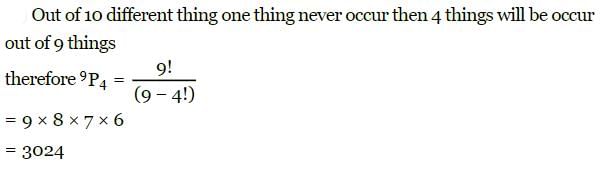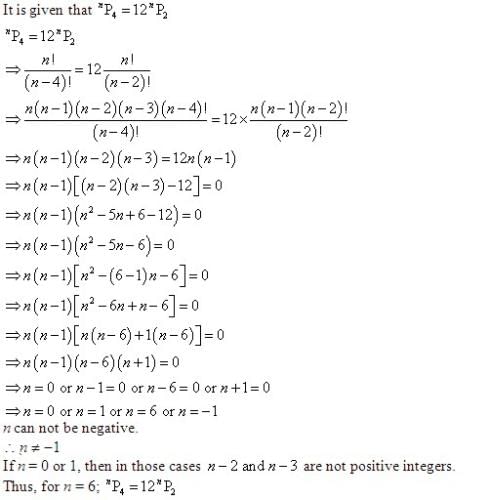All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 5: Permutations and Combinations for CA Foundation Exam
The number of ways the letters of the word COMPUTER can be rearranged is
- a)40320
- b)40319
- c)40318
- d)none of these
Correct answer is 'A'. Can you explain this answer?
The number of ways the letters of the word COMPUTER can be rearranged is
a)
40320
b)
40319
c)
40318
d)
none of these
|
|
Aarav Sharma answered |
Since all letters in the word "COMPUTER" are distinct then the arrangements is 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40320
The number of numbers lying between 10 and 1000 can be formed with the digits 2,3,4,0,8,9 is
- a)124
- b)120
- c)125
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of numbers lying between 10 and 1000 can be formed with the digits 2,3,4,0,8,9 is
a)
124
b)
120
c)
125
d)
none of these

|
Dhruv Mehra answered |
Case 1: two digit numbers:
We can choose the tens digit any of 5 ways (0 cannot be chosen)
We can then choose the units digit any of 5 ways, because 0 can be chosen.
That's 5 x 5 or 25 two digit numbers
Case 2: three digit numbers:
We can choose the hundreds digit any of 5 ways (0 cannot be chosen)
We can then choose the tens digit any of 5 ways, because 0 can be chosen.
We can then choose the units digit any of the 4 remaining ways.
That's 5 x 5 x 4 = 100 three-digit numbers
So, total: 25+100 = 125
How many permutations can be formed from the letters of the word " DRAUGHT" if both vowels may not be separated?- a)720
- b)1,440
- c)140
- d)1,000
Correct answer is option 'A'. Can you explain this answer?
How many permutations can be formed from the letters of the word " DRAUGHT" if both vowels may not be separated?
a)
720
b)
1,440
c)
140
d)
1,000
|
|
Preeti Khanna answered |
The vowels are never being separated.
So, vowels a & u are taken together and considered as one letter.
So, there are 6 letters in the word draught
The number of ways in which it can be arranged are given by =6!=720.
But the internal arrangement can be done of a and u in 2 ways.
Hence the total arrangements are 720×2=1440.
The number of arrangements of the letters in the word FAILURE, so that vowels are always coming together is
- a)576
- b)575
- c)570
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of arrangements of the letters in the word FAILURE, so that vowels are always coming together is
a)
576
b)
575
c)
570
d)
none of these

|
Freedom Institute answered |
In the word FAILURE, there are 4 odd position for letters and 3 even positions.
Now we have 3 consonants and 4 places.
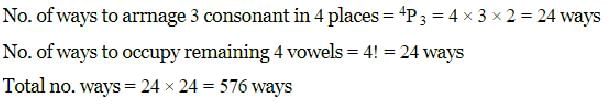
Now we have 3 consonants and 4 places.
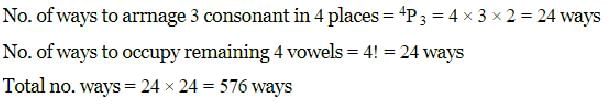
There are 5 speakers A, B, C, D and E. The number of ways in which A will speak always before B is- a)24
- b)
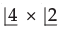
- c)
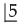
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
There are 5 speakers A, B, C, D and E. The number of ways in which A will speak always before B is
a)
24
b)
c)
d)
none of these

|
Srsps answered |
. Treat A and B as a Single Unit
Since Speaker A must always speak immediately before Speaker B, we can consider them as a single combined entity, denoted as AB.
- Combined Units to Arrange:
- AB (A and B together)
- C
- D
- E
This effectively reduces the problem to arranging 4 units instead of 5.
2. Calculate the Number of Arrangements
- Number of Units to Arrange: 4 (AB, C, D, E)
- Number of Ways to Arrange 4 Units:
- This is given by 4 factorial, written as 4!
- 4! = 4 × 3 × 2 × 1 = 24
3. Arranging Within the Combined Unit (AB)
- Since A must always come before B within the combined unit AB, there's only 1 way to arrange them (A followed by B).
- Number of Arrangements for AB: 1
4. Total Number of Arrangements
- Total Ways = Arrangements of Units × Arrangements within AB
- Total Ways = 4! × 1 = 24
If . nP3 : nP2 = 3 : 1, then n is equal to- a)7
- b)4
- c)5
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If . nP3 : nP2 = 3 : 1, then n is equal to
a)
7
b)
4
c)
5
d)
none of these

|
Freedom Institute answered |
We are given the ratio of permutations nP3 : nP2 = 3 : 1, and we need to find the value of n.
First, recall the formula for permutations:
P(n, r) = n! / (n - r)!
P(n, r) = n! / (n - r)!
Using this formula, we can express the permutations:
nP3 = n! / (n - 3)! = n(n-1)(n-2)
nP2 = n! / (n - 2)! = n(n-1)
Now, we substitute these into the given ratio:
(n(n-1)(n-2)) / (n(n-1)) = 3 / 1
nP2 = n! / (n - 2)! = n(n-1)
Now, we substitute these into the given ratio:
(n(n-1)(n-2)) / (n(n-1)) = 3 / 1
On simplifying:
(n-2) = 3
(n-2) = 3
Solving for n:
n = 3 + 2 = 5
Therefore, the value of n is 5.
n = 3 + 2 = 5
Therefore, the value of n is 5.
The number of ways in which the letters of the word DOGMATIC can be arranged is- a)40319
- b)40320
- c)40321
- d)none of these
Correct answer is 'A'. Can you explain this answer?
The number of ways in which the letters of the word DOGMATIC can be arranged is
a)
40319
b)
40320
c)
40321
d)
none of these

|
Dhruv Mehra answered |
Answer is b) 40320
All letters in the word are distinct.
So, 8 letters can be permuted in 8! = 40,320 ways.
In nPr = n (n–1) (n–2) ………………(n–r–1), the number of factor is- a)n
- b)r–1
- c)n–r
- d)r
Correct answer is option 'D'. Can you explain this answer?
In nPr = n (n–1) (n–2) ………………(n–r–1), the number of factor is
a)
n
b)
r–1
c)
n–r
d)
r

|
Srsps answered |
The expression nPr = n (n–1) (n–2) ………………(n–r–1) represents the number of permutations of r objects taken from a set of n objects.
The formula shows a sequence of factors starting from n and decreasing by 1 until we have r terms. The first factor is n, the second is n-1, and so on, until the last factor, which is n-r+1.
The total number of factors in this sequence is r, because there are r terms in the product:
- n (n–1) (n–2) ………………(n–r+1)
Therefore, the number of factors is r.
The number of arrangements of 10 different things taken 4 at a time in which one particular thing always occurs is- a)2015
- b)2016
- c)2014
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The number of arrangements of 10 different things taken 4 at a time in which one particular thing always occurs is
a)
2015
b)
2016
c)
2014
d)
none of these

|
Sameer Rane answered |
Here, if 1 thing always occur then we will fix that place. Now 3 places are remaining and 9 things are remaining.
For, rest 3 places total selections of things are (93)(93)and total arrangements of 4 things is 4!4!..
Answer = (9/3)∗4!=84∗24=2016(9/3)∗4!=84∗24=2016
There are 10 trains plying between Calcutta and Delhi. The number of ways in which a person can go from Calcutta to Delhi and return by a different train is
- a)99
- b)90
- c)80
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
There are 10 trains plying between Calcutta and Delhi. The number of ways in which a person can go from Calcutta to Delhi and return by a different train is
a)
99
b)
90
c)
80
d)
none of these
|
|
Rajat Patel answered |
To determine the number of ways a person can go from Calcutta to Delhi and return by a different train among 10 available trains, we can break down the problem as follows:
- Choose a train for the journey from Calcutta to Delhi: There are 10 choices.
- Choose a different train for the return journey from Delhi to Calcutta: After choosing one train for the outgoing journey, 9 other trains remain for the return journey.
Therefore, the total number of ways to make the round trip using different trains for each leg is:
10 × 9 = 90
So, the correct answer is Option 2: 90.
The number of diagonals in a decagon is- a)30
- b)35
- c)45
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The number of diagonals in a decagon is
a)
30
b)
35
c)
45
d)
none of these

|
Shanaya Deshpande answered |
Hint: The number of diagonals in a polygon of n sides is 1/2n (n–3).
The number of words that can be made by rearranging the letters of the word APURNA so that vowels and consonants appear alternate is- a)18
- b)35
- c)36
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of words that can be made by rearranging the letters of the word APURNA so that vowels and consonants appear alternate is
a)
18
b)
35
c)
36
d)
none of these

|
Srsps answered |
We are asked to find the number of words that can be made by rearranging the letters of the word "APURNA" such that vowels and consonants alternate.
Step 1: Identify Vowels and Consonants
The word "APURNA" consists of the following letters: - Vowels: A, U, A (3 vowels) - Consonants: P, R, N (3 consonants)
The word "APURNA" consists of the following letters: - Vowels: A, U, A (3 vowels) - Consonants: P, R, N (3 consonants)
Step 2: Arrangement of Vowels and Consonants
Since the vowels and consonants must alternate, we have two possible patterns: 1. Vowel, Consonant, Vowel, Consonant, Vowel, Consonant 2. Consonant, Vowel, Consonant, Vowel, Consonant, Vowel Since there are 3 vowels and 3 consonants, both patterns are possible.
Since the vowels and consonants must alternate, we have two possible patterns: 1. Vowel, Consonant, Vowel, Consonant, Vowel, Consonant 2. Consonant, Vowel, Consonant, Vowel, Consonant, Vowel Since there are 3 vowels and 3 consonants, both patterns are possible.
Step 3: Calculating the Number of Arrangements
The vowels A, U, A are not all distinct. So, we need to account for the repetition of A. - The number of ways to arrange the vowels is: 3!/2! = 3 (since there are two A's). - The consonants P, R, N are all distinct, so the number of ways to arrange the consonants is: 3! = 6
Therefore, the total number of ways to arrange the vowels and consonants alternately is: Total = 2 x 3 x 6 = 36 (multiplied by 2 for the two possible patterns).
The total number of ways to rearrange the letters of the word "APURNA" such that vowels and consonants alternate is 36.
The vowels A, U, A are not all distinct. So, we need to account for the repetition of A. - The number of ways to arrange the vowels is: 3!/2! = 3 (since there are two A's). - The consonants P, R, N are all distinct, so the number of ways to arrange the consonants is: 3! = 6
Therefore, the total number of ways to arrange the vowels and consonants alternately is: Total = 2 x 3 x 6 = 36 (multiplied by 2 for the two possible patterns).
The total number of ways to rearrange the letters of the word "APURNA" such that vowels and consonants alternate is 36.
The number of ways in which 7 boys sit in a round table so that two particular boys may sit together is- a)240
- b)200
- c)120
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of ways in which 7 boys sit in a round table so that two particular boys may sit together is
a)
240
b)
200
c)
120
d)
none of these
|
|
Arun Khanna answered |
The 2 boys can be arranged in 2 ways; they form a unit.
So now you have 6 units.
At a round table those 6 can be arranged is 5! ways.
--------------
Total # of arrangements = 2*5! = 2*120 = 240 ways
If 5Pr = 60, then the value of r is- a)3
- b)2
- c)4
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If 5Pr = 60, then the value of r is
a)
3
b)
2
c)
4
d)
none of these

|
Dhruv Mehra answered |
5Pr=60
⇒5!/(5−r)! = 60
⇒120/(5−r)! = 60
⇒(5−r)! = 2
since 2! = 2
hence, 5−r = 2 or r = 3
The number of different factors the number 75600 has is- a)120
- b)121
- c)119
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of different factors the number 75600 has is
a)
120
b)
121
c)
119
d)
none of these
|
|
Rajeev Kumar answered |
75600 = 756*100 = 7*108*100 =7*4*27*100=7*(3^3)*(4)*(4)*(5)*(5) = 7*(3^3)*(2^4)*(5^2)
thus the powers of the prime factors are, 1, 3, 4, 2
thus number of factors are,
(1+1)(1+3)(1+4)(1+2) = 120
thus the powers of the prime factors are, 1, 3, 4, 2
thus number of factors are,
(1+1)(1+3)(1+4)(1+2) = 120
m+nP2 = 56, m–nP2 = 30 then- a)m =6, n = 2
- b)m = 7, n= 1
- c)m=4,n=4
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
m+nP2 = 56, m–nP2 = 30 then
a)
m =6, n = 2
b)
m = 7, n= 1
c)
m=4,n=4
d)
None of these

|
Srsps answered |
We are given the following two permutation equations:
m+nP2 = 56
m–nP2 = 30
First, recall the formula for permutations:
m–nP2 = 30
First, recall the formula for permutations:
P(n, r) = n! / (n - r)!
For P2, this simplifies to:
P(n, 2) = n(n-1)
Now, let's substitute the given values into the permutation formula:
For P2, this simplifies to:
P(n, 2) = n(n-1)
Now, let's substitute the given values into the permutation formula:
m+nP2 = (m+n)(m+n-1) = 56
m–nP2 = (m-n)(m-n-1) = 30
We now have the system of equations:
m–nP2 = (m-n)(m-n-1) = 30
We now have the system of equations:
(m+n)(m+n-1) = 56
(m-n)(m-n-1) = 30
Let's solve each equation:
(m-n)(m-n-1) = 30
Let's solve each equation:
1. Solve for m + n:
(m+n)(m+n-1) = 56
(m+n)(m+n-1) = 56
m+n = 8 (since 8×7 = 56)
2. Solve for m - n:
(m-n)(m-n-1) = 30
(m-n)(m-n-1) = 30
m-n = 6 (since 6×5 = 30)
Now, we have:
m + n = 8
m - n = 6
Adding these two equations:
(m+n) + (m-n) = 8 + 6
2m = 14
m = 7
Substituting m = 7 into m + n = 8:
7 + n = 8
n = 1
Therefore, m = 7 and n = 1.
(m+n)(m+n-1) = 56
(m+n)(m+n-1) = 56
m+n = 8 (since 8×7 = 56)
2. Solve for m - n:
(m-n)(m-n-1) = 30
(m-n)(m-n-1) = 30
m-n = 6 (since 6×5 = 30)
Now, we have:
m + n = 8
m - n = 6
Adding these two equations:
(m+n) + (m-n) = 8 + 6
2m = 14
m = 7
Substituting m = 7 into m + n = 8:
7 + n = 8
n = 1
Therefore, m = 7 and n = 1.
In nPr , the restriction is- a)n > r
- b)n ≥r
- c)n ≤ r
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
In nPr , the restriction is
a)
n > r
b)
n ≥r
c)
n ≤ r
d)
none of these

|
Freedom Institute answered |
The expression nPr refers to the number of permutations of r objects selected from a total of n objects.
The formula for permutations is:
P(n, r) = n! / (n - r)!
In order for this formula to be valid, the value of n must be greater than or equal to r. This is because we cannot select more objects than we have available. Therefore, the restriction is:
In order for this formula to be valid, the value of n must be greater than or equal to r. This is because we cannot select more objects than we have available. Therefore, the restriction is:
n ≥ r (Option B)
So, for the permutation formula nPr to work, it is required that n ≥ r.
So, for the permutation formula nPr to work, it is required that n ≥ r.
The number of ways a person can contribute to a fund out of 1 ten-rupee note, 1 fiverupee note, 1 two-rupee and 1 one rupee note is- a)15
- b)25
- c)10
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of ways a person can contribute to a fund out of 1 ten-rupee note, 1 fiverupee note, 1 two-rupee and 1 one rupee note is
a)
15
b)
25
c)
10
d)
none of these

|
Freedom Institute answered |
We are asked to find the number of ways a person can contribute to a fund out of the following notes:
- 1 ten-rupee note
- 1 five-rupee note
- 1 two-rupee note
- 1 one-rupee note
Step 1: Understanding the Problem
- The person can choose to contribute or not contribute each note to the fund. - For each note, there are two options: - Contribute the note. - Do not contribute the note.
Step 2: Number of Choices for Each Note
- For the ten-rupee note, the person can either contribute or not contribute, so there are 2 choices. - For the five-rupee note, there are also 2 choices. - For the two-rupee note, there are 2 choices. - For the one-rupee note, there are 2 choices.
Step 3: Total Number of Ways to Contribute
Since the choices for each note are independent, the total number of ways to contribute to the fund is the product of the choices for each note:
2 choices (for ten-rupee) × 2 choices (for five-rupee) × 2 choices (for two-rupee) × 2 choices (for one-rupee) = 2 × 2 × 2 × 2 = 16
2 choices (for ten-rupee) × 2 choices (for five-rupee) × 2 choices (for two-rupee) × 2 choices (for one-rupee) = 2 × 2 × 2 × 2 = 16
Step 4: Subtracting the Case of Contributing Nothing
- One of these 16 ways corresponds to the case where the person does not contribute any money (i.e., they choose "not contribute" for all notes). - Since the problem asks for the number of ways to contribute (not to not contribute), we subtract this case of contributing nothing. Therefore, the total number of ways to contribute to the fund is: 16 - 1 = 15
The number of ways the person can contribute to the fund is 15.
4 digit numbers to be formed out of the figures 0, 1, 2, 3, 4 (no digit is repeated) then number of such numbers is
- a)120
- b)20
- c)96.
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
4 digit numbers to be formed out of the figures 0, 1, 2, 3, 4 (no digit is repeated) then number of such numbers is
a)
120
b)
20
c)
96.
d)
none of these

|
Anirban Khanna answered |
There are 4 ways to pick the 1st digit (can't use 0 for the 1st digit).
There are 4 remaining ways to pick the 2nd digit. Can pick 0, but not the digit picked for the 1st digit.
There are 3 remaining ways to pick the 3rd digit.
There are 2 remaining ways to pick the 4th digit.
Answer: (4)(4)(3)(2) = 96 ways.
There are 4 remaining ways to pick the 2nd digit. Can pick 0, but not the digit picked for the 1st digit.
There are 3 remaining ways to pick the 3rd digit.
There are 2 remaining ways to pick the 4th digit.
Answer: (4)(4)(3)(2) = 96 ways.
The number of ways in which 6 men can be arranged in a row so that the particular 3 men sit together, is- a)4P4
- b)4P4 × 3P3
- c)
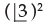
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The number of ways in which 6 men can be arranged in a row so that the particular 3 men sit together, is
a)
4P4
b)
4P4 × 3P3
c)
d)
none of these

|
Satyabrata Sahoo answered |
GIven,
6 men and 3 particular men are consecutive
let those 3 particular men be considered together as a single item
∴ Now 4 items in total can be arranged in 4! ways and those 3 men which are considered as a single item can be arranged in 3! ways among themselves.
i.e.,
4p4 × 3p3
ways
Hence option B is correct
The number of 4 digit numbers formed with the digits 1, 1, 2, 2, 3, 4 is- a)100
- b)101
- c)201
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The number of 4 digit numbers formed with the digits 1, 1, 2, 2, 3, 4 is
a)
100
b)
101
c)
201
d)
none of these

|
Srsps answered |
We are asked to find the number of 4-digit numbers that can be formed using the digits 1, 1, 2, 2, 3, 4.
Step 1: Understanding the Problem
We need to form a 4-digit number using the digits 1, 1, 2, 2, 3, 4, and we can repeat digits as long as they are available. The key thing to note is that some of the digits are repeated (1 and 2 each appear twice), so we need to consider this repetition when calculating the total number of different 4-digit numbers.
We need to form a 4-digit number using the digits 1, 1, 2, 2, 3, 4, and we can repeat digits as long as they are available. The key thing to note is that some of the digits are repeated (1 and 2 each appear twice), so we need to consider this repetition when calculating the total number of different 4-digit numbers.
Step 2: Case Analysis
We can form the 4-digit number by choosing different combinations of digits. Since there are 6 digits in total but only 4 digits need to be selected, we can have multiple cases based on the selection of digits:
We can form the 4-digit number by choosing different combinations of digits. Since there are 6 digits in total but only 4 digits need to be selected, we can have multiple cases based on the selection of digits:
Case 1: Two 1’s and Two 2’s
If we choose two 1's and two 2's, we need to arrange the four digits: 1, 1, 2, 2. The number of distinct arrangements of these digits is calculated as:
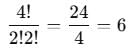
Case 2: Two 1’s and One 2, One 3
If we choose two 1's, one 2, and one 3, we need to arrange the digits: 1, 1, 2, 3. The number of distinct arrangements of these digits is:
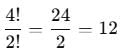
Case 3: Two 1’s and One 2, One 4
If we choose two 1's, one 2, and one 4, we need to arrange the digits: 1, 1, 2, 4. The number of distinct arrangements of these digits is:
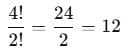
Case 4: One 1, One 2, One 3, One 4
If we choose one 1, one 2, one 3, and one 4, we need to arrange the digits: 1, 2, 3, 4. The number of distinct arrangements of these digits is:
4! = 24
Step 3: Total Number of Arrangements
Now, we add up all the distinct arrangements from each case:
6+12+12+24=54
The total number of distinct 4-digit numbers that can be formed is 54.
If we choose two 1's and two 2's, we need to arrange the four digits: 1, 1, 2, 2. The number of distinct arrangements of these digits is calculated as:
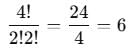
Case 2: Two 1’s and One 2, One 3
If we choose two 1's, one 2, and one 3, we need to arrange the digits: 1, 1, 2, 3. The number of distinct arrangements of these digits is:
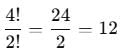
Case 3: Two 1’s and One 2, One 4
If we choose two 1's, one 2, and one 4, we need to arrange the digits: 1, 1, 2, 4. The number of distinct arrangements of these digits is:
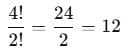
Case 4: One 1, One 2, One 3, One 4
If we choose one 1, one 2, one 3, and one 4, we need to arrange the digits: 1, 2, 3, 4. The number of distinct arrangements of these digits is:
4! = 24
Step 3: Total Number of Arrangements
Now, we add up all the distinct arrangements from each case:
6+12+12+24=54
The total number of distinct 4-digit numbers that can be formed is 54.
The number of ways in which 8 sweats of different sizes can be distributed among 8 persons of different ages so that the largest sweat always goes to be younger assuming that each one of then gets a sweat is- a)
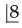
- b)5040
- c)5039
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The number of ways in which 8 sweats of different sizes can be distributed among 8 persons of different ages so that the largest sweat always goes to be younger assuming that each one of then gets a sweat is
a)
b)
5040
c)
5039
d)
none of these

|
Quantronics answered |
The number of ways in which 8 sweets of different sizes can be distributed among 8 persons of different ages so that the largest sweat goes to the younger assuming that each one of them gets a sweet.
Since the largest goes to the youngest, that leaves 7 sweets to distribute to 7 people.
7P7 = 7! = 5040 ways
Since the largest goes to the youngest, that leaves 7 sweets to distribute to 7 people.
7P7 = 7! = 5040 ways
Every two persons shakes hands with each other in a party and the total number of hand shakes is 66. The number of guests in the party is- a)11
- b)12
- c)13
- d)14
Correct answer is option 'B'. Can you explain this answer?
Every two persons shakes hands with each other in a party and the total number of hand shakes is 66. The number of guests in the party is
a)
11
b)
12
c)
13
d)
14

|
Srsps answered |
Let the number of people be x
For a hand shake we need 2 people so selecting 2 person form x can be done in xC2 ways.
Therefore xC2=66
x!/(x-2)!2!=66
x(x-1)/2=66
x(x-1)=132
Solving this we get x=12
So there must be 12 persons in the party.
A candidate is required to answer 6 out of 12 questions which are divided into two groups containing 6 questions in each group. He is not permitted to attempt not more than four from any group. The number of choices are.- a)750
- b)850
- c)800
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A candidate is required to answer 6 out of 12 questions which are divided into two groups containing 6 questions in each group. He is not permitted to attempt not more than four from any group. The number of choices are.
a)
750
b)
850
c)
800
d)
none of these

|
Freedom Institute answered |
We are asked to find the number of ways a candidate can answer 6 out of 12 questions, where the questions are divided into two groups of 6 questions each, and the candidate is not allowed to attempt more than 4 questions from any group.
Step 1: Understanding the Constraints
- The candidate must answer 6 questions in total. - The questions are divided into two groups: - Group 1: 6 questions - Group 2: 6 questions - The candidate cannot answer more than 4 questions from any one group. Therefore, the candidate can answer the questions in the following combinations: 1. Answer 4 questions from Group 1 and 2 questions from Group 2. 2. Answer 3 questions from Group 1 and 3 questions from Group 2. 3. Answer 2 questions from Group 1 and 4 questions from Group 2.
Step 2: Calculating the Number of Ways for Each Case
- Case 1: Answer 4 questions from Group 1 and 2 questions from Group 2: - The number of ways to choose 4 questions from Group 1 (6 questions) is C(6, 4) = 15. - The number of ways to choose 2 questions from Group 2 (6 questions) is C(6, 2) = 15. - So, the total for this case is 15 × 15 = 225.
- Case 2: Answer 3 questions from Group 1 and 3 questions from Group 2: - The number of ways to choose 3 questions from Group 1 (6 questions) is C(6, 3) = 20. - The number of ways to choose 3 questions from Group 2 (6 questions) is C(6, 3) = 20. - So, the total for this case is 20 × 20 = 400.
- Case 3: Answer 2 questions from Group 1 and 4 questions from Group 2: - The number of ways to choose 2 questions from Group 1 (6 questions) is C(6, 2) = 15. - The number of ways to choose 4 questions from Group 2 (6 questions) is C(6, 4) = 15. - So, the total for this case is 15 × 15 = 225.
Step 3: Total Number of Choices
Adding up the results from all three cases:
Adding up the results from all three cases:
Total Choices = 225 + 400 + 225 = 850
The total number of ways the candidate can answer 6 out of 12 questions, with the given constraints, is 850.
The total number of ways the candidate can answer 6 out of 12 questions, with the given constraints, is 850.
The number of ways the letters of the word “Triangle” to be arranged so that the word ’angle’ will be always present is
- a)20
- b)60
- c)24
- d)32
Correct answer is option 'C'. Can you explain this answer?
The number of ways the letters of the word “Triangle” to be arranged so that the word ’angle’ will be always present is
a)
20
b)
60
c)
24
d)
32

|
Srsps answered |
angle would be 1 word so total letters would be 4 [ Tri + angle ] these 4 letters can be arranged in 4! ie 24 ways
If 18Cr = 18Cr+2, the value of rC5 is- a)55
- b)50
- c)56
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If 18Cr = 18Cr+2, the value of rC5 is
a)
55
b)
50
c)
56
d)
none of these

|
Srsps answered |
We are given the equation 18Cr = 18C(r+2) and are asked to find the value of rC5.
Step 1: Understand the given equation
The given equation is:
18Cr = 18C(r+2)
The given equation is:
18Cr = 18C(r+2)
Using the property of combinations, we know that nCk = nC(n-k). Therefore, we can equate the two combinations:
18Cr = 18C(18-r-2) (since r + 2 = 18 - r)
This simplifies to:
r = 18 - r - 2
18Cr = 18C(18-r-2) (since r + 2 = 18 - r)
This simplifies to:
r = 18 - r - 2
Step 2: Solve for r
Now, solving for r:
r + r = 18 - 2
2r = 16
r = 8
r + r = 18 - 2
2r = 16
r = 8
Step 3: Find the value of rC5
Now that we know r = 8, we need to find 8C5.
We use the combination formula:
8C5 = 8! / (5!3!) = (8 × 7 × 6) / (3 × 2 × 1)
Now that we know r = 8, we need to find 8C5.
We use the combination formula:
8C5 = 8! / (5!3!) = (8 × 7 × 6) / (3 × 2 × 1)
Now, simplifying the factorials:
8C5 = 336 / 6 = 56
8C5 = 336 / 6 = 56
Final Answer:
The value of rC5 is 56.
The value of rC5 is 56.
The number of 4 digit numbers greater than 5000 can be formed out of the digits 3,4,5,6 and 7(no. digit is repeated). The number of such is
- a)72
- b)27
- c)70
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of 4 digit numbers greater than 5000 can be formed out of the digits 3,4,5,6 and 7(no. digit is repeated). The number of such is
a)
72
b)
27
c)
70
d)
none of these

|
Dhruv Mehra answered |
To form a 4-digit number greater than 5000 using the digits 3, 4, 5, 6, and 7 without repetition, we need to consider the following:
- The first digit has to be either 5, 6, or 7.
- The remaining digits can be any of the remaining digits, i.e., 4 digits out of the 4 available.
For the first digit, there are 3 choices (5, 6, or 7).
Then, for the remaining three digits, we have 4 choices for the second digit, 3 choices for the third digit, and 2 choices for the fourth digit, since we cannot repeat any digit.
So, the total number of such 4-digit numbers is 3×4×3×2 =72.
Out of 7 gents and 4 ladies a committee of 5 is to be formed. The number of committees such that each committee includes at least one lady is- a)400
- b)440
- c)441
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Out of 7 gents and 4 ladies a committee of 5 is to be formed. The number of committees such that each committee includes at least one lady is
a)
400
b)
440
c)
441
d)
none of these

|
Srsps answered |
We are given 7 gents and 4 ladies, and a committee of 5 members is to be formed. The condition is that each committee must include at least one lady. We need to find the number of such committees.
Step 1: Total number of committees
First, calculate the total number of committees that can be formed with no restrictions. The total number of ways to select 5 people from 11 (7 gents and 4 ladies) is given by the combination formula:
Total committees = 11C5 = (11 * 10 * 9 * 8 * 7) / (5 * 4 * 3 * 2 * 1) = 462
First, calculate the total number of committees that can be formed with no restrictions. The total number of ways to select 5 people from 11 (7 gents and 4 ladies) is given by the combination formula:
Total committees = 11C5 = (11 * 10 * 9 * 8 * 7) / (5 * 4 * 3 * 2 * 1) = 462
Step 2: Committees with no ladies
Next, calculate the number of committees that can be formed with no ladies (i.e., all gents). This is simply selecting 5 gents from 7:
Committees with no ladies = 7C5 = (7 * 6) / (2 * 1) = 21
Next, calculate the number of committees that can be formed with no ladies (i.e., all gents). This is simply selecting 5 gents from 7:
Committees with no ladies = 7C5 = (7 * 6) / (2 * 1) = 21
Step 3: Committees with at least one lady
The number of committees with at least one lady is found by subtracting the number of committees with no ladies from the total number of committees:
Committees with at least one lady = Total committees - Committees with no ladies = 462 - 21 = 441
The number of committees that include at least one lady is 441.
The number of committees with at least one lady is found by subtracting the number of committees with no ladies from the total number of committees:
Committees with at least one lady = Total committees - Committees with no ladies = 462 - 21 = 441
The number of committees that include at least one lady is 441.
The Supreme Court has given a 6 to 3 decision upholding a lower court; the number of ways it can give a majority decision reversing the lower court is- a)256
- b)276
- c)245
- d)226
Correct answer is option 'A'. Can you explain this answer?
The Supreme Court has given a 6 to 3 decision upholding a lower court; the number of ways it can give a majority decision reversing the lower court is
a)
256
b)
276
c)
245
d)
226

|
Sagarika Patel answered |
To reverse the decision, at least 5 out of the 9 judges must vote in favor of reversing the decision.
Therefore, required number of ways
= 9C5+9C6+9C7+9C8+9C9
=126+84+36+9+1
= 256
Five bulbs of which three are defective are to be tried in two bulb points in a dark room.Number of trials the room shall be lighted is- a)6
- b)8
- c)5
- d)7
Correct answer is option 'D'. Can you explain this answer?
Five bulbs of which three are defective are to be tried in two bulb points in a dark room.Number of trials the room shall be lighted is
a)
6
b)
8
c)
5
d)
7
|
|
Rajat Patel answered |
5 bulbs
3 defective
2 good
2 bulbs placed in a room.
how many trials required to get the room to light.
-----
you only need 1 good bulb to light the room.
the number of possible combinations would be C(5,2) which is equal to 10 possible combinations.
the number of possible combinations of 2 that would involve only defective bulbs would be C(3,2) which is equal to 3.
10 - 3 leaves 7 combinations where the room will be lighted.
let's see if this works out.
let d1, d2, d3 represent the defective bulbs.
let g1, g2 represent the good bulbs.
the total possible combinations are:
d1, d2 = room is dark *****
d1, d3 = room is dark *****
d1, g1 = room is light
d1, g2 = room is light
d2, d3 = room is dark *****
d2, g1 = room is light
d2, g2 = room is light
d3, g1 = room is light
d3, g2 = room is light
g1, g2 = room is light
there are 3 possible situations where the room will still be dark.
there are 7 possible situations where the room will be light.
5 persons are sitting in a round table in such way that Tallest Person is always on the right– side of the shortest person; the number of such arrangements is- a)6
- b)8
- c)24
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
5 persons are sitting in a round table in such way that Tallest Person is always on the right– side of the shortest person; the number of such arrangements is
a)
6
b)
8
c)
24
d)
none of these

|
Pallabi Deshpande answered |
There are 5 persons,so total arrangements in case of circular permutation is (n-1)!,
Here according to the condition tallest person is always right of shortest person(note: there is only one tallest and shortest person).
Therefor take both tallest and shortest person as one person so we have 4 persons.
Total arrangements of 4 person is
(4-1)! . That is 3!
Answer is 6
In your college Union Election you have to choose candidates. Out of 5 candidates 3 are to be elected and you are entitled to vote for any number of candidates but not exceeding the number to be elected. You can do it in ________ ways.- a)25
- b)5
- c)10
- d)None
Correct answer is option 'A'. Can you explain this answer?
In your college Union Election you have to choose candidates. Out of 5 candidates 3 are to be elected and you are entitled to vote for any number of candidates but not exceeding the number to be elected. You can do it in ________ ways.
a)
25
b)
5
c)
10
d)
None

|
Disha Joshi answered |
Solution:
To solve this problem, we can use the combination formula as we need to choose 3 candidates out of 5.
The formula for combination is:
nCr = n! / r! * (n-r)!
where n = total number of candidates and r = number of candidates to be elected.
Putting n = 5 and r = 3, we get:
5C3 = 5! / 3! * (5-3)!
= 5! / 3! * 2!
= (5 * 4 * 3 * 2 * 1) / (3 * 2 * 1 * 2 * 1)
= 10
Therefore, there are 10 ways to choose 3 candidates out of 5.
But the question states that we can vote for any number of candidates, not exceeding the number to be elected. So, we can vote for 0, 1, 2 or 3 candidates.
The number of ways to choose 0 candidates is 1 (not voting for anyone).
The number of ways to choose 1 candidate is 5 (choosing any one from 5 candidates).
The number of ways to choose 2 candidates is 10 (as we calculated above).
The number of ways to choose 3 candidates is also 10 (same as choosing 2 candidates out of 5).
Therefore, the total number of ways to choose candidates is:
1 + 5 + 10 + 10 = 26
Hence, option 'D' (None) is incorrect and the correct answer is option 'A' (25).
To solve this problem, we can use the combination formula as we need to choose 3 candidates out of 5.
The formula for combination is:
nCr = n! / r! * (n-r)!
where n = total number of candidates and r = number of candidates to be elected.
Putting n = 5 and r = 3, we get:
5C3 = 5! / 3! * (5-3)!
= 5! / 3! * 2!
= (5 * 4 * 3 * 2 * 1) / (3 * 2 * 1 * 2 * 1)
= 10
Therefore, there are 10 ways to choose 3 candidates out of 5.
But the question states that we can vote for any number of candidates, not exceeding the number to be elected. So, we can vote for 0, 1, 2 or 3 candidates.
The number of ways to choose 0 candidates is 1 (not voting for anyone).
The number of ways to choose 1 candidate is 5 (choosing any one from 5 candidates).
The number of ways to choose 2 candidates is 10 (as we calculated above).
The number of ways to choose 3 candidates is also 10 (same as choosing 2 candidates out of 5).
Therefore, the total number of ways to choose candidates is:
1 + 5 + 10 + 10 = 26
Hence, option 'D' (None) is incorrect and the correct answer is option 'A' (25).
Find the number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included.- a)39,000
- b)37,600
- c)39,600
- d)36,000
Correct answer is option 'C'. Can you explain this answer?
Find the number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included.
a)
39,000
b)
37,600
c)
39,600
d)
36,000

|
Ankita Mukherjee answered |
Given: 12 things and we have to select 5 things such that one particular thing must always be included.
To find: Number of arrangements of 5 things taken out of 12 things.
Solution:
Let's consider the given particular thing as one of the 5 selected things. Then we have to select 4 more things from the remaining 11 things.
Number of ways of selecting 4 things out of 11 things = 11C4
Number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included = 11C4 × 4!
[Because once we select the 5 things, we can arrange them in 5! ways.]
Now, let's simplify the expression for 11C4:
11C4 = (11 × 10 × 9 × 8) / (4 × 3 × 2 × 1) = 330
Therefore, the number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included = 330 × 4! = 39,600
Hence, the correct option is (c) 39,600.
To find: Number of arrangements of 5 things taken out of 12 things.
Solution:
Let's consider the given particular thing as one of the 5 selected things. Then we have to select 4 more things from the remaining 11 things.
Number of ways of selecting 4 things out of 11 things = 11C4
Number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included = 11C4 × 4!
[Because once we select the 5 things, we can arrange them in 5! ways.]
Now, let's simplify the expression for 11C4:
11C4 = (11 × 10 × 9 × 8) / (4 × 3 × 2 × 1) = 330
Therefore, the number of arrangements of 5 things taken out of 12 things, in which one particular thing must always be included = 330 × 4! = 39,600
Hence, the correct option is (c) 39,600.
The number of ways in which 15 mangoes can be equally divided among 3 students is- a)
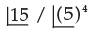
- b)
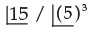
- c)
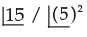
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The number of ways in which 15 mangoes can be equally divided among 3 students is
a)
b)
c)
d)
none of these

|
Sai Kulkarni answered |
To determine the number of ways to divide 15 mangoes equally among 3 students, we can follow these steps:
- The total number of mangoes is 15.
- Since there are 3 students, we need to divide the mangoes by the number of students.
- Each student would receive:
- 15 mangoes ÷ 3 students = 5 mangoes per student.
- Now, we need to consider the different ways to distribute the mangoes.
- Since each student receives the same number of mangoes, the arrangement is straightforward:
- There is only 1 way to equally distribute 15 mangoes among 3 students, as each gets 5.
Conclusion: The number of ways to equally divide 15 mangoes among 3 students is 1.
At an election there are 5 candidates and 3 members are to be elected. A voter is entitled to vote for any number of candidates not greater than the number to be elected. The number of ways a voter choose to vote is
- a)20
- b)22
- c)26
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
At an election there are 5 candidates and 3 members are to be elected. A voter is entitled to vote for any number of candidates not greater than the number to be elected. The number of ways a voter choose to vote is
a)
20
b)
22
c)
26
d)
none of these

|
Freedom Institute answered |


A polygon has 44 diagonals then the number of its sides are:- a)8
- b)9
- c)10
- d)11
Correct answer is option 'D'. Can you explain this answer?
A polygon has 44 diagonals then the number of its sides are:
a)
8
b)
9
c)
10
d)
11

|
Maheshwar Goyal answered |
Solution:
To find the number of sides of a polygon that has 44 diagonals, we can use the formula:
Number of diagonals of an n-sided polygon = n(n-3)/2
where n is the number of sides.
We are given that the number of diagonals in the polygon is 44. So, we can set up the equation:
44 = n(n-3)/2
Multiplying both sides by 2 gives:
88 = n(n-3)
Expanding the right-hand side gives:
88 = n^2 - 3n
Rearranging gives:
n^2 - 3n - 88 = 0
We can now solve for n using the quadratic formula:
n = (-b ± sqrt(b^2 - 4ac)) / 2a
where a = 1, b = -3, and c = -88.
Plugging in these values gives:
n = (3 ± sqrt(3^2 - 4(1)(-88))) / 2(1)
n = (3 ± sqrt(361)) / 2
n = (3 ± 19) / 2
We take the positive root since the number of sides of a polygon cannot be negative. So:
n = (3 + 19) / 2
n = 11
Therefore, the polygon has 11 sides.
To find the number of sides of a polygon that has 44 diagonals, we can use the formula:
Number of diagonals of an n-sided polygon = n(n-3)/2
where n is the number of sides.
We are given that the number of diagonals in the polygon is 44. So, we can set up the equation:
44 = n(n-3)/2
Multiplying both sides by 2 gives:
88 = n(n-3)
Expanding the right-hand side gives:
88 = n^2 - 3n
Rearranging gives:
n^2 - 3n - 88 = 0
We can now solve for n using the quadratic formula:
n = (-b ± sqrt(b^2 - 4ac)) / 2a
where a = 1, b = -3, and c = -88.
Plugging in these values gives:
n = (3 ± sqrt(3^2 - 4(1)(-88))) / 2(1)
n = (3 ± sqrt(361)) / 2
n = (3 ± 19) / 2
We take the positive root since the number of sides of a polygon cannot be negative. So:
n = (3 + 19) / 2
n = 11
Therefore, the polygon has 11 sides.
There are 12 points in a plane of which 5 are collinear. The number of triangles is
- a)200
- b)211
- c)210
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
There are 12 points in a plane of which 5 are collinear. The number of triangles is
a)
200
b)
211
c)
210
d)
none of these
|
|
Aditya Kumar answered |
Explanation
- Given that there are 12 points in a plane.
- Out of these 12 points, 5 are collinear.
- To find the number of triangles that can be formed using these 12 points, we can use the combination formula.
- The number of ways to choose 3 points out of 12 is given by 12C3 = 220.
- However, we need to subtract the number of triangles that can be formed using the collinear points.
- Since 5 points are collinear, we can form triangles using these points as well.
- The number of ways to choose 3 points out of 5 collinear points is given by 5C3 = 10.
- So, the total number of triangles that can be formed using the 12 points is 220 - 10 = 210.
- Therefore, the correct answer is option C: 210.
- Given that there are 12 points in a plane.
- Out of these 12 points, 5 are collinear.
- To find the number of triangles that can be formed using these 12 points, we can use the combination formula.
- The number of ways to choose 3 points out of 12 is given by 12C3 = 220.
- However, we need to subtract the number of triangles that can be formed using the collinear points.
- Since 5 points are collinear, we can form triangles using these points as well.
- The number of ways to choose 3 points out of 5 collinear points is given by 5C3 = 10.
- So, the total number of triangles that can be formed using the 12 points is 220 - 10 = 210.
- Therefore, the correct answer is option C: 210.
The number of different words that can be formed with 12 consonants and 5 vowels by taking 4 consonants and 3 vowels in each word is- a)12c4 × 5c3
- b)17c7
- c)
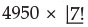
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of different words that can be formed with 12 consonants and 5 vowels by taking 4 consonants and 3 vowels in each word is
a)
12c4 × 5c3
b)
17c7
c)
d)
none of these

|
Srsps answered |
- Selecting and Arranging the Consonants:
- Selection: Choose 4 consonants out of 12.
- Arrangement: Arrange the selected 4 consonants in order.
- Number of Ways: This is represented by the permutation notation 12P4.
- Selecting and Arranging the Vowels:
- Selection: Choose 3 vowels out of 5.
- Arrangement: Arrange the selected 3 vowels in order.
- Number of Ways: This is represented by the permutation notation 5P3.
- Combining Consonants and Vowels:
- After selecting and arranging the consonants and vowels separately, we need to arrange all 7 letters together to form a word.
- Number of Ways: The 7 letters can be arranged in 7! (7 factorial) ways.
- Total Number of Different Words:
- Multiply the number of ways to arrange consonants, vowels, and the combined letters.
- Total Ways = 12P4 × 5P3 × 7! = 4950 x 7!
-
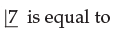
- a)5040
- b)4050
- c)5050
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
5040
b)
4050
c)
5050
d)
none of these

|
Srsps answered |
We are asked to find the value of 7! (7 factorial).
Step 1: Definition of Factorial
The factorial of a number n, denoted as n!, is the product of all positive integers from 1 to n.
The factorial of a number n, denoted as n!, is the product of all positive integers from 1 to n.
Step 2: Calculating 7!
For 7!, we multiply all integers from 1 to 7:
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1
For 7!, we multiply all integers from 1 to 7:
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1
Now, let's perform the multiplication:
7 × 6 = 42
42 × 5 = 210
210 × 4 = 840
840 × 3 = 2520
2520 × 2 = 5040
5040 × 1 = 5040
Step 3: Final Answer
Therefore, the value of 7! is 5040.
42 × 5 = 210
210 × 4 = 840
840 × 3 = 2520
2520 × 2 = 5040
5040 × 1 = 5040
Step 3: Final Answer
Therefore, the value of 7! is 5040.
Chapter doubts & questions for Chapter 5: Permutations and Combinations - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 5: Permutations and Combinations - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup