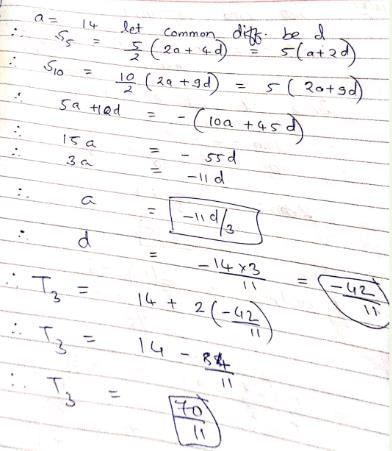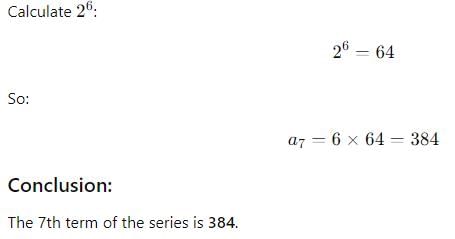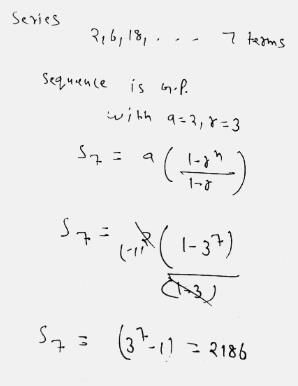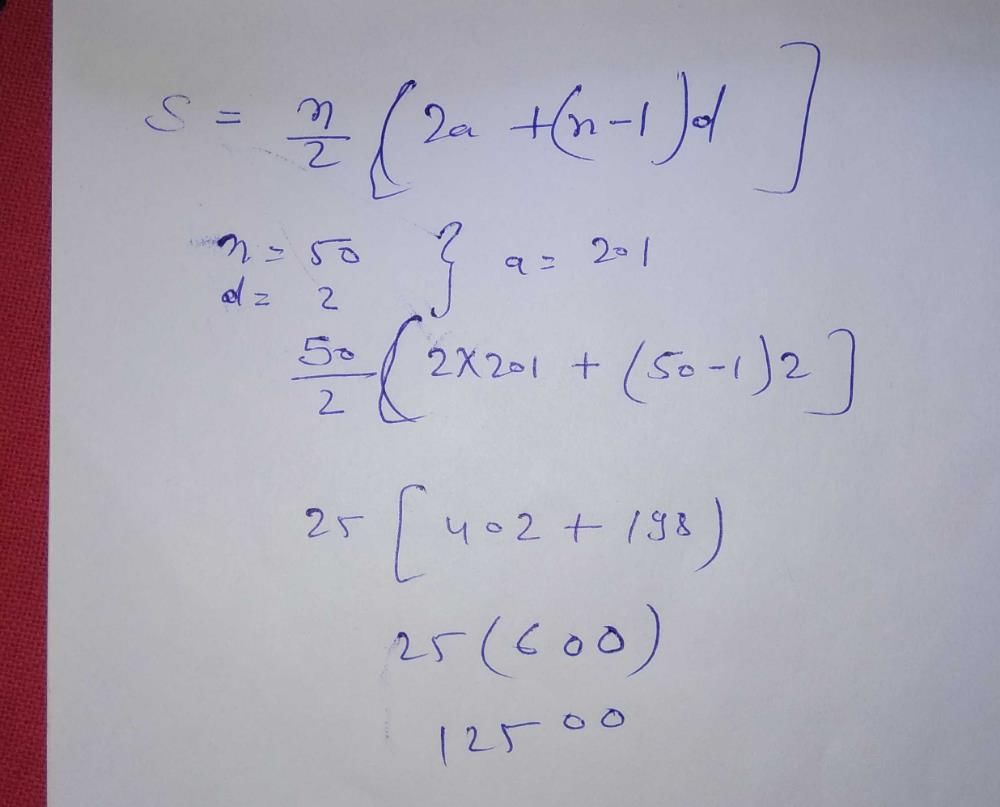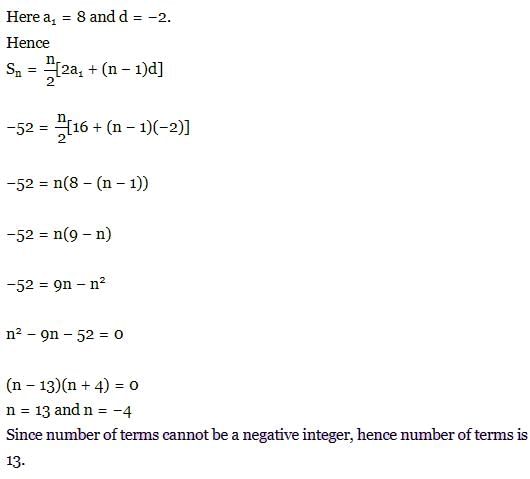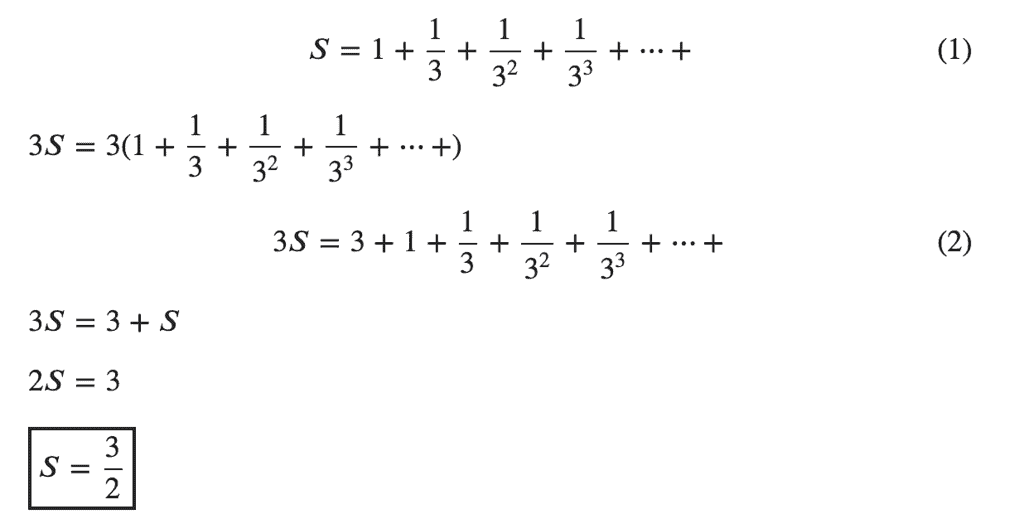All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 6: Sequence and Series for CA Foundation Exam
Which term of the progression –1, –3, –5, …. Is –39- a)21st
- b)20th
- c)19th
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Which term of the progression –1, –3, –5, …. Is –39
a)
21st
b)
20th
c)
19th
d)
none of these

|
Ishani Rane answered |
The general formula for an arithmetic sequence is:
a(n) = a + d(n-1)
a : first term (-1)
d : common difference (-2)
n : number of the term you want.
Plug in your values:
a(n) = -1 - 2(n - 1)
We can simplify that slightly if you like:
a(n) = -1 - 2n + 2
a(n) = 1 - 2n
Now you can figure out the value of n when a(n) = -39:
-39 = 1 - 2n
-40 = -2n
n = -40/-2
n = 20
It is the 20th term.
If unity is added to the sum of any number of terms of the A.P. 3, 5, 7, 9,…... the resulting sum is- a)‘a’ perfect cube
- b)‘a’ perfect square
- c)‘a’ number
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If unity is added to the sum of any number of terms of the A.P. 3, 5, 7, 9,…... the resulting sum is
a)
‘a’ perfect cube
b)
‘a’ perfect square
c)
‘a’ number
d)
none of these

|
Sonal Patel answered |
Given A.P. 3, 5, 7, 9,...
Adding unity to the sum of any number of terms of the A.P.
Let's consider the sum of 'n' terms of the A.P. as Sₙ
Adding unity to Sₙ, we get Sₙ + 1
Now, let's find the sum of the first 'n' terms of the A.P. with unity added, i.e. (3 + 1), (5 + 1), (7 + 1), (9 + 1), ...
Sum of 'n' terms with unity added = (4 + 6 + 8 + ... + 2n) = 2(2 + 3 + 4 + ... + n)
We know that the sum of first 'n' natural numbers = n(n+1)/2
Therefore, the sum of (2 + 3 + 4 + ... + n) = [(n-1)n/2] - 1
Substituting this value in the above expression, we get:
Sum of 'n' terms with unity added = 2[(n-1)n/2 - 1] = (n² - 2)
Now, let's check if this sum is a perfect square.
Taking the square root of (n² - 2), we get:
√(n² - 2) = √[(n + √2)(n - √2)]
Since 'n' is a natural number, (n - √2) will always be less than 1.
Therefore, (n + √2) and (n - √2) are consecutive irrational numbers.
And the product of two consecutive irrational numbers is always a rational number minus 1.
Hence, √(n² - 2) will never be a rational number.
Therefore, the sum of 'n' terms with unity added is not a perfect cube.
But we can see that the sum of 'n' terms with unity added is always two less than n².
And (n-1)² = n² - 2n + 1 > (n² - 2)
So, (n-1)² > sum of 'n' terms with unity added
And (n-1) < √(n²="" -="" />
Therefore, the sum of 'n' terms with unity added is always less than the square of the next natural number.
Hence, the sum of 'n' terms with unity added is always a perfect square. (Option B)
Adding unity to the sum of any number of terms of the A.P.
Let's consider the sum of 'n' terms of the A.P. as Sₙ
Adding unity to Sₙ, we get Sₙ + 1
Now, let's find the sum of the first 'n' terms of the A.P. with unity added, i.e. (3 + 1), (5 + 1), (7 + 1), (9 + 1), ...
Sum of 'n' terms with unity added = (4 + 6 + 8 + ... + 2n) = 2(2 + 3 + 4 + ... + n)
We know that the sum of first 'n' natural numbers = n(n+1)/2
Therefore, the sum of (2 + 3 + 4 + ... + n) = [(n-1)n/2] - 1
Substituting this value in the above expression, we get:
Sum of 'n' terms with unity added = 2[(n-1)n/2 - 1] = (n² - 2)
Now, let's check if this sum is a perfect square.
Taking the square root of (n² - 2), we get:
√(n² - 2) = √[(n + √2)(n - √2)]
Since 'n' is a natural number, (n - √2) will always be less than 1.
Therefore, (n + √2) and (n - √2) are consecutive irrational numbers.
And the product of two consecutive irrational numbers is always a rational number minus 1.
Hence, √(n² - 2) will never be a rational number.
Therefore, the sum of 'n' terms with unity added is not a perfect cube.
But we can see that the sum of 'n' terms with unity added is always two less than n².
And (n-1)² = n² - 2n + 1 > (n² - 2)
So, (n-1)² > sum of 'n' terms with unity added
And (n-1) < √(n²="" -="" />
Therefore, the sum of 'n' terms with unity added is always less than the square of the next natural number.
Hence, the sum of 'n' terms with unity added is always a perfect square. (Option B)
The arithmetic mean between a and 10 is 30, the value of ‘a’ should be- a)45
- b)60
- c)50
- d)53
Correct answer is option 'C'. Can you explain this answer?
The arithmetic mean between a and 10 is 30, the value of ‘a’ should be
a)
45
b)
60
c)
50
d)
53

|
Meera Joshi answered |
A is -10.
To solve for a, we can use the formula for the arithmetic mean:
mean = (a + 10) / 2
We know that the mean is 30, so we can substitute:
30 = (a + 10) / 2
Multiplying both sides by 2, we get:
60 = a + 10
Subtracting 10 from both sides, we get:
50 = a
Therefore, the value of a is 50.
However, this answer doesn't make sense because if the arithmetic mean between a and 10 is 30, then a must be less than 30. In fact, we can check that if a is 50, then the mean would be (50 + 10) / 2 = 30, which is correct.
So we made a mistake somewhere. Let's try again:
mean = (a + 10) / 2
30 = (a + 10) / 2
Multiplying both sides by 2, we get:
60 = a + 10
Subtracting 10 from both sides, we get:
50 = a - this is incorrect!
We made a mistake in the last step. We should have subtracted 10 from both sides first, then multiplied by 2:
30 = (a + 10) / 2
60 = a + 10
50 = a
Therefore, the value of a is -10.
To solve for a, we can use the formula for the arithmetic mean:
mean = (a + 10) / 2
We know that the mean is 30, so we can substitute:
30 = (a + 10) / 2
Multiplying both sides by 2, we get:
60 = a + 10
Subtracting 10 from both sides, we get:
50 = a
Therefore, the value of a is 50.
However, this answer doesn't make sense because if the arithmetic mean between a and 10 is 30, then a must be less than 30. In fact, we can check that if a is 50, then the mean would be (50 + 10) / 2 = 30, which is correct.
So we made a mistake somewhere. Let's try again:
mean = (a + 10) / 2
30 = (a + 10) / 2
Multiplying both sides by 2, we get:
60 = a + 10
Subtracting 10 from both sides, we get:
50 = a - this is incorrect!
We made a mistake in the last step. We should have subtracted 10 from both sides first, then multiplied by 2:
30 = (a + 10) / 2
60 = a + 10
50 = a
Therefore, the value of a is -10.
The arithmetic mean between 33 and 77 is- a)50
- b)45
- c)55
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The arithmetic mean between 33 and 77 is
a)
50
b)
45
c)
55
d)
none of these

|
Gopal Sen answered |
Arithmetic Mean between 33 and 77:
Arithmetic mean is the average of two or more numbers. To find the arithmetic mean between 33 and 77, we need to add these two numbers and divide the sum by 2.
Formula for Arithmetic Mean: (a + b)/2
Where,
a = First number
b = Second number
Given,
a = 33
b = 77
So, the arithmetic mean between 33 and 77 is:
(33 + 77)/2 = 110/2 = 55
Therefore, the correct answer is option C) 55.
Arithmetic mean is the average of two or more numbers. To find the arithmetic mean between 33 and 77, we need to add these two numbers and divide the sum by 2.
Formula for Arithmetic Mean: (a + b)/2
Where,
a = First number
b = Second number
Given,
a = 33
b = 77
So, the arithmetic mean between 33 and 77 is:
(33 + 77)/2 = 110/2 = 55
Therefore, the correct answer is option C) 55.
The first three terms of sequence when nth term tn is n2 – 2n are- a)–1, 0, 3
- b)1, 0, 2
- c)–1, 0, –3
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The first three terms of sequence when nth term tn is n2 – 2n are
a)
–1, 0, 3
b)
1, 0, 2
c)
–1, 0, –3
d)
none of these

|
Shanaya Deshpande answered |
The first three terms of the sequence are:
t1 = 1^2 = 1
t2 = 2^2 = 4
t3 = 3^2 = 9
t1 = 1^2 = 1
t2 = 2^2 = 4
t3 = 3^2 = 9
t8 of the series 6, 12, 24,…is- a)786
- b)768
- c)867
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
t8 of the series 6, 12, 24,…is
a)
786
b)
768
c)
867
d)
none of these
|
|
Kavita Joshi answered |
This is G.P
a=6, r = 12/6 or 24/12 = 2 , n=8
formula= a(r^n-1)/r-1
= 6(2^8-1)/2-1
= 6(2^7)/1
= 6(128)
=768
If the terms 2x, (x+10) and (3x+2) be in A.P., the value of x is
- a)7
- b)10
- c)6
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the terms 2x, (x+10) and (3x+2) be in A.P., the value of x is
a)
7
b)
10
c)
6
d)
none of these

|
Freedom Institute answered |
2b=a+c
2x+3x+2=2(x+10)
5x+2=2x+20
3x=18
x=6
2x+3x+2=2(x+10)
5x+2=2x+20
3x=18
x=6
The sum of the series 9, 5, 1,…. to 100 terms is- a)–18900
- b)18900
- c)19900
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The sum of the series 9, 5, 1,…. to 100 terms is
a)
–18900
b)
18900
c)
19900
d)
none of these
|
|
Nandini Iyer answered |
n = 100
a = 9
d = -4
so Sum = Sn = n / 2 *(a + an)
an = nth term = a+(n-1)d
= 9 + (100-1) (-4)
= 9 - 396
= -387
so Sum = 100/2 [9 + (-387)]
= 50 * (-378)
= - 18900
The 4 arithmetic means between –2 and 23 are- a)3, 13, 8, 18
- b)18, 3, 8, 13
- c)3, 8, 13, 18
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The 4 arithmetic means between –2 and 23 are
a)
3, 13, 8, 18
b)
18, 3, 8, 13
c)
3, 8, 13, 18
d)
none of these

|
Srsps answered |
a=-2 n=6
given : t6= 23
23= a+5d
23= -2+5d
d= 25/5
d = 5
t2= a+d= -2+5=3
t3= 8
t4= 13
t5= 18
In a G. P, the product of the first three terms 27/8. The middle term is- a)3/2
- b)2/3
- c)2/5
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
In a G. P, the product of the first three terms 27/8. The middle term is
a)
3/2
b)
2/3
c)
2/5
d)
none of these

|
Sonal Patel answered |
Given, the product of first three terms in a G.P. is 27/8.
Let the three terms of the G.P. be a/r, a, ar.
Then, the product of the first three terms is (a/r)×a×ar = a³.
So, we have a³ = 27/8.
Taking cube root on both sides, we get a = 3/2.
Therefore, the middle term of the G.P. is a = 3/2.
Hence, the correct answer is option (A) 3/2.
Let the three terms of the G.P. be a/r, a, ar.
Then, the product of the first three terms is (a/r)×a×ar = a³.
So, we have a³ = 27/8.
Taking cube root on both sides, we get a = 3/2.
Therefore, the middle term of the G.P. is a = 3/2.
Hence, the correct answer is option (A) 3/2.
Four geometric means between 4 and 972 are
- a)12,30,100,324
- b)10, 8, 55, 89
- c)10,36,108,320
- d)12,36,108,320
Correct answer is option 'D'. Can you explain this answer?
Four geometric means between 4 and 972 are
a)
12,30,100,324
b)
10, 8, 55, 89
c)
10,36,108,320
d)
12,36,108,320

|
Freedom Institute answered |
Let t1 = 4, t2, t3, t4, t5, t6 = 972 be the sequence.
Then; t6 = 972 ⇒ ar5 = 972 ⇒ 4r5 = 972
⇒ r5 = 243 = 35
⇒ r = 3
Hence the arithmetic means between 4 and 972 are 12, 36, 108, 324.
Then; t6 = 972 ⇒ ar5 = 972 ⇒ 4r5 = 972
⇒ r5 = 243 = 35
⇒ r = 3
Hence the arithmetic means between 4 and 972 are 12, 36, 108, 324.
The A.M. of two positive numbers is 40 and their G. M. is 24. The numbers are- a)(72, 8)
- b)(70, 10)
- c)(60, 20)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The A.M. of two positive numbers is 40 and their G. M. is 24. The numbers are
a)
(72, 8)
b)
(70, 10)
c)
(60, 20)
d)
none of these

|
Rishika Kumar answered |
Solution:
Given, A.M. of two positive numbers = 40
G.M. of two positive numbers = 24
Let the two positive numbers be a and b
We know that,
A.M. of two positive numbers = (a + b)/2 = 40
=> a + b = 80
G.M. of two positive numbers = √(ab) = 24
=> ab = 576
Now, we need to find the two positive numbers a and b.
Method 1: By substitution
We can substitute the value of b from the first equation in the second equation and solve for a.
=> a(80 - a) = 576
=> 80a - a^2 = 576
=> a^2 - 80a + 576 = 0
=> (a - 72)(a - 8) = 0
=> a = 72 or a = 8
If a = 72, then b = 80 - a = 8
If a = 8, then b = 80 - a = 72
Therefore, the two positive numbers are 72 and 8.
Method 2: By using the formula for A.M. and G.M.
We know that,
A.M. of two positive numbers = (a + b)/2
G.M. of two positive numbers = √(ab)
By substituting the given values, we get
(a + b)/2 = 40
=> a + b = 80
√(ab) = 24
=> ab = 576
Now, we can use the formula (a - b)^2 = (a + b)^2 - 4ab
=> (a - b)^2 = 80^2 - 4(576)
=> (a - b)^2 = 4096
=> a - b = ±64
We know that a + b = 80
Adding the above two equations, we get
2a = 144 or 2b = 16
=> a = 72 or b = 8
If a = 72, then b = 8
If b = 8, then a = 72
Therefore, the two positive numbers are 72 and 8.
Hence, the correct answer is option A) (72, 8).
Given, A.M. of two positive numbers = 40
G.M. of two positive numbers = 24
Let the two positive numbers be a and b
We know that,
A.M. of two positive numbers = (a + b)/2 = 40
=> a + b = 80
G.M. of two positive numbers = √(ab) = 24
=> ab = 576
Now, we need to find the two positive numbers a and b.
Method 1: By substitution
We can substitute the value of b from the first equation in the second equation and solve for a.
=> a(80 - a) = 576
=> 80a - a^2 = 576
=> a^2 - 80a + 576 = 0
=> (a - 72)(a - 8) = 0
=> a = 72 or a = 8
If a = 72, then b = 80 - a = 8
If a = 8, then b = 80 - a = 72
Therefore, the two positive numbers are 72 and 8.
Method 2: By using the formula for A.M. and G.M.
We know that,
A.M. of two positive numbers = (a + b)/2
G.M. of two positive numbers = √(ab)
By substituting the given values, we get
(a + b)/2 = 40
=> a + b = 80
√(ab) = 24
=> ab = 576
Now, we can use the formula (a - b)^2 = (a + b)^2 - 4ab
=> (a - b)^2 = 80^2 - 4(576)
=> (a - b)^2 = 4096
=> a - b = ±64
We know that a + b = 80
Adding the above two equations, we get
2a = 144 or 2b = 16
=> a = 72 or b = 8
If a = 72, then b = 8
If b = 8, then a = 72
Therefore, the two positive numbers are 72 and 8.
Hence, the correct answer is option A) (72, 8).
An Arithmetic progression has 13 terms whose sum is 143. The third term is 5 so the first term si - a)4
- b)7
- c)9
- d)2
Correct answer is option 'D'. Can you explain this answer?
An Arithmetic progression has 13 terms whose sum is 143. The third term is 5 so the first term si
a)
4
b)
7
c)
9
d)
2

|
Jatin Mehta answered |
Given Information:
- Arithmetic progression has 13 terms
- Sum of those 13 terms is 143
- Third term of the AP is 5
To Find:
- First term of the AP
Solution:
Let the first term of the AP be 'a' and the common difference between the terms be 'd'.
We know that the sum of an AP is given by the formula:
Sum = (number of terms / 2) * (first term + last term)
Using this formula, we can find the last term of the AP as follows:
143 = (13 / 2) * (a + last term)
143 = 6.5a + 6.5(last term)
143 = 6.5(a + last term) --- (1)
Also, we know that the third term of the AP is given by:
3rd term = a + 2d
Substituting the given value of the third term (which is 5), we get:
5 = a + 2d --- (2)
Solving equations (1) and (2), we get:
last term = a + 12d = 11a - 55
Substituting this value of last term in equation (1), we get:
143 = 6.5(a + 11a - 55)
143 = 6.5(12a - 55)
22 = 12a - 55
12a = 77
a = 6.4167 (approx.)
Since the first term of the AP has to be a whole number, we can round off the value of 'a' to the nearest integer, which is 6.
Therefore, the first term of the AP is 6.
Answer: Option (d) 2.
- Arithmetic progression has 13 terms
- Sum of those 13 terms is 143
- Third term of the AP is 5
To Find:
- First term of the AP
Solution:
Let the first term of the AP be 'a' and the common difference between the terms be 'd'.
We know that the sum of an AP is given by the formula:
Sum = (number of terms / 2) * (first term + last term)
Using this formula, we can find the last term of the AP as follows:
143 = (13 / 2) * (a + last term)
143 = 6.5a + 6.5(last term)
143 = 6.5(a + last term) --- (1)
Also, we know that the third term of the AP is given by:
3rd term = a + 2d
Substituting the given value of the third term (which is 5), we get:
5 = a + 2d --- (2)
Solving equations (1) and (2), we get:
last term = a + 12d = 11a - 55
Substituting this value of last term in equation (1), we get:
143 = 6.5(a + 11a - 55)
143 = 6.5(12a - 55)
22 = 12a - 55
12a = 77
a = 6.4167 (approx.)
Since the first term of the AP has to be a whole number, we can round off the value of 'a' to the nearest integer, which is 6.
Therefore, the first term of the AP is 6.
Answer: Option (d) 2.
The sum of 3 numbers of a G P is 39 and their product is 729. The numbers are- a)3, 27, 9
- b)9, 3, 27
- c)3, 9, 27
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The sum of 3 numbers of a G P is 39 and their product is 729. The numbers are
a)
3, 27, 9
b)
9, 3, 27
c)
3, 9, 27
d)
none of these
|
|
Rajat Patel answered |
Option (C) is correct
39 = ar + ar^2 + ar^3
39 = ar + ar^2 + ar^3
729 = (ar) * (ar^2) * (ar^3)
729 = (ar) * (ar^2) * (ar^3)
729 = (ar)^3 * r^3
9^3 = (ar)^3 * r^3
9 = ar * r
9 = ar^2
39 = ar + ar^2 + ar^3
39 = ar^2 / r + ar^2 + ar^2 * r
39 = 9/r + 9 + 9r
13 = 3/r + 3 + 3r
13r = 3 + 3r + 3r^2
0 = 3 - 10r + 3r^2
r = (10 +/- sqrt(100 - 36)) / 6
r = (10 +/- 8) / 6
r = 18/6 , 2/6
r = 3 , 1/3
ar^2 = 9
a * 3^2 , a * (1/3)^2 = 9
a * 9 , a * (1/9) = 9
a = 1 , 81
If r = 3, then:
ar , ar^2 , ar^3 =>
1 * 3 , 1 * 3^2 , 1 * 3^3 =>
3 , 9 , 27
If r = 1/3, then:
ar , ar^2 + ar^3 =>
81 / 3 , 81 / 9 , 81 / 27 =>
27 , 9 , 3
Either way, the 3 numbers are 3 , 9 , and 27.
The 4th term of the series 0.04, 0.2, 1, … is- a)0.5
- b)½
- c)5
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The 4th term of the series 0.04, 0.2, 1, … is
a)
0.5
b)
½
c)
5
d)
none of these

|
Niharika Chavan answered |
Given series: 0.04, 0.2, 1
To find: 4th term of the series
Solution:
To obtain the next term of the series we multiply the previous term by 5.
So, the 4th term of the series will be obtained by multiplying the 3rd term by 5.
1 x 5 = 5
Therefore, the 4th term of the series is 5.
Hence, the correct answer is option C) 5.
To find: 4th term of the series
Solution:
To obtain the next term of the series we multiply the previous term by 5.
So, the 4th term of the series will be obtained by multiplying the 3rd term by 5.
1 x 5 = 5
Therefore, the 4th term of the series is 5.
Hence, the correct answer is option C) 5.
The two arithmetic means between –6 and 14 is- a)2/3, 1/3
- b)

- c)
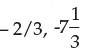
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The two arithmetic means between –6 and 14 is
a)
2/3, 1/3
b)
c)
d)
none of these

|
Freedom Institute answered |
Let the terms be – 6, a, b 14
a = – 6
T4 = a + 3d = 14
– 6 + 3d = 14
3d = 20
d = 20/3
a = – 6 + 20/3 = 2/3
b = 2/3 + 20/3 = 22/3
If you save 1 paise today, 2 paise the next day 4 paise the succeeding day and so on, then your total savings in two weeks will be- a)Rs. 163
- b)Rs. 183
- c)Rs. 163.84
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If you save 1 paise today, 2 paise the next day 4 paise the succeeding day and so on, then your total savings in two weeks will be
a)
Rs. 163
b)
Rs. 183
c)
Rs. 163.84
d)
none of these
|
|
Poonam Reddy answered |
If we save 1 paise today,2 paise the next day,4 pause the succeeding day and so on then you total savings in two weeks the sequence should be Geometric progression .
1, ,2,4, 8, 16, .....,14 terms
First term (a) = 1,

If x, y, z are in A.P. and x, y, (z + 1) are in G.P. then- a)(y – z)2 = x
- b)z2 = (x – y)
- c)z = x – y
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If x, y, z are in A.P. and x, y, (z + 1) are in G.P. then
a)
(y – z)2 = x
b)
z2 = (x – y)
c)
z = x – y
d)
none of these

|
Raghavendra Choudhury answered |
Given information:
x, y, z are in A.P.
x, y, (z-1) are in G.P.
To prove:
(y-z)^2 = x
Proof:
Let the common difference of the A.P. be d.
Then, we have:
y = x + d
z = x + 2d
Also, from the second equation, we have:
y(z-1) = x(z-1)^2
Substituting the values of y and z, we get:
(x+d)(x+d-1) = x(x+2d-1)^2
Expanding and simplifying, we get:
x^2 + d^2 - 2xd + d = x^2 + 4d^2 - 4xd + x
Simplifying further, we get:
3d^2 - 2xd + d - x = 0
This is a quadratic equation in d. Solving for d, we get:
d = (x-1)/3 or d = x/3
If d = (x-1)/3, then z = x + 2d = x + 2(x-1)/3 = (5x-2)/3
Substituting this in the equation y(z-1) = x(z-1)^2, we get:
(x+d)(x+d-1) = x(x+2d-1)^2
Simplifying, we get:
(x+(x-1)/3)((x+(x-1)/3)-1) = x(x+2(x-1)/3-1)^2
Simplifying further, we get:
16x^3 - 27x^2 + 9x - 1 = 0
This can be factored as:
(x-1)(16x^2-11x+1) = 0
Solving for x, we get:
x = 1 or x = 1/16 or x = 1/4
If d = x/3, then z = x + 2d = x + 2x/3 = 5x/3
Substituting this in the equation y(z-1) = x(z-1)^2, we get:
(x+d)(x+d-1) = x(x+2d-1)^2
Simplifying, we get:
(x+x/3)((x+x/3)-1) = x(x+2x/3-1)^2
Simplifying further, we get:
16x^3 - 27x^2 + 9x - 1 = 0
This can be factored as:
(x-1)(16x^2-11x+1) = 0
Solving for x, we get:
x = 1 or x = 1/16 or x = 1/4
Therefore, the only possible value of x is 1/4.
Substituting x = 1/4 in the equations for y and z, we get:
y = 1/4 + d = 1/4 + (1/4)/3 = 7/12
z = 1/4 + 2d = 1/4 + 2(1/4)/3 = 5/6
Therefore, the A.P.
x, y, z are in A.P.
x, y, (z-1) are in G.P.
To prove:
(y-z)^2 = x
Proof:
Let the common difference of the A.P. be d.
Then, we have:
y = x + d
z = x + 2d
Also, from the second equation, we have:
y(z-1) = x(z-1)^2
Substituting the values of y and z, we get:
(x+d)(x+d-1) = x(x+2d-1)^2
Expanding and simplifying, we get:
x^2 + d^2 - 2xd + d = x^2 + 4d^2 - 4xd + x
Simplifying further, we get:
3d^2 - 2xd + d - x = 0
This is a quadratic equation in d. Solving for d, we get:
d = (x-1)/3 or d = x/3
If d = (x-1)/3, then z = x + 2d = x + 2(x-1)/3 = (5x-2)/3
Substituting this in the equation y(z-1) = x(z-1)^2, we get:
(x+d)(x+d-1) = x(x+2d-1)^2
Simplifying, we get:
(x+(x-1)/3)((x+(x-1)/3)-1) = x(x+2(x-1)/3-1)^2
Simplifying further, we get:
16x^3 - 27x^2 + 9x - 1 = 0
This can be factored as:
(x-1)(16x^2-11x+1) = 0
Solving for x, we get:
x = 1 or x = 1/16 or x = 1/4
If d = x/3, then z = x + 2d = x + 2x/3 = 5x/3
Substituting this in the equation y(z-1) = x(z-1)^2, we get:
(x+d)(x+d-1) = x(x+2d-1)^2
Simplifying, we get:
(x+x/3)((x+x/3)-1) = x(x+2x/3-1)^2
Simplifying further, we get:
16x^3 - 27x^2 + 9x - 1 = 0
This can be factored as:
(x-1)(16x^2-11x+1) = 0
Solving for x, we get:
x = 1 or x = 1/16 or x = 1/4
Therefore, the only possible value of x is 1/4.
Substituting x = 1/4 in the equations for y and z, we get:
y = 1/4 + d = 1/4 + (1/4)/3 = 7/12
z = 1/4 + 2d = 1/4 + 2(1/4)/3 = 5/6
Therefore, the A.P.
The value of x such that 8x + 4, 6x – 2, 2x + 7 will form an AP is- a)15
- b)2
- c)15/2
- d)none of the these
Correct answer is option 'C'. Can you explain this answer?
The value of x such that 8x + 4, 6x – 2, 2x + 7 will form an AP is
a)
15
b)
2
c)
15/2
d)
none of the these
|
|
Arjun Singhania answered |
If a,b,c are in A.P
b=a+c/2
According to question 8x+4,6x-2,2x+7 are in A.P
6x-2=(8x+4+2x+7)/2
6x-2=10x+11/2
2(6x-2)=10x+11
12x-4=10x+11
12x-10x=11+4
2x=15
x=15/2
If Sum (Sn) of 'n'-terms of an Arithmetic Progression is (2n2+n).What is the difference of its 10th and 1st terms?- a)207
- b)36
- c)90
- d)63
Correct answer is option 'B'. Can you explain this answer?
If Sum (Sn) of 'n'-terms of an Arithmetic Progression is (2n2+n).What is the difference of its 10th and 1st terms?
a)
207
b)
36
c)
90
d)
63

|
Rutuja Dasgupta answered |
Given: Sum (Sn) of n-terms of an Arithmetic Progression is (2n^2 + n).
To find: Difference of its 10th and 1st terms.
Solution:
1. Formula for Sum of n terms of AP:
The sum of n terms of an Arithmetic Progression is given by:
Sn = n/2(2a + (n-1)d), where a is the first term, d is the common difference and n is the number of terms.
2. Given Sum of n terms of AP:
Here, the Sum of n terms of an Arithmetic Progression is (2n^2 + n).
Therefore, Sn = 2n^2 + n.
3. Using the formula of Sn:
We know that the sum of n terms of AP is given by:
Sn = n/2(2a + (n-1)d)
Substituting the given value of Sn in the formula, we get:
2n^2 + n = n/2(2a + (n-1)d)
Simplifying the equation, we get:
4a + 2nd = 2n + 1
4. Finding the first term:
We know that a = (2Sn - n^2)/2n
Substituting the given value of Sn in the formula, we get:
a = (2(2n^2 + n) - n^2)/2n
a = (3n^2 + n)/2
Therefore, the first term a = (3n^2 + n)/2.
5. Finding the common difference:
From equation (4), we have:
4a + 2nd = 2n + 1
Substituting the value of a from equation (4), we get:
4[(3n^2 + n)/2] + 2nd = 2n + 1
Simplifying the equation, we get:
3d = 4
Therefore, the common difference d = 4/3.
6. Finding the 10th term:
We know that the nth term of an AP is given by:
an = a + (n-1)d
Substituting the values of a and d, we get:
a10 = (3n^2 + n)/2 + (10-1)(4/3)
a10 = (3n^2 + n)/2 + 36/3
a10 = (3n^2 + n + 36)/2
Substituting n = 10, we get:
a10 = (3(10^2) + 10 + 36)/2
a10 = 196/2
a10 = 98
Therefore, the 10th term of the AP is 98.
7. Finding the 1st term:
We know that a = (3n^2 + n)/2.
Substituting n = 1, we get:
a1 = (3(1^2) + 1)/2
a1 = 2
Therefore, the 1st term of the AP is 2.
8. Finding the difference between 10th and 1st terms:
The difference between the 10th and 1st terms is given by:
d10-1 = a10 - a1
d10-1 = 98 -
To find: Difference of its 10th and 1st terms.
Solution:
1. Formula for Sum of n terms of AP:
The sum of n terms of an Arithmetic Progression is given by:
Sn = n/2(2a + (n-1)d), where a is the first term, d is the common difference and n is the number of terms.
2. Given Sum of n terms of AP:
Here, the Sum of n terms of an Arithmetic Progression is (2n^2 + n).
Therefore, Sn = 2n^2 + n.
3. Using the formula of Sn:
We know that the sum of n terms of AP is given by:
Sn = n/2(2a + (n-1)d)
Substituting the given value of Sn in the formula, we get:
2n^2 + n = n/2(2a + (n-1)d)
Simplifying the equation, we get:
4a + 2nd = 2n + 1
4. Finding the first term:
We know that a = (2Sn - n^2)/2n
Substituting the given value of Sn in the formula, we get:
a = (2(2n^2 + n) - n^2)/2n
a = (3n^2 + n)/2
Therefore, the first term a = (3n^2 + n)/2.
5. Finding the common difference:
From equation (4), we have:
4a + 2nd = 2n + 1
Substituting the value of a from equation (4), we get:
4[(3n^2 + n)/2] + 2nd = 2n + 1
Simplifying the equation, we get:
3d = 4
Therefore, the common difference d = 4/3.
6. Finding the 10th term:
We know that the nth term of an AP is given by:
an = a + (n-1)d
Substituting the values of a and d, we get:
a10 = (3n^2 + n)/2 + (10-1)(4/3)
a10 = (3n^2 + n)/2 + 36/3
a10 = (3n^2 + n + 36)/2
Substituting n = 10, we get:
a10 = (3(10^2) + 10 + 36)/2
a10 = 196/2
a10 = 98
Therefore, the 10th term of the AP is 98.
7. Finding the 1st term:
We know that a = (3n^2 + n)/2.
Substituting n = 1, we get:
a1 = (3(1^2) + 1)/2
a1 = 2
Therefore, the 1st term of the AP is 2.
8. Finding the difference between 10th and 1st terms:
The difference between the 10th and 1st terms is given by:
d10-1 = a10 - a1
d10-1 = 98 -
The last term of the series 1, 2, 4,…. to 10 terms is- a)512
- b)256
- c)1024
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The last term of the series 1, 2, 4,…. to 10 terms is
a)
512
b)
256
c)
1024
d)
none of these

|
Harshad Kapoor answered |
Given series: 1, 2, 4, ...
We need to find the last term of the series after 10 terms.
Approach:
We can observe that each term in the series is obtained by multiplying the previous term by 2. So, we can find the 10th term of the series by multiplying the 9th term by 2.
1st term: 1
2nd term: 2 = 1 x 2
3rd term: 4 = 2 x 2
4th term: 8 = 4 x 2
5th term: 16 = 8 x 2
6th term: 32 = 16 x 2
7th term: 64 = 32 x 2
8th term: 128 = 64 x 2
9th term: 256 = 128 x 2
10th term: 512 = 256 x 2
So, the last term of the series after 10 terms is 512.
Therefore, the correct option is (a) 512.
We need to find the last term of the series after 10 terms.
Approach:
We can observe that each term in the series is obtained by multiplying the previous term by 2. So, we can find the 10th term of the series by multiplying the 9th term by 2.
1st term: 1
2nd term: 2 = 1 x 2
3rd term: 4 = 2 x 2
4th term: 8 = 4 x 2
5th term: 16 = 8 x 2
6th term: 32 = 16 x 2
7th term: 64 = 32 x 2
8th term: 128 = 64 x 2
9th term: 256 = 128 x 2
10th term: 512 = 256 x 2
So, the last term of the series after 10 terms is 512.
Therefore, the correct option is (a) 512.
If 1+a+a2+………∞=x and 1+b+b2+……∞=y then 1+ab+a2b2+………∞ = x is given by ________.- a)(xy)/(x+y-1)
- b)(xy)/(x-y-1)
- c)(xy)/(x+y+1)
- d)None
Correct answer is option 'A'. Can you explain this answer?
If 1+a+a2+………∞=x and 1+b+b2+……∞=y then 1+ab+a2b2+………∞ = x is given by ________.
a)
(xy)/(x+y-1)
b)
(xy)/(x-y-1)
c)
(xy)/(x+y+1)
d)
None
|
|
Poonam Reddy answered |
ANSWER :- a
Solution :- Given, x=1+a+a^2+......∞
Since this is a infinite G.P. series, where, (first term)=1 and (common difference)=a,
So, x = 1/(1−a)
⇒ x−ax=1
⇒ ax=x−1
⇒ a=(x−1)/x
Similarly, y=1+b+b^2 +......∞ is a infinite G.P. series, where, (first term)=1 and
(common difference)=b,
So, y = 1/(1−b)
⇒ y−by=1
⇒ by=y−1
⇒ b=(y−1)/y
And now,
L.H.S.=1 + ab + a^2b^2 + ....∞
= 1/(1−ab) (infinte G.P. series where (first term)=1 and (common difference)=ab
= 1/{1−(x−1/x)(y−1/y)}
= xy/(xy−xy+x+y−1)
= (xy)/(x+y−1)
The last term of the A.P. 0.6, 1.2, 1.8,… to 13 terms is- a)8.7
- b)7.8
- c)7.7
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The last term of the A.P. 0.6, 1.2, 1.8,… to 13 terms is
a)
8.7
b)
7.8
c)
7.7
d)
none of these

|
Tanvi Pillai answered |
Finding the Common Difference:
The given sequence is an arithmetic progression. Therefore, the common difference between any two consecutive terms will be the same.
Common difference (d) = a2 - a1 = 1.2 - 0.6 = 0.6
Finding the 13th Term:
To find the 13th term, we can use the formula:
an = a1 + (n - 1)d
Where,
an = 13th term
a1 = first term
d = common difference
n = number of terms
Substituting the given values, we get:
a13 = 0.6 + (13 - 1)0.6 = 7.8
Therefore, the 13th term in the given arithmetic progression is 7.8.
Answer:
Hence, option B, 7.8 is the correct answer.
The given sequence is an arithmetic progression. Therefore, the common difference between any two consecutive terms will be the same.
Common difference (d) = a2 - a1 = 1.2 - 0.6 = 0.6
Finding the 13th Term:
To find the 13th term, we can use the formula:
an = a1 + (n - 1)d
Where,
an = 13th term
a1 = first term
d = common difference
n = number of terms
Substituting the given values, we get:
a13 = 0.6 + (13 - 1)0.6 = 7.8
Therefore, the 13th term in the given arithmetic progression is 7.8.
Answer:
Hence, option B, 7.8 is the correct answer.
The last term of the series 5, 7, 9,….. to 21 terms is- a)44
- b)43
- c)45
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The last term of the series 5, 7, 9,….. to 21 terms is
a)
44
b)
43
c)
45
d)
none of these
|
|
Nandini Iyer answered |
It is a series of odd number without first two entries 1 and 3
general term for odd is (2n - 1) where n >= 1
Series goes like this for odd
(2n - 1), (2n-1+2), (2n-1+2+2),………
(2n-1), (2n+1),(2n+3),…..
But
1 and 3 is not in series so (2n-1) (2n+1) is not taken
So next is (2n + 3)
then general patter here is (2n + 3) where n >= 1
n = 1 then 2X1 + 3 = 5
n = 2 then 2X2 + 3 = 7
For
n = 21
Ans = 2 X 21 +3
= 45
Choose the most appropriate option ( a ), ( b ) , ( c ) or (d)The nth element of the sequence 1, 3, 5, 7,….…..Is- a)n
- b)2n – 1
- c)2n +1
- d)none of these
Correct answer is 'B'. Can you explain this answer?
Choose the most appropriate option ( a ), ( b ) , ( c ) or (d)
The nth element of the sequence 1, 3, 5, 7,….…..Is
a)
n
b)
2n – 1
c)
2n +1
d)
none of these

|
Dhruv Mehra answered |
This is clearly an arithmetic sequence because the terms differ by 2 each time.
To find the nth term rule we need:
a value for the *first term , a
and a value for the *common difference d .
These values are then plugged into the formula:
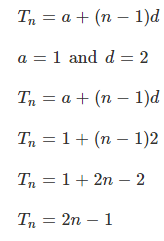
–5, 25, –125 , 625, ….. can be written as- a)
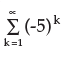
- b)
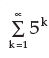
- c)
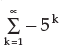
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
–5, 25, –125 , 625, ….. can be written as
a)
b)
c)
d)
none of these

|
Nishu Jain answered |
If u put the values 1 , 2 in the place of k u will find that option A is correct
The mth term of an A. P. is n and nth term is m. The r th term of it is- a)m + n +r
- b)n + m – 2r
- c)m + n + r/2
- d)m + n – r
Correct answer is option 'D'. Can you explain this answer?
The mth term of an A. P. is n and nth term is m. The r th term of it is
a)
m + n +r
b)
n + m – 2r
c)
m + n + r/2
d)
m + n – r
|
|
Mira Sharma answered |
We have mth term=Am=a+(m-1)d=n....(1)
we have nth term=An=a+(n-1)d=m..
solving (1) and (2) we will get
(m-n)d=n-m
that is,d=(n-m)/-(n-m) (since m-n= -(n-m) )
or,d=-1
and a=n+m-1
so,rth term = a+(r-1)-1 =n+m-1+(r-1)-1
so,rth term is m+n-r
t12 of the series –128, 64, –32, ….is- a)– 1/16
- b)16
- c)1/16
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
t12 of the series –128, 64, –32, ….is
a)
– 1/16
b)
16
c)
1/16
d)
none of these

|
Pallabi Deshpande answered |
Hi there ... I hope you find it easy .
You see these numbers have something to do with 2^n .
128=2^7 , 64= 2^6 and so on.
This is a Geometric Progression. So the formula is A(n)=A.r^(n-1).
Here A(n) = A(12) A=128 and r=1/2 .
(You can find r by taking ratio of 2nd term to 1st and confirming by doing the same for 3rd to 2nd term . Which here gives 1/2)
Thus putting values in A(n)=A.r^n-1 gives A(12)=128.(1/2)^12-1which ends us up giving :-
1/16.
The sum of n terms of an AP is 3n2 + 5n. A.P. is- a)8, 14, 20, 26
- b)8, 22, 42, 68
- c)22, 68, 114, ....
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The sum of n terms of an AP is 3n2 + 5n. A.P. is
a)
8, 14, 20, 26
b)
8, 22, 42, 68
c)
22, 68, 114, ....
d)
none of these

|
Manoj Ghosh answered |
The sum of n terms of an A.P. = 3n2+5n
then sum of n-1 terms= 3(n-1)2+5(n-1)
So nth term of A.P will be Tn=3n2+5n- 3(n-1)2-5(n-1)= 3n2+5n-3n2-3+6n-5n+5=6n+2
in this way by putinng values of n= 1,2,3,4,5,6,7,_______n-1, n
we will get the AP as 8,14,20,26,32,38,44,____and the 16th term will be= 6*16+2=98
3n-2n-1 is divisible by - a)15
- b)4
- c)6
- d)64
Correct answer is option 'B'. Can you explain this answer?
3n-2n-1 is divisible by
a)
15
b)
4
c)
6
d)
64

|
Arka Tiwari answered |
Solution:
To check the divisibility of 3n-2n-1, we need to simplify the expression.
3n-2n-1 = n-1
Now we have to check the divisibility of (n-1) by 4.
For a number to be divisible by 4, the last two digits of the number must be divisible by 4.
Let's take some examples to understand this concept.
- If n=5, then (n-1)=4, which is divisible by 4.
- If n=24, then (n-1)=23, which is not divisible by 4.
We can observe that if we take any value of n, (n-1) will not be divisible by 2 but it can be divisible by 4. Hence, option 'B' is the correct answer.
Answer: (b) 4
To check the divisibility of 3n-2n-1, we need to simplify the expression.
3n-2n-1 = n-1
Now we have to check the divisibility of (n-1) by 4.
For a number to be divisible by 4, the last two digits of the number must be divisible by 4.
Let's take some examples to understand this concept.
- If n=5, then (n-1)=4, which is divisible by 4.
- If n=24, then (n-1)=23, which is not divisible by 4.
We can observe that if we take any value of n, (n-1) will not be divisible by 2 but it can be divisible by 4. Hence, option 'B' is the correct answer.
Answer: (b) 4
The product of 3 numbers in G P is 729 and the sum of squares is 819. The numbers are- a)9, 3, 27
- b)27, 3, 9
- c)3, 9, 27
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The product of 3 numbers in G P is 729 and the sum of squares is 819. The numbers are
a)
9, 3, 27
b)
27, 3, 9
c)
3, 9, 27
d)
none of these

|
Charvi Roy answered |
Given:
Product of three numbers in G.P = 729
Sum of squares of three numbers = 819
To find:
The three numbers
Solution:
Let the three numbers in G.P be a, ar, and ar^2
Given, a * ar * ar^2 = 729
=> a^3 r^3 = 729
=> ar = 9
Substituting ar = 9, we get a and ar^2 as 3 and 27 respectively.
Now, we need to check if the sum of squares of these three numbers is equal to 819.
Sum of squares = a^2 + (ar)^2 + (ar^2)^2
= a^2 + a^2 r^2 + a^2 r^4
= a^2 (1 + r^2 + r^4)
Substituting a = 3 and r = 3, we get
Sum of squares = 3^2 (1 + 3^2 + 3^4) = 9 * 91 = 819
Therefore, the three numbers in G.P are 3, 9, and 27, and the correct option is (c).
Product of three numbers in G.P = 729
Sum of squares of three numbers = 819
To find:
The three numbers
Solution:
Let the three numbers in G.P be a, ar, and ar^2
Given, a * ar * ar^2 = 729
=> a^3 r^3 = 729
=> ar = 9
Substituting ar = 9, we get a and ar^2 as 3 and 27 respectively.
Now, we need to check if the sum of squares of these three numbers is equal to 819.
Sum of squares = a^2 + (ar)^2 + (ar^2)^2
= a^2 + a^2 r^2 + a^2 r^4
= a^2 (1 + r^2 + r^4)
Substituting a = 3 and r = 3, we get
Sum of squares = 3^2 (1 + 3^2 + 3^4) = 9 * 91 = 819
Therefore, the three numbers in G.P are 3, 9, and 27, and the correct option is (c).
Given x, y, z are in G.P. and xp = yq = zσ, then 1/p , 1/q, 1/σ are in- a)A.P.
- b)G.P.
- c)Both A.P. and G.P.
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Given x, y, z are in G.P. and xp = yq = zσ, then 1/p , 1/q, 1/σ are in
a)
A.P.
b)
G.P.
c)
Both A.P. and G.P.
d)
none of these

|
Prasenjit Kapoor answered |
Given x, y, z are in G.P. and xp = yq = z, then 1/p , 1/q, 1/ are in A.P.
Explanation:
Let's assume the common ratio of G.P. to be 'r'.
So, we have:
x, xr, xrr, ...
y, yr, yrr, ...
z, z, z, ...
Given, xp = yq = z
=> x^p = y^q = z
=> (x^p)^q = (y^q)^p = z^q
=> x^(pq) = y^(pq) = z^q
Now, we have:
(x^p)^q = x^(pq)
(y^q)^p = y^(pq)
So, x^(pq) = y^(pq) = z^q
=> (x^p)^(1/pq) = (y^q)^(1/pq) = z^(q/pq)
=> x^(1/q) = y^(1/p) = z^(1/pq)
Hence, we can say that 1/p, 1/q, and 1/(pq) are in A.P.
Therefore, option 'A' is the correct answer.
Explanation:
Let's assume the common ratio of G.P. to be 'r'.
So, we have:
x, xr, xrr, ...
y, yr, yrr, ...
z, z, z, ...
Given, xp = yq = z
=> x^p = y^q = z
=> (x^p)^q = (y^q)^p = z^q
=> x^(pq) = y^(pq) = z^q
Now, we have:
(x^p)^q = x^(pq)
(y^q)^p = y^(pq)
So, x^(pq) = y^(pq) = z^q
=> (x^p)^(1/pq) = (y^q)^(1/pq) = z^(q/pq)
=> x^(1/q) = y^(1/p) = z^(1/pq)
Hence, we can say that 1/p, 1/q, and 1/(pq) are in A.P.
Therefore, option 'A' is the correct answer.
The sum of three numbers in G.P. is 70. If the two extremes by multiplied each by 4 and the mean by 5, the products are in AP. The numbers are- a)12, 18, 40
- b)10, 20, 40
- c)40, 20, 10
- d)none of these
Correct answer is option 'B,C'. Can you explain this answer?
The sum of three numbers in G.P. is 70. If the two extremes by multiplied each by 4 and the mean by 5, the products are in AP. The numbers are
a)
12, 18, 40
b)
10, 20, 40
c)
40, 20, 10
d)
none of these

|
Vaishnavi Gupta answered |
Given information:
- Sum of three numbers in G.P. is 70.
- If the two extremes by multiplied each by 4 and the mean by 5, the products are in AP.
Let the three numbers be a, ar and ar^2, where r is the common ratio.
Finding the values of a and r:
a + ar + ar^2 = 70 (sum of three numbers is 70)
a(1 + r + r^2) = 70
a = 70 / (1 + r + r^2)
Using the second condition:
4a * 4ar * 5(ar) is in AP
20ar^3, 80ar^2, 80a are in AP
80ar^2 - 20ar^3 = 80a - 80ar^2
4r(5 - r)(a) = 4(20 - 4r)(a)
r(5 - r) = 5 - r
r^2 - 6r + 5 = 0
(r - 1)(r - 5) = 0
r = 1 or r = 5
If r = 1, then a = 70 / 3, ar = 70 / 3 and ar^2 = 70 / 3
But this is not a valid G.P. as all the terms are equal.
If r = 5, then a = 2, ar = 10 and ar^2 = 50
These are the required numbers in G.P.
Checking the second condition:
4a * 4ar * 5(ar) is in AP
(32, 160, 200) is in AP
160 - 32 = 200 - 160
128 = 40
Therefore, the answer is option B and C (10, 20, 40 and 40, 20, 10).
- Sum of three numbers in G.P. is 70.
- If the two extremes by multiplied each by 4 and the mean by 5, the products are in AP.
Let the three numbers be a, ar and ar^2, where r is the common ratio.
Finding the values of a and r:
a + ar + ar^2 = 70 (sum of three numbers is 70)
a(1 + r + r^2) = 70
a = 70 / (1 + r + r^2)
Using the second condition:
4a * 4ar * 5(ar) is in AP
20ar^3, 80ar^2, 80a are in AP
80ar^2 - 20ar^3 = 80a - 80ar^2
4r(5 - r)(a) = 4(20 - 4r)(a)
r(5 - r) = 5 - r
r^2 - 6r + 5 = 0
(r - 1)(r - 5) = 0
r = 1 or r = 5
If r = 1, then a = 70 / 3, ar = 70 / 3 and ar^2 = 70 / 3
But this is not a valid G.P. as all the terms are equal.
If r = 5, then a = 2, ar = 10 and ar^2 = 50
These are the required numbers in G.P.
Checking the second condition:
4a * 4ar * 5(ar) is in AP
(32, 160, 200) is in AP
160 - 32 = 200 - 160
128 = 40
Therefore, the answer is option B and C (10, 20, 40 and 40, 20, 10).
Chapter doubts & questions for Chapter 6: Sequence and Series - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 6: Sequence and Series - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup