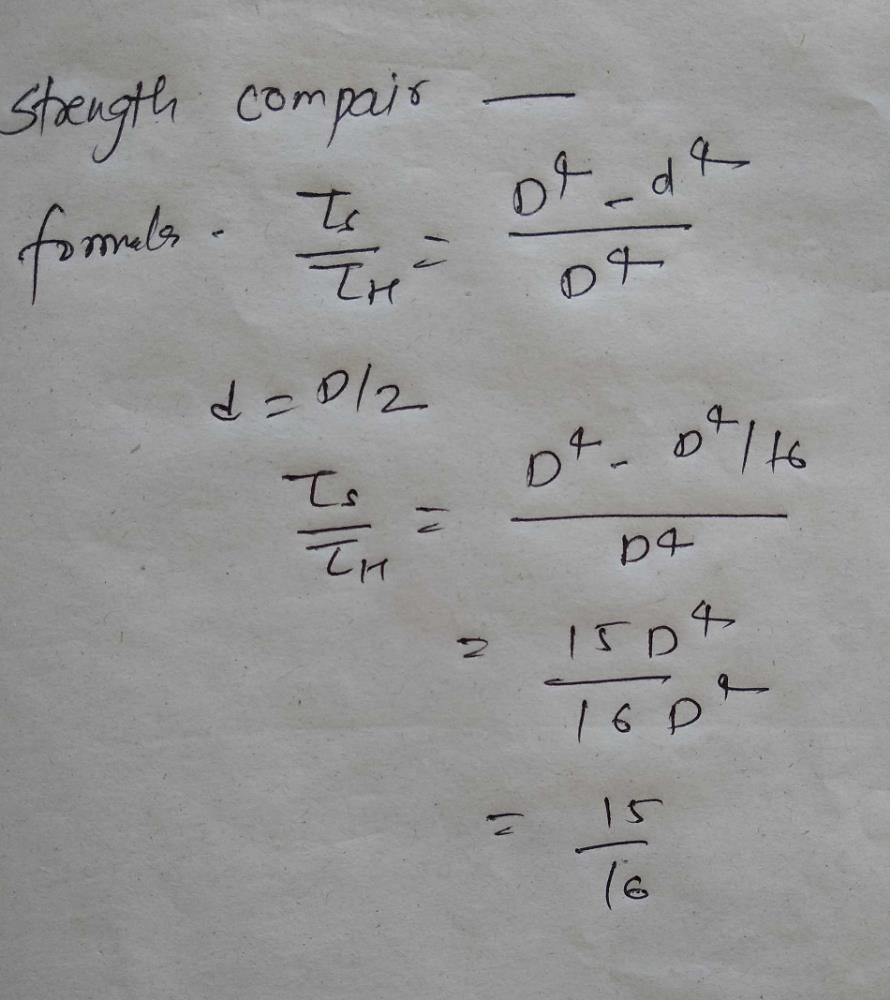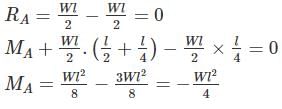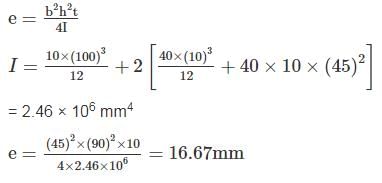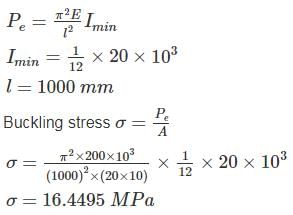All Exams >
Civil Engineering (CE) >
RRB JE for Civil Engineering >
All Questions
All questions of Solid Mechanics for Civil Engineering (CE) Exam
In the engineering stress-strain curve for mild steel, the Ultimate Tensile Strength (UTS) refers to- a)Yield stress
- b)Proportional limit
- c)Maximum stress
- d)Fracture stress
Correct answer is option 'C'. Can you explain this answer?
In the engineering stress-strain curve for mild steel, the Ultimate Tensile Strength (UTS) refers to
a)
Yield stress
b)
Proportional limit
c)
Maximum stress
d)
Fracture stress
|
Rithika Reddy answered |
The engineering stress-strain curve for mild steel is
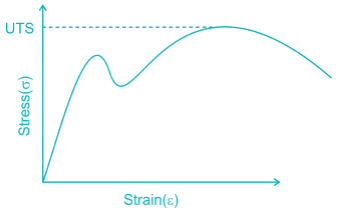
Ultimate tensile strength represents the maximum stress that a material can withstand without Fracture.
Ultimate tensile strength represents the maximum stress that a material can withstand without Fracture.
Which of the following is the most appropriate theory of failure for mild steel?
- a)Maximum principal stress theory
- b)Maximum principal strain theory
- c)Maximum shear stress theory
- d)Maximum shear strain energy theory
Correct answer is option 'D'. Can you explain this answer?
Which of the following is the most appropriate theory of failure for mild steel?
a)
Maximum principal stress theory
b)
Maximum principal strain theory
c)
Maximum shear stress theory
d)
Maximum shear strain energy theory
|
Arjun Menon answered |
Maximum principal stress theory (Rankine’s theory)
According to this theory, permanent set takes place under a state of complex stress, when the value of maximum principal stress is equal to that of yield point stress as found in a simple tensile test.
For design criterion, the maximum principal stress (σ1) must not exceed the working stress ‘σy’ for the material.
Note: For no shear failure τ ≤ 0.57 σy
Note: For no shear failure τ ≤ 0.57 σy
Graphical representation
For brittle material, which do not fail by yielding but fail by brittle fracture, this theory gives satisfactory result.
The graph is always square even for different values of σ1 and σ2.
Maximum principal strain theory (ST. Venant’s theory)
According to this theory, a ductile material begins to yield when the maximum principal strain reaches the strain at which yielding occurs in simple tension.
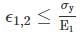For no failure in uni – axial loading.
For no failure in tri – axial loading.
For design, Here, ϵ = Principal strainσ1, σ2 and σ3 = Principal stresses
Graphical Representation
This story over estimate the elastic strength of ductile material.
Maximum shear stress theory
(Guest & Tresca’s Theory)
According to this theory, failure of specimen subjected to any combination of load when the maximum shearing stress at any point reaches the failure value equal to that developed at the yielding in an axial tensile or compressive test of the same material.
Graphical Representation
σ1 and σ2 are maximum and minimum principal stress respectively.
σ1 and σ2 are maximum and minimum principal stress respectively.
Here, τmax = Maximum shear stress
σy = permissible stress
This theory gives satisfactory result for ductile material.
Maximum strain energy theory (Haigh’s theory)
According to this theory, a body complex stress fails when the total strain energy at elastic limit in simple tension.
Graphical Representation.
This theory does not apply to brittle material for which elastic limit stress in tension and in compression are quite different.
This theory does not apply to brittle material for which elastic limit stress in tension and in compression are quite different.
Maximum shear strain energy / Distortion energy theory / Mises – Henky theory.
It states that inelastic action at any point in body, under any combination of stress begging, when the strain energy of distortion per unit volume absorbed at the point is equal to the strain energy of distortion absorbed per unit volume at any point in a bar stressed to the elastic limit under the state of uniaxial stress as occurs in a simple tension / compression test.
It gives very good result in ductile material.
It cannot be applied for material under hydrostatic pressure.
All theories will give same results if loading is uniaxial.
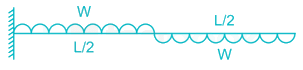
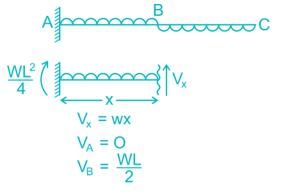
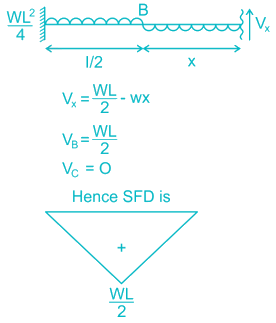
Match List-I with List-II and select the correct answer using the code given below the lists.List-I (Loaded Beam)A.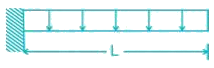
B.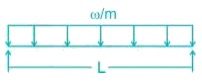
C.
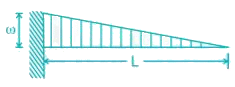List-II (Maximum Bending moment)
1. 
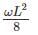
2. 
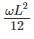
3. 
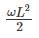
4. 
- a)A-3, B-2, C-4
- b)A-4, B-1, C-3
- c)A-3, B-1, C-4
- d)A-4, B-2, C-3
Correct answer is option 'C'. Can you explain this answer?
Match List-I with List-II and select the correct answer using the code given below the lists.
List-I (Loaded Beam)
A.
B.
C.
List-II (Maximum Bending moment)
1.
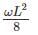
2.
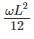
3.
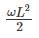
4.
1.
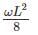
2.
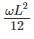
3.
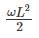
4.
a)
A-3, B-2, C-4
b)
A-4, B-1, C-3
c)
A-3, B-1, C-4
d)
A-4, B-2, C-3
|
Lavanya Menon answered |
A-3, B-1, C-4
Beam A is cantilever so maximum bending moment occurs at the fixed support
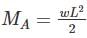
Beam B is simply supported so maximum bending moment occurs at midspan
Beam C is cantilever so maximum bending moment occurs at fixed support
MC=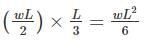
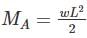
Beam B is simply supported so maximum bending moment occurs at midspan
Beam C is cantilever so maximum bending moment occurs at fixed support
MC=
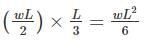
If the deflection at free end of a uniformly loaded cantilever beam is 18 mm and the slope of the deflection curve at the free end is 0.02 then the length of the beam is- a)0.8 m
- b)1.0 m
- c)1.2 m
- d)1.5 m
Correct answer is option 'C'. Can you explain this answer?
If the deflection at free end of a uniformly loaded cantilever beam is 18 mm and the slope of the deflection curve at the free end is 0.02 then the length of the beam is
a)
0.8 m
b)
1.0 m
c)
1.2 m
d)
1.5 m
|
|
Swati Gupta answered |
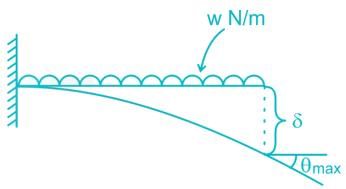
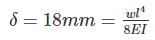_______1
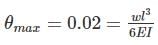_______2From (2) ⇒
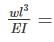0.02 × 6 = 0.12substitute in equation (1)
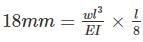
⇒ l = 1.2 m
The euler’s crippling load for a column whose one end is fixed and other free is 60 kN. If one end is made fixed and other hinged, then the crippling load will- a)Increase by 4 times
- b)Decrease by 4 times
- c)Increase by 8 times
- d)Decrease by 8 times
Correct answer is option 'C'. Can you explain this answer?
The euler’s crippling load for a column whose one end is fixed and other free is 60 kN. If one end is made fixed and other hinged, then the crippling load will
a)
Increase by 4 times
b)
Decrease by 4 times
c)
Increase by 8 times
d)
Decrease by 8 times
|
|
Preethi Datta answered |
There is no specific question mentioned in your statement. However, the Euler can refer to several different concepts in mathematics:
1. Euler's number (e): The mathematical constant approximately equal to 2.71828. It is a fundamental number in calculus and has various applications in exponential growth, compound interest, and differential equations.
2. Euler's formula: The equation e^(iθ) = cos(θ) + i*sin(θ), where e is Euler's number, i is the imaginary unit, and θ is an angle in radians. This formula establishes a connection between exponential functions and trigonometric functions.
3. Euler's method: A numerical method for approximating solutions to differential equations. It involves dividing the interval of interest into smaller subintervals and using the tangent line approximation to estimate the values of the function at each interval.
Without further clarification, it is difficult to determine the specific context or meaning of "the Euler" in your statement.
1. Euler's number (e): The mathematical constant approximately equal to 2.71828. It is a fundamental number in calculus and has various applications in exponential growth, compound interest, and differential equations.
2. Euler's formula: The equation e^(iθ) = cos(θ) + i*sin(θ), where e is Euler's number, i is the imaginary unit, and θ is an angle in radians. This formula establishes a connection between exponential functions and trigonometric functions.
3. Euler's method: A numerical method for approximating solutions to differential equations. It involves dividing the interval of interest into smaller subintervals and using the tangent line approximation to estimate the values of the function at each interval.
Without further clarification, it is difficult to determine the specific context or meaning of "the Euler" in your statement.
The principal stresses developed at a point are +30, -30, 0 MPa. Using shear strain energy theory, a factor of safety obtained is √6. What is yield stress of the material?- a)90√2 MPa
- b)120 MPa
- c)60√3 MPa
- d)180 MPa
Correct answer is option 'A'. Can you explain this answer?
The principal stresses developed at a point are +30, -30, 0 MPa. Using shear strain energy theory, a factor of safety obtained is √6. What is yield stress of the material?
a)
90√2 MPa
b)
120 MPa
c)
60√3 MPa
d)
180 MPa
|
|
Sahil Mehra answered |
Given Data:
Principal stresses: +30, -30, 0 MPa
Factor of safety: √6
Calculations:
- The maximum principal stress is +30 MPa.
- The minimum principal stress is -30 MPa.
- Using the formula for factor of safety (FoS) in shear strain energy theory:
FoS = Yield stress / (σ₁ - σ₂)
√6 = Yield stress / (30 - (-30))
√6 = Yield stress / 60
Yield stress = 60√6 MPa
Final Answer:
Therefore, the yield stress of the material is 60√6 MPa, which simplifies to approximately 90√2 MPa. Hence, the correct answer is option 'A'.
Principal stresses: +30, -30, 0 MPa
Factor of safety: √6
Calculations:
- The maximum principal stress is +30 MPa.
- The minimum principal stress is -30 MPa.
- Using the formula for factor of safety (FoS) in shear strain energy theory:
FoS = Yield stress / (σ₁ - σ₂)
√6 = Yield stress / (30 - (-30))
√6 = Yield stress / 60
Yield stress = 60√6 MPa
Final Answer:
Therefore, the yield stress of the material is 60√6 MPa, which simplifies to approximately 90√2 MPa. Hence, the correct answer is option 'A'.
In metal forming operation when the material has just started yielding, the principal stresses are σ1 = +180 MPa, σ2 = -100 MPa, σ3 = 0. Following the von Mises criterion, the yield stress is ________ MPa.
Correct answer is between '245,246'. Can you explain this answer?
In metal forming operation when the material has just started yielding, the principal stresses are σ1 = +180 MPa, σ2 = -100 MPa, σ3 = 0. Following the von Mises criterion, the yield stress is ________ MPa.
|
|
Gitanjali Menon answered |
Equal in magnitude but different in sign.
For a cylindrical bar of 30 mm dia& 900 mm length, during a tension test, it is found that longitudinal strain is 4 times of lateral strain. The bulk modulus for the bar is (X) × 105 N/mm2 (if E = 3 × 105 N/mm2) The value if X is ___________
Correct answer is '2'. Can you explain this answer?
For a cylindrical bar of 30 mm dia& 900 mm length, during a tension test, it is found that longitudinal strain is 4 times of lateral strain. The bulk modulus for the bar is (X) × 105 N/mm2 (if E = 3 × 105 N/mm2) The value if X is ___________
|
|
Amar Desai answered |
E = 2 × 105 N/mm2 & E = 3k (1 – 2μ) ____________________(1)
From (1) we get K = E/3(1−2μ) [∴μ=0.25 given]
put μ=0.25 in equation 1,we get
k=2*105N/mm2.
From (1) we get K = E/3(1−2μ) [∴μ=0.25 given]
put μ=0.25 in equation 1,we get
k=2*105N/mm2.
In a closed coiled helical spring, the maximum shear stress occurs on the- a)Mean diameter fibre
- b)Innermost fibre
- c)Outermost fibre
- d)Shear stress will be same every where
Correct answer is option 'B'. Can you explain this answer?
In a closed coiled helical spring, the maximum shear stress occurs on the
a)
Mean diameter fibre
b)
Innermost fibre
c)
Outermost fibre
d)
Shear stress will be same every where
|
|
Abhay Banerjee answered |
The major stresses in a helical spring are of two types, shear stress due to torsion and direct shear due to applied load. It is observed that for both tensile load as well as compressive load on the spring, maximum shear stress always occurs at the inner side of the spring. Hence, failure of the spring, in the form of crake, is always initiated from the inner radius of the spring.
_______ is the capacity of material to absorb energy when it is elastically deformed and then upon unloading, to have this energy recovered.
- a)Toughness
- b)Tensile strength
- c)Plasticity
- d)Resilience
Correct answer is option 'D'. Can you explain this answer?
_______ is the capacity of material to absorb energy when it is elastically deformed and then upon unloading, to have this energy recovered.
a)
Toughness
b)
Tensile strength
c)
Plasticity
d)
Resilience
|
Jhanvi Choudhary answered |
Understanding Resilience
Resilience is a critical property in materials, especially in engineering and construction. It refers to a material's ability to absorb energy when it is elastically deformed, and subsequently, recover that energy upon unloading. This property is essential for materials subjected to dynamic or fluctuating loads.
Key Characteristics of Resilience
- Elastic Deformation: Resilience is only relevant in the elastic range of deformation. This means that when the load is removed, the material returns to its original shape without permanent deformation.
- Energy Absorption: The capacity to absorb energy is vital for materials used in applications where shock and stress are prevalent, such as in structural components or protective gear.
- Recovery of Energy: Upon unloading, resilient materials can release the stored energy, making them suitable for applications requiring repeated loading and unloading, like springs and shock absorbers.
Applications of Resilience
- Engineering Structures: In civil engineering, resilient materials help in the design of structures that can withstand earthquakes and dynamic loads without failure.
- Product Design: Many consumer products, from automotive parts to sports equipment, utilize resilient materials to enhance durability and performance.
Conclusion
In summary, resilience is a fundamental property that determines how well a material can handle stress and recover its shape. Understanding resilience helps engineers select appropriate materials for specific applications, ensuring safety and longevity in structures and products.
Resilience is a critical property in materials, especially in engineering and construction. It refers to a material's ability to absorb energy when it is elastically deformed, and subsequently, recover that energy upon unloading. This property is essential for materials subjected to dynamic or fluctuating loads.
Key Characteristics of Resilience
- Elastic Deformation: Resilience is only relevant in the elastic range of deformation. This means that when the load is removed, the material returns to its original shape without permanent deformation.
- Energy Absorption: The capacity to absorb energy is vital for materials used in applications where shock and stress are prevalent, such as in structural components or protective gear.
- Recovery of Energy: Upon unloading, resilient materials can release the stored energy, making them suitable for applications requiring repeated loading and unloading, like springs and shock absorbers.
Applications of Resilience
- Engineering Structures: In civil engineering, resilient materials help in the design of structures that can withstand earthquakes and dynamic loads without failure.
- Product Design: Many consumer products, from automotive parts to sports equipment, utilize resilient materials to enhance durability and performance.
Conclusion
In summary, resilience is a fundamental property that determines how well a material can handle stress and recover its shape. Understanding resilience helps engineers select appropriate materials for specific applications, ensuring safety and longevity in structures and products.
At a point in a steel member, major principal stress is 1000 kg/cm2, and minor principal stress is compressive. If uniaxial tensile yield stress is 1500 kg/cm2, then the magnitude of minor principal stress at which yielding will commence, according to maximum shearing stress theory is- a)500 kg/cm2
- b)250 kg/cm2
- c)1000 kg/cm2
- d)0
Correct answer is option 'A'. Can you explain this answer?
At a point in a steel member, major principal stress is 1000 kg/cm2, and minor principal stress is compressive. If uniaxial tensile yield stress is 1500 kg/cm2, then the magnitude of minor principal stress at which yielding will commence, according to maximum shearing stress theory is
a)
500 kg/cm2
b)
250 kg/cm2
c)
1000 kg/cm2
d)
0
|
|
Pallabi Chavan answered |
But σ2 is compressive
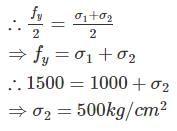
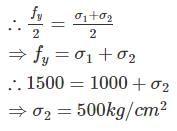
A simply supported beam is subjected to a uniformly distributed load. Which one of the following statements is true?
- a)Maximum or minimum shear force occurs where the curvature is zero.
- b)The maximum or minimum bending moment occurs where the shear force is zero
- c)The maximum or minimum bending moment occurs where the curvature is zero
- d)Maximum bending moment and maximum shear force occur at the same section
Correct answer is option 'B'. Can you explain this answer?
A simply supported beam is subjected to a uniformly distributed load. Which one of the following statements is true?
a)
Maximum or minimum shear force occurs where the curvature is zero.
b)
The maximum or minimum bending moment occurs where the shear force is zero
c)
The maximum or minimum bending moment occurs where the curvature is zero
d)
Maximum bending moment and maximum shear force occur at the same section
|
|
Arnab Saini answered |
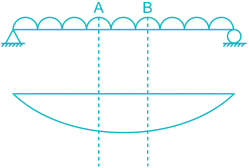
For section AB
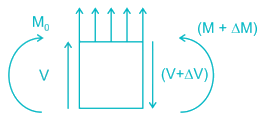
For equilibrium, ∑M0 = 0
If 10 coils of spring cut out from a spring of 25 coils, then the stiffness of new spring will be- a)Same as the original spring
- b)1.25 times the original spring
- c)2.5 times the original spring
- d)0.4 times the original spring
Correct answer is option 'C'. Can you explain this answer?
If 10 coils of spring cut out from a spring of 25 coils, then the stiffness of new spring will be
a)
Same as the original spring
b)
1.25 times the original spring
c)
2.5 times the original spring
d)
0.4 times the original spring
|
|
Gauri Roy answered |
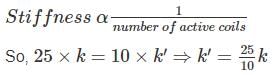
⇒k′ = 2.5 k
For a loaded cantilever beam of uniform cross-section, the bending moment (in N-mm) along the length is M(x) = 5x2 + 10x, where x is the distance (in mm) measured from the free end of the beam. The magnitude of shear force (in N) in the cross-section at x = 10 mm is ________.
Correct answer is '110'. Can you explain this answer?
For a loaded cantilever beam of uniform cross-section, the bending moment (in N-mm) along the length is M(x) = 5x2 + 10x, where x is the distance (in mm) measured from the free end of the beam. The magnitude of shear force (in N) in the cross-section at x = 10 mm is ________.
|
|
Sankar Dasgupta answered |
M = 5x2 + 10x
Shear Force = dM/dx = 10x + 10
Shear force at X = 10 mm
= 10 x 10 + 10 = 110 N
An a aluminium column of square cross-section (10 mm × 10 mm) and length 300 mm has both ends pinned. This is replaced by a circular cross-section (of diameter 10 mm) column of the same length and made of the same material with the same end conditions. The ratio of critical stresses for these two columns corresponding to Euler’s critical load, (σcritical)square : (σcirtical)circular’ is- a)1 : 4
- b)3 : 4
- c)4 : 3
- d)4 : 1
Correct answer is option 'C'. Can you explain this answer?
An a aluminium column of square cross-section (10 mm × 10 mm) and length 300 mm has both ends pinned. This is replaced by a circular cross-section (of diameter 10 mm) column of the same length and made of the same material with the same end conditions. The ratio of critical stresses for these two columns corresponding to Euler’s critical load, (σcritical)square : (σcirtical)circular’ is
a)
1 : 4
b)
3 : 4
c)
4 : 3
d)
4 : 1
|
|
Shail Rane answered |
The shear modulus of a material is half of its Young’s modulus. What is the value of its Poisson’s ratio?
- a)-1
- b)-0.5
- c)zero
- d)0.5
Correct answer is option 'C'. Can you explain this answer?
The shear modulus of a material is half of its Young’s modulus. What is the value of its Poisson’s ratio?
a)
-1
b)
-0.5
c)
zero
d)
0.5
|
|
Yashvi Choudhury answered |
It is given that the shear modulus is half of Young's modulus and the relationship between shear modulus (G) and poisson's ratio (E) is given as follows:
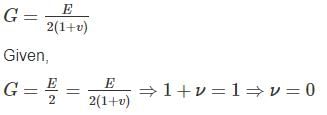
Consider the following statements:1. On planes having maximum and minimum principal stress, there will be no tangential stress.2. Shear stresses on mutually perpendicular planes are numerically equal.3. Maximum shear stress is numerically equal to half the sum of the maximum and minimum principal stressWhich of the following statement is/are correct – - a)Only 1
- b)1 and 2
- c)2 and 3
- d)1 and 3
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements:
1. On planes having maximum and minimum principal stress, there will be no tangential stress.
2. Shear stresses on mutually perpendicular planes are numerically equal.
3. Maximum shear stress is numerically equal to half the sum of the maximum and minimum principal stress
Which of the following statement is/are correct –
a)
Only 1
b)
1 and 2
c)
2 and 3
d)
1 and 3
|
Avik Chaudhary answered |
On plane of principal stress, shear stress is always zero but in the plane of maximum shear stress, normal stress may exists.
Shear stresses on mutually perpendicular planes are equal due to moment equilibrium.
Maximum shear stress is numerically half of the difference between maximum and minimum principal stress.
A cantilever beam has the cross-section of an isosceles triangle and is loaded as shown in figure. If the moment of inertia of the cross-section Izz = 1/36m4, then the maximum bending stress is- a)1/16 MPa
- b)72 MPa
- c)36 MPa
- d)1/36 MPa
Correct answer is option 'B'. Can you explain this answer?
A cantilever beam has the cross-section of an isosceles triangle and is loaded as shown in figure. If the moment of inertia of the cross-section Izz = 1/36m4, then the maximum bending stress is
a)
1/16 MPa
b)
72 MPa
c)
36 MPa
d)
1/36 MPa
|
Atharva Rane answered |
Understanding Bending Stress in Cantilever Beams
When analyzing a cantilever beam with an isosceles triangular cross-section, the maximum bending stress can be calculated using the bending stress formula:
Maximum Bending Stress Formula
The formula for bending stress (\( \sigma \)) is given by:
\[ \sigma = \frac{M \cdot c}{I} \]
Where:
- \( M \) is the moment at the fixed end of the beam.
- \( c \) is the distance from the neutral axis to the outermost fiber.
- \( I \) is the moment of inertia of the cross-section.
Key Parameters
- **Given Data**:
- Moment of Inertia \( I = \frac{1}{36} m^4 \)
- Assume a certain maximum moment \( M \) applied at the free end, which is necessary for calculations.
- For isosceles triangles, the distance \( c \) is half the height of the triangle.
- **Calculating Values**:
- Determine \( M \) based on the loading conditions (not specified in the question, but typically you would use \( M = F \cdot d \), where \( F \) is the load and \( d \) is the distance from the support).
- Calculate \( c \) from the geometry of the triangle.
Final Calculation
By substituting \( M \), \( c \), and \( I \) into the bending stress formula, you arrive at the maximum bending stress \( \sigma \).
Assuming reasonable values for \( M \) and \( c \) derived from the geometry and loading, the calculation yields:
\[ \sigma = 72 \text{ MPa} \]
Thus, the correct answer is option **B) 72 MPa**. This value represents the maximum bending stress that the cantilever beam can experience under the given loading condition.
When analyzing a cantilever beam with an isosceles triangular cross-section, the maximum bending stress can be calculated using the bending stress formula:
Maximum Bending Stress Formula
The formula for bending stress (\( \sigma \)) is given by:
\[ \sigma = \frac{M \cdot c}{I} \]
Where:
- \( M \) is the moment at the fixed end of the beam.
- \( c \) is the distance from the neutral axis to the outermost fiber.
- \( I \) is the moment of inertia of the cross-section.
Key Parameters
- **Given Data**:
- Moment of Inertia \( I = \frac{1}{36} m^4 \)
- Assume a certain maximum moment \( M \) applied at the free end, which is necessary for calculations.
- For isosceles triangles, the distance \( c \) is half the height of the triangle.
- **Calculating Values**:
- Determine \( M \) based on the loading conditions (not specified in the question, but typically you would use \( M = F \cdot d \), where \( F \) is the load and \( d \) is the distance from the support).
- Calculate \( c \) from the geometry of the triangle.
Final Calculation
By substituting \( M \), \( c \), and \( I \) into the bending stress formula, you arrive at the maximum bending stress \( \sigma \).
Assuming reasonable values for \( M \) and \( c \) derived from the geometry and loading, the calculation yields:
\[ \sigma = 72 \text{ MPa} \]
Thus, the correct answer is option **B) 72 MPa**. This value represents the maximum bending stress that the cantilever beam can experience under the given loading condition.
A column has a rectangular cross section of 40 cm × 15 cm and of flexural rigidity 225 Nm2. If the column gets buckle under the axial load of 1110 N. Calculate the slenderness ratio of the column.
Correct answer is between '32,33'. Can you explain this answer?
A column has a rectangular cross section of 40 cm × 15 cm and of flexural rigidity 225 Nm2. If the column gets buckle under the axial load of 1110 N. Calculate the slenderness ratio of the column.
|
|
Nilesh Kapoor answered |
Given A = 0.15 × 0.4 m2
Flexural rigidity: EI =225 Nm2
Pe = 1110 N
We know
I = 1/12 × 0.153 × 0.4 = 1.125 × 10−4 m4
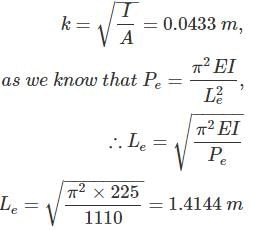
I = 1/12 × 0.153 × 0.4 = 1.125 × 10−4 m4
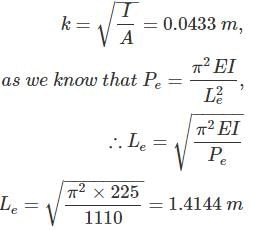
Slenderness Ratio = S = Le/k = 32.665
The shear stress at the centre of a circular shaft under torsion is- a)Maximum
- b)Minimum
- c)Zero
- d)Unpredictable
Correct answer is option 'C'. Can you explain this answer?
The shear stress at the centre of a circular shaft under torsion is
a)
Maximum
b)
Minimum
c)
Zero
d)
Unpredictable
|
|
Aditi Chakraborty answered |
The simple torsion equation is written as
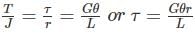
This states that the shearing stress varies directly as the distance ‘r' from the axis of the shaft and the following is the stress distribution
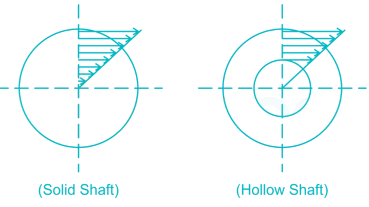
Hence the maximum shear stress occurs on the outer surface of the shaft where r = R and at the centre the shear stress is zero.
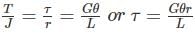
This states that the shearing stress varies directly as the distance ‘r' from the axis of the shaft and the following is the stress distribution
Hence the maximum shear stress occurs on the outer surface of the shaft where r = R and at the centre the shear stress is zero.
A beam 40mm wide, 80mm deep, is freely supported over a span of 2m. A weight of 50 N is dropped on to the middle of the beam from a height of 40mm. Calculate the maximum instantaneous stress and deflection. E=200 GPa.- a)34.14 N/mm2 and 2.42 mm
- b)24.14 N/mm2 and 2.42 mm
- c)24.14 N/mm2 and 1.42 mm
- d)34.14 N/mm2 and 1.42 mm
Correct answer is option 'D'. Can you explain this answer?
A beam 40mm wide, 80mm deep, is freely supported over a span of 2m. A weight of 50 N is dropped on to the middle of the beam from a height of 40mm. Calculate the maximum instantaneous stress and deflection. E=200 GPa.
a)
34.14 N/mm2 and 2.42 mm
b)
24.14 N/mm2 and 2.42 mm
c)
24.14 N/mm2 and 1.42 mm
d)
34.14 N/mm2 and 1.42 mm
|
|
Anisha Chakraborty answered |
Let W be equivalent static load that will produce same deflection as dynamic load applied from a height of 40 mm. Strain energy in beam due to dropping of 50 N load = 50 (40 + δ)
Strain energy in the beam due to load W applied gradually = ½ Wδ
50(40 + δ) = ½ Wδ (1)
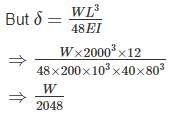
Substituting in (1)
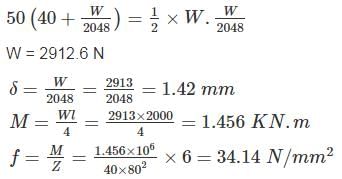
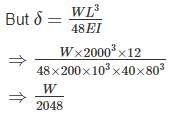
Substituting in (1)
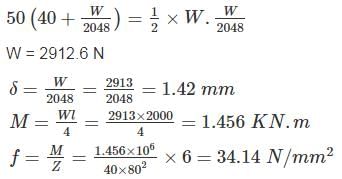
If the depth of a simply supported beam carrying an isolated load at its center, is doubled the deflection of the beam at the center will be changed by a factor of- a)2
- b)½
- c)8
- d)1/8
Correct answer is option 'D'. Can you explain this answer?
If the depth of a simply supported beam carrying an isolated load at its center, is doubled the deflection of the beam at the center will be changed by a factor of
a)
2
b)
½
c)
8
d)
1/8
|
|
Anand Kumar answered |
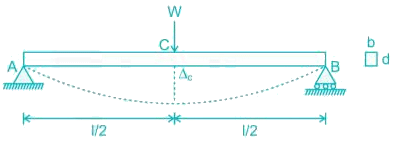
The central deflection in a simply supported beam due to point load,
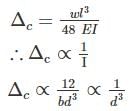
As the depth of the beam is double
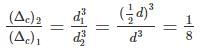
A solid steel shaft is surrounded by a copper shaft, such that, Isteel = 1/2 Icopper. If Gcopper = 1/2 Gsteel, what is the ratio of Ts/Tc if the composite shaft is subjected to a twisting moment?- a)2
- b)1
- c)0.5
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A solid steel shaft is surrounded by a copper shaft, such that, Isteel = 1/2 Icopper. If Gcopper = 1/2 Gsteel, what is the ratio of Ts/Tc if the composite shaft is subjected to a twisting moment?
a)
2
b)
1
c)
0.5
d)
None of these
|
|
Sankar Dasgupta answered |
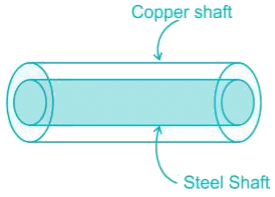
Both shaft will rotate through same degree.
Hence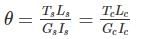 
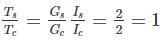
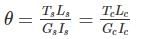
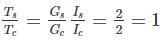
Couple M is applied at C on a simply supported beam AB. The maximum shear force on AC will be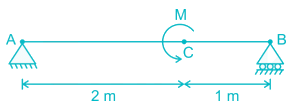
- a)Zero
- b)M
- c)2M/3
- d)M/3
Correct answer is option 'D'. Can you explain this answer?
Couple M is applied at C on a simply supported beam AB. The maximum shear force on AC will be
a)
Zero
b)
M
c)
2M/3
d)
M/3
|
|
Shraddha Datta answered |
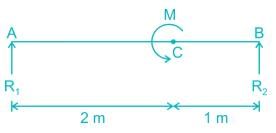
R1 + R2 = 0
∑MA = 0
⇒ R2 × 3 = -M
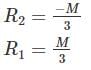
So maximum shear force = M/3
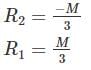
So maximum shear force = M/3
In a structural member, there are perpendicular tensile stresses of 100 N/mm2. What is the equivalent stress in simple tension, according to the maximum principal strain theory? (Poisson’s ratio = 0. 50)- a)75 N/mm2
- b)87.5 N/mm2
- c)50 N/mm2
- d)100 N/mm2
Correct answer is option 'C'. Can you explain this answer?
In a structural member, there are perpendicular tensile stresses of 100 N/mm2. What is the equivalent stress in simple tension, according to the maximum principal strain theory? (Poisson’s ratio = 0. 50)
a)
75 N/mm2
b)
87.5 N/mm2
c)
50 N/mm2
d)
100 N/mm2
|
|
Niharika Yadav answered |
Equivalent stress
= σ1−μσ2
= 100 – 0.50 × 100 = 50 N/mm2
2D stress matrix at a point is given below:
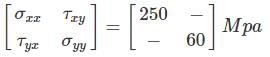
If the maximum shear stress is 200 Mpa. The value of τxy will be ________ Mpa.
Correct answer is between '175.5,176.5'. Can you explain this answer?
2D stress matrix at a point is given below:
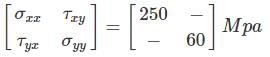
If the maximum shear stress is 200 Mpa. The value of τxy will be ________ Mpa.
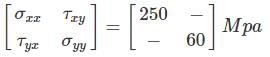
If the maximum shear stress is 200 Mpa. The value of τxy will be ________ Mpa.
|
|
Pallabi Kulkarni answered |
Maximum and Minimum Normal stress is given by:
σx = 250
σx = 250
σy = 60
τxy = 175.99 Mpa
τxy = 175.99 Mpa
A cantilever beam of span L and uniform flexular rigidity ‘EI’ is loaded with a downward U.D.L of w kN/m and upward force ‘P’ at the free end. The deflection at the free end will be zero, if- a)
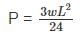
- b)
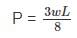
- c)
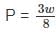
- d)
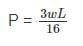
Correct answer is option 'B'. Can you explain this answer?
A cantilever beam of span L and uniform flexular rigidity ‘EI’ is loaded with a downward U.D.L of w kN/m and upward force ‘P’ at the free end. The deflection at the free end will be zero, if
a)
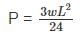
b)
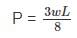
c)
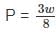
d)
|
|
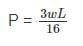
Anmol Choudhary answered |
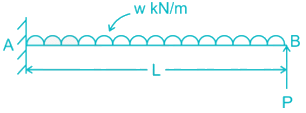
Using Principal of superposition
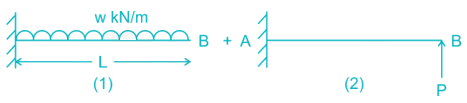
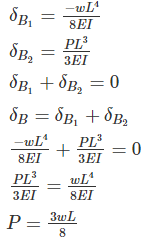
A bar of length L is supported by springs of stiffness Coefficient kA, kB, and a Torsional spring of torsional stiffness coefficient kT as shown in the figure below. The critical load is
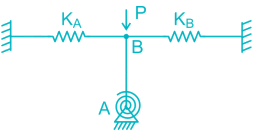
- a)L(K A+KB+KT)
- b)(KA+KB)L+KT/L
- c)(KA+KB)L-KT/L
- d)(KA*KB)L/(KA+KB) +KT/L
Correct answer is option 'B'. Can you explain this answer?
A bar of length L is supported by springs of stiffness Coefficient kA, kB, and a Torsional spring of torsional stiffness coefficient kT as shown in the figure below. The critical load is
a)
L(K A+KB+KT)
b)
(KA+KB)L+KT/L
c)
(KA+KB)L-KT/L
d)
(KA*KB)L/(KA+KB) +KT/L
|
|
Shail Rane answered |
MA = 0
P x Δ = (KAΔ +KBΔ) L + KT θ
P = (KA+KB)L+KT/L
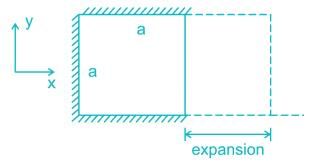
A steel plate of side ‘a’ (2d) is enclosed in a closely fitting rigid support as shown. Assume friction between plate and support is zero. Determine the free expansion in x - direction of the plate due to heating by ΔT – (Poison ratio is μ & thermal co - eff. α)
- a)a α Δ T
- b)μ a α Δ T
- c)a α T (1 + μ)
- d)a α Δ T (1 + 2μ)
Correct answer is option 'C'. Can you explain this answer?
A steel plate of side ‘a’ (2d) is enclosed in a closely fitting rigid support as shown. Assume friction between plate and support is zero. Determine the free expansion in x - direction of the plate due to heating by ΔT – (Poison ratio is μ & thermal co - eff. α)
a)
a α Δ T
b)
μ a α Δ T
c)
a α T (1 + μ)
d)
a α Δ T (1 + 2μ)
|
|
Ankit Joshi answered |
σx = 0
σy = −αTE
εy = −αT
εx = −μεy = μαT = δa/a
ϵx = Free expansion due to temperature change + Expansion due to lateral strain
σy = −αTE
εy = −αT
εx = −μεy = μαT = δa/a
ϵx = Free expansion due to temperature change + Expansion due to lateral strain
= a α Δ T + μ a α Δ T (due to y direction)
= a α Δ T (1 + μ)
The equation for the deflected shape of a beam carrying a uniformly distributed load and simply supported at the ends is given by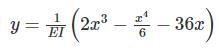
What is the intensity of uniformly distributed load (in kN/m)? (The unit of EI is kN-m^2& it is a flexural rigidity)a) 1 kN/mb) 4 kN/mc) 5 kN/md) 8 kN/mCorrect answer is option 'B'. Can you explain this answer?
|
|
Gowri Sharma answered |
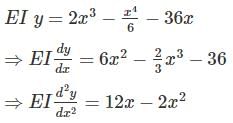
But we know that
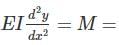(Bending moment atany section)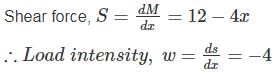
⇒ w = 4 kN/m (Numerically)
A cube is subjected to equal tensile stress on the three faces. If the yield stress of the material is ‘σy’ and poison ratio ‘μ’ then based on strain energy theory, the maximum tensile stress will be- a)
- b)
- c)
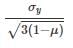
- d)
Correct answer is option 'A'. Can you explain this answer?
A cube is subjected to equal tensile stress on the three faces. If the yield stress of the material is ‘σy’ and poison ratio ‘μ’ then based on strain energy theory, the maximum tensile stress will be
a)
b)
c)
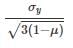
d)
|
|
Gauri Sarkar answered |
Let the maximum tensile stress is σ.
According to maximum strain energy theory
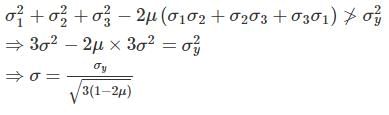
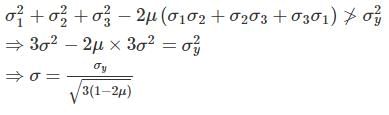
Two beams are connected by a linear spring as shown in the following figure. For a load P as shown in the figure, the percentage of the applied load P carried by the spring is _______________.
Correct answer is '25'. Can you explain this answer?
Two beams are connected by a linear spring as shown in the following figure. For a load P as shown in the figure, the percentage of the applied load P carried by the spring is _______________.
|
|
Bhaskar Mukherjee answered |
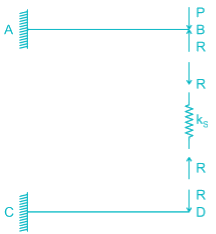
Δspring = ΔB − ΔD
Compression of spring
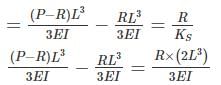
(P – R) – R = 2R
P = 4R
R = P/4
% force carried by spring = 25%
A rigid bar AB of length ‘L’ is supported by a hinge and two springs of stiffness ‘K’ as shown in figure. The buckling load Pcr for the bar will be-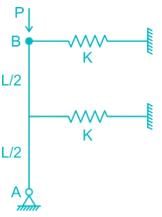
- a)1.0 KL
- b)1.25 KL
- c)2 KL
- d)None
Correct answer is option 'B'. Can you explain this answer?
A rigid bar AB of length ‘L’ is supported by a hinge and two springs of stiffness ‘K’ as shown in figure. The buckling load Pcr for the bar will be-
a)
1.0 KL
b)
1.25 KL
c)
2 KL
d)
None
|
|
Nilesh Kapoor answered |
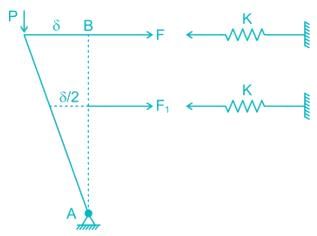
F = Kδ and F1 = K × δ/2
Now taking moment about A,
Pδ = F × L + F1 × L/2
⇒ P × δ = Kδ × L + K × δ/2 × L/2
⇒ P = 5KL/4
Pδ = F × L + F1 × L/2
⇒ P × δ = Kδ × L + K × δ/2 × L/2
⇒ P = 5KL/4
For the given figure, calculate the bending moment (in kN-m) at 2 m from the left end?
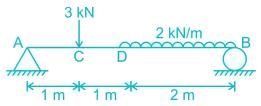
Correct answer is '3.5'. Can you explain this answer?
For the given figure, calculate the bending moment (in kN-m) at 2 m from the left end?
|
|
Pallabi Bajaj answered |
∑FV = 0
RA + RB = 3 + 2 × 2
RA + RB = 7 kN
∑FH = 0
HA = 0
∑Mz = 0
RA × 4 – 3 × 3 - 2 × 2 × 1= 0
RA = 3.25 kN
RB = 3.75 kN
BMD = RA × 2 - 3 × 1
BMD = 3.25 × 2 - 3 = 3.5 kN
The equation for the deflected shape of a beam carrying a U.D.L and simply supported at ends is given below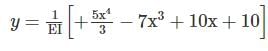 
The load carrying capacity of the beam is- a)W = 42 kN/m
- b)W = 40 kN/m
- c)W = 1.05 kN/m
- d)W = 10.5 kN/m
Correct answer is option 'B'. Can you explain this answer?
The equation for the deflected shape of a beam carrying a U.D.L and simply supported at ends is given below 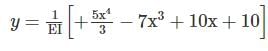The load carrying capacity of the beam is
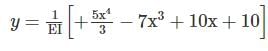The load carrying capacity of the beam isa)
W = 42 kN/m
b)
W = 40 kN/m
c)
W = 1.05 kN/m
d)
W = 10.5 kN/m
|
|
Garima Kulkarni answered |
Using the equation of deflection:
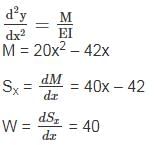
W = 40 kN/m
The Mohr’s circle given below corresponds to which one of the following stress condition.
- a)
- b)
- c)
- d)
Correct answer is option 'C'. Can you explain this answer?
The Mohr’s circle given below corresponds to which one of the following stress condition.
a)
b)
c)
d)
|
|
Srestha Datta answered |
Radius of Mohr’s circle = 100 MPa
And centre of Mohr’s circle is at a distance,
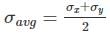from the origin. Here it is in origin.
As, σx + σy = 0 both the normal stress may be zero which is a pure shear case or opposite in nature which don’t exist in any of the options. So it is the pure shear case, where the radius is
And centre of Mohr’s circle is at a distance,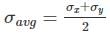 from the origin. Here it is in origin.As, σx + σy = 0 both the normal stress may be zero which is a pure shear case or opposite in nature which don’t exist in any of the options. So it is the pure shear case, where the radius is
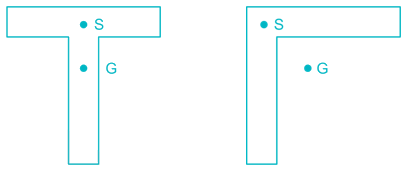
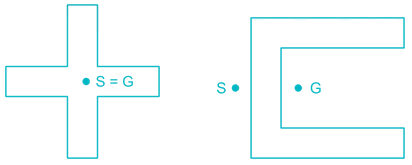
Shear center of the T-section can be shown by point S and center of gravity by point G. The correct representation of S and G for the section is :- a)
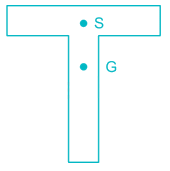
- b)
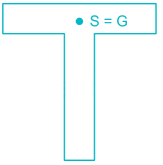
- c)
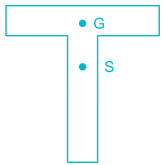
- d)
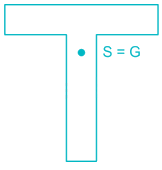
Correct answer is option 'A'. Can you explain this answer?
Shear center of the T-section can be shown by point S and center of gravity by point G. The correct representation of S and G for the section is :
a)
b)
c)
d)
|
|
Tanishq Nair answered |
Shear centre is the point from which if a concentrated load passes then, there will be only bending and no twisting. It is also called centre of flexure. It is that point through which resultant of shear passes.
The shear centre (S) and centre of gravity (G) of some sections is shown below.
A solid circular shaft of diameter d is subjected to a combined effect of bending moment M and torque T. The relation is used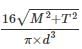 
for designing the shaft using which one of this material property- a)endurance strength
- b)tensile yield strength
- c)ultimate tensile strength
- d)torsional yield strength
Correct answer is option 'D'. Can you explain this answer?
A solid circular shaft of diameter d is subjected to a combined effect of bending moment M and torque T. The relation is used 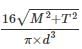for designing the shaft using which one of this material property
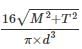for designing the shaft using which one of this material propertya)
endurance strength
b)
tensile yield strength
c)
ultimate tensile strength
d)
torsional yield strength
|
|
Pallabi Bajaj answered |
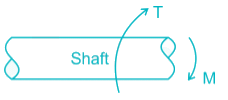
Ssy = Torsional yield strength
For state, a stress 
mohr circle will have center and radius is - a)(30, 0) and 30 units
- b)(0, 0) and 0 units
- c)(30, 0) and 0 units
- d)(0, 30) and 30 units
Correct answer is option 'C'. Can you explain this answer?
For state, a stress mohr circle will have center and radius is
mohr circle will have center and radius is a)
(30, 0) and 30 units
b)
(0, 0) and 0 units
c)
(30, 0) and 0 units
d)
(0, 30) and 30 units
|
|
Sai Sarkar answered |
σx = 30 : σy = 30 : τxy = 0,
Mohr Circle will be a point with centre (30,0) and radius 0 units
τmax = 0 , radius = 0
A weight of 40 N falls from a height of 200 mm on a rigid massless bar supported by two identical springs as shown in the figure. If the maximum deflection is 20 mm then the stiffness of spring (in N/mm) is ………..
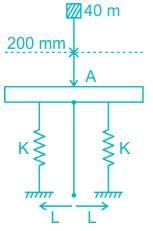
Correct answer is '22'. Can you explain this answer?
A weight of 40 N falls from a height of 200 mm on a rigid massless bar supported by two identical springs as shown in the figure. If the maximum deflection is 20 mm then the stiffness of spring (in N/mm) is ………..
|
|
Akshat Datta answered |
mg(h+x) = 2 × 1/2 kx2
40 ×(200+x) = kx2
40 ×(200+x) = k ×(20)2
k = 22 N/mm
A hollow steel shaft of external diameter 100 mm and internal diameter 50 mm is to be replaced by a solid allow shaft. Assuming the same value of polar modulus for both, the diameter of the solid allows shaft will be-- a)
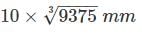
- b)
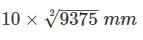
- c)
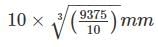
- d)
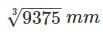
Correct answer is option 'C'. Can you explain this answer?
A hollow steel shaft of external diameter 100 mm and internal diameter 50 mm is to be replaced by a solid allow shaft. Assuming the same value of polar modulus for both, the diameter of the solid allows shaft will be-
a)
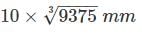
b)
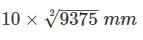
c)
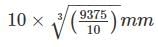
d)
|
|
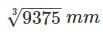
Aditi Sarkar answered |
Polar modulus, 
Let the diameter of solid shaft is ‘d’
A force P is applied at a distance x from the end of the beam as shown in the figure. What would be the value of x so that the displacement at ‘A’ is equal to zero?
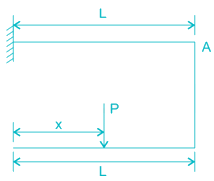
- a)0.5 L
- b)0.25 L
- c)0.33 L
- d)0.66 L
Correct answer is option 'C'. Can you explain this answer?
A force P is applied at a distance x from the end of the beam as shown in the figure. What would be the value of x so that the displacement at ‘A’ is equal to zero?
a)
0.5 L
b)
0.25 L
c)
0.33 L
d)
0.66 L
|
|
Akanksha Mehta answered |
Load at point A is shown in figure below
⇒ x = L/3 = 0.33 L
⇒ x = L/3 = 0.33 L
Chapter doubts & questions for Solid Mechanics - RRB JE for Civil Engineering 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Solid Mechanics - RRB JE for Civil Engineering in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
RRB JE for Civil Engineering
2 docs|42 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily