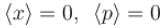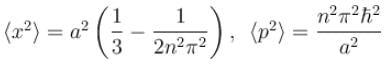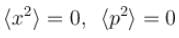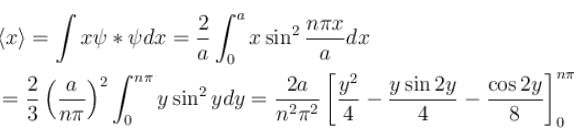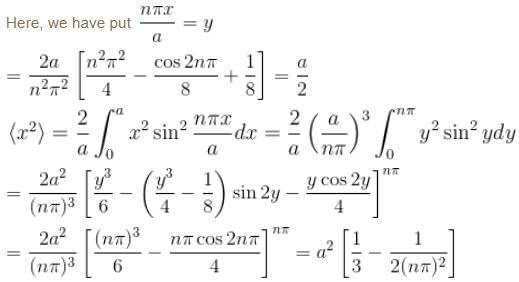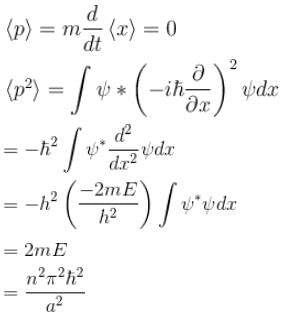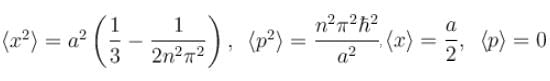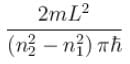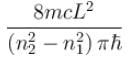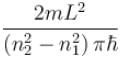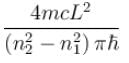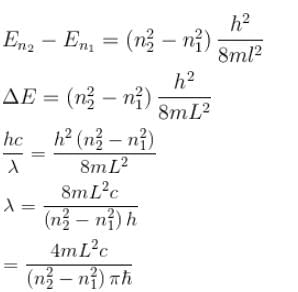All Exams >
Physics >
Topic wise Tests for IIT JAM Physics >
All Questions
All questions of Application of Schrodinger Wave Equation for Physics Exam
The solution to the Schrodinger equation for a particle bound in a one-dimensional, infinitely deep potential well, indexed by a quantum number n, indicates that in the middle of the well, the probability density vanishes for.- a)all states except the ground state
- b)states of even n(n = 2, 4...)
- c)Ground state (n = 1) only.
- d)states of odd n(n = 1, 2, 3...)
Correct answer is option 'B'. Can you explain this answer?
The solution to the Schrodinger equation for a particle bound in a one-dimensional, infinitely deep potential well, indexed by a quantum number n, indicates that in the middle of the well, the probability density vanishes for.
a)
all states except the ground state
b)
states of even n(n = 2, 4...)
c)
Ground state (n = 1) only.
d)
states of odd n(n = 1, 2, 3...)
|
Vedika Singh answered |
For particle in a box
For ψ1(x), probability density does not vanish in the middle
for
for
probability density vanishes in the middle
Similarly, it does not vanish for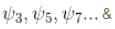 
vanishes for 
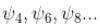in the middle of the well.
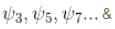vanishes for 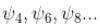in the middle of the well.The correct answer is: states of even n(n = 2, 4...)
For a quantum wave particle, E = _____________ - a)ℏ ω
- b)ℏ k
- c)ℏ ω/2
- d)ℏ k/2
Correct answer is option 'A'. Can you explain this answer?
For a quantum wave particle, E = _____________
a)
ℏ ω
b)
ℏ k
c)
ℏ ω/2
d)
ℏ k/2
|
|
Vedika Singh answered |
The Energy of a wave particle is given as ℏ ω while the momentum of the particle is given as ℏ k. These are the desired relation.
For a particle of mass m, being acted upon by a force with potential energy function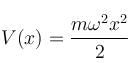 
a one-dimensional simple harmonic oscillator. If there is a wall at x = 0 so that V = ∞ for x < 0, then the energy levels are equal to :- a)
- b)
- c)
- d)
Correct answer is option 'D'. Can you explain this answer?
For a particle of mass m, being acted upon by a force with potential energy function 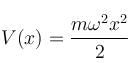a one-dimensional simple harmonic oscillator. If there is a wall at x = 0 so that V = ∞ for x < 0, then the energy levels are equal to :
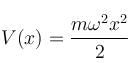a one-dimensional simple harmonic oscillator. If there is a wall at x = 0 so that V = ∞ for x < 0, then the energy levels are equal to :a)
b)
c)
d)
|
Pie Academy answered |
The probability distributions for the quantum states of the oscillator without the barrier.
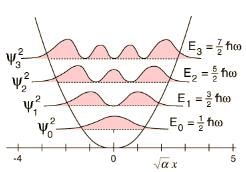
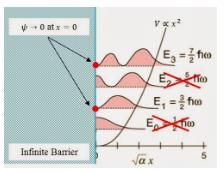
Infinite barrier at the origin means a node at origin, or the wave function goes to zero at x = 0.
By symmetry, the ground state will disappear, as well all the even states. Odd values remain
Consider the solutions to particle in one dimensional box of length, L.
Which of the following is true for the group of functions ψ2(x)- a)They form a complete set
- b)They are mutually orthogonal
- c)As we go up in energy, each successive state has one more node. i.e. ψ1(x) has none, ψ2(x) has one, ψ3(x) has 2 and so on
- d)They are alternately even and odd with respect to the centre of the well
Correct answer is option 'A,B,C,D'. Can you explain this answer?
Consider the solutions to particle in one dimensional box of length, L.
Which of the following is true for the group of functions ψ2(x)
a)
They form a complete set
b)
They are mutually orthogonal
c)
As we go up in energy, each successive state has one more node. i.e. ψ1(x) has none, ψ2(x) has one, ψ3(x) has 2 and so on
d)
They are alternately even and odd with respect to the centre of the well
|
|
Pie Academy answered |
The solution of a symmetric infinite potential well consists of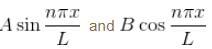 
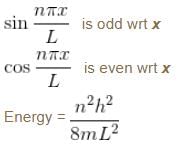
Now, any function can be written as a linear combination of these functions (sin and cos)
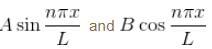
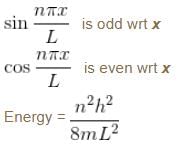
Now, any function can be written as a linear combination of these functions (sin and cos)
∴ They form a complete let
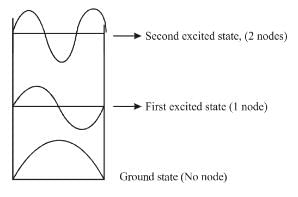
The correct answers are: They are alternately even and odd with respect to the centre of the well, As we go up in energy, each successive state has one more node. i.e. ψ1(x) has none, ψ2(x) has one, ψ3(x) has 2 and so on, They are mutually orthogonal, They form a complete set
For a wave function ψ(x) , its time dependence can be seen from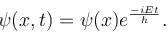 
Select the correct option.- a)Neither of |ψ(x)|2 & |ψ(x, t)2 has any time dependence
- b)If ψ(x) is normalised, then ψ(x, t) has to be normalised
- c)|ψ(x)|2 has no time dependence, |ψ(x, t)|2 is time dependent
- d)If ψ(x) is normalised ψ(x, t) may or may not be normalised
Correct answer is option 'A,B'. Can you explain this answer?
For a wave function ψ(x) , its time dependence can be seen from 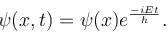Select the correct option.
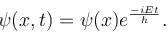Select the correct option.a)
Neither of |ψ(x)|2 & |ψ(x, t)2 has any time dependence
b)
If ψ(x) is normalised, then ψ(x, t) has to be normalised
c)
|ψ(x)|2 has no time dependence, |ψ(x, t)|2 is time dependent
d)
If ψ(x) is normalised ψ(x, t) may or may not be normalised
|
Jayant Mishra answered |
is normalised, so is 
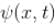& neither of 
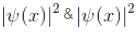has any time dependence.The correct answers are: If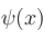 
is normalised, then 
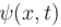has to be normalised, Neither of 
& 
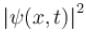has any time dependence
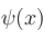is normalised, then 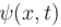has to be normalised, Neither of & 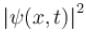has any time dependenceFor a particle in a one dimensional box,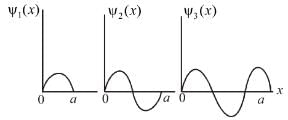
There is zero probability of finding the particle at- a)
- b)x = 0 & x = a for ψ2(x)
- c)x = 0 & x = a/2 & x = a for ψ2(x)
- d)x = 0 & x = a for ψ1(x)
Correct answer is option 'C,D'. Can you explain this answer?
For a particle in a one dimensional box,
There is zero probability of finding the particle at
a)
b)
x = 0 & x = a for ψ2(x)
c)
x = 0 & x = a/2 & x = a for ψ2(x)
d)
x = 0 & x = a for ψ1(x)
|
|
Vedika Singh answered |
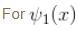
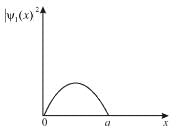
Probability is 0 at x = 0 & a
For
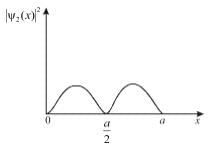
Probability density is zero at x = 0, a/2 , a
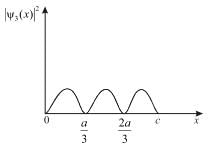
Probability density zero at x = 0,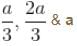 
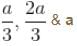
The correct answers are:
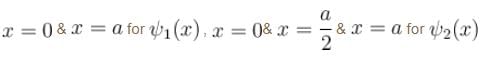
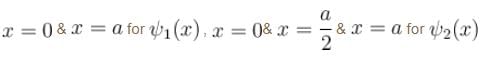
Consider the potential of the form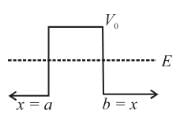
V(x) = 0 for x < a
= V0 for a < x b
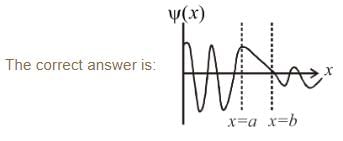
= 0 for x > bWhich of the following wave functions is possible for a particle incident from the left with energy E < V0- a)
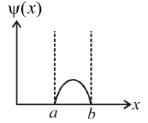
- b)
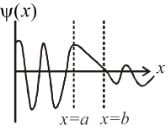
- c)
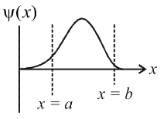
- d)
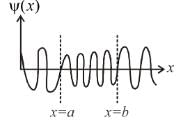
Correct answer is option 'B'. Can you explain this answer?
Consider the potential of the form
V(x) = 0 for x < a
= V0 for a < x b
= 0 for x > b
= V0 for a < x b
= 0 for x > b
Which of the following wave functions is possible for a particle incident from the left with energy E < V0
a)
b)
c)
d)
|
|
Pie Academy answered |
Solving the Schrodinger equation for the region from a to b.
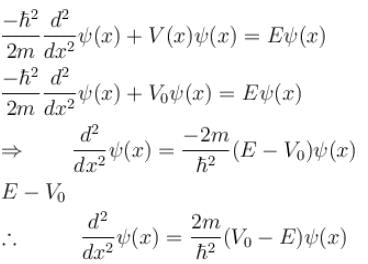
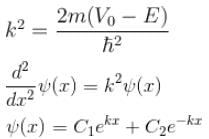
So, in the region from x = a to b, the wave function are in the form of exponential rise/fall.
If the nucleus is seen as a cubical box of length 10–14 m, then compute the minimum energy of a nucleon confined to the nucleus. Mass of nucleon = 1.6 × 10–27 kg - a)10 MeV
- b)6 MeV
- c)10 KeV
- d)6 KeV
Correct answer is option 'B'. Can you explain this answer?
If the nucleus is seen as a cubical box of length 10–14 m, then compute the minimum energy of a nucleon confined to the nucleus. Mass of nucleon = 1.6 × 10–27 kg
a)
10 MeV
b)
6 MeV
c)
10 KeV
d)
6 KeV
|
|
Vedika Singh answered |
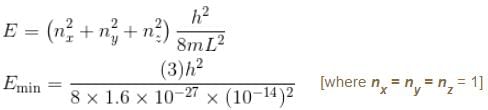
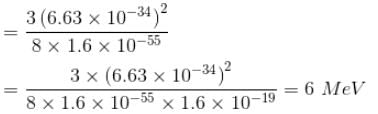
The correct answer is: 6 MeV
Consider two cases of one dimensional potential well. The first case is an infinite potential will V = 0, for a < x < 0 the second case is a finite potential well. Which of the following is true? [for E < V0]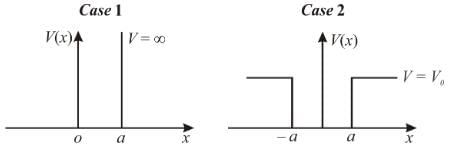
- a)
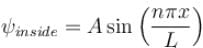for infinite case & 
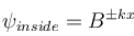for finite case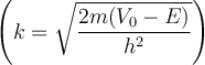 
- b)
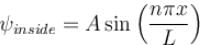for infinite case & 
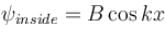for finite case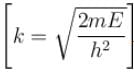 
- c)
for infinite case & 
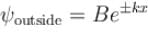for the finite case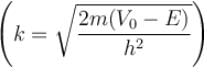 
- d)
for infinite case &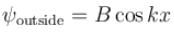 
for the finite case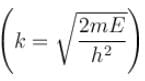 
Correct answer is option 'B,C'. Can you explain this answer?
Consider two cases of one dimensional potential well. The first case is an infinite potential will V = 0, for a < x < 0 the second case is a finite potential well. Which of the following is true? [for E < V0]
a)
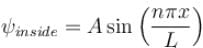for infinite case & 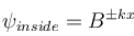for finite case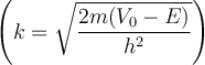 b)
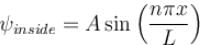for infinite case & 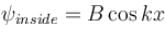for finite case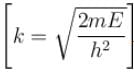 c)
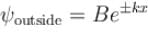for infinite case & for the finite case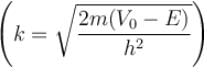 d)
for infinite case & 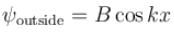for the finite case |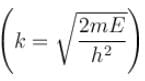
|
Jayant Mishra answered |
The correct answers are: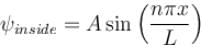 
for infinite case & 
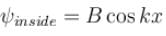for finite case 
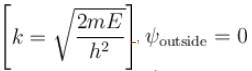for infinite case & 
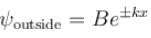for the finite case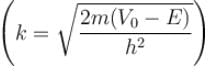 
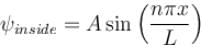for infinite case & 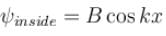for finite case 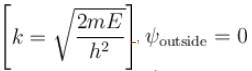for infinite case & 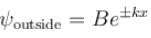for the finite case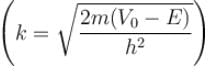 
Which of the following is true in case of a free particle?- a)The Schrodinger equation yields the solution to be
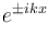(linear combination of the two) - b)The solutions of the Schrodinger equation are both energy and momentum eigenfunctions
- c)The solutions are not momentum eigenfunctions
- d)The solutions are not energy eigenfunction
Correct answer is option 'A,B'. Can you explain this answer?
Which of the following is true in case of a free particle?
a)
The Schrodinger equation yields the solution to be 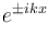(linear combination of the two)
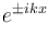(linear combination of the two) b)
The solutions of the Schrodinger equation are both energy and momentum eigenfunctions
c)
The solutions are not momentum eigenfunctions
d)
The solutions are not energy eigenfunction
|
|
Jayant Mishra answered |
The Schrodinger equation solution are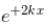 
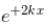
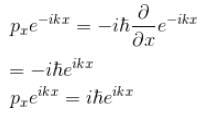
∴ momentum eigenfunction.
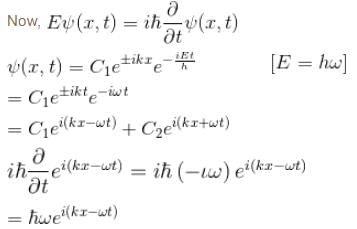
The correct answers are: The Schrodinger equation yields the solution to be 
(linear combination of the two), The solutions of the Schrodinger equation are both energy and momentum eigenfunctions
(linear combination of the two), The solutions of the Schrodinger equation are both energy and momentum eigenfunctionsWhich of the following is true for a quantum harmonic oscillator?- a)A spectrum of evenly spaced energy levels
- b)A non zero probability of finding the oscillator outside the classical turning points
- c)A ground state that is characterized by zero kinetic energy.
- d)A potential energy function that is linear in the position coordinate
Correct answer is option 'A,B'. Can you explain this answer?
Which of the following is true for a quantum harmonic oscillator?
a)
A spectrum of evenly spaced energy levels
b)
A non zero probability of finding the oscillator outside the classical turning points
c)
A ground state that is characterized by zero kinetic energy.
d)
A potential energy function that is linear in the position coordinate
|
|
Jayant Mishra answered |
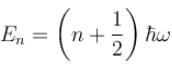for a harmonic oscillator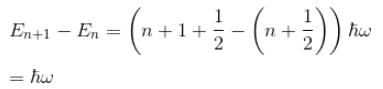
∴ evenly spaced.
The correct answers are: A spectrum of evenly spaced energy levels, A non zero probability of finding the oscillator outside the classical turning points
The Steady-state form of Schrodinger wave equation is _____________
- a)Linear
- b)Quadratic
- c)Differential equation
- d)Derivable
Correct answer is option 'A'. Can you explain this answer?
The Steady-state form of Schrodinger wave equation is _____________
a)
Linear
b)
Quadratic
c)
Differential equation
d)
Derivable
|
|
Vedika Singh answered |
The Steady-state Schrodinger Wave equation is a linear in the wave function Ψ. It means, that no term has \Psi with a degree greater than 1.
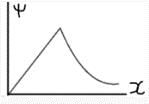
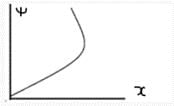
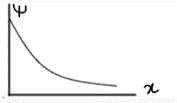
Which of the following can be the solution of Schrondinger's equation?- a)
- b)
- c)
- d)
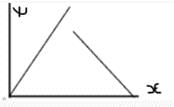
Correct answer is option 'C'. Can you explain this answer?
Which of the following can be the solution of Schrondinger's equation?
a)
b)
c)
d)
|
|
Pie Academy answered |
Concept:
- Schrodinger wave equation is a mathematical expression that describes the energy and position of the electron in space and time, taking into account the matter wave nature of the electron inside an atom.
- It is based on three considerations. They are:
- Classical plane wave equation, (wave which satisfies
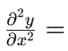
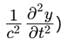
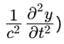
- Broglie’s Hypothesis of matter-wave, (the wavelength of matter-wave is inversely proportional to the linear momentum.)
- Conservation of Energy. (total energy = kinetic + potential)
- Classical plane wave equation, (wave which satisfies
Schrodinger equation gives us a detailed account of the form of the wave functions or probability waves that control the motion of some smaller particles.
The equation also describes how these waves are influenced by external factors.
Moreover, the equation makes use of the energy conservation concept that offers details about the behavior of an electron that is attached to the nucleus.
Explanation:
- For a wave to be a solution of Schrodinger's equation it must satisfy the following conditions:
- The wave function must be a single value.
- The wave function must be continuous.
- The wave function must be finite.
- The wave function must be differentiable at every point in space.
Hence the correct option is 3.
A particle is in the second excited state (n=3) of a one-dimensional infinite potential well of width a. Which of the following is correct for the expectation values of x, x2, and p2?- a)
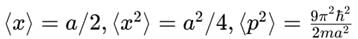
- b)
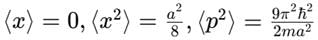
- c)
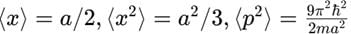
- d)
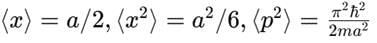
Correct answer is option 'A'. Can you explain this answer?
A particle is in the second excited state (n=3) of a one-dimensional infinite potential well of width a. Which of the following is correct for the expectation values of x, x2, and p2?
a)
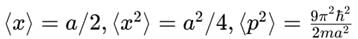
b)
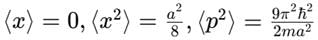
c)
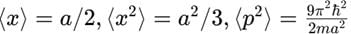
d)
|
|
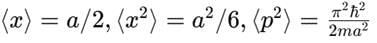
Pie Academy answered |
Wavefunction for n=3n = 3n=3:
The wavefunction is
The wavefunction is
:
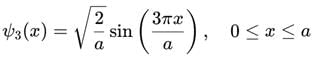
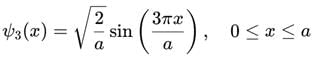
Expectation value of xxx:
For all stationary states in an infinite potential well, the wavefunction is symmetric or antisymmetric around x = a / 2.
For all stationary states in an infinite potential well, the wavefunction is symmetric or antisymmetric around x = a / 2.
Hence, ⟨x⟩ = a / 2.
Expectation value of x2:
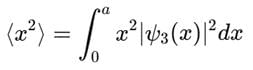
- This integral evaluates to a2 / 4 for n = 3.
- Expectation value of p2:
From the energy eigenvalue relation:
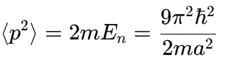
A particle is in the ground state of a one-dimensional infinite potential well with boundaries at x=0 and x=a. Which of the following statements is correct?- a)The probability density is maximum at the center of the well (x = a / 2).
- b)The expectation value of position, ⟨x⟩, is zero.
- c)The energy eigenvalue of the ground state is inversely proportional to a2.
- d)The expectation value of kinetic energy is zero.
Correct answer is option 'A'. Can you explain this answer?
A particle is in the ground state of a one-dimensional infinite potential well with boundaries at x=0 and x=a. Which of the following statements is correct?
a)
The probability density is maximum at the center of the well (x = a / 2).
b)
The expectation value of position, ⟨x⟩, is zero.
c)
The energy eigenvalue of the ground state is inversely proportional to a2.
d)
The expectation value of kinetic energy is zero.
|
|
Pie Academy answered |
Wavefunction for the Ground State:
- The ground state wavefunction for an infinite potential well is:
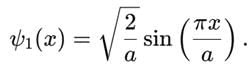
- The corresponding probability density is:
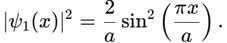
This is maximum at x = a/2 because sin2 reaches its peak value (1) at the center of the well.
Expectation Value of Position (⟨x⟩):
- The wavefunction is symmetric about x = a/2, so the expectation value of position is:
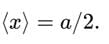
- Hence, it is not zero.
- Energy Eigenvalue of the Ground State:The energy eigenvalue for the ground state (n=1) is
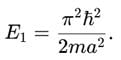
- The energy is inversely proportional to a2, as larger aaa allows the particle to occupy lower-energy states.
- Expectation Value of Kinetic Energy:The expectation value of kinetic energy is nonzero because the particle is confined, and its wavefunction has a curvature (derivative). For the ground state:
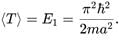
Which of the following can be a wave function? - a)tan x
- b)cot x
- c)sec x
- d)sin x
Correct answer is option 'D'. Can you explain this answer?
Which of the following can be a wave function?
a)
tan x
b)
cot x
c)
sec x
d)
sin x
|
|
Pie Academy answered |
A wave function must satisfy the following key properties:
- Single-valued: The wave function must have a unique value for every point in space.
- Continuous and finite: It must not have any discontinuities or infinite values.
- Normalizable: The integral of the squared wave function over all space must converge to a finite value.
Now, analyzing the options:
- Option A: tanx
The tangent function has discontinuities at x = π/2, 3π/2,…, making it invalid as a wave function. - Option B: cotx
The cotangent function has discontinuities at x = 0, π, 2π,…, so it cannot represent a wave function. - Option C: secx
The secant function has discontinuities at x = π/2, 3π/2,…, disqualifying it as a wave function. - Option D: sinx
The sine function is continuous, finite, and single-valued across all points. It satisfies the criteria for a valid wave function.
For the above cases of one-dimensional infinite and finite potential wells which of the following is true?- a)Energy levels are the same in both cases
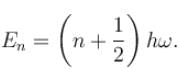
- b)Energy levels are same,
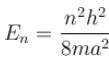in both cases. - c)Energy levels are different
- d)None of the above.
Correct answer is option 'B'. Can you explain this answer?
For the above cases of one-dimensional infinite and finite potential wells which of the following is true?
a)
Energy levels are the same in both cases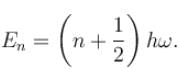
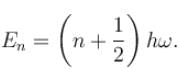
b)
Energy levels are same, 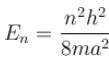in both cases.
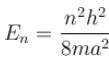in both cases. c)
Energy levels are different
d)
None of the above.
|
|
Pie Academy answered |
- Energy Levels for an Infinite Potential Well: In a one-dimensional infinite potential well, the energy levels are quantized and given by:
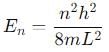where:- n is the quantum number (n = 1, 2, 3,…),
- h is Planck's constant,
- m is the particle's mass,
- L is the width of the well.
- Energy Levels for a Finite Potential Well: In a finite potential well, the energy levels are also quantized but slightly lower than those in the infinite potential well due to the finite height of the potential, which allows tunneling effects. However, the functional form remains approximately the same for lower energy levels:
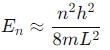for sufficiently deep wells. - Harmonic Oscillator Energy Levels: The energy levels given in Option A:
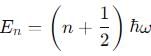represent the quantized energy levels for a quantum harmonic oscillator, not a potential well. Hence, Option A is incorrect.
Analysis of Options:
- Option A: Incorrect, as this describes the energy levels of a quantum harmonic oscillator, not a one-dimensional potential well.
- Option B: Correct, because the energy levels for both the infinite and finite potential wells are approximately given by
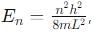, especially for deep finite wells. - Option C: Incorrect, as the energy levels are approximately the same in form for both cases, differing only due to tunneling effects in the finite case.
- Option D: Incorrect, as Option B is correct.
An electron is trapped in an infinite well of width 1cm. For what value of n will the electron have an energy of 2eV?- a)~ 105
- b)~ 109
- c)~ 108
- d)~ 107
Correct answer is option 'D'. Can you explain this answer?
An electron is trapped in an infinite well of width 1cm. For what value of n will the electron have an energy of 2eV?
a)
~ 105
b)
~ 109
c)
~ 108
d)
~ 107
|
|
Pie Academy answered |
Given En = 2 eV = 2 × 1.602×10−19J, we solve for n:
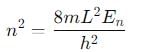
Substitute the values:
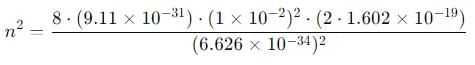
Taking the square root:
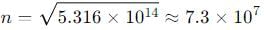
~ 107
If a particle is confined to a one dimensional box of length a with the centre of the box at x = 0. Then, choose the correct option.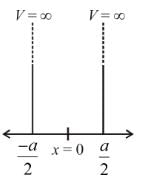
- a)The energy levels are
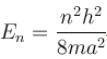
- b)Both the normalization constant and the energy levels are different from the case of the box centered at x = a/2
- c)The normalization constant will be same as in the case of a box centered at x = a/2
- d)The solutions of this case can be obtained by substituting x by
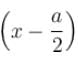in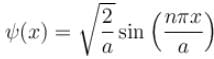 
Correct answer is option 'A,C,D'. Can you explain this answer?
If a particle is confined to a one dimensional box of length a with the centre of the box at x = 0. Then, choose the correct option.
a)
The energy levels are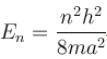
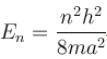
b)
Both the normalization constant and the energy levels are different from the case of the box centered at x = a/2
c)
The normalization constant will be same as in the case of a box centered at x = a/2
d)
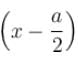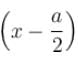The solutions of this case can be obtained by substituting x by in
in |
|
Vedika Singh answered |
The case of a symmetric one dimensional box, is similar to the box from x = 0 to a. The wave functions can be derived from the later case by putting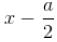 
in place of x.
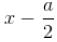in place of x.The correct answers are: The solutions of this case can be obtained by substituting x by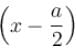 
in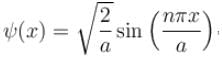 
The normalization constant will be same as in the case of a box centered x = a/2 , The energy levels are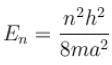 
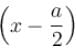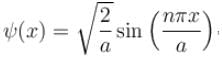in The normalization constant will be same as in the case of a box centered x = a/2 , The energy levels are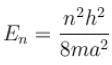 
Chapter doubts & questions for Application of Schrodinger Wave Equation - Topic wise Tests for IIT JAM Physics 2025 is part of Physics exam preparation. The chapters have been prepared according to the Physics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Physics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Application of Schrodinger Wave Equation - Topic wise Tests for IIT JAM Physics in English & Hindi are available as part of Physics exam.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily