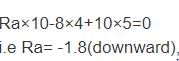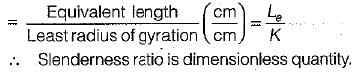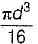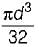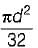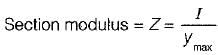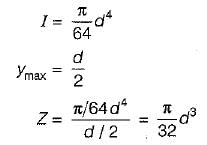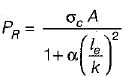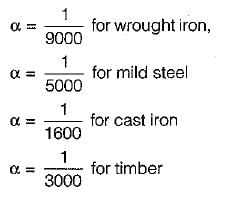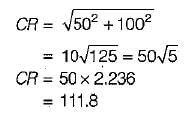All Exams >
Mechanical Engineering >
Topicwise Question Bank for Mechanical Engineering >
All Questions
All questions of Strength of Materials (SOM) for Mechanical Engineering Exam
Limit of proportionality depends upon
- a)type of loading
- b)type of material
- c)area of cross-section
- d)all of the above
Correct answer is option 'B'. Can you explain this answer?
Limit of proportionality depends upon
a)
type of loading
b)
type of material
c)
area of cross-section
d)
all of the above
|
Gaurav Kapoor answered |
The material and its properties. Different materials have different limits of proportionality, which is the maximum stress a material can withstand before it no longer behaves in a linearly elastic manner. It also depends on the temperature and the strain rate.
The permanent mode of deformation of a material known as ____________- a)Plasticity
- b)Elasticity
- c)Slip deformation
- d)Twinning deformation
Correct answer is option 'A'. Can you explain this answer?
The permanent mode of deformation of a material known as ____________
a)
Plasticity
b)
Elasticity
c)
Slip deformation
d)
Twinning deformation
|
Sarita Yadav answered |
Plasticity is defined as the property of a material due to which it is permanently deformed due to loading. Elasticity is the temporary form of deformation. Twinning and Slip are mechanisms of Plastic deformation.
Strain is defined as ratio of- a)change in volume to original volume
- b)change in length to original length.
- c)change in cross-sectional area to original cross-sectional area
- d)any one of the above
Correct answer is option 'D'. Can you explain this answer?
Strain is defined as ratio of
a)
change in volume to original volume
b)
change in length to original length.
c)
change in cross-sectional area to original cross-sectional area
d)
any one of the above
|
Neha Joshi answered |
The strain is defined as the ratio of change in dimension to the original dimension.
If ‘δl’ changes in the length and ‘l’ is the original length, strain = δl/l
Important Terms:
- The ratio of change in length to the original length is called the longitudinal strain.
- The ratio of change in diameter/breadth to original diameter/breadth is called the lateral strain.
- The volumetric strain of a deformed body is defined as the ratio of the change in volume of the body to the deformation to its original volume.
- Shear strain is defined as the strain accompanying a shearing action. It is the angle in radian measure through which the body gets distorted when subjected to external shearing action.
For a beam of uniform strength, if its depth is kept constant, then its width will vary in proportion to- a)bending moment {M)
- b)√M
- c)M2
- d)M-1
Correct answer is option 'A'. Can you explain this answer?
For a beam of uniform strength, if its depth is kept constant, then its width will vary in proportion to
a)
bending moment {M)
b)
√M
c)
M2
d)
M-1
|
|
Sarita Yadav answered |
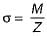
for beam of uniform strength, σ = constant at any section
so, M α Z
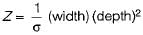
∴ M α width
Two closed coil springs are made from the same small diameter wire, one wound on 10 cm diameter core and the other on 5 cm diameter core. If each spring had N coils, then the ratio of their spring constants should be- a)1/16
- b)1/8
- c)1/4
- d)1/2
Correct answer is option 'B'. Can you explain this answer?
Two closed coil springs are made from the same small diameter wire, one wound on 10 cm diameter core and the other on 5 cm diameter core. If each spring had N coils, then the ratio of their spring constants should be
a)
1/16
b)
1/8
c)
1/4
d)
1/2
|
|
Mrinalini Sharma answered |
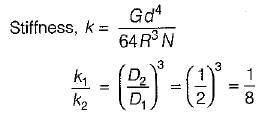
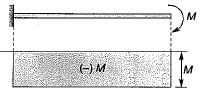
The state of stresses on an element is as shown in following figure.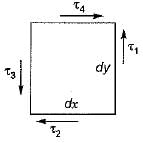
The necessary and sufficient condition for its equilibrium is- a)τ1 - τ3 and τ2 = τ4
- b)τ1= τ4 and τ2 = τ3
- c)τ1 = 2τ4 and τ2 = 2 τ3
- d)τ1 = τ2 = τ3 = τ4
Correct answer is option 'D'. Can you explain this answer?
The state of stresses on an element is as shown in following figure.
The necessary and sufficient condition for its equilibrium is
a)
τ1 - τ3 and τ2 = τ4
b)
τ1= τ4 and τ2 = τ3
c)
τ1 = 2τ4 and τ2 = 2 τ3
d)
τ1 = τ2 = τ3 = τ4
|
|
Sanvi Kapoor answered |
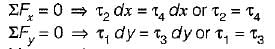
Moment about upper right corner = 0
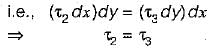
Moment about lower left corner = 0
Young's modulus is defined as the ratio of- a)volumetric stress and volumetric strain
- b)lateral stress and lateral strain
- c)longitudinal stress and lateral strain
- d)longitudinal stress and longitudinal strain
Correct answer is option 'D'. Can you explain this answer?
Young's modulus is defined as the ratio of
a)
volumetric stress and volumetric strain
b)
lateral stress and lateral strain
c)
longitudinal stress and lateral strain
d)
longitudinal stress and longitudinal strain
|
Megha Choudhury answered |
The linear relationship between stress and strain for a bar in simple tension or compression can be expressed by the equation
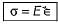
in which Eis a constant of proportionality known as modulus of elasticity for the material. The modulus of elasticity is the slope of the stress- strain diagram in the linearly elastic region and its value depends upon the particular material being used.
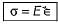
in which Eis a constant of proportionality known as modulus of elasticity for the material. The modulus of elasticity is the slope of the stress- strain diagram in the linearly elastic region and its value depends upon the particular material being used.
Shear force at any point on the beam is the algebraic sum of- a)all vertical forces
- b)all horizontal forces
- c)forces on either side of the point
- d)components of horizontal and vertical forces
Correct answer is option 'C'. Can you explain this answer?
Shear force at any point on the beam is the algebraic sum of
a)
all vertical forces
b)
all horizontal forces
c)
forces on either side of the point
d)
components of horizontal and vertical forces
|
Zoya Sharma answered |
-
Shear force at any point on the beam is the algebraic sum of
forces on either side of the point.A bar of square cross - section has b ee n subjected to an axial tensile load. A plane normal to the axis of loading will have- a)maximum shear stress and minimum normal stress
- b)maximum shear stress as well as maximum normal stress
- c)maximum normal stress and zero shear stress
- d)minimum normal stress and zero shear stress
Correct answer is option 'C'. Can you explain this answer?
A bar of square cross - section has b ee n subjected to an axial tensile load. A plane normal to the axis of loading will have
a)
maximum shear stress and minimum normal stress
b)
maximum shear stress as well as maximum normal stress
c)
maximum normal stress and zero shear stress
d)
minimum normal stress and zero shear stress
|
|
Sanvi Kapoor answered |
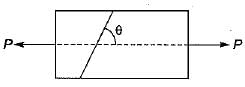
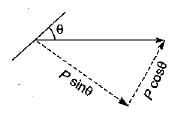
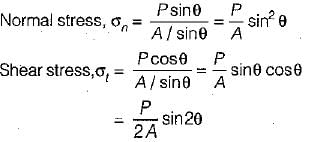
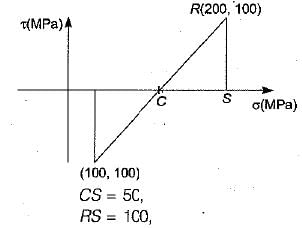
For the plane normal to the axis of loading,
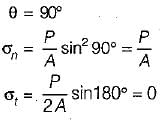
A Mohr’s circle reduces to a point when the body is subjected to- a)pure shear
- b)uniaxial stress only
- c)equal and opposite axial stresses on two mutually perpendicular planes, the planes being free of shear
- d)equal axial stresses on two mutually perpendicular planes, the planes being free of shear
Correct answer is option 'D'. Can you explain this answer?
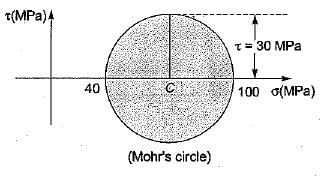
A Mohr’s circle reduces to a point when the body is subjected to
a)
pure shear
b)
uniaxial stress only
c)
equal and opposite axial stresses on two mutually perpendicular planes, the planes being free of shear
d)
equal axial stresses on two mutually perpendicular planes, the planes being free of shear
|
|
Neha Joshi answered |
When the normal stresses on the two mutually perpendicular planes are equal and alike then radius of Mohr’s circle will be zero.
i.e.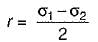
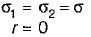
Hence Mohr’s circle reduces to a point.
i.e.
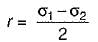
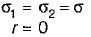
Hence Mohr’s circle reduces to a point.
A cast-iron pipe of 750 mm diameter is used to carry water under a head of 60 m. Water is the thickness of pipe if the permissible stress is to be 20 MPa?- a)11 mm
- b)12 mm
- c)13 mm
- d)14 mm
Correct answer is option 'A'. Can you explain this answer?
A cast-iron pipe of 750 mm diameter is used to carry water under a head of 60 m. Water is the thickness of pipe if the permissible stress is to be 20 MPa?
a)
11 mm
b)
12 mm
c)
13 mm
d)
14 mm
|
Yash Patel answered |
Pressure = ρgH = 1000 x 9,81 x 60
= 588.6 kPa
∴ P = 0.5886 MPa
= 588.6 kPa
∴ P = 0.5886 MPa
Complimentary shear stresses are- a)equal both in magnitude and sign
- b)equal in magnitude but opposite in sign
- c)unequal in magnitude but of same sign
- d)equal in magnitude, and the direction may be same or opposite
Correct answer is option 'B'. Can you explain this answer?
Complimentary shear stresses are
a)
equal both in magnitude and sign
b)
equal in magnitude but opposite in sign
c)
unequal in magnitude but of same sign
d)
equal in magnitude, and the direction may be same or opposite
|
|
Kajal Tiwari answered |
**Complimentary Shear Stresses:**
Complimentary shear stresses refer to shear stresses acting on two mutually perpendicular planes in a solid material. These shear stresses are equal in magnitude but opposite in sign.
**Explanation:**
When a solid material is subjected to shear stress, it deforms and experiences internal forces. These internal forces can be resolved into normal stresses and shear stresses acting on different planes within the material.
When considering shear stresses on two mutually perpendicular planes, they are called complimentary shear stresses. The magnitudes of these shear stresses are equal, but their signs are opposite.
**Example:**
Let's consider a simple example to understand this concept. Suppose a rectangular block is subjected to shear stress along the x-axis. The shear stress acting on the xz-plane will be positive, indicating a shear force in the positive x-direction. Simultaneously, the shear stress acting on the yz-plane will be negative, indicating a shear force in the negative x-direction.
This means that the shear stress acting on the xz-plane and the shear stress acting on the yz-plane are equal in magnitude but opposite in sign. They are complimentary shear stresses.
**Importance:**
Complimentary shear stresses are essential in understanding the distribution of internal forces within a material. They help in analyzing the deformation and failure of structural components when subjected to shear stress. By considering the complimentary shear stresses, engineers can design structures that can withstand these forces without failure.
In conclusion, complimentary shear stresses are equal in magnitude but opposite in sign. They play a significant role in understanding the behavior of materials under shear stress and are essential in engineering design and analysis.
Complimentary shear stresses refer to shear stresses acting on two mutually perpendicular planes in a solid material. These shear stresses are equal in magnitude but opposite in sign.
**Explanation:**
When a solid material is subjected to shear stress, it deforms and experiences internal forces. These internal forces can be resolved into normal stresses and shear stresses acting on different planes within the material.
When considering shear stresses on two mutually perpendicular planes, they are called complimentary shear stresses. The magnitudes of these shear stresses are equal, but their signs are opposite.
**Example:**
Let's consider a simple example to understand this concept. Suppose a rectangular block is subjected to shear stress along the x-axis. The shear stress acting on the xz-plane will be positive, indicating a shear force in the positive x-direction. Simultaneously, the shear stress acting on the yz-plane will be negative, indicating a shear force in the negative x-direction.
This means that the shear stress acting on the xz-plane and the shear stress acting on the yz-plane are equal in magnitude but opposite in sign. They are complimentary shear stresses.
**Importance:**
Complimentary shear stresses are essential in understanding the distribution of internal forces within a material. They help in analyzing the deformation and failure of structural components when subjected to shear stress. By considering the complimentary shear stresses, engineers can design structures that can withstand these forces without failure.
In conclusion, complimentary shear stresses are equal in magnitude but opposite in sign. They play a significant role in understanding the behavior of materials under shear stress and are essential in engineering design and analysis.
A shaft subjected to torsion experiences a pure shear stress τ on the surface. The maximum principal stress on the surface which is at 45° to the axis will have a value of- a)τ cos 45°
- b)2τ cos 45°
- c)τ cos2 45°
- d)2τ sin 45° cos 45°
Correct answer is option 'D'. Can you explain this answer?
A shaft subjected to torsion experiences a pure shear stress τ on the surface. The maximum principal stress on the surface which is at 45° to the axis will have a value of
a)
τ cos 45°
b)
2τ cos 45°
c)
τ cos2 45°
d)
2τ sin 45° cos 45°
|
Arnav Menon answered |
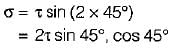
The Young's modulus and the Poisson’s ratio for a certain material are stated to be 1000 GPa and 0.25 respectively. The bulk modulus of the material will be about
- a)450 GPa
- b)600 GPa
- c)66.67 GPa
- d)400 GPa
Correct answer is option 'C'. Can you explain this answer?
The Young's modulus and the Poisson’s ratio for a certain material are stated to be 1000 GPa and 0.25 respectively. The bulk modulus of the material will be about
a)
450 GPa
b)
600 GPa
c)
66.67 GPa
d)
400 GPa
|
|
Prerna Kaur answered |
E = 3 K ( 1 - 2 v )
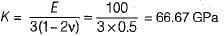
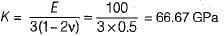
The material in which large deformation is possible before the absolute failure or rupture is termed as- a)brittle
- b)elastic
- c)ductile
- d)plastic
Correct answer is option 'C'. Can you explain this answer?
The material in which large deformation is possible before the absolute failure or rupture is termed as
a)
brittle
b)
elastic
c)
ductile
d)
plastic
|
Partho Jain answered |
Explanation:
In materials science and engineering, the ability of a material to undergo large deformation without fracturing or rupturing is referred to as ductility. Ductility is an important mechanical property of materials and is often desired in applications where the material needs to undergo extensive deformation without failure.
Ductile Materials:
Ductile materials exhibit plastic deformation before failure. Plastic deformation occurs when the material is subjected to an applied load and undergoes a permanent change in shape without fracturing or rupturing. This is in contrast to brittle materials, which undergo little to no plastic deformation before failure.
Brittle Materials:
Brittle materials, such as glass or ceramic, have very limited plastic deformation capabilities. They tend to fracture or rupture at relatively low strains or stresses without undergoing any significant plastic deformation. This makes them more prone to sudden failure under applied loads.
Elastic Materials:
Elastic materials, on the other hand, exhibit reversible deformation. When an elastic material is subjected to an applied load, it deforms temporarily but returns to its original shape once the load is removed. These materials can undergo small deformations without permanent damage or failure.
Importance of Ductility:
Ductility is an important property in various engineering applications. For example, in the construction industry, materials used for structural purposes need to be ductile to withstand loads and deformations caused by earthquakes, wind, or other external forces. Ductile materials are also preferred in metal forming processes such as forging, rolling, or extrusion, where extensive plastic deformation is required.
Conclusion:
In summary, the material in which large deformation is possible before absolute failure or rupture is termed as ductile. Ductile materials can undergo significant plastic deformation without fracturing or rupturing, making them desirable for various engineering applications.
Which stress comes when there is an eccentric load applied? - a)Shear stress
- b)Bending stress
- c)Tensile stress
- d)Thermal stress
Correct answer is option 'B'. Can you explain this answer?
Which stress comes when there is an eccentric load applied?
a)
Shear stress
b)
Bending stress
c)
Tensile stress
d)
Thermal stress
|
Pranav Singh answered |
When there is an eccentric load it means that the load is at some distance from the axis. This causes compression in one side and tension on the other. This causes bending stress.
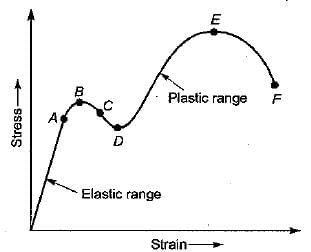
A thin mid steel wire is loaded by adding loads in equal increments till it breaks. The extensions noted with increasing loads will behave as under- a)uniform throughout
- b)first increase and then decrease
- c)increase uniformly first and then increase rapidly
- d)increase rapidly first and then uniformly
Correct answer is option 'C'. Can you explain this answer?
A thin mid steel wire is loaded by adding loads in equal increments till it breaks. The extensions noted with increasing loads will behave as under
a)
uniform throughout
b)
first increase and then decrease
c)
increase uniformly first and then increase rapidly
d)
increase rapidly first and then uniformly
|
|
Neha Joshi answered |
At first, the strain is proportional to strain or elongation is proportional to the load giving a straight-line relationship.
A further increase in the load after yield load will cause marked deformation in the whole volume of the metal. The maximum load which the specimen can withstand without failure is called the load at the ultimate strength.
A cantilever beam rectangular in cross-section is subjected to an isolated load at its free end. If the width of the beam is doubled, the deflection of the free end will be changed in the ratio of- a)8
- b)1/8
- c)1/2
- d)2
Correct answer is option 'C'. Can you explain this answer?
A cantilever beam rectangular in cross-section is subjected to an isolated load at its free end. If the width of the beam is doubled, the deflection of the free end will be changed in the ratio of
a)
8
b)
1/8
c)
1/2
d)
2
|
|
Lakshmi Datta answered |
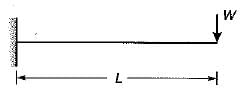
initial width, b1 = b
final width, b2 = 2b
Deflection,
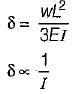
But
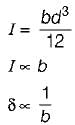
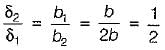
If the crushing stress in the material of a mild steel column is 3300 kg/cm2. Euler’s formula for crippling load is applicable for slenderness ratio equal to/greater than- a)40
- b)50
- c)60
- d)80
Correct answer is option 'D'. Can you explain this answer?
If the crushing stress in the material of a mild steel column is 3300 kg/cm2. Euler’s formula for crippling load is applicable for slenderness ratio equal to/greater than
a)
40
b)
50
c)
60
d)
80
|
Sai Reddy answered |
For Euler’s formula to be applicable the critical stress must not exceed the proportional limit.
Now crushing stress in mild steel
= 3300 kg/cm2
= 330 N/mm2
But stress at proportional limit in mild steel
= 250 M/mm2
Euler’s buckling stress
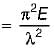
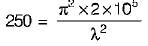
λ = 88.55 ≈ 89
Thus slenderness ratio should be more than or equal to 89 ideally. Option (d) is the most close one.
Now crushing stress in mild steel
= 3300 kg/cm2
= 330 N/mm2
But stress at proportional limit in mild steel
= 250 M/mm2
Euler’s buckling stress
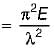
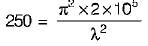
λ = 88.55 ≈ 89
Thus slenderness ratio should be more than or equal to 89 ideally. Option (d) is the most close one.
The value of shear stress which is induced in the shaft due to the applied couple varies- a)from maximum at the center to zero at circumference
- b)from zero at the center to maximum at the circumference
- c)from maximum at the center to minimum at the circumference
- d)from minimum at the center to maximum at the circumference
Correct answer is option 'B'. Can you explain this answer?
The value of shear stress which is induced in the shaft due to the applied couple varies
a)
from maximum at the center to zero at circumference
b)
from zero at the center to maximum at the circumference
c)
from maximum at the center to minimum at the circumference
d)
from minimum at the center to maximum at the circumference
|
|
Sahil Mehra answered |
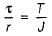
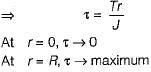
A shell may be termed as thin if the ratio of thickness of the wall to the diameter of the shell is less than one to- a)5
- b)1/10
- c)1/20
- d)15
Correct answer is option 'C'. Can you explain this answer?
A shell may be termed as thin if the ratio of thickness of the wall to the diameter of the shell is less than one to
a)
5
b)
1/10
c)
1/20
d)
15
|
Kalyan Chakraborty answered |
Correct Answer :- C
Explanation : T < Di/10 - Di/15 = Thin shell.
T > Di/10 - Di/15 = Thick shell.
i.e. 1/20
The point of contra-flexure occurs only in- a)cantilever beam
- b)overhanging beam
- c)continuous beam
- d)simply supported beam
Correct answer is option 'B'. Can you explain this answer?
The point of contra-flexure occurs only in
a)
cantilever beam
b)
overhanging beam
c)
continuous beam
d)
simply supported beam
|
|
Arjun Menon answered |
Point of Contra-flexure in Beams
The point of contra-flexure is a point on a beam where the bending moment changes sign. It is a point where the beam changes from being concave upwards to concave downwards or vice versa. This point occurs only in overhanging beams.
Overhanging Beams
An overhanging beam is a beam that has one or both ends extending beyond its supports. These beams are commonly used in construction, especially in bridges and buildings. Overhanging beams can be cantilever beams or simply supported beams.
Cantilever Beams
A cantilever beam is a type of overhanging beam that is supported on one end only. It is characterized by having a fixed support at one end and a free end at the other. Cantilever beams are often used in construction for balconies, bridges, and other structures.
Simply Supported Beams
A simply supported beam is a type of overhanging beam that is supported on both ends. It is characterized by having a support at each end and a free span in the middle. Simply supported beams are commonly used in construction for roofs, floors, and other structures.
Continuous Beams
A continuous beam is a type of beam that is supported by more than two supports. It is characterized by having a continuous span with multiple supports along its length. Continuous beams are commonly used in construction for bridges, buildings, and other structures.
Conclusion
In conclusion, the point of contra-flexure occurs only in overhanging beams, specifically in cantilever beams. This point is important in the design and analysis of beams because it affects the maximum bending moment and the stresses in the beam. Understanding the behavior of beams at the point of contra-flexure is essential for ensuring the safety and stability of structures.
The point of contra-flexure is a point on a beam where the bending moment changes sign. It is a point where the beam changes from being concave upwards to concave downwards or vice versa. This point occurs only in overhanging beams.
Overhanging Beams
An overhanging beam is a beam that has one or both ends extending beyond its supports. These beams are commonly used in construction, especially in bridges and buildings. Overhanging beams can be cantilever beams or simply supported beams.
Cantilever Beams
A cantilever beam is a type of overhanging beam that is supported on one end only. It is characterized by having a fixed support at one end and a free end at the other. Cantilever beams are often used in construction for balconies, bridges, and other structures.
Simply Supported Beams
A simply supported beam is a type of overhanging beam that is supported on both ends. It is characterized by having a support at each end and a free span in the middle. Simply supported beams are commonly used in construction for roofs, floors, and other structures.
Continuous Beams
A continuous beam is a type of beam that is supported by more than two supports. It is characterized by having a continuous span with multiple supports along its length. Continuous beams are commonly used in construction for bridges, buildings, and other structures.
Conclusion
In conclusion, the point of contra-flexure occurs only in overhanging beams, specifically in cantilever beams. This point is important in the design and analysis of beams because it affects the maximum bending moment and the stresses in the beam. Understanding the behavior of beams at the point of contra-flexure is essential for ensuring the safety and stability of structures.
If a material had a modulus of elasticity of 2.1 kgf/cm2 and a modulus of rigidity of 0.8 kgf/cm2 then what will be the approximate value of the Poissons ratio?- a)0.26
- b)0.31
- c)0.47
- d)0.43
Correct answer is option 'B'. Can you explain this answer?
If a material had a modulus of elasticity of 2.1 kgf/cm2 and a modulus of rigidity of 0.8 kgf/cm2 then what will be the approximate value of the Poissons ratio?
a)
0.26
b)
0.31
c)
0.47
d)
0.43
|
Telecom Tuners answered |
On using E = 2G(1 + μ) we can put the values of E and G to get the Poissons value.
Principal stresses at a point in an elastic materia! are 100 MPa tensile 5 and 50 MPa tensile. Whal is the factor of safety against failure based on maximum shear strain energy theory? The elastic limit in simple tension is 173.2 MPa and Poisson’s ratio 0.3.- a)1.25
- b)1.78
- c)2
- d)2.39
Correct answer is option 'C'. Can you explain this answer?
Principal stresses at a point in an elastic materia! are 100 MPa tensile 5 and 50 MPa tensile. Whal is the factor of safety against failure based on maximum shear strain energy theory? The elastic limit in simple tension is 173.2 MPa and Poisson’s ratio 0.3.
a)
1.25
b)
1.78
c)
2
d)
2.39
|
|
Muskaan Sen answered |
∴
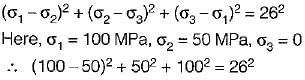
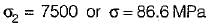
Factor of safety,
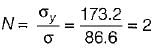
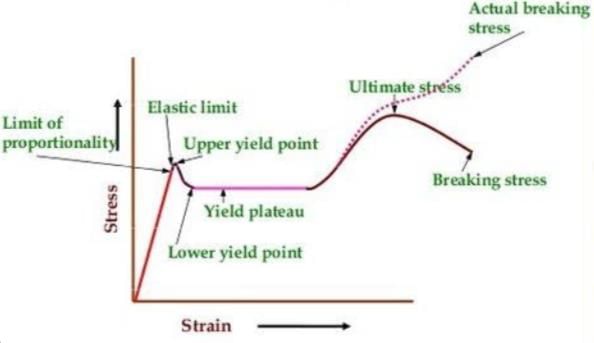
The linear relation between the stress and strain of a material is valid until
- a)fracture stress
- b)proportional limit
- c)ultimate stress
- d)elastic limit
Correct answer is option 'D'. Can you explain this answer?
The linear relation between the stress and strain of a material is valid until
a)
fracture stress
b)
proportional limit
c)
ultimate stress
d)
elastic limit
|
Arshiya Dey answered |
Hooke’s law holds up to the proportional limit.
Hooke’s law in terms of stress and strain is Stress∝Strain→σ∝ε→σ=Eε
The constant of proportionality is called the elastic modulus or Young’s modulus, E. It has the same units as stress. E is a property of the material used.
A spherical ball of 0.5 x 103 mm3 volume is subjected to a volumetric stress of 0.5 MPa. If bulk modulus of the bail material is 16 GPa, the change in volume of the ball would be approximately equal to- a)0.0156 mm3
- b)1.56 x 10-4mm3
- c)0.156 mm3
- d)0.00156 mm3
Correct answer is option 'A'. Can you explain this answer?
A spherical ball of 0.5 x 103 mm3 volume is subjected to a volumetric stress of 0.5 MPa. If bulk modulus of the bail material is 16 GPa, the change in volume of the ball would be approximately equal to
a)
0.0156 mm3
b)
1.56 x 10-4mm3
c)
0.156 mm3
d)
0.00156 mm3
|
|
Telecom Tuners answered |
Bulk modulus
Resilience of a material is considered when it is subjected to
- a)fatigue
- b)creep
- c)shock loading
- d)resonant condition
Correct answer is option 'C'. Can you explain this answer?
Resilience of a material is considered when it is subjected to
a)
fatigue
b)
creep
c)
shock loading
d)
resonant condition
|
Rutuja Deshpande answered |
It is the property of materials to absorb energy and to resist shock and impact loads. It is measured by the amount of energy absorbed per unit volume within elastic limit this property is essential for spring materials. The resilience of material should be considered when it is subjected to shock loading.
In a tensile testing experiment on a specimen of 1 cm2 area, the maximum load observed was 5 tonnes and neck area 0.25 cm2. The ultimate tensile strength of specimen is
- a)4 tonnes/cm2
- b)5 tonnes/cm2
- c)16 tonnes/cm2
- d)22 tonnes/cm2
Correct answer is option 'B'. Can you explain this answer?
In a tensile testing experiment on a specimen of 1 cm2 area, the maximum load observed was 5 tonnes and neck area 0.25 cm2. The ultimate tensile strength of specimen is
a)
4 tonnes/cm2
b)
5 tonnes/cm2
c)
16 tonnes/cm2
d)
22 tonnes/cm2
|
Sinjini Bose answered |
Ultimate tensile strength is corresponding to the maximum load and cross-sectional area of the specimen at the start of the test.
Ultimate tensile strength =
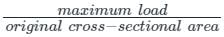
Area = 1 cm2 and maximum load = 5 tonnes
So ultimate tensile strength = 5 tonnes/1 cm2 = 5 tonnes/cm2
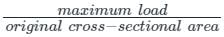
Area = 1 cm2 and maximum load = 5 tonnes
So ultimate tensile strength = 5 tonnes/1 cm2 = 5 tonnes/cm2
The point of contraflexure in a beam is at the location where the
- a)deflection changes sign
- b)beam develops crack
- c)radius of curvature changes sign
- d)bending moment is zero
Correct answer is option 'D'. Can you explain this answer?
The point of contraflexure in a beam is at the location where the
a)
deflection changes sign
b)
beam develops crack
c)
radius of curvature changes sign
d)
bending moment is zero
|
Atharva Rane answered |
Explanation:
The point of contraflexure in a beam is the location where the shear force is maximum. Contraflexure refers to the change in sign of the bending moment along the length of the beam. It occurs when the beam is subjected to a combination of loading conditions that cause the bending moment to change direction.
When a beam is loaded, it experiences both bending moment and shear force. The bending moment causes the beam to bend and the shear force causes the beam to shear. The distribution of bending moment and shear force along the length of the beam is influenced by the type and magnitude of the applied loads.
Shear Force and Bending Moment:
Shear force is the internal force that tends to shear or cut a beam along its cross-section. It is responsible for the transverse loads that act on a beam. Bending moment, on the other hand, is the internal moment that causes a beam to bend. It is responsible for the sagging or hogging of the beam.
Contraflexure:
Contraflexure occurs when the bending moment changes sign along the length of the beam. This means that the beam changes from sagging to hogging or vice versa. The point of contraflexure is the location where this sign change occurs.
Significance of Contraflexure:
The point of contraflexure is an important location in the beam as it indicates the transition from one bending moment condition to another. It is often associated with the maximum shear force in the beam. At the point of contraflexure, the shear force is at its maximum value.
The maximum shear force occurs at the point of contraflexure because it is the location where the bending moment changes sign. This change in sign results in a rapid change in the internal forces and stresses within the beam, leading to the maximum shear force.
Conclusion:
In summary, the point of contraflexure in a beam is the location where the shear force is maximum. It occurs when the bending moment changes sign along the length of the beam. The maximum shear force at the point of contraflexure is a result of the rapid change in internal forces and stresses within the beam.
The point of contraflexure in a beam is the location where the shear force is maximum. Contraflexure refers to the change in sign of the bending moment along the length of the beam. It occurs when the beam is subjected to a combination of loading conditions that cause the bending moment to change direction.
When a beam is loaded, it experiences both bending moment and shear force. The bending moment causes the beam to bend and the shear force causes the beam to shear. The distribution of bending moment and shear force along the length of the beam is influenced by the type and magnitude of the applied loads.
Shear Force and Bending Moment:
Shear force is the internal force that tends to shear or cut a beam along its cross-section. It is responsible for the transverse loads that act on a beam. Bending moment, on the other hand, is the internal moment that causes a beam to bend. It is responsible for the sagging or hogging of the beam.
Contraflexure:
Contraflexure occurs when the bending moment changes sign along the length of the beam. This means that the beam changes from sagging to hogging or vice versa. The point of contraflexure is the location where this sign change occurs.
Significance of Contraflexure:
The point of contraflexure is an important location in the beam as it indicates the transition from one bending moment condition to another. It is often associated with the maximum shear force in the beam. At the point of contraflexure, the shear force is at its maximum value.
The maximum shear force occurs at the point of contraflexure because it is the location where the bending moment changes sign. This change in sign results in a rapid change in the internal forces and stresses within the beam, leading to the maximum shear force.
Conclusion:
In summary, the point of contraflexure in a beam is the location where the shear force is maximum. It occurs when the bending moment changes sign along the length of the beam. The maximum shear force at the point of contraflexure is a result of the rapid change in internal forces and stresses within the beam.
Youngs modulus of elasticity and Poissons ratio of a material are 1.25 x 102 MPa and 0.34 respectively. The modulus of rigidity of the material is __________- a)0.9469 MPa
- b)0.8375 MPa
- c)0.4664 MPa
- d)0.4025 MPa
Correct answer is option 'C'. Can you explain this answer?
Youngs modulus of elasticity and Poissons ratio of a material are 1.25 x 102 MPa and 0.34 respectively. The modulus of rigidity of the material is __________
a)
0.9469 MPa
b)
0.8375 MPa
c)
0.4664 MPa
d)
0.4025 MPa
|
|
Rajat Basu answered |
Modulus of Rigidity Calculation:
1. Given Values:
- Young's Modulus (E) = 1.25 x 10^2 MPa
- Poisson's Ratio (ν) = 0.34
2. Formula for Modulus of Rigidity (G):
G = E / (2 * (1 + ν))
3. Calculate Modulus of Rigidity:
G = 1.25 x 10^2 / (2 * (1 + 0.34))
G = 1.25 x 10^2 / (2 * 1.34)
G = 1.25 x 10^2 / 2.68
G ≈ 0.4664 MPa
Therefore, the Modulus of Rigidity of the material is approximately 0.4664 MPa, which corresponds to option (c).
1. Given Values:
- Young's Modulus (E) = 1.25 x 10^2 MPa
- Poisson's Ratio (ν) = 0.34
2. Formula for Modulus of Rigidity (G):
G = E / (2 * (1 + ν))
3. Calculate Modulus of Rigidity:
G = 1.25 x 10^2 / (2 * (1 + 0.34))
G = 1.25 x 10^2 / (2 * 1.34)
G = 1.25 x 10^2 / 2.68
G ≈ 0.4664 MPa
Therefore, the Modulus of Rigidity of the material is approximately 0.4664 MPa, which corresponds to option (c).
If the length of a column is double, the criteria load becomes- a)1/2 of the original value
- b)1/4 of the original value
- c) 1/8 of the original value 8
- d) 1/16 of the original value 16
Correct answer is option 'B'. Can you explain this answer?
If the length of a column is double, the criteria load becomes
a)
1/2 of the original value
b)
1/4 of the original value
c)
1/8 of the original value 8
d)
1/16 of the original value 16
|
|
Nandini Basak answered |
Understanding Column Load and Length Relationship
When analyzing the behavior of columns under axial load, the length of the column plays a crucial role in determining its load-bearing capacity.
Impact of Length on Load Capacity
- Buckling Load Formula: The critical load at which a column buckles can be defined by Euler's formula: P = (π²EI) / (KL)², where:
- P = critical load
- E = modulus of elasticity
- I = moment of inertia
- K = column effective length factor
- L = length of the column
- Doubling the Length: If the length (L) of the column is doubled, the new length becomes 2L. Substituting this into the formula gives:
- P_new = (π²EI) / (K(2L))² = (π²EI) / (4K²L²)
- Load Reduction: Comparing the original load (P) with the new load (P_new):
- P_new = P / 4
This indicates that when the length of the column is doubled, the critical buckling load becomes one-fourth of the original load.
Conclusion
Thus, when the length of a column is increased to double its original value, the capacity to carry load decreases to one-fourth of the original value, confirming that the correct answer is option 'B'.
When analyzing the behavior of columns under axial load, the length of the column plays a crucial role in determining its load-bearing capacity.
Impact of Length on Load Capacity
- Buckling Load Formula: The critical load at which a column buckles can be defined by Euler's formula: P = (π²EI) / (KL)², where:
- P = critical load
- E = modulus of elasticity
- I = moment of inertia
- K = column effective length factor
- L = length of the column
- Doubling the Length: If the length (L) of the column is doubled, the new length becomes 2L. Substituting this into the formula gives:
- P_new = (π²EI) / (K(2L))² = (π²EI) / (4K²L²)
- Load Reduction: Comparing the original load (P) with the new load (P_new):
- P_new = P / 4
This indicates that when the length of the column is doubled, the critical buckling load becomes one-fourth of the original load.
Conclusion
Thus, when the length of a column is increased to double its original value, the capacity to carry load decreases to one-fourth of the original value, confirming that the correct answer is option 'B'.
A steel rod of length 300 mm is held between two fixed supports so that the rod cannot elongate or contract in the axial direction. If the temperature of the rod is raised by 20°C, the axial stress induced in the rod due to this rise in temperature is
(Take E = 200 GPa, α = 11.5 x 10-6/°C)- a)46 MPa (Tension)
- b)46 MPa (Compression)
- c)23 MPa (Tension)
- d)23 MPa (Compression)
Correct answer is option 'B'. Can you explain this answer?
A steel rod of length 300 mm is held between two fixed supports so that the rod cannot elongate or contract in the axial direction. If the temperature of the rod is raised by 20°C, the axial stress induced in the rod due to this rise in temperature is
(Take E = 200 GPa, α = 11.5 x 10-6/°C)
(Take E = 200 GPa, α = 11.5 x 10-6/°C)
a)
46 MPa (Tension)
b)
46 MPa (Compression)
c)
23 MPa (Tension)
d)
23 MPa (Compression)
|
|
Anuj Chauhan answered |
In order to determine the change in length of the steel rod, we need to use the coefficient of linear expansion of steel. The coefficient of linear expansion for steel is typically around 12 x 10^-6 per degree Celsius.
Given that the temperature of the rod is raised by 20 degrees Celsius, we can calculate the change in length using the formula:
ΔL = αLΔT
where ΔL is the change in length, α is the coefficient of linear expansion, L is the original length of the rod, and ΔT is the change in temperature.
Plugging in the given values:
ΔL = (12 x 10^-6) x (300 mm) x (20 degrees Celsius)
ΔL = 0.072 mm
Therefore, the steel rod will increase in length by 0.072 mm when the temperature is raised by 20 degrees Celsius.
Given that the temperature of the rod is raised by 20 degrees Celsius, we can calculate the change in length using the formula:
ΔL = αLΔT
where ΔL is the change in length, α is the coefficient of linear expansion, L is the original length of the rod, and ΔT is the change in temperature.
Plugging in the given values:
ΔL = (12 x 10^-6) x (300 mm) x (20 degrees Celsius)
ΔL = 0.072 mm
Therefore, the steel rod will increase in length by 0.072 mm when the temperature is raised by 20 degrees Celsius.
What are the materials which show direction dependent properties?- a)Homogeneous materials
- b)Viscoelastic materials
- c)Isotropic materials
- d)Anisotropic materials
Correct answer is option 'D'. Can you explain this answer?
What are the materials which show direction dependent properties?
a)
Homogeneous materials
b)
Viscoelastic materials
c)
Isotropic materials
d)
Anisotropic materials
|
|
Mrinalini Sharma answered |
Anisotropy is the property in which material possess different properties in different directions.
A steel rod passes through a brass tube which is closed by thin rigid washers and fastened by nuts screwed to the rod. Which type of stress will be induced in the tube when the nut is tightened on the bolt?- a)tensile
- b)compressive
- c)shear
- d)bending
Correct answer is option 'B'. Can you explain this answer?
A steel rod passes through a brass tube which is closed by thin rigid washers and fastened by nuts screwed to the rod. Which type of stress will be induced in the tube when the nut is tightened on the bolt?
a)
tensile
b)
compressive
c)
shear
d)
bending
|
Stuti Bajaj answered |
When nut is tightened on the bolt, rod is subjected to tensile stress and brass tube is subjected to compressive state of stress.
What is the phenomenon of progressive extension of the material i.e. strain increasing with the time at a constant load, called?- a)Plasticity
- b)Yielding
- c)Creeping
- d)Breaking
Correct answer is option 'C'. Can you explain this answer?
What is the phenomenon of progressive extension of the material i.e. strain increasing with the time at a constant load, called?
a)
Plasticity
b)
Yielding
c)
Creeping
d)
Breaking
|
|
Dishani Desai answered |
When metals are subjected to constant loads, metals tends to deform continuously. This continuous deformation of metals under constant loads is called as creep.
Consider the following statements about truestress-strain method/curve:
1. It is more sensitive to changes in both metallurgical and mechanical conditions.
2. It gives a more accurate picture of the ductility.
3. It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests etc.
4. It can be used for compression tests as well.Which of the above statements are correct?- a)1, 2 and 3
- b)1, 3 and 4
- c)2, 3 and 4
- d)1, 2, 3 and 4
Correct answer is option 'D'. Can you explain this answer?
Consider the following statements about truestress-strain method/curve:
1. It is more sensitive to changes in both metallurgical and mechanical conditions.
2. It gives a more accurate picture of the ductility.
3. It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests etc.
4. It can be used for compression tests as well.
1. It is more sensitive to changes in both metallurgical and mechanical conditions.
2. It gives a more accurate picture of the ductility.
3. It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests etc.
4. It can be used for compression tests as well.
Which of the above statements are correct?
a)
1, 2 and 3
b)
1, 3 and 4
c)
2, 3 and 4
d)
1, 2, 3 and 4
|
|
Nitya Nambiar answered |
Truestress-strain method/curve is a widely used method in materials testing to determine the mechanical behavior of a material under load. It provides valuable information about the material's strength, ductility, and other mechanical properties. Let's analyze each statement to determine their correctness:
Statement 1: It is more sensitive to changes in both metallurgical and mechanical conditions.
- This statement is correct. The truestress-strain method takes into account the instantaneous cross-sectional area of the specimen, which changes during deformation. This makes it more sensitive to changes in the material's mechanical and metallurgical conditions compared to the engineering stress-strain method.
Statement 2: It gives a more accurate picture of the ductility.
- This statement is correct. The truestress-strain curve provides a more accurate representation of the material's ductility because it considers the actual change in cross-sectional area during deformation. It accounts for the necking phenomenon that occurs in many materials under tension, which is crucial for accurately assessing the material's ability to deform before failure.
Statement 3: It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests, etc.
- This statement is correct. The truestress-strain values obtained from tensile testing can be correlated with stress-strain values obtained from other testing methods like torsion, impact, and combined stress tests. This allows for a better understanding of the material's behavior under different loading conditions and helps in predicting its performance in various applications.
Statement 4: It can be used for compression tests as well.
- This statement is correct. While the truestress-strain method is commonly used in tensile testing, it can also be applied to compression testing. The concept of truestress and truestrain can be extended to compression tests by considering the instantaneous cross-sectional area and volume changes during deformation.
In conclusion, all the given statements about the truestress-strain method/curve are correct. It is a sensitive method that provides a more accurate picture of ductility, can be correlated with other test results, and can be used for both tension and compression testing.
Statement 1: It is more sensitive to changes in both metallurgical and mechanical conditions.
- This statement is correct. The truestress-strain method takes into account the instantaneous cross-sectional area of the specimen, which changes during deformation. This makes it more sensitive to changes in the material's mechanical and metallurgical conditions compared to the engineering stress-strain method.
Statement 2: It gives a more accurate picture of the ductility.
- This statement is correct. The truestress-strain curve provides a more accurate representation of the material's ductility because it considers the actual change in cross-sectional area during deformation. It accounts for the necking phenomenon that occurs in many materials under tension, which is crucial for accurately assessing the material's ability to deform before failure.
Statement 3: It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests, etc.
- This statement is correct. The truestress-strain values obtained from tensile testing can be correlated with stress-strain values obtained from other testing methods like torsion, impact, and combined stress tests. This allows for a better understanding of the material's behavior under different loading conditions and helps in predicting its performance in various applications.
Statement 4: It can be used for compression tests as well.
- This statement is correct. While the truestress-strain method is commonly used in tensile testing, it can also be applied to compression testing. The concept of truestress and truestrain can be extended to compression tests by considering the instantaneous cross-sectional area and volume changes during deformation.
In conclusion, all the given statements about the truestress-strain method/curve are correct. It is a sensitive method that provides a more accurate picture of ductility, can be correlated with other test results, and can be used for both tension and compression testing.
For a circular column having its ends hinged, the slenderness ratio is 160. The L/d ratio of the column is- a)80
- b)57
- c)40
- d)20
Correct answer is option 'C'. Can you explain this answer?
For a circular column having its ends hinged, the slenderness ratio is 160. The L/d ratio of the column is
a)
80
b)
57
c)
40
d)
20
|
|
Anshul Chakraborty answered |
Slenderness ratio,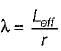 
where r is the least radius of gyration and Leff is effective length
∴
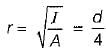
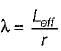
where r is the least radius of gyration and Leff is effective length
∴
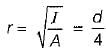
A straight bar having a constant cross-sectional area A, length L and weight W is hanging vertically. If E is the Young’s modulus of the material, total increase in length of the bar due to its own weight only is- a)WL/2 AE
- b)WL/AE
- c)2WL/AE
- d)4WL/AE
Correct answer is option 'A'. Can you explain this answer?
A straight bar having a constant cross-sectional area A, length L and weight W is hanging vertically. If E is the Young’s modulus of the material, total increase in length of the bar due to its own weight only is
a)
WL/2 AE
b)
WL/AE
c)
2WL/AE
d)
4WL/AE
|
Diya Dasgupta answered |
's modulus of the material of the bar, then the strain in the bar can be determined using the formula:
strain = stress / Young's modulus
The stress on the bar can be determined using the formula:
stress = weight / cross-sectional area
Therefore, substituting the values, we have:
stress = W / A
And the strain can be calculated as:
strain = (W / A) / E
The strain represents the amount of deformation or elongation that the bar undergoes under the applied stress.
strain = stress / Young's modulus
The stress on the bar can be determined using the formula:
stress = weight / cross-sectional area
Therefore, substituting the values, we have:
stress = W / A
And the strain can be calculated as:
strain = (W / A) / E
The strain represents the amount of deformation or elongation that the bar undergoes under the applied stress.
Chapter doubts & questions for Strength of Materials (SOM) - Topicwise Question Bank for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Strength of Materials (SOM) - Topicwise Question Bank for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Topicwise Question Bank for Mechanical Engineering
45 videos|314 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily