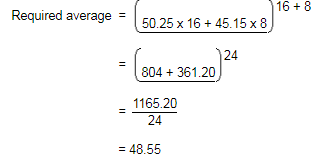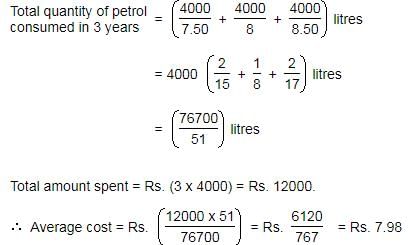All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Averages for UPSC CSE Exam
Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?
- a)82
- b)81
- c)81.5
- d)84.5
Correct answer is option 'C'. Can you explain this answer?
Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?
a)
82
b)
81
c)
81.5
d)
84.5

|
Nipun Tuteja answered |
Avg speed of train = 2xy/x+y
⇒ [2(84)(56)]/(84+56)
⇒ [2(84)(56)]/140
= 67.2km/hr
⇒ [2(84)(56)]/(84+56)
⇒ [2(84)(56)]/140
= 67.2km/hr
There are 7 members in a family whose average age is 25 years. Ram who is 12 years old is the second youngest in the family. Find the average age of the family in years just before Ram was born?
- a)15.167
- b)18.2
- c)13
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
There are 7 members in a family whose average age is 25 years. Ram who is 12 years old is the second youngest in the family. Find the average age of the family in years just before Ram was born?
a)
15.167
b)
18.2
c)
13
d)
Cannot be determined
|
|
Rajeev Kumar answered |
In order to find the average age of the family before Ram was born, we need to know the age of the youngest member of the family.
Since, we do not know the age of the youngest member, we can not calculate the total age of the family before Ram was born.
Hence, we can not calculate the answer with the given conditions.
Since, we do not know the age of the youngest member, we can not calculate the total age of the family before Ram was born.
Hence, we can not calculate the answer with the given conditions.
Thus, D is the right choice.
Can you explain the answer of this question below:The average of 20 numbers is zero. Of them, How many of them may be greater than zero , at the most?
- A:1
- B:20
- C:0
- D:19
The answer is D.

|
Ishita Das answered |
Average of 20 numbers = 0.
 Sum of 20 numbers (0 x 20) = 0.
Sum of 20 numbers (0 x 20) = 0.It is quite possible that 19 of these numbers may be positive and if their sum is a then 20th number is (-a).
Can you explain the answer of this question below: A car owner buys diesel at Rs.7.50, Rs. 8 and Rs. 8.50 per litre for three successive years. What approximately is the average cost per litre of diesel if he spends Rs. 4000 each year?
- A:Rs. 8
- B:Rs. 7.98
- C:Rs. 6.2
- D:Rs. 8.1
The answer is B.

|
Ishani Rane answered |
Average cost per litre of petrol = Total amount / Total quantity of petrol
Re. 4000 is spent each year, so total amount spent = 3 * Rs. 4000 = Rs. 12,000
Total quantity of petrol consumed in 3 years = (4000/7.50) + (4000/8) + (4000/8.50) litres
= 533.3 + 500 + 470.6 = 1505
Average cost = Total amount / Total quantity
= 12000/1504 = 7.98
To find quickly, you can take cube root of (7.50 * 8 * 8.50), and it will be slightly less than 8.
The correct option is B.
A library has an average of 510 visitors on Sundays and 240 on other days. What is the average number of visitors per day in a month of 30 days beginning with a Sunday?
- a)290
- b)304
- c)285
- d)270
Correct answer is option 'C'. Can you explain this answer?
a)
290
b)
304
c)
285
d)
270

|
Ishani Rane answered |
Since the month begins with a Sunday, to there will be five Sundays in the month.
Required average = [510 x 5 + 240 x 25] 30
= 8550/30
= 285
A batsman makes a score of 87 runs in the 17th inning and thus increases his averages by 3. What is his average after 17th inning?
- a)39
- b)35
- c)42
- d)40.5
Correct answer is option 'A'. Can you explain this answer?
a)
39
b)
35
c)
42
d)
40.5

|
Manoj Ghosh answered |
Let the average after 17 innings = x
Total runs scored in 17 innings = 17x
then average after 16 innings = (x-3)
Total runs scored in 16 innings = 16(x-3)
We know that Total runs scored in 16 innings + 87 = Total runs scored in 17 innings
=> 16(x-3) + 87 = 17x
=> 16x - 48 + 87 = 17x
=> x = 39
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?- a)6.25
- b)5.5
- c)7.4
- d)5
Correct answer is 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?
a)
6.25
b)
5.5
c)
7.4
d)
5

|
Ishani Rane answered |
For the 1st 10 overs the score will be 10*3.2=32so the remaining score is 282-32=250remaining overs = 40so the run rate 250/40=6.25ans is 6.25
The average number of runs scored by Virat Kohli in four matches is 48. In the fifth match, Kohli scores some runs such that his average now becomes 60. In the 6th innings he scores 12 runs more than his fifth innings and now the average of his last five innings becomes 78. How many runs did he score in his first innings? (He does not remain not out in any of the innings)- a)30
- b)50
- c)70
- d)90
Correct answer is option 'A'. Can you explain this answer?
The average number of runs scored by Virat Kohli in four matches is 48. In the fifth match, Kohli scores some runs such that his average now becomes 60. In the 6th innings he scores 12 runs more than his fifth innings and now the average of his last five innings becomes 78. How many runs did he score in his first innings? (He does not remain not out in any of the innings)
a)
30
b)
50
c)
70
d)
90

|
Quantronics answered |
Runs scored by Kohli in first 4 innings = 48*4 = 192
Average of 5 innings is 60, so total runs scored after 5 innings = 60*5 = 300
Hence runs scored by Kohli in fifth inning = 300 – 192 = 108
It is given that in 6th innings he scores 12 runs more than this, so he must score 120 in the sixth inning. Hence total runs scored in 6 innings = 300+120 = 420
Now average of last five innings is 78, so runs scored in last innings = 390
Hence runs scored in first inning = 420 – 390 = 30.
Average of 5 innings is 60, so total runs scored after 5 innings = 60*5 = 300
Hence runs scored by Kohli in fifth inning = 300 – 192 = 108
It is given that in 6th innings he scores 12 runs more than this, so he must score 120 in the sixth inning. Hence total runs scored in 6 innings = 300+120 = 420
Now average of last five innings is 78, so runs scored in last innings = 390
Hence runs scored in first inning = 420 – 390 = 30.
The average monthly income of P and Q is Rs. 5050. The average monthly income of Q and R is Rs. 6250 and the average monthly income of P and R is Rs. 5200. The monthly income of P is:
- a)3500
- b)4000
- c)4050
- d)5000
Correct answer is 'B'. Can you explain this answer?
a)
3500
b)
4000
c)
4050
d)
5000

|
Arya Roy answered |
Let monthly income of A = a
monthly income of B = b
monthly income of C = c
a + b = 2 * 5050 .... (Equation 1)
b + c = 2 * 6250 .... (Equation 2)
a + c = 2 * 5200 .... (Equation 3)
(Equation 1) + (Equation 3) - (Equation 2)
= a + b + a + c - (b + c) = (2 * 5050) + (2 * 5200) - (2 * 6250)
= 2a = 2(5050 + 5200 - 6250)
= a = 4000
i.e., Monthly income of A = 4000
If the average marks of three batches of 55, 60 and 45 students respectively is 50, 55, 60, what is the average marks of all the students?
- a)53.23
- b)54.68
- c)51.33
- d)50
Correct answer is 'B'. Can you explain this answer?
a)
53.23
b)
54.68
c)
51.33
d)
50

|
Manoj Ghosh answered |
Total marks of first batch(55) is= 55*50=2750
Total marks of second batch (60) is= 60*55=3300
Total marks of third batch(45)= 45*60=2700
Total marks of second batch= 2750+3300+2700 = 8750
Total number of Students= 55+60+45 =160
Avg= 8750/160= 54.68
The captain of a cricket team of 11 members is 26 years old and the wicket keeper is 3 years older. If the ages of these two are excluded, the average age of the remaining players is one year less than the average age of the whole team. Find out the average age of the team.
- a)23 years
- b)20 years
- c)24 years
- d)21 years
Correct answer is option 'A'. Can you explain this answer?
a)
23 years
b)
20 years
c)
24 years
d)
21 years

|
Pallabi Deshpande answered |
Number of members in the team = 11
Let the average age of of the team = x
=> Sum of the ages of all the 11 members of the team / 11 = x
=> Sum of the ages of all the 11 members of the team = 11 x
Age of the captain = 26
Age of the wicket keeper = 26 + 3 = 29
Sum of the ages of 9 members of the team excluding captain and wicket keeper
= 11x − 26 − 29 =11x − 55
Average age of 9 members of the team excluding captain and wicket keeper
= 11x−55 / 9
Given that
11x−55 / 9 =(x−1)
⇒11x−55=9(x−1)
⇒11x−55=9x−9
⇒2x=46
⇒x = 46/2 = 23 years
The average age of husband, wife and their child 3 years ago was 27 years and that of wife and the child 5 years ago was 20 years. What is the present age of the husband?
- a)40
- b)32
- c)28
- d)30
Correct answer is option 'A'. Can you explain this answer?
a)
40
b)
32
c)
28
d)
30

|
Arya Roy answered |
Sum of the present ages of husband, wife and child = (27 x 3 + 3 x 3) years = 90 years.
Sum of the present ages of wife and child (20 x 2 + 5 x 2) years = 50 years.
Husband's present age = (90 - 50) years = 40 years.
The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, what is the weight of B?- a)31 kg
- b)28 kg
- c)32 kg
- d)30 kg
Correct answer is option 'A'. Can you explain this answer?
The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, what is the weight of B?
a)
31 kg
b)
28 kg
c)
32 kg
d)
30 kg
|
|
Kavya Saxena answered |
Let A, B, C represent their respective weights. Then, we have:
A + B + C = (45 x 3) = 135 .... (i)
A + B = (40 x 2) = 80 .... (ii)
B + C = (43 x 2) = 86 ....(iii)
Adding (ii) and (iii), we get: A + 2B + C = 166 .... (iv)
Subtracting (i) from (iv), we get : B = 31.
 B's weight = 31 kg.
B's weight = 31 kg.The average weight of a class of 10 students is increased by 2 kg when one student of 30kg left and another student joined. After a few months, this new student left and another student joined whose weight was 10 less than the student who left now. What is the difference between the final and initial averages?
- a)11
- b)1
- c)111
- d)121
Correct answer is option 'B'. Can you explain this answer?
The average weight of a class of 10 students is increased by 2 kg when one student of 30kg left and another student joined. After a few months, this new student left and another student joined whose weight was 10 less than the student who left now. What is the difference between the final and initial averages?
a)
11
b)
1
c)
111
d)
121
|
|
Rajeev Kumar answered |
Change in total weight of 10 students = difference in weight of the student who joined and the student
=> weigth of first student who left = 30 + (10×2) = 50
weight of the student who joined last = 50 – 10 = 40...
Thus change in average weight = (40 – 30)/10 = 1...
Thus change in average weight = (40 – 30)/10 = 1...
There are two divisions A and B of a class, consisting of 36 and 44 students respectively. If the average weight of divisions A is 40 kg and that of division b is 35 kg. What is the average weight of the whole class?
- a)38.25
- b)37.25
- c)38.5
- d)37
Correct answer is option 'B'. Can you explain this answer?
a)
38.25
b)
37.25
c)
38.5
d)
37

|
Ishani Rane answered |
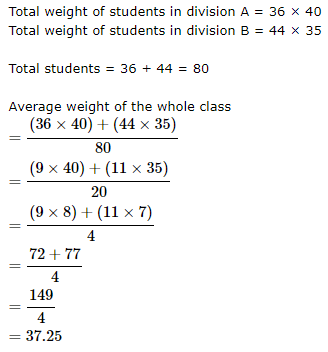
The average of 20 numbers is zero. Of them, How many of them may be greater than zero , at the most?
- a)1
- b)20
- c)0
- d)19
Correct answer is 'D'. Can you explain this answer?
a)
1
b)
20
c)
0
d)
19

|
Priyanka Datta answered |
Average of 20 numbers = 0.
 Sum of 20 numbers (0 x 20) = 0.
Sum of 20 numbers (0 x 20) = 0.It is quite possible that 19 of these numbers may be positive and if their sum is a then 20th number is (-a).
A student needed to find the arithmetic mean of the numbers 3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14 and x. He found the mean to be 12. What is the value of x?
- a)12
- b)5
- c)7
- d)9
Correct answer is option 'C'. Can you explain this answer?
a)
12
b)
5
c)
7
d)
9

|
Arya Roy answered |
Mean = Sum / Total count
12 = (3+11+7+9+15+13+8+19+17+21+14+x) / 12
12*12 = 137 + x
144 = 137 + x
x = 144 - 137
x = 7
A grocer has a sale of Rs. 6435, Rs. 6927, Rs. 6855, Rs. 7230 and Rs. 6562 for 5 consecutive months. How much sale must he have in the sixth month so that he gets an average sale of Rs. 6500?
- a)4800
- b)4991
- c)5004
- d)5000
Correct answer is option 'B'. Can you explain this answer?
a)
4800
b)
4991
c)
5004
d)
5000

|
Pallabi Deshpande answered |
Total sale for 5 months = Rs. (6435 + 6927 + 6855 + 7230 + 6562) = Rs. 34009.
Required sale = Rs. [ (6500 x 6) - 34009 ]
= Rs.(39000 - 34009)
= Rs.4991.
The average age of a family of 5 members is 20 years. If the age of the youngest member is 10 years, what was the average age of the family at the birth of the youngest member?- a)12.50
- b)15.25
- c)21.25
- d)18.75
Correct answer is option 'D'. Can you explain this answer?
The average age of a family of 5 members is 20 years. If the age of the youngest member is 10 years, what was the average age of the family at the birth of the youngest member?
a)
12.50
b)
15.25
c)
21.25
d)
18.75
|
|
Rajeev Kumar answered |
At present the total age of the family = 5 × 20 =100
The total age of the family at the time of the birth of the youngest member,
= 100 - 10 - (10 × 4)
= 50
Therefore, average age of the family at the time of birth of the youngest member,
= 50/4 =12.5
The total age of the family at the time of the birth of the youngest member,
= 100 - 10 - (10 × 4)
= 50
Therefore, average age of the family at the time of birth of the youngest member,
= 50/4 =12.5
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?- a)6.25
- b)5.5
- c)7.4
- d)5
Correct answer is option 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?
a)
6.25
b)
5.5
c)
7.4
d)
5

|
Arya Roy answered |
Runs scored in the first 10 overs = 10 * 3.2 = 32
Total runs = 282
Remaining runs to be scored = 282 - 32 = 250
Remaining overs = 40
Run rate needed =250/40 = 6.25
A family consists of two grandparents, two parents and three grandchildren. The average age of the grandparents is 67 years, that of the parents is 35 years and that of the grandchildren is 6 years. The average age of the family is
- a)32 2/7 years
- b)31 5/7 years
- c)28 1/7 years
- d)30 5/7 years
Correct answer is option 'B'. Can you explain this answer?
a)
32 2/7 years
b)
31 5/7 years
c)
28 1/7 years
d)
30 5/7 years

|
Ishani Rane answered |
Total age of the grandparents = 67 * 2
Total age of the parents = 35 * 2
Total age of the grandchildren = 6 * 3
Average age of the family
= (67 *2 ) + (35*2) + (6*2) / 7
= 134 + 70 + 18 / 7
= 22/7
= 31 5/7
The average of 20 numbers is zero. Of them, How many of them may be greater than zero , at the most?
- a)1
- b)20
- c)0
- d)19
Correct answer is option 'D'. Can you explain this answer?
a)
1
b)
20
c)
0
d)
19
|
|
Sagar Sharma answered |
Problem:
The average of 20 numbers is zero. How many of them may be greater than zero, at the most?
Solution:
To find the maximum number of numbers that can be greater than zero, we need to understand the concept of average and the properties of numbers.
Understanding the Average:
The average of a set of numbers is found by summing all the numbers in the set and then dividing the sum by the total number of numbers.
Properties of Numbers:
1. The sum of positive numbers is always greater than zero.
2. The sum of negative numbers is always less than zero.
3. The sum of positive and negative numbers can be zero if the sum of positive numbers equals the sum of negative numbers.
Explanation:
Given that the average of 20 numbers is zero, we can conclude that the sum of these 20 numbers is also zero.
Let's assume that there are 'x' numbers greater than zero and 'y' numbers less than or equal to zero.
Since the sum of these 20 numbers is zero, we can write the equation:
(x * positive number) + (y * non-positive number) = 0
To maximize the number of numbers greater than zero, we need to minimize the number of non-positive numbers. The smallest non-positive number is zero. Therefore, we can rewrite the equation as:
(x * positive number) + (y * 0) = 0
Simplifying the equation, we get:
x * positive number = 0
In order for this equation to be true, the value of 'x' must be zero. This means that there can be zero numbers greater than zero in the set of 20 numbers.
Therefore, the maximum number of numbers that can be greater than zero is 0.
Hence, the correct answer is option 'C' - 0.
The average of 20 numbers is zero. How many of them may be greater than zero, at the most?
Solution:
To find the maximum number of numbers that can be greater than zero, we need to understand the concept of average and the properties of numbers.
Understanding the Average:
The average of a set of numbers is found by summing all the numbers in the set and then dividing the sum by the total number of numbers.
Properties of Numbers:
1. The sum of positive numbers is always greater than zero.
2. The sum of negative numbers is always less than zero.
3. The sum of positive and negative numbers can be zero if the sum of positive numbers equals the sum of negative numbers.
Explanation:
Given that the average of 20 numbers is zero, we can conclude that the sum of these 20 numbers is also zero.
Let's assume that there are 'x' numbers greater than zero and 'y' numbers less than or equal to zero.
Since the sum of these 20 numbers is zero, we can write the equation:
(x * positive number) + (y * non-positive number) = 0
To maximize the number of numbers greater than zero, we need to minimize the number of non-positive numbers. The smallest non-positive number is zero. Therefore, we can rewrite the equation as:
(x * positive number) + (y * 0) = 0
Simplifying the equation, we get:
x * positive number = 0
In order for this equation to be true, the value of 'x' must be zero. This means that there can be zero numbers greater than zero in the set of 20 numbers.
Therefore, the maximum number of numbers that can be greater than zero is 0.
Hence, the correct answer is option 'C' - 0.
The average weight of a class is 54 kg. A student, whose weight is 145 kg, joined the class and the average weight of the class now becomes a prime number less than 72. Find the total number of students in the class now.- a)7
- b)13
- c)15
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
The average weight of a class is 54 kg. A student, whose weight is 145 kg, joined the class and the average weight of the class now becomes a prime number less than 72. Find the total number of students in the class now.
a)
7
b)
13
c)
15
d)
Cannot be determined
|
|
Rajeev Kumar answered |
Let the original number of students in the class be N.
Total weight of the class = 54N
New total weight of the class = 54N + 145
New average weight of the class = (54N + 145)/(N+1) = (54N + 54)/(N+1) + 91/(N+1) = 54 + 91/(N+1).
Since the new average is an integer, (N+1) should be a factor of 91.
If N+1 = 7, the new average becomes 54 + 91/7 = 54 + 13 = 67
and if N+1 = 13, then the new average becomes 54 + 91/13 = 54 + 7 = 61
Both 67 and 61 are prime numbers less than 72. So, we cannot uniquely determine the number of students in the class.
Total weight of the class = 54N
New total weight of the class = 54N + 145
New average weight of the class = (54N + 145)/(N+1) = (54N + 54)/(N+1) + 91/(N+1) = 54 + 91/(N+1).
Since the new average is an integer, (N+1) should be a factor of 91.
If N+1 = 7, the new average becomes 54 + 91/7 = 54 + 13 = 67
and if N+1 = 13, then the new average becomes 54 + 91/13 = 54 + 7 = 61
Both 67 and 61 are prime numbers less than 72. So, we cannot uniquely determine the number of students in the class.
The average weight of 8 person's increases by 2.5 kg when a new person comes in place of one of them weighing 65 kg. What is the weight of the new person?
- a)75 Kg
- b)50 Kg
- c)85 Kg
- d)80 Kg
Correct answer is option 'C'. Can you explain this answer?
a)
75 Kg
b)
50 Kg
c)
85 Kg
d)
80 Kg

|
Gowri Chakraborty answered |
Total weight increased = (8 x 2.5) kg = 20 kg.
Weight of new person = (65 + 20) kg = 85 kg.
Arun obtained 76, 65, 82, 67 and 85 marks (out in 100) in English, Mathematics, Chemistry, Biology and Physics. What is his average mark?
- a)53
- b)54
- c)72
- d)75
Correct answer is option 'D'. Can you explain this answer?
a)
53
b)
54
c)
72
d)
75

|
Manoj Ghosh answered |
Average = (76 + 65 + 82 + 67 + 85 )/ 5 = 375/5 = 75.
A car owner buys diesel at Rs.7.50, Rs. 8 and Rs. 8.50 per litre for three successive years. What approximately is the average cost per litre of diesel if he spends Rs. 4000 each year?
- a)Rs. 8
- b)Rs. 7.98
- c)Rs. 6.2
- d)Rs. 8.1
Correct answer is option 'B'. Can you explain this answer?
a)
Rs. 8
b)
Rs. 7.98
c)
Rs. 6.2
d)
Rs. 8.1

|
Ishani Rane answered |
Total quantity of petrol consumed in 3 years =(4000/7.50+4000/8+4000/8.50) liters
= 4000(2/15+1/8+2/17) liters
= 76700/51 liters
Total amount spent = Rs. (3 x 4000) = Rs. 12000.
Average cost = Rs. (12000*51/76700) = Rs. 7.98.
There are n weights in a bag measuring 1kg, 2kg and so on till n kg. These weights are divided into 3 parts. The first part contains the weights 1kg, 4kg, 7kg, and so on. The second part contains the weights 2kg, 5kg, 8kg and so on. The third part contains the remaining weights. The average weights any two of the three parts is equal to the weight present in those parts but the average weight of the remaining one part is not equal to the weight present in that part. Which of the following can be a possible value of n?- a)90
- b)93
- c)96
- d)88
Correct answer is option 'D'. Can you explain this answer?
There are n weights in a bag measuring 1kg, 2kg and so on till n kg. These weights are divided into 3 parts. The first part contains the weights 1kg, 4kg, 7kg, and so on. The second part contains the weights 2kg, 5kg, 8kg and so on. The third part contains the remaining weights. The average weights any two of the three parts is equal to the weight present in those parts but the average weight of the remaining one part is not equal to the weight present in that part. Which of the following can be a possible value of n?
a)
90
b)
93
c)
96
d)
88
|
|
Rajeev Kumar answered |
We know that if in an AP the number of terms in a series is odd, the average of the terms of the series is equal to the middle term of the series. However if the number of terms in the series is even, the average of all the terms of the series is not equal to one of the terms of the series. Hence the three part contain terms 2x+1, 2x+1, 2x or 2x-1, 2x-1, 2x
Hence the total number of parts = 2x+1+2x+1+2x or 2x-1+2x-1+2x = 6x+2 or 6x-2
Among the options, the only number of the form 6x+2 or 6x-2 is 88. Hence 88 can be the required value of n.
Hence the total number of parts = 2x+1+2x+1+2x or 2x-1+2x-1+2x = 6x+2 or 6x-2
Among the options, the only number of the form 6x+2 or 6x-2 is 88. Hence 88 can be the required value of n.
Consider a class of 40 students whose average weight is 40 kgs. m new students join this class whose average weight is n kgs. If it is known that m + n = 50, what is the maximum possible average weight of the class now?
- a)40.18 Kgs
- b)40.56 Kgs
- c)40.67 Kgs
- d)40.49 Kgs
Correct answer is option 'B'. Can you explain this answer?
Consider a class of 40 students whose average weight is 40 kgs. m new students join this class whose average weight is n kgs. If it is known that m + n = 50, what is the maximum possible average weight of the class now?
a)
40.18 Kgs
b)
40.56 Kgs
c)
40.67 Kgs
d)
40.49 Kgs
|
|
Rajeev Kumar answered |
If the overall average weight has to increase after the new people are added, the average weight of the new entrants has to be higher than 40.
So, n > 40
Consequently, m has to be < 10 (as n + m = 50)
Working with the “differences"? approach, we know that the total additional weight added by “m"? students would be (n - 40) each, above the already existing average of 40. m(n - 40) is the total extra additional weight added, which is shared amongst 40 + m students.
So, m * (n−40)(m+40)(n−40)(m+40) has to be maximum for the overall average to be maximum.
At this point, use the trial and error approach (or else, go with the answer options) to arrive at the answer.
So, n > 40
Consequently, m has to be < 10 (as n + m = 50)
Working with the “differences"? approach, we know that the total additional weight added by “m"? students would be (n - 40) each, above the already existing average of 40. m(n - 40) is the total extra additional weight added, which is shared amongst 40 + m students.
So, m * (n−40)(m+40)(n−40)(m+40) has to be maximum for the overall average to be maximum.
At this point, use the trial and error approach (or else, go with the answer options) to arrive at the answer.
The maximum average occurs when m = 5, and n = 45
And the average is 40 + (45 – 40) * 545545 = 40 + 5959 = 40.56 kgs
And the average is 40 + (45 – 40) * 545545 = 40 + 5959 = 40.56 kgs
The question is "what is the maximum possible average weight of the class now?"
Hence, the answer is "40.56 kgs".
A car owner buys petrol at Rs.7.50, Rs. 8 and Rs. 8.50 per litre for three successive years. What approximately is the average cost per litre of petrol if he spends Rs. 4000 each year?
- a)Rs. 8
- b)Rs. 7.98
- c)Rs. 6.2
- d)Rs. 8.1
Correct answer is option 'B'. Can you explain this answer?
a)
Rs. 8
b)
Rs. 7.98
c)
Rs. 6.2
d)
Rs. 8.1

|
Arya Roy answered |
Average cost per litre of petrol = Total amount / Total quantity of petrol
Re. 4000 is spent each year, so total amount spent = 3 * Rs. 4000 = Rs. 12,000
Total quantity of petrol consumed in 3 years = (4000/7.50) + (4000/8) + (4000/8.50) litres
= 533.3 + 500 + 470.6 = 1505
Average cost = Total amount / Total quantity
= 12000/1504 = 7.98
To find quickly, you can take cube root of (7.50 * 8 * 8.50), and it will be slightly less than 8.
The average monthly income of P and Q is Rs. 5050. The average monthly income of Q and R is Rs. 6250 and the average monthly income of P and R is Rs. 5200. The monthly income of P is:
- a)3500
- b)4000
- c)4050
- d)5000
Correct answer is option 'B'. Can you explain this answer?
a)
3500
b)
4000
c)
4050
d)
5000

|
Sameer Rane answered |
Let monthly income of A = a
monthly income of B = b
monthly income of C = c
a + b = 2 x 5050 .... (Equation 1)
b + c = 2 x 6250 .... (Equation 2)
a + c = 2 x 5200 .... (Equation 3)
(Equation 1) + (Equation 3) - (Equation 2)
=> a + b + a + c - (b + c) = (2 x 5050) + (2 x 5200) - (2 x 6250)
=> 2a = 2(5050 + 5200 - 6250)
=> a = 4000
i.e., Monthly income of A = 4000
Chapter doubts & questions for Averages - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Averages - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily