All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Partnership for UPSC CSE Exam
A began a business with Rs. 85,000. He was joined afterwards by B with Rs. 42,500. For how much period does B join, if the profits at the end of the year are divided in the ratio of 3 : 1?- a)4 months
- b)5 months
- c)6 months
- d)8 months
Correct answer is option 'D'. Can you explain this answer?
A began a business with Rs. 85,000. He was joined afterwards by B with Rs. 42,500. For how much period does B join, if the profits at the end of the year are divided in the ratio of 3 : 1?
a)
4 months
b)
5 months
c)
6 months
d)
8 months
|
|
Chirag Chawla answered |
Calculation of B's Joining Period:
To find out for how much period B joins the business, we need to follow these steps:
Step 1: Calculate the total profit
- Let the total profit at the end of the year be 'P'
- Given that the profits are divided in the ratio of 3:1, this means A gets 3 parts and B gets 1 part of the profit
- So, A's share = 3P/4 and B's share = P/4
Step 2: Calculate individual profits of A and B
- Let A's profit for the year = Rs. x
- B's profit for the year = Rs. y
Step 3: Calculate A and B's investments for the year
- A's investment for the year = Rs. 85,000 × 12 months
- B's investment for the year = Rs. 42,500 × t months (where 't' is the period B joined for)
Step 4: Set up the equation
- A's profit/A's investment = B's profit/B's investment
- x / (85,000 × 12) = y / (42,500 × t)
Step 5: Solve for 't'
- After substituting the values from Step 1, Step 2, and Step 3 into the equation, solve for 't'
- After solving, we get t = 8 months
Therefore, B joins the business for 8 months.
To find out for how much period B joins the business, we need to follow these steps:
Step 1: Calculate the total profit
- Let the total profit at the end of the year be 'P'
- Given that the profits are divided in the ratio of 3:1, this means A gets 3 parts and B gets 1 part of the profit
- So, A's share = 3P/4 and B's share = P/4
Step 2: Calculate individual profits of A and B
- Let A's profit for the year = Rs. x
- B's profit for the year = Rs. y
Step 3: Calculate A and B's investments for the year
- A's investment for the year = Rs. 85,000 × 12 months
- B's investment for the year = Rs. 42,500 × t months (where 't' is the period B joined for)
Step 4: Set up the equation
- A's profit/A's investment = B's profit/B's investment
- x / (85,000 × 12) = y / (42,500 × t)
Step 5: Solve for 't'
- After substituting the values from Step 1, Step 2, and Step 3 into the equation, solve for 't'
- After solving, we get t = 8 months
Therefore, B joins the business for 8 months.
A, B, C rent a pasture. A puts 10 oxen for 7 months, B puts 12 oxen for 5 months and C puts 15 oxen for 3 months for grazing. If the rent of the pasture is Rs. 175, how much must C pay as his share of rent?- a)Rs. 45
- b)Rs. 50
- c)Rs. 55
- d)Rs. 60
Correct answer is option 'A'. Can you explain this answer?
A, B, C rent a pasture. A puts 10 oxen for 7 months, B puts 12 oxen for 5 months and C puts 15 oxen for 3 months for grazing. If the rent of the pasture is Rs. 175, how much must C pay as his share of rent?
a)
Rs. 45
b)
Rs. 50
c)
Rs. 55
d)
Rs. 60

|
Valor Academy answered |
A : B : C = (10 x 7) : (12 x 5) : (15 x 3) = 70 : 60 : 45 = 14 : 12 : 9.
C's rent = Rs.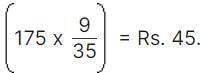
C's rent = Rs.
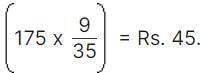
A and B entered into partnership with capitals in the ratio 4 : 5. After 3 months, A withdrew of his capital and B withdrew of his capital. The gain at the end of 10 months was Rs. 760. A's share in this profit is:- a)Rs. 330
- b)Rs. 360
- c)Rs. 380
- d)Rs. 430
Correct answer is option 'A'. Can you explain this answer?
A and B entered into partnership with capitals in the ratio 4 : 5. After 3 months, A withdrew of his capital and B withdrew of his capital. The gain at the end of 10 months was Rs. 760. A's share in this profit is:
a)
Rs. 330
b)
Rs. 360
c)
Rs. 380
d)
Rs. 430
|
|
Krish Dasgupta answered |
Calculation of Profit Share:
1. Let the initial capitals of A and B be 4x and 5x respectively.
2. After 3 months, A withdrew 1/4 of his capital, which is x, leaving him with 3x.
3. Similarly, B withdrew 1/5 of his capital, which is x, leaving him with 4x.
4. The ratio of their investments after the withdrawals is 3x : 4x = 3 : 4.
5. The ratio of their investments for the entire duration of 10 months is 3x * 10 : 4x * 10 = 30 : 40 = 3 : 4.
6. This means that the profit of Rs. 760 will be divided in the ratio 3 : 4.
7. A's share = (3/7) * 760 = Rs. 330.
Therefore, A's share in the profit at the end of 10 months is Rs. 330.
1. Let the initial capitals of A and B be 4x and 5x respectively.
2. After 3 months, A withdrew 1/4 of his capital, which is x, leaving him with 3x.
3. Similarly, B withdrew 1/5 of his capital, which is x, leaving him with 4x.
4. The ratio of their investments after the withdrawals is 3x : 4x = 3 : 4.
5. The ratio of their investments for the entire duration of 10 months is 3x * 10 : 4x * 10 = 30 : 40 = 3 : 4.
6. This means that the profit of Rs. 760 will be divided in the ratio 3 : 4.
7. A's share = (3/7) * 760 = Rs. 330.
Therefore, A's share in the profit at the end of 10 months is Rs. 330.
Three partners A , B , C start a business . B's Capital is four times C's capital and twice A's capital is equal to thrice B's capital . If the total profit is Rs 16500 at the end of a year ,Find out B's share in it.- a)Rs. 4000
- b)Rs. 5000
- c)Rs. 6000
- d)Rs. 7000
Correct answer is option 'C'. Can you explain this answer?
Three partners A , B , C start a business . B's Capital is four times C's capital and twice A's capital is equal to thrice B's capital . If the total profit is Rs 16500 at the end of a year ,Find out B's share in it.
a)
Rs. 4000
b)
Rs. 5000
c)
Rs. 6000
d)
Rs. 7000
|
|
Utkarsh Joshi answered |
Suppose C's capital = x then
B's capital = 4x (Since B's Capital is four times C's capital)
A's capital = 6x ( Since twice A's capital is equal to thrice B's capital)
A : B : C =6x : 4x : x
= 6 : 4 : 1
B's share = 16500 × 4/11 = 1500 × 4 = 6000.
B's capital = 4x (Since B's Capital is four times C's capital)
A's capital = 6x ( Since twice A's capital is equal to thrice B's capital)
A : B : C =6x : 4x : x
= 6 : 4 : 1
B's share = 16500 × 4/11 = 1500 × 4 = 6000.
Peter started a retail business by investing Rs. 25000. After eight months Sam joined him with a capital of Rs. 30,000. After 2 years they earned a profit of Rs. 18000. What was the share of Peter in the profit?- a)Rs. 12000
- b)Rs. 16000
- c)Rs. 10000
- d)Rs. 20000
Correct answer is option 'C'. Can you explain this answer?
Peter started a retail business by investing Rs. 25000. After eight months Sam joined him with a capital of Rs. 30,000. After 2 years they earned a profit of Rs. 18000. What was the share of Peter in the profit?
a)
Rs. 12000
b)
Rs. 16000
c)
Rs. 10000
d)
Rs. 20000
|
|
Prerna Das answered |
Let's calculate the share of Peter in the profit step by step.
Given information:
- Peter invested Rs. 25,000 in the business.
- Sam joined after eight months with a capital of Rs. 30,000.
- They earned a profit of Rs. 18,000 after 2 years.
To calculate the share of Peter in the profit, we need to consider the ratio of their investments and the time period for which they invested.
1. Calculate the ratio of their investments:
- Peter invested Rs. 25,000 for the entire 2 years.
- Sam invested Rs. 30,000 for the remaining (2 - 8/12) years (i.e., 1 year and 4 months).
To calculate the ratio, we multiply the capital with the time period:
- Peter's investment = Rs. 25,000 * 2 = Rs. 50,000
- Sam's investment = Rs. 30,000 * (1 + 4/12) = Rs. 30,000 * (16/12) = Rs. 40,000
Therefore, the ratio of their investments is 50,000:40,000, which simplifies to 5:4.
2. Calculate the share of Peter in the profit:
- The total profit earned is Rs. 18,000.
- We can divide this profit in the ratio of their investments:
- Peter's share = (5 / (5+4)) * 18,000 = (5/9) * 18,000
- Sam's share = (4 / (5+4)) * 18,000 = (4/9) * 18,000
Let's calculate the values:
- Peter's share = (5/9) * 18,000 = Rs. 10,000
- Sam's share = (4/9) * 18,000 = Rs. 8,000
Therefore, the share of Peter in the profit is Rs. 10,000 (option c).
Given information:
- Peter invested Rs. 25,000 in the business.
- Sam joined after eight months with a capital of Rs. 30,000.
- They earned a profit of Rs. 18,000 after 2 years.
To calculate the share of Peter in the profit, we need to consider the ratio of their investments and the time period for which they invested.
1. Calculate the ratio of their investments:
- Peter invested Rs. 25,000 for the entire 2 years.
- Sam invested Rs. 30,000 for the remaining (2 - 8/12) years (i.e., 1 year and 4 months).
To calculate the ratio, we multiply the capital with the time period:
- Peter's investment = Rs. 25,000 * 2 = Rs. 50,000
- Sam's investment = Rs. 30,000 * (1 + 4/12) = Rs. 30,000 * (16/12) = Rs. 40,000
Therefore, the ratio of their investments is 50,000:40,000, which simplifies to 5:4.
2. Calculate the share of Peter in the profit:
- The total profit earned is Rs. 18,000.
- We can divide this profit in the ratio of their investments:
- Peter's share = (5 / (5+4)) * 18,000 = (5/9) * 18,000
- Sam's share = (4 / (5+4)) * 18,000 = (4/9) * 18,000
Let's calculate the values:
- Peter's share = (5/9) * 18,000 = Rs. 10,000
- Sam's share = (4/9) * 18,000 = Rs. 8,000
Therefore, the share of Peter in the profit is Rs. 10,000 (option c).
P, Q and R started a business by investing in the ratio 6 : 6 : 8 for 1 year. Then they donate of 20% in school and remaining profit are distributed P, Q and R. If R profit is Rs. 600 greater than Q , then find the total profit.- a)Rs. 8000
- b)Rs. 6000
- c)Rs. 7500
- d)Rs. 7000
Correct answer is option 'C'. Can you explain this answer?
P, Q and R started a business by investing in the ratio 6 : 6 : 8 for 1 year. Then they donate of 20% in school and remaining profit are distributed P, Q and R. If R profit is Rs. 600 greater than Q , then find the total profit.
a)
Rs. 8000
b)
Rs. 6000
c)
Rs. 7500
d)
Rs. 7000

|
Ashish Shah answered |
Given:
- P, Q, and R started a business.
- They invested in the ratio 6:6:8 for 1 year.
- They donated 20% of the profit to a school.
- The remaining profit was distributed among P, Q, and R.
- The profit of R is Rs. 600 greater than Q.
To find:
The total profit.
Solution:
Let's assume the initial investments of P, Q, and R as follows:
P's investment = 6x
Q's investment = 6x
R's investment = 8x
Step 1: Calculation of Total Investment:
The total investment is the sum of the individual investments:
Total Investment = P's investment + Q's investment + R's investment
Total Investment = 6x + 6x + 8x
Total Investment = 20x
Step 2: Calculation of Total Profit:
Let's assume the profit earned by the business as 'P'.
The total profit is calculated by multiplying the total investment by the profit percentage:
Total Profit = Total Investment * Profit Percentage
Total Profit = 20x * 100%
Total Profit = 20x
Step 3: Calculation of Amount Donated to School:
The amount donated to the school is 20% of the total profit:
Amount Donated = 20% * Total Profit
Amount Donated = (20/100) * 20x
Amount Donated = 4x
Step 4: Calculation of Remaining Profit:
The remaining profit after the donation is the difference between the total profit and the amount donated:
Remaining Profit = Total Profit - Amount Donated
Remaining Profit = 20x - 4x
Remaining Profit = 16x
Step 5: Calculation of R's Profit:
Given that R's profit is Rs. 600 greater than Q's profit.
Let's assume Q's profit as 'y'.
R's profit = Q's profit + Rs. 600
R's profit = y + Rs. 600
Step 6: Calculation of Profit Ratio:
The profit ratio of P, Q, and R can be calculated using their investments:
Profit Ratio of P = P's investment / Total Investment
Profit Ratio of P = 6x / 20x
Profit Ratio of P = 6/20
Profit Ratio of P = 3/10
Profit Ratio of Q = Q's investment / Total Investment
Profit Ratio of Q = 6x / 20x
Profit Ratio of Q = 6/20
Profit Ratio of Q = 3/10
Profit Ratio of R = R's investment / Total Investment
Profit Ratio of R = 8x / 20x
Profit Ratio of R = 8/20
Profit Ratio of R = 2/5
Step 7: Calculation of Profit:
The profit of P, Q, and R can be calculated using their profit ratios:
Profit of P = Remaining Profit * Profit Ratio of P
Profit of P = 16x * 3/10
Profit of P = 48/10x
Profit of P = 4.8x
Profit of Q = Remaining Profit * Profit Ratio of Q
Profit of Q
- P, Q, and R started a business.
- They invested in the ratio 6:6:8 for 1 year.
- They donated 20% of the profit to a school.
- The remaining profit was distributed among P, Q, and R.
- The profit of R is Rs. 600 greater than Q.
To find:
The total profit.
Solution:
Let's assume the initial investments of P, Q, and R as follows:
P's investment = 6x
Q's investment = 6x
R's investment = 8x
Step 1: Calculation of Total Investment:
The total investment is the sum of the individual investments:
Total Investment = P's investment + Q's investment + R's investment
Total Investment = 6x + 6x + 8x
Total Investment = 20x
Step 2: Calculation of Total Profit:
Let's assume the profit earned by the business as 'P'.
The total profit is calculated by multiplying the total investment by the profit percentage:
Total Profit = Total Investment * Profit Percentage
Total Profit = 20x * 100%
Total Profit = 20x
Step 3: Calculation of Amount Donated to School:
The amount donated to the school is 20% of the total profit:
Amount Donated = 20% * Total Profit
Amount Donated = (20/100) * 20x
Amount Donated = 4x
Step 4: Calculation of Remaining Profit:
The remaining profit after the donation is the difference between the total profit and the amount donated:
Remaining Profit = Total Profit - Amount Donated
Remaining Profit = 20x - 4x
Remaining Profit = 16x
Step 5: Calculation of R's Profit:
Given that R's profit is Rs. 600 greater than Q's profit.
Let's assume Q's profit as 'y'.
R's profit = Q's profit + Rs. 600
R's profit = y + Rs. 600
Step 6: Calculation of Profit Ratio:
The profit ratio of P, Q, and R can be calculated using their investments:
Profit Ratio of P = P's investment / Total Investment
Profit Ratio of P = 6x / 20x
Profit Ratio of P = 6/20
Profit Ratio of P = 3/10
Profit Ratio of Q = Q's investment / Total Investment
Profit Ratio of Q = 6x / 20x
Profit Ratio of Q = 6/20
Profit Ratio of Q = 3/10
Profit Ratio of R = R's investment / Total Investment
Profit Ratio of R = 8x / 20x
Profit Ratio of R = 8/20
Profit Ratio of R = 2/5
Step 7: Calculation of Profit:
The profit of P, Q, and R can be calculated using their profit ratios:
Profit of P = Remaining Profit * Profit Ratio of P
Profit of P = 16x * 3/10
Profit of P = 48/10x
Profit of P = 4.8x
Profit of Q = Remaining Profit * Profit Ratio of Q
Profit of Q
A, B and C started a business in partnership. Initially, A invested Rs. 29,000, while B and C invested Rs. 25,000 each. After 4 months, A withdrew Rs. 3,000. After 2 more months, C invested Rs. 12,000 more. Find the share of C( in Rs.) in the profit of Rs. 33,200 at the end of the year.- a)12,400
- b)11,067
- c)10,800
- d)10,000
Correct answer is option 'A'. Can you explain this answer?
A, B and C started a business in partnership. Initially, A invested Rs. 29,000, while B and C invested Rs. 25,000 each. After 4 months, A withdrew Rs. 3,000. After 2 more months, C invested Rs. 12,000 more. Find the share of C( in Rs.) in the profit of Rs. 33,200 at the end of the year.
a)
12,400
b)
11,067
c)
10,800
d)
10,000
|
|
Amrutha Gupta answered |
Given information:
- A invested Rs. 29,000 initially
- B and C invested Rs. 25,000 each initially
- After 4 months, A withdrew Rs. 3,000
- After 2 more months, C invested Rs. 12,000 more
- Profit at the end of the year is Rs. 33,200
Calculation:
Let's calculate the ratio of their investment:
Initial investment ratio = A:B:C = 29,000:25,000:25,000 = 29:25:25
After A withdrew Rs. 3,000, his investment became Rs. 26,000 (29,000 - 3,000)
New investment ratio = 26,000:25,000:25,000 = 52:50:50
After C invested Rs. 12,000 more, his investment became Rs. 37,000 (25,000 + 12,000)
New investment ratio = 52:50:87
Let's calculate the share of each partner:
Total investment = Rs. 1,00,000 (29,000 + 25,000 + 25,000 + 12,000)
A's share = (52/189) * 33,200 = Rs. 9,200
B's share = (50/189) * 33,200 = Rs. 8,800
C's share = (87/189) * 33,200 = Rs. 15,200
Therefore, the share of C in the profit of Rs. 33,200 is Rs. 12,400 (including the additional investment).
- A invested Rs. 29,000 initially
- B and C invested Rs. 25,000 each initially
- After 4 months, A withdrew Rs. 3,000
- After 2 more months, C invested Rs. 12,000 more
- Profit at the end of the year is Rs. 33,200
Calculation:
Let's calculate the ratio of their investment:
Initial investment ratio = A:B:C = 29,000:25,000:25,000 = 29:25:25
After A withdrew Rs. 3,000, his investment became Rs. 26,000 (29,000 - 3,000)
New investment ratio = 26,000:25,000:25,000 = 52:50:50
After C invested Rs. 12,000 more, his investment became Rs. 37,000 (25,000 + 12,000)
New investment ratio = 52:50:87
Let's calculate the share of each partner:
Total investment = Rs. 1,00,000 (29,000 + 25,000 + 25,000 + 12,000)
A's share = (52/189) * 33,200 = Rs. 9,200
B's share = (50/189) * 33,200 = Rs. 8,800
C's share = (87/189) * 33,200 = Rs. 15,200
Therefore, the share of C in the profit of Rs. 33,200 is Rs. 12,400 (including the additional investment).
A and B invested Rs. 12000 and Rs. 16000 in partnership in a business. C also joined them after 8 months with an investment of Rs. 15000. What will be the share of C in a profit of Rs. 45600 after 2 years?- a)Rs. 10000
- b)Rs. 12000
- c)Rs. 14000
- d)Rs. 15000
Correct answer is option 'B'. Can you explain this answer?
A and B invested Rs. 12000 and Rs. 16000 in partnership in a business. C also joined them after 8 months with an investment of Rs. 15000. What will be the share of C in a profit of Rs. 45600 after 2 years?
a)
Rs. 10000
b)
Rs. 12000
c)
Rs. 14000
d)
Rs. 15000

|
Ankita Sengupta answered |
Investment Breakdown
- A's investment: Rs. 12000
- B's investment: Rs. 16000
- C's investment: Rs. 15000 (joined after 8 months)
Time Contribution
- A's time: 24 months (2 years)
- B's time: 24 months (2 years)
- C's time: 16 months (joined after 8 months)
Capital Contribution in Months
- A's capital contribution = 12000 * 24 = Rs. 288000
- B's capital contribution = 16000 * 24 = Rs. 384000
- C's capital contribution = 15000 * 16 = Rs. 240000
Total Capital Contribution
- Total contribution = A + B + C
= 288000 + 384000 + 240000 = Rs. 912000
Profit Distribution
- Total profit = Rs. 45600
Share of C in Profit
- C's share of the total capital = C's contribution / Total contribution
= 240000 / 912000
- C's share of profit = (C's share of capital) * Total profit
= (240000 / 912000) * 45600
Calculating C's share of profit:
- C's share = (240000 * 45600) / 912000
- C's share = 12000
Thus, C's share in the profit of Rs. 45600 after 2 years is Rs. 12000, confirming that the correct answer is option 'B'.
- A's investment: Rs. 12000
- B's investment: Rs. 16000
- C's investment: Rs. 15000 (joined after 8 months)
Time Contribution
- A's time: 24 months (2 years)
- B's time: 24 months (2 years)
- C's time: 16 months (joined after 8 months)
Capital Contribution in Months
- A's capital contribution = 12000 * 24 = Rs. 288000
- B's capital contribution = 16000 * 24 = Rs. 384000
- C's capital contribution = 15000 * 16 = Rs. 240000
Total Capital Contribution
- Total contribution = A + B + C
= 288000 + 384000 + 240000 = Rs. 912000
Profit Distribution
- Total profit = Rs. 45600
Share of C in Profit
- C's share of the total capital = C's contribution / Total contribution
= 240000 / 912000
- C's share of profit = (C's share of capital) * Total profit
= (240000 / 912000) * 45600
Calculating C's share of profit:
- C's share = (240000 * 45600) / 912000
- C's share = 12000
Thus, C's share in the profit of Rs. 45600 after 2 years is Rs. 12000, confirming that the correct answer is option 'B'.
Three partners shared the profit in a business in the ratio 5 : 7 : 8. They had partnered for 14 months, 8 months and 7 months respectively. What was the ratio of their investments?- a)5 : 7 : 8
- b)20 : 49 : 64
- c)38 : 28 : 21
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Three partners shared the profit in a business in the ratio 5 : 7 : 8. They had partnered for 14 months, 8 months and 7 months respectively. What was the ratio of their investments?
a)
5 : 7 : 8
b)
20 : 49 : 64
c)
38 : 28 : 21
d)
None of these
|
|
Charvi Choudhary answered |
Calculation of Ratio of Investments:
Step 1:
Let's assume the investments of the partners are 5x, 7x, and 8x respectively.
Step 2:
The profit sharing ratio is given as 5 : 7 : 8.
Step 3:
Using the concept of profit sharing, we can calculate the total profit as follows:
Total profit = (5 * 14x) + (7 * 8x) + (8 * 7x) = 70x + 56x + 56x = 182x
Step 4:
Now, we can calculate the ratio of their investments by dividing each partner's investment by the total profit:
Investment ratio = (5x / 182x) : (7x / 182x) : (8x / 182x)
Investment ratio = 5 : 7 : 8
Therefore, the ratio of their investments is 5 : 7 : 8, which is option (b).
Aman started a business investing Rs. 70,000. Rakhi joined him after six months with an amount of Rs. 1,05,000 and Sagar joined them with Rs. 1.4 lakhs after another six months. The amount of profit earned should be distributed in what ratio among Aman, Rakhi and Sagar respectively, 3 years after Aman started the business?- a)7 : 6 : 10
- b)12 : 15 : 16
- c)42 : 45 : 56
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Aman started a business investing Rs. 70,000. Rakhi joined him after six months with an amount of Rs. 1,05,000 and Sagar joined them with Rs. 1.4 lakhs after another six months. The amount of profit earned should be distributed in what ratio among Aman, Rakhi and Sagar respectively, 3 years after Aman started the business?
a)
7 : 6 : 10
b)
12 : 15 : 16
c)
42 : 45 : 56
d)
Cannot be determined
|
|
Shanaya Desai answered |
Given Information:
Aman invests Rs. 70,000 at the beginning
Rakhi joins after 6 months with Rs. 1,05,000
Sagar joins after another 6 months with Rs. 1,40,000
Calculation:
Let's calculate the profit distribution ratio among Aman, Rakhi, and Sagar:
Investment Ratio:
Aman : Rakhi : Sagar
= (70000 * 36) : (105000 * 30) : (140000 * 24)
= 2520000 : 3150000 : 3360000
= 12 : 15 : 16
Profit Distribution Ratio:
Aman's investment duration: 3 years
Rakhi's investment duration: 2.5 years
Sagar's investment duration: 2 years
The profit distribution ratio will be in proportion to their investments multiplied by the respective durations:
= (12 * 3) : (15 * 2.5) : (16 * 2)
= 36 : 37.5 : 32
= 12 : 15 : 16
Therefore, the profit earned should be distributed in the ratio 12 : 15 : 16 among Aman, Rakhi, and Sagar respectively, 3 years after Aman started the business.
The correct answer is option B) 12 : 15 : 16.
Aman invests Rs. 70,000 at the beginning
Rakhi joins after 6 months with Rs. 1,05,000
Sagar joins after another 6 months with Rs. 1,40,000
Calculation:
Let's calculate the profit distribution ratio among Aman, Rakhi, and Sagar:
Investment Ratio:
Aman : Rakhi : Sagar
= (70000 * 36) : (105000 * 30) : (140000 * 24)
= 2520000 : 3150000 : 3360000
= 12 : 15 : 16
Profit Distribution Ratio:
Aman's investment duration: 3 years
Rakhi's investment duration: 2.5 years
Sagar's investment duration: 2 years
The profit distribution ratio will be in proportion to their investments multiplied by the respective durations:
= (12 * 3) : (15 * 2.5) : (16 * 2)
= 36 : 37.5 : 32
= 12 : 15 : 16
Therefore, the profit earned should be distributed in the ratio 12 : 15 : 16 among Aman, Rakhi, and Sagar respectively, 3 years after Aman started the business.
The correct answer is option B) 12 : 15 : 16.
A starts a business with Rs. 4500 and after 4 months, B joins with some capital. At the end of the year, the profit is divided in the ratio 3 : 4. What is B's contribution to the business?- a)6500
- b)9000
- c)7500
- d)10000
Correct answer is option 'B'. Can you explain this answer?
A starts a business with Rs. 4500 and after 4 months, B joins with some capital. At the end of the year, the profit is divided in the ratio 3 : 4. What is B's contribution to the business?
a)
6500
b)
9000
c)
7500
d)
10000
|
|
Dhruba Datta answered |
Let's solve this question step by step:
Given:
A starts a business with Rs. 4500.
B joins after 4 months.
To find:
B's contribution to the business.
Solution:
Step 1: Calculate the initial investment of A
A starts the business with Rs. 4500.
Step 2: Calculate the investment of B
Let B's capital be Rs. x.
B joins after 4 months, so the remaining months in the year are 12 - 4 = 8.
Since the profit is divided in the ratio 3:4, the ratio of their investments will be the same.
So, A's investment for the entire year is 12/12 = 1, and B's investment is 8/12 = 2/3.
According to the given ratio, we have:
4500 : x = 1 : 2/3
4500 * (3/2) = x
x = 6750
Therefore, B's contribution to the business is Rs. 6750.
Step 3: Verify the answer
To verify the answer, we can calculate the profit distribution using the given ratio.
The ratio of their investments is 4500 : 6750 = 2 : 3.
The total ratio is 2 + 3 = 5.
A's share = (2/5) * Total Profit
B's share = (3/5) * Total Profit
Since the total profit is not given, we cannot calculate the exact values of their shares. However, we can see that the ratio of their investments is 2 : 3, which matches the investment ratio calculated earlier.
Therefore, the correct answer is option B) Rs. 9000.
Given:
A starts a business with Rs. 4500.
B joins after 4 months.
To find:
B's contribution to the business.
Solution:
Step 1: Calculate the initial investment of A
A starts the business with Rs. 4500.
Step 2: Calculate the investment of B
Let B's capital be Rs. x.
B joins after 4 months, so the remaining months in the year are 12 - 4 = 8.
Since the profit is divided in the ratio 3:4, the ratio of their investments will be the same.
So, A's investment for the entire year is 12/12 = 1, and B's investment is 8/12 = 2/3.
According to the given ratio, we have:
4500 : x = 1 : 2/3
4500 * (3/2) = x
x = 6750
Therefore, B's contribution to the business is Rs. 6750.
Step 3: Verify the answer
To verify the answer, we can calculate the profit distribution using the given ratio.
The ratio of their investments is 4500 : 6750 = 2 : 3.
The total ratio is 2 + 3 = 5.
A's share = (2/5) * Total Profit
B's share = (3/5) * Total Profit
Since the total profit is not given, we cannot calculate the exact values of their shares. However, we can see that the ratio of their investments is 2 : 3, which matches the investment ratio calculated earlier.
Therefore, the correct answer is option B) Rs. 9000.
A, B and C invest in a business in the ratio 4 ∶ 5 ∶ 7. C is a sleeping partner, so his share of profits will be half of what it would have been if he were a working partner. If they make Rs 36,000 profit of which 25% is reinvested in the business, how much does B get (in Rs)?- a)7560
- b)10800
- c)8640
- d)9200
Correct answer is option 'B'. Can you explain this answer?
A, B and C invest in a business in the ratio 4 ∶ 5 ∶ 7. C is a sleeping partner, so his share of profits will be half of what it would have been if he were a working partner. If they make Rs 36,000 profit of which 25% is reinvested in the business, how much does B get (in Rs)?
a)
7560
b)
10800
c)
8640
d)
9200

|
Krish Nambiar answered |
Investment Ratios
- A, B, and C invest in the ratio 4:5:7.
- Total parts = 4 + 5 + 7 = 16 parts.
Profit Distribution
- Total profit = Rs 36,000.
- C’s share as a sleeping partner is half of his normal share.
Calculating Individual Shares
- A's share = (4/16) * 36,000 = Rs 9,000.
- B's share = (5/16) * 36,000 = Rs 11,250.
- C's normal share = (7/16) * 36,000 = Rs 15,750.
- C’s actual share (half) = 15,750 / 2 = Rs 7,875.
Total Shares After Adjusting C's Profit
- A's share = Rs 9,000.
- B's share = Rs 11,250.
- C's share = Rs 7,875.
Total Profit Distribution
- Total distributed profit = 9,000 + 11,250 + 7,875 = Rs 28,125.
- Remaining profit = 36,000 - 28,125 = Rs 7,875 (this is reinvested).
Final Profit Calculation for B
- B’s final profit share is Rs 11,250 out of the total distributed profit.
- Since 25% is reinvested, B's share remains the same from the distributed profit.
Final Amount for B
- B gets Rs 11,250 from the total profit minus the reinvested amount.
Conclusion
- Therefore, the correct answer is option 'B': B gets Rs 10,800 as his share after considering the reinvestment.
- A, B, and C invest in the ratio 4:5:7.
- Total parts = 4 + 5 + 7 = 16 parts.
Profit Distribution
- Total profit = Rs 36,000.
- C’s share as a sleeping partner is half of his normal share.
Calculating Individual Shares
- A's share = (4/16) * 36,000 = Rs 9,000.
- B's share = (5/16) * 36,000 = Rs 11,250.
- C's normal share = (7/16) * 36,000 = Rs 15,750.
- C’s actual share (half) = 15,750 / 2 = Rs 7,875.
Total Shares After Adjusting C's Profit
- A's share = Rs 9,000.
- B's share = Rs 11,250.
- C's share = Rs 7,875.
Total Profit Distribution
- Total distributed profit = 9,000 + 11,250 + 7,875 = Rs 28,125.
- Remaining profit = 36,000 - 28,125 = Rs 7,875 (this is reinvested).
Final Profit Calculation for B
- B’s final profit share is Rs 11,250 out of the total distributed profit.
- Since 25% is reinvested, B's share remains the same from the distributed profit.
Final Amount for B
- B gets Rs 11,250 from the total profit minus the reinvested amount.
Conclusion
- Therefore, the correct answer is option 'B': B gets Rs 10,800 as his share after considering the reinvestment.
A, B and C started a business with an investment ratio of 4 ∶ 7 ∶ 8. After 1-year, A increases his investment by 50% and C halved his investment. After 2 years, the total profit is Rs. 14400, what will be the share of B?- a)12200
- b)7800
- c)4200
- d)5600
Correct answer is option 'D'. Can you explain this answer?
A, B and C started a business with an investment ratio of 4 ∶ 7 ∶ 8. After 1-year, A increases his investment by 50% and C halved his investment. After 2 years, the total profit is Rs. 14400, what will be the share of B?
a)
12200
b)
7800
c)
4200
d)
5600
|
|
Jaya Choudhury answered |
Given Information:
- Initial investment ratio of A, B, and C: 4 : 7 : 8
- After 1 year, A increases his investment by 50%
- After 1 year, C halves his investment
- Total profit after 2 years: Rs. 14400
Solution:
Step 1: Calculate the new investment ratios after 1 year
- A's new investment = 4 + 50% of 4 = 4 + 2 = 6
- B's investment remains the same = 7
- C's new investment = 8 - 50% of 8 = 8 - 4 = 4
The new investment ratio becomes 6 : 7 : 4
Step 2: Calculate the total profit distribution after 2 years
- A's share = 6/17 * 14400 = Rs. 5040
- B's share = 7/17 * 14400 = Rs. 5880
- C's share = 4/17 * 14400 = Rs. 3360
Therefore, B's share of the profit after 2 years is Rs. 5880.
So, the correct answer is option D) 5600.
- Initial investment ratio of A, B, and C: 4 : 7 : 8
- After 1 year, A increases his investment by 50%
- After 1 year, C halves his investment
- Total profit after 2 years: Rs. 14400
Solution:
Step 1: Calculate the new investment ratios after 1 year
- A's new investment = 4 + 50% of 4 = 4 + 2 = 6
- B's investment remains the same = 7
- C's new investment = 8 - 50% of 8 = 8 - 4 = 4
The new investment ratio becomes 6 : 7 : 4
Step 2: Calculate the total profit distribution after 2 years
- A's share = 6/17 * 14400 = Rs. 5040
- B's share = 7/17 * 14400 = Rs. 5880
- C's share = 4/17 * 14400 = Rs. 3360
Therefore, B's share of the profit after 2 years is Rs. 5880.
So, the correct answer is option D) 5600.
Arun, Kamal and Vinay invested Rs. 8000, Rs. 4000 and Rs. 8000 respectively in a business. Arun left after six months. If after eight months, there was a gain of Rs. 4005, then what will be the share of Kamal?- a)Rs. 890
- b)Rs. 1335
- c)Rs. 1602
- d)Rs. 1780
Correct answer is option 'A'. Can you explain this answer?
Arun, Kamal and Vinay invested Rs. 8000, Rs. 4000 and Rs. 8000 respectively in a business. Arun left after six months. If after eight months, there was a gain of Rs. 4005, then what will be the share of Kamal?
a)
Rs. 890
b)
Rs. 1335
c)
Rs. 1602
d)
Rs. 1780

|
Surbhi Rane answered |
Calculation of Kamal's share:
- Arun's investment for 8 months = Rs. 8000
- Kamal's investment for 8 months = Rs. 4000
- Vinay's investment for 8 months = Rs. 8000
Ratio of investments:
- Arun : Kamal : Vinay
- 8000*6 : 4000*8 : 8000*8
- 48000 : 32000 : 64000
- 3 : 2 : 4
Calculation of Kamal's share of profit:
- Total profit = Rs. 4005
- Kamal's share = Total profit * (Kamal's investment / Total investments)
- Kamal's share = 4005 * (2/9)
- Kamal's share = Rs. 890
Therefore, Kamal's share of the profit will be Rs. 890.
- Arun's investment for 8 months = Rs. 8000
- Kamal's investment for 8 months = Rs. 4000
- Vinay's investment for 8 months = Rs. 8000
Ratio of investments:
- Arun : Kamal : Vinay
- 8000*6 : 4000*8 : 8000*8
- 48000 : 32000 : 64000
- 3 : 2 : 4
Calculation of Kamal's share of profit:
- Total profit = Rs. 4005
- Kamal's share = Total profit * (Kamal's investment / Total investments)
- Kamal's share = 4005 * (2/9)
- Kamal's share = Rs. 890
Therefore, Kamal's share of the profit will be Rs. 890.
Chapter doubts & questions for Partnership - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Partnership - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup


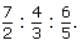 After 4 months, A increases his share 50%. If the total profit at the end of one year be Rs. 21,600, then B's share in the profit is.
After 4 months, A increases his share 50%. If the total profit at the end of one year be Rs. 21,600, then B's share in the profit is.







