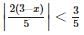All Exams >
JEE >
Mathematics (Maths) for JEE Main & Advanced >
All Questions
All questions of Inequalities for JEE Exam
Find the value of x when x is a natural number and 24x< 100.- a){5,6,……..∞}
- b){1,2,3,4}
- c){1,2,3,4,5}
- d){0,1,2,3,4}
Correct answer is option 'B'. Can you explain this answer?
Find the value of x when x is a natural number and 24x< 100.
a)
{5,6,……..∞}
b)
{1,2,3,4}
c)
{1,2,3,4,5}
d)
{0,1,2,3,4}
|
Shreya Gupta answered |
We are given: 24x < 100
24x < 100
=> 24x /24 < 100/24 [Dividing both sides by positive number.]
=> x < 25/6
When x is a natural number, in this case, the following values of x make the statement true
x = 1, 2, 3, 4.
The solution set of the inequality is {1, 2, 3, 4}.
What is the region represented by x > 0 and y < 0?- a)2nd quadrant
- b)3rd quadrant
- c)4th quadrant
- d)1st quadrant
Correct answer is option 'C'. Can you explain this answer?
What is the region represented by x > 0 and y < 0?
a)
2nd quadrant
b)
3rd quadrant
c)
4th quadrant
d)
1st quadrant
|
|
Suresh Reddy answered |
If x >0 then x will be positive and y less than 0 means it gets negative value
that means it lies in 4th quadrant.
that means it lies in 4th quadrant.
The solution of the inequality 3(2-x)≥2(1-x) for real x is :- a)x < 4
- b)x > 4
- c)x ≤4
- d)x ≥ 4
Correct answer is option 'C'. Can you explain this answer?
The solution of the inequality 3(2-x)≥2(1-x) for real x is :
a)
x < 4
b)
x > 4
c)
x ≤4
d)
x ≥ 4
|
Mohit Rajpoot answered |
3(2 - x) ≥ 2(1 - x)
6 - 3x ≥ 2 - 2x
4 ≥ x
6 - 3x ≥ 2 - 2x
4 ≥ x
Find the solution for the pair of solution x > 1 and x > -1- a)No solution
- b)-1 < x < 1
- c)x < -1
- d)x > 1
Correct answer is option 'D'. Can you explain this answer?
Find the solution for the pair of solution x > 1 and x > -1
a)
No solution
b)
-1 < x < 1
c)
x < -1
d)
x > 1
|
Riya Banerjee answered |
x > 1 and x > -1
Take two points 1,-1 on number line
Therefore x > 1
Take two points 1,-1 on number line
Therefore x > 1
If -5x+2<7x -4, then x is- a)<3/2
- b)<1/2
- c)>1/2
- d)>3/2
Correct answer is option 'C'. Can you explain this answer?
If -5x+2<7x -4, then x is
a)
<3/2
b)
<1/2
c)
>1/2
d)
>3/2
|
Pooja Shah answered |
-5x + 2 < 7x - 4
6 < 12x
x > 1/2
6 < 12x
x > 1/2
Solve: 30x < 200, when x is a natural number:
- a){2, 3, 4, 5, 6}
- b){1, 2, 3, 4, 5, 6}
- c){4, 5, 6, 7, 8, 9}
- d){1, 2, 3, 4, 5, 6, 7}
Correct answer is option 'B'. Can you explain this answer?
Solve: 30x < 200, when x is a natural number:
a)
{2, 3, 4, 5, 6}
b)
{1, 2, 3, 4, 5, 6}
c)
{4, 5, 6, 7, 8, 9}
d)
{1, 2, 3, 4, 5, 6, 7}
|
Learners Habitat answered |
We are given 30x < 200
When x is a natural number, in this case the following values of x make the statement true.
1, 2, 3, 4, 5, 6.
The solution set of the inequality is {1, 2, 3, 4, 5, 6}.
When x is a natural number, in this case the following values of x make the statement true.
1, 2, 3, 4, 5, 6.
The solution set of the inequality is {1, 2, 3, 4, 5, 6}.
The solution of 4x-2 > 6 is- a)x > 2
- b)x < 6
- c)x = 4
- d)x > 4
Correct answer is option 'A'. Can you explain this answer?
The solution of 4x-2 > 6 is
a)
x > 2
b)
x < 6
c)
x = 4
d)
x > 4
|
|
Arjun Kumar answered |
According to the laws of inequality, answer should be x is less than 2.
Find all pairs of consecutive odd natural numbers, both of which are larger than 10, such that their sum is less than 40.- a)(11 , 13) , (13 , 15) , (15 , 17) , (17 , 21)
- b)(9 , 11) , (13 , 15) , (15 , 17) , (17 , 19)
- c)(11 , 13) , (13 , 15) , (17 , 19) , (19 , 21)
- d)(11 , 13) , (13 , 15) , (15 , 17) , (17 , 19)
Correct answer is option 'D'. Can you explain this answer?
Find all pairs of consecutive odd natural numbers, both of which are larger than 10, such that their sum is less than 40.
a)
(11 , 13) , (13 , 15) , (15 , 17) , (17 , 21)
b)
(9 , 11) , (13 , 15) , (15 , 17) , (17 , 19)
c)
(11 , 13) , (13 , 15) , (17 , 19) , (19 , 21)
d)
(11 , 13) , (13 , 15) , (15 , 17) , (17 , 19)
|
|
Dipika Patel answered |
**Explanation:**
To find the pairs of consecutive odd natural numbers that satisfy the given conditions, we need to consider the following:
1. The numbers should be consecutive odd natural numbers.
2. Both numbers should be larger than 10.
3. The sum of the two numbers should be less than 40.
Let's analyze each option to see if it satisfies these conditions:
**Option A: (11, 13), (13, 15), (15, 17), (17, 21)**
- (11, 13): The sum is 24, which is less than 40. This pair satisfies all conditions.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (15, 17): The sum is 32, which is less than 40. This pair satisfies all conditions.
- (17, 21): The sum is 38, which is less than 40. This pair satisfies all conditions.
**Option B: (9, 11), (13, 15), (15, 17), (17, 19)**
- (9, 11): The numbers are not larger than 10. This pair does not satisfy the second condition.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (15, 17): The sum is 32, which is less than 40. This pair satisfies all conditions.
- (17, 19): The sum is 36, which is not less than 40. This pair does not satisfy the third condition.
**Option C: (11, 13), (13, 15), (17, 19), (19, 21)**
- (11, 13): The sum is 24, which is less than 40. This pair satisfies all conditions.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (17, 19): The sum is 36, which is not less than 40. This pair does not satisfy the third condition.
- (19, 21): The sum is 40, which is not less than 40. This pair does not satisfy the third condition.
**Option D: (11, 13), (13, 15), (15, 17), (17, 19)**
- (11, 13): The sum is 24, which is less than 40. This pair satisfies all conditions.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (15, 17): The sum is 32, which is less than 40. This pair satisfies all conditions.
- (17, 19): The sum is 36, which is not less than 40. This pair does not satisfy the third condition.
Therefore, the correct answer is **Option D: (11, 13), (13, 15), (15, 17), (17, 19)** as it is the only option where all the pairs satisfy all the given conditions.
To find the pairs of consecutive odd natural numbers that satisfy the given conditions, we need to consider the following:
1. The numbers should be consecutive odd natural numbers.
2. Both numbers should be larger than 10.
3. The sum of the two numbers should be less than 40.
Let's analyze each option to see if it satisfies these conditions:
**Option A: (11, 13), (13, 15), (15, 17), (17, 21)**
- (11, 13): The sum is 24, which is less than 40. This pair satisfies all conditions.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (15, 17): The sum is 32, which is less than 40. This pair satisfies all conditions.
- (17, 21): The sum is 38, which is less than 40. This pair satisfies all conditions.
**Option B: (9, 11), (13, 15), (15, 17), (17, 19)**
- (9, 11): The numbers are not larger than 10. This pair does not satisfy the second condition.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (15, 17): The sum is 32, which is less than 40. This pair satisfies all conditions.
- (17, 19): The sum is 36, which is not less than 40. This pair does not satisfy the third condition.
**Option C: (11, 13), (13, 15), (17, 19), (19, 21)**
- (11, 13): The sum is 24, which is less than 40. This pair satisfies all conditions.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (17, 19): The sum is 36, which is not less than 40. This pair does not satisfy the third condition.
- (19, 21): The sum is 40, which is not less than 40. This pair does not satisfy the third condition.
**Option D: (11, 13), (13, 15), (15, 17), (17, 19)**
- (11, 13): The sum is 24, which is less than 40. This pair satisfies all conditions.
- (13, 15): The sum is 28, which is less than 40. This pair satisfies all conditions.
- (15, 17): The sum is 32, which is less than 40. This pair satisfies all conditions.
- (17, 19): The sum is 36, which is not less than 40. This pair does not satisfy the third condition.
Therefore, the correct answer is **Option D: (11, 13), (13, 15), (15, 17), (17, 19)** as it is the only option where all the pairs satisfy all the given conditions.
A solution is to be kept between 30∘C and 35∘C What is the range of temperature in degree Fahrenheit ?- a)Between 40∘F and 60∘F
- b)Between 30∘Fand 35∘F
- c)Between 86∘F and 95∘F
- d)Between 76∘F and 105∘F
Correct answer is option 'C'. Can you explain this answer?
A solution is to be kept between 30∘C and 35∘C What is the range of temperature in degree Fahrenheit ?
a)
Between 40∘F and 60∘F
b)
Between 30∘Fand 35∘F
c)
Between 86∘F and 95∘F
d)
Between 76∘F and 105∘F
|
Manoj Patel answered |
Explanation:
To convert Celsius to Fahrenheit, we use the formula:
F = (9/5)C + 32
where F is the temperature in Fahrenheit and C is the temperature in Celsius.
Let's find the Fahrenheit equivalents of the given temperature range:
Lower limit:
F = (9/5)30 + 32 = 86F
Upper limit:
F = (9/5)35 + 32 = 95F
Therefore, the range of temperature in degree Fahrenheit is between 86F and 95F.
Answer:
Option (c) is correct. The range of temperature in degree Fahrenheit is between 86F and 95F.
To convert Celsius to Fahrenheit, we use the formula:
F = (9/5)C + 32
where F is the temperature in Fahrenheit and C is the temperature in Celsius.
Let's find the Fahrenheit equivalents of the given temperature range:
Lower limit:
F = (9/5)30 + 32 = 86F
Upper limit:
F = (9/5)35 + 32 = 95F
Therefore, the range of temperature in degree Fahrenheit is between 86F and 95F.
Answer:
Option (c) is correct. The range of temperature in degree Fahrenheit is between 86F and 95F.
Identify solution set for [| 4 −− x | + 1 < 3?- a)(2 , 6)
- b)(3 , 6)
- c)(2 , 4)
- d)(2 , 3)
Correct answer is option 'A'. Can you explain this answer?
Identify solution set for [| 4 −− x | + 1 < 3?
a)
(2 , 6)
b)
(3 , 6)
c)
(2 , 4)
d)
(2 , 3)
|
Neha Joshi answered |
|4 − x| + 1 < 3
⇒ 4 − x + 1 < 3
Add −4 and −1 on both sides, we get
4 − x + 1 − 4 − 1 < 3 − 4 − 1
⇒ − x < −2
Multiply both sides by −1, we get
x > 2
Also,|4−x| + 1 < 3
⇒ −(4−x) + 1 < 3
⇒ − 4 + x + 1 < 3
Add 4 and −1 on both sides, we get
− 4 + x + 1 + 4 − 1 < 3 + 4 − 1
⇒ x < 6
Thus, x ∈ (2,6).
⇒ 4 − x + 1 < 3
Add −4 and −1 on both sides, we get
4 − x + 1 − 4 − 1 < 3 − 4 − 1
⇒ − x < −2
Multiply both sides by −1, we get
x > 2
Also,|4−x| + 1 < 3
⇒ −(4−x) + 1 < 3
⇒ − 4 + x + 1 < 3
Add 4 and −1 on both sides, we get
− 4 + x + 1 + 4 − 1 < 3 + 4 − 1
⇒ x < 6
Thus, x ∈ (2,6).
A connected planar graph having 6 vertices, 7 edges contains _____________ regions.- a)15
- b)2
- c)1
- d)11
Correct answer is option 'B'. Can you explain this answer?
A connected planar graph having 6 vertices, 7 edges contains _____________ regions.
a)
15
b)
2
c)
1
d)
11
|
Lavanya Menon answered |
By euler’s formula the relation between vertices(n), edges(q) and regions(r) is given by n-q+r=2.
In a game a person wins a TV if in four throws of a dice he get sum greater than 20 .In three throws he got numbers as 5,3,6. What should be his fourth throw so that he wins a TV?- a)5 or 6
- b)never wins.
- c)5
- d)6
Correct answer is option 'B'. Can you explain this answer?
In a game a person wins a TV if in four throws of a dice he get sum greater than 20 .In three throws he got numbers as 5,3,6. What should be his fourth throw so that he wins a TV?
a)
5 or 6
b)
never wins.
c)
5
d)
6
|
Krithika Kulkarni answered |
Method to Solve :
Numbers obtained in three throws are 6, 5 and 4.
Let the number obtained in fourth throw be x.
Now, Sum > 20
6 + 5 + 4 + x > 20
15 + x > 20
x > 20 – 15
x > 5
He must get a 6 in the fourth throw to win the game.
Let the number obtained in fourth throw be x.
Now, Sum > 20
6 + 5 + 4 + x > 20
15 + x > 20
x > 20 – 15
x > 5
He must get a 6 in the fourth throw to win the game.
Solve the system of inequalities − 2 < 1 − 3x < 7- a)− 2 < x < 2
- b)− 1 < x < 1
- c)− 2 < x < 1
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Solve the system of inequalities − 2 < 1 − 3x < 7
a)
− 2 < x < 2
b)
− 1 < x < 1
c)
− 2 < x < 1
d)
none of these
|
Bhargavi Mishra answered |
Step 1: Understanding the Inequality
We have the compound inequality:
-2 < 1="" -="" 3x="" />< 7="" this="" means="" we="" need="" to="" solve="" two="" inequalities:="" 1.="" -2="" />< 1="" -="" 3x="" 2.="" 1="" -="" 3x="" />< 7="" />Step 2: Solving the First Inequality
Let's solve -2 < 1="" -="" 3x:="" -="" add="" 3x="" to="" both="" sides:="" 3x="" -="" 2="" />< 1="" -="" add="" 2="" to="" both="" sides:="" 3x="" />< 3="" -="" divide="" by="" 3:="" x="" />< 1="" />Step 3: Solving the Second Inequality
Now, let's solve 1 - 3x < 7:="" -="" subtract="" 1="" from="" both="" sides:="" -3x="" />< 6="" -="" divide="" by="" -3="" (remember="" to="" flip="" the="" inequality="" sign):="" x="" /> -2
Step 4: Combining the Results
From our computations, we have two results:
- x < 1="" -="" x="" /> -2
Putting these together, we get:
-2 < x="" />< 1="" />Step 5: Conclusion
The solution to the system of inequalities is:
-2 < x="" />< 1="" thus,="" the="" correct="" answer="" is="" option="" 'c':="" -2="" />< x="" />< 1.="" />
We have the compound inequality:
-2 < 1="" -="" 3x="" />< 7="" this="" means="" we="" need="" to="" solve="" two="" inequalities:="" 1.="" -2="" />< 1="" -="" 3x="" 2.="" 1="" -="" 3x="" />< 7="" />Step 2: Solving the First Inequality
Let's solve -2 < 1="" -="" 3x:="" -="" add="" 3x="" to="" both="" sides:="" 3x="" -="" 2="" />< 1="" -="" add="" 2="" to="" both="" sides:="" 3x="" />< 3="" -="" divide="" by="" 3:="" x="" />< 1="" />Step 3: Solving the Second Inequality
Now, let's solve 1 - 3x < 7:="" -="" subtract="" 1="" from="" both="" sides:="" -3x="" />< 6="" -="" divide="" by="" -3="" (remember="" to="" flip="" the="" inequality="" sign):="" x="" /> -2
Step 4: Combining the Results
From our computations, we have two results:
- x < 1="" -="" x="" /> -2
Putting these together, we get:
-2 < x="" />< 1="" />Step 5: Conclusion
The solution to the system of inequalities is:
-2 < x="" />< 1="" thus,="" the="" correct="" answer="" is="" option="" 'c':="" -2="" />< x="" />< 1.="" />
The graphical representation of x > 2 on number line is- a)
- b)
- c)
- d)
Correct answer is option 'C'. Can you explain this answer?
The graphical representation of x > 2 on number line is
a)
b)
c)
d)
|
Knowledge Hub answered |
x>2, the value of x is greater than 2. the value goes till infinity.
if X is equal or greater than 2 then we use solid dot, but it is only greater than 2
so the option c is correct.
if X is equal or greater than 2 then we use solid dot, but it is only greater than 2
so the option c is correct.
Given that x is an integer, find the values of x which satisfy the simultaneous linear inequalities 2 + x < 6 and 2 −3x < − 1.- a)1 , 2 , 3
- b)2 , 3
- c)2 , 3, 4,
- d)1 , 2, 3, 4.
Correct answer is option 'B'. Can you explain this answer?
Given that x is an integer, find the values of x which satisfy the simultaneous linear inequalities 2 + x < 6 and 2 −3x < − 1.
a)
1 , 2 , 3
b)
2 , 3
c)
2 , 3, 4,
d)
1 , 2, 3, 4.
|
EduRev JEE answered |
Given Inequalities:
- 2 + x < 6
- 2 −3x < − 1
Step 1: Solve the first inequality 2 + x < 6
Subtract 2 from both sides:
x < 6 - 2
Simplifying:
x < 4
Thus, from the first inequality, we have:
x < 4
Step 2: Solve the second inequality 2 - 3x < -1
Subtract 2 from both sides:
- 3x < -1 - 2
Simplifying:
- 3x < -3
Now, divide both sides by -3, and remember to reverse the inequality sign when dividing by a negative number:
x > 1
Step 3: Combine the results
From the first inequality, we know x < 4.
From the second inequality, we know x > 1.
Thus, the solution for x must satisfy both:
1 < x < 4
The integer values of xxx that lie between 1 and 4 are:
x = 2, 3
The correct option is: B: 2, 3
Subtract 2 from both sides:
x < 6 - 2
Simplifying:
x < 4
Thus, from the first inequality, we have:
x < 4
Step 2: Solve the second inequality 2 - 3x < -1
Subtract 2 from both sides:
- 3x < -1 - 2
Simplifying:
- 3x < -3
Now, divide both sides by -3, and remember to reverse the inequality sign when dividing by a negative number:
x > 1
Step 3: Combine the results
From the first inequality, we know x < 4.
From the second inequality, we know x > 1.
Thus, the solution for x must satisfy both:
1 < x < 4
The integer values of xxx that lie between 1 and 4 are:
x = 2, 3
The correct option is: B: 2, 3
Which one of them is the solution for x, when x is integer and 12 x > 30?- a)-1
- b)3
- c)1
- d)0
Correct answer is option 'B'. Can you explain this answer?
Which one of them is the solution for x, when x is integer and 12 x > 30?
a)
-1
b)
3
c)
1
d)
0
|
Gaurav Kumar answered |
12x > 30
x > 30/12
x > 2.5
x is an integer. So, minimum value of x is 3.
x > 30/12
x > 2.5
x is an integer. So, minimum value of x is 3.
Find the solution for the pair of inequations x > 1 and x < -1- a)no solution
- b)x < -1
- c)-1 < x < 1
- d)x > 1
Correct answer is option 'A'. Can you explain this answer?
Find the solution for the pair of inequations x > 1 and x < -1
a)
no solution
b)
x < -1
c)
-1 < x < 1
d)
x > 1
|
|
Pooja Shah answered |
x > 1 means x is greater than 1 in this equation the values of x can be 2,3,4,5.............∞
x < -1 means is less than -1 therefore values of x can be -2, -3, -4, -5............ -∞
So no common point for x
Hence there will be no solution
x < -1 means is less than -1 therefore values of x can be -2, -3, -4, -5............ -∞
So no common point for x
Hence there will be no solution
Solve the inequality 3 −− 2x ≤ 9- a)x ≥ − 6
- b)x ≥ − 3
- c)x ≤ − 3
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
Solve the inequality 3 −− 2x ≤ 9
a)
x ≥ − 6
b)
x ≥ − 3
c)
x ≤ − 3
d)
none of these.
|
|
Raghav Bansal answered |
3 − 2x ≤ 9
-2x ≤ 6
-x ≤ 3
-3 ≤ x
-2x ≤ 6
-x ≤ 3
-3 ≤ x
The solution to |3x – 1| + 1 < 3 is- a)2 < x < 3/4
- b)-1/3 < x < 1
- c)-1/3 < x < 1/4
- d)-3 < x < 3
Correct answer is option 'B'. Can you explain this answer?
The solution to |3x – 1| + 1 < 3 is
a)
2 < x < 3/4
b)
-1/3 < x < 1
c)
-1/3 < x < 1/4
d)
-3 < x < 3
|
|
Neha Joshi answered |
|3x - 1| + 1 < 3
|3x -1| < 2
Opening mod, we get
3x - 1 < 2, -3x + 1 > 2
3x < 3, -3x > 1
x < 1, x > -1/3
-1/3 < x < 1
|3x -1| < 2
Opening mod, we get
3x - 1 < 2, -3x + 1 > 2
3x < 3, -3x > 1
x < 1, x > -1/3
-1/3 < x < 1
For a student to qualify for a certain course, the average of his marks in the permitted 3 attempts must be more than 60. His first two attempts yielded only 45 and 62 marks respectively. What is the minimum score required in the third attempt to qualify?- a)73
- b)91
- c)83
- d)89
Correct answer is option 'A'. Can you explain this answer?
For a student to qualify for a certain course, the average of his marks in the permitted 3 attempts must be more than 60. His first two attempts yielded only 45 and 62 marks respectively. What is the minimum score required in the third attempt to qualify?
a)
73
b)
91
c)
83
d)
89
|
Tejas Verma answered |
No of attempts = 3
Average = (45+62+x)/3=60
x=73
Average = (45+62+x)/3=60
x=73
IQ of a person is given by the formula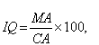 
where MA is mental age and CA is the chronological age. If 
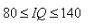for a group of 12 years old children, find the range of their mental age.- a)9.6 to 14.8
- b)9.6 and 16.8
- c)9.6 to 16.8
- d)14.8 to 16.8
Correct answer is option 'C'. Can you explain this answer?
IQ of a person is given by the formula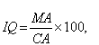
where MA is mental age and CA is the chronological age. If 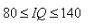for a group of 12 years old children, find the range of their mental age.
for a group of 12 years old children, find the range of their mental age.a)
9.6 to 14.8
b)
9.6 and 16.8
c)
9.6 to 16.8
d)
14.8 to 16.8
|
|
Raghav Bansal answered |
IQ = (MA*100)/CA
and 80 ≤ IQ ≤ 140
80 ≤ (MA*100)/CA ≤ 140
80 ≤ (MA*100)/12 ≤ 140
960 ≤ (MA*100) ≤ 1680
9.6 ≤ MA ≤ 16.8
and 80 ≤ IQ ≤ 140
80 ≤ (MA*100)/CA ≤ 140
80 ≤ (MA*100)/12 ≤ 140
960 ≤ (MA*100) ≤ 1680
9.6 ≤ MA ≤ 16.8
If 5x+6<2x-3, then- a)x>-3
- b)x<-3
- c)x>3
- d)x<3
Correct answer is option 'B'. Can you explain this answer?
If 5x+6<2x-3, then
a)
x>-3
b)
x<-3
c)
x>3
d)
x<3
|
|
Rohit Jain answered |
5x+6<2x-3
5x-2x < -3-6
3x < -9
x<-3
5x-2x < -3-6
3x < -9
x<-3
Find the value of x which satisfies 5x – 3 < 7, where x is a natural number.- a){1, 2}
- b)1
- c)(1,∞)
- d)[1,∞)
Correct answer is option 'B'. Can you explain this answer?
Find the value of x which satisfies 5x – 3 < 7, where x is a natural number.
a)
{1, 2}
b)
1
c)
(1,∞)
d)
[1,∞)
|
Vikas Saini answered |
From inequality it comes out to be x less than 2 but it is also a natural no. so 1,2 is the. only answer in this case
Which of the following is correct ?- a)If 0 > -7 , then 0 < 7
- b)If 8 > 1 , then -8 > -1
- c)If -4 < 7 , then 4 < - 7
- d)If -2 < 5 , then 2 > 5
Correct answer is option 'A'. Can you explain this answer?
Which of the following is correct ?
a)
If 0 > -7 , then 0 < 7
b)
If 8 > 1 , then -8 > -1
c)
If -4 < 7 , then 4 < - 7
d)
If -2 < 5 , then 2 > 5
|
|
EduRev JEE answered |
We are given a set of inequalities and asked to identify which one is correct. Let's analyze each option one by one.
Option A: If 0 > -7 , then 0 < 7
Option A: If 0 > -7 , then 0 < 7
- The inequality 0 > -7 is true because 0 is indeed greater than -7.
- The statement 0 < 7 is also true because 0 is less than 7.
- Since both parts of this conditional are true, Option A is correct.
Option B: If 8 > 1, then -8 > -1
- The inequality 8 > 1 is true because 8 is greater than 1.
- However, the statement −8 > −1 is false because -8 is smaller than -1. As numbers become more negative, they become smaller.
- Therefore, Option B is incorrect.
Option C: If -4 < 7 , then 4 < - 7
- The inequality −4 < 7 is true because -4 is smaller than 7.
- However, the statement 4 < −7 is false because 4 is greater than -7, not less.
- Therefore, Option C is incorrect.
Option D: If -2 < 5 , then 2 > 5
- The inequality −2 < 5 is true because -2 is smaller than 5.
- However, the statement 2 > 5 is false because 2 is less than 5, not greater.
- Therefore, Option D is incorrect.
Option A is the correct one, as both parts of the statement are true.
Which of the following is not a linear inequality?- a)ax2 + bx + c < 0
- b)ax + by + c ≥ 0
- c)ax + b < 0
- d)ax + by + c ≤ 0
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a linear inequality?
a)
ax2 + bx + c < 0
b)
ax + by + c ≥ 0
c)
ax + b < 0
d)
ax + by + c ≤ 0
|
Shubham Rajput answered |
A is a quadratic equation not a linear equality because square of a function can't be negative
A pack of coffee powder contains a mixture of x grams of coffee and y grams of choco. The amount of coffee powder is greater than that of choco and each pack is atleast 10 grams. Which of the following inequations describe the conditions given ?
- a)x + y < 12 ; x > y
- b)x + y ≥ 10 ; x > y
- c)x + y < 10 ; x < y
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A pack of coffee powder contains a mixture of x grams of coffee and y grams of choco. The amount of coffee powder is greater than that of choco and each pack is atleast 10 grams. Which of the following inequations describe the conditions given ?
a)
x + y < 12 ; x > y
b)
x + y ≥ 10 ; x > y
c)
x + y < 10 ; x < y
d)
none of these
|
Nabanita Nambiar answered |
The coffee powder is greater than choco
hence, x>y
each pack is at least 10 gm
Hence, x+y≥10
hence, x>y
each pack is at least 10 gm
Hence, x+y≥10
The inequations -4x+1≥0 and 3-4x<0 have the common solutions given by
- a){}
- b){0,2}
- c){-2,2}
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The inequations -4x+1≥0 and 3-4x<0 have the common solutions given by
a)
{}
b)
{0,2}
c)
{-2,2}
d)
None of these
|
Abhishek Dasgupta answered |
-4x+1≥0 and 3-4x<0
1 ≥ 4x and 3 < 4x
1/4 ≥ x and 3/4 < x
so x ∈ (-∞,1/4] U (3/4 , ∞ )
In the first four papers each of 100 marks, Rishi got 95, 72, 73, 83 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks, find the range of marks he should score in the fifth paper .
- a)52 ≤ × < 77
- b)73 < × < 100
- c)25 < × < 75
- d)75 < × < 80
Correct answer is option 'A'. Can you explain this answer?
In the first four papers each of 100 marks, Rishi got 95, 72, 73, 83 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks, find the range of marks he should score in the fifth paper .
a)
52 ≤ × < 77
b)
73 < × < 100
c)
25 < × < 75
d)
75 < × < 80
|
Ayush Joshi answered |
Suppose Richard scores x in the fifth paper. Then,75
The longest side of a triangle is three times the shortest side and the third side is 2cm shorter than the longest side if the perimeter of the triangles at least 61cm, find the minimum length of the shortest side.- a)16 cm
- b)11 cm
- c)61 cm
- d)9 cm
Correct answer is option 'D'. Can you explain this answer?
The longest side of a triangle is three times the shortest side and the third side is 2cm shorter than the longest side if the perimeter of the triangles at least 61cm, find the minimum length of the shortest side.
a)
16 cm
b)
11 cm
c)
61 cm
d)
9 cm
|
Manish Aggarwal answered |
Let the shortest side of the triangle be x cm.
Then, the longest side will be 3x and the third side will be 3x − 2.
∴ Perimeter of the triangle ≥ 61
⇒ x + 3x + 3x − 2 ≥ 61
⇒ 7x ≥ 61 + 2
Dividing throughout by ⇒ x ≥ 9( Dividing throughout by 7)
Hence, the minumum length of the shortest side is 9 cm.
Then, the longest side will be 3x and the third side will be 3x − 2.
∴ Perimeter of the triangle ≥ 61
⇒ x + 3x + 3x − 2 ≥ 61
⇒ 7x ≥ 61 + 2
Dividing throughout by ⇒ x ≥ 9( Dividing throughout by 7)
Hence, the minumum length of the shortest side is 9 cm.
If a < b then -a ______ - b- a)–a < -b
- b)–a ≤ -b
- c)–a ≥ -b
- d)-a > -b
Correct answer is option 'D'. Can you explain this answer?
If a < b then -a ______ - b
a)
–a < -b
b)
–a ≤ -b
c)
–a ≥ -b
d)
-a > -b
|
|
Bhargavi Sen answered |
If a person ate only fruits and vegetables for a week, they may experience several potential benefits. These can include:
1. Increased nutrient intake: Fruits and vegetables are rich in essential vitamins, minerals, and antioxidants. Eating a variety of fruits and vegetables can provide a wide range of nutrients necessary for optimal health.
2. Improved digestion: Fruits and vegetables are high in fiber, which can promote healthy digestion and prevent constipation. The high water content in many fruits and vegetables can also help maintain hydration and promote regular bowel movements.
3. Enhanced immune function: Fruits and vegetables are packed with immune-boosting nutrients like vitamin C, beta-carotene, and antioxidants. These nutrients can support a strong immune system, helping to fight off infections and diseases.
4. Weight management: Fruits and vegetables are generally low in calories and high in fiber, which can help with weight management. The high fiber content can promote feelings of fullness and reduce overall calorie intake.
5. Improved skin health: Fruits and vegetables contain antioxidants that can help protect the skin from damage caused by free radicals. Additionally, the high water content in fruits and vegetables can contribute to hydrated and healthy-looking skin.
6. Reduced risk of chronic diseases: A diet rich in fruits and vegetables has been associated with a lower risk of chronic diseases such as heart disease, certain types of cancer, and diabetes. The various nutrients and antioxidants found in fruits and vegetables may help protect against these conditions.
However, it is important to note that a balanced diet should include a variety of food groups to ensure all essential nutrients are obtained. It is recommended to consult with a healthcare professional or registered dietitian before making any significant changes to your diet.
1. Increased nutrient intake: Fruits and vegetables are rich in essential vitamins, minerals, and antioxidants. Eating a variety of fruits and vegetables can provide a wide range of nutrients necessary for optimal health.
2. Improved digestion: Fruits and vegetables are high in fiber, which can promote healthy digestion and prevent constipation. The high water content in many fruits and vegetables can also help maintain hydration and promote regular bowel movements.
3. Enhanced immune function: Fruits and vegetables are packed with immune-boosting nutrients like vitamin C, beta-carotene, and antioxidants. These nutrients can support a strong immune system, helping to fight off infections and diseases.
4. Weight management: Fruits and vegetables are generally low in calories and high in fiber, which can help with weight management. The high fiber content can promote feelings of fullness and reduce overall calorie intake.
5. Improved skin health: Fruits and vegetables contain antioxidants that can help protect the skin from damage caused by free radicals. Additionally, the high water content in fruits and vegetables can contribute to hydrated and healthy-looking skin.
6. Reduced risk of chronic diseases: A diet rich in fruits and vegetables has been associated with a lower risk of chronic diseases such as heart disease, certain types of cancer, and diabetes. The various nutrients and antioxidants found in fruits and vegetables may help protect against these conditions.
However, it is important to note that a balanced diet should include a variety of food groups to ensure all essential nutrients are obtained. It is recommended to consult with a healthcare professional or registered dietitian before making any significant changes to your diet.
By solving the inequality 3(a - 6) < 4 + a, the answer will be- a)a < 9
- b)a < 12
- c)a < 13
- d)a < 11
Correct answer is option 'D'. Can you explain this answer?
By solving the inequality 3(a - 6) < 4 + a, the answer will be
a)
a < 9
b)
a < 12
c)
a < 13
d)
a < 11
|
Harsh Rajput answered |
To solve inequality,take < as="." />
3(a+6)=4+a
3a+18=4+a
2a=22
a=11
replace = with
so a<11>
3(a+6)=4+a
3a+18=4+a
2a=22
a=11
replace = with
so a<11>
A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3 cm longer than the shortest and third length is to be twice as long as the shortest. What are the possible lengths for the shortest board if the third piece is to be at least 5 cm longer than the second?- a)5 ≤ × ≤ 91
- b)3 ≤ × ≤ 5
- c)3 ≤ × ≤ 91
- d)8 ≤ × ≤ 22
Correct answer is option 'D'. Can you explain this answer?
A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3 cm longer than the shortest and third length is to be twice as long as the shortest. What are the possible lengths for the shortest board if the third piece is to be at least 5 cm longer than the second?
a)
5 ≤ × ≤ 91
b)
3 ≤ × ≤ 5
c)
3 ≤ × ≤ 91
d)
8 ≤ × ≤ 22
|
|
Ashwin Verma answered |
Let x be the length of the shortest board.
The second length is x+3.
The third length is 2x.
The third length is at least 5 cm longer than the second: 2x ≥ (x+3)+5
2x ≥ x+8
x ≥ 8
The possible lengths for the shortest board are x ≥ 8. Answer: \boxed{8}.
The second length is x+3.
The third length is 2x.
The third length is at least 5 cm longer than the second: 2x ≥ (x+3)+5
2x ≥ x+8
x ≥ 8
The possible lengths for the shortest board are x ≥ 8. Answer: \boxed{8}.
Identify the solution set for –( x – 3 ) + 5 – 2x- a)(−∞,−1)
- b)(−∞,−2)
- c)(−∞,−5)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Identify the solution set for –( x – 3 ) + 5 – 2x
a)
(−∞,−1)
b)
(−∞,−2)
c)
(−∞,−5)
d)
none of these
|
|
EduRev JEE answered |
Given inequality:
3(a - 6) < 4 + a
Step 1: Expand the left-hand side
3a - 18 < 4 + a
Step 2: Move all terms involving aaa to one side and constants to the other side
Subtract aaa from both sides:
3a - a - 18 < 4
This simplifies to:
2a - 18 < 4
Step 3: Add 18 to both sides
2a < 22
Step 4: Divide both sides by 2
a < 11
The correct option is D: a < 11.
Find the pairs of consecutive even positive integers both of which are smaller than 10 and their sum of more than 11- a)(4, 8)
- b)(6, 8)
- c)(6, 8) and (4, 8)
- d)(6, 4)(4, 2)
Correct answer is option 'B'. Can you explain this answer?
Find the pairs of consecutive even positive integers both of which are smaller than 10 and their sum of more than 11
a)
(4, 8)
b)
(6, 8)
c)
(6, 8) and (4, 8)
d)
(6, 4)(4, 2)
|
Geetika Shah answered |
Let x be the smaller of the two consecutive even positive integers .
Then the other integer is x+2.
Since both the integers are smaller than 10,x<10 ....(1)
Also the sum of the two integers is more than 11.
x+(x+2)>11
⇒ 2x+2>11
⇒ 2x>11−2
⇒ 2x>9
⇒ x>9/2
⇒ x>4.5....(2)
From (1) and (2) we obtain 4.5>x>11
Since x is an even number, x can take the values 6,8 and 10.
Thus the required possible pairs are (6,8).
Then the other integer is x+2.
Since both the integers are smaller than 10,x<10 ....(1)
Also the sum of the two integers is more than 11.
x+(x+2)>11
⇒ 2x+2>11
⇒ 2x>11−2
⇒ 2x>9
⇒ x>9/2
⇒ x>4.5....(2)
From (1) and (2) we obtain 4.5>x>11
Since x is an even number, x can take the values 6,8 and 10.
Thus the required possible pairs are (6,8).
Given that x is an integer, find the values of x which satisfy both 2x + 3 > 7 and x + 4 < 10- a)4 , 5
- b)3
- c)4
- d)3 , 4 , 5
Correct answer is option 'D'. Can you explain this answer?
Given that x is an integer, find the values of x which satisfy both 2x + 3 > 7 and x + 4 < 10
a)
4 , 5
b)
3
c)
4
d)
3 , 4 , 5
|
Vishal Kumar answered |
Common between 2 and 6 . 3 , 4,5 are answer
By solving the inequality 6x - 7 > 5, the answer will be- a)x > 6
- b)x < 5
- c)x < 7
- d)x > 2
Correct answer is option 'D'. Can you explain this answer?
By solving the inequality 6x - 7 > 5, the answer will be
a)
x > 6
b)
x < 5
c)
x < 7
d)
x > 2
|
|
Meera Nambiar answered |
To solve the inequality 6x - 7, we need to isolate x on one side of the inequality symbol. Here's the step-by-step solution:
1. Add 7 to both sides of the inequality: 6x - 7 + 7 > 0 + 7
This simplifies to: 6x > 7
2. Divide both sides of the inequality by 6: (6x)/6 > 7/6
This simplifies to: x > 7/6
Therefore, the solution to the inequality 6x - 7 is x > 7/6.
1. Add 7 to both sides of the inequality: 6x - 7 + 7 > 0 + 7
This simplifies to: 6x > 7
2. Divide both sides of the inequality by 6: (6x)/6 > 7/6
This simplifies to: x > 7/6
Therefore, the solution to the inequality 6x - 7 is x > 7/6.
If a , b , c are real numbers such that a ≥ b , c > 0, then- a)ac < bc
- b)ac > bc
- c)ac ≥ bc
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If a , b , c are real numbers such that a ≥ b , c > 0, then
a)
ac < bc
b)
ac > bc
c)
ac ≥ bc
d)
none of these
|
|
Palak Joshi answered |
We know that $a$, $b$, and $c$ are real numbers such that $a< />
We can use the fact that $a< />
Now we can rewrite $ac+bc$ as $c(a+b)=c(a+\frac{a+c}{2})=\frac{3}{2}ac+\frac{1}{2}c^2$. Since $a+c=4$, we can substitute $c=4-a$ to get $ac+bc=\frac{3}{2}a(4-a)+\frac{1}{2}(4-a)^2=\frac{1}{2}(a-2)^2+\frac{7}{2}$.
The minimum value of $(a-2)^2$ is 0, which occurs when $a=2$. Therefore, the minimum value of $ac+bc$ is $\frac{7}{2}$, which occurs when $a=2$, $b=3$, and $c=4$.
We can use the fact that $a< />
Now we can rewrite $ac+bc$ as $c(a+b)=c(a+\frac{a+c}{2})=\frac{3}{2}ac+\frac{1}{2}c^2$. Since $a+c=4$, we can substitute $c=4-a$ to get $ac+bc=\frac{3}{2}a(4-a)+\frac{1}{2}(4-a)^2=\frac{1}{2}(a-2)^2+\frac{7}{2}$.
The minimum value of $(a-2)^2$ is 0, which occurs when $a=2$. Therefore, the minimum value of $ac+bc$ is $\frac{7}{2}$, which occurs when $a=2$, $b=3$, and $c=4$.
If x < 0 then | x | is equal to- a)x
- b)0
- c)1
- d)−x
Correct answer is option 'D'. Can you explain this answer?
If x < 0 then | x | is equal to
a)
x
b)
0
c)
1
d)
−x
|
|
Kalyan Yadav answered |
Is greater than 5, then x + 2 is greater than 7.
What is the solution set for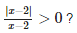 
- a)(2 , ∞)
- b)(0 , 2)
- c)(-∞ , - 2)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
What is the solution set for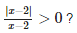
a)
(2 , ∞)
b)
(0 , 2)
c)
(-∞ , - 2)
d)
none of these
|
Mani Kandan answered |
X=-2,2
x+2 ×-2 x+2/x-2
(-infinity,-2) (+) (-) ( - )
(-2,2) ( + ) ( - ) ( - )
(2,infinity ) ( + ) ( + ) ( +)
so answer is A=(2,infinity )
x+2 ×-2 x+2/x-2
(-infinity,-2) (+) (-) ( - )
(-2,2) ( + ) ( - ) ( - )
(2,infinity ) ( + ) ( + ) ( +)
so answer is A=(2,infinity )
In a game a person wins a TV if in four throws of a dice he get sum greater than 20 .In three throws he got numbers as 5,3,6. What should be his fourth throw so that he wins a TV?- a)5 or 6
- b)5
- c)6
- d)no one wins
Correct answer is option 'D'. Can you explain this answer?
In a game a person wins a TV if in four throws of a dice he get sum greater than 20 .In three throws he got numbers as 5,3,6. What should be his fourth throw so that he wins a TV?
a)
5 or 6
b)
5
c)
6
d)
no one wins
|
|
Lavanya Menon answered |
Numbers obtained in three throws are 3, 5 and 6.
Let the number obtained in fourth throw be x.
Now, Sum > 20
=> 5 + 3 + 6 + x > 20
=> 14 + x > 20
=> x > 20 – 14
=> x > 6 (no one wins)
Let the number obtained in fourth throw be x.
Now, Sum > 20
=> 5 + 3 + 6 + x > 20
=> 14 + x > 20
=> x > 20 – 14
=> x > 6 (no one wins)
The graphical solution of -1 < x < 2 on number line is- a)
- b)
- c)
- d)
Correct answer is option 'D'. Can you explain this answer?
The graphical solution of -1 < x < 2 on number line is
a)
b)
c)
d)
|
|
Mohit Mittal answered |
D is correct as x between -1 and 2 and excluding -1 and 2
What is the solution set for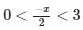 
- a)(5 , 6)
- b)(- 6 , 6)
- c)(- 6 , 0)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
What is the solution set for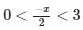
a)
(5 , 6)
b)
(- 6 , 6)
c)
(- 6 , 0)
d)
none of these
|
Tarun Kaushik answered |
Given Inequality:
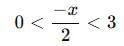
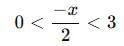
Step 1: Break down the inequality
We need to solve both parts of the compound inequality:
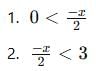
Step 2: Solve each part separately
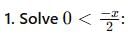
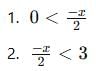
Step 2: Solve each part separately
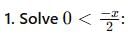
Multiply both sides of the inequality by 2 to get rid of the denominator:
0 < -x
Now, multiply both sides by -1 (which reverses the inequality):
x < 0
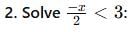
Multiply both sides by 2 to eliminate the denominator:
-x < 6
Multiply both sides by -1 (which reverses the inequality):
x > -6
Step 3: Combine the results
From both inequalities, we now have:
-6 < x < 0
The solution set is x ∈ (−6, 0), which corresponds to Option C.
0 < -x
Now, multiply both sides by -1 (which reverses the inequality):
x < 0
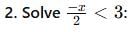
Multiply both sides by 2 to eliminate the denominator:
-x < 6
Multiply both sides by -1 (which reverses the inequality):
x > -6
Step 3: Combine the results
From both inequalities, we now have:
-6 < x < 0
The solution set is x ∈ (−6, 0), which corresponds to Option C.
x = 4, 5 and 6 are the solutions for:
- a)x > 4 and x < 7
- b)x ≥ 4 and x ≤ 7
- c)x ≥ 4 and x < 7
- d)x > 4 and x > 7
Correct answer is option 'C'. Can you explain this answer?
x = 4, 5 and 6 are the solutions for:
a)
x > 4 and x < 7
b)
x ≥ 4 and x ≤ 7
c)
x ≥ 4 and x < 7
d)
x > 4 and x > 7
|
Foothill Academy answered |
To determine which statement matches the solutions x=4,5 and 6, let's analyze each option:
a) x > 4 and x < 7
- This means 4 < x < 7.
- The solutions x = 5,6 do not satisfy this condition because it does not contain 4.
b) x ≥ 4 and x ≤ 7
- This means 4 ≤ x ≤ 7.
- The solution x = 4,5,6,7 do not satisfy this condition as it contains 7 also .
c) x ≥ 4 and x < 7
- This means 4 ≤ x < 7.
- The solutions x=4,5,6 satisfy this condition because they are all greater than or equal to 4 and strictly less than 7.
d) x > 4 and x > 7
- This means x > 7.
- The solutions x = 4,5,6 do not satisfy this condition because none of them are greater than 7.
Therefore, after analyzing each option, we conclude that the solutions x=4,5,6 correspond to statement:
c) x ≥ 4 and x < 7
By solving the inequality 6x - 7 > 5, the answer will be- a)x > 6
- b)x < 5
- c)x < 7
- d)x > 2
Correct answer is option 'D'. Can you explain this answer?
By solving the inequality 6x - 7 > 5, the answer will be
a)
x > 6
b)
x < 5
c)
x < 7
d)
x > 2
|
|
Shraddha Deshpande answered |
To solve the inequality 6x - 7 < 0,="" we="" need="" to="" isolate="" the="" variable="" />
Adding 7 to both sides of the inequality, we get:
6x - 7 + 7 < 0="" +="" />
Simplifying, we have:
6x < />
Dividing both sides of the inequality by 6 (since the coefficient of x is 6), we get:
x < />
Therefore, the solution to the inequality 6x - 7 < 0="" is="" x="" />< 7/6.="" />
Adding 7 to both sides of the inequality, we get:
6x - 7 + 7 < 0="" +="" />
Simplifying, we have:
6x < />
Dividing both sides of the inequality by 6 (since the coefficient of x is 6), we get:
x < />
Therefore, the solution to the inequality 6x - 7 < 0="" is="" x="" />< 7/6.="" />
Chapter doubts & questions for Inequalities - Mathematics (Maths) for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Inequalities - Mathematics (Maths) for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Mathematics (Maths) for JEE Main & Advanced
172 videos|487 docs|154 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup