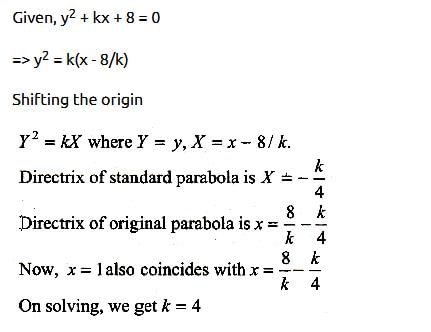All Exams >
JEE >
Mathematics (Maths) for JEE Main & Advanced >
All Questions
All questions of Parabola for JEE Exam
The equation of the parabola with vertex at (0, 0) and focus at (0, – 2) is:- a)y2 = – 2x
- b)x2 = – 8y
- c)y2 = – 8x
- d)x2 = – 4y
Correct answer is option 'B'. Can you explain this answer?
The equation of the parabola with vertex at (0, 0) and focus at (0, – 2) is:
a)
y2 = – 2x
b)
x2 = – 8y
c)
y2 = – 8x
d)
x2 = – 4y

|
Praveen Kumar answered |
Given the vertex of the parabola is (0,0) and focus is at (0,-2).
This gives the axis of the parabola is the positive y− axis.
Then the equation of the parabola will be x^2 = 4ay where a = -2.
So the equation of the parabola is x2 = -8y.
This gives the axis of the parabola is the positive y− axis.
Then the equation of the parabola will be x^2 = 4ay where a = -2.
So the equation of the parabola is x2 = -8y.
Any point on the parabola whose focus is (0,1) and the directrix is x + 2 = 0 is given by- a)(t2 + 1, 2t – 1)
- b)(t2, 2t)
- c)(t2 + 1, 2t + 1)
- d)(t2 – 1, 2t + 1)
Correct answer is option 'D'. Can you explain this answer?
Any point on the parabola whose focus is (0,1) and the directrix is x + 2 = 0 is given by
a)
(t2 + 1, 2t – 1)
b)
(t2, 2t)
c)
(t2 + 1, 2t + 1)
d)
(t2 – 1, 2t + 1)
|
|
Pooja Shah answered |
f(0,1),d(x+2=0)
Distance of any point on parabola and focus is equal to distance of point and directrix.
fP=(h−0)2+(k−1)2= (h2+k2+1−2k)1/2
Distance of point (h,k) and line x+2=0
Using point line distance formula.
dP=h+2
[h2+k2+1−2k]1/2=h+2
h2+k2+1−2k = h2+4+4h
k2−2k+1−4−4h=0
replacing h→x,k→y y2−2y+1−4−4x=0
(y−1)2=4(x+1) …(1)
Let Y=y−1,X=x+1 then (1) becomes
Y^2=4aX2
Here a=1 any point on this parabola will be of the form (at2,2at)=(t2,2at)
⇒X=t2 ⇒x+1=t2
⇒x=t2−1
⇒Y2=2t
⇒y−1 = 2t ⇒ y = 2t+1
∴ Any point on the parabola (y−1)2=4(x+1) is
= (t2−1,2t+1)
Distance of any point on parabola and focus is equal to distance of point and directrix.
fP=(h−0)2+(k−1)2= (h2+k2+1−2k)1/2
Distance of point (h,k) and line x+2=0
Using point line distance formula.
dP=h+2
[h2+k2+1−2k]1/2=h+2
h2+k2+1−2k = h2+4+4h
k2−2k+1−4−4h=0
replacing h→x,k→y y2−2y+1−4−4x=0
(y−1)2=4(x+1) …(1)
Let Y=y−1,X=x+1 then (1) becomes
Y^2=4aX2
Here a=1 any point on this parabola will be of the form (at2,2at)=(t2,2at)
⇒X=t2 ⇒x+1=t2
⇒x=t2−1
⇒Y2=2t
⇒y−1 = 2t ⇒ y = 2t+1
∴ Any point on the parabola (y−1)2=4(x+1) is
= (t2−1,2t+1)
A variable chord PQ of the parabola y = 4x2 substends a right angle at the vertex. Then the locus of points of intersection of the tangents at P and Q is- a)4y + 1= 16x2
- b)y + 4 = 0
- c)4y + 4 = 4x2
- d)4y + 1 = 0
Correct answer is option 'D'. Can you explain this answer?
A variable chord PQ of the parabola y = 4x2 substends a right angle at the vertex. Then the locus of points of intersection of the tangents at P and Q is
a)
4y + 1= 16x2
b)
y + 4 = 0
c)
4y + 4 = 4x2
d)
4y + 1 = 0
|
|
Krishna Iyer answered |
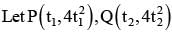
Slope of OP x slope of OQ = -1
⇒ 4t1.4t2 = -1
Eq of tangent at
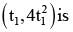
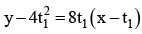
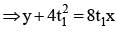
Eq of tangent at
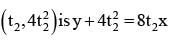
Let (x1 , y1) is the point of intersection
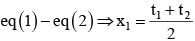
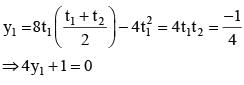
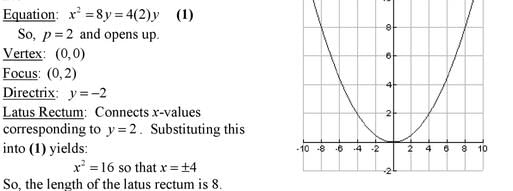
The equation 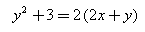 represents a parabola with the vertex at
represents a parabola with the vertex at- a)

- b)

- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
The equation 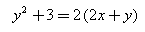 represents a parabola with the vertex at
represents a parabola with the vertex at
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
y2+3=2(2x+y) represents parabola.
y2+3=4x+2y
y2−2y+3=4x
y2−2y+1+3=4x+1
(y−1)2=4x−2
(y−1)2=4(x−1/2)
So, the vertex of parabola=(1/2,1) and axis is parallel to x axis.
a=1
Focus=(1/2+1,1)
=(3/2,1)
y2+3=4x+2y
y2−2y+3=4x
y2−2y+1+3=4x+1
(y−1)2=4x−2
(y−1)2=4(x−1/2)
So, the vertex of parabola=(1/2,1) and axis is parallel to x axis.
a=1
Focus=(1/2+1,1)
=(3/2,1)
The line 4x – 7y + 10 = 0 intersects the parabola, y2 = 4x at the points A & B. The co-ordinates of the point of intersection of the tangents drawn at the points A & B are- a)
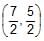
- b)
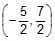
- c)
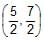
- d)
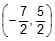
Correct answer is option 'C'. Can you explain this answer?
The line 4x – 7y + 10 = 0 intersects the parabola, y2 = 4x at the points A & B. The co-ordinates of the point of intersection of the tangents drawn at the points A & B are
a)
b)
c)
d)
|
|
Yash Patel answered |
ky=[4(x+h)]/2
=> 2ky=2(x+h)
2ky=4x+4h =>4x−2ky+4h=0
4x−7y+10=0
4h=10 => h=5/2
2k=7 => k=7/2
point of intersection of tangent at p and q is (5/2,7/2)
=> 2ky=2(x+h)
2ky=4x+4h =>4x−2ky+4h=0
4x−7y+10=0
4h=10 => h=5/2
2k=7 => k=7/2
point of intersection of tangent at p and q is (5/2,7/2)
From the focus of the parabola y2 = 8x as centre, a circle is described so that a common chord of the curves is equidistant from the vertex and focus of the parabola. The equation of the circle is- a) (x – 2)2 + y2 = 3
- b) (x – 2)2 + y2 = 9
- c)(x + 2)2 + y2 = 9
- d)None
Correct answer is option 'B'. Can you explain this answer?
From the focus of the parabola y2 = 8x as centre, a circle is described so that a common chord of the curves is equidistant from the vertex and focus of the parabola. The equation of the circle is
a)
(x – 2)2 + y2 = 3
b)
(x – 2)2 + y2 = 9
c)
(x + 2)2 + y2 = 9
d)
None
|
|
Geetika Shah answered |
Focus of parabola y2 = 8x is (2,0). Equation of circle with centre (2,0) is (x−2)2 + y2 = r2
Let AB is common chord and Q is mid point i.e. (1,0)
AQ2 = y2 = 8x
= 8×1 = 8
∴ r2 = AQ2 + QS2
= 8 + 1 = 9
So required circle is (x−2)2 + y2 = 9
Let AB is common chord and Q is mid point i.e. (1,0)
AQ2 = y2 = 8x
= 8×1 = 8
∴ r2 = AQ2 + QS2
= 8 + 1 = 9
So required circle is (x−2)2 + y2 = 9
A parabola whose axis is along the y-axis, vertex is (0,0) and point from the first and second quadrants lie on it, has the equation of the type- a)
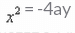
- b)
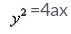
- c)
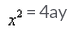
- d)
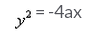
Correct answer is option 'C'. Can you explain this answer?
A parabola whose axis is along the y-axis, vertex is (0,0) and point from the first and second quadrants lie on it, has the equation of the type
a)
b)
c)
d)
|
|
Rohini Verma answered |
As the quadrants lies in first and second quadrant
y = -a Focus(0,a)
x2 = 4ay
y = -a Focus(0,a)
x2 = 4ay
The …… of a conic is the chord passing through the focus and perpendicular to the axis.- a)Latus-rectum
- b)Directrix
- c)Line of axis
- d)Y-axis
Correct answer is option 'A'. Can you explain this answer?
The …… of a conic is the chord passing through the focus and perpendicular to the axis.
a)
Latus-rectum
b)
Directrix
c)
Line of axis
d)
Y-axis

|
Jitendra Meena answered |
Answer is A. As latus rectum is a line that passes through the focus and also is perpendicular to the axis
Which one of the following equations represents parametrically, parabolic profile ?- a)x = 3 cost ; y = 4 sint
- b) x2 – 2 = – cost ; y = 4 cos2
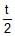
- c)
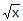 = tan t ;
= tan t ; 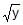 = sec t
= sec t - d) x =
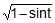 ; y = sin
; y = sin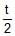 + cos
+ cos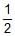
Correct answer is option 'B'. Can you explain this answer?
Which one of the following equations represents parametrically, parabolic profile ?
a)
x = 3 cost ; y = 4 sint
b)
x2 – 2 = – cost ; y = 4 cos2 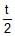
c)
d)
x = 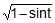 ; y = sin
; y = sin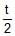 + cos
+ cos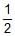
|
|
Hansa Sharma answered |
x2 − 2 = −2cost
⇒ x2 = 2 − 2cost
⇒x2 = 2(1−cost)
⇒x2 = 2(1−(1−2sin2 t/2))
⇒x2 = 4sin2 t/2
We have y = 4cos2 t/2
⇒cos2 t/2= y/4
We know the identity, sin2 t/2 + cos2 t/2 = 1
⇒ x2/4 + y/4 = 1
⇒ x2 = 4−y represents a parabolic profile.
⇒ x2 = 2 − 2cost
⇒x2 = 2(1−cost)
⇒x2 = 2(1−(1−2sin2 t/2))
⇒x2 = 4sin2 t/2
We have y = 4cos2 t/2
⇒cos2 t/2= y/4
We know the identity, sin2 t/2 + cos2 t/2 = 1
⇒ x2/4 + y/4 = 1
⇒ x2 = 4−y represents a parabolic profile.
If the focus of a parabola is (-2,1) and the directrix has the equation x + y = 3 then the vertex is- a)(2,-1)
- b)(-1,2)
- c)(0,3)
- d)(-1,1/2)
Correct answer is option 'B'. Can you explain this answer?
If the focus of a parabola is (-2,1) and the directrix has the equation x + y = 3 then the vertex is
a)
(2,-1)
b)
(-1,2)
c)
(0,3)
d)
(-1,1/2)
|
|
Riya Banerjee answered |
x+y=3 m=−1
(−2,1)m = 1
y−1 = 1(x+2)
y−1 = x+2
x−y+3 = 0
x−y+3 = 0
x+y−3 = 0
2x = 0
x = 0; y = 3
Vertex=
Midpoint of focus and directrix = (0−2)/2,(3+1)/2
=(−1,2)
(−2,1)m = 1
y−1 = 1(x+2)
y−1 = x+2
x−y+3 = 0
x−y+3 = 0
x+y−3 = 0
2x = 0
x = 0; y = 3
Vertex=
Midpoint of focus and directrix = (0−2)/2,(3+1)/2
=(−1,2)
The straight line x + y = k + 1 touches the parabola y = x(1 – x) if- a)k = -1
- b)k = 0
- c)k = 1
- d)k takes any real value
Correct answer is option 'B'. Can you explain this answer?
The straight line x + y = k + 1 touches the parabola y = x(1 – x) if
a)
k = -1
b)
k = 0
c)
k = 1
d)
k takes any real value

|
Nishanth Verma answered |
Method to Solve :
x+y-1=0. or. y=1-x (1)
y^2. = kx .(2)
On putting y=1-x from eq.(1)
(1-x)^2=k.x
1–2x+x^2 =kx
x^2 - (k+2)x+1 = 0
The given line is tangent to the parabola which touches the parabola one and only one point. means both the roots are same.
D or. b^ - 4 a.c. =0
{-(k+2)}^2. - 4.1.1. =0
(k+2)^2. = 4
(k+2) = +/-(2)
k= -2 +/-2
k= -2+2 or. -2–2.
k =0. , - 4. Answer.
y^2. = kx .(2)
On putting y=1-x from eq.(1)
(1-x)^2=k.x
1–2x+x^2 =kx
x^2 - (k+2)x+1 = 0
The given line is tangent to the parabola which touches the parabola one and only one point. means both the roots are same.
D or. b^ - 4 a.c. =0
{-(k+2)}^2. - 4.1.1. =0
(k+2)^2. = 4
(k+2) = +/-(2)
k= -2 +/-2
k= -2+2 or. -2–2.
k =0. , - 4. Answer.
The equation 2x2 – 3xy + 5y2 + 6x – 3y + 5 = 0 represents.- a)A parabola
- b)An ellipse
- c)A hyperbola
- d)A pair of straight lines
Correct answer is option 'B'. Can you explain this answer?
The equation 2x2 – 3xy + 5y2 + 6x – 3y + 5 = 0 represents.
a)
A parabola
b)
An ellipse
c)
A hyperbola
d)
A pair of straight lines
|
|
Pooja Shah answered |
Comparing the equation with the standard form ax2+2hxy+by2+2gx+2fy+c=0
a=2,h=−3/2,b=5,g=3,f=−3/2,c=5
Δ=abc+2fgh−af2−bg2−ch2
=(2)(5)(5)+2(−3/2)(3)(−3/2)−(2)(−3/2)2−(5)(3)2−(5)(−3/2)2
=50+27/2−9/2−45−225/4
=−169/4 is not equal to 0
Descriminant =h2−ab
=(−3/2)2−(2)(5)
= 9/4−10
= −31/4<0
So, the curve represents either a circle or an ellipse
a is not equal to b and
Δ/a+b = −(169/4)/2+5
=−169/28<0
So, the curve represents a ellipse.
a=2,h=−3/2,b=5,g=3,f=−3/2,c=5
Δ=abc+2fgh−af2−bg2−ch2
=(2)(5)(5)+2(−3/2)(3)(−3/2)−(2)(−3/2)2−(5)(3)2−(5)(−3/2)2
=50+27/2−9/2−45−225/4
=−169/4 is not equal to 0
Descriminant =h2−ab
=(−3/2)2−(2)(5)
= 9/4−10
= −31/4<0
So, the curve represents either a circle or an ellipse
a is not equal to b and
Δ/a+b = −(169/4)/2+5
=−169/28<0
So, the curve represents a ellipse.
Locus of the point of intersection of the perpendicular tangents of the curve y2 + 4y – 6x – 2 = 0 is- a) 2x – 1 = 0
- b)2x + 3 = 0
- c)2y + 3 = 0
- d)2x + 5 = 0
Correct answer is option 'C'. Can you explain this answer?
Locus of the point of intersection of the perpendicular tangents of the curve y2 + 4y – 6x – 2 = 0 is
a)
2x – 1 = 0
b)
2x + 3 = 0
c)
2y + 3 = 0
d)
2x + 5 = 0
|
|
Geetika Shah answered |
Given parabola is, y2+4y−6x−2=0
⇒ y2+4y+4=6x+6=6(x+1)
⇒ (y+2)2 = 6(x+1)
shifting origin to (−1,−2)
Y2 = 4aX where a = 3/2
We know locus of point of intersection of perpendicular tangent is directrix of the parabola itself
Hence required locus is X=−a ⇒ x+1=−3/2
⇒ 2x+5=0
⇒ y2+4y+4=6x+6=6(x+1)
⇒ (y+2)2 = 6(x+1)
shifting origin to (−1,−2)
Y2 = 4aX where a = 3/2
We know locus of point of intersection of perpendicular tangent is directrix of the parabola itself
Hence required locus is X=−a ⇒ x+1=−3/2
⇒ 2x+5=0
The locus of a point such that two tangents drawn from it to the parabola y2 = 4ax are such that the slope of one is double the other is- a) y2 =
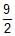 ax
ax - b) y2 =
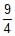 ax
ax - c) y2 = 9ax
- d)x2 = 4ay
Correct answer is option 'A'. Can you explain this answer?
The locus of a point such that two tangents drawn from it to the parabola y2 = 4ax are such that the slope of one is double the other is
a)
y2 = 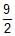 ax
ax
b)
y2 = 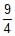 ax
ax
c)
y2 = 9ax
d)
x2 = 4ay

|
Knowledge Hub answered |
Let the point be (h, k)
Now equation of tangent to the parabola y2 = 4ax whose slope is m is
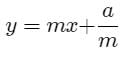
as it passes through (h, k)]
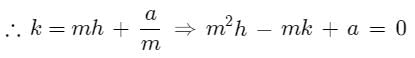
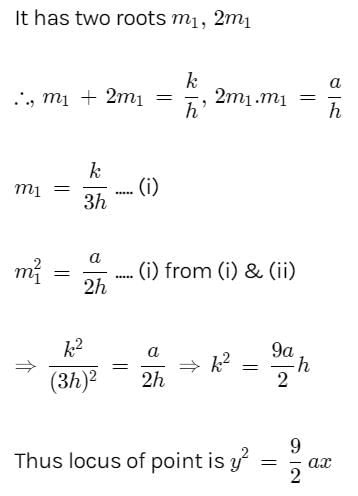
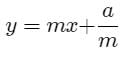
as it passes through (h, k)]
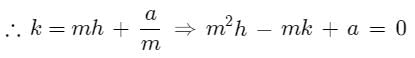
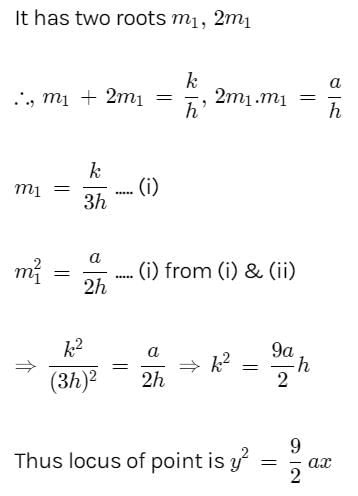
T is a point on the tangent to a parabola y2 = 4ax at its point P. TL and TN are the perpendiculars on the focal radius SP and the directrix of the parabola respectively. Then- a)SL = 2 (TN)
- b)3 (SL) = 2 (TN)
- c)SL = TN
- d)2 (SL) = 3 (TN)
Correct answer is option 'C'. Can you explain this answer?
T is a point on the tangent to a parabola y2 = 4ax at its point P. TL and TN are the perpendiculars on the focal radius SP and the directrix of the parabola respectively. Then
a)
SL = 2 (TN)
b)
3 (SL) = 2 (TN)
c)
SL = TN
d)
2 (SL) = 3 (TN)

|
Anjana Desai answered |
D
The point of intersection of the curves whose parametric equations are x = t2 + 1, y = 2t and x = 2s, y = 2/s is given by- a)(1, –3)
- b)(2, 2)
- c)(–2, 4)
- d)(1, 2)
Correct answer is option 'B'. Can you explain this answer?
The point of intersection of the curves whose parametric equations are x = t2 + 1, y = 2t and x = 2s, y = 2/s is given by
a)
(1, –3)
b)
(2, 2)
c)
(–2, 4)
d)
(1, 2)
|
|
Bhargavi Joshi answered |
For intersection of both the curve we must have,
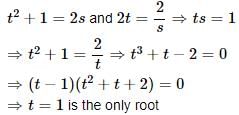
Therefore, the point of intersection is (2,2)(2,2)
Hence, option 'B' is correct.
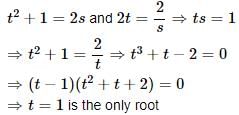
Therefore, the point of intersection is (2,2)(2,2)
Hence, option 'B' is correct.
PN is an ordinate of the parabola y2 = 4ax. A straight line is drawn parallel to the axis to bisect NP and meets the curve in Q. NQ meets the tangent at the vertex in a point T such that AT = kNP, then the value of k is (where A is the vertex)- a)3/2
- b)2/3
- c)1
- d)none
Correct answer is option 'B'. Can you explain this answer?
PN is an ordinate of the parabola y2 = 4ax. A straight line is drawn parallel to the axis to bisect NP and meets the curve in Q. NQ meets the tangent at the vertex in a point T such that AT = kNP, then the value of k is (where A is the vertex)
a)
3/2
b)
2/3
c)
1
d)
none
|
|
Naina Sharma answered |
The equation of parabola be y2=4ax
let the point P be (at2,2at)
PN is ordinate ⇒N(at2,0)
Equation of straight line bisecting NP is
y=at
substituting y in equation of parabola
a2t2 = 4ax
⇒x = 4at2
So the coordinates of Q are (4at2 ,at)
Equation of NQ is y−0 = (at−0)/(at2/4 - at2)(x−at2)
y= −4/3t(x−at2)
Put x=0
y = −4/3t(0−at^2)
⇒y=4at/3
⇒AT = 4at/3
NP = 2at
AT/NP = (4at/3)/2at
= ⅔
AT = 2/3NP
let the point P be (at2,2at)
PN is ordinate ⇒N(at2,0)
Equation of straight line bisecting NP is
y=at
substituting y in equation of parabola
a2t2 = 4ax
⇒x = 4at2
So the coordinates of Q are (4at2 ,at)
Equation of NQ is y−0 = (at−0)/(at2/4 - at2)(x−at2)
y= −4/3t(x−at2)
Put x=0
y = −4/3t(0−at^2)
⇒y=4at/3
⇒AT = 4at/3
NP = 2at
AT/NP = (4at/3)/2at
= ⅔
AT = 2/3NP
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =- a)6
- b)9
- c)3
- d)12
Correct answer is option 'B'. Can you explain this answer?
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =
a)
6
b)
9
c)
3
d)
12
|
|
Rajesh Gupta answered |
x2 + y2 + 6x − 6y + 5 = 0
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
Focus and vertex of the parabola that touches x-axis at (1, 0) and x = y at (1, 1) are (h, k) and (p, q) then the value of 25(p q h k)
- a) 35
- b) 37
- c) 33
- d) 39
Correct answer is option 'B'. Can you explain this answer?
Focus and vertex of the parabola that touches x-axis at (1, 0) and x = y at (1, 1) are (h, k) and (p, q) then the value of 25(p q h k)
a)
35b)
37c)
33d)
39|
|
Poonam Reddy answered |
The x-axis touches at A(1, 0) and x = y touches at B(1, 1). Hence the equation to the curve through these points is given by y(y – x) + k(x – 1)2 = 0. For this to represent a parabola, 4k = 1. The equation is x2 – 4xy + 4y2 – 2x + 1 = 0. Vertex 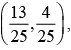 focus
focus 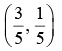
Two parabolas y2 = 4a(x – l1) and x2 = 4a(y – l2) always touch one another, the quantities l1 and l2 are both variable. Locus of their point of contact has the equation- a)xy = a2
- b) xy = 2a2
- c)xy = 4a2
- d)None
Correct answer is option 'C'. Can you explain this answer?
Two parabolas y2 = 4a(x – l1) and x2 = 4a(y – l2) always touch one another, the quantities l1 and l2 are both variable. Locus of their point of contact has the equation
a)
xy = a2
b)
xy = 2a2
c)
xy = 4a2
d)
None
|
|
Gaurav Kumar answered |
Let P(x1 , y1) be point of contact of two parabola. tangents at P of the two parabolas are
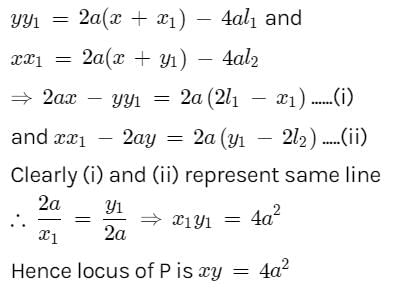
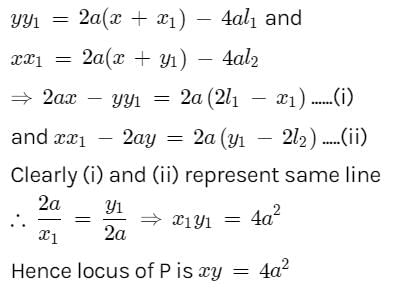
The number of points on X-axis which are at a distance c units (c < 3) from (2, 3) is- a)1
- b)0
- c)3
- d)2
Correct answer is option 'B'. Can you explain this answer?
The number of points on X-axis which are at a distance c units (c < 3) from (2, 3) is
a)
1
b)
0
c)
3
d)
2

|
Mohit Rajpoot answered |
Distance of 'c' units from (2,3)
Let the no: of points be (x,0)
By distance formula
{(2−x)2+(3−0)2}=c
4−4x+x2+9=c
⇒x2−4x+13 = c:c=2,2
There are the points of c,such that when they are applied back to the equations,the number of points will become zero.
Let the no: of points be (x,0)
By distance formula
{(2−x)2+(3−0)2}=c
4−4x+x2+9=c
⇒x2−4x+13 = c:c=2,2
There are the points of c,such that when they are applied back to the equations,the number of points will become zero.
In a knockout tournament 16 equally skilled players namely P1, P2, -------- P16 are participating. In each round players are divided in pairs at random and winner from each pair moves in the next round. If P2 reaches the semifinal, then the probability that P1 will win the tournament is.- a)3/64
- b)1/16
- c)1/20
- d)1/15
Correct answer is option 'C'. Can you explain this answer?
In a knockout tournament 16 equally skilled players namely P1, P2, -------- P16 are participating. In each round players are divided in pairs at random and winner from each pair moves in the next round. If P2 reaches the semifinal, then the probability that P1 will win the tournament is.
a)
3/64
b)
1/16
c)
1/20
d)
1/15
|
|
Anjali Sharma answered |
Let E1 = P1 win the tournament, E2 = P2 reaches the semifinal since all players are equally skilled and there are 4 persons in the semifinal 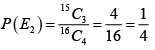
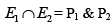 both are in semifinal and P1 wins in semifinal and final
both are in semifinal and P1 wins in semifinal and final
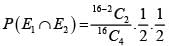
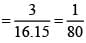
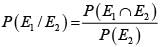
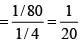
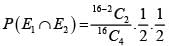
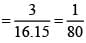
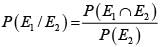
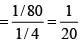
Directrix of a parabola is x + y = 2. If it's focus is origin, then latus rectum of the parabola is equal to- a)√2 units
- b)2 units
- c)4√2 units
- d) 4 units
Correct answer is option 'C'. Can you explain this answer?
Directrix of a parabola is x + y = 2. If it's focus is origin, then latus rectum of the parabola is equal to
a)
√2 units
b)
2 units
c)
4√2 units
d)
4 units
|
|
Aaradhya Solankir answered |
Ritu Singh ,
There is not answer in the given options. What Saroj Bala said is wrong because there it's considered the vertex as origin , but in the question the focus is given as origin...
There is not answer in the given options. What Saroj Bala said is wrong because there it's considered the vertex as origin , but in the question the focus is given as origin...
A parabola has focus at (0, 0) and passes through the points (4, 3) and (–4, –3). The number of lattice points (x, y) on the parabola such that |4x + 3y| < 1000 is- a)20
- b)100
- c)40
- d)80
Correct answer is option 'D'. Can you explain this answer?
A parabola has focus at (0, 0) and passes through the points (4, 3) and (–4, –3). The number of lattice points (x, y) on the parabola such that |4x + 3y| < 1000 is
a)
20
b)
100
c)
40
d)
80

|
Devansh Joshi answered |
The expression you'll find is 4x+3y=1250n+50p−25, n being a integer and p being a positive integer that is less than 125050
Then, you can build a simple excel file to exhaust the answers from 1250n+25
Then, you can build a simple excel file to exhaust the answers from 1250n+25
to 1250n+1225. It turns out that only when n=0 or 1 are the criteria satisfied, and in each case there are 20 of the pairs.
So B.40
The equation of the tangent at the vertex of the parabola x2 + 4x + 2y = 0 is- a)x = –2
- b)x = 2
- c)y = 2
- d)y = –2.
Correct answer is option 'C'. Can you explain this answer?
The equation of the tangent at the vertex of the parabola x2 + 4x + 2y = 0 is
a)
x = –2
b)
x = 2
c)
y = 2
d)
y = –2.
|
|
Akshay Chauhan answered |
-2
To find the equation of the tangent at the vertex of the parabola, we need to first find the coordinates of the vertex. We can do this by completing the square:
x^2 + 4x + 2y = 0
x^2 + 4x + 4 + 2y = 4
(x + 2)^2 = -2y + 4
So the vertex is at (-2, 2).
Next, we need to find the slope of the tangent at the vertex. We can do this by taking the derivative of the equation of the parabola:
2x + 4 + 0 = 0
2x = -4
x = -2
So the slope of the tangent at the vertex is 2(-2) + 4 = 0.
Finally, we can use the point-slope form of a line to find the equation of the tangent:
y - 2 = 0(x + 2)
y - 2 = 0
y = 2
So the equation of the tangent at the vertex is y = 2.
To find the equation of the tangent at the vertex of the parabola, we need to first find the coordinates of the vertex. We can do this by completing the square:
x^2 + 4x + 2y = 0
x^2 + 4x + 4 + 2y = 4
(x + 2)^2 = -2y + 4
So the vertex is at (-2, 2).
Next, we need to find the slope of the tangent at the vertex. We can do this by taking the derivative of the equation of the parabola:
2x + 4 + 0 = 0
2x = -4
x = -2
So the slope of the tangent at the vertex is 2(-2) + 4 = 0.
Finally, we can use the point-slope form of a line to find the equation of the tangent:
y - 2 = 0(x + 2)
y - 2 = 0
y = 2
So the equation of the tangent at the vertex is y = 2.
The locus of the centre of a circle, which touches externally the circle x2 + y2 − 6x − 6y + 14 = 0 and also touches Y-axis, is given by the equation- a)x2−6x−10y+14=0
- b)x2−10x−6y+14=0
- c)y2−6x−10y+14=0
- d)y2−10x−6y+14=0
Correct answer is option 'D'. Can you explain this answer?
The locus of the centre of a circle, which touches externally the circle x2 + y2 − 6x − 6y + 14 = 0 and also touches Y-axis, is given by the equation
a)
x2−6x−10y+14=0
b)
x2−10x−6y+14=0
c)
y2−6x−10y+14=0
d)
y2−10x−6y+14=0

|
Nipun Tuteja answered |
Let the equation of circle be x2+y2+2gx+2fy+c=0.
Then the radius,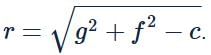
Centre: (−g,−f).
But since circle touches Y-axis, the absolute value of abscissa is equal to the radius, |−g|=r.
⇒g2=r2⇒g2=g2+f2−c
⇒c=f2
Centre of the circle, x2+y2−6x−6y+14=0: (3,3)
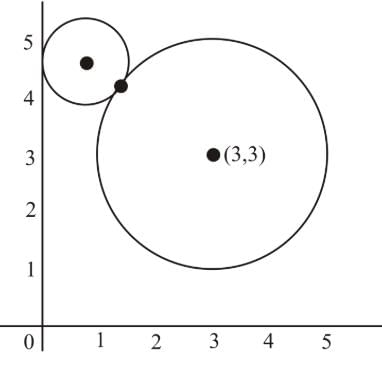
As the two circles touch externally, the distance between
centres is equal to the sum of radii.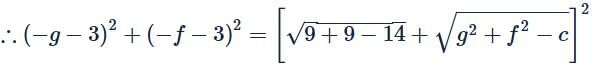
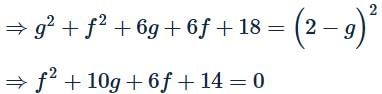
Hence, locus of the centre (−g,−f) obtained by substituting −g=x, −f=y⇒g=−x, f=−y, is y2−10x−6y+14=0.
Then the radius,
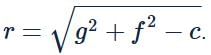
Centre: (−g,−f).
But since circle touches Y-axis, the absolute value of abscissa is equal to the radius, |−g|=r.
⇒g2=r2⇒g2=g2+f2−c
⇒c=f2
Centre of the circle, x2+y2−6x−6y+14=0: (3,3)

As the two circles touch externally, the distance between
centres is equal to the sum of radii.
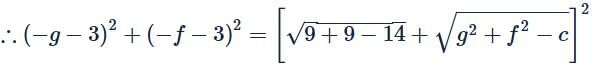
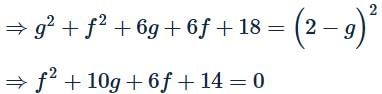
Hence, locus of the centre (−g,−f) obtained by substituting −g=x, −f=y⇒g=−x, f=−y, is y2−10x−6y+14=0.
The equations x = at2, y = 4at ; t ∈ R represent- a)a parabola
- b)a circle
- c)an ellipse
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
The equations x = at2, y = 4at ; t ∈ R represent
a)
a parabola
b)
a circle
c)
an ellipse
d)
a hyperbola

|
Anjali Mehla answered |
Firstly I think you have to know the equation of a parabola and it's proff
The locus of mid–point of family of chords λx + y - 5 = 0 (parameter) of the parabola x2 = 20y is- a)y2 = 10(x - 5)
- b)x2 = 10(y - 5)
- c)x2 + y2 = 25
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The locus of mid–point of family of chords λx + y - 5 = 0 (parameter) of the parabola x2 = 20y is
a)
y2 = 10(x - 5)
b)
x2 = 10(y - 5)
c)
x2 + y2 = 25
d)
none of these
|
|
Parth Majumdar answered |
λx + y - 5 = 0 is the focal chord
Since it passes through (0, 5)
Let h, k be the mid point of all such chord h = 5(t1 + t2),
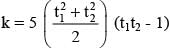
On eliminating t1, t2
x2 = 10 (y - 5).
Since it passes through (0, 5)
Let h, k be the mid point of all such chord h = 5(t1 + t2),
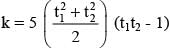
On eliminating t1, t2
x2 = 10 (y - 5).
The line x + y = 6 is a normal to the parabola y2 = 8x at the point- a)(18, - 12)
- b)(4, 2)
- c)(2, 4)
- d)(3, 3)
Correct answer is option 'C'. Can you explain this answer?
The line x + y = 6 is a normal to the parabola y2 = 8x at the point
a)
(18, - 12)
b)
(4, 2)
c)
(2, 4)
d)
(3, 3)

|
Devika Banerjee answered |
Method to Solve :
From the given equation of the parabola, we can find the focus to be4a = 8, this implies, a = 2
The condition for a line y = mx + c, to be a tangent to the parabola, then c = a/m
The given line is x - y +2 = 0
or y = x+2, where m = 1 and c = 2
c = a/m = 2/1 satifies the condition for the line to be a tangent.
Hence the given line is a tangent to the parabola.
The condition for a line y = mx + c, to be a tangent to the parabola, then c = a/m
The given line is x - y +2 = 0
or y = x+2, where m = 1 and c = 2
c = a/m = 2/1 satifies the condition for the line to be a tangent.
Hence the given line is a tangent to the parabola.
The line y = c is a tangent to the parabola 7/2 if c is equal to- a)a
- b)0
- c)2a
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The line y = c is a tangent to the parabola 7/2 if c is equal to
a)
a
b)
0
c)
2a
d)
none of these
|
|
Sravya Nair answered |
y = x is tangent to the parabola
y=ax2+c
if a= then c=?
y′ =2ax
y’ = 2(7/2)x =1
x = 1/7
1/7 = 2(1/7)2 + c
c = 1/7 * 2/49
c = 7/2
y=ax2+c
if a= then c=?
y′ =2ax
y’ = 2(7/2)x =1
x = 1/7
1/7 = 2(1/7)2 + c
c = 1/7 * 2/49
c = 7/2
If the tangents at two points (1, 2) and (3, 6) as a parabola intersect at the point (– 1, 1), then the slope of the directrix of the parabola is - a)√2
- b)-2
- c)-1
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the tangents at two points (1, 2) and (3, 6) as a parabola intersect at the point (– 1, 1), then the slope of the directrix of the parabola is
a)
√2
b)
-2
c)
-1
d)
none of these

|
Manisha Choudhary answered |
If the tangents at P and Q intersect at T, then axis of parabola is parallel to TR, where R is the mid point of P and Q. So, slope of the axis is 1.
∴ slope of the directrix = – 1.
∴ slope of the directrix = – 1.
If the line x + y – 1 = 0 touches the parabola y2 = kx , then the value of k is- a)4
- b)–4
- c)2
- d)–2
Correct answer is option 'B'. Can you explain this answer?
If the line x + y – 1 = 0 touches the parabola y2 = kx , then the value of k is
a)
4
b)
–4
c)
2
d)
–2
|
|
Pragati Kumar answered |
I'm sorry, but there is no information or context given to determine what is being asked. Please provide more details or clarify your question.
The tangent and normal at the point P(4, 4) to the parabola, y2 = 4x intersect the x–axis at the points Q and R respectively. Then the cirucm centre of the ΔPQR is- a)(2, 0)
- b)(2, 1)
- c)(1, 0)
- d)(1, 2)
Correct answer is option 'C'. Can you explain this answer?
The tangent and normal at the point P(4, 4) to the parabola, y2 = 4x intersect the x–axis at the points Q and R respectively. Then the cirucm centre of the ΔPQR is
a)
(2, 0)
b)
(2, 1)
c)
(1, 0)
d)
(1, 2)

|
Pragati Patel answered |
Eq. of tangent 2y = x + 4
∴ Q ≡ (-4,0)
Eq. of normal is y - 4 = -2 (x - 4)
⇒ y + 2x = 12
Clearly QR is diameter of the required circle.
⇒ (x + 4) (x – 6) + y2 = 0
⇒ x2 + y2 – 2x – 24 = 0
centre (1, 0)
A and B are two distinct points, Locus of a point P satisfying |PA| + |PB| = 2k, a constant is- a)nothing can be said
- b)the line segment [AB]
- c)an ellipse
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
A and B are two distinct points, Locus of a point P satisfying |PA| + |PB| = 2k, a constant is
a)
nothing can be said
b)
the line segment [AB]
c)
an ellipse
d)
a hyperbola
|
|
Ram Mohith answered |
I think the locus of P is an ellipse because if yo... moreu take any point on the ellipse then the sum of distance from focii to that
All chords of the parabola y2 = 4x which subtend right angle at the origin are concurrent at the point:- a)(1, 0)
- b)(2, 0)
- c)(3, 0)
- d)(4, 0)
Correct answer is option 'D'. Can you explain this answer?
All chords of the parabola y2 = 4x which subtend right angle at the origin are concurrent at the point:
a)
(1, 0)
b)
(2, 0)
c)
(3, 0)
d)
(4, 0)

|
Akash Shah answered |
Let y = mx+ c be such chord with extremities A and B .
∴ The combined equation of the pair of lines OA and OB is
∴ Coeff of x2 + Coeff of y2 = 0

∴ c = -4 m
∴ The chord equation is y = m (x- 4) .
∴ The combined equation of the pair of lines OA and OB is

∴ Coeff of x2 + Coeff of y2 = 0

∴ c = -4 m
∴ The chord equation is y = m (x- 4) .
If (h, k) is a point on the axis of parabola 2(x -1)2 + 2 (y -1)2 = (x + y + 2)2 from where three distinct normals can be drawn, then- a)h > 2
- b)h < 4
- c)h > 8
- d)h < 8
Correct answer is option 'A'. Can you explain this answer?
If (h, k) is a point on the axis of parabola 2(x -1)2 + 2 (y -1)2 = (x + y + 2)2 from where three distinct normals can be drawn, then
a)
h > 2
b)
h < 4
c)
h > 8
d)
h < 8
|
|
Shounak Shah answered |
∴ Focus= (1,1) . Directrix is x+y+2 =0
Axis is x-y=0 and z= (-1,-1)
Vertex = (0,0). Parameter a = √2
The distance of the point from vertex and lie on axis from which 3 normals can be drawn must be greater 2a = 2√2. Hence point on axis at a distance 2√2 is (2,2), Hence h>2
Let PSQ be the focal chord of the parabola, y2 = 8x. If the length of SP = 6 then, l(SQ) is equal to(where S is the focus)- a)3
- b)4
- c)6
- d)None
Correct answer is option 'A'. Can you explain this answer?
Let PSQ be the focal chord of the parabola, y2 = 8x. If the length of SP = 6 then, l(SQ) is equal to(where S is the focus)
a)
3
b)
4
c)
6
d)
None
|
|
Bijoy Sen answered |
Since the semi latus rectum of a parabola is the harmonic mean between the segment of any focal chord of a parabola, therefore,SP,4,SQ are in H.P.
⇒4=2(SP.SQ)/(SP+SQ)
⇒4=2*6.SQ/(6+SQ)
⇒SQ=3
⇒4=2(SP.SQ)/(SP+SQ)
⇒4=2*6.SQ/(6+SQ)
⇒SQ=3
Equation of common tangent of parabola y2 = 8x and x2 + y = 0 is- a)y = 2x + 1
- b)x = y + 1
- c)2x - y + 1 = 0
- d)x + 2y + 1 = 0
Correct answer is option 'A'. Can you explain this answer?
Equation of common tangent of parabola y2 = 8x and x2 + y = 0 is
a)
y = 2x + 1
b)
x = y + 1
c)
2x - y + 1 = 0
d)
x + 2y + 1 = 0

|
Athira Datta answered |
if it is common tangent, then m3 = 8 m = 2.
The combined equation to two parabolas, both have their axis along x-axis, is given by y4 - y2 (4x + 4 - 2 sin22α) + sin22α (4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°
is- a)another parabola
- b)circle
- c)a line midway between the tangents at vertices
- d)a line midway between their directrices
Correct answer is option 'D'. Can you explain this answer?
The combined equation to two parabolas, both have their axis along x-axis, is given by y4 - y2 (4x + 4 - 2 sin22α) + sin22α (4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°
is
is
a)
another parabola
b)
circle
c)
a line midway between the tangents at vertices
d)
a line midway between their directrices

|
Milan Roy answered |
The parabolas are y2 = 4sin2 α(x + sin2α) and y2 = 4cos2 α(x + cos2α), hence the locus is x + cos2α + sin2α = 0 ⇒ x + 1 = 0
Assume the point as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)
as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)
Similarly A3(-2, 0), A4 (0, -2√2) etc.
Assume the point
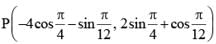 as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)
as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)Similarly A3(-2, 0), A4 (0, -2√2) etc.
Point on the curve y2 = 4(x- 10) which is nearest to the line x + y = 4 may be- a)(11, 2)
- b)(10, 0)
- c)(11, -2)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Point on the curve y2 = 4(x- 10) which is nearest to the line x + y = 4 may be
a)
(11, 2)
b)
(10, 0)
c)
(11, -2)
d)
None of these
|
|
Anjali Banerjee answered |
P(x0 , y0) : pt on curve nearest to line.
Normal at P is perpendicular to the line Normal at P has slope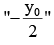
∴ y0 = 2 and x0 = 11; P(11, -2)
Normal at P is perpendicular to the line Normal at P has slope
∴ y0 = 2 and x0 = 11; P(11, -2)
Chapter doubts & questions for Parabola - Mathematics (Maths) for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Parabola - Mathematics (Maths) for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup










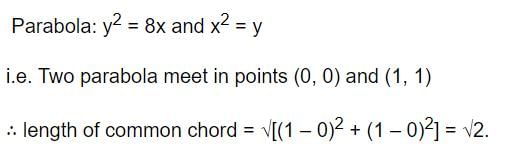
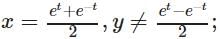 t ∈ R represents
t ∈ R represents