All Exams >
Computer Science Engineering (CSE) >
Algorithms >
All Questions
All questions of Recurrence Relations for Computer Science Engineering (CSE) Exam
When n = 22k for some k ≥ 0, the recurrence relation
T(n) = √(2) T(n/2) + √n, T(1) = 1
evaluates to :- a)√(n) (log n + 1)
- b)√(n) (log n )
- c)√(n) log √(n)
- d)n log √(n)
Correct answer is option 'A'. Can you explain this answer?
When n = 22k for some k ≥ 0, the recurrence relation
T(n) = √(2) T(n/2) + √n, T(1) = 1
evaluates to :
T(n) = √(2) T(n/2) + √n, T(1) = 1
evaluates to :
a)
√(n) (log n + 1)
b)
√(n) (log n )
c)
√(n) log √(n)
d)
n log √(n)
|
|
Ravi Singh answered |
Please note that the question is asking about exact solution. Master theorem provides results in the form of asymptotic notations. So we can't apply Master theorem here. We can solve this recurrence using simple expansion or recurrence tree method.
T(n) = √(2) T(n/2) + √n = √(2) [√(2) T(n/4) + √(n/2) ] + √n = 2 T(n/4) + √2 √(n/2) +√n = 2[ √2 T(n/8) + √(n/4) ]+√2 √(n/2)+√n = √(2^3) T(n/8)+ 2 √(n/4) + √2 √(n/2) +√n = √(2^3) T(n/8)+√n +√n +√n = √(2^3) T(n/(2^3))+3√n ............................................. = √(2^k) T(n/(2^k))+k√n = √(2^logn) + logn √n = √n + logn √n = √n(logn +1)
Alternate Solution : This question can be easily done by substitution method look: T(1)= 1; GIVEN. Now use n=2 in the given recurrence relation which gives 2*(1.414) (since value of root over 2 is 1.414) now by looking at the options use n=2 which satisfies option A.
For parameters a and b, both of which are ω(1), T(n)=T(n1/a)+1, and T(b)=1. Then T(n) is- a)Θ(logalogbn)
- b)Θ(logabn)
- c)Θ(logblogan)
- d)Θ(log2log2n)
Correct answer is option 'A'. Can you explain this answer?
For parameters a and b, both of which are ω(1), T(n)=T(n1/a)+1, and T(b)=1. Then T(n) is
a)
Θ(logalogbn)
b)
Θ(logabn)
c)
Θ(logblogan)
d)
Θ(log2log2n)
|
|
Ravi Singh answered |
Given,
T(n) = T(n1/a)+1, T(b) = 1
Now, using iterative method,
= T(n) = [T(n1/a2)+1] + 1 = [T(n1/a3)+1] + 2 = [T(n1/a4)+1] + 3 . . . = [T(n1/ak)+1] + (k-1) = T(n1/ak) + k
Let,
→ n1/ak = b → log(n1/ak) = log(b) → ak = log(n) / log (b) = logb(n) → k = logalogb(n)
Therefore,
= T(n1/ak) + k = T(b) + logalogb(n) = 1 + logalogb(n) = Θ(logalogb(n))
Option (A) is correct.
The running time of an algorithm is represented by the following recurrence relation:if n <= 3 then T(n) = n else T(n) = T(n/3) + cn Which one of the following represents the time complexity of the algorithm?
(A)  (n)
(n)
(B)  (n log n)
(n log n)
(C)  (n^2)
(n^2)
(D)  (n^2log n)
(n^2log n)- a)A
- b)B
- c)C
- d)D
Correct answer is option 'A'. Can you explain this answer?
The running time of an algorithm is represented by the following recurrence relation:
if n <= 3 then T(n) = n
else T(n) = T(n/3) + cn
Which one of the following represents the time complexity of the algorithm?
(A) (n)
(n)
(B) (n log n)
(n log n)
(C) (n^2)
(n^2)
(D) (n^2log n)
(n^2log n)
(A)
(B)
(C)
(D)
a)
A
b)
B
c)
C
d)
D

|
Riverdale Learning Institute answered |
T(n) = cn + T(n/3)
= cn + cn/3 + T(n/9)
= cn + cn/3 + cn/9 + T(n/27)
Taking the sum of infinite GP series. The value of T(n) will be less than this sum.
T(n) = cn(1/(1-1/3))
= 3cn/2
or we can say
cn = T(n) = 3cn/2
Therefore T(n) =  (n)
(n)
Consider the following recurrence relation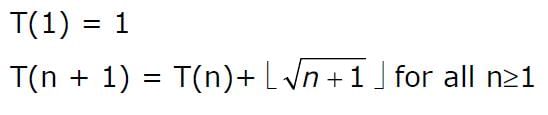 The value of T(m2) for m ≥ 1 is
The value of T(m2) for m ≥ 1 is- a)(m/6) (21m - 39) + 4
- b)(m/6) (4m2 - 3m + 5)
- c)(m/2) (m2.5 - 11m + 20) - 5
- d)(m/6) (5m3 - 34m2 + 137m - 104) + (5/6)
Correct answer is option 'B'. Can you explain this answer?
Consider the following recurrence relation
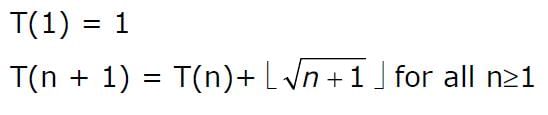
The value of T(m2) for m ≥ 1 is
a)
(m/6) (21m - 39) + 4
b)
(m/6) (4m2 - 3m + 5)
c)
(m/2) (m2.5 - 11m + 20) - 5
d)
(m/6) (5m3 - 34m2 + 137m - 104) + (5/6)
|
|
Sanya Agarwal answered |
One easy way to solve this is to try putting different
values of m.
values of m.
For example, we know T(1) = 1. If we put m = 1, only A
and B satisfy the result.
and B satisfy the result.
m = 2
T(2) = T(1) + 1 = 2
T(3) = T(2) + 1 = 3
T(4) = T(3) + 2 = 5
T(3) = T(2) + 1 = 3
T(4) = T(3) + 2 = 5
Both A & B produce 5
m = 3
T(9) = T(4) + 2*5 + 1 = 5 + 10 + 1 = 16
Both A & B produce 16
T(9) = T(4) + 2*5 + 1 = 5 + 10 + 1 = 16
Both A & B produce 16
m = 4
T(16) = T(9) + 3*7 + 1 = 16 + 21 + 1 = 38
Only B produces 38, A produces 34 which doesn't match
T(16) = T(9) + 3*7 + 1 = 16 + 21 + 1 = 38
Only B produces 38, A produces 34 which doesn't match
The solution to the recurrence equation T(2k) = 3 T(2k-1) + 1, T (1) = 1, is:- a)2k
- b)(3k + 1 - 1)/2
- c)3log2k
- d)2log3k
Correct answer is option 'B'. Can you explain this answer?
The solution to the recurrence equation T(2k) = 3 T(2k-1) + 1, T (1) = 1, is:
a)
2k
b)
(3k + 1 - 1)/2
c)
3log2k
d)
2log3k
|
|
Neha Mishra answered |
Solution:
To solve the recurrence equation T(2k) = 3 T(2k-1) - 1, we need to find a pattern in the terms and then find a closed-form solution.
Pattern of Terms:
Let's find the values of T(1), T(2), T(4), T(8), T(16), and T(32) to observe a pattern:
T(1) = 1
T(2) = 3 T(1) - 1 = 3(1) - 1 = 2
T(4) = 3 T(2) - 1 = 3(2) - 1 = 5
T(8) = 3 T(4) - 1 = 3(5) - 1 = 14
T(16) = 3 T(8) - 1 = 3(14) - 1 = 41
T(32) = 3 T(16) - 1 = 3(41) - 1 = 122
We can observe that the terms are increasing rapidly, but there doesn't seem to be a clear pattern.
Finding a Closed-Form Solution:
Let's try to find a closed-form solution for T(k) by substituting k = 2^m:
T(2^m) = 3 T(2^m-1) - 1
Let's divide both sides by T(2^m-1):
T(2^m) / T(2^m-1) = 3 - 1 / T(2^m-1)
Since T(2^m) / T(2^m-1) is a ratio of consecutive terms, it should approach a constant value as m increases.
Let's assume the ratio approaches a constant value R:
R = 3 - 1 / R
Simplifying the equation:
R^2 = 3 - 1
R^2 = 2
Taking the square root of both sides:
R = √2
Now, let's express T(2^m) in terms of m using the formula T(k) = R^(m-1) T(2):
T(2^m) = √2^(m-1) T(2)
Substituting k = 2^m:
T(k) = √2^(log2(k)-1) T(2)
Simplifying:
T(k) = 2^(log2(k)/2 - 1/2) T(2)
Since T(2) = 2 - 1 / 2 = 1/2:
T(k) = 2^(log2(k)/2 - 1/2) / 2 = (2^(log2(k)/2 - 1/2) - 1) / 2
Simplifying further:
T(k) = (2^(log2(k)/2) - 2^(-1/2)) / 2
T(k) = (2^(log2(k)/2) - 1) / 2
Finally, let's substitute k = 2k to get the solution in terms of k:
T(2k) = (2^(log2(2k)/2) - 1) / 2
T(
To solve the recurrence equation T(2k) = 3 T(2k-1) - 1, we need to find a pattern in the terms and then find a closed-form solution.
Pattern of Terms:
Let's find the values of T(1), T(2), T(4), T(8), T(16), and T(32) to observe a pattern:
T(1) = 1
T(2) = 3 T(1) - 1 = 3(1) - 1 = 2
T(4) = 3 T(2) - 1 = 3(2) - 1 = 5
T(8) = 3 T(4) - 1 = 3(5) - 1 = 14
T(16) = 3 T(8) - 1 = 3(14) - 1 = 41
T(32) = 3 T(16) - 1 = 3(41) - 1 = 122
We can observe that the terms are increasing rapidly, but there doesn't seem to be a clear pattern.
Finding a Closed-Form Solution:
Let's try to find a closed-form solution for T(k) by substituting k = 2^m:
T(2^m) = 3 T(2^m-1) - 1
Let's divide both sides by T(2^m-1):
T(2^m) / T(2^m-1) = 3 - 1 / T(2^m-1)
Since T(2^m) / T(2^m-1) is a ratio of consecutive terms, it should approach a constant value as m increases.
Let's assume the ratio approaches a constant value R:
R = 3 - 1 / R
Simplifying the equation:
R^2 = 3 - 1
R^2 = 2
Taking the square root of both sides:
R = √2
Now, let's express T(2^m) in terms of m using the formula T(k) = R^(m-1) T(2):
T(2^m) = √2^(m-1) T(2)
Substituting k = 2^m:
T(k) = √2^(log2(k)-1) T(2)
Simplifying:
T(k) = 2^(log2(k)/2 - 1/2) T(2)
Since T(2) = 2 - 1 / 2 = 1/2:
T(k) = 2^(log2(k)/2 - 1/2) / 2 = (2^(log2(k)/2 - 1/2) - 1) / 2
Simplifying further:
T(k) = (2^(log2(k)/2) - 2^(-1/2)) / 2
T(k) = (2^(log2(k)/2) - 1) / 2
Finally, let's substitute k = 2k to get the solution in terms of k:
T(2k) = (2^(log2(2k)/2) - 1) / 2
T(
What is the worst-case number of arithmetic operations performed by recursive binary search on a sorted array of size n?- a)Θ(√n)
- b)Θ(log2(n))
- c)Θ(n2)
- d)Θ(n)
Correct answer is option 'C'. Can you explain this answer?
What is the worst-case number of arithmetic operations performed by recursive binary search on a sorted array of size n?
a)
Θ(√n)
b)
Θ(log2(n))
c)
Θ(n2)
d)
Θ(n)
|
|
Yash Verma answered |
Worst-case number of arithmetic operations in recursive binary search:
Binary search is a divide and conquer algorithm that searches for a target value within a sorted array. In the worst-case scenario, the target value is not present in the array, leading to the maximum number of comparisons.
Reasoning:
- In each recursive call of binary search, the array is divided into two halves.
- This process continues until the target value is found or the subarray size becomes 0.
- In the worst-case scenario, the target value is not present in the array, and the recursion reaches the base case with a single element or an empty subarray.
Analysis:
- At each step of the recursion, the algorithm performs a constant number of arithmetic operations to calculate the mid-point and compare the target value.
- The number of recursive calls required to reduce the array size to 1 in the worst-case scenario is logarithmic with respect to the size of the array (log2(n)).
- Hence, the worst-case number of arithmetic operations performed by recursive binary search on a sorted array of size n is Theta(n) due to Theta(n) comparisons in the worst case.
Therefore, the correct answer is option 'C' - Theta(n^2).
Binary search is a divide and conquer algorithm that searches for a target value within a sorted array. In the worst-case scenario, the target value is not present in the array, leading to the maximum number of comparisons.
Reasoning:
- In each recursive call of binary search, the array is divided into two halves.
- This process continues until the target value is found or the subarray size becomes 0.
- In the worst-case scenario, the target value is not present in the array, and the recursion reaches the base case with a single element or an empty subarray.
Analysis:
- At each step of the recursion, the algorithm performs a constant number of arithmetic operations to calculate the mid-point and compare the target value.
- The number of recursive calls required to reduce the array size to 1 in the worst-case scenario is logarithmic with respect to the size of the array (log2(n)).
- Hence, the worst-case number of arithmetic operations performed by recursive binary search on a sorted array of size n is Theta(n) due to Theta(n) comparisons in the worst case.
Therefore, the correct answer is option 'C' - Theta(n^2).
The worst-case running time of Merge sort algorithm is described by the following recurrence relation :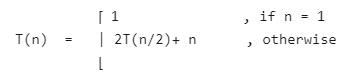 Given recurrence equation evaluates to -
Given recurrence equation evaluates to -- a)2k T(n/2k) + kn
- b)2k T(nk/2) + kn
- c)nk T(n/2k)
- d)T(n/2k) + kn
Correct answer is option 'A'. Can you explain this answer?
The worst-case running time of Merge sort algorithm is described by the following recurrence relation :
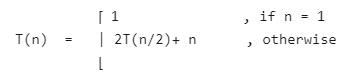
Given recurrence equation evaluates to -
a)
2k T(n/2k) + kn
b)
2k T(nk/2) + kn
c)
nk T(n/2k)
d)
T(n/2k) + kn
|
|
Sanya Agarwal answered |
T(n) = 2T (n/2) + n = 21 T(n/21) + 1.n [ k = 1] = 2k-1 T(n/2k-1) + (k-1)n = 2k-1 (2T(n/2k + n/2k-1) + (k-1)n = 2k T(n/2k) + kn
Option (A) is Correct.
Consider the following three functions.f1 = 10nf2 = nlognf3 = n√nWhich one of the following options arranges the functions in the increasing order of asymptotic growth rate?- a)f3,f2,f1
- b)f2,f1,f3
- c)f1,f2,f3
- d)f2,f3,f1
Correct answer is option 'D'. Can you explain this answer?
Consider the following three functions.
f1 = 10n
f2 = nlogn
f3 = n√n
Which one of the following options arranges the functions in the increasing order of asymptotic growth rate?
a)
f3,f2,f1
b)
f2,f1,f3
c)
f1,f2,f3
d)
f2,f3,f1
|
|
Sanya Agarwal answered |
On comparing power of these given functions : f1 has n in power. f2 has logn in power. f3 has √n in power. Hence, f2, f3, f1 is in increasing order. Note that you can take the log of each function then compare.
Consider the recurrence relation a1 = 8, an = 6n2 + 2n + an-1. Let a99 = k x 104. The value of K is _____ Note : This question was asked as Numerical Answer Type.- a)190
- b)296
- c)198
- d)200
Correct answer is option 'C'. Can you explain this answer?
Consider the recurrence relation a1 = 8, an = 6n2 + 2n + an-1. Let a99 = k x 104. The value of K is _____ Note : This question was asked as Numerical Answer Type.
a)
190
b)
296
c)
198
d)
200
|
|
Arka Dasgupta answered |
To solve the given recurrence relation and find the value of k in a99 = k x 104, we can use the method of iteration.
1. Finding the pattern:
Let's find the values of a2, a3, a4, and a5 using the given recurrence relation:
a2 = 6(2^2) - 2(2) + a1 = 24 - 4 + 8 = 28
a3 = 6(3^2) - 2(3) + a2 = 54 - 6 + 28 = 76
a4 = 6(4^2) - 2(4) + a3 = 96 - 8 + 76 = 164
a5 = 6(5^2) - 2(5) + a4 = 150 - 10 + 164 = 304
By observing the pattern, we can see that the values of a2, a3, a4, a5 are 28, 76, 164, and 304 respectively.
2. Writing the general term:
From the pattern, we can deduce that the general term of the given recurrence relation can be written as:
an = 6n^2 - 2n + (n-1)^2 + 4
3. Finding the value of a99:
Using the general term, we can find the value of a99:
a99 = 6(99^2) - 2(99) + (99-1)^2 + 4
= 6(9801) - 198 + 98^2 + 4
= 58806 - 198 + 9604 + 4
= 68816
4. Finding the value of k:
Given that a99 = k x 104, we can equate the two expressions:
68816 = k x 104
k = 68816 / 104
k ≈ 661.538
Rounded to the nearest whole number, k ≈ 662.
Therefore, the value of k is approximately 662, which corresponds to option C.
1. Finding the pattern:
Let's find the values of a2, a3, a4, and a5 using the given recurrence relation:
a2 = 6(2^2) - 2(2) + a1 = 24 - 4 + 8 = 28
a3 = 6(3^2) - 2(3) + a2 = 54 - 6 + 28 = 76
a4 = 6(4^2) - 2(4) + a3 = 96 - 8 + 76 = 164
a5 = 6(5^2) - 2(5) + a4 = 150 - 10 + 164 = 304
By observing the pattern, we can see that the values of a2, a3, a4, a5 are 28, 76, 164, and 304 respectively.
2. Writing the general term:
From the pattern, we can deduce that the general term of the given recurrence relation can be written as:
an = 6n^2 - 2n + (n-1)^2 + 4
3. Finding the value of a99:
Using the general term, we can find the value of a99:
a99 = 6(99^2) - 2(99) + (99-1)^2 + 4
= 6(9801) - 198 + 98^2 + 4
= 58806 - 198 + 9604 + 4
= 68816
4. Finding the value of k:
Given that a99 = k x 104, we can equate the two expressions:
68816 = k x 104
k = 68816 / 104
k ≈ 661.538
Rounded to the nearest whole number, k ≈ 662.
Therefore, the value of k is approximately 662, which corresponds to option C.
Select the correct asymptotic complexity of an algorithm with runtime T(n, n) where
T(x, c) = Θ(x) for c <= 2,
T(c, y) = Θ(y) for c <= 2, and
T(x, y) = Θ(x+y) + T(x/2, y/2)- a)Θ(nLogn)
- b)Θ(n2)
- c)Θ(n)
- d)Θ(n2Logn)
Correct answer is option 'C'. Can you explain this answer?
Select the correct asymptotic complexity of an algorithm with runtime T(n, n) where
T(x, c) = Θ(x) for c <= 2,
T(c, y) = Θ(y) for c <= 2, and
T(x, y) = Θ(x+y) + T(x/2, y/2)
T(x, c) = Θ(x) for c <= 2,
T(c, y) = Θ(y) for c <= 2, and
T(x, y) = Θ(x+y) + T(x/2, y/2)
a)
Θ(nLogn)
b)
Θ(n2)
c)
Θ(n)
d)
Θ(n2Logn)
|
|
Sanya Agarwal answered |
The recurrence is
T(x, y) = Θ(x+y) + T(x/2, y/2)
It can be written as below.
T(x, y) = Θ(x+y) + Θ((x+y)/2) + Θ((x+y)/4) + Θ((x+y)/8) .....
T(x, y) = Θ((x+y) + (x+y)/2 + (x+y)/4 + (x+y)/8 ..... )
The above expression forms a geometric series with ratio as 2 and starting element as (x+y)/2 T(x, y) is upper bounded by Θ(x+y) as sum of infinite series is 2(x+y). It is lower bounded by (x+y)
T(x, y) = Θ(x+y) + T(x/2, y/2)
It can be written as below.
T(x, y) = Θ(x+y) + Θ((x+y)/2) + Θ((x+y)/4) + Θ((x+y)/8) .....
T(x, y) = Θ((x+y) + (x+y)/2 + (x+y)/4 + (x+y)/8 ..... )
The above expression forms a geometric series with ratio as 2 and starting element as (x+y)/2 T(x, y) is upper bounded by Θ(x+y) as sum of infinite series is 2(x+y). It is lower bounded by (x+y)
What is the value of following recurrence.T(n) = T(n/4) + T(n/2) + cn2
T(1) = c
T(0) = 0
Where c is a positive constant- a)O(n3)
- b)O(n2)
- c)O(n2 Logn)
- d)O(nLogn)
Correct answer is option 'B'. Can you explain this answer?
What is the value of following recurrence.
T(n) = T(n/4) + T(n/2) + cn2
T(1) = c
T(0) = 0
Where c is a positive constant
T(1) = c
T(0) = 0
Where c is a positive constant
a)
O(n3)
b)
O(n2)
c)
O(n2 Logn)
d)
O(nLogn)
|
|
Sanya Agarwal answered |
Following is the initial recursion tree for the given recurrence relation.
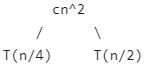
If we further break down the expression T(n/4) and T(n/2), we get following recursion tree.
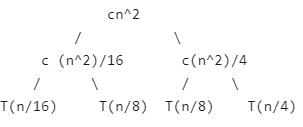
Breaking down further gives us following
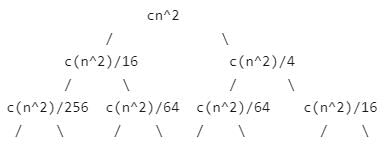
To know the value of T(n), we need to calculate sum of tree nodes level by level. If we sum the above tree level by level, we get the following series T(n) = c(n^2 + 5(n^2)/16 + 25(n^2)/256) + ....
The above series is geometrical progression with ratio 5/16 To get an upper bound, we can sum the above series for infinite terms. We get the sum as (n^2) / (1 - 5/16) which is O(n^2)
What is the time complexity for the following C module? Assume that n>0 . int module(int n) { if (n == 1) return 1; else return (n + module(n-1)); }- a)O(n)
- b)O(log n)
- c)O(n2)
- d)O(n!)
Correct answer is option 'A'. Can you explain this answer?
What is the time complexity for the following C module? Assume that n>0 . int module(int n) { if (n == 1) return 1; else return (n + module(n-1)); }
a)
O(n)
b)
O(log n)
c)
O(n2)
d)
O(n!)
|
|
Sanya Agarwal answered |
F(n) = (n + f(n-1)) → n + (n-1 + f(n-2))→ n + (n-1 + (n-2 (+...+ (n-(n-1) + f(1))) Time complexity of of code is = O(n)
Consider the following recurrence. T(n) = T(√n) + θ(Log Log n) What is the value of recurrence?
(A) θ( (Log Log n)2)
(B) θ(Log Log n)
(B) θ(n)
(B) θ(Log Log Log n)- a)A
- b)B
- c)C
- d)D
Correct answer is option 'A'. Can you explain this answer?
Consider the following recurrence. T(n) = T(√n) + θ(Log Log n) What is the value of recurrence?
(A) θ( (Log Log n)2)
(B) θ(Log Log n)
(B) θ(n)
(B) θ(Log Log Log n)
(A) θ( (Log Log n)2)
(B) θ(Log Log n)
(B) θ(n)
(B) θ(Log Log Log n)
a)
A
b)
B
c)
C
d)
D
|
|
Sanya Agarwal answered |
Change of variables: let m = lg n. Recurrence becomes S(m) = S(m/2) + θ(lgm). Case 2 of master’s theorem applies, so T(n) = θ( (log Log n) ^ 2).
Standard planning algorithms assume environment to be __________.- a)Both deterministic and fully observable
- b)Neither deterministic nor fully observable
- c)Deterministic but not fully observable
- d)Not deterministic but fully observable
Correct answer is option 'A'. Can you explain this answer?
Standard planning algorithms assume environment to be __________.
a)
Both deterministic and fully observable
b)
Neither deterministic nor fully observable
c)
Deterministic but not fully observable
d)
Not deterministic but fully observable
|
|
Sanya Agarwal answered |
Standard planning algorithms assume environment to be both deterministic and fully observable. So, option (A) is correct.
Consider the following recurrence relation.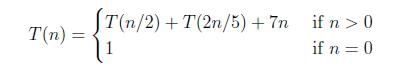 Which one of the following options is correct?
Which one of the following options is correct?- a)T(n) = Θ(n5/2)
- b)T(n) = Θ(nlogn)
- c)T(n) = Θ(n)
- d)T(n) = Θ((logn)5/2)
Correct answer is option 'C'. Can you explain this answer?
Consider the following recurrence relation.
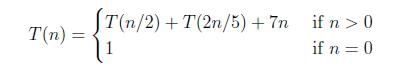
Which one of the following options is correct?
a)
T(n) = Θ(n5/2)
b)
T(n) = Θ(nlogn)
c)
T(n) = Θ(n)
d)
T(n) = Θ((logn)5/2)
|
|
Sanya Agarwal answered |
Given, recurrence relation can be written as, T(n) = T(n/2) + T(2n/5) + 7n T(n) = T((5/2)n/5) + T(2n/5) + 7n Since, sum of numerator (5/2+2 = 4.5) is less than denominator (5), so time complexity would be function itself. Hence, T(n) = Θ(7n) = Θ(n)
Chapter doubts & questions for Recurrence Relations - Algorithms 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Recurrence Relations - Algorithms in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Algorithms
81 videos|113 docs|33 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









