All Exams >
Electronics and Communication Engineering (ECE) >
Electromagnetics >
All Questions
All questions of Coordinate System & Vector Analysis for Electronics and Communication Engineering (ECE) Exam
The energy stored in the inductor 100mH with a current of 2A is- a)0.2
- b)0.4
- c)0.6
- d)0.8
Correct answer is option 'A'. Can you explain this answer?
The energy stored in the inductor 100mH with a current of 2A is
a)
0.2
b)
0.4
c)
0.6
d)
0.8

|
EduRev GATE answered |
Answer: a
Explanation: dw = ei dt = Li di, W = L∫ i.di
Energy E = 0.5LI2 = 0.5 X 0.1 X 22 = 0.2 Joule.
Explanation: dw = ei dt = Li di, W = L∫ i.di
Energy E = 0.5LI2 = 0.5 X 0.1 X 22 = 0.2 Joule.
Find the Laplace equation value of the following potential field
V = x2 – y2 + z2- a)0
- b)2
- c)4
- d)6
Correct answer is option 'B'. Can you explain this answer?
Find the Laplace equation value of the following potential field
V = x2 – y2 + z2
V = x2 – y2 + z2
a)
0
b)
2
c)
4
d)
6
|
|
Lavanya Menon answered |
Answer: b
Explanation: (Del) V = 2x – 2y + 2z
(Del)2 V = 2 – 2 + 2= 2, which is non zero value. Thus it doesn’t satisfy Laplace equation.
Explanation: (Del) V = 2x – 2y + 2z
(Del)2 V = 2 – 2 + 2= 2, which is non zero value. Thus it doesn’t satisfy Laplace equation.
Curl of gradient of a vector is- a)Unity
- b)Zero
- c)Null vector
- d)Depends on the constants of the vector
Correct answer is option 'C'. Can you explain this answer?
Curl of gradient of a vector is
a)
Unity
b)
Zero
c)
Null vector
d)
Depends on the constants of the vector
|
|
Srishti Choudhary answered |
Answer: c
Explanation: Gradient of any function leads to a vector. Similarly curl of that vector gives another vector, which is always zero for all constants of the vector. A zero value in vector is always termed as null vector(not simply a zero).
Explanation: Gradient of any function leads to a vector. Similarly curl of that vector gives another vector, which is always zero for all constants of the vector. A zero value in vector is always termed as null vector(not simply a zero).
The divergence of a vector is a scalar. State True/False. - a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The divergence of a vector is a scalar. State True/False.
a)
True
b)
False
|
|
Zoya Sharma answered |
Answer: a
Explanation: Divergence can be computed only for a vector. Since it is the measure of outward flow of flux from a small closed surface as the volume shrinks to zero, the result will be directionless (scalar).
Explanation: Divergence can be computed only for a vector. Since it is the measure of outward flow of flux from a small closed surface as the volume shrinks to zero, the result will be directionless (scalar).
Identify the nature of the field, if the divergence is zero and curl is also zero.- a)Solenoidal, irrotational
- b)Divergent, rotational
- c)Solenoidal, irrotational
- d)Divergent, rotational
Correct answer is option 'C'. Can you explain this answer?
Identify the nature of the field, if the divergence is zero and curl is also zero.
a)
Solenoidal, irrotational
b)
Divergent, rotational
c)
Solenoidal, irrotational
d)
Divergent, rotational

|
Rahul Chatterjee answered |
Since the vector field does not diverge (moves in a straight path), the divergence is zero. Also, the path does not possess any curls, so the field is irrotational.
Hence option (C) is correct
To learn more about Divergence and Curl of a vector click on the link given below:
Let S be the portion of the plane z = 2x + 2y − 100 which lies inside the cylinder x2 + y2 = 1. If the surface area of S is απ, then the value of α is equal to ___________.- a)3
- b)4
- c)6
- d)8
Correct answer is option 'A'. Can you explain this answer?
Let S be the portion of the plane z = 2x + 2y − 100 which lies inside the cylinder x2 + y2 = 1. If the surface area of S is απ, then the value of α is equal to ___________.
a)
3
b)
4
c)
6
d)
8

|
EduRev GATE answered |
�� is the portion of the plane z = 2x + 2y − 100 which lies inside the cylinder x2 + y2 = 1.
zx = 2, zy = 2
then surface area of S
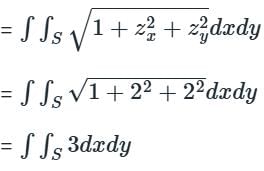
Now, the cylinder is x2 + y2 = 1
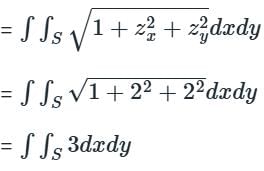
Now, the cylinder is x2 + y2 = 1
Let x = cosθ, y = sin θ
then surface area of S

Given area S = απ

Given area S = απ
Hnece α = 3
Given D = e-xsin y i – e-xcos y j
Find divergence of D.- a)3
- b)2
- c)1
- d)0
Correct answer is option 'D'. Can you explain this answer?
Given D = e-xsin y i – e-xcos y j
Find divergence of D.
Find divergence of D.
a)
3
b)
2
c)
1
d)
0
|
|
Debanshi Basak answered |
Answer: d
Explanation: Div (D) = Dx(e-xsin y) + Dy(-e-xcos y ) = -e-xsin y + e-xsin y = 0.
Explanation: Div (D) = Dx(e-xsin y) + Dy(-e-xcos y ) = -e-xsin y + e-xsin y = 0.
According to gauss theorem, the electric flux on a closed surface depends on?- a)The area of open surface
- b)Charge enclosed
- c)Magnetic field of charge
- d)Charge outside the sphere
Correct answer is option 'B'. Can you explain this answer?
According to gauss theorem, the electric flux on a closed surface depends on?
a)
The area of open surface
b)
Charge enclosed
c)
Magnetic field of charge
d)
Charge outside the sphere
|
|
Pooja Patel answered |
CONCEPT
- Electric Flux: It is defined as the number of electric field lines passing through the perpendicular unit area.
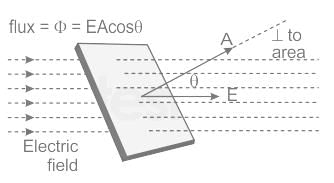
- Electric Flux = (Φ) = EA⊥ [E = electric field, A = perpendicular area]
- Electric flux (Φ) = EA cos θ [where θ is the angle between area plane and electric field]
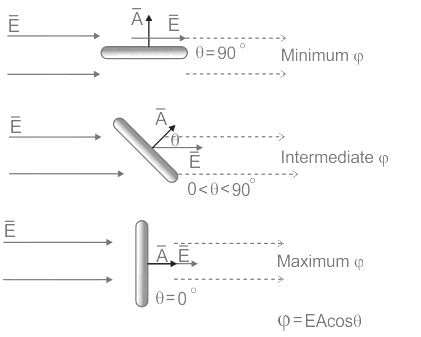
- The flux is maximum when the angle is 0°
- Gauss Law: According to gauss’s law, total electric flux through a closed surface enclosing a charge is 1/ϵ0 times the magnitude of charge enclosed.
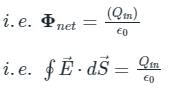
Where, Φ = electric flux, Qin = charge enclosed the sphere, ϵ0 = permittivity of space (8.85 × 10-12 C2/Nm2), dS = surface area
According to gauss’s law,
The flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ϵ0.
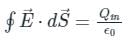
Electric flux on a closed surface only depends on the enclosed charge.
∴ Option 2 is correct
The Stoke’s theorem uses which of the following operation?- a)Divergence
- b)Gradient
- c)Curl
- d)Laplacian
Correct answer is option 'C'. Can you explain this answer?
The Stoke’s theorem uses which of the following operation?
a)
Divergence
b)
Gradient
c)
Curl
d)
Laplacian
|
|
Malavika Nair answered |
Answer: c
Explanation: ∫A.dl = ∫∫ Curl (A).ds is the expression for Stoke’s theorem. It is clear that the theorem uses curl operation.
Explanation: ∫A.dl = ∫∫ Curl (A).ds is the expression for Stoke’s theorem. It is clear that the theorem uses curl operation.
Find the value of divergence theorem for the field D = 2xy i + x2 j for the rectangular parallelepiped given by x = 0 and 1, y = 0 and 2, z = 0 and 3.- a)10
- b)12
- c)14
- d)16
Correct answer is option 'B'. Can you explain this answer?
Find the value of divergence theorem for the field D = 2xy i + x2 j for the rectangular parallelepiped given by x = 0 and 1, y = 0 and 2, z = 0 and 3.
a)
10
b)
12
c)
14
d)
16
|
|
Prisha Sen answered |
Answer: b
Explanation: Div (D) = 2y
∫∫∫Div (D) dv = ∫∫∫ 2y dx dy dz. On integrating, x = 0->1, y = 0->2 and z = 0->3, we get Q = 12.
Explanation: Div (D) = 2y
∫∫∫Div (D) dv = ∫∫∫ 2y dx dy dz. On integrating, x = 0->1, y = 0->2 and z = 0->3, we get Q = 12.
False statement among the following statements regarding Coulombs law is:- a)Gives the force between two charges Q1 and Q2
- b)The magnitude of the force of attraction (or repulsion) between two-point charges is directly proportional to the product of the quantity of the two charges
- c)The magnitude of the force of attraction (or repulsion) between two-point charges is inversely proportional to the square of the distance between them.
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
False statement among the following statements regarding Coulombs law is:
a)
Gives the force between two charges Q1 and Q2
b)
The magnitude of the force of attraction (or repulsion) between two-point charges is directly proportional to the product of the quantity of the two charges
c)
The magnitude of the force of attraction (or repulsion) between two-point charges is inversely proportional to the square of the distance between them.
d)
None of the above
|
|
Ankita Das answered |
Understanding Coulomb's Law
Coulomb's Law describes the electrostatic interaction between charged particles. It is essential to evaluate each statement to determine the falsehood.
Statement Analysis
- a) Gives the force between two charges Q1 and Q2
- This statement is true. Coulomb's Law quantifies the force exerted between two point charges, Q1 and Q2.
- b) The magnitude of the force of attraction (or repulsion) between two-point charges is directly proportional to the product of the quantity of the two charges
- This statement is also true. According to Coulomb's Law, the force is directly proportional to the product of the magnitudes of the two charges.
- c) The magnitude of the force of attraction (or repulsion) between two-point charges is inversely proportional to the square of the distance between them
- This statement is true as well. The force decreases as the square of the distance between the charges increases, demonstrating an inverse square relationship.
Conclusion
- d) None of the above
- This option is correct. Since all previous statements (a, b, and c) accurately reflect Coulomb's Law, there are no false statements among them. Thus, option 'd' is the correct answer.
Coulomb's Law is foundational in electrostatics, providing critical insight into how charged bodies interact. Understanding these principles is essential for further studies in electrical engineering and physics.
Coulomb's Law describes the electrostatic interaction between charged particles. It is essential to evaluate each statement to determine the falsehood.
Statement Analysis
- a) Gives the force between two charges Q1 and Q2
- This statement is true. Coulomb's Law quantifies the force exerted between two point charges, Q1 and Q2.
- b) The magnitude of the force of attraction (or repulsion) between two-point charges is directly proportional to the product of the quantity of the two charges
- This statement is also true. According to Coulomb's Law, the force is directly proportional to the product of the magnitudes of the two charges.
- c) The magnitude of the force of attraction (or repulsion) between two-point charges is inversely proportional to the square of the distance between them
- This statement is true as well. The force decreases as the square of the distance between the charges increases, demonstrating an inverse square relationship.
Conclusion
- d) None of the above
- This option is correct. Since all previous statements (a, b, and c) accurately reflect Coulomb's Law, there are no false statements among them. Thus, option 'd' is the correct answer.
Coulomb's Law is foundational in electrostatics, providing critical insight into how charged bodies interact. Understanding these principles is essential for further studies in electrical engineering and physics.
Find the charged enclosed by a sphere of charge density ρ and radius a. - a)ρ (4πa2)
- b)ρ(4πa3/3)
- c)ρ(2πa2)
- d)ρ(2πa3/3)
Correct answer is option 'B'. Can you explain this answer?
Find the charged enclosed by a sphere of charge density ρ and radius a.
a)
ρ (4πa2)
b)
ρ(4πa3/3)
c)
ρ(2πa2)
d)
ρ(2πa3/3)
|
|
Prateek Mehra answered |
Answer: b
Explanation: The charge enclosed by the sphere is Q = ∫∫∫ ρ dv.
Where, dv = r2 sin θ dr dθ dφ and on integrating with r = 0->a, φ = 0->2π and θ = 0->π, we get Q = ρ(4πa3/3).
Explanation: The charge enclosed by the sphere is Q = ∫∫∫ ρ dv.
Where, dv = r2 sin θ dr dθ dφ and on integrating with r = 0->a, φ = 0->2π and θ = 0->π, we get Q = ρ(4πa3/3).
The mathematical perception of the gradient is said to be- a)Tangent
- b)Chord
- c)Slope
- d)Arc
Correct answer is option 'C'. Can you explain this answer?
The mathematical perception of the gradient is said to be
a)
Tangent
b)
Chord
c)
Slope
d)
Arc
|
|
Aman Datta answered |
Answer: c
Explanation: The gradient is the rate of change of space of flux in electromagnetics. This is analogous to the slope in mathematics.
Explanation: The gradient is the rate of change of space of flux in electromagnetics. This is analogous to the slope in mathematics.
The path traversal in calculating the Green’s theorem is- a)Clockwise
- b)Anticlockwise
- c)Inwards
- d)Outwards
Correct answer is option 'B'. Can you explain this answer?
The path traversal in calculating the Green’s theorem is
a)
Clockwise
b)
Anticlockwise
c)
Inwards
d)
Outwards
|
|
Kajal Yadav answered |
Answer: b
Explanation: The Green’s theorem calculates the area traversed by the functions in the region in the anticlockwise direction. This converts the line integral to surface integral.
Explanation: The Green’s theorem calculates the area traversed by the functions in the region in the anticlockwise direction. This converts the line integral to surface integral.
Given the potential V = 25 sin θ, in free space, determine whether V satisfies Laplace’s equation.- a)No
- b)Yes
- c)Data sufficient
- d)Potential is not defined
Correct answer is option 'A'. Can you explain this answer?
Given the potential V = 25 sin θ, in free space, determine whether V satisfies Laplace’s equation.
a)
No
b)
Yes
c)
Data sufficient
d)
Potential is not defined
|
|
Avantika Kaur answered |
Sorry, the question seems to be incomplete as it does not specify any unit for the potential V and it cuts off after "sin". Please provide more information or context so that I can assist you better.
4. The gradient of xi + yj + zk is- a)0
- b)1
- c)2
- d)3
Correct answer is option 'D'. Can you explain this answer?
4. The gradient of xi + yj + zk is
a)
0
b)
1
c)
2
d)
3
|
|
Naveen Kapoor answered |
Answer: d
Explanation: Grad (xi + yj + zk) = 1 + 1 + 1 = 3. In other words, the gradient of any position vector is 3.
Explanation: Grad (xi + yj + zk) = 1 + 1 + 1 = 3. In other words, the gradient of any position vector is 3.
Find the curl of A = (y cos ax)i + (y + ex)k- a)2i – ex j – cos ax k
- b)i – ex j – cos ax k
- c)2i – ex j + cos ax k
- d)i – ex j + cos ax k
Correct answer is option 'B'. Can you explain this answer?
Find the curl of A = (y cos ax)i + (y + ex)k
a)
2i – ex j – cos ax k
b)
i – ex j – cos ax k
c)
2i – ex j + cos ax k
d)
i – ex j + cos ax k
|
|
Ishan Chawla answered |
Answer: b
Explanation: Curl A = i(Dy(y + ex)) – j (Dx(y + ex) – Dz(y cos ax)) + k(-Dy(y cos ax))
= 1.i – j(ex) – k cos ax = i – ex j – cos ax k.
Explanation: Curl A = i(Dy(y + ex)) – j (Dx(y + ex) – Dz(y cos ax)) + k(-Dy(y cos ax))
= 1.i – j(ex) – k cos ax = i – ex j – cos ax k.
An electric field is given as E = 6y2z i + 12xyz j + 6xy2 k. An incremental path is given by dl = -3 i + 5 j – 2 k mm. The work done in moving a 2mC charge along the path if the location of the path is at p(0,2,5) is (in Joule)- a)0.64
- b)0.72
- c)0.78
- d)0.80
Correct answer is option 'B'. Can you explain this answer?
An electric field is given as E = 6y2z i + 12xyz j + 6xy2 k. An incremental path is given by dl = -3 i + 5 j – 2 k mm. The work done in moving a 2mC charge along the path if the location of the path is at p(0,2,5) is (in Joule)
a)
0.64
b)
0.72
c)
0.78
d)
0.80
|
|
Sanchita Choudhary answered |
Answer: b
Explanation: W = -Q E.dl
W = -2 X 10-3 X (6y2z i + 12xyz j + 6xy2 k) . (-3 i + 5 j -2 k)
At p(0,2,5), W = -2(-18.22.5) X 10-3 = 0.72 J.
Explanation: W = -Q E.dl
W = -2 X 10-3 X (6y2z i + 12xyz j + 6xy2 k) . (-3 i + 5 j -2 k)
At p(0,2,5), W = -2(-18.22.5) X 10-3 = 0.72 J.
The Gauss divergence theorem converts- a)line to surface integral
- b)line to volume integral
- c)surface to line integral
- d)surface to volume integral
Correct answer is option 'D'. Can you explain this answer?
The Gauss divergence theorem converts
a)
line to surface integral
b)
line to volume integral
c)
surface to line integral
d)
surface to volume integral
|
|
Debanshi Basak answered |
Answer: d
Explanation: The divergence theorem for a function F is given by ∫∫ F.dS = ∫∫∫ Div (F).dV. Thus it converts surface to volume integral
Explanation: The divergence theorem for a function F is given by ∫∫ F.dS = ∫∫∫ Div (F).dV. Thus it converts surface to volume integral
The electric flux from a cube of side ‘a’ is ‘Φ’. What will be its value if the side of the cube is made ‘2a’ and the charge enclosed is made half?- a)Φ/2
- b)Φ
- c)4 Φ
- d)2 Φ
Correct answer is option 'A'. Can you explain this answer?
The electric flux from a cube of side ‘a’ is ‘Φ’. What will be its value if the side of the cube is made ‘2a’ and the charge enclosed is made half?
a)
Φ/2
b)
Φ
c)
4 Φ
d)
2 Φ
|
|
Sushant Mukherjee answered |
Understanding Electric Flux
Electric flux is defined as the flow of electric field through a surface. According to Gauss's Law, the electric flux (Φ) through a closed surface is proportional to the charge (Q) enclosed by that surface:
Φ = Q / ε₀
where ε₀ is the permittivity of free space.
Scenario 1: Original Cube
- Consider a cube with side length 'a.'
- The electric flux through this cube is given as Φ.
- The charge enclosed in this cube is Q.
Scenario 2: Modified Cube
- The side of the cube is now doubled to '2a.'
- The volume of the cube increases, but the charge enclosed is halved (Q/2).
Applying Gauss's Law
- For the new cube, using Gauss's Law:
Φ' = Q' / ε₀
- Since the new charge Q' = Q/2, we have:
Φ' = (Q/2) / ε₀
Relating New Flux to Original Flux
- The original flux Φ was:
Φ = Q / ε₀
- Therefore, substituting Q' into the equation for the new electric flux:
Φ' = (1/2) * (Q / ε₀) = (1/2) * Φ
Final Answer
- The electric flux for the cube with side '2a' and half the enclosed charge is:
Φ' = Φ / 2
Thus, the correct answer is option 'A' (Φ/2).
Electric flux is defined as the flow of electric field through a surface. According to Gauss's Law, the electric flux (Φ) through a closed surface is proportional to the charge (Q) enclosed by that surface:
Φ = Q / ε₀
where ε₀ is the permittivity of free space.
Scenario 1: Original Cube
- Consider a cube with side length 'a.'
- The electric flux through this cube is given as Φ.
- The charge enclosed in this cube is Q.
Scenario 2: Modified Cube
- The side of the cube is now doubled to '2a.'
- The volume of the cube increases, but the charge enclosed is halved (Q/2).
Applying Gauss's Law
- For the new cube, using Gauss's Law:
Φ' = Q' / ε₀
- Since the new charge Q' = Q/2, we have:
Φ' = (Q/2) / ε₀
Relating New Flux to Original Flux
- The original flux Φ was:
Φ = Q / ε₀
- Therefore, substituting Q' into the equation for the new electric flux:
Φ' = (1/2) * (Q / ε₀) = (1/2) * Φ
Final Answer
- The electric flux for the cube with side '2a' and half the enclosed charge is:
Φ' = Φ / 2
Thus, the correct answer is option 'A' (Φ/2).
If a function is described by F = (3x + z, y2 − sin x2z, xz + yex5), then the divergence theorem value in the region 0<x<1, 0<y<3 and 0<z<2 will be- a)13
- b)26
- c)39
- d)51
Correct answer is option 'C'. Can you explain this answer?
If a function is described by F = (3x + z, y2 − sin x2z, xz + yex5), then the divergence theorem value in the region 0<x<1, 0<y<3 and 0<z<2 will be
a)
13
b)
26
c)
39
d)
51
|
|
Ishani Iyer answered |
The function is not properly described as it is missing information about the variables and their relationships. Please provide more context or a complete description of the function.
Curl is defined as the angular velocity at every point of the vector field. State True/False. - a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Curl is defined as the angular velocity at every point of the vector field. State True/False.
a)
True
b)
False
|
|
Athul Banerjee answered |
Answer: a
Explanation: Curl is defined as the circulation of a vector per unit area. It is the cross product of the del operator and any vector field. Circulation implies the angular at every point of the vector field. It is obtained by multiplying the component of the vector parallel to the specified closed path at each point along it, by the differential path length and summing the results.
Explanation: Curl is defined as the circulation of a vector per unit area. It is the cross product of the del operator and any vector field. Circulation implies the angular at every point of the vector field. It is obtained by multiplying the component of the vector parallel to the specified closed path at each point along it, by the differential path length and summing the results.
The Poisson equation cannot be determined from Laplace equation. State True/False. - a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
The Poisson equation cannot be determined from Laplace equation. State True/False.
a)
True
b)
False
|
|
Vaibhav Joshi answered |
Answer: b
Explanation: The Poisson equation is a general case for Laplace equation. If volume charge density exists for a field, then (Del)2V= -ρv/ε, which is called Poisson equation.
Explanation: The Poisson equation is a general case for Laplace equation. If volume charge density exists for a field, then (Del)2V= -ρv/ε, which is called Poisson equation.
The resistivity of a material with resistance 200 ohm, length 10m and area twice that of the length is- a)200
- b)300
- c)400
- d)500
Correct answer is option 'C'. Can you explain this answer?
The resistivity of a material with resistance 200 ohm, length 10m and area twice that of the length is
a)
200
b)
300
c)
400
d)
500
|
|
Anoushka Choudhury answered |
Answer: c
Explanation: Resistance calculated from Ohm’s law and Stoke’s theorem will be R = ρL/A. To get resistivity, ρ = RA/L = 200 X 20/10 = 400.
Explanation: Resistance calculated from Ohm’s law and Stoke’s theorem will be R = ρL/A. To get resistivity, ρ = RA/L = 200 X 20/10 = 400.
The divergence theorem for a surface consisting of a sphere is computed in which coordinate system?- a)Cartesian
- b)Cylindrical
- c)Spherical
- d)Depends on the function
Correct answer is option 'D'. Can you explain this answer?
The divergence theorem for a surface consisting of a sphere is computed in which coordinate system?
a)
Cartesian
b)
Cylindrical
c)
Spherical
d)
Depends on the function
|
|
Saranya Mishra answered |
Answer: d
Explanation: Seeing the surface as sphere, we would immediately choose spherical system, but it is wrong. The divergence operation is performed in that coordinate system in which the function belongs to. It is independent of the surface region.
Explanation: Seeing the surface as sphere, we would immediately choose spherical system, but it is wrong. The divergence operation is performed in that coordinate system in which the function belongs to. It is independent of the surface region.
Find the value of Green’s theorem for F = x2 and G = y2 is- a)0
- b)1
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
Find the value of Green’s theorem for F = x2 and G = y2 is
a)
0
b)
1
c)
2
d)
3
|
|
Sarthak Yadav answered |
Answer: a
Explanation: ∫∫(dG/dx – dF/dy)dx dy = ∫∫(0 – 0)dx dy = 0. The value of Green’s theorem gives zero for the functions given.
Explanation: ∫∫(dG/dx – dF/dy)dx dy = ∫∫(0 – 0)dx dy = 0. The value of Green’s theorem gives zero for the functions given.
Which of the following Maxwell equations use curl operation?- a)Maxwell 1st and 2nd equation
- b)Maxwell 3rd and 4th equation
- c)All the four equations
- d)None of the equations
Correct answer is option 'A'. Can you explain this answer?
Which of the following Maxwell equations use curl operation?
a)
Maxwell 1st and 2nd equation
b)
Maxwell 3rd and 4th equation
c)
All the four equations
d)
None of the equations
|
|
Rajesh Saha answered |
Answer: a
Explanation: Maxwell 1st equation, Curl (H) = J (Ampere law)
Maxwell 2nd equation, Curl (E) = -D(B)/Dt (Faraday’s law)
Maxwell 3rd equation, Div (D) = Q (Gauss law for electric field)
Maxwell 4th equation, Div (B) = 0(Gauss law for magnetic field)
It is clear that only 1st and 2nd equations use the curl operation.
Explanation: Maxwell 1st equation, Curl (H) = J (Ampere law)
Maxwell 2nd equation, Curl (E) = -D(B)/Dt (Faraday’s law)
Maxwell 3rd equation, Div (D) = Q (Gauss law for electric field)
Maxwell 4th equation, Div (B) = 0(Gauss law for magnetic field)
It is clear that only 1st and 2nd equations use the curl operation.
Find the potential between two points p(1,-1,0) and q(2,1,3) with E = 40xy i + 20x2 j + 2 k- a)104
- b)105
- c)106
- d)107
Correct answer is option 'C'. Can you explain this answer?
Find the potential between two points p(1,-1,0) and q(2,1,3) with E = 40xy i + 20x2 j + 2 k
a)
104
b)
105
c)
106
d)
107
|
|
Jaya Datta answered |
Answer: c
Explanation: V = -∫ E.dl = -∫ (40xy dx + 20x2 dy + 2 dz) , from q to p.
On integrating, we get 106 volts.
Explanation: V = -∫ E.dl = -∫ (40xy dx + 20x2 dy + 2 dz) , from q to p.
On integrating, we get 106 volts.
The curl of a curl of a vector gives a- a)Scalar
- b)Vector
- c)Zero value
- d)Non zero value
Correct answer is option 'B'. Can you explain this answer?
The curl of a curl of a vector gives a
a)
Scalar
b)
Vector
c)
Zero value
d)
Non zero value
|
|
Nilanjan Saini answered |
Answer: b
Explanation: Curl is always defined for vectors only. The curl of a vector is a vector only. The curl of the resultant vector is also a vector only.
Explanation: Curl is always defined for vectors only. The curl of a vector is a vector only. The curl of the resultant vector is also a vector only.
When gradient of a function is zero, the function lies parallel to the x-axis. State True/False. - a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
When gradient of a function is zero, the function lies parallel to the x-axis. State True/False.
a)
True
b)
False
|
|
Harsh Kulkarni answered |
True
Explanation:
When the gradient of a function is zero, it means that the derivative of the function with respect to the independent variable is zero at that point. In the case of a function of one variable, such as f(x), the derivative represents the rate of change of the function with respect to x.
When the derivative is zero, it means that the function is not changing at that point, and hence the graph of the function is parallel to the x-axis. This is because the slope of the tangent line to the graph at that point is zero, which means that the tangent line is horizontal and parallel to the x-axis.
To understand this concept further, let's consider an example:
Let's say we have a function f(x) = x^2. The derivative of this function with respect to x is f'(x) = 2x.
To find the points where the gradient is zero, we set the derivative equal to zero and solve for x:
2x = 0
x = 0
So, at x = 0, the gradient of the function is zero. This means that the function f(x) = x^2 is parallel to the x-axis at x = 0.
In general, when the gradient of a function is zero, it means that the function is not changing at that point and is parallel to the x-axis. Therefore, the statement "When the gradient of a function is zero, the function lies parallel to the x-axis" is true.
Explanation:
When the gradient of a function is zero, it means that the derivative of the function with respect to the independent variable is zero at that point. In the case of a function of one variable, such as f(x), the derivative represents the rate of change of the function with respect to x.
When the derivative is zero, it means that the function is not changing at that point, and hence the graph of the function is parallel to the x-axis. This is because the slope of the tangent line to the graph at that point is zero, which means that the tangent line is horizontal and parallel to the x-axis.
To understand this concept further, let's consider an example:
Let's say we have a function f(x) = x^2. The derivative of this function with respect to x is f'(x) = 2x.
To find the points where the gradient is zero, we set the derivative equal to zero and solve for x:
2x = 0
x = 0
So, at x = 0, the gradient of the function is zero. This means that the function f(x) = x^2 is parallel to the x-axis at x = 0.
In general, when the gradient of a function is zero, it means that the function is not changing at that point and is parallel to the x-axis. Therefore, the statement "When the gradient of a function is zero, the function lies parallel to the x-axis" is true.
If a function is said to be harmonic, then- a)Curl(Grad V) = 0
- b)Div(Curl V) = 0
- c)Div(Grad V) = 0
- d)Grad(Curl V) = 0
Correct answer is option 'C'. Can you explain this answer?
If a function is said to be harmonic, then
a)
Curl(Grad V) = 0
b)
Div(Curl V) = 0
c)
Div(Grad V) = 0
d)
Grad(Curl V) = 0
|
|
Sneha Bose answered |
Answer: c
Explanation: Though option a & b are also correct, for harmonic fields, the Laplacian of electric potential is zero. Now, Laplacian refers to Div(Grad V), which is zero for harmonic fields.
Explanation: Though option a & b are also correct, for harmonic fields, the Laplacian of electric potential is zero. Now, Laplacian refers to Div(Grad V), which is zero for harmonic fields.
Compute the charge enclosed by a cube of 2m each edge centered at the origin and with the edges parallel to the axes. Given D = 10y3/3 j.- a)20
- b)70/3
- c)80/3
- d)30
Correct answer is option 'C'. Can you explain this answer?
Compute the charge enclosed by a cube of 2m each edge centered at the origin and with the edges parallel to the axes. Given D = 10y3/3 j.
a)
20
b)
70/3
c)
80/3
d)
30
|
|
Sahana Sarkar answered |
Answer: c
Explanation: Div(D) = 10y2
∫∫∫Div (D) dv = ∫∫∫ 10y2 dx dy dz. On integrating, x = -1->1, y = -1->1 and z = -1->1, we get Q = 80/3.
Explanation: Div(D) = 10y2
∫∫∫Div (D) dv = ∫∫∫ 10y2 dx dy dz. On integrating, x = -1->1, y = -1->1 and z = -1->1, we get Q = 80/3.
Find the Laplace equation value of the following potential field
V = ρ cosφ + z- a)0
- b)1
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
Find the Laplace equation value of the following potential field
V = ρ cosφ + z
V = ρ cosφ + z
a)
0
b)
1
c)
2
d)
3
|
|
Dipanjan Nambiar answered |
Answer: a
Explanation: (Del)2 (ρ cosφ + z)= (cos φ/r) – (cos φ/r) + 0
= 0, this satisfies Laplace equation. The value is 0.
Explanation: (Del)2 (ρ cosφ + z)= (cos φ/r) – (cos φ/r) + 0
= 0, this satisfies Laplace equation. The value is 0.
Find the value of Stoke’s theorem for A = x i + y j + z k. The state of the function will be- a)Solenoidal
- b)Divergent
- c)Rotational
- d)Curl free
Correct answer is option 'D'. Can you explain this answer?
Find the value of Stoke’s theorem for A = x i + y j + z k. The state of the function will be
a)
Solenoidal
b)
Divergent
c)
Rotational
d)
Curl free
|
|
Maulik Choudhury answered |
Answer: Since curl is required, we need not bother about divergence property. The curl of the function will be i(0-0) – j(0-0) + k(0-0) = 0. The curl is zero, thus the function is said to be irrotational or curl free.
Find the Gauss value for a position vector in Cartesian system from the origin to one unit in three dimensions.- a)0
- b)3
- c)-3
- d)1
Correct answer is option 'B'. Can you explain this answer?
Find the Gauss value for a position vector in Cartesian system from the origin to one unit in three dimensions.
a)
0
b)
3
c)
-3
d)
1
|
|
Neha Nambiar answered |
Answer: b
Explanation: The position vector in Cartesian system is given by R = x i + y j + z k. Div(R) = 1 + 1 + 1 = 3. By divergence theorem, ∫∫∫3.dV, where V is a cube with x = 0->1, y = 0->1 and z = 0->1. On integrating, we get 3 units.
Explanation: The position vector in Cartesian system is given by R = x i + y j + z k. Div(R) = 1 + 1 + 1 = 3. By divergence theorem, ∫∫∫3.dV, where V is a cube with x = 0->1, y = 0->1 and z = 0->1. On integrating, we get 3 units.
Divergence theorem computes to zero for a solenoidal function. State True/False.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Divergence theorem computes to zero for a solenoidal function. State True/False.
a)
True
b)
False
|
|
Sushant Mukherjee answered |
Answer: a
Explanation: The divergence theorem is given by, ∫∫ F.dS = ∫∫∫ Div (F).dV, for a function F. If the function is solenoidal, its divergence will be zero. Thus the theorem computes to zero.
Explanation: The divergence theorem is given by, ∫∫ F.dS = ∫∫∫ Div (F).dV, for a function F. If the function is solenoidal, its divergence will be zero. Thus the theorem computes to zero.
A field in which a test charge around any closed surface in static path is zero is called- a)Solenoidal
- b)Rotational
- c)Irrotational
- d)Conservative
Correct answer is option 'D'. Can you explain this answer?
A field in which a test charge around any closed surface in static path is zero is called
a)
Solenoidal
b)
Rotational
c)
Irrotational
d)
Conservative
|
|
Bibek Saha answered |
Answer: d
Explanation: Work done in moving a charge in a closed path is zero. It is expressed as, ∫ E.dl = 0. The field having this property is called conservative or lamellar field.
Explanation: Work done in moving a charge in a closed path is zero. It is expressed as, ∫ E.dl = 0. The field having this property is called conservative or lamellar field.
Compute the divergence of the vector xi + yj + zk.- a)0
- b)1
- c)2
- d)3
Correct answer is option 'D'. Can you explain this answer?
Compute the divergence of the vector xi + yj + zk.
a)
0
b)
1
c)
2
d)
3
|
|
Aman Jain answered |
Answer: d
Explanation: The vector given is a position vector. The divergence of any position vector is always 3.
Explanation: The vector given is a position vector. The divergence of any position vector is always 3.
Evaluate Gauss law for D = 5r2/2 i in spherical coordinates with r = 4m and θ = π/2 as volume integral.- a)600
- b)588.9
- c)577.8
- d)599.7
Correct answer is option 'B'. Can you explain this answer?
Evaluate Gauss law for D = 5r2/2 i in spherical coordinates with r = 4m and θ = π/2 as volume integral.
a)
600
b)
588.9
c)
577.8
d)
599.7
|
|
Nayanika Kaur answered |
Answer: b
Explanation: ∫∫ D.ds = ∫∫∫ Div (D) dv, where RHS needs to be computed.
The divergence of D given is, Div(D) = 5r and dv = r2 sin θ dr dθ dφ. On integrating, r = 0->4, φ = 0->2π and θ = 0->π/4, we get Q = 588.9.
Explanation: ∫∫ D.ds = ∫∫∫ Div (D) dv, where RHS needs to be computed.
The divergence of D given is, Div(D) = 5r and dv = r2 sin θ dr dθ dφ. On integrating, r = 0->4, φ = 0->2π and θ = 0->π/4, we get Q = 588.9.
Find the divergence of the field, P = x2yz i + xz k- a)xyz + 2x
- b)2xyz + x
- c)xyz + 2z
- d)2xyz + z
Correct answer is option 'B'. Can you explain this answer?
Find the divergence of the field, P = x2yz i + xz k
a)
xyz + 2x
b)
2xyz + x
c)
xyz + 2z
d)
2xyz + z
|
|
Gaurav Chauhan answered |
Answer: b
Explanation: Div(P) = Dx(x2yz) + Dy(0) + Dz(xz) = 2xyz + x, which is option b. For different values of x,y,z the divergence of the field varies.
Explanation: Div(P) = Dx(x2yz) + Dy(0) + Dz(xz) = 2xyz + x, which is option b. For different values of x,y,z the divergence of the field varies.
Find the value of Stoke’s theorem for y i + z j + x k.- a)i + j
- b)j + k
- c)i + j + k
- d)–i – j – k
Correct answer is option 'D'. Can you explain this answer?
Find the value of Stoke’s theorem for y i + z j + x k.
a)
i + j
b)
j + k
c)
i + j + k
d)
–i – j – k
|
|
Aniket Choudhury answered |
Answer: d
Explanation: The curl of y i + z j + x k is i(0-1) – j(1-0) + k(0-1) =
-i –j –k. Since the curl is zero, the value of Stoke’s theorem is zero. The function is said to be irrotational.
Explanation: The curl of y i + z j + x k is i(0-1) – j(1-0) + k(0-1) =
-i –j –k. Since the curl is zero, the value of Stoke’s theorem is zero. The function is said to be irrotational.
The Laplacian operator cannot be used in which one the following?- a)Two dimensional heat equation
- b)Two dimensional wave equation
- c)Poisson equation
- d)Maxwell equation
Correct answer is option 'D'. Can you explain this answer?
The Laplacian operator cannot be used in which one the following?
a)
Two dimensional heat equation
b)
Two dimensional wave equation
c)
Poisson equation
d)
Maxwell equation
|
|
Anirban Gupta answered |
Answer: d
Explanation: The first three options are general cases of Laplacian equation. Maxwell equation uses only divergence and curl, which is first order differential equation, whereas Laplacian operator is second order differential equation. Thus Maxwell equation will not employ Laplacian operator.
Explanation: The first three options are general cases of Laplacian equation. Maxwell equation uses only divergence and curl, which is first order differential equation, whereas Laplacian operator is second order differential equation. Thus Maxwell equation will not employ Laplacian operator.
Find whether the vector is solenoidal, E = yz i + xz j + xy k- a)Yes, solenoidal
- b)No, non-solenoidal
- c)Solenoidal with negative divergence
- d)Variable divergence
Correct answer is option 'A'. Can you explain this answer?
Find whether the vector is solenoidal, E = yz i + xz j + xy k
a)
Yes, solenoidal
b)
No, non-solenoidal
c)
Solenoidal with negative divergence
d)
Variable divergence
|
|
Sarthak Yadav answered |
Answer: a
Explanation: Div(E) = Dx(yz) + Dy(xz) + Dz(xy) = 0. The divergence is zero, thus vector is divergentless or solenoidal.
Explanation: Div(E) = Dx(yz) + Dy(xz) + Dz(xy) = 0. The divergence is zero, thus vector is divergentless or solenoidal.
Find the gradient of t = x2y+ ez at the point p(1,5,-2)- a)i + 10j + 0.135k
- b)10i + j + 0.135k
- c)i + 0.135j + 10k
- d)10i + 0.135j + k
Correct answer is option 'B'. Can you explain this answer?
Find the gradient of t = x2y+ ez at the point p(1,5,-2)
a)
i + 10j + 0.135k
b)
10i + j + 0.135k
c)
i + 0.135j + 10k
d)
10i + 0.135j + k
|
|
Sanskriti Bajaj answered |
Answer: b
Explanation: Grad(t) = 2xy i + x2 j + ez k. On substituting p(1,5,-2), we get 10i + j + 0.135k
Explanation: Grad(t) = 2xy i + x2 j + ez k. On substituting p(1,5,-2), we get 10i + j + 0.135k
Calculate the Green’s value for the functions F = y2 and G = x2 for the region x = 1 and y = 2 from origin.- a)0
- b)2
- c)-2
- d)1
Correct answer is option 'C'. Can you explain this answer?
Calculate the Green’s value for the functions F = y2 and G = x2 for the region x = 1 and y = 2 from origin.
a)
0
b)
2
c)
-2
d)
1
|
|
Ishan Chawla answered |
Answer: c
Explanation: ∫∫(dG/dx – dF/dy)dx dy = ∫∫(2x – 2y)dx dy. On integrating for x = 0->1 and y = 0->2, we get Green’s value as -2.
Explanation: ∫∫(dG/dx – dF/dy)dx dy = ∫∫(2x – 2y)dx dy. On integrating for x = 0->1 and y = 0->2, we get Green’s value as -2.
Find the Laplace equation value of the following potential field V = r cos θ + φ- a)3
- b)2
- c)1
- d)0
Correct answer is option 'D'. Can you explain this answer?
Find the Laplace equation value of the following potential field V = r cos θ + φ
a)
3
b)
2
c)
1
d)
0
|
|
Nayanika Kaur answered |
Answer: d
Explanation: (Del)2 (r cos θ + φ) = (2 cosθ/r) – (2 cosθ/r) + 0
= 0, this satisfies Laplace equation. This value is 0.
Explanation: (Del)2 (r cos θ + φ) = (2 cosθ/r) – (2 cosθ/r) + 0
= 0, this satisfies Laplace equation. This value is 0.
Find the divergence of the vector yi + zj + xk.- a)-1
- b)0
- c)1
- d)3
Correct answer is option 'B'. Can you explain this answer?
Find the divergence of the vector yi + zj + xk.
a)
-1
b)
0
c)
1
d)
3
|
|
Pallabi Pillai answered |
Answer: b
Explanation: Div (yi + zj + xk) = Dx(y) + Dy(z) + Dz(x), which is zero. Here D refers to partial differentiation.
Explanation: Div (yi + zj + xk) = Dx(y) + Dy(z) + Dz(x), which is zero. Here D refers to partial differentiation.
The electric field of a point charge is a linear function of the value of the charge. It is the principle applied to an electric field and states that the total resultant field at a point is the vector sum of the individual components of the field at a point. Identify the principle mentioned in the context.- a)Superposition principle of fields
- b)Coulomb's Law
- c)Ampere circuital Law
- d)Insulation
Correct answer is option 'A'. Can you explain this answer?
The electric field of a point charge is a linear function of the value of the charge. It is the principle applied to an electric field and states that the total resultant field at a point is the vector sum of the individual components of the field at a point. Identify the principle mentioned in the context.
a)
Superposition principle of fields
b)
Coulomb's Law
c)
Ampere circuital Law
d)
Insulation

|
Cstoppers Instructors answered |
CONCEPT:
Superposition Principle:
Superposition Principle:
- The principle of superposition states that when a number of charges are interacting, the total force on a given charge is the vector sum of the forces exerted on it due to all other charges.
- The force between two charges is not affected by the presence of other charges.
- This is used to calculate the following parameter at the observation point, to any configuration of charges.
- Net force.
- Net electric field.
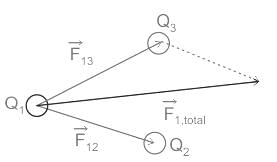
Coulomb's law in Electrostatics:
- It state’s that force of interaction between two stationary point charges is directly proportional to the product of the charges, and inversely proportional to the square of the distance between them and acts along the straight line joining the two charges.
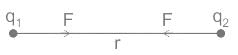
F ∝ q1 × q2
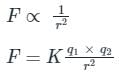
Where K = constant called electrostatic force constant.
- The value of K depends on the nature of the medium between the two charges and the system of units chosen
The conductivity of a material with current density 1 unit and electric field 200 μV is- a)2000
- b)3000
- c)4000
- d)5000
Correct answer is option 'D'. Can you explain this answer?
The conductivity of a material with current density 1 unit and electric field 200 μV is
a)
2000
b)
3000
c)
4000
d)
5000
|
|
Siddharth Khanna answered |
Answer: d
Explanation: The current density is given by, J = σE. To find conductivity, σ = J/E = 1/200 X 10-6 = 5000.
Explanation: The current density is given by, J = σE. To find conductivity, σ = J/E = 1/200 X 10-6 = 5000.
If D = 2xy i + 3yz j + 4xz k, how much flux passes through x = 3 plane for which -1<y<2 and 0<z<4?- a)12
- b)24
- c)36
- d)48
Correct answer is option 'C'. Can you explain this answer?
If D = 2xy i + 3yz j + 4xz k, how much flux passes through x = 3 plane for which -1<y<2 and 0<z<4?
a)
12
b)
24
c)
36
d)
48
|
|
Jyoti Basak answered |
Answer: c
Explanation: By Gauss law, ψ = ∫∫ D.ds, where ds = dydz i at the x-plane. Put x = 3 and integrate at -1<y<2 and 0<z<4, we get 12 X 3 = 36.
Explanation: By Gauss law, ψ = ∫∫ D.ds, where ds = dydz i at the x-plane. Put x = 3 and integrate at -1<y<2 and 0<z<4, we get 12 X 3 = 36.
Chapter doubts & questions for Coordinate System & Vector Analysis - Electromagnetics 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Coordinate System & Vector Analysis - Electromagnetics in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Electromagnetics
12 videos|85 docs|90 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily










