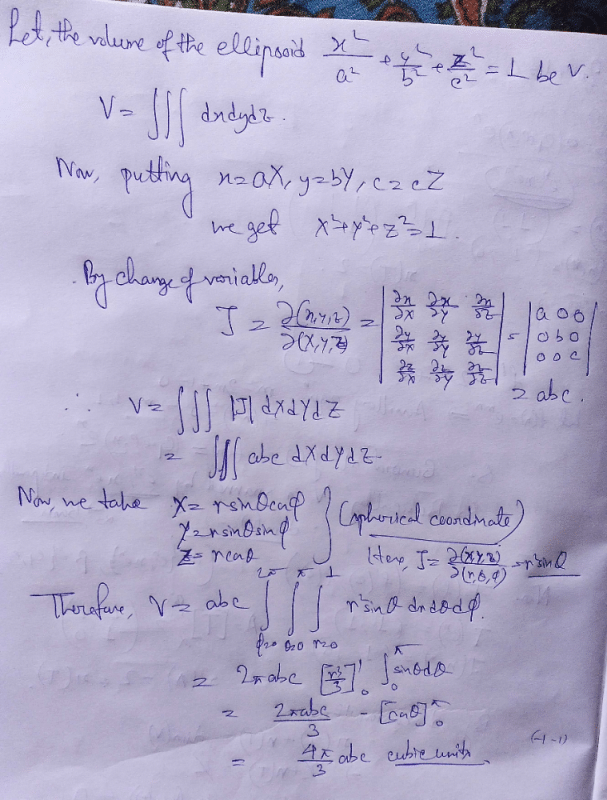All Exams >
Mathematics >
Mathematics for Competitive Exams >
All Questions
All questions of Functions of One, Two or Three Variable for Mathematics Exam
If f(x) = x5 - 20x3 + 240 x, then f(x) is
- a)monotonically decreasing everywhere
- b)monotonically decreasing on (0, ∞)
- c)monotonically increasing everywhere
- d)monotonically increasing only in (-∞, 0)
Correct answer is option 'C'. Can you explain this answer?
If f(x) = x5 - 20x3 + 240 x, then f(x) is
a)
monotonically decreasing everywhere
b)
monotonically decreasing on (0, ∞)
c)
monotonically increasing everywhere
d)
monotonically increasing only in (-∞, 0)
|
|
Chirag Verma answered |
Solution : c)
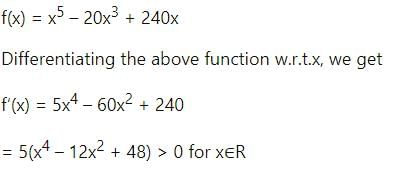
Hence Monotonicaly increasing
The function f(x) = - 2x3 - 9x2 - 12x + 1 is an increasing function in the interval- a)-2 < x < -1
- b)-2 < x < 1
- c)- l < x < 2
- d)1 < x < 2
Correct answer is option 'A'. Can you explain this answer?
The function f(x) = - 2x3 - 9x2 - 12x + 1 is an increasing function in the interval
a)
-2 < x < -1
b)
-2 < x < 1
c)
- l < x < 2
d)
1 < x < 2

|
Vivek Kumar answered |
Given that
f(x) = - 2x3 - 9x2 - 12x + 1
- + -
- 2 - 1
implies f'(x) = - 6x2 - 18x - 12
= -6[x2 + 3x + 2]
= - 6[(x + l ) ( x + 2)]
implies f'(x) > 0, V x ∈ (-2, -1)
Hence, f(x) is increasing in the interval (-2, -1)
f(x) = - 2x3 - 9x2 - 12x + 1
- + -
- 2 - 1
implies f'(x) = - 6x2 - 18x - 12
= -6[x2 + 3x + 2]
= - 6[(x + l ) ( x + 2)]
implies f'(x) > 0, V x ∈ (-2, -1)
Hence, f(x) is increasing in the interval (-2, -1)
 dx dy is equal to
dx dy is equal to- a)4 log 8 + e
- b)8 log 8 - 16
- c)8 log 8 - 16 + e
- d) e - 16
Correct answer is option 'C'. Can you explain this answer?
 dx dy is equal to
dx dy is equal toa)
4 log 8 + e
b)
8 log 8 - 16
c)
8 log 8 - 16 + e
d)
e - 16

|
Pavan Kishore answered |
First integrate w.r.t x taking y as const
then u get function in terms of pure y and then integrate w.r.t y and asusual substitution
then u get function in terms of pure y and then integrate w.r.t y and asusual substitution
Let f(x) = xn | x | for real x. Then f(x) is differentiable at origin, if x is equal to which one of the following ?- a)1
- b)0
- c)Any real number
- d)Any positive intege
Correct answer is option 'D'. Can you explain this answer?
Let f(x) = xn | x | for real x. Then f(x) is differentiable at origin, if x is equal to which one of the following ?
a)
1
b)
0
c)
Any real number
d)
Any positive intege
|
|
Chirag Verma answered |
Given that f(x) 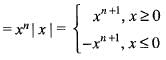
Since, f(x) is differentiable at x = 0 therefore, we have
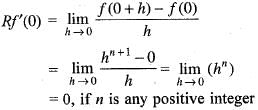

Since, f(x) is differentiable at x = 0 therefore, we have
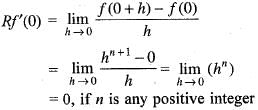
Let
f(x, y) = 2x2 - xy + 2y2 Then at (1, 2)- a)
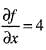
- b)
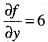
- c)
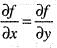
- d)
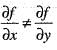
Correct answer is option 'D'. Can you explain this answer?
Let
f(x, y) = 2x2 - xy + 2y2 Then at (1, 2)
f(x, y) = 2x2 - xy + 2y2 Then at (1, 2)
a)
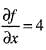
b)
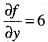
c)
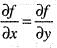
d)
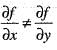
|
|
Chirag Verma answered |
We are given that
f(x, y) = 2x2 - xy + 2y2
then,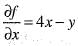
Hence,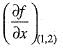 = 4 x 1 - 2 = 2
= 4 x 1 - 2 = 2
and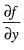 = - x + 4y
= - x + 4y
Hence,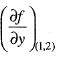 = - l + 4x 2 = 7
= - l + 4x 2 = 7
Thus,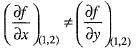
Hence, option (d) is correct.
f(x, y) = 2x2 - xy + 2y2
then,
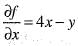
Hence,
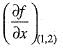 = 4 x 1 - 2 = 2
= 4 x 1 - 2 = 2and
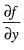 = - x + 4y
= - x + 4yHence,
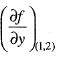 = - l + 4x 2 = 7
= - l + 4x 2 = 7Thus,
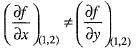
Hence, option (d) is correct.
Let f : R2 —> R be defined by
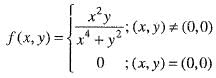
Then, the directional derivative direction of f at (0 , 0) in the direction o f the vector 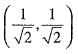 is
is- a)1/√2
- b)1/2
- c)1/2√2
- d)1/4√2
Correct answer is option 'A'. Can you explain this answer?
Let f : R2 —> R be defined by
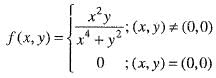
Then, the directional derivative direction of f at (0 , 0) in the direction o f the vector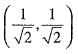 is
is
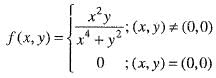
Then, the directional derivative direction of f at (0 , 0) in the direction o f the vector
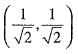 is
isa)
1/√2
b)
1/2
c)
1/2√2
d)
1/4√2

|
Veda Institute answered |
we are given that u = 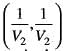 and a = (0,0). we have directional derivative at a in the direction u as
and a = (0,0). we have directional derivative at a in the direction u as
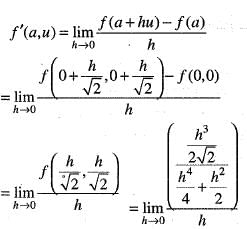
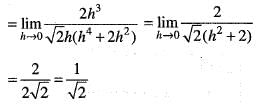
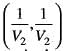 and a = (0,0). we have directional derivative at a in the direction u as
and a = (0,0). we have directional derivative at a in the direction u as 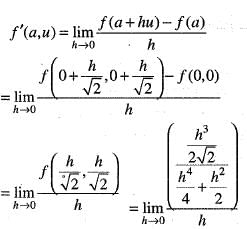
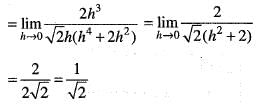
If f(x) is real-valued function defined on [0, ∞] such that f(0) = 0 and 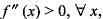 then the function h(x)
then the function h(x) 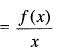 is
is- a)increasing in [0,∞]
- b)decreasing in [0, 1]
- c)increasing in [0, 1] and decreasing in [1, ∞]
- d)decreasing in [0, 1] and increasing in [ 1 , ∞]
Correct answer is option 'A'. Can you explain this answer?
If f(x) is real-valued function defined on [0, ∞] such that f(0) = 0 and 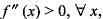 then the function h(x)
then the function h(x) 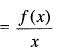 is
is
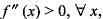 then the function h(x)
then the function h(x) 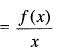 is
isa)
increasing in [0,∞]
b)
decreasing in [0, 1]
c)
increasing in [0, 1] and decreasing in [1, ∞]
d)
decreasing in [0, 1] and increasing in [ 1 , ∞]

|
Veda Institute answered |
Given that,
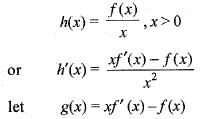
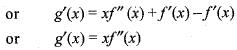
Since, f''(x) > 0 and x > 0, therefore g'(x) > 0, 0 => g (x) is strictly increasing function in [0, ∞]
0 => g (x) is strictly increasing function in [0, ∞]
since, h'(x)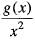
=> h'(x) > 0,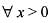
or h (x) is increasing in [0, ∞]
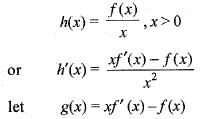
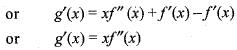
Since, f''(x) > 0 and x > 0, therefore g'(x) > 0,
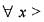 0 => g (x) is strictly increasing function in [0, ∞]
0 => g (x) is strictly increasing function in [0, ∞]since, h'(x)
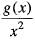
=> h'(x) > 0,
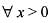
or h (x) is increasing in [0, ∞]
If is α repeated root of the polynomial equation f(x) = 0, then- a) f(a) = 0 but f'(a) ≠ 0
- b)f(a) ≠ 0 but f'(α) = 0
- c)f'(α) ≠ 0 and f'(α) = 0
- d) f(α) = 0 and f'(α) = 0
Correct answer is option 'D'. Can you explain this answer?
If is α repeated root of the polynomial equation f(x) = 0, then
a)
f(a) = 0 but f'(a) ≠ 0
b)
f(a) ≠ 0 but f'(α) = 0
c)
f'(α) ≠ 0 and f'(α) = 0
d)
f(α) = 0 and f'(α) = 0
|
|
Arnav Chawla answered |
Repeating Root of a Polynomial Equation
An repeated root of a polynomial equation means that the root is a solution to the equation with a multiplicity greater than 1. In this case, if α is a repeated root of the polynomial equation f(x) = 0, it means that when you substitute α into the polynomial equation, it gives you 0.
Understanding the Options
a) f(α) = 0 but f(α) ≠ 0
This option is contradictory because if f(α) = 0, then f(α) cannot be not equal to 0.
b) f(α) ≠ 0 but f(α) = 0
This option is also contradictory because if f(α) = 0, then f(α) cannot be not equal to 0.
c) f(α) ≠ 0 and f(α) = 0
This option is contradictory because it states that f(α) is not equal to 0 and at the same time equal to 0.
Correct Answer: Option 'D'
d) f(α) = 0 and f(α) = 0
This option correctly states that when a root is repeated, it must satisfy the polynomial equation with a value of 0. Therefore, the correct answer is option 'D'.
If f(x) and g(x) are real number function defined on 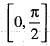 and
and 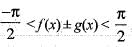 , , then which of following is correct?
, , then which of following is correct?- a)cos (f(x)) = sin (g (x)),
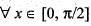
- b) cos (f(x)) > sin (g (x)),
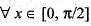
- c)cos (f(x)) < sin (g(x),
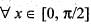
- d) None of the above
Correct answer is option 'C'. Can you explain this answer?
If f(x) and g(x) are real number function defined on 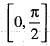 and
and 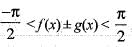 , , then which of following is correct?
, , then which of following is correct?
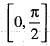 and
and 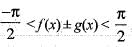 , , then which of following is correct?
, , then which of following is correct?a)
cos (f(x)) = sin (g (x)),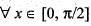
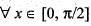
b)
cos (f(x)) > sin (g (x)), 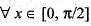
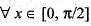
c)
cos (f(x)) < sin (g(x), 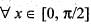
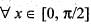
d)
None of the above
|
|
Chirag Verma answered |
Here, 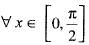
cos f(x) - sin (g(x))
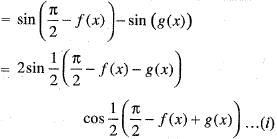
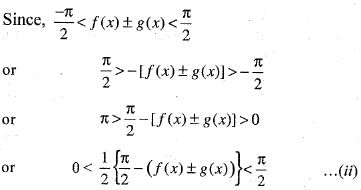
using eq. (ii) in eq. (i), then we obtain cos (f (x)) - sin (g (x)) > 0
or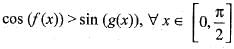
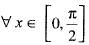
cos f(x) - sin (g(x))
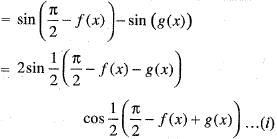
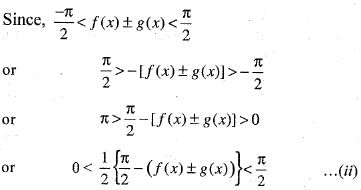
using eq. (ii) in eq. (i), then we obtain cos (f (x)) - sin (g (x)) > 0
or
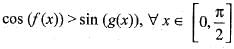
The value of ‘C’ in Rolle’s theorem, where -π/2 < C < π/2 and f(x) = cos x is equal to- a)π/4
- b)π/3
- c)π
- d)0
Correct answer is option 'D'. Can you explain this answer?
The value of ‘C’ in Rolle’s theorem, where -π/2 < C < π/2 and f(x) = cos x is equal to
a)
π/4
b)
π/3
c)
π
d)
0

|
Veda Institute answered |
Clearly, f(x) = cos x is continuous as well as differentiable in interval 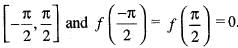
Then by Rolle’s theorem we have
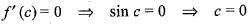
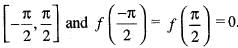
Then by Rolle’s theorem we have
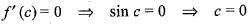
f(x) = x6 - x - 1, x ∈ [1, 2], consider the following statements
(i) f is increasing on [1, 2]
(ii) f has root in [1, 2]
(iii) f is decreasing in [1, 2]
(iv) f has no root in [1 ,2]
Q. which of the above is/are correct?- a)I and II
- b)I and IV
- c)II and III
- d)III and IV
Correct answer is option 'A'. Can you explain this answer?
f(x) = x6 - x - 1, x ∈ [1, 2], consider the following statements
(i) f is increasing on [1, 2]
(ii) f has root in [1, 2]
(iii) f is decreasing in [1, 2]
(iv) f has no root in [1 ,2]
Q. which of the above is/are correct?
(i) f is increasing on [1, 2]
(ii) f has root in [1, 2]
(iii) f is decreasing in [1, 2]
(iv) f has no root in [1 ,2]
Q. which of the above is/are correct?
a)
I and II
b)
I and IV
c)
II and III
d)
III and IV
|
|
Chirag Verma answered |
Given that f(x) = x6 - x - 1
or f'(x) = 6x5- 1
or f'(x) > 0,
Clearly, f(x) is continuous in the interval [1, 2]
Such that f(1) f(2) < 0, therefore , f(x ) has atleast one root between [1, 2]
or f'(x) = 6x5- 1
or f'(x) > 0,
Clearly, f(x) is continuous in the interval [1, 2]
Such that f(1) f(2) < 0, therefore , f(x ) has atleast one root between [1, 2]
Let l = { 1 } ∪ { 2 } 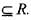 For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then
For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then- a)φ is discontinuous some where or R
- b)φ is continuous on R but not differentiable only at x = 1
- c)φ is continuous on R but not differentiable only at x = 1 and 2
- d)φ is continuous on R but not differentiable only at
x = 1, 3/2 and 2
Correct answer is option 'D'. Can you explain this answer?
Let l = { 1 } ∪ { 2 } 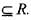 For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then
For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then
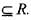 For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} then
For x ∈ R, let φ(x) = dis (x, l) = ln f{| x —y | : y ∈ l} thena)
φ is discontinuous some where or R
b)
φ is continuous on R but not differentiable only at x = 1
c)
φ is continuous on R but not differentiable only at x = 1 and 2
d)
φ is continuous on R but not differentiable only at
x = 1, 3/2 and 2
x = 1, 3/2 and 2
|
|
Chirag Verma answered |
Given that,
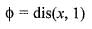
= ln f{|x -.y| : y ∈ 1}
where l = { l } ∪ { 2 }
= ln f{| x -l| ,| x -2 | }
the graph of the φ(x) is given by.
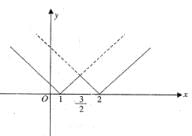
Clearly, the graph of the function have sharp edges at x = 1,3/2 and 2. Therefore, f(x) is not differentiable at x
= 1, 3/2 and 2.
Hence, φ(x) is continuous on R but not
differentiable at x = 1, 3/2 and 2
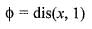
= ln f{|x -.y| : y ∈ 1}
where l = { l } ∪ { 2 }
= ln f{| x -l| ,| x -2 | }
the graph of the φ(x) is given by.

Clearly, the graph of the function have sharp edges at x = 1,3/2 and 2. Therefore, f(x) is not differentiable at x
= 1, 3/2 and 2.
Hence, φ(x) is continuous on R but not
differentiable at x = 1, 3/2 and 2
If f(x+y) = f (x) . f(y) for all x and y. Suppose that f(3) = 3 and f'(0) = 11 then , f'(3) is equal to- a)22
- b)33
- c)28
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If f(x+y) = f (x) . f(y) for all x and y. Suppose that f(3) = 3 and f'(0) = 11 then , f'(3) is equal to
a)
22
b)
33
c)
28
d)
None of these
|
|
Chirag Verma answered |
Given that f'(0) = 11
implies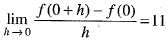
implies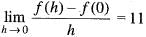
implies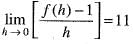
[Since f(3 + 0) = f(3) - f(0)
=> f(3) = f(3) • (0)]
implies f(0) = 1 Now we have
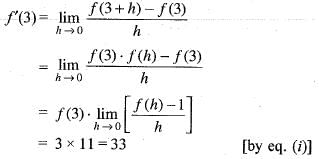
implies
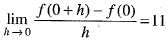
implies
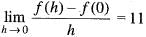
implies
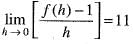
[Since f(3 + 0) = f(3) - f(0)
=> f(3) = f(3) • (0)]
implies f(0) = 1 Now we have
The equation of the curve for which the square of the ordinate is twice the rectangle contained by the abscissa and the intercept of the normal on x-axis and passing through (2, 1) is- a)x2 + y2 − x = 0
- b)4x2 + 2y2 − 9y = 0
- c)2x2 + 4y2 − 9x = 0
- d)4x2 + 2y2 − 9x = 0
Correct answer is option 'D'. Can you explain this answer?
The equation of the curve for which the square of the ordinate is twice the rectangle contained by the abscissa and the intercept of the normal on x-axis and passing through (2, 1) is
a)
x2 + y2 − x = 0
b)
4x2 + 2y2 − 9y = 0
c)
2x2 + 4y2 − 9x = 0
d)
4x2 + 2y2 − 9x = 0
|
|
Vikram Kapoor answered |
∵ Equation of normal at (x, y) is
Y − y = dx/dy (X − x)
Put, y = 0
Then, X = x + y dy/dx
Given, y2 = 2x X
⇒ y2 = 2x ( x + y dy/dx)
⇒ dy/dx = (y2 − 2x2)/(2xy) = ((y/x)2 − 2)/ ( 2y/x)
Put y = vx, we get dx/dy = v + x dv/dx
Then, v + x dv/dx = v2−2/2v
On integrating both sides, we get
ln (2 + v2) + ln|x| = ln c
⇒ ln (|x|(2 + v2)) = ln c
⇒ |x| ( 2 + y2/x2) = c
∵ It passes through (2, 1), then 2 (2 + 1 4 ) = c
⇒ c = 9/2
Then, |x| ( 2 + y2/x2) = 9/2
⇒ 2x2 + y2 = 9/2 |x|
⇒ 4x2 + 2y2 = 9|x|
Y − y = dx/dy (X − x)
Put, y = 0
Then, X = x + y dy/dx
Given, y2 = 2x X
⇒ y2 = 2x ( x + y dy/dx)
⇒ dy/dx = (y2 − 2x2)/(2xy) = ((y/x)2 − 2)/ ( 2y/x)
Put y = vx, we get dx/dy = v + x dv/dx
Then, v + x dv/dx = v2−2/2v
On integrating both sides, we get
ln (2 + v2) + ln|x| = ln c
⇒ ln (|x|(2 + v2)) = ln c
⇒ |x| ( 2 + y2/x2) = c
∵ It passes through (2, 1), then 2 (2 + 1 4 ) = c
⇒ c = 9/2
Then, |x| ( 2 + y2/x2) = 9/2
⇒ 2x2 + y2 = 9/2 |x|
⇒ 4x2 + 2y2 = 9|x|
Let f : R --> R be given by f(x) = [x] the greatest integer less than or equal to x. Then- a)The points at which f is not continuous is countable
- b)The points at which f is not continuous is R
- c)f is strictly decreasing
- d)f is strictly increasing
Correct answer is option 'A'. Can you explain this answer?
Let f : R --> R be given by f(x) = [x] the greatest integer less than or equal to x. Then
a)
The points at which f is not continuous is countable
b)
The points at which f is not continuous is R
c)
f is strictly decreasing
d)
f is strictly increasing
|
|
Ananya Patel answered |
R be a function. The domain of the function f is the set of all real numbers, R, and the codomain is also the set of all real numbers, R.
Let f(x) = | sin πx |,  then
then- a)f is continuous nowhere
- b)f is continuous everywhere and differentiable nowhere.
- c)f is continuous everywhere and differentiable every where except at integral values of x.
- d)f is differentiable everywhere.
Correct answer is option 'C'. Can you explain this answer?
Let f(x) = | sin πx |,  then
then
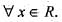 then
thena)
f is continuous nowhere
b)
f is continuous everywhere and differentiable nowhere.
c)
f is continuous everywhere and differentiable every where except at integral values of x.
d)
f is differentiable everywhere.
|
|
Chirag Verma answered |
The graph of the function f(x) = | sinπx | is y =f(x)
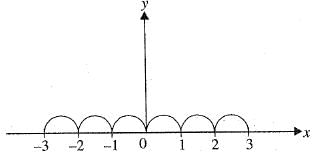
clearly, the graph have sharp edges at the points 0, ±1, ± 2, ±3, .. therefore function is continuous everywhere but not differentiable everywhere except at integral values of x.

clearly, the graph have sharp edges at the points 0, ±1, ± 2, ±3, .. therefore function is continuous everywhere but not differentiable everywhere except at integral values of x.
If f(x) = 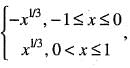 then
then- a)Rolle’s theorem does not apply to f in [-1,1]
- b)Rolle’s theorem apply to f in [-1, 1]
- c)f is not continuous at x = 0
- d)f'(0) = 0
Correct answer is option 'A'. Can you explain this answer?
If f(x) = 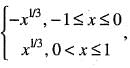 then
then
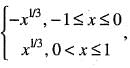 then
thena)
Rolle’s theorem does not apply to f in [-1,1]
b)
Rolle’s theorem apply to f in [-1, 1]
c)
f is not continuous at x = 0
d)
f'(0) = 0
|
|
Chirag Verma answered |
Given that,
f(x) =
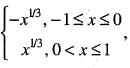
Clearly the given function is not differentiable at x = 0. Therefore, Roll’s theorem does not apply to f in [-1,1]
f(x) =
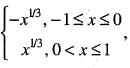
Clearly the given function is not differentiable at x = 0. Therefore, Roll’s theorem does not apply to f in [-1,1]
The function f(x) = | x + 2 | is not differentiable at a point- a)x = 2
- b)x = - 2
- c) x = - 1
- d)x = 1
Correct answer is option 'B'. Can you explain this answer?
The function f(x) = | x + 2 | is not differentiable at a point
a)
x = 2
b)
x = - 2
c)
x = - 1
d)
x = 1

|
Veda Institute answered |
Given that
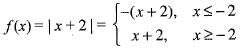
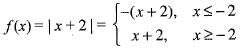
Clearly, the rule of the function is changing at x = 0, so we shall test the differentiability of f(x) only at the point x = -2 obviously, being polynomial, at all other points the function is differentiable.
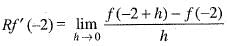

Since Lf '(- 2) ≠ R'f(- 2) , therefore , f(x) is not differentiable at x = - 2 .
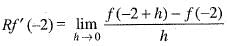

Since Lf '(- 2) ≠ R'f(- 2) , therefore , f(x) is not differentiable at x = - 2 .
A function f : R-->R satisfies the e q .f(x +y) = f(x).f(y),  and f(x) ≠ 0,
and f(x) ≠ 0, 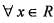 . If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal to
. If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal to
- a)2 f(x),

- b)4f(x),
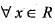
- c)0,
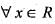 - { 0 }
- { 0 }
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
A function f : R-->R satisfies the e q .f(x +y) = f(x).f(y), 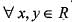 and f(x) ≠ 0,
and f(x) ≠ 0, 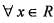 . If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal to
. If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal to
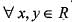 and f(x) ≠ 0,
and f(x) ≠ 0, 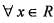 . If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal to
. If f(x) is differentiate at 0 a n d f'(0 ) = 2 then f'(x) is equal toa)
2 f(x), 

b)
4f(x), 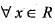
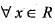
c)
0, 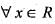 - { 0 }
- { 0 }
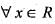 - { 0 }
- { 0 }d)
None of the above
|
|
Chirag Verma answered |
We have
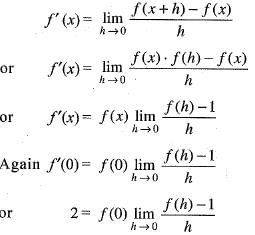
Now f(0 + 0)= f(0)- f(0)
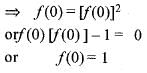
[Since f(x) 0 ,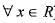 ]
]
from eq. (ii) we get
Gives
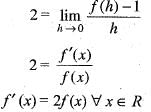
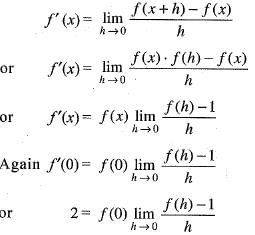
Now f(0 + 0)= f(0)- f(0)
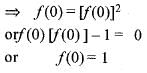
[Since f(x) 0 ,
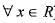 ]
]from eq. (ii) we get
Gives
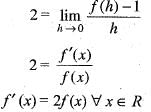
If the function defined as
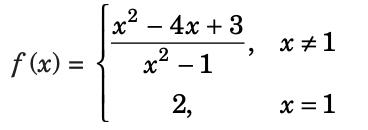
Then, the function f (x) has- a)a discontinuity of second kind at the point x = 1
- b)a discontinuity of second kind at the point x = 0
- c)a removable discontinuity at the point x = 1
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If the function defined as
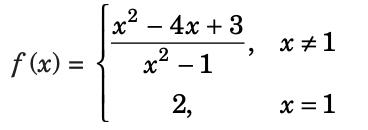
Then, the function f (x) has
Then, the function f (x) has
a)
a discontinuity of second kind at the point x = 1
b)
a discontinuity of second kind at the point x = 0
c)
a removable discontinuity at the point x = 1
d)
None of these

|
Veda Institute answered |
So, the function is not continuous at the point x = 1. The discontinuity is of the first kind and can be removed by defining function as f (x) = – 1.
If we expand sinx by Taylor’s series about 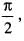 then a1, a7, a4, a3 are
then a1, a7, a4, a3 are- a)
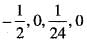
- b)
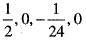
- c)
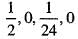
- d)
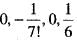
Correct answer is option 'A'. Can you explain this answer?
If we expand sinx by Taylor’s series about 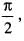 then a1, a7, a4, a3 are
then a1, a7, a4, a3 are
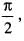 then a1, a7, a4, a3 are
then a1, a7, a4, a3 area)
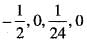
b)
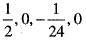
c)
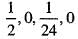
d)
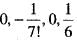

|
Veda Institute answered |
Given function f(x) = sin x
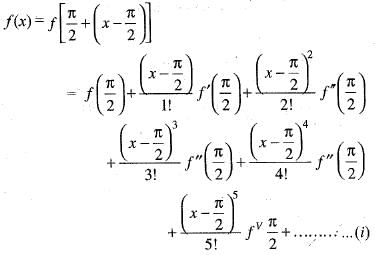
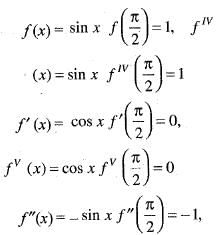
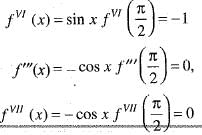
the value of a2, a7 a4, a3 in (i) are
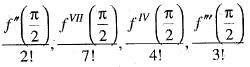
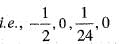
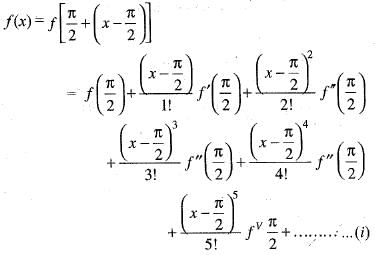
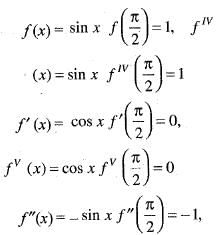
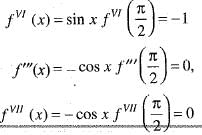
the value of a2, a7 a4, a3 in (i) are
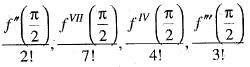
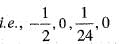
A function is said to be ______________ if and only if f(a) = f(b) implies that a = b for all a and b in the domain of f. - a)One-to-many
- b)One-to-one
- c)Many-to-many
- d)Many-to-one
Correct answer is option 'B'. Can you explain this answer?
A function is said to be ______________ if and only if f(a) = f(b) implies that a = b for all a and b in the domain of f.
a)
One-to-many
b)
One-to-one
c)
Many-to-many
d)
Many-to-one
|
|
Chirag Verma answered |
A function is one-to-one if and only if f(a) ≠ f(b) whenever a ≠ b.
Let A be a 3 x 4 matrix of rank 2. Then the rank of ATA, where AT denotes the transpose of A. is,- a)exactly 2
- b)exactly 1
- c)at most 3, and atleast 2
- d)at most 2, but not necessarily 2
Correct answer is option 'A'. Can you explain this answer?
Let A be a 3 x 4 matrix of rank 2. Then the rank of ATA, where AT denotes the transpose of A. is,
a)
exactly 2
b)
exactly 1
c)
at most 3, and atleast 2
d)
at most 2, but not necessarily 2
|
|
Pooja Choudhury answered |
We know Rank A = Rank AT= 2
and also we know Rank (AB) £ min {Rank A, Rank B} as here we are taking product of matrix with its transpose.
Thus Rank (ATA) = 2
and also we know Rank (AB) £ min {Rank A, Rank B} as here we are taking product of matrix with its transpose.
Thus Rank (ATA) = 2
The value of ‘C’ of Lagrange’s mean value theorem for f( x ) = x (x - 1) in [1 ,2] is given by- a)5/4
- b)3/2
- c)7/4
- d)11/6
Correct answer is option 'B'. Can you explain this answer?
The value of ‘C’ of Lagrange’s mean value theorem for f( x ) = x (x - 1) in [1 ,2] is given by
a)
5/4
b)
3/2
c)
7/4
d)
11/6
|
|
Chirag Verma answered |
Clearly f(x) = x2 - x is continuous in the interval [1, 2] and differentiable in the open interval [1,2]. therefore,
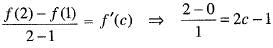 or 2 = 2c - 1
or 2 = 2c - 1
or c = 3/2
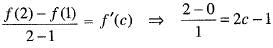 or 2 = 2c - 1
or 2 = 2c - 1or c = 3/2
If 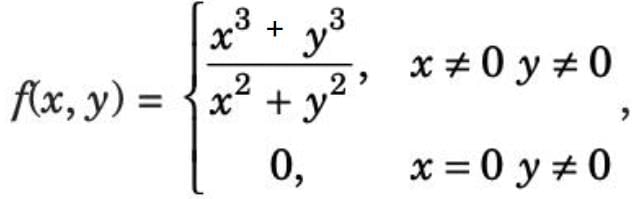 then
then
- a)f does not exist at (0, 0)
- b)f is continuous at (0, 0)
- c)f is not continuous at (0, 0)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If 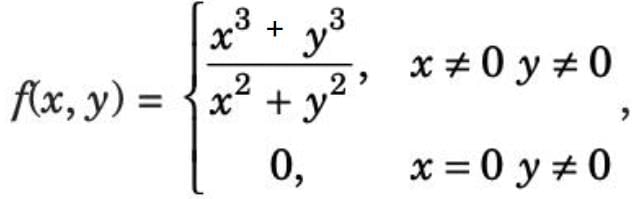 then
then
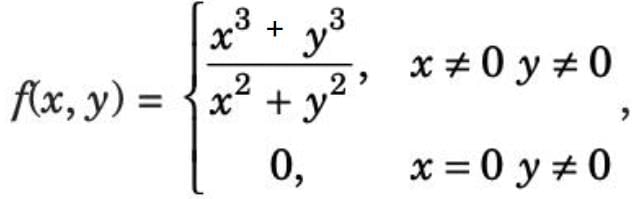 then
thena)
f does not exist at (0, 0)
b)
f is continuous at (0, 0)
c)
f is not continuous at (0, 0)
d)
none of these
|
|
Chirag Verma answered |
Limit along x → 0 and y → 0:
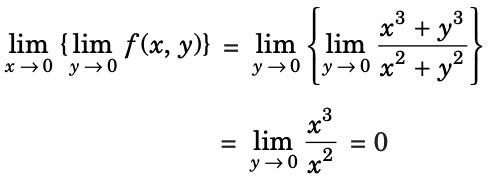
Limit along y → 0 and x → 0
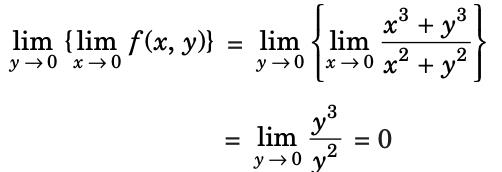
Limit along the y = mx, then
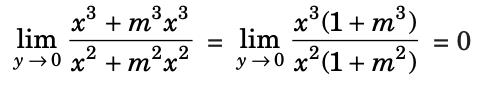
Since the limit along any path is the same, the limit exists.
Limit along y → 0 and x → 0
Limit along the y = mx, then
Since the limit along any path is the same, the limit exists.
Let
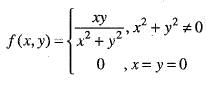
then- a)f(x, y) is continuous at origin
- b)f(x, y) has removable discontinuity of (0,0)
- c)f(x, y) is not differentiable at (0, 0)
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Let
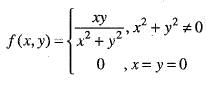
then
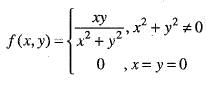
then
a)
f(x, y) is continuous at origin
b)
f(x, y) has removable discontinuity of (0,0)
c)
f(x, y) is not differentiable at (0, 0)
d)
None of these

|
Veda Institute answered |
ANSWER :- c
Solution :- Consider an approach along the line y=x; then f(x,y)=x^2/(x^2+x^2) = 1/2
for all x≠0. On the other hand, if we approach (0,0) along the line y=2x
f(x,y)=(2x)^2/[x^2+4x^2]
=2/5
So there are two different paths toward the origin, each giving a different limit. Hence, the limit does not exist.
Or more simply, approach along y=0
Therefore , f(x, y) is not differentiable at origin
Let
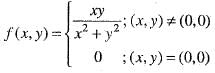
Then,- a)f is continuous at (0, 0) and the partial derivatives fx, fy exists at every point o f R2
- b)f is discontinuous at (0,0) and fx, fy does not exists at every point o f R2
- c)f is discontinuous at (0, 0) a n d fx , fy exists at (0,0)
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Let
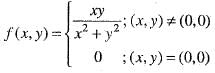
Then,
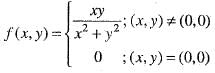
Then,
a)
f is continuous at (0, 0) and the partial derivatives fx, fy exists at every point o f R2
b)
f is discontinuous at (0,0) and fx, fy does not exists at every point o f R2
c)
f is discontinuous at (0, 0) a n d fx , fy exists at (0,0)
d)
None of the above
|
|
Chirag Verma answered |
Let us suppose (x, y) approaches (0, 0) along the line y = mx. Which is a line through the origin. Put y = mx and allows x —> 0, we get
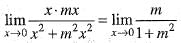
which depends on m, therefore the limit of f(x, y) at (0, 0) does not exists. Hence, f(x, y) is discontinuous at origin.
Now,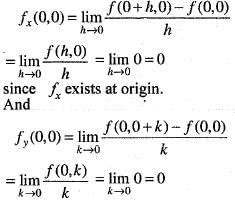
since fy exists at origin.
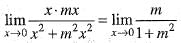
which depends on m, therefore the limit of f(x, y) at (0, 0) does not exists. Hence, f(x, y) is discontinuous at origin.
Now,
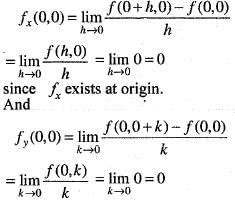
since fy exists at origin.
At what point will be function be continuous ?- a)At all points of Z
- b)At all points of R ~ Z
- c)At all points of R
- d)Whenever X ∈ Z
Correct answer is option 'D'. Can you explain this answer?
At what point will be function be continuous ?
a)
At all points of Z
b)
At all points of R ~ Z
c)
At all points of R
d)
Whenever X ∈ Z
|
|
Chirag Verma answered |
Let f be the function defined on R by setting f (x) = 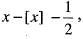 when x is not an integer , f(x ) = 0, then f is continuous, when x is an integer.
when x is not an integer , f(x ) = 0, then f is continuous, when x is an integer.
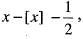 when x is not an integer , f(x ) = 0, then f is continuous, when x is an integer.
when x is not an integer , f(x ) = 0, then f is continuous, when x is an integer.If f(x) is twice differentiable and | f(x) | < α, f'(x)| < β, in the range x > α, then which of the following is correct?- a)

- b)
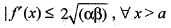
- c)
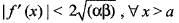
- d)
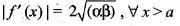
Correct answer is option 'C'. Can you explain this answer?
If f(x) is twice differentiable and | f(x) | < α, f'(x)| < β, in the range x > α, then which of the following is correct?
a)

b)
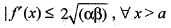
c)
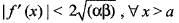
d)
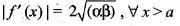

|
Veda Institute answered |
Let x > a and n a positive number then
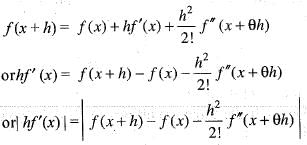

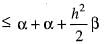
or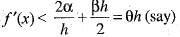
Now, for maxima or minima of f(h), we have

or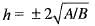
and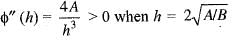
Hence, the least value of φ(h)
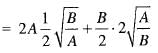
= 2√AB
thus,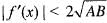
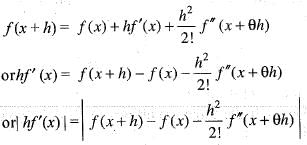

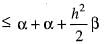
or
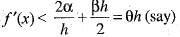
Now, for maxima or minima of f(h), we have

or
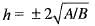
and
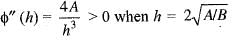
Hence, the least value of φ(h)
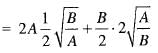
= 2√AB
thus,
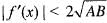
If f(x) is differentiable on interval l and 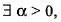 such that |f'(x)| ≤ a on l, then f(x) is
such that |f'(x)| ≤ a on l, then f(x) is- a) Continuous but not uniformly continuous on l
- b)Uniformly continuous but not continuous on l
- c)Uniformly continuous but not differentiable on l
- d)Continuous, uniformly continuous and differentiable on l
Correct answer is option 'A'. Can you explain this answer?
If f(x) is differentiable on interval l and 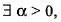 such that |f'(x)| ≤ a on l, then f(x) is
such that |f'(x)| ≤ a on l, then f(x) is
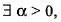 such that |f'(x)| ≤ a on l, then f(x) is
such that |f'(x)| ≤ a on l, then f(x) isa)
Continuous but not uniformly continuous on l
b)
Uniformly continuous but not continuous on l
c)
Uniformly continuous but not differentiable on l
d)
Continuous, uniformly continuous and differentiable on l
|
|
Chirag Verma answered |
For xy ∈ l, by Lagrange’s mean value theorem
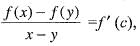 where x < c < y
where x < c < y
implies f(x)- f(y) = (x - y) f '(c )
implies |f(x) - f(y) | = x - y || f'(c)|
for a given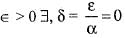 such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.
such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.
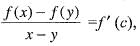 where x < c < y
where x < c < yimplies f(x)- f(y) = (x - y) f '(c )
implies |f(x) - f(y) | = x - y || f'(c)|
for a given
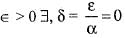 such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.
such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.Let
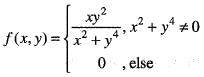
Then, the directional derivative at c = (0, 0) in the direction u = (a1, a2) is- a)

- b)
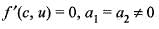
- c)
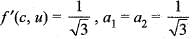
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Let
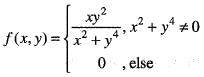
Then, the directional derivative at c = (0, 0) in the direction u = (a1, a2) is
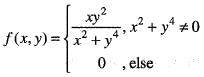
Then, the directional derivative at c = (0, 0) in the direction u = (a1, a2) is
a)

b)
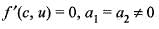
c)
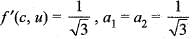
d)
None of these

|
Veda Institute answered |
We are given that

Then, the directional derivative at c = (0, 0) in the direction u(a1, a2) is
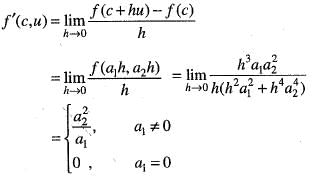
and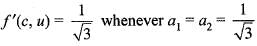
Hence, option (c) is correct.

Then, the directional derivative at c = (0, 0) in the direction u(a1, a2) is
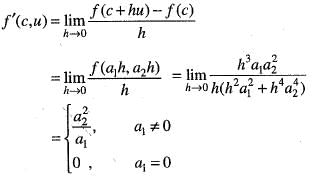
and
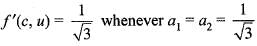
Hence, option (c) is correct.
Consider the following conditions
(i) f(x) is well defined at x = a
(ii) 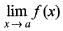 must exist.
must exist.
(iii) f(x) is continuous.
(iv) f(x) ≠ 0 at x = a
Q. which of these conditions are necessary for a function f(x) to be derivable at a point x = a of its domain?- a)I and II
- b)III and IV
- c)I, II and III
- d)I, II and IV
Correct answer is option 'A'. Can you explain this answer?
Consider the following conditions
(i) f(x) is well defined at x = a
(ii)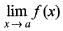 must exist.
must exist.
(iii) f(x) is continuous.
(iv) f(x) ≠ 0 at x = a
Q. which of these conditions are necessary for a function f(x) to be derivable at a point x = a of its domain?
(i) f(x) is well defined at x = a
(ii)
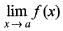 must exist.
must exist.(iii) f(x) is continuous.
(iv) f(x) ≠ 0 at x = a
Q. which of these conditions are necessary for a function f(x) to be derivable at a point x = a of its domain?
a)
I and II
b)
III and IV
c)
I, II and III
d)
I, II and IV

|
Veda Institute answered |
The necessary condition for a function f(x) to be derivable at a point x = a of its domain.
(i) f(x) is well defined at x = a
(ii)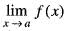 must exist.
must exist.
(iv) f (x) is continuous.
(i) f(x) is well defined at x = a
(ii)
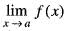 must exist.
must exist.(iv) f (x) is continuous.
The inverse of function f(x) = x3 + 2 is ____________ - a)f -1 (y) = (y – 2)1/2
- b)f -1 (y) = (y – 2)1/3
- c)f -1 (y) = (y)1/3
- d)f -1 (y) = (y – 2)
Correct answer is option 'B'. Can you explain this answer?
The inverse of function f(x) = x3 + 2 is ____________
a)
f -1 (y) = (y – 2)1/2
b)
f -1 (y) = (y – 2)1/3
c)
f -1 (y) = (y)1/3
d)
f -1 (y) = (y – 2)
|
|
Chirag Verma answered |
To find the inverse of the function equate f(x) then find the value of x in terms of y such that f -1 (y) = x.
Let
f(x,y) = x3 + y3- 63 (x + y) + 12xy,
then- a)the function has three stationary points
- b)the function is minimum at (-7, -7)
- c)the function is maximum at (3, 3)
- d)the function has neither minimum nor a maximum at (5,-1)
Correct answer is option 'D'. Can you explain this answer?
Let
f(x,y) = x3 + y3- 63 (x + y) + 12xy,
then
f(x,y) = x3 + y3- 63 (x + y) + 12xy,
then
a)
the function has three stationary points
b)
the function is minimum at (-7, -7)
c)
the function is maximum at (3, 3)
d)
the function has neither minimum nor a maximum at (5,-1)
|
|
Rudra Sethi answered |
Given Function:
The given function is:
f(x,y) = x^3y^3 - 63xy + 12xy
Stationary Points:
To find the stationary points of the function, we need to find the values of x and y where the partial derivatives of the function with respect to x and y are equal to zero.
Taking the partial derivative of f(x,y) with respect to x:
∂f/∂x = 3x^2y^3 - 63y + 12y
Taking the partial derivative of f(x,y) with respect to y:
∂f/∂y = 3x^3y^2 - 63x + 12x
Setting both partial derivatives equal to zero and solving for x and y, we get:
3x^2y^3 - 63y + 12y = 0
3x^3y^2 - 63x + 12x = 0
The Function has Three Stationary Points:
To determine the number of stationary points, we need to solve the system of equations formed by setting the partial derivatives equal to zero.
By solving the system of equations, we can find the values of x and y where the function has stationary points. If the system has three distinct solutions, then the function has three stationary points.
The Function is Minimum at (-7, -7):
To determine whether the function is a minimum or maximum at a specific point, we need to consider the second-order partial derivatives of the function.
Calculating the second-order partial derivatives of f(x,y):
∂^2f/∂x^2 = 6xy^3
∂^2f/∂y^2 = 6x^3y
∂^2f/∂x∂y = 9x^2y^2 - 63
∂^2f/∂y∂x = 9x^2y^2 - 63
To determine the nature of the critical point, we can use the second-order partial derivatives test. However, in this case, we can see that the second-order partial derivatives are not needed to determine the nature of the point.
The Function is Maximum at (3, 3):
Similarly, to determine whether the function is a minimum or maximum at a specific point, we need to consider the second-order partial derivatives of the function.
Calculating the second-order partial derivatives of f(x,y):
∂^2f/∂x^2 = 6xy^3
∂^2f/∂y^2 = 6x^3y
∂^2f/∂x∂y = 9x^2y^2 - 63
∂^2f/∂y∂x = 9x^2y^2 - 63
To determine the nature of the critical point, we can use the second-order partial derivatives test. However, in this case, we can see that the second-order partial derivatives are not needed to determine the nature of the point.
The Function has Neither Minimum nor Maximum at (5, -1):
To determine whether the function has a minimum or maximum at a specific point, we need to consider the
The given function is:
f(x,y) = x^3y^3 - 63xy + 12xy
Stationary Points:
To find the stationary points of the function, we need to find the values of x and y where the partial derivatives of the function with respect to x and y are equal to zero.
Taking the partial derivative of f(x,y) with respect to x:
∂f/∂x = 3x^2y^3 - 63y + 12y
Taking the partial derivative of f(x,y) with respect to y:
∂f/∂y = 3x^3y^2 - 63x + 12x
Setting both partial derivatives equal to zero and solving for x and y, we get:
3x^2y^3 - 63y + 12y = 0
3x^3y^2 - 63x + 12x = 0
The Function has Three Stationary Points:
To determine the number of stationary points, we need to solve the system of equations formed by setting the partial derivatives equal to zero.
By solving the system of equations, we can find the values of x and y where the function has stationary points. If the system has three distinct solutions, then the function has three stationary points.
The Function is Minimum at (-7, -7):
To determine whether the function is a minimum or maximum at a specific point, we need to consider the second-order partial derivatives of the function.
Calculating the second-order partial derivatives of f(x,y):
∂^2f/∂x^2 = 6xy^3
∂^2f/∂y^2 = 6x^3y
∂^2f/∂x∂y = 9x^2y^2 - 63
∂^2f/∂y∂x = 9x^2y^2 - 63
To determine the nature of the critical point, we can use the second-order partial derivatives test. However, in this case, we can see that the second-order partial derivatives are not needed to determine the nature of the point.
The Function is Maximum at (3, 3):
Similarly, to determine whether the function is a minimum or maximum at a specific point, we need to consider the second-order partial derivatives of the function.
Calculating the second-order partial derivatives of f(x,y):
∂^2f/∂x^2 = 6xy^3
∂^2f/∂y^2 = 6x^3y
∂^2f/∂x∂y = 9x^2y^2 - 63
∂^2f/∂y∂x = 9x^2y^2 - 63
To determine the nature of the critical point, we can use the second-order partial derivatives test. However, in this case, we can see that the second-order partial derivatives are not needed to determine the nature of the point.
The Function has Neither Minimum nor Maximum at (5, -1):
To determine whether the function has a minimum or maximum at a specific point, we need to consider the
Let
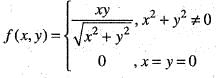
- a)f(x, y) is continuous at origin
- b)f(x, y) is differentiable at origin
- c)fx(0,0) ≠ 0
- d) fy(0 ,0) ≠ 0
Correct answer is option 'A'. Can you explain this answer?
Let
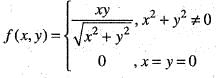
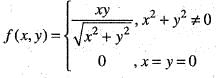
a)
f(x, y) is continuous at origin
b)
f(x, y) is differentiable at origin
c)
fx(0,0) ≠ 0
d)
fy(0 ,0) ≠ 0

|
Veda Institute answered |
We are given that 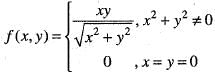
Let us take ε > 0 and x2 + y2 ≠ 0.
Now consider,

We know that,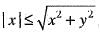
or equivalently
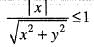
Thus,
| f(x ,y )-0 | ≤ | y | = 0- |x| + 1 • |y|
take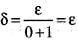
Therefore, for given ε > 0, there exists δ > 0 such that
|f(x, y) - 0 | < ε. whenever 0<|x|<δ,
0< |y |< δ
Hence,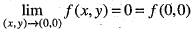
Thus, f(x,y) is continuous at (0, 0).
Hence, option (a) is correct.
Now,
f(0 + h ,0 + k) - f(0,0) = f(h , k) - f(*0,0)
= 0 • h + 0 • k + •
• 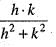
So that A = 0, B = 0 which does not depends on h and k and

Now approaching along h = mk, we get
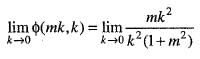
which depends on m. Therefore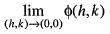 does not exists. Hence, f(x, y) is not differentiable at origin. Hence, option (b) is incorrect.
does not exists. Hence, f(x, y) is not differentiable at origin. Hence, option (b) is incorrect.
Next,
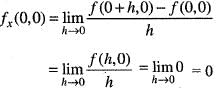 Hence, option (c) is incorrect.
Hence, option (c) is incorrect.
And,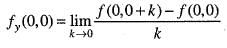

Hence, option (d) is incorrect.
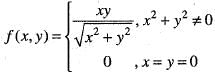
Let us take ε > 0 and x2 + y2 ≠ 0.
Now consider,

We know that,
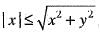
or equivalently
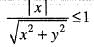
Thus,
| f(x ,y )-0 | ≤ | y | = 0- |x| + 1 • |y|
take
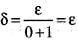
Therefore, for given ε > 0, there exists δ > 0 such that
|f(x, y) - 0 | < ε. whenever 0<|x|<δ,
0< |y |< δ
Hence,
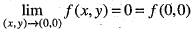
Thus, f(x,y) is continuous at (0, 0).
Hence, option (a) is correct.
Now,
f(0 + h ,0 + k) - f(0,0) = f(h , k) - f(*0,0)
= 0 • h + 0 • k +
 •
• 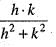
So that A = 0, B = 0 which does not depends on h and k and

Now approaching along h = mk, we get
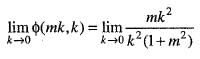
which depends on m. Therefore
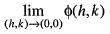 does not exists. Hence, f(x, y) is not differentiable at origin. Hence, option (b) is incorrect.
does not exists. Hence, f(x, y) is not differentiable at origin. Hence, option (b) is incorrect.Next,
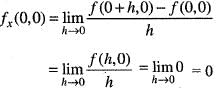 Hence, option (c) is incorrect.
Hence, option (c) is incorrect.And,
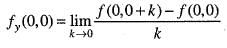

Hence, option (d) is incorrect.
Let
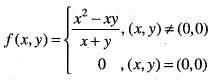
Then,- a)fx(0,0) = 2
- b)fy(0,0) = 0
- c)fx(0 ,0) = 0
- d)fy(0 , 0) = 1
Correct answer is option 'B'. Can you explain this answer?
Let
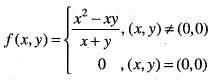
Then,
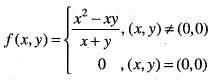
Then,
a)
fx(0,0) = 2
b)
fy(0,0) = 0
c)
fx(0 ,0) = 0
d)
fy(0 , 0) = 1
|
|
Chirag Verma answered |
We are given that
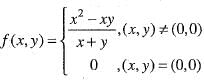
Now,
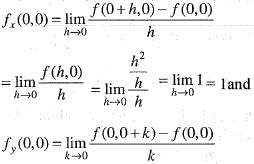

Hence, option (b) is correct,
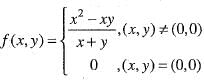
Now,
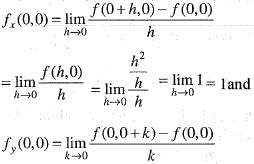

Hence, option (b) is correct,
Using Rolle’s theorem, the equation. 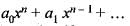
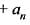 = 0 has atleast one root between 0 and 1, if
= 0 has atleast one root between 0 and 1, if- a)
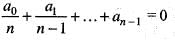
- b)
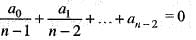
- c)
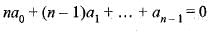
- d)
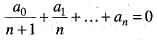
Correct answer is option 'D'. Can you explain this answer?
Using Rolle’s theorem, the equation. 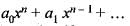
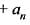 = 0 has atleast one root between 0 and 1, if
= 0 has atleast one root between 0 and 1, if
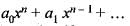
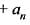 = 0 has atleast one root between 0 and 1, if
= 0 has atleast one root between 0 and 1, ifa)
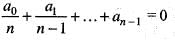
b)
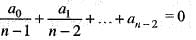
c)
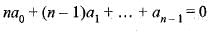
d)
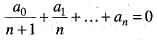
|
|
Chirag Verma answered |
Consider the function f defined by
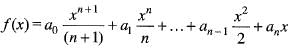 Since , f(x) is a polynomial, it is continuous and differentiable
Since , f(x) is a polynomial, it is continuous and differentiable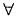 x. Consequently f(x) is continuous in the closed interval [0, 1] and differentiable in the open interval [0,1] Also , f(0) = 0 and
x. Consequently f(x) is continuous in the closed interval [0, 1] and differentiable in the open interval [0,1] Also , f(0) = 0 and
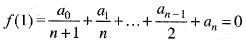
i.e. , f(0) = f(1)
Thus, all the three conditions of Rolle’s theorem are satisfied
Hence, there is atleast one value of x in the open interval [0, 1]
where f'(x) = 0
i.e., cos xn + a1.xn-1 + . . . + an-1 + an = 0
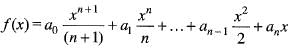 Since , f(x) is a polynomial, it is continuous and differentiable
Since , f(x) is a polynomial, it is continuous and differentiable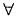 x. Consequently f(x) is continuous in the closed interval [0, 1] and differentiable in the open interval [0,1] Also , f(0) = 0 and
x. Consequently f(x) is continuous in the closed interval [0, 1] and differentiable in the open interval [0,1] Also , f(0) = 0 and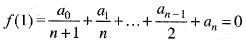
i.e. , f(0) = f(1)
Thus, all the three conditions of Rolle’s theorem are satisfied
Hence, there is atleast one value of x in the open interval [0, 1]
where f'(x) = 0
i.e., cos xn + a1.xn-1 + . . . + an-1 + an = 0
The derivative of the function f(x) = x2m is- a)even function
- b)odd function
- c)constant function
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The derivative of the function f(x) = x2m is
a)
even function
b)
odd function
c)
constant function
d)
None of these
|
|
Ishika Singhania answered |
The derivative of the function f(x) = x^2m is an odd function.
Explanation:
To find the derivative of the function f(x), we can use the power rule of differentiation. According to the power rule, if we have a function f(x) = x^n, the derivative of f(x) is given by:
f'(x) = n * x^(n-1)
In this case, the function f(x) = x^2m can be written as f(x) = (x^2)^m. Applying the power rule, we can find the derivative as follows:
f'(x) = m * (x^2)^(m-1) * 2x
Simplifying further:
f'(x) = 2mx^(2m-1)
Odd Function:
An odd function is a function that satisfies the property f(-x) = -f(x) for all values of x in the domain of the function. In other words, if we replace x with -x in the function and negate the result, it should be equal to the function itself.
Let's substitute -x for x in the derivative we found:
f'(-x) = 2m(-x)^(2m-1)
Now let's negate the result:
-f'(x) = -2m(-x)^(2m-1)
If we simplify this expression, we get:
-f'(x) = 2m(-x)^(2m-1)
We can observe that -f'(x) = f'(-x), which means that the derivative of f(x) satisfies the property of an odd function.
Conclusion:
The derivative of the function f(x) = x^2m is an odd function.
Explanation:
To find the derivative of the function f(x), we can use the power rule of differentiation. According to the power rule, if we have a function f(x) = x^n, the derivative of f(x) is given by:
f'(x) = n * x^(n-1)
In this case, the function f(x) = x^2m can be written as f(x) = (x^2)^m. Applying the power rule, we can find the derivative as follows:
f'(x) = m * (x^2)^(m-1) * 2x
Simplifying further:
f'(x) = 2mx^(2m-1)
Odd Function:
An odd function is a function that satisfies the property f(-x) = -f(x) for all values of x in the domain of the function. In other words, if we replace x with -x in the function and negate the result, it should be equal to the function itself.
Let's substitute -x for x in the derivative we found:
f'(-x) = 2m(-x)^(2m-1)
Now let's negate the result:
-f'(x) = -2m(-x)^(2m-1)
If we simplify this expression, we get:
-f'(x) = 2m(-x)^(2m-1)
We can observe that -f'(x) = f'(-x), which means that the derivative of f(x) satisfies the property of an odd function.
Conclusion:
The derivative of the function f(x) = x^2m is an odd function.
Which of the following function is not called the Euler’s integral of the first kind?- a)
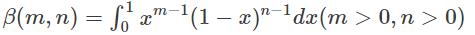
- b)

- c)
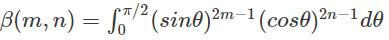
- d)

Correct answer is option 'C'. Can you explain this answer?
Which of the following function is not called the Euler’s integral of the first kind?
a)
b)
c)
d)

|
Veda Institute answered |
Euler’s integral of the first kind is nothing but Beta function. So, here only 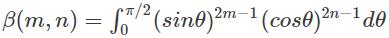 is not the definition of Beta function.
is not the definition of Beta function.
Consider the function f(x) = 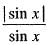 , then which one of the following is correct?
, then which one of the following is correct?- a)f (x) is every where differentiable except x = 0
- b)
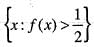 is empty set.
is empty set. - c)set of point which f(x) ≥ -1 is countable
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
Consider the function f(x) = 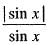 , then which one of the following is correct?
, then which one of the following is correct?
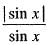 , then which one of the following is correct?
, then which one of the following is correct?a)
f (x) is every where differentiable except x = 0
b)
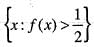 is empty set.
is empty set.c)
set of point which f(x) ≥ -1 is countable
d)
None of the above

|
Veda Institute answered |
Given that
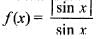
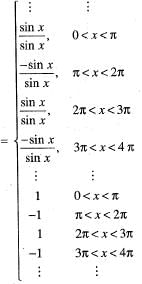
It is clear that f(x) is not continuous at the points x = nπ, n ∈ z, therefore it is not differentiable at the points.
Which f(x) > 1/2, and f (x) ≥ - 1, also there points are not countable.
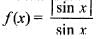
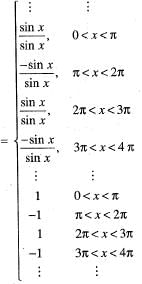
It is clear that f(x) is not continuous at the points x = nπ, n ∈ z, therefore it is not differentiable at the points.
Which f(x) > 1/2, and f (x) ≥ - 1, also there points are not countable.
The function sin xh is- a)differentiable
- b)non-differentiable
- c)discontinuous
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
The function sin xh is
a)
differentiable
b)
non-differentiable
c)
discontinuous
d)
None of the above

|
Veda Institute answered |
Sin x is differentiable and xn is also differentiable.
Hence, sin xn is also differentiable.
Hence, sin xn is also differentiable.
Let f(x, y) =  then
then- a)f(x, y) is continuous at origin
- b)fx exists at origin but not equal to zero.
- c) fy exists at origin but not equal to zero.
- d)None of these.
Correct answer is option 'A'. Can you explain this answer?
Let f(x, y) =  then
then
 then
thena)
f(x, y) is continuous at origin
b)
fx exists at origin but not equal to zero.
c)
fy exists at origin but not equal to zero.
d)
None of these.
|
|
Chirag Verma answered |
We are given that
f(x,y) =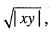
Let us take ε > 0 and (x, y) ≠ (0, 0). Consider
|f(x,y) - 0| =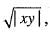
Let x = r cos θ, y = r sin θ
Therefore,
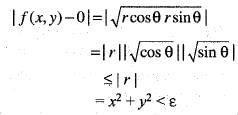
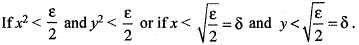 Hence for given ε > 0, there exists δ > 0 such that
Hence for given ε > 0, there exists δ > 0 such that
 Therefore, f(x, y) is continuous at (0, 0). Hence option (a) is correct.
Therefore, f(x, y) is continuous at (0, 0). Hence option (a) is correct.
Next,

Hence, option (c) is incorrect.
f(x,y) =
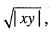
Let us take ε > 0 and (x, y) ≠ (0, 0). Consider
|f(x,y) - 0| =
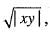
Let x = r cos θ, y = r sin θ
Therefore,
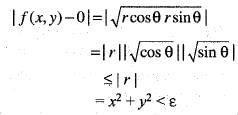
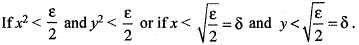 Hence for given ε > 0, there exists δ > 0 such that
Hence for given ε > 0, there exists δ > 0 such that Therefore, f(x, y) is continuous at (0, 0). Hence option (a) is correct.
Therefore, f(x, y) is continuous at (0, 0). Hence option (a) is correct.Next,

Hence, option (c) is incorrect.
Let
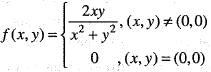
then,- a)fx does not exists at origin
- b)fy exists at origin
- c)fy does not exists at origin
- d)None
Correct answer is option 'B'. Can you explain this answer?
Let
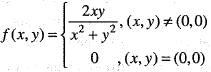
then,
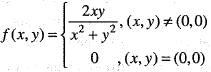
then,
a)
fx does not exists at origin
b)
fy exists at origin
c)
fy does not exists at origin
d)
None

|
Veda Institute answered |
We are given that
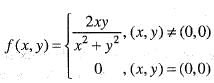
Now,
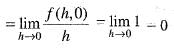
and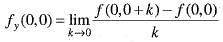
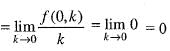
Hence, option (b) is correct.
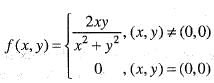
Now,

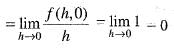
and
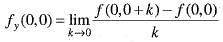
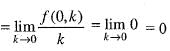
Hence, option (b) is correct.
Chapter doubts & questions for Functions of One, Two or Three Variable - Mathematics for Competitive Exams 2025 is part of Mathematics exam preparation. The chapters have been prepared according to the Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Functions of One, Two or Three Variable - Mathematics for Competitive Exams in English & Hindi are available as part of Mathematics exam.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Mathematics for Competitive Exams
98 videos|37 docs|32 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup
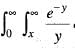 dydx by changing the order of integration is
dydx by changing the order of integration is 
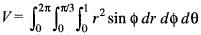

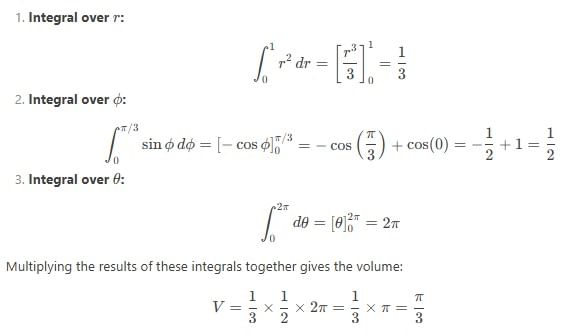
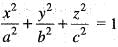 is
is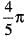 abc cubic units
abc cubic units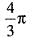 abc cubic units
abc cubic units