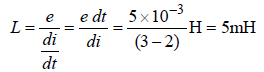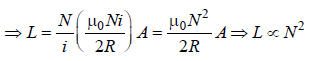All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Electromagnetic Induction for NEET Exam
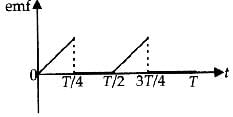
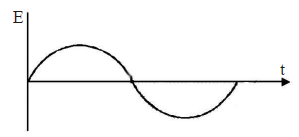
The current i in a coil varies with time as shown in the figure. The variation of induced emf with time would be [2011]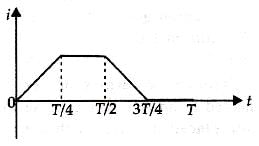
- a)
- b)
- c)
- d)
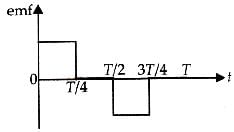
Correct answer is option 'A'. Can you explain this answer?
The current i in a coil varies with time as shown in the figure. The variation of induced emf with time would be [2011]
a)
b)
c)
d)
|
Krishna Iyer answered |
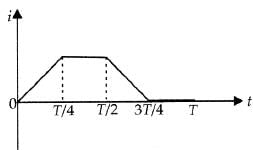
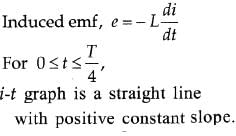
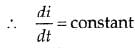
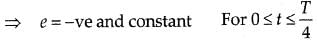
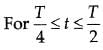
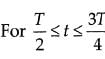
i-t graph is a straight line with negative constant slope.
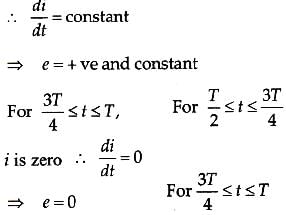
From this analysis, the variation of induced emf with time as shown in the figure below.
A rectangular coil of 20 turns and area of crosssection 25 sq. cm has a resistance of 100Ω. If amagnetic field which is perpendicular to the planeof coil changes at a rate of 1000 tesla per second,the current in the coil is [1992]- a)1 A
- b)50 A
- c)0.5 A
- d)5 A
Correct answer is option 'C'. Can you explain this answer?
A rectangular coil of 20 turns and area of crosssection 25 sq. cm has a resistance of 100Ω. If amagnetic field which is perpendicular to the planeof coil changes at a rate of 1000 tesla per second,the current in the coil is [1992]
a)
1 A
b)
50 A
c)
0.5 A
d)
5 A
|
Abhishek Desai answered |
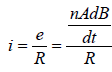
A wire loop is rotated in a magnetic field. Thefrequency of change of direction of the inducede.m.f. is [NEET 2013]- a)twice per revolution
- b)four times per revolution
- c)six times per revolution
- d)once per revolution
Correct answer is option 'A'. Can you explain this answer?
A wire loop is rotated in a magnetic field. Thefrequency of change of direction of the inducede.m.f. is [NEET 2013]
a)
twice per revolution
b)
four times per revolution
c)
six times per revolution
d)
once per revolution
|
Sarthak Saini answered |
This is the case of periodic EMI
From graph, it is clear that direction is
changing once in 1/2 cycle.
changing once in 1/2 cycle.
If the number of turns per unit length of a coil ofsolenoid is doubled, the self-inductance of thesolenoid will [1991]- a)remain unchanged
- b)be halved
- c)be doubled
- d)become four times
Correct answer is option 'D'. Can you explain this answer?
If the number of turns per unit length of a coil ofsolenoid is doubled, the self-inductance of thesolenoid will [1991]
a)
remain unchanged
b)
be halved
c)
be doubled
d)
become four times
|
Rohan Unni answered |
Self inductance of a solenoid =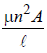 
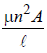
So, self induction ∝ n2
So, inductance becomes 4 times when n is doubled.
So, inductance becomes 4 times when n is doubled.
A long solenoid has 500 turns. When a currentof 2 ampere is passed through it, the resultingmagnetic flux linked with each turn of thesolenoid is 4 ×10–3 Wb. The self- inductance ofthe solenoid is [2008]- a)2.5 henry
- b)2.0 henry
- c)1.0 henry
- d)40 henry
Correct answer is option 'C'. Can you explain this answer?
A long solenoid has 500 turns. When a currentof 2 ampere is passed through it, the resultingmagnetic flux linked with each turn of thesolenoid is 4 ×10–3 Wb. The self- inductance ofthe solenoid is [2008]
a)
2.5 henry
b)
2.0 henry
c)
1.0 henry
d)
40 henry
|
Prisha Roy answered |
To find the magnetic flux linked with each turn of the solenoid, we can use the formula:
Magnetic Flux (Φ) = Number of Turns (N) * Magnetic Flux Density (B) * Area (A)
Given that the solenoid has 500 turns and a current of 2 amperes is passed through it, we can calculate the magnetic flux density using Ampere's Law:
Magnetic Flux Density (B) = (μ₀ * N * I) / L
Where:
- μ₀ is the permeability of free space (4π * 10^-7 T m/A)
- N is the number of turns (500)
- I is the current (2 A)
- L is the length of the solenoid (unknown)
Substituting the given values, we have:
B = (4π * 10^-7 T m/A) * 500 turns * 2 A / L
Now, we can substitute the magnetic flux density into the formula for magnetic flux:
Φ = N * B * A
Given that the magnetic flux linked with each turn of the solenoid is 4 units, we can write:
4 = 500 turns * B * A
Substituting the value of B, we have:
4 = 500 turns * ((4π * 10^-7 T m/A) * 500 turns * 2 A / L) * A
Simplifying the equation, we find:
4 = 500^2 * (4π * 10^-7 T m/A) * 2 A * A / L
Now, we can solve for L:
L = 500^2 * (4π * 10^-7 T m/A) * 2 A * A / 4
L = 500^2 * (π * 10^-7 T m/A) * 1000 A m^2 / 4
L = 125,000 * π * 10^-7 T m/A * 1000 A m^2 / 4
L = 125,000 * π * 10^-7 T m * 250
L = 125,000 * π * 2.5 * 10^-4 T m
Finally, we can calculate the length of the solenoid:
L = 125,000 * π * 2.5 * 10^-4 T m
L ≈ 0.981 meters
Therefore, the length of the solenoid is approximately 0.981 meters.
Magnetic Flux (Φ) = Number of Turns (N) * Magnetic Flux Density (B) * Area (A)
Given that the solenoid has 500 turns and a current of 2 amperes is passed through it, we can calculate the magnetic flux density using Ampere's Law:
Magnetic Flux Density (B) = (μ₀ * N * I) / L
Where:
- μ₀ is the permeability of free space (4π * 10^-7 T m/A)
- N is the number of turns (500)
- I is the current (2 A)
- L is the length of the solenoid (unknown)
Substituting the given values, we have:
B = (4π * 10^-7 T m/A) * 500 turns * 2 A / L
Now, we can substitute the magnetic flux density into the formula for magnetic flux:
Φ = N * B * A
Given that the magnetic flux linked with each turn of the solenoid is 4 units, we can write:
4 = 500 turns * B * A
Substituting the value of B, we have:
4 = 500 turns * ((4π * 10^-7 T m/A) * 500 turns * 2 A / L) * A
Simplifying the equation, we find:
4 = 500^2 * (4π * 10^-7 T m/A) * 2 A * A / L
Now, we can solve for L:
L = 500^2 * (4π * 10^-7 T m/A) * 2 A * A / 4
L = 500^2 * (π * 10^-7 T m/A) * 1000 A m^2 / 4
L = 125,000 * π * 10^-7 T m/A * 1000 A m^2 / 4
L = 125,000 * π * 10^-7 T m * 250
L = 125,000 * π * 2.5 * 10^-4 T m
Finally, we can calculate the length of the solenoid:
L = 125,000 * π * 2.5 * 10^-4 T m
L ≈ 0.981 meters
Therefore, the length of the solenoid is approximately 0.981 meters.
An inductor may store energy in [1990]- a)its electric field
- b)its coils
- c)its magnetic field
- d)both in electric and magnetic fields
Correct answer is option 'C'. Can you explain this answer?
An inductor may store energy in [1990]
a)
its electric field
b)
its coils
c)
its magnetic field
d)
both in electric and magnetic fields
|
Nilotpal Gupta answered |
An inductor stores energy in its magnetic field.
A varying current in a coil changes from 10A tozero in 0.5 sec. If the average e.m.f induced inthe coil is 220V, the self-inductance of the coil is [1995]- a)5 H
- b)6 H
- c)11 H
- d)12 H
Correct answer is option 'C'. Can you explain this answer?
A varying current in a coil changes from 10A tozero in 0.5 sec. If the average e.m.f induced inthe coil is 220V, the self-inductance of the coil is [1995]
a)
5 H
b)
6 H
c)
11 H
d)
12 H
|
Krish Saha answered |
Initial current (I1) = 10 A; Final current
(I2)= 0; Time (t) = 0.5 sec and induced e.m.f.
(ε) = 220 V.
Induced e.m.f. (ε)
(I2)= 0; Time (t) = 0.5 sec and induced e.m.f.
(ε) = 220 V.
Induced e.m.f. (ε)
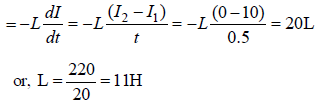
[where L = Self inductance of coil]
The magnetic flux through a circuit of resistance R changes by an amount Δφ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by [2004]- a)
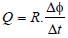
- b)
- c)
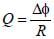
- d)
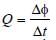
Correct answer is option 'C'. Can you explain this answer?
The magnetic flux through a circuit of resistance R changes by an amount Δφ in a time Δt. Then the total quantity of electric charge Q that passes any point in the circuit during the time Δt is represented by [2004]
a)
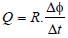
b)
c)
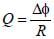
d)
|
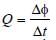
Akshat Chavan answered |
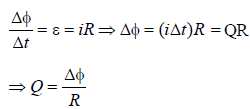
In an inductor of self-inductance L = 2 mH,current changes with time according to relationi = t2e–t. At what time emf is zero? [2001]- a)4s
- b)3s
- c)2s
- d)1s
Correct answer is option 'C'. Can you explain this answer?
In an inductor of self-inductance L = 2 mH,current changes with time according to relationi = t2e–t. At what time emf is zero? [2001]
a)
4s
b)
3s
c)
2s
d)
1s
|
Krish Chakraborty answered |
L = 2mH, i = t2e–t
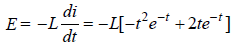
when E = 0,
–e–t t2 + 2te–t = 0
or, 2t e–t = e–t t2
⇒t = 2 sec.
–e–t t2 + 2te–t = 0
or, 2t e–t = e–t t2
⇒t = 2 sec.
The total charge induced in a conducting loopwhen it is moved in a magnetic field depend on [1992]- a)the rate of change of magnetic flux
- b)initial magnetic flux only
- c)the total change in magnetic flux
- d)final magnetic flux only
Correct answer is option 'C'. Can you explain this answer?
The total charge induced in a conducting loopwhen it is moved in a magnetic field depend on [1992]
a)
the rate of change of magnetic flux
b)
initial magnetic flux only
c)
the total change in magnetic flux
d)
final magnetic flux only
|
Bhavana Das answered |
Total Charge Induced in a Conducting Loop
The phenomenon of induced charge in a conducting loop when it is moved in a magnetic field is governed by Faraday's law of electromagnetic induction.
Understanding the Induction Process
- When a conducting loop moves through a magnetic field, the magnetic flux through the loop changes.
- According to Faraday's law, the induced electromotive force (emf) in a closed loop is directly related to the rate of change of magnetic flux through the loop.
Factors Affecting Induced Charge
- The total charge induced in the loop depends on the total change in magnetic flux (option C).
- It is not just the initial or final magnetic flux that matters, but the total difference between the initial and final states of the magnetic flux.
Key Points to Remember
- Total Change in Magnetic Flux: This is the difference between the magnetic flux at the start and at the end of the movement. The greater this difference, the larger the induced charge.
- Rate of Change vs. Total Change: While the rate of change of magnetic flux is important for calculating induced emf, the total charge induced is ultimately determined by the total change in flux over the entire movement.
Conclusion
In summary, the total charge induced in a conducting loop when moved through a magnetic field is primarily dependent on the total change in magnetic flux, confirming that option C is indeed the correct choice. Understanding this principle is vital in applications like electric generators and transformers, where electromagnetic induction plays a crucial role.
The phenomenon of induced charge in a conducting loop when it is moved in a magnetic field is governed by Faraday's law of electromagnetic induction.
Understanding the Induction Process
- When a conducting loop moves through a magnetic field, the magnetic flux through the loop changes.
- According to Faraday's law, the induced electromotive force (emf) in a closed loop is directly related to the rate of change of magnetic flux through the loop.
Factors Affecting Induced Charge
- The total charge induced in the loop depends on the total change in magnetic flux (option C).
- It is not just the initial or final magnetic flux that matters, but the total difference between the initial and final states of the magnetic flux.
Key Points to Remember
- Total Change in Magnetic Flux: This is the difference between the magnetic flux at the start and at the end of the movement. The greater this difference, the larger the induced charge.
- Rate of Change vs. Total Change: While the rate of change of magnetic flux is important for calculating induced emf, the total charge induced is ultimately determined by the total change in flux over the entire movement.
Conclusion
In summary, the total charge induced in a conducting loop when moved through a magnetic field is primarily dependent on the total change in magnetic flux, confirming that option C is indeed the correct choice. Understanding this principle is vital in applications like electric generators and transformers, where electromagnetic induction plays a crucial role.
A conductor of length 0.4 m is moving with aspeed of 7 m/s perpendicular to a magnetic fieldof intensity 0.9 Wb/m2. The induced e.m.f.across the conductor is [1995]- a)1.26 V
- b)2.52 V
- c)5.04 V
- d)25.2 V
Correct answer is option 'B'. Can you explain this answer?
A conductor of length 0.4 m is moving with aspeed of 7 m/s perpendicular to a magnetic fieldof intensity 0.9 Wb/m2. The induced e.m.f.across the conductor is [1995]
a)
1.26 V
b)
2.52 V
c)
5.04 V
d)
25.2 V
|
Ayush Sengupta answered |
Length of conductor (l) = 0.4 m; Speed (v) = 7 m/s and magnetic field (B) = 0.9 Wb/ m2.
Induced e.m.f. (V) = Blv sin θ = 0.9 × 0.4 × 7
× sin 90º = 2.52 V.
Induced e.m.f. (V) = Blv sin θ = 0.9 × 0.4 × 7
× sin 90º = 2.52 V.
A rectangular, a square, a circular and an elliptical loop, all in the (x – y) plane, are moving out of a uniform magnetic field with a constant velocity, 
The magnetic field is directed along the negative z axis direction. The induced emf, during the passage of these loops, out of the field region, will not remain constant for [2009]- a)the circular and the elliptical loops.
- b)only the elliptical loop.
- c)any of the four loops.
- d)the rectangular, circular and elliptical loops.
Correct answer is option 'A'. Can you explain this answer?
A rectangular, a square, a circular and an elliptical loop, all in the (x – y) plane, are moving out of a uniform magnetic field with a constant velocity, The magnetic field is directed along the negative z axis direction. The induced emf, during the passage of these loops, out of the field region, will not remain constant for [2009]
The magnetic field is directed along the negative z axis direction. The induced emf, during the passage of these loops, out of the field region, will not remain constant for [2009]a)
the circular and the elliptical loops.
b)
only the elliptical loop.
c)
any of the four loops.
d)
the rectangular, circular and elliptical loops.
|
Pankaj Banerjee answered |
The induced emf will remain constant only in the case of rectangular and square loops. In case of the circular and the elliptical loops, the rate of change of area of the loops during their passage out of the field is not constant, hence induced emf will not remain constant for them.
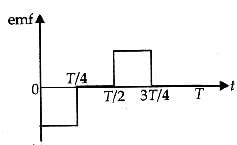
In a coil of resistance 10 Ω, the induced current developed by changing magnetic flux through it, is shown in figure as a function of time. The magnitude of change in flux through the coil in Weber is : [2012M]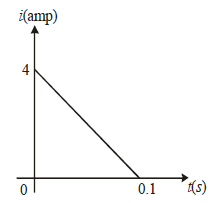
- a)8
- b)2
- c)6
- d)4
Correct answer is option 'B'. Can you explain this answer?
In a coil of resistance 10 Ω, the induced current developed by changing magnetic flux through it, is shown in figure as a function of time. The magnitude of change in flux through the coil in Weber is : [2012M]
a)
8
b)
2
c)
6
d)
4
|
|
Akshat Chavan answered |
The charge through the coil = area of
current-time(i – t) graph
current-time(i – t) graph
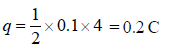
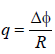∵ Change in flux (Δφ ) = q × R
Δφ = 2 Weber
Two coils have a mutual inductance 0.005 H.The current changes in the first coil accordingto equation I = I0 sin ωt, where I0 = 10A and ω = 100π radian/sec. The maximum value of e.m.f.in the second coil is [1998]- a)2π
- b)5π
- c)π
- d)4π
Correct answer is option 'B'. Can you explain this answer?
Two coils have a mutual inductance 0.005 H.The current changes in the first coil accordingto equation I = I0 sin ωt, where I0 = 10A and ω = 100π radian/sec. The maximum value of e.m.f.in the second coil is [1998]
a)
2π
b)
5π
c)
π
d)
4π
|
|
Rohan Unni answered |
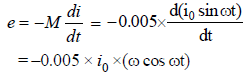
emax . = 0.005x i0 xω (when cos ωt = –1)
= 0.005 × 10 × 100π = 5πV
= 0.005 × 10 × 100π = 5πV
As a result of change in the magnetic flux linkedto the closed loop shown in the Fig,
an e.m.f. V volt is induced in the loop. The work done (joules) in taking a charge Q coulomb once along the loop is[2005]- a)QV
- b)2QV
- c)QV/2
- d)Zero
Correct answer is option 'A'. Can you explain this answer?
As a result of change in the magnetic flux linkedto the closed loop shown in the Fig,
an e.m.f. V volt is induced in the loop. The work done (joules) in taking a charge Q coulomb once along the loop is
[2005]
a)
QV
b)
2QV
c)
QV/2
d)
Zero
|
|
Sarthak Saini answered |
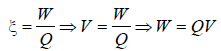
A conducting circular loop is placed in a uniformmagnetic field of 0.04 T with its planeperpendicular to the magnetic field. The radiusof the loop starts shrinking at 2 mm/s. The induced emf in the loop when the radius is 2 cmis [2009]- a)4.8 πμV
- b)0.8 πμV
- c)1.6 πμV
- d)3.2 πμV
Correct answer is option 'D'. Can you explain this answer?
A conducting circular loop is placed in a uniformmagnetic field of 0.04 T with its planeperpendicular to the magnetic field. The radiusof the loop starts shrinking at 2 mm/s. The induced emf in the loop when the radius is 2 cmis [2009]
a)
4.8 πμV
b)
0.8 πμV
c)
1.6 πμV
d)
3.2 πμV
|
|
Nilotpal Gupta answered |
Induced emf in the loop is given by
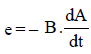where A is the area of the loop.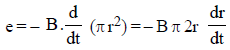
r = 2cm = 2 × 10–2 m
dr = 2 mm = 2 × 10–3 m
dt = 1s
dr = 2 mm = 2 × 10–3 m
dt = 1s
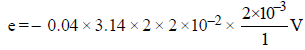
= 0.32 π × 10–5V
= 3.2 π ×10–6V
= 3.2 πμV
= 3.2 π ×10–6V
= 3.2 πμV
A current of 2.5 A flows through a coil ofinductance 5 H. The magnetic flux linked withthe coil is [NEET Kar. 2013]- a)2 Wb
- b)0.5 Wb
- c)12.5 Wb
- d)Zero
Correct answer is option 'C'. Can you explain this answer?
A current of 2.5 A flows through a coil ofinductance 5 H. The magnetic flux linked withthe coil is [NEET Kar. 2013]
a)
2 Wb
b)
0.5 Wb
c)
12.5 Wb
d)
Zero
|
Maheshwar Saini answered |
Given: current I = 2.5 A
Inductance, L = 5H
Magnatic flux, φ=?
We know, φ = LI ⇒ 5 × 2.5 Wb = 12.5 Wb
Inductance, L = 5H
Magnatic flux, φ=?
We know, φ = LI ⇒ 5 × 2.5 Wb = 12.5 Wb
The current in self inductance L = 40 mH is to beincreased uniformly from 1 amp to 11 amp in 4 milliseconds. The e.m.f. induced in the inductorduring the process is [1990]- a)100 volt
- b)0.4 volt
- c)4.0 volt
- d)440 volt
Correct answer is option 'A'. Can you explain this answer?
The current in self inductance L = 40 mH is to beincreased uniformly from 1 amp to 11 amp in 4 milliseconds. The e.m.f. induced in the inductorduring the process is [1990]
a)
100 volt
b)
0.4 volt
c)
4.0 volt
d)
440 volt
|
Rajat Roy answered |
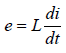
Given that L = 40 × 10–3 H,
di = 11 A – 1 A = 10 A
and dt = 4 × 10–3 s
di = 11 A – 1 A = 10 A
and dt = 4 × 10–3 s
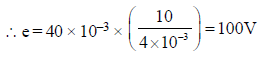
A coil of resistance 400Ω is placed in a magneticfield. If the magnetic flux φ(wb) linked with thecoil varies with time t (sec) as φ = 50t2 + 4. Thecurrent in the coil at t = 2 sec is : [2012]- a)0.5 A
- b)0.1 A
- c)2 A
- d)1 A
Correct answer is option 'A'. Can you explain this answer?
A coil of resistance 400Ω is placed in a magneticfield. If the magnetic flux φ(wb) linked with thecoil varies with time t (sec) as φ = 50t2 + 4. Thecurrent in the coil at t = 2 sec is : [2012]
a)
0.5 A
b)
0.1 A
c)
2 A
d)
1 A
|
Abhijeet Goyal answered |
According, to Faraday’s law of induction
Induced e.m.f.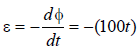
Induced e.m.f.
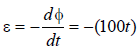
Induced current i at t = 2 sec.
Two coils of self inductances 2 mH and 8 mH areplaced so close together that the effective fluxin one coil is completely linked with the other.The mutual inductance between these coils is [2006]- a)6 mH
- b)4 mH
- c)16 mH
- d)10 mH
Correct answer is option 'B'. Can you explain this answer?
Two coils of self inductances 2 mH and 8 mH areplaced so close together that the effective fluxin one coil is completely linked with the other.The mutual inductance between these coils is [2006]
a)
6 mH
b)
4 mH
c)
16 mH
d)
10 mH
|
|
Ayush Sengupta answered |
Mutual Inductance of two coils
A magnetic field of 2 × 10–2 T acts at right anglesto a coil of area 100 cm2, with 50 turns. Theaverage e.m.f. induced in the coil is 0.1 V, when itis removed from the field in t sec. The value of t is- a)10 s
- b)0.1 s [1991]
- c)0.01 s
- d)1 s
Correct answer is option 'B'. Can you explain this answer?
A magnetic field of 2 × 10–2 T acts at right anglesto a coil of area 100 cm2, with 50 turns. Theaverage e.m.f. induced in the coil is 0.1 V, when itis removed from the field in t sec. The value of t is
a)
10 s
b)
0.1 s [1991]
c)
0.01 s
d)
1 s
|
|
Krish Chakraborty answered |
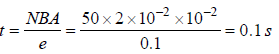
A conducting circular loop is placed in a uniform magnetic field, B = 0.025 T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1 mm s–1. The induced e.m.f. when the radius is 2 cm, is [2010]- a)2πμV
- b)πμV
- c)
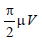
- d)2μV
Correct answer is option 'B'. Can you explain this answer?
A conducting circular loop is placed in a uniform magnetic field, B = 0.025 T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1 mm s–1. The induced e.m.f. when the radius is 2 cm, is [2010]
a)
2πμV
b)
πμV
c)
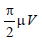
d)
2μV
|
|
Abhishek Desai answered |
Magnetic flux linked with the loop
When r = 2 cm, dr/dt = 1 mms-1
e = 0.025× π×2 ×2 ×10–2×10–3
= 0.100 × π× 10–5 = π × 10–6 V = πμV
= 0.100 × π× 10–5 = π × 10–6 V = πμV
Chapter doubts & questions for Electromagnetic Induction - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Electromagnetic Induction - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
NEET Past Year Papers
86 docs|146 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily