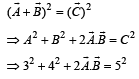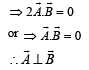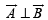All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Motion in a Plane for NEET Exam
Two boys are standing at the ends A and B of a ground where AB = a. The boy at B starts running in a direction perpendicular to AB with velocity v1. The boy at A starts running simultaneously with velocity v and catches the oth er boy in a time t, where t is [2005]- a)
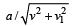 a /(v + v1)
a /(v + v1) - b)a /(v + v1)
- c)a /(v–v1)
- d)
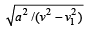
Correct answer is option 'D'. Can you explain this answer?
Two boys are standing at the ends A and B of a ground where AB = a. The boy at B starts running in a direction perpendicular to AB with velocity v1. The boy at A starts running simultaneously with velocity v and catches the oth er boy in a time t, where t is [2005]
a)
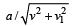 a /(v + v1)
a /(v + v1)b)
a /(v + v1)
c)
a /(v–v1)
d)
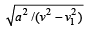
|
|
Vishal Kumar answered |

A stone is tied to a string of length ℓ and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u.
The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is [2004]- a)

- b)
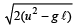
- c)
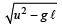
- d)
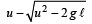
Correct answer is option 'B'. Can you explain this answer?
A stone is tied to a string of length ℓ and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u.
The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is [2004]
The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is [2004]
a)

b)
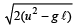
c)
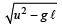
d)
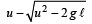

|
Adit Raj answered |
Are resultant vector nikal do..
DeltaV=Vf-Vi
option B aaega..
photo upload nhi ho rha hai warna me kr deta
The angle between two vectors of magnitude 12 and 18 units when their resultant is 24 units, is[1999]- a)63º 51´
- b)75º 52´
- c)82º 31´
- d)89º 16´
Correct answer is option 'B'. Can you explain this answer?
The angle between two vectors of magnitude 12 and 18 units when their resultant is 24 units, is[1999]
a)
63º 51´
b)
75º 52´
c)
82º 31´
d)
89º 16´

|
Snehal Shah answered |
We know that, R2 = A2 + B2 + 2 AB cosθ
(24)2 = (12)2 + (18)2 + 2(12)(18) cos θ
(24)2 = (12)2 + (18)2 + 2(12)(18) cos θ

For angles of projection of a projectile (45° – θ) and (45° + θ), the horizontal ranges described by the projectile are in the ratio of [2006]- a)1: 3
- b)1 : 2
- c)2 : 1
- d)1 : 1
Correct answer is option 'D'. Can you explain this answer?
For angles of projection of a projectile (45° – θ) and (45° + θ), the horizontal ranges described by the projectile are in the ratio of [2006]
a)
1: 3
b)
1 : 2
c)
2 : 1
d)
1 : 1

|
Arpita Tiwari answered |
(45º – θ) & (45º + θ) are complementary angles as 45º – θ + 45º + θ = 90º. We know that if angle of projection of two projectiles make complementary angles, their ranges are equal.
In this case also, the range will be same. So the ratio is 1 : 1.
In this case also, the range will be same. So the ratio is 1 : 1.
If a vector 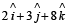 is perpendicular to the vector
is perpendicular to the vector 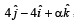 then the value of α is [2005]
then the value of α is [2005]- a)1/2
- b)–1/2
- c)1
- d)–1
Correct answer is option 'B'. Can you explain this answer?
If a vector 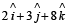 is perpendicular to the vector
is perpendicular to the vector 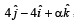 then the value of α is [2005]
then the value of α is [2005]
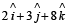 is perpendicular to the vector
is perpendicular to the vector 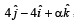 then the value of α is [2005]
then the value of α is [2005]a)
1/2
b)
–1/2
c)
1
d)
–1

|
Shounak Nair answered |
For two vectors to be perpendicular to each other
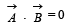
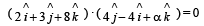
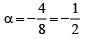
The cir cular motion of a particle with constant speed is [2005]- a)periodic but not simple harmonic
- b)simple harmonic but not periodic
- c)periodic and simple harmonic
- d)neither periodic nor simple harmonic
Correct answer is option 'A'. Can you explain this answer?
The cir cular motion of a particle with constant speed is [2005]
a)
periodic but not simple harmonic
b)
simple harmonic but not periodic
c)
periodic and simple harmonic
d)
neither periodic nor simple harmonic

|
Rajat Roy answered |
In circular motion of a particle with constant speed, particle repeats its motion after a regular interval of time but does not oscillate about a fixed point. So, motion of particle is periodic but not simple harmonic.
The vector sum of two forces is perpendicular to their vector differences. In that case, the forces[2003]- a)can not be pr edicted
- b)are equal to each other
- c)are equal to each other in magnitude
- d)are not equal to each other in magnitude
Correct answer is option 'C'. Can you explain this answer?
The vector sum of two forces is perpendicular to their vector differences. In that case, the forces[2003]
a)
can not be pr edicted
b)
are equal to each other
c)
are equal to each other in magnitude
d)
are not equal to each other in magnitude
|
|
Satakshi Kumari answered |

If the angle between the vectors 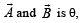 the value of the product
the value of the product 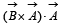 is equal to [2005]
is equal to [2005]- a)BA2 sinθ
- b)BA2 cosθ
- c)BA2 sinθ cosθ
- d)zero
Correct answer is option 'D'. Can you explain this answer?
If the angle between the vectors 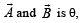 the value of the product
the value of the product 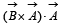 is equal to [2005]
is equal to [2005]
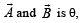 the value of the product
the value of the product 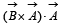 is equal to [2005]
is equal to [2005]a)
BA2 sinθ
b)
BA2 cosθ
c)
BA2 sinθ cosθ
d)
zero
|
|
Satakshi Kumari answered |
Direction of vector product of 2 vector is perpendicular to both vector
means if A×B=C then C is perpendicular to A as well as B .
now apply this concept on your question
let B×A=C ,
A.(B×C)=A.C
where C is perpendicular to both vector A&B
so angle b/w C and A is 90
A.C=0
means if A×B=C then C is perpendicular to A as well as B .
now apply this concept on your question
let B×A=C ,
A.(B×C)=A.C
where C is perpendicular to both vector A&B
so angle b/w C and A is 90
A.C=0
A particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is [2011]- a)15 m/s2
- b)25 m/s2
- c)36 m/s2
- d)5 m/s2
Correct answer is option 'D'. Can you explain this answer?
A particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is [2011]
a)
15 m/s2
b)
25 m/s2
c)
36 m/s2
d)
5 m/s2
|
|
Simran Nair answered |
To find the speed of the particle, we can use the formula:
speed = distance / time
Since the particle moves in a circle, the distance it travels in one complete revolution is the circumference of the circle, which is 2πr, where r is the radius of the circle.
Given that the radius is 5 cm, the distance the particle travels in one complete revolution is:
distance = 2π(5 cm) = 10π cm
Since the time period is 0.2 seconds, the time it takes for the particle to complete one revolution is 0.2 seconds.
Therefore, the speed of the particle is:
speed = distance / time = (10π cm) / (0.2 s) = 50π cm/s
So, the speed of the particle is 50π cm/s.
speed = distance / time
Since the particle moves in a circle, the distance it travels in one complete revolution is the circumference of the circle, which is 2πr, where r is the radius of the circle.
Given that the radius is 5 cm, the distance the particle travels in one complete revolution is:
distance = 2π(5 cm) = 10π cm
Since the time period is 0.2 seconds, the time it takes for the particle to complete one revolution is 0.2 seconds.
Therefore, the speed of the particle is:
speed = distance / time = (10π cm) / (0.2 s) = 50π cm/s
So, the speed of the particle is 50π cm/s.
The resultant of 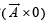 will be equal to [1992]
will be equal to [1992]- a)zero
- b)A
- c)zero vector
- d)unit vector
Correct answer is option 'C'. Can you explain this answer?
The resultant of 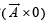 will be equal to [1992]
will be equal to [1992]
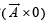 will be equal to [1992]
will be equal to [1992]a)
zero
b)
A
c)
zero vector
d)
unit vector

|
Mehul Iyer answered |
When a vector is multiplied with a scalar, the result is a vector.
A particle starting from the origin (0, 0) moves in a straight line in the (x, y) plane. Its coordinates at a later time are 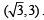 . The path of the particle makes with the x-axis an angle of [2007]
. The path of the particle makes with the x-axis an angle of [2007]- a)45o
- b)60o
- c)0o
- d)30o
Correct answer is option 'B'. Can you explain this answer?
A particle starting from the origin (0, 0) moves in a straight line in the (x, y) plane. Its coordinates at a later time are 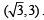 . The path of the particle makes with the x-axis an angle of [2007]
. The path of the particle makes with the x-axis an angle of [2007]
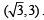 . The path of the particle makes with the x-axis an angle of [2007]
. The path of the particle makes with the x-axis an angle of [2007]a)
45o
b)
60o
c)
0o
d)
30o

|
Dipanjan Mehta answered |
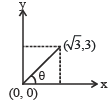
Let θ be the angle which the particle makes with x axis.
From figure,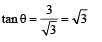
From figure,
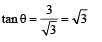
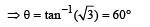
From a 10 m high building a stone 'A' is dropped, and simultaneously another identical stone 'B' is thrown horizontally with an initial speed of 5 ms–1. Which one of the following statements is true?[2002]- a)It is not possible to calculate which one of the two stones will reach the ground first
- b)Both th e stones ('A' an d 'B') will r each the ground simultaneously
- c)'A' stone reaches the ground earlier than 'B'
- d)'B' stone reaches the ground earlier than 'A'
Correct answer is option 'B'. Can you explain this answer?
From a 10 m high building a stone 'A' is dropped, and simultaneously another identical stone 'B' is thrown horizontally with an initial speed of 5 ms–1. Which one of the following statements is true?[2002]
a)
It is not possible to calculate which one of the two stones will reach the ground first
b)
Both th e stones ('A' an d 'B') will r each the ground simultaneously
c)
'A' stone reaches the ground earlier than 'B'
d)
'B' stone reaches the ground earlier than 'A'

|
Maheshwar Saini answered |

h and g are same for both the balls, so time of fall ‘t’ will also be the same for both of them (h is vertical height]
Two particles of mass M and m are moving in a circle of radii R and r. If their time-periods are same, what will be the ratio of their linear velocities? [2001]- a)MR : mr
- b)M : m
- c)R : r
- d)1 : 1
Correct answer is option 'C'. Can you explain this answer?
Two particles of mass M and m are moving in a circle of radii R and r. If their time-periods are same, what will be the ratio of their linear velocities? [2001]
a)
MR : mr
b)
M : m
c)
R : r
d)
1 : 1

|
Devansh Mehra answered |
Linear velocity v = rω
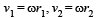
[ω is same in both cases because time period is same]
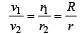
A bullet is fired from a gun with a speed of 1000 m/s in order to hit a target 100 m away. At what height above the target should the gun be aimed? (The resistance of air is negligible and g = 10 m/s2) [1995]- a)5 cm
- b)10 cm
- c)15 cm
- d)20 cm
Correct answer is option 'A'. Can you explain this answer?
A bullet is fired from a gun with a speed of 1000 m/s in order to hit a target 100 m away. At what height above the target should the gun be aimed? (The resistance of air is negligible and g = 10 m/s2) [1995]
a)
5 cm
b)
10 cm
c)
15 cm
d)
20 cm

|
Raghav Khanna answered |
Speed of the bullet (v) = 1000 m/s and horizontal distance of the target (s) = 100 m.
Time taken to cover the horizontal distance
Time taken to cover the horizontal distance
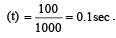
During this time, the bullet will fall down vertically due to gravitational acceleration.
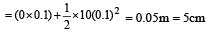
A missile is fired for maximum range with an initial velocity of 20 m/s. If g = 10 m/s2, the range of the missile is [2011]- a)40 m
- b)50 m
- c)60 m
- d)20 m
Correct answer is option 'A'. Can you explain this answer?
A missile is fired for maximum range with an initial velocity of 20 m/s. If g = 10 m/s2, the range of the missile is [2011]
a)
40 m
b)
50 m
c)
60 m
d)
20 m

|
Ashwini Khanna answered |
For maximum range, the angle of projection, θ = 45°.
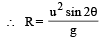
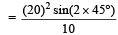
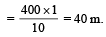
A stone tied to the end of a string of 1 m long is whirled in a horizontal circle with a constant speed. If the stone makes 22 revolutions in 44 seconds, what is the magnitude and direction of acceleration of the stone? [2005]- a)π2 ms–2 and direction along the radius towards the centre
- b)π2 ms–2 and direction along the radius away from the centre
- c)π2 ms–2 and direction along the tangent to the circle
- d)π2/4 ms–2 and direction along the radius towards the centre
Correct answer is option 'A'. Can you explain this answer?
A stone tied to the end of a string of 1 m long is whirled in a horizontal circle with a constant speed. If the stone makes 22 revolutions in 44 seconds, what is the magnitude and direction of acceleration of the stone? [2005]
a)
π2 ms–2 and direction along the radius towards the centre
b)
π2 ms–2 and direction along the radius away from the centre
c)
π2 ms–2 and direction along the tangent to the circle
d)
π2/4 ms–2 and direction along the radius towards the centre
|
|
Puja Chakraborty answered |
First, we need to find the angular velocity (ω) of the stone:
Number of revolutions = 22
Time taken = 44 seconds
Therefore, frequency (f) = number of revolutions / time taken = 22/44 = 0.5 Hz
Angular velocity (ω) = 2πf = 2π(0.5) = π rad/s
Next, we can use the formula for centripetal acceleration (ac) to find the magnitude of acceleration:
ac = ω2r
where r is the radius of the circle (1 m).
ac = (π)2(1) = 9.87 m/s2
The direction of acceleration is towards the center of the circle (i.e. radially inward).
Therefore, the magnitude of acceleration of the stone is 9.87 m/s2 and the direction is radially inward.
Number of revolutions = 22
Time taken = 44 seconds
Therefore, frequency (f) = number of revolutions / time taken = 22/44 = 0.5 Hz
Angular velocity (ω) = 2πf = 2π(0.5) = π rad/s
Next, we can use the formula for centripetal acceleration (ac) to find the magnitude of acceleration:
ac = ω2r
where r is the radius of the circle (1 m).
ac = (π)2(1) = 9.87 m/s2
The direction of acceleration is towards the center of the circle (i.e. radially inward).
Therefore, the magnitude of acceleration of the stone is 9.87 m/s2 and the direction is radially inward.
A body of mass 0.4 kg is whi rled in a vertical circle making 2 rev/sec. If the radius of the circle is 1.2 m, then tension in the string when the body is at th e top of the circle, is [1999]- a)41.56 N
- b)89.86 N
- c)109.86 N
- d)115.86 N.
Correct answer is option 'A'. Can you explain this answer?
A body of mass 0.4 kg is whi rled in a vertical circle making 2 rev/sec. If the radius of the circle is 1.2 m, then tension in the string when the body is at th e top of the circle, is [1999]
a)
41.56 N
b)
89.86 N
c)
109.86 N
d)
115.86 N.

|
Raghav Khanna answered |
Given : Mass (m) = 0.4 kg Its frequency (n) = 2 rev/sec Radius (r) =1.2 m.
We know that linear velocity of the body (v) = ωr = (2πn)r
= 2 × 3.14 × 1.2 × 2 = 15.08 m/s.
Therefore, tension in the string when the body is at the top of the circle (T)
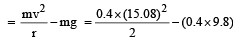
= 45.78 - 3.92 = 41.56 N
A bus is moving on a straight road towards north with a uniform speed of 50 km/hour turns through 90°. If the speed remains unchanged after turning, the increase in the velocity of bus in the turning process is [1989]- a)70.7 km/hour along south-west direction
- b)zero
- c)50 km/hour along west
- d)70.7 km/hour along north-west direction.
Correct answer is option 'A'. Can you explain this answer?
A bus is moving on a straight road towards north with a uniform speed of 50 km/hour turns through 90°. If the speed remains unchanged after turning, the increase in the velocity of bus in the turning process is [1989]
a)
70.7 km/hour along south-west direction
b)
zero
c)
50 km/hour along west
d)
70.7 km/hour along north-west direction.

|
Soumya Ahuja answered |
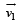 = 50 km h-1 due North;
= 50 km h-1 due North;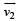 = 50 km h-1 due West. Angle between
= 50 km h-1 due West. Angle between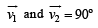
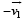 = 50 km h-1 due South
= 50 km h-1 due South∴ Change in velocity
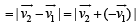
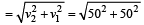 = 70.7 km/h
= 70.7 km/hThe direction of this change in velocity is in South-West.
When milk is churned, cream gets separated due to[1991]- a)centripetal force
- b)centrifugal force
- c)frictional force
- d)gravitational force
Correct answer is option 'B'. Can you explain this answer?
When milk is churned, cream gets separated due to[1991]
a)
centripetal force
b)
centrifugal force
c)
frictional force
d)
gravitational force

|
Mahi Shah answered |
Cream gets separated from a churned milk due to centrifugal force.
Six vectors, 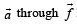 have the magnitudes and directions indicated in the figure. Which of the following statements is true? [2010]
have the magnitudes and directions indicated in the figure. Which of the following statements is true? [2010]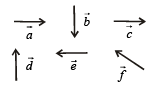
- a)
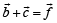
- b)
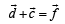
- c)
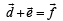
- d)
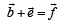
Correct answer is option 'C'. Can you explain this answer?
Six vectors, 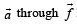 have the magnitudes and directions indicated in the figure. Which of the following statements is true? [2010]
have the magnitudes and directions indicated in the figure. Which of the following statements is true? [2010]
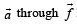 have the magnitudes and directions indicated in the figure. Which of the following statements is true? [2010]
have the magnitudes and directions indicated in the figure. Which of the following statements is true? [2010]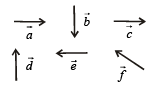
a)
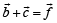
b)
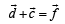
c)
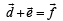
d)
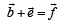

|
Mahesh Saini answered |
Using the law of vector addition, 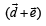 is as shown in the fig.
is as shown in the fig.
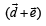 is as shown in the fig.
is as shown in the fig.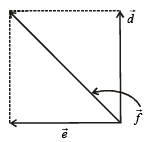

A ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving in a horizontal circle. The string will break if the tension is more than 25 N. What is the maximum speed with which the ball can be moved? [1998]- a)14 m/s
- b)3 m/s
- c)5 m/s
- d)3.92 m/s
Correct answer is option 'A'. Can you explain this answer?
A ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving in a horizontal circle. The string will break if the tension is more than 25 N. What is the maximum speed with which the ball can be moved? [1998]
a)
14 m/s
b)
3 m/s
c)
5 m/s
d)
3.92 m/s
|
|
Maulik Chakraborty answered |
Given data:
Mass of the ball, m = 0.25 kg
Length of the string, l = 1.96 m
Maximum tension, T = 25 N
Formula:
The centripetal force required to keep the ball moving in a circle is provided by the tension in the string. This can be calculated using the formula:
T = mv^2 / r
where T is the tension, m is the mass of the ball, v is the speed of the ball, and r is the radius of the circle (which is equal to the length of the string).
Calculations:
Given that the maximum tension is 25 N, we can rearrange the formula to find the maximum speed:
25 = 0.25 * v^2 / 1.96
v^2 = 25 * 1.96 / 0.25
v^2 = 196
v = √196
v = 14 m/s
Therefore, the maximum speed with which the ball can be moved is 14 m/s. Hence, option 'A' is correct.
Mass of the ball, m = 0.25 kg
Length of the string, l = 1.96 m
Maximum tension, T = 25 N
Formula:
The centripetal force required to keep the ball moving in a circle is provided by the tension in the string. This can be calculated using the formula:
T = mv^2 / r
where T is the tension, m is the mass of the ball, v is the speed of the ball, and r is the radius of the circle (which is equal to the length of the string).
Calculations:
Given that the maximum tension is 25 N, we can rearrange the formula to find the maximum speed:
25 = 0.25 * v^2 / 1.96
v^2 = 25 * 1.96 / 0.25
v^2 = 196
v = √196
v = 14 m/s
Therefore, the maximum speed with which the ball can be moved is 14 m/s. Hence, option 'A' is correct.
A boat which has a speed of 5 km/hr in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. The velocity of the river water in km/hr is [1998, 2000]- a)3
- b)4
- c)
- d)1
Correct answer is option 'A'. Can you explain this answer?
A boat which has a speed of 5 km/hr in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. The velocity of the river water in km/hr is [1998, 2000]
a)
3
b)
4
c)
d)
1

|
Ayush Choudhury answered |
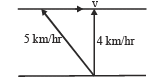
Speed along the shortest path
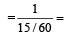 4 km/hr
4 km/hrSpeed of water 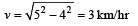
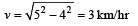
A car runs at a constant speed on a circular track of radius 100 m, taking 62.8 seconds in every circular loop. The average velocity and average speed for each circular loop respectively, is [2006]- a)0, 10 m/s
- b)10 m/s, 10 m/s
- c)10 m/s, 0
- d)0, 0
Correct answer is option 'A'. Can you explain this answer?
A car runs at a constant speed on a circular track of radius 100 m, taking 62.8 seconds in every circular loop. The average velocity and average speed for each circular loop respectively, is [2006]
a)
0, 10 m/s
b)
10 m/s, 10 m/s
c)
10 m/s, 0
d)
0, 0
|
|
Vivek Godara answered |
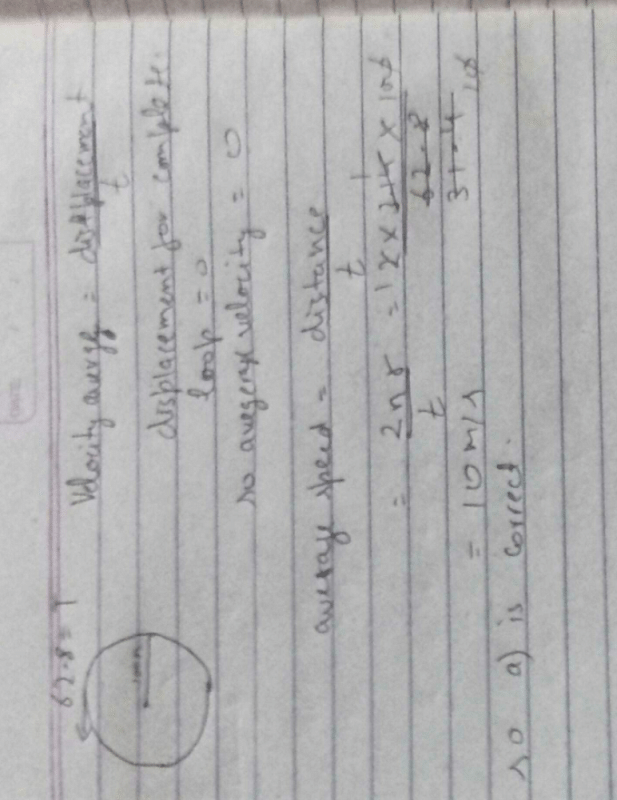
A stone tied with a string, is rotated in a vertical circle. The minimum speed with which the string has to be rotated [1999]- a)is independent of the mass of the stone
- b)is independent of the length of the str ing
- c)decreases with increasing mass of the stone
- d)decreases with in creasing length of the string
Correct answer is option 'A'. Can you explain this answer?
A stone tied with a string, is rotated in a vertical circle. The minimum speed with which the string has to be rotated [1999]
a)
is independent of the mass of the stone
b)
is independent of the length of the str ing
c)
decreases with increasing mass of the stone
d)
decreases with in creasing length of the string
|
|
Palak Basu answered |
The Minimum Speed Required for a Stone in Vertical Circle
The problem is about finding the minimum speed required for a stone attached to a string to move in a vertical circle. The answer is option 'A', which means that the minimum speed is independent of the mass of the stone. Here's how we can arrive at this conclusion:
Force Analysis
When the stone is moving in a vertical circle, it experiences two types of forces: tension and gravity. At the top of the circle, the tension force is directed downwards, while the gravity force is directed downwards as well. At the bottom of the circle, the tension force is directed upwards, while the gravity force is directed downwards as well.
Minimum Speed
To keep the stone moving in a circular path, the tension force must be larger than the gravity force at all points in the circle. Therefore, the minimum speed required for the stone to move in a vertical circle is the speed that makes the tension force just equal to the gravity force at the top of the circle.
Mathematical Analysis
Let's assume that the mass of the stone is m, the length of the string is L, and the speed of the stone is v. Then, the tension force T and the gravity force mg are given by:
T = mv^2/L
mg = m g
where g is the acceleration due to gravity. Equating these two forces at the top of the circle, we get:
mv^2/L = m g
which simplifies to:
v^2 = g L
Therefore, the minimum speed required for the stone to move in a vertical circle is:
v = √(g L)
Conclusion
The minimum speed required for a stone attached to a string to move in a vertical circle is independent of the mass of the stone. This is because the mass of the stone cancels out in the equation for the minimum speed. Therefore, the answer is option 'A'.
The problem is about finding the minimum speed required for a stone attached to a string to move in a vertical circle. The answer is option 'A', which means that the minimum speed is independent of the mass of the stone. Here's how we can arrive at this conclusion:
Force Analysis
When the stone is moving in a vertical circle, it experiences two types of forces: tension and gravity. At the top of the circle, the tension force is directed downwards, while the gravity force is directed downwards as well. At the bottom of the circle, the tension force is directed upwards, while the gravity force is directed downwards as well.
Minimum Speed
To keep the stone moving in a circular path, the tension force must be larger than the gravity force at all points in the circle. Therefore, the minimum speed required for the stone to move in a vertical circle is the speed that makes the tension force just equal to the gravity force at the top of the circle.
Mathematical Analysis
Let's assume that the mass of the stone is m, the length of the string is L, and the speed of the stone is v. Then, the tension force T and the gravity force mg are given by:
T = mv^2/L
mg = m g
where g is the acceleration due to gravity. Equating these two forces at the top of the circle, we get:
mv^2/L = m g
which simplifies to:
v^2 = g L
Therefore, the minimum speed required for the stone to move in a vertical circle is:
v = √(g L)
Conclusion
The minimum speed required for a stone attached to a string to move in a vertical circle is independent of the mass of the stone. This is because the mass of the stone cancels out in the equation for the minimum speed. Therefore, the answer is option 'A'.
If a body A of mass M is thrown with velocity v at an angle of 30° to the horizontal and another body B of the same mass is thrown with the same speed at an angle of 60° to the horizontal, the ratio of horizontal range of A to B will be [1992]- a)1 : 3
- b)1 : 1
- c)
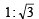
- d)
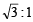
Correct answer is option 'B'. Can you explain this answer?
If a body A of mass M is thrown with velocity v at an angle of 30° to the horizontal and another body B of the same mass is thrown with the same speed at an angle of 60° to the horizontal, the ratio of horizontal range of A to B will be [1992]
a)
1 : 3
b)
1 : 1
c)
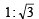
d)
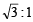

|
Ritika Khanna answered |
Horizontal range is same wh en an gle of projection with the horizonatal is θ and (90° – θ).
A ball whose kinetic energy is E, is thrown at an angle of 45º with the horizontal. Its kinetic energy at the highest point of its flight will be [1997]- a)E
- b)
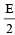
- c)
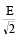
- d)0
Correct answer is option 'B'. Can you explain this answer?
A ball whose kinetic energy is E, is thrown at an angle of 45º with the horizontal. Its kinetic energy at the highest point of its flight will be [1997]
a)
E
b)
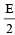
c)
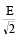
d)
0

|
Shivani Tiwari answered |
Kinetic energy is E
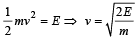
Velocity at highest point
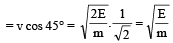
[∴ at the highest point there is only horizontal velocity]
K.E. at highest point 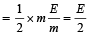
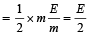
A body is whirled in a horizontal circle of radius 20 cm. It has an angular velocity of 10 rad/s.What is its linear velocity at any point on circular path[1996]- a)
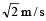
- b)2 m/s
- c)10 m/s
- d)20 m/s
Correct answer is option 'B'. Can you explain this answer?
A body is whirled in a horizontal circle of radius 20 cm. It has an angular velocity of 10 rad/s.What is its linear velocity at any point on circular path[1996]
a)
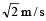
b)
2 m/s
c)
10 m/s
d)
20 m/s

|
Shivani Rane answered |
Radius of circular path = 20 cm = 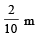
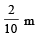
Angular speed of body = 10 rad/s
Linear velocity = radius × Angular speed
A block of mass m is in contact with the cart C as shown in the Figure. [2010]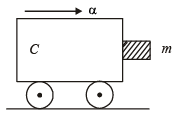 The coefficient of static friction between the block and the cart is μ . The acceleration α of the cart that will prevent the block from falling satisfies:
The coefficient of static friction between the block and the cart is μ . The acceleration α of the cart that will prevent the block from falling satisfies:- a)
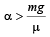
- b)
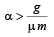
- c)
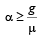
- d)
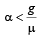
Correct answer is option 'C'. Can you explain this answer?
A block of mass m is in contact with the cart C as shown in the Figure. [2010]

The coefficient of static friction between the block and the cart is μ . The acceleration α of the cart that will prevent the block from falling satisfies:
a)
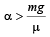
b)
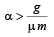
c)
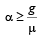
d)
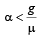

|
Ayush Chavan answered |
Forces acting on the block are as shown in the fig. Normal reaction N is provided by the force mα due to acceleration α
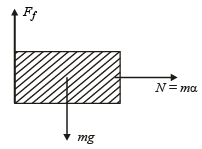
∴ N = mα For the block not to fall, frictional force,
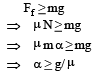
A particle moves along a circle of radius 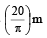 with constant tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is [2003]
with constant tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is [2003]- a)40πm/s2
- b)40 m/s2
- c)640πm/s2
- d)160πm/s2
Correct answer is option 'B'. Can you explain this answer?
A particle moves along a circle of radius 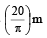 with constant tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is [2003]
with constant tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is [2003]
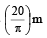 with constant tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is [2003]
with constant tangential acceleration. If the velocity of the particle is 80 m/s at the end of the second revolution after motion has begun, the tangential acceleration is [2003]a)
40πm/s2
b)
40 m/s2
c)
640πm/s2
d)
160πm/s2

|
Abhijeet Goyal answered |
Circumference 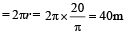
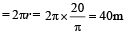
Distance travelled in 2 revolutions = 2 × 40 = 80 m
Initial velocity = u = 0
Final velocity v = 80m/sec
Applying the formula, v2 = u2 + 2as
(80)2 = 02 + 2 × a × 80 ⇒ a = 40 m/sec2
Initial velocity = u = 0
Final velocity v = 80m/sec
Applying the formula, v2 = u2 + 2as
(80)2 = 02 + 2 × a × 80 ⇒ a = 40 m/sec2
Which of the following is not a vector quantity?- a)sp eed
- b)velocity [1995]
- c)torque
- d)displacement
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a vector quantity?
a)
sp eed
b)
velocity [1995]
c)
torque
d)
displacement

|
Ruchi Chopra answered |
A vector quantity has both magnitude and direction. In the given options, speed has only magnitude, therefore, it is non- vector or scalar quantity.
Two projectiles ar e fir ed from t he same point with the same speed at angles of projection 60º and 30º respectively. Which one of the following is true? [2000]- a)Their maximum height will be same
- b)Their range will be same
- c)Their landing velocity will be same
- d)Their time of flight will be same
Correct answer is option 'B'. Can you explain this answer?
Two projectiles ar e fir ed from t he same point with the same speed at angles of projection 60º and 30º respectively. Which one of the following is true? [2000]
a)
Their maximum height will be same
b)
Their range will be same
c)
Their landing velocity will be same
d)
Their time of flight will be same

|
Mahi Shah answered |
Given, u1 = u2 = u, θ1 = 60º, θ2 = 30º In 1st case, we know that range
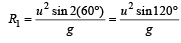
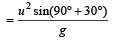

In 2nd case, when θ2 = 30º, then
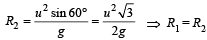
[we get same value of ranges].
Th e position vector of a par ticle is 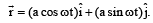 . The velocity of the particle is [1995]
. The velocity of the particle is [1995]- a)directed towards the origin
- b)directed away from the origin
- c)par allel to the position vector
- d)per pendicular to the position vector
Correct answer is option 'D'. Can you explain this answer?
Th e position vector of a par ticle is 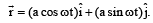 . The velocity of the particle is [1995]
. The velocity of the particle is [1995]
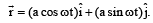 . The velocity of the particle is [1995]
. The velocity of the particle is [1995]a)
directed towards the origin
b)
directed away from the origin
c)
par allel to the position vector
d)
per pendicular to the position vector

|
Anu Bajaj answered |
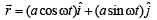

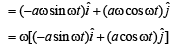
Slope of position vector = 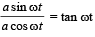 & slope of velocity vector
& slope of velocity vector
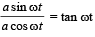 & slope of velocity vector
& slope of velocity vector
∴ velocity is perpendicular to the displacement.
A person swims in a river aiming to reach exactly opposite point on the bank of a river. His speed of swimming is 0.5 m/s at an angle 120º with the direction of flow of water. The speed of water in stream is [1999]- a)1.0 m/s
- b)0.5 m/s
- c)0.25 m/s
- d)0.43 m/s.
Correct answer is option 'C'. Can you explain this answer?
A person swims in a river aiming to reach exactly opposite point on the bank of a river. His speed of swimming is 0.5 m/s at an angle 120º with the direction of flow of water. The speed of water in stream is [1999]
a)
1.0 m/s
b)
0.5 m/s
c)
0.25 m/s
d)
0.43 m/s.

|
Prisha Singh answered |
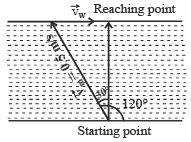
Velocity of person 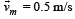
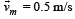
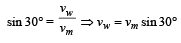
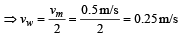
The maximum range of a gun of horizontal terrain is 16 km. If g = 10 ms–2, then muzzle velocity of a shell must be [1990]- a)160 ms–1
- b)

- c)400 ms–1
- d)800 ms–1
Correct answer is option 'C'. Can you explain this answer?
The maximum range of a gun of horizontal terrain is 16 km. If g = 10 ms–2, then muzzle velocity of a shell must be [1990]
a)
160 ms–1
b)

c)
400 ms–1
d)
800 ms–1

|
Shivani Rane answered |
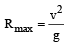 = 16000 [16km = 16000m]
= 16000 [16km = 16000m]or v = (16000g )½ = (16000 x10)½
= 400 ms –1
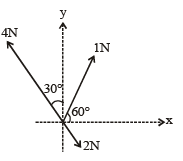 Three forces acting on a body are shown in the figure. To have the resultant force only along the y- direction, the magnitude of the minimum additional force needed is: [2008]
Three forces acting on a body are shown in the figure. To have the resultant force only along the y- direction, the magnitude of the minimum additional force needed is: [2008]- a)0.5 N
- b)1.5 N
- c)

- d)
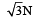
Correct answer is option 'A'. Can you explain this answer?

Three forces acting on a body are shown in the figure. To have the resultant force only along the y- direction, the magnitude of the minimum additional force needed is: [2008]
a)
0.5 N
b)
1.5 N
c)

d)
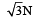

|
Dipanjan Mehta answered |
Th e componen ts of 1N and 2N forces along + x axis = 1 cos60° + 2 sin30°
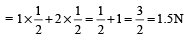

The component of 4 N force along –x-axis
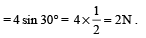
Therefore, if a force of 0.5N is applied along + x-axis, the resultant force along x-axis will become zero and the resultant force will be obtained only along y-axis.
Chapter doubts & questions for Motion in a Plane - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Motion in a Plane - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily
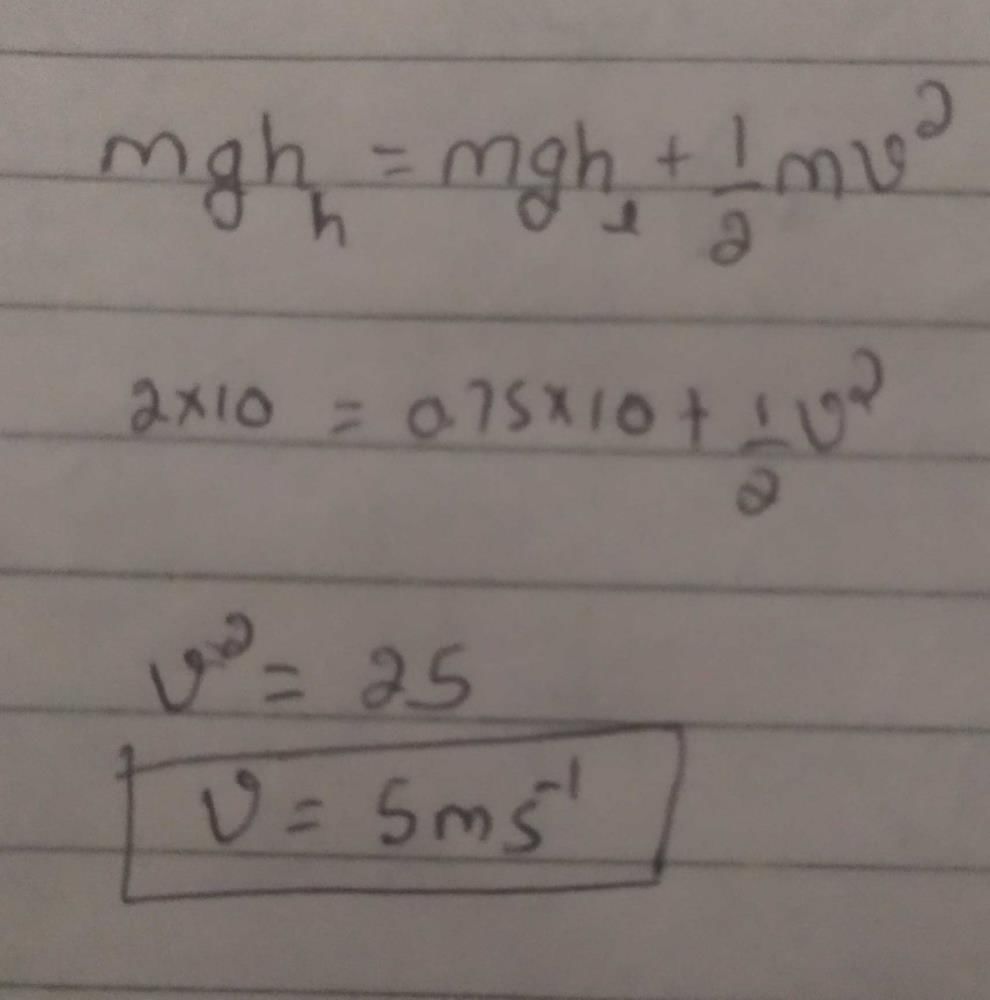

 are such that
are such that 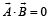 and
and 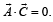 Then the vector parallel to
Then the vector parallel to 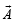 is [NEET Kar. 2013]
is [NEET Kar. 2013]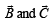
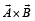
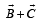
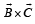

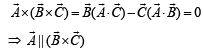
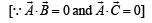
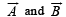 are two vectors and θ is the angle between them, if
are two vectors and θ is the angle between them, if 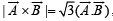 , the valueof θ is[2007]
, the valueof θ is[2007]
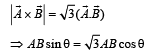
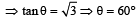


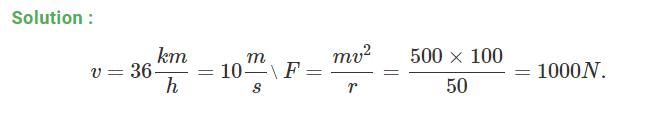
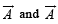 is θ. The value of the triple product
is θ. The value of the triple product 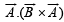 is [1989]
is [1989]
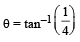

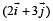 and acceleration
and acceleration 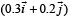 . The magnitude of velocity after 10 seconds will be : [2012]
. The magnitude of velocity after 10 seconds will be : [2012] 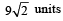
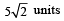
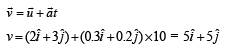
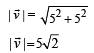
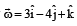 and position vector
and position vector  [1999]
[1999]
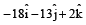
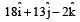
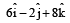
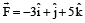 acting at the point
acting at the point 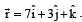 . [1997]
. [1997]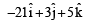
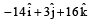

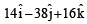

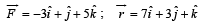
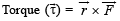
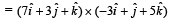
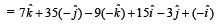
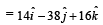
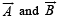 are such that
are such that 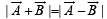 The angle between the two vectors is [1991, 1996, 2001, 2006]
The angle between the two vectors is [1991, 1996, 2001, 2006]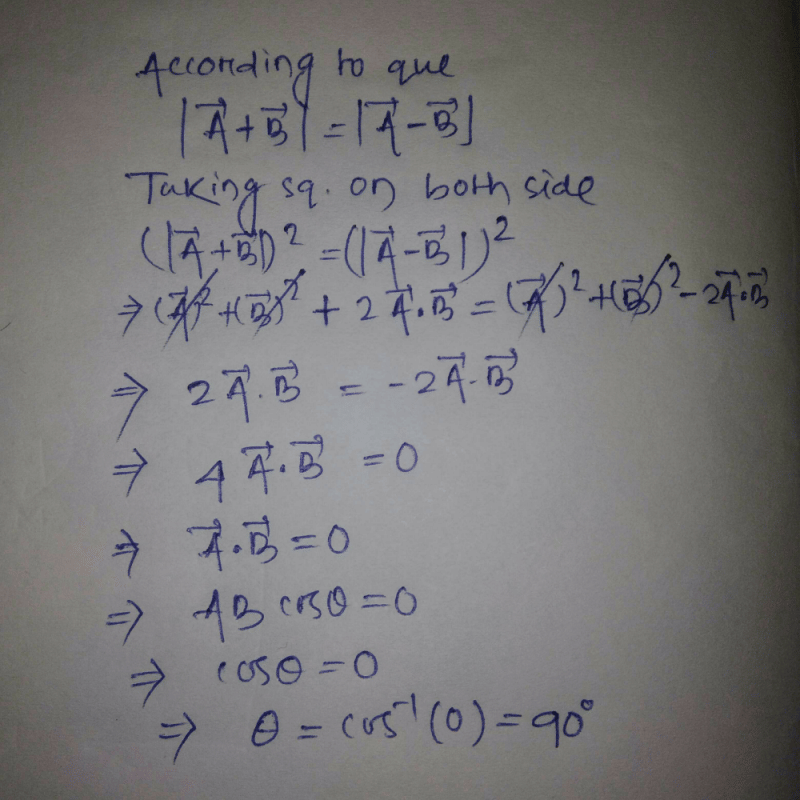
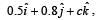 , the value of c is [1999]
, the value of c is [1999]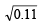
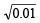
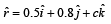
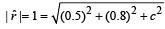
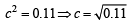
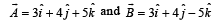 will be
will be
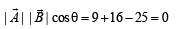
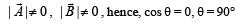
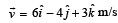 under the in fluence of a constant force
under the in fluence of a constant force 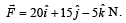 The instantaneous power applied to the particle is [2000]
The instantaneous power applied to the particle is [2000]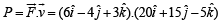
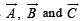 are 3, 4 and 5 units respectively. If
are 3, 4 and 5 units respectively. If 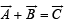 , thenthe angle between
, thenthe angle between 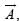 and
and  is [1988]
is [1988]