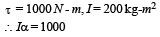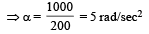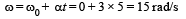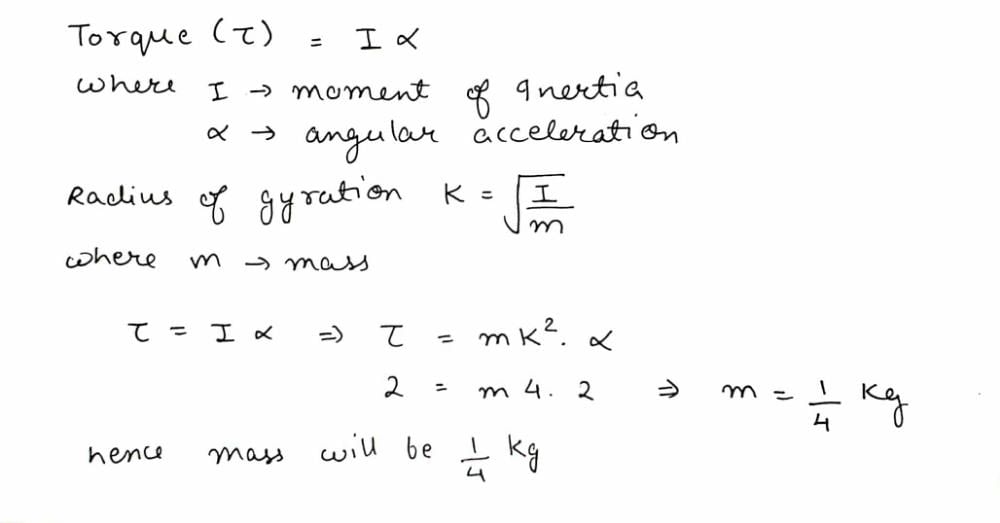All questions of System of Particles and Rotational Motion for NEET Exam
The centre of mass of a body is locateda)outside the systemb)inside or outside the systemc)inside the systemd)at the centre of systemCorrect answer is option 'B'. Can you explain this answer?
|
|
Suresh Iyer answered |
Example
(i) Centre of mass of a uniform rod lies at its geometrical centre which lies within the rod
(ii) Centre of mass of a uniform ring lies at its geometrical centre which lies outside the ring.
Can you explain the answer of this question below:Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
- A:
10 m/s
- B:
5 m/s
- C:
15 m/s
- D:
20 m/s
The answer is a.
Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
10 m/s
5 m/s
15 m/s
20 m/s

|
EduRev JEE answered |
Velocity of lighter block (v1) = 0m/s
Velocity of centre of mass,
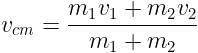
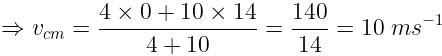
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
- a)Is zero
- b)Remains constant
- c)Goes on increasing
- d)Goes on decreasing
Correct answer is option 'B'. Can you explain this answer?
|
|
Krishna Iyer answered |
L = mv×y
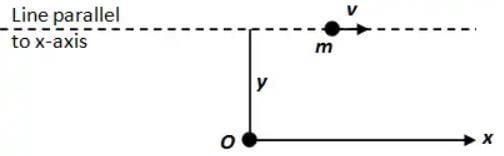
⇒ L = constant
A person standing on a rotating platform with his hands lowered outstretches his arms. The angular momentum of the person- a)becomes zero
- b)decreases
- c)remains constant
- d)inreases
Correct answer is option 'C'. Can you explain this answer?
|
|
Suresh Reddy answered |
here outstretching the hands means internal forces are working.. so moment of inertia increases in this case and to make angular momentum constant when angular velocity decreases.
There are two objects of masses 1 kg and 2 kg located at (1, 2) and (-1, 3) respectively. The coordinates of the centre of mass are- a)( 2, -1 )
- b)( 8/3 ,-1/3 )
- c)( -1/3 , 8/3 )
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
|
|
Riya Banerjee answered |
Body B has mass of 2kg and location (-1,3)
(1+2) xc = (1 * 1) + (2 * -1)
xc = -1/3
mcyc = m1y1 + m2y2
(1 + 2) yc = (1 * 2) + (2 * 3)
yc= 8/3
A solid sphere, a hollow sphere and a ring are released from top of an inclined plane (frictionless) so that they slide down the plane. Then maximum acceleration down the plane is for (no rolling) [AIEEE 2002]- a)Solid sphere
- b)Hollow sphere
- c)Ring
- d)All same
Correct answer is option 'D'. Can you explain this answer?
|
|
Preeti Iyer answered |
The moment of inertia of two spheres of equal masses is equal. If one of the spheres is solid of radius  m and the other is a hollow sphere. What is the radius of the hollow sphere?
m and the other is a hollow sphere. What is the radius of the hollow sphere?- a)5 m
- b)√3 m
- c)3√3 m
- d)3 m
Correct answer is option 'C'. Can you explain this answer?
 m and the other is a hollow sphere. What is the radius of the hollow sphere?
m and the other is a hollow sphere. What is the radius of the hollow sphere?

|
Sushil Kumar answered |
moment of inertia of hollow sphere Ih =2/3MR2
given mass of solid sphere =√45 kg.
Is=Ih
2MR2/5=2MR2/3
given their masses are equal 2 (√45)2/5= 2 R2/3
45/5=R2/3
9=R2/3
9×3=R2
27=R2
√27=R
√3×9=R
3√3 m=R.
A right triangular plate ABC of mass m is free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is : 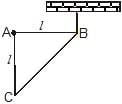
- a)
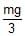
- b)
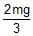
- c)
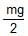
- d)mg
Correct answer is option 'B'. Can you explain this answer?

|
Crafty Classes answered |
Force of magnitude mg is acting downwards at its COM.
Moment balance around B gives:
mg(2L/3)−FA(L)=0
(Moment= × =rFsin(θ)=F(rsin(θ))=Fr⊥)
∴FA=2mg/3
The motion of a potter’s wheel is an example of
- a)rolling motion
- b)rotatory motion
- c)translatory motion
- d)precessional motion
Correct answer is option 'B'. Can you explain this answer?
|
|
Anjali Iyer answered |
The centre of mass of a system of particles does not depend on
- a)masses of the particles
- b)forces on the particles
- c)relative distances between the particles
- d)position of the particles
Correct answer is option 'B'. Can you explain this answer?
|
|
Neha Joshi answered |
An engine develops a power of 360 kw, when rotating at 30 revolutions per second. The Torque required to deliver this power is- a)191.08 Nm
- b)19108 Nm
- c)1910.8 Nm
- d)19.108 Nm
Correct answer is option 'C'. Can you explain this answer?
|
|
Preeti Iyer answered |
P=τω or τ=P/ω
Here P=360KW=360000 Watt
ω=30 x 2π rad/sec,
ω=60π rad/sec
now,
τ=360000 /60×3.14Nm
τ= 1910.8 Nm
If a shell at rest explodes then the centre of mass of the fragments
- a)remains at rest
- b)Moves along a parabolic path
- c)Moves along a straight line
- d)moves along an elliptical path
Correct answer is option 'A'. Can you explain this answer?
|
|
Gaurav Kumar answered |
The mass of an electron is 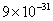 kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of
kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of 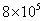 m/s. The angular momentum of electron is
m/s. The angular momentum of electron is- a)2.24 x 10-4 kgm2s-1
- b)3.24 x 10-34 kgm2s-1
- c)4.24 x10-34 kgm2s-1
- d)2.24 x 10-34 kgm2s-1
Correct answer is option 'B'. Can you explain this answer?
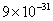 kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of
kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of 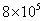 m/s. The angular momentum of electron is
m/s. The angular momentum of electron is|
|
Krishna Iyer answered |
V=8x105m/s
L=mvr
=9x10-31 x 4.5 x 10-10 x 8 x 105 = 3.24 x 10-34 kgm2s-1
Two rings have their moment of inertia in the ratio 2:1 and their diameters are in the ratio 2:1. The ratio of their masses will be:- a)1:2
- b)2:1
- c)1:4
- d)1:1
Correct answer is option 'A'. Can you explain this answer?
|
|
Suresh Reddy answered |
Where m is mass of the ring and r is its radius
When we have ratio of I = 2:1
And ratio of r = 2:1
We get ratio of r2 = 4:1
Thus to make this ratio 2:1 , that ratio of masses must be 1:2
Moment of inertia of a circular wire of mass M and radius R about its diameter is[AIEEE 2002]- a)
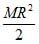
- b)MR2
- c) 2MR2
- d)
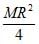
Correct answer is option 'A'. Can you explain this answer?
|
|
Krishna Iyer answered |
MOI through centre (z-axis) is MR², so, by applying perpendicular axis theorem
Ix + Iy = Iz and since Ix = Iy and both are about diameter
Iz = MR², so, 2Ix = MR² MOI about diameter is MR²/2
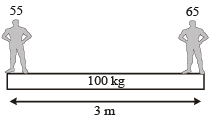
Two persons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat.The length of the boat is 3.0 m and weighs 100 kg. The 55 kg man walks up to the 65 kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by : [2012]- a)3.0 m
- b)2.3 m
- c)zero
- d)0.75 m
Correct answer is option 'C'. Can you explain this answer?

|
Ayush Sengupta answered |
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along : [2012]- a)a line perpendicular to the plane of rotation
- b)the line making an angle of 45° to the plane of rotation
- c)the radius
- d)the tangent to the orbit
Correct answer is option 'A'. Can you explain this answer?
|
|
Cute Princess answered |
If a man of mass M jumps to the ground from height h and his centre of mass moves a distance x in the time taken by him to hit the ground, the average force acting on him is (assuming his retardation to be constant during his impact with the ground)- a)
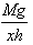
- b)
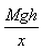
- c)
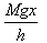
- d)
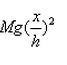
Correct answer is option 'B'. Can you explain this answer?
|
|
Neha Joshi answered |
Work done = Change in potential energy
⇒ Fx = Mgh
⇒ F =
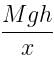
There are two circular iron discs A and B having masses in the ratio 1:2 and diameter in the ratio 2:1. The ratio of their moment of inertia is- a)4:1
- b)1:3
- c)2:1
- d)8:1
Correct answer is option 'C'. Can you explain this answer?
|
|
Preeti Iyer answered |
Mass of A=1,
Mass of B=2.
diameter if A=2,
diameter if B=1.
radius (r) of A=d/2=2/2=1.
radius (r) of B=d/2=1/2.
we know ,
moment of inertia of disc=MR2/2.
moment of inertia (I)of A/moment of inertia (I)of B=MR2/2/MR2/2.
(I) of A/(I) of B=1×12/2/2×(1/2)2/2.
=1×1/2/2×(1/4)/2.
=1/2/(1/2)/2.
=1/2/1/4.
=4/2.
=2/1.
When external forces acting on a body are zero, then its centre of mass- a)remains stationary
- b)moves with uniform velocity
- c)either remains stationary or moves with uniform velocity
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
|
|
Naina Sharma answered |
A homogeneous cubical brick lies motionless on a rough inclined surface. The half of the brick which applies greater pressure on the plane is : 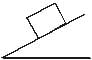
- a) Left half
- b)Right half
- c)Both applies equal pressure
- d)The answer depend upon coefficient of friction
Correct answer is option 'A'. Can you explain this answer?

|
Mohit Rajpoot answered |
mgcosx acts perpendicular to flow of the object.
The pressure of right half comes on left half hence left half has maximum pressure.
There are some passengers inside a stationary railway compartment. The centre of masses of the compartment itself(without the passengers) is C1, while the centre of mass of the compartment plus passengers’ system is C2. if the passengers moves about inside the compartment
- a)both C1 and C2 will move with respect to the ground
- b)neither C1 nor C2 will move with respect to the ground
- c)C1 will move but C2 will be stationary with respect to the ground
- d)C2 will move but C1 will be stationary with respect to the ground
Correct answer is option 'C'. Can you explain this answer?
|
|
Lavanya Menon answered |
Can you explain the answer of this question below:The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by 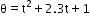 . The linear velocity of the particle
. The linear velocity of the particle
- A:
1.84 m/s
- B:
1.80 m/s
- C:
1.82 m/s
- D:
1.88 m/s
The answer is a.
The angular position of a particle (in radians), along a circle of radius 0.8 m is given by the function in time (seconds) by 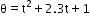 . The linear velocity of the particle
. The linear velocity of the particle
1.84 m/s
1.80 m/s
1.82 m/s
1.88 m/s

|
Knowledge Hub answered |
So, as we know,
After differentiating angular velocity with respect to t,
Linear velocity=2t+2.3=ω
Now,
Velocity=r x ω(where r is 0.8m)
=0.8x2.3
=1.84m/s
Moment of inertia of a solid sphere of mass M and radius R is ______- a)MR2
- b)2/5MR2
- c)2/3MR2
- d)1/2MR2
Correct answer is option 'B'. Can you explain this answer?
|
|
Sarita Pandey answered |
A small object of uniform density rolls up a curved surface with an initial velocity ‘ν’. It reaches upto a maximum height of 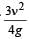 with respect to the initial position. The object is a [NEET 2013]
with respect to the initial position. The object is a [NEET 2013]- a)solid sphere
- b)hollow sphere
- c)disc
- d)ring
Correct answer is option 'C'. Can you explain this answer?
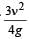 with respect to the initial position. The object is a [NEET 2013]
with respect to the initial position. The object is a [NEET 2013]|
|
Pallavi Sarkar answered |
A solid sphere and a hollow sphere of the same mass have the same moments of inertia about their respective diameters, the ratio of their radii is- a)(5)1/2 : (3)1/2
- b) (3)1/2 : (5)1/2
- c)3 : 2
- d)2 : 3
Correct answer is option 'A'. Can you explain this answer?
|
|
Gaurav Kumar answered |
moment of inertia of hollow sphere IH=2/3mHRH2 As per question Is=IH
Now,
2/5msRs2=2/3mHRH2
as the masses are equal the ratio of their radii will be
Rs2 /RH2 =2/3/2/5=√5/3=(5)1/2: (3)1/2
A particle of mass 1 kg is fired from the origin of the co-ordinate axis-making angle 45 with the horizontal. After time t its position vector is 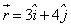 and velocity
and velocity 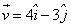 . What is the angular momentum of the particle at that instant?
. What is the angular momentum of the particle at that instant?- a)-25
- b)-7
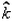
- c)25
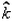
- d)7
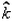
Correct answer is option 'A'. Can you explain this answer?
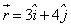 and velocity
and velocity 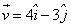 . What is the angular momentum of the particle at that instant?
. What is the angular momentum of the particle at that instant?|
|
Anaya Patel answered |
Therefore,
A rigid body is one
- a)the sum of distances of all particles from the axis remains constant
- b)in which the distance between all pairs of particles remains fixed
- c)whose centre of mass follows a parabolic path
- d)that deforms and comes back to its original shape after getting deformed
Correct answer is option 'B'. Can you explain this answer?
|
|
Krishna Iyer answered |
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4 kg m2.- a)12 kg m2
- b)3 kg m2
- c)6 kg m2
- d)9 kg m2
Correct answer is option 'C'. Can you explain this answer?
|
|
Naina Sharma answered |
MR2/2 = 4, MR2 = 8 then substitute in (1) you will get I = 12, this is for tangent perpendicular to plane then divide by 2 you will get tangent along the plane
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the initial angular acceleration of the rod is [NEET 2013]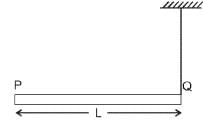
- a)g /L
- b)2g/L
- c)
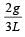
- d)
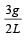
Correct answer is option 'D'. Can you explain this answer?

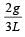
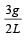
|
|
Wahid Khan answered |
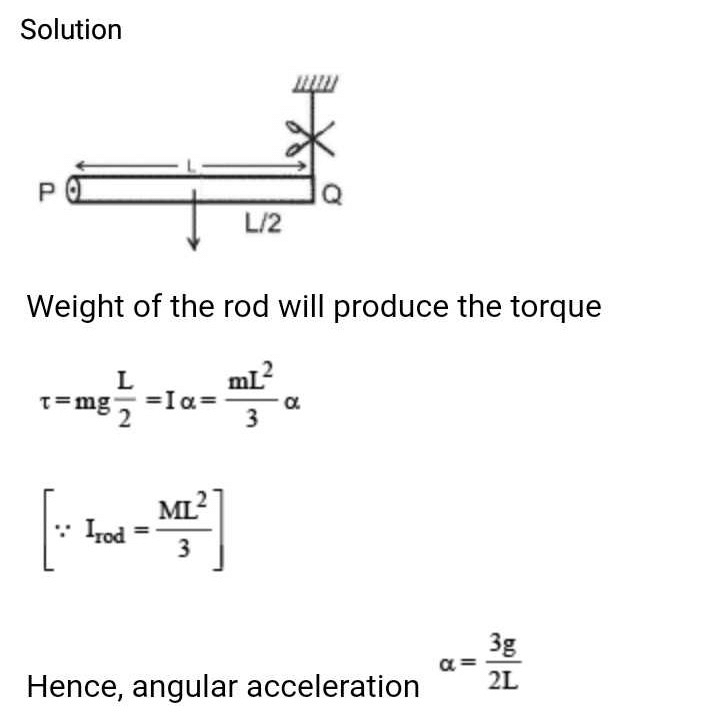
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is- a)4 unit
- b)6 unit
- c)8 unit
- d)10 unit
Correct answer is option 'D'. Can you explain this answer?
|
|
Krishna Iyer answered |
MI of a disc about its diameter = mr2/4 = 2
And also MI about a point on its rim = mr2/4 + mr2
= 5mr2/4
= 5 x 2 = 10
A CD accelerates uniformly from rest to 200 spins per minute in 8 seconds. If the rate of change of speed is constant, determine the instantaneous acceleration in rad/s2 .- a)200.2 π rad/s2
- b)25 rad/ s2
- c)20.9 rad/ s2
- d)2.6 rad/ s2
Correct answer is option 'D'. Can you explain this answer?
|
|
Varun Kapoor answered |
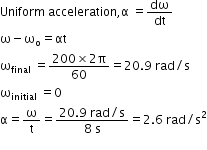
The moment of inertia and rotational kinetic energy of a fly wheel are 20kg-m2 and 1000 joule respectively. Its angular frequency per minute would be -- a)600/π
- b)25/π2
- c)5/π
- d)300/π
Correct answer is option 'D'. Can you explain this answer?
|
|
Riya Banerjee answered |
A mixer grinder rotates clockwise, its angular velocity will be :- a)zero
- b)negative
- c)uniform but not zero
- d)positive
Correct answer is option 'B'. Can you explain this answer?
|
|
Ashish Roy answered |
A mixer grinder is a device that is used for grinding and mixing various ingredients. It consists of a motor and a set of blades that rotate at high speeds to perform the grinding and mixing tasks. When the mixer grinder is turned on, the motor starts rotating the blades in a clockwise direction.
**Angular Velocity:**
Angular velocity is a measure of how quickly an object rotates or moves around a central point. It is defined as the rate of change of angular displacement with respect to time. The direction of the angular velocity is determined by the direction of rotation. In the case of a mixer grinder rotating clockwise, the angular velocity will be negative.
**Direction of Angular Velocity:**
The direction of angular velocity is determined by the right-hand rule. According to the right-hand rule, if the fingers of the right hand curl in the direction of rotation, the thumb will point in the direction of the angular velocity vector. In the case of a mixer grinder rotating clockwise, the fingers of the right hand curl in the clockwise direction, and the thumb points in the opposite direction, which is counterclockwise or negative.
**Significance of Negative Angular Velocity:**
A negative angular velocity indicates that the object is rotating in the opposite direction compared to the conventional positive direction. In the case of a mixer grinder, a negative angular velocity means that the blades are rotating counterclockwise when viewed from above. This counterclockwise rotation is necessary for the blades to effectively grind and mix the ingredients.
**Conclusion:**
In conclusion, a mixer grinder rotates clockwise, which means its angular velocity will be negative. The negative angular velocity indicates that the blades are rotating counterclockwise when viewed from above, allowing them to efficiently perform the grinding and mixing tasks.
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved ? [2002]- a)Linear momentum
- b)Angular momentum
- c)Kinetic energy
- d)Moment of inertia
Correct answer is option 'B'. Can you explain this answer?

|
Krish Khanna answered |
L = Iω = constant
A solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same, which one of the following will not be affected ? [AIEEE 2004]- a)Moment of inertia
- b) Angular momentum
- c)Angular velocity
- d)Rotational kinetic energy
Correct answer is option 'B'. Can you explain this answer?
|
|
Jayant Mishra answered |
An automobile engine develops 100H.P. when rotating at a speed of 1800 rad/min. The torque it delivers is- a)3.33 W-s
- b)200W-s
- c)248.7 W-s
- d)2487 W-s
Correct answer is option 'D'. Can you explain this answer?

|
Manish Aggarwal answered |
If three balls of same radius are placed touching each other on a horizontal surface such that they will form an equilateral triangle, when their centers are joined. What will be the position of the centre of mass of the system?- a)At the point of intersection of the medians.
- b)At the line joining the centers of any two balls.
- c)At the centre of one of the ball.
- d)At the horizontal surface.
Correct answer is option 'A'. Can you explain this answer?
|
|
Neha Joshi answered |
When a shell was following a parabolic path in the air, it explodes somewhere in its flight. The centre of mass of fragments will continue to move in- a)any direction
- b)horizontal direction
- c)same parabolic path
- d)vertical direction
Correct answer is option 'C'. Can you explain this answer?
|
|
Riya Banerjee answered |
If the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is[2002]- a)2.5 m
- b)1 m
- c)1.5 m
- d)2 m
Correct answer is option 'D'. Can you explain this answer?
|
|
Sakshi Sharma answered |
Let the linear density of the rod at distance x from one end be ρ(x).
We know that the mass of an element of length dx at a distance x from one end is given by dm = ρ(x) dx.
The total mass of the rod is given by integrating the above expression from 0 to 3m:
M = ∫₀³ ρ(x) dx
We also know that the position of the centre of gravity of the rod is given by:
x_bar = (1/M) ∫₀³ x ρ(x) dx
Substituting dm = ρ(x) dx in the above expression, we get:
x_bar = (1/M) ∫₀³ x dm
x_bar = (1/M) ∫₀³ x ρ(x) dx
x_bar = (1/M) ∫₀³ x (kx) dx (since ρ(x) is proportional to x)
x_bar = (k/M) ∫₀³ x² dx
x_bar = (k/M) [x³/3]₀³
x_bar = (k/M) [3³/3]
x_bar = 3k/M
But we know that M = ∫₀³ ρ(x) dx
M = k ∫₀³ x dx
M = k [x²/2]₀³
M = k (9/2)
Therefore, x_bar = 3k/M = 3k/(k(9/2)) = 2/3 * 3 = 2m
Hence, the distance of the centre of gravity of the rod from one end is 2m, which is option D.
A thin horizontal circular disc is rotating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.[AIEEE 2011]- a)Continuously decreases
- b)Remains unchanged
- c)First increases and then decreases
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
|
|
Om Desai answered |
L=mr2×ω
Since r first decreases then increases.
So due to conservation of angular momentum L first increases then decreases.
Can you explain the answer of this question below:An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
- A:
y = +5 cm
- B:
y = +20 cm
- C:
y = -20 cm
- D:
y = -5 cm
The answer is d.
An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
y = +5 cm
y = +20 cm
y = -20 cm
y = -5 cm

|
Ambition Institute answered |
⇒ net external force during this process is 0 i.e. center mass will not change.
Let positon of larger fragment be y.
⇒ (m/4 * 15) + (3m/4 * y) = 0
⇒ y = - 5 cm
A wheel of radius 1m r olls for war d half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially in contact with the ground is [2002]- a)π
- b)2π
- c)
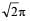
- d)
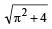
Correct answer is option 'D'. Can you explain this answer?
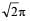
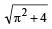

|
Sarthak Saini answered |
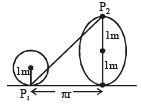
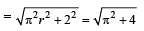 [∵ r = 1m]
[∵ r = 1m]A player caught a cricket ball of mass 150 g moving at a rate of 20 m/s. If the catching process is completed in 0.1 s, the force of the blow exerted by the ball on the hand of the player is equal to [AIEEE 2006]- a) 150 N
- b)3 N
- c)30 N
- d) 300 N
Correct answer is option 'C'. Can you explain this answer?
|
|
Lavanya Menon answered |
F = 150 × 20 / 0.1 × 1000
F = 30N
Three masses are placed on the x-axis : 300g at origin, 500g at x = 40cm and 400g at x = 70 cm.The distance of the centre of mass from the origin is : [2012M]- a)40 cm
- b)45 cm
- c)50 cm
- d)30 cm
Correct answer is option 'A'. Can you explain this answer?
|
|
Jhanvi Tiwari answered |
To find the centre of mass of the system, we can use the formula:
Xcm = (m1x1 + m2x2 + m3x3)/M
where m1, m2, m3 are the masses of the three particles, x1, x2, x3 are their respective distances from the origin, and M = m1 + m2 + m3 is the total mass of the system.
Substituting the given values, we get:
Xcm = (0.3 kg x 0 m + 0.5 kg x 0.4 m + 0.4 kg x 0.7 m)/(0.3 kg + 0.5 kg + 0.4 kg)
Xcm = 0.12 m + 0.2 m + 0.28 m / 1.2 kg
Xcm = 0.6 m
Therefore, the distance of the centre of mass from the origin is 0.6 m or 60 cm.
Answer:
The correct option is (A) 40 cm.
Chapter doubts & questions for System of Particles and Rotational Motion - Topic-wise MCQ Tests for NEET 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Contact Support
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|