Class 11 Exam > Class 11 Questions > Moment of inertia of a solid sphere of mass M...
Start Learning for Free
Moment of inertia of a solid sphere of mass M and radius R is ______
- a)MR2
- b)2/5MR2
- c)2/3MR2
- d)1/2MR2
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
Moment of inertia of a solid sphere of mass M and radius R is ______a)...
Fact.
Most Upvoted Answer
Moment of inertia of a solid sphere of mass M and radius R is ______a)...
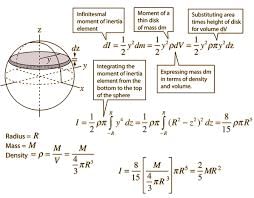
Hence, Moment of Inertia of a solid sphere is 2/5MR^2...
Community Answer
Moment of inertia of a solid sphere of mass M and radius R is ______a)...
Moment of Inertia of a Solid Sphere
The moment of inertia of an object is a measure of its resistance to rotational motion. It depends on the mass distribution of the object and its axis of rotation.
The moment of inertia of a solid sphere can be calculated using the formula:
I = (2/5) * M * R^2
where:
I is the moment of inertia
M is the mass of the sphere
R is the radius of the sphere
Explanation:
1. Definition of Moment of Inertia:
The moment of inertia, I, of an object is defined as the sum of the products of the masses of its particles and the square of their distances from the axis of rotation.
2. Mass Distribution of a Solid Sphere:
A solid sphere has a uniform mass distribution, meaning that the mass is evenly distributed throughout the entire object.
3. Calculating Moment of Inertia for a Solid Sphere:
To calculate the moment of inertia of a solid sphere, we can consider it as a collection of infinitesimally small mass elements. Each small mass element can be considered as a point mass.
4. Infinitesimal Mass Element:
Let's consider a small mass element of radius r and mass dm. The moment of inertia of this small mass element with respect to an axis passing through its center is given by the formula:
dI = r^2 * dm
5. Mass Element in a Solid Sphere:
In a solid sphere, the mass element dm can be expressed in terms of the total mass M and the volume element dV. The volume of a small spherical shell is given by:
dV = 4πr^2 * dr
The mass of the small shell can be calculated using the density ρ of the material:
dm = ρ * dV = ρ * 4πr^2 * dr
6. Integrating to Find the Moment of Inertia:
To find the moment of inertia of the entire sphere, we need to integrate the moment of inertia of each small mass element over the entire sphere.
I = ∫ (r^2 * dm)
Substituting the expression for dm, we get:
I = ∫ (r^2 * ρ * 4πr^2 * dr)
7. Simplifying the Integral:
We can simplify the integral by factoring out the constants:
I = 4πρ * ∫ (r^4 * dr)
8. Evaluating the Integral:
Integrating the expression, we get:
I = 4πρ * [r^5 / 5] + C
9. Applying Limits to the Integral:
To apply limits to the integral, we consider the radius of the sphere, R, as the upper limit and 0 as the lower limit:
I = (4πρ * R^5 / 5) - (4πρ * 0^5 / 5)
Since the density of the sphere is uniform, we can replace ρ with M / V, where V is the volume of the sphere:
I = (4π * (M / V) * R^5 / 5) - (4π * (M / V) * 0^5 / 5)
10. Simplifying Further:
The volume of a sphere can be expressed as V = (4/3)πR^3. Substituting this in the equation, we get:
I =
The moment of inertia of an object is a measure of its resistance to rotational motion. It depends on the mass distribution of the object and its axis of rotation.
The moment of inertia of a solid sphere can be calculated using the formula:
I = (2/5) * M * R^2
where:
I is the moment of inertia
M is the mass of the sphere
R is the radius of the sphere
Explanation:
1. Definition of Moment of Inertia:
The moment of inertia, I, of an object is defined as the sum of the products of the masses of its particles and the square of their distances from the axis of rotation.
2. Mass Distribution of a Solid Sphere:
A solid sphere has a uniform mass distribution, meaning that the mass is evenly distributed throughout the entire object.
3. Calculating Moment of Inertia for a Solid Sphere:
To calculate the moment of inertia of a solid sphere, we can consider it as a collection of infinitesimally small mass elements. Each small mass element can be considered as a point mass.
4. Infinitesimal Mass Element:
Let's consider a small mass element of radius r and mass dm. The moment of inertia of this small mass element with respect to an axis passing through its center is given by the formula:
dI = r^2 * dm
5. Mass Element in a Solid Sphere:
In a solid sphere, the mass element dm can be expressed in terms of the total mass M and the volume element dV. The volume of a small spherical shell is given by:
dV = 4πr^2 * dr
The mass of the small shell can be calculated using the density ρ of the material:
dm = ρ * dV = ρ * 4πr^2 * dr
6. Integrating to Find the Moment of Inertia:
To find the moment of inertia of the entire sphere, we need to integrate the moment of inertia of each small mass element over the entire sphere.
I = ∫ (r^2 * dm)
Substituting the expression for dm, we get:
I = ∫ (r^2 * ρ * 4πr^2 * dr)
7. Simplifying the Integral:
We can simplify the integral by factoring out the constants:
I = 4πρ * ∫ (r^4 * dr)
8. Evaluating the Integral:
Integrating the expression, we get:
I = 4πρ * [r^5 / 5] + C
9. Applying Limits to the Integral:
To apply limits to the integral, we consider the radius of the sphere, R, as the upper limit and 0 as the lower limit:
I = (4πρ * R^5 / 5) - (4πρ * 0^5 / 5)
Since the density of the sphere is uniform, we can replace ρ with M / V, where V is the volume of the sphere:
I = (4π * (M / V) * R^5 / 5) - (4π * (M / V) * 0^5 / 5)
10. Simplifying Further:
The volume of a sphere can be expressed as V = (4/3)πR^3. Substituting this in the equation, we get:
I =

|
Explore Courses for Class 11 exam
|

|
Question Description
Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer?.
Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? for Class 11 2025 is part of Class 11 preparation. The Question and answers have been prepared according to the Class 11 exam syllabus. Information about Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for Class 11 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer?.
Solutions for Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 11.
Download more important topics, notes, lectures and mock test series for Class 11 Exam by signing up for free.
Here you can find the meaning of Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Moment of inertia of a solid sphere of mass M and radius R is ______a)MR2b)2/5MR2c)2/3MR2d)1/2MR2Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice Class 11 tests.

|
Explore Courses for Class 11 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















