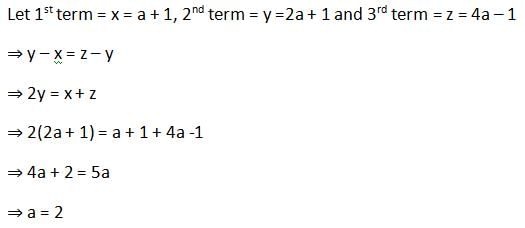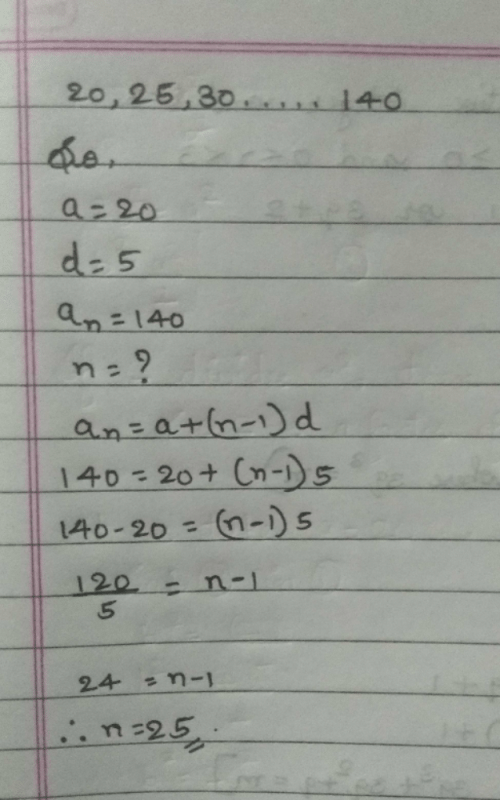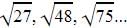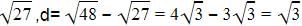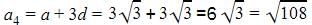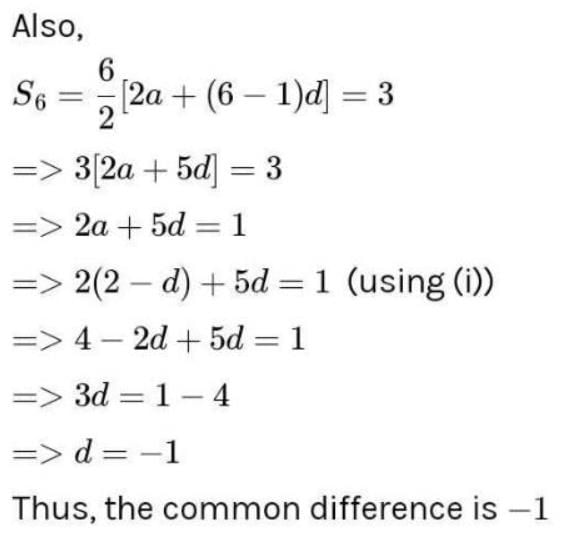All Exams >
Class 10 >
Online MCQ Tests for Class 10 >
All Questions
All questions of Arithmetic Progressions for Class 10 Exam
The 5th term of an A.P. is 18, the common difference is 2. What is the first term ?
- a)8
- b)9
- c)10
- d)7
Correct answer is option 'C'. Can you explain this answer?
The 5th term of an A.P. is 18, the common difference is 2. What is the first term ?
a)
8
b)
9
c)
10
d)
7
|
Indu Gupta answered |
5th term of AP is 18 and common difference is 2
We have, l = a + (n - 1)d
Where l = 18,a = ?,n = 5,d = 2
Substituting the values,
18 = a+8
a = 10
We have, l = a + (n - 1)d
Where l = 18,a = ?,n = 5,d = 2
Substituting the values,
18 = a+8
a = 10
The next term of the given series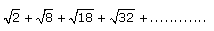 
would be- a)
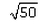
- b)
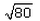
- c)
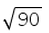
- d)
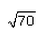
Correct answer is option 'A'. Can you explain this answer?
The next term of the given series 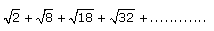would be
would bea)
b)
c)
d)
|
Krishna Iyer answered |
We have an AP :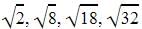 
Here a=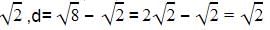
l=a+(n-1)d
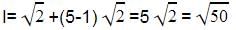
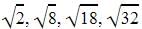
Here a=
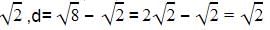
l=a+(n-1)d
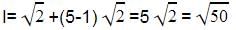
The 6th term from the end of the AP: 5, 2, -1 , -4 , . . . , -31 is
- a)-16
- b)-19
- c)-22
- d)-25
Correct answer is option 'A'. Can you explain this answer?
The 6th term from the end of the AP: 5, 2, -1 , -4 , . . . , -31 is
a)
-16
b)
-19
c)
-22
d)
-25
|
Let's Tute answered |
The given AP is 5, 2, -1, -4 ... ...., -31
d = 2 - 5 = -3, so d for the AP starting from the last term is 3.
The first term = l = -31
We know, an = a+(n−1)d
a6 from the end = −31+(5)3
a6 from the end = −16
d = 2 - 5 = -3, so d for the AP starting from the last term is 3.
The first term = l = -31
We know, an = a+(n−1)d
a6 from the end = −31+(5)3
a6 from the end = −16
The list of numbers -10, -6, -2, 2,... is
- a)An AP with d = -16
- b)An AP with d = 4
- c)An AP with d = -4
- d)Not an AP
Correct answer is option 'B'. Can you explain this answer?
The list of numbers -10, -6, -2, 2,... is
a)
An AP with d = -16
b)
An AP with d = 4
c)
An AP with d = -4
d)
Not an AP
|
|
Krishna Iyer answered |
a1=-10
a2=-6
so the common difference
d=(-6 - (-10)) = (-6 +10) = 4
a2=-6
so the common difference
d=(-6 - (-10)) = (-6 +10) = 4
Two APs have same common difference. The first term of one of these is -1 and that of the other is - 8. Then the difference between their 4th term is - a)-1
- b)-8
- c)7
- d)-9
Correct answer is option 'C'. Can you explain this answer?
Two APs have same common difference. The first term of one of these is -1 and that of the other is - 8. Then the difference between their 4th term is
a)
-1
b)
-8
c)
7
d)
-9
|
Amit Sharma answered |
Correct Answer :- c
Explanation : ad1 = -1
ad2 = -8
4th term of ad1 is
a4 = a + 3d
a4 = -1 + 3d.....(1)
Similarly ad2 is
a4 = -8 + 3d.......(2)
Subtracting (2) from (1), we get
-1 + 3d -(-8 + 3d)
=> 7
The 11th and 13th terms of an AP are 35 and 41 respectively, its common difference is- a)38
- b)32
- c)6
- d)3
Correct answer is option 'D'. Can you explain this answer?
The 11th and 13th terms of an AP are 35 and 41 respectively, its common difference is
a)
38
b)
32
c)
6
d)
3
|
Raghav Bansal answered |
11th term is 35 so a+10d = 35 => equation 1
13th term is 41 so a+12d = 41 => equation 2
solve both equations by elimination method
we get common difference as 3
Give that an A.P. has term as 5 and common differences as 2. What is the A.p.?- a)5,7,9,11,13…
- b)5,7,9,10,11,12…
- c)5,6,8,10,12…
- d)5,6,7,8,9,10…
Correct answer is option 'A'. Can you explain this answer?
Give that an A.P. has term as 5 and common differences as 2. What is the A.p.?
a)
5,7,9,11,13…
b)
5,7,9,10,11,12…
c)
5,6,8,10,12…
d)
5,6,7,8,9,10…
|
|
Krishna Iyer answered |
A¹=5 d=2
a²=a¹+d =5+2=7
a³=a²+d =7+2 =9
a⁴=a³+d=9+2=11
A5 =a⁴+d=11+2=13
Therefore 5,7,9,11,13 is an AP.
a²=a¹+d =5+2=7
a³=a²+d =7+2 =9
a⁴=a³+d=9+2=11
A5 =a⁴+d=11+2=13
Therefore 5,7,9,11,13 is an AP.
Progressions with equal common difference are known as- a)Arithmetic Progression
- b)Geometric Progression
- c)Harmonic Progression
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Progressions with equal common difference are known as
a)
Arithmetic Progression
b)
Geometric Progression
c)
Harmonic Progression
d)
none of these
|
Sonal Joshi answered |
Progressions with equal common difference are known as Arithmetic Progression.
The common difference and the next two terms of the A.P are….
- a)
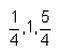
- b)
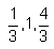
- c)
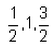
- d)
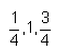
Correct answer is option 'A'. Can you explain this answer?
The common difference and the next two terms of the A.P are….
a)
b)
c)
d)
|
|
ᴄᴀᴘᴛᴀɪɴ ᴅᴇᴠɪʟ answered |
AP=0,1/4,1/2,3/4,
a=0,
d=1/4-0=1/4,
now atq,
a5=a+4d,
=0+4(1/4)=1,
a6=a+5d,
=0+5/4=5/4
a=0,
d=1/4-0=1/4,
now atq,
a5=a+4d,
=0+4(1/4)=1,
a6=a+5d,
=0+5/4=5/4
Which term of the AP: 18, 23, 28, 33,... is 98?- a)18th
- b)17th
- c)16th
- d)15th
Correct answer is option 'B'. Can you explain this answer?
Which term of the AP: 18, 23, 28, 33,... is 98?
a)
18th
b)
17th
c)
16th
d)
15th
|
|
Arun Sharma answered |
98=a+(n-1)d
98=18+(n-1)5
80=(n-1)5
16=n-1
17=n
this explains that 98 is 17th term of the AP
If 18, a, b, -3 are in AP, then a + b is equal to- a)19
- b)7
- c)11
- d)15
Correct answer is option 'D'. Can you explain this answer?
If 18, a, b, -3 are in AP, then a + b is equal to
a)
19
b)
7
c)
11
d)
15
|
Pooja Shah answered |
We know
AM is ( a + b)/2
(a+b) = [ {18+(-3) }/2] X 2 = 15
An AP consists of 31 terms. If its 16th term is m, then sum of all the terms of this AP is- a)16 m
- b)47 m
- c)31 m
- d)52m
Correct answer is option 'C'. Can you explain this answer?
An AP consists of 31 terms. If its 16th term is m, then sum of all the terms of this AP is
a)
16 m
b)
47 m
c)
31 m
d)
52m
|
Ashish Choudhary answered |
Here,
a16=p
=>a+15d=p
=>a=p-15d
Let all terms be '31' in this AP
Therefore,
Sn=31/2[(2a+(n-1)]
Sn=31/2[2(p-15d)+(31-1)d]
Sn=31/2[2p-30d+30d]
Sn=31/2 x 2p
Sn=31
The 21st term of the AP whose first two terms are -3 and 4, is- a)17
- b)137
- c)143
- d)-143
Correct answer is option 'B'. Can you explain this answer?
The 21st term of the AP whose first two terms are -3 and 4, is
a)
17
b)
137
c)
143
d)
-143
|
Vivek Rana answered |
a1=-3,
a2=4,
d=4-(-3)=7,
a21=?,
a21=a+(n-1)d
=-3+(21-1)7
= -3+(20)(7)
= -3+140
=137
a2=4,
d=4-(-3)=7,
a21=?,
a21=a+(n-1)d
=-3+(21-1)7
= -3+(20)(7)
= -3+140
=137
Which term of the A.P. 63, 84, …… is 399?- a)13th
- b)17th
- c)23rd
- d)16th
Correct answer is option 'B'. Can you explain this answer?
Which term of the A.P. 63, 84, …… is 399?
a)
13th
b)
17th
c)
23rd
d)
16th
|
|
Anita Menon answered |
The correct answer is b
A=21
d=21
n=?
420=21+(n-1)21
(n-1)*21=399
n-1=399/21
n-1=19
n=19+1=20
therefore the 20th term of the AP is 420
The sum of first 16 terms of the AP : 10, 6, 2,... is - a)-320
- b)320
- c)-352
- d)-400
Correct answer is option 'A'. Can you explain this answer?
The sum of first 16 terms of the AP : 10, 6, 2,... is
a)
-320
b)
320
c)
-352
d)
-400
|
|
Arun Sharma answered |
The formula for the sum of first n terms of a AP is n/2(2a+(n-1)d)
here n=16 a=10 d=6-10=2-6=-4
so sum of first 16 terms=16/2(2·10+(16-1)·-4)
=8(20+15·-4)
=8(20-60)
=8(-40)
=-320
here n=16 a=10 d=6-10=2-6=-4
so sum of first 16 terms=16/2(2·10+(16-1)·-4)
=8(20+15·-4)
=8(20-60)
=8(-40)
=-320
Which term of the AP : 21, 42, 63, 84, ... is 210 ?
- a)9th
- b)10th
- c)11th
- d)12th
Correct answer is option 'B'. Can you explain this answer?
Which term of the AP : 21, 42, 63, 84, ... is 210 ?
a)
9th
b)
10th
c)
11th
d)
12th
|
|
Priyanshu Intelligent answered |
Here , a=21 and d = 42-21 = 21
Since, a+(n-1) d = an
Then , 210 = 21+(n-1)*21
210 = 21 + 21n - 21
21n = 210
n = 10.
Therefore, 10 th term of this AP is 210.
Hence, option b) is correct answer.
Since, a+(n-1) d = an
Then , 210 = 21+(n-1)*21
210 = 21 + 21n - 21
21n = 210
n = 10.
Therefore, 10 th term of this AP is 210.
Hence, option b) is correct answer.
Is the sequence, whose general term is 5n2 + 2n + 3 an AP?
- a)No
- b)Insufficent information
- c)Yes
- d)Depends on n
Correct answer is option 'A'. Can you explain this answer?
Is the sequence, whose general term is 5n2 + 2n + 3 an AP?
a)
No
b)
Insufficent information
c)
Yes
d)
Depends on n
|
|
Ananya Das answered |
We have the sequence 5n2+2n+3
It will be in AP if it satisfies an-an-1=d where d is a constant.
Here, an=5n2+2n+3
And, an-1=5(n-1)2+2(n-1)+3=5(n2+1-2n)+2n-2+3
=5n2+5-10n+2n+1=5n2-8n+6
an-an-1=5n2+2n+3-(5n2-8n+6)
=5n2+2n+3-5n2+8n-6
=10n-3, which depends on a variable , so its not constant.
It will be in AP if it satisfies an-an-1=d where d is a constant.
Here, an=5n2+2n+3
And, an-1=5(n-1)2+2(n-1)+3=5(n2+1-2n)+2n-2+3
=5n2+5-10n+2n+1=5n2-8n+6
an-an-1=5n2+2n+3-(5n2-8n+6)
=5n2+2n+3-5n2+8n-6
=10n-3, which depends on a variable , so its not constant.
… is:
For an A.P. the third and the fifth terms are given as 10 and 16 .What is the fourth term and the common difference?
- a)22,4
- b)4,6
- c)13,3
- d)22,6
Correct answer is option 'C'. Can you explain this answer?
For an A.P. the third and the fifth terms are given as 10 and 16 .What is the fourth term and the common difference?
a)
22,4
b)
4,6
c)
13,3
d)
22,6
|
Aisha Negi answered |
Abe yrr we are given third term means a+ 2d and fifth term means a+ 4d now make two equation separately i.e, a+ 2d = 10 ------ eq1 and a+ 4d = 16 ---------eq2 now eliminate both the equation and Iam sure ans will be 13, 3
The common difference and the next two terms of the A.P are….1.8, 2.0, 2.2, 2.4,….- a)3.1, 6.2 , 9.3
- b)0.2 , 3.4,3.6
- c)0.2 , 2.6 , 2.8
- d)1.0, 3.0,4.0
Correct answer is option 'C'. Can you explain this answer?
The common difference and the next two terms of the A.P are….1.8, 2.0, 2.2, 2.4,….
a)
3.1, 6.2 , 9.3
b)
0.2 , 3.4,3.6
c)
0.2 , 2.6 , 2.8
d)
1.0, 3.0,4.0
|
|
Himaja Ammu answered |
Common difference us 0.2 and next 2 terms r 2.6 ,2.8.3.0
What is the sum of the first 50 multiples of 3?
- a)3255
- b)3825
- c)4325
- d)4455
Correct answer is option 'B'. Can you explain this answer?
What is the sum of the first 50 multiples of 3?
a)
3255
b)
3825
c)
4325
d)
4455
|
|
Let's Tute answered |
sum=n/2x(2a+(n-1)d )
=50/2(2x3+ (50-1)3 )
= 25 ( 6+49x3 )
= 25x 153
= 3825
=50/2(2x3+ (50-1)3 )
= 25 ( 6+49x3 )
= 25x 153
= 3825
The sum of (a + b), (a – b), (a – 3b), …….. to 22nd term is- a)22a – 440b
- b)22a – 400b
- c)22a + 440b
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The sum of (a + b), (a – b), (a – 3b), …….. to 22nd term is
a)
22a – 440b
b)
22a – 400b
c)
22a + 440b
d)
none of these
|
Mukund Narayan answered |
First u calculate difference between a+ b and a- b and then use the formula
The sum of first five multiples of 3 is- a)45
- b)55
- c)65
- d)75
Correct answer is option 'A'. Can you explain this answer?
The sum of first five multiples of 3 is
a)
45
b)
55
c)
65
d)
75
|
|
Amit Kumar answered |
First five multiple of 3 are:
3, 6, 9, 12, 15
Here first term, a = 3
common difference, d = 6 – 3 = 3
Number of term, n = 5
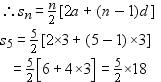
⇒ s5 = 9 × 5 = 45
Ramesh’s salary in February 2008 is Rs. 10,000. If he’s promised an increase of Rs. 1000 every year, what would be his salary in Feb 2011?- a)Rs. 13,000
- b)Rs.14,000
- c)Rs. 12,000
- d)Rs. 15,000
Correct answer is option 'A'. Can you explain this answer?
Ramesh’s salary in February 2008 is Rs. 10,000. If he’s promised an increase of Rs. 1000 every year, what would be his salary in Feb 2011?
a)
Rs. 13,000
b)
Rs.14,000
c)
Rs. 12,000
d)
Rs. 15,000
|
|
Anita Menon answered |
So this is an AP with a=10,000 , d= 1000
So after 4 years
l=a+(n-1)d=10000+(4 -1)1000=10000+3000=13000
So after 4 years
l=a+(n-1)d=10000+(4 -1)1000=10000+3000=13000
If for an A.P. Sn=n2+7n what is its third term?- a)21
- b)20
- c)15
- d)12
Correct answer is option 'D'. Can you explain this answer?
If for an A.P. Sn=n2+7n what is its third term?
a)
21
b)
20
c)
15
d)
12
|
Ananya shah answered |
Given:
First term (a) = 1
Last term (l) = 11
Sum of terms = 36
To find: Number of terms (n)
Formula:
The sum of n terms of an arithmetic progression is given as:
S = n/2 [2a + (n-1)d]
where,
a = first term
d = common difference
l = last term
n = number of terms
Approach:
1. Using the given values, we can find the common difference (d) of the arithmetic progression.
2. Then, we can substitute the values of a, d, and l in the formula for the sum of n terms and simplify the equation to get the value of n.
Calculation:
Common difference (d) = l - a
= 11 - 1
= 10
Substituting the values in the formula for sum of n terms:
36 = n/2 [2(1) + (n-1)(10)]
36 = n/2 [2 + 10n - 10]
36 = n/2 [10n - 8]
72 = n(5n - 4)
5n² - 4n - 72 = 0
(n - 6)(5n + 12) = 0
n = 6 or -12/5
Since the number of terms cannot be negative, the answer is n = 6.
Therefore, the number of terms in the arithmetic progression is 6.
Answer: b) 6
First term (a) = 1
Last term (l) = 11
Sum of terms = 36
To find: Number of terms (n)
Formula:
The sum of n terms of an arithmetic progression is given as:
S = n/2 [2a + (n-1)d]
where,
a = first term
d = common difference
l = last term
n = number of terms
Approach:
1. Using the given values, we can find the common difference (d) of the arithmetic progression.
2. Then, we can substitute the values of a, d, and l in the formula for the sum of n terms and simplify the equation to get the value of n.
Calculation:
Common difference (d) = l - a
= 11 - 1
= 10
Substituting the values in the formula for sum of n terms:
36 = n/2 [2(1) + (n-1)(10)]
36 = n/2 [2 + 10n - 10]
36 = n/2 [10n - 8]
72 = n(5n - 4)
5n² - 4n - 72 = 0
(n - 6)(5n + 12) = 0
n = 6 or -12/5
Since the number of terms cannot be negative, the answer is n = 6.
Therefore, the number of terms in the arithmetic progression is 6.
Answer: b) 6
An athlete wants to improve his stamina, so he decides to increase the distance he runs by half a kilometer every day. If he starts with 5 km on first day, find how much he runs on the 10 th day- a)6 Km
- b)7.5Km
- c)9.5Km
- d)10 Km
Correct answer is option 'C'. Can you explain this answer?
An athlete wants to improve his stamina, so he decides to increase the distance he runs by half a kilometer every day. If he starts with 5 km on first day, find how much he runs on the 10 th day
a)
6 Km
b)
7.5Km
c)
9.5Km
d)
10 Km
|
|
Amit Kumar answered |
Distance increased every day is the common difference for the AP which is 0.5
Initial distance is 5 km , so a=5
To find the distance at 10th day, so n=10
l=a+(n-1)d
=5+(10-1)0.5
=5+4.5=9.5km
Initial distance is 5 km , so a=5
To find the distance at 10th day, so n=10
l=a+(n-1)d
=5+(10-1)0.5
=5+4.5=9.5km
Find the next two terms of the A.P.:- -10, -6,-2…- a)4,8
- b)-4,-8
- c)2,6
- d)6,10
Correct answer is option 'C'. Can you explain this answer?
Find the next two terms of the A.P.:- -10, -6,-2…
a)
4,8
b)
-4,-8
c)
2,6
d)
6,10
|
|
Amit Sharma answered |
We have A.P.: -10, -6,-2…
So a= -10, d=-6+10=-2+6=4
l=a+(n-1)d
For fourth term,
= -10+(3)*4=-10+12=2
For 5th term
= -10+4*4=6
So a= -10, d=-6+10=-2+6=4
l=a+(n-1)d
For fourth term,
= -10+(3)*4=-10+12=2
For 5th term
= -10+4*4=6
The 16th term of the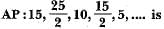 
- a)45/2
- b)-45/2
- c)105/2
- d)-25
Correct answer is option 'B'. Can you explain this answer?
The 16th term of the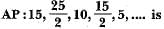
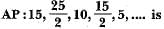
a)
45/2
b)
-45/2
c)
105/2
d)
-25
|
|
Raghav Bansal answered |
A= 15
d = a2 - a1
d = 25 / 2 - 15
d = ( 30 - 25 / 2 )
d = - 5/ 2
16th term of an AP = a + 15 d
15 +( 15 × ( -5 / 2 ))
15 + (-75 / 2 )
= - 45 / 2
d = a2 - a1
d = 25 / 2 - 15
d = ( 30 - 25 / 2 )
d = - 5/ 2
16th term of an AP = a + 15 d
15 +( 15 × ( -5 / 2 ))
15 + (-75 / 2 )
= - 45 / 2
If Ss = 32, S4 = 28 ~~ What is ts =?- a)36
- b)24
- c)8
- d)4
Correct answer is option 'D'. Can you explain this answer?
If Ss = 32, S4 = 28 ~~ What is ts =?
a)
36
b)
24
c)
8
d)
4
|
Amitabh sinha answered |
Given, Ss= 32 and S4 = 28
To find, ts=?
We know that the sum of an arithmetic progression (AP) is given by the formula:
Sn = n/2[2a + (n-1)d]
where Sn is the sum of first n terms, a is the first term, d is the common difference and n is the number of terms.
Let's find the common difference (d) of this AP.
S4 = 4/2[2a + (4-1)d] = 2[2a + 3d] = 4a + 6d
Given that S4 = 28, we have:
4a + 6d = 28
Similarly, for Ss, we have:
Ss = s/2[2a + (s-1)d] = s/2[a + a + (s-1)d] = (s/2)[2a + (s-1)d]
Given that Ss = 32, we have:
(s/2)[2a + (s-1)d] = 32
Dividing both sides by 4, we get:
(s/8)[2a + (s-1)d] = 8
Now, we can substitute the value of a + 3d from the equation 4a + 6d = 28 into the above equation, to get:
(s/8)[2(a + 3d) + (s-4)d] = 8
Simplifying this, we get:
s^2 - 16s + 64 = 0
This is a quadratic equation that can be factored as:
(s-8)(s-8) = 0
Therefore, the only possible value of s is 8.
Hence, the answer is option D, ts = 4.
To find, ts=?
We know that the sum of an arithmetic progression (AP) is given by the formula:
Sn = n/2[2a + (n-1)d]
where Sn is the sum of first n terms, a is the first term, d is the common difference and n is the number of terms.
Let's find the common difference (d) of this AP.
S4 = 4/2[2a + (4-1)d] = 2[2a + 3d] = 4a + 6d
Given that S4 = 28, we have:
4a + 6d = 28
Similarly, for Ss, we have:
Ss = s/2[2a + (s-1)d] = s/2[a + a + (s-1)d] = (s/2)[2a + (s-1)d]
Given that Ss = 32, we have:
(s/2)[2a + (s-1)d] = 32
Dividing both sides by 4, we get:
(s/8)[2a + (s-1)d] = 8
Now, we can substitute the value of a + 3d from the equation 4a + 6d = 28 into the above equation, to get:
(s/8)[2(a + 3d) + (s-4)d] = 8
Simplifying this, we get:
s^2 - 16s + 64 = 0
This is a quadratic equation that can be factored as:
(s-8)(s-8) = 0
Therefore, the only possible value of s is 8.
Hence, the answer is option D, ts = 4.
The angles of a triangle in A.P. the smallest being half of the greatest. So what are the angles ?- a)45°, 55°, 90°
- b)50°, 25°, 75°
- c)60°, 40°, 80°
- d)40°, 60°, 30°
Correct answer is 'C'. Can you explain this answer?
The angles of a triangle in A.P. the smallest being half of the greatest. So what are the angles ?
a)
45°, 55°, 90°
b)
50°, 25°, 75°
c)
60°, 40°, 80°
d)
40°, 60°, 30°
|
|
Rajiv Gupta answered |
Let a-d, a, a+d be the three angles of the triangle that form AP.Now, 2(a-d)=a+d2a-2d=a+da=3d (eq. 1)Now by angle sum property,(a-d)+a+(a+d)=1803a=180a=60 (eq.2)from (1) and (2),3d=60d=20Now, the angles are,a-d=60-20=40a=60a+d=60+20=80
Which term of A.P. 5, 13, 21, is 189- a)21
- b)22
- c)23
- d)24
Correct answer is option 'D'. Can you explain this answer?
Which term of A.P. 5, 13, 21, is 189
a)
21
b)
22
c)
23
d)
24
|
|
ᴄᴀᴘᴛᴀɪɴ ᴅᴇᴠɪʟ answered |
A=5,
d=13-5=8,
an=189,
an=a+(n-1)d,
189=5+(n-1)8,
184/8=n-1,
23+1=n
n=24
d=13-5=8,
an=189,
an=a+(n-1)d,
189=5+(n-1)8,
184/8=n-1,
23+1=n
n=24
The first negative term of the sequence 114, 109, 104 ………… is- a)21
- b)23
- c)24
- d)22
Correct answer is option 'C'. Can you explain this answer?
The first negative term of the sequence 114, 109, 104 ………… is
a)
21
b)
23
c)
24
d)
22
|
|
Krishna Iyer answered |
l=a+(n-1)d , d=109-114=-5
First negative term will be
0 > a+(n-1)d
0 > 114+(n-1)(-5)
0 > 114-5n+5
5n > 119
n > 119/5=23.8
So the first negative term will be 24th term.
First negative term will be
0 > a+(n-1)d
0 > 114+(n-1)(-5)
0 > 114-5n+5
5n > 119
n > 119/5=23.8
So the first negative term will be 24th term.
For an A.P the sum of first 30 terms is -1155,the common difference is -3and the thirtieth term is -82. What is the first term?- a)10
- b)8
- c)5
- d)12
Correct answer is option 'C'. Can you explain this answer?
For an A.P the sum of first 30 terms is -1155,the common difference is -3and the thirtieth term is -82. What is the first term?
a)
10
b)
8
c)
5
d)
12
|
|
Vivek Rana answered |
l = a + (n - 1)d
Where l = -82,a = ?,d = -3,n = 30
-82 = a + 29 (- 3)
a = 5
Where l = -82,a = ?,d = -3,n = 30
-82 = a + 29 (- 3)
a = 5
If p – 1, p + 3, 3p – 1 are in A.P., then p is equal to:- a)-4
- b)4
- c)2
- d)-2
Correct answer is option 'B'. Can you explain this answer?
If p – 1, p + 3, 3p – 1 are in A.P., then p is equal to:
a)
-4
b)
4
c)
2
d)
-2
|
|
Kiran Mehta answered |
We have given that
p-1,p+3 , 3p-1 are in A.P
p-1,p+3 , 3p-1 are in A.P
we have to find p= ?
solution :-
we know that :
if a,b,c are in AP
then 2b = a + c
we know that :
if a,b,c are in AP
then 2b = a + c
here
=> 2(p+3) = { (p-1) + ( 3p -1) }
=> 2(p+3) = { (p-1) + ( 3p -1) }
=> 2p +6 = 4p -2
=> 2p = 8
=> p = 4
For what values of k can the following numbers form an A.P:2k-1,k+2,2k- a)3/ 2
- b)5/ 2
- c)2/ 3
- d)2/ 5
Correct answer is option 'B'. Can you explain this answer?
For what values of k can the following numbers form an A.P:2k-1,k+2,2k
a)
3/ 2
b)
5/ 2
c)
2/ 3
d)
2/ 5
|
|
Krishna Iyer answered |
If 2k-1,k+2,2k are in AP, the difference of two consecutive terms will be same.
Therefore,
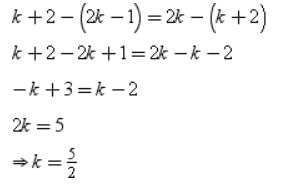
Therefore,
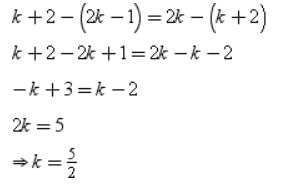
The sum of all 2-digit odd positive numbers is :- a)2475
- b)2530
- c)4905
- d)5049
Correct answer is option 'A'. Can you explain this answer?
The sum of all 2-digit odd positive numbers is :
a)
2475
b)
2530
c)
4905
d)
5049
|
Ishan Choudhury answered |
Here a = 11 and d = 2, tn= 99, n = ?
Sum of the n terms = (n/2)[2a+(n -1)d]
But tn = a + (n -1)d
⇒ 99 = 11+ (n-1)2
⇒ 99 -11 = (n-1)2
⇒ 88/2 = (n-1)
∴ n = 45.
subsitute n = 45 in sum of the n terms we obtain
⇒ s45 = (45/2)(2×11 + (45 -1)2)
⇒ s45 = (45/2)(110)
⇒ s45 = 45×55.
⇒ s45 = 2475.
∴ sum of all two digit odd positive numbers = 2475.
Sum of the n terms = (n/2)[2a+(n -1)d]
But tn = a + (n -1)d
⇒ 99 = 11+ (n-1)2
⇒ 99 -11 = (n-1)2
⇒ 88/2 = (n-1)
∴ n = 45.
subsitute n = 45 in sum of the n terms we obtain
⇒ s45 = (45/2)(2×11 + (45 -1)2)
⇒ s45 = (45/2)(110)
⇒ s45 = 45×55.
⇒ s45 = 2475.
∴ sum of all two digit odd positive numbers = 2475.
The weights of 11 students selected for a team are noted in ascending order and are in A. P. The lowest value is 45 Kg, and the middle value is 55 Kg. What is the difference between the two values placed consecutively ?
- a)4
- b)2
- c)6
- d)3
Correct answer is option 'B'. Can you explain this answer?
The weights of 11 students selected for a team are noted in ascending order and are in A. P. The lowest value is 45 Kg, and the middle value is 55 Kg. What is the difference between the two values placed consecutively ?
a)
4
b)
2
c)
6
d)
3
|
Nk Classes answered |
as there are 11 students so 6 th student would be middle one
a=45
a+(6-1)d=55
a+5d=55
45+5d=55
5d=10
d=2
a=45
a+(6-1)d=55
a+5d=55
45+5d=55
5d=10
d=2
Amit starts his exercise regime with 25 push ups on Monday. He plans to increase 5 push ups every following Monday. How many push ups will he be doing on the 3rd Monday since he started?- a)60
- b)70
- c)35
- d)45
Correct answer is option 'C'. Can you explain this answer?
Amit starts his exercise regime with 25 push ups on Monday. He plans to increase 5 push ups every following Monday. How many push ups will he be doing on the 3rd Monday since he started?
a)
60
b)
70
c)
35
d)
45
|
|
Pooja Shah answered |
On 1st Monday he did 25
on 2nd next he did 25+5=30
on 3rd Monday he did 30+5=35
on 2nd next he did 25+5=30
on 3rd Monday he did 30+5=35
Chapter doubts & questions for Arithmetic Progressions - Online MCQ Tests for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Arithmetic Progressions - Online MCQ Tests for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup