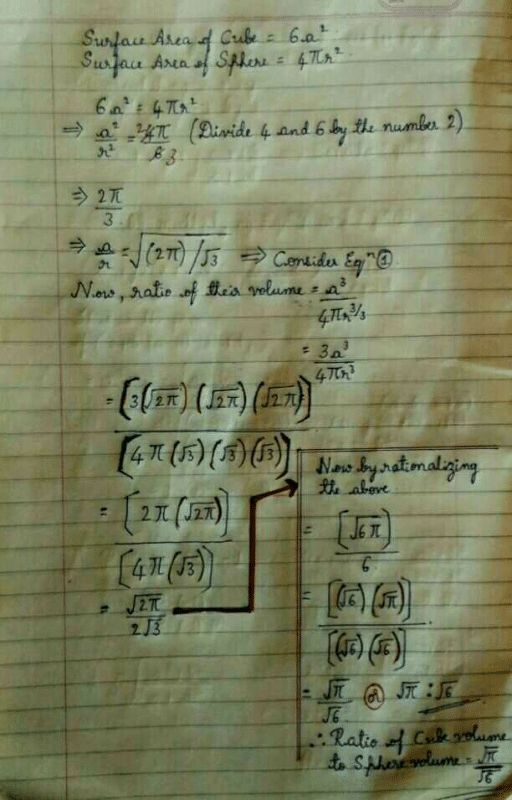All Exams >
Class 10 >
Online MCQ Tests for Class 10 >
All Questions
All questions of Surface Area and Volumes for Class 10 Exam
If a solid metallic sphere of radius 8 cm is melted and recasted into n spherical solid balls of radius 1 cm, then n =- a)500
- b)510
- c)512
- d)516
Correct answer is option 'C'. Can you explain this answer?
If a solid metallic sphere of radius 8 cm is melted and recasted into n spherical solid balls of radius 1 cm, then n =
a)
500
b)
510
c)
512
d)
516
|
Imk Pathshala answered |
In order to find the number of balls carved from larger sphere we need to divide the larger ball to small ball
A hollow cylindrical pipe is 21 cm long. If its outer and inner diameters are 10 cm and 6 cm respectively, then the volume of the metal used in making the pipe is (Take π = 22/7)- a)1048 cm3
- b)1056 cm3
- c)1060 cm3
- d)1064 cm3
Correct answer is option 'B'. Can you explain this answer?
A hollow cylindrical pipe is 21 cm long. If its outer and inner diameters are 10 cm and 6 cm respectively, then the volume of the metal used in making the pipe is (Take π = 22/7)
a)
1048 cm3
b)
1056 cm3
c)
1060 cm3
d)
1064 cm3
|
Krishna Iyer answered |
The height of the cylindrical pipe=21cm
inner radius=6cm
outer radius=10cm
volume of the metal used to make the Pipe=Π(R2-r2)h
=22/7×(102-62)
=1056cm
inner radius=6cm
outer radius=10cm
volume of the metal used to make the Pipe=Π(R2-r2)h
=22/7×(102-62)
=1056cm
3
If a marble of radius 2.1 cm is put into a cylindrical cup full of water of radius 5 cm and height 6 cm, then how much water flows out of the cylindricall cup?
- a)38.8 cm3
- b)55.4 cm3
- c)19.4 cm3
- d)471.4 cm3
Correct answer is option 'A'. Can you explain this answer?
If a marble of radius 2.1 cm is put into a cylindrical cup full of water of radius 5 cm and height 6 cm, then how much water flows out of the cylindricall cup?
a)
38.8 cm3
b)
55.4 cm3
c)
19.4 cm3
d)
471.4 cm3
|
|
Imk Pathshala answered |
Given, a marble of radius 2.1 cm is put into a cylindrical cup full of water of radius 5 cm and height 6 cm.
We have to find the quantity of water that flows out of the cylindrical cup.
We know that when the marble is put inside the cylindrical cup full of water the volume of water displaced is equal to the volume of the marble.
So, volume of water that flows out = volume of the marble
Volume of sphere = (4/3)πr3
Given, radius = 2.1 cm
So, volume of marble = (4/3)(22/7)(2.1)3
= 38.808 cm³
Therefore, the volume of the water that flows out is 38.8 cm³
If the radius and height of a cylinder are in the ratio 5 : 7 and its volume is 550 cm3, then its radius is equal to (Take π = 22/7)
a) 5 cmb) 7cmc) 6 cmd) 10 cmCorrect answer is option 'A'. Can you explain this answer?
|
Arun Yadav answered |
The answer is c.
Let the radius = r = 5x and height = h = 7x
Let the radius = r = 5x and height = h = 7x
So, the volume of the cylinder = π r^2 h
= 22/7 x (5x)^2 x 7x
= 22/7 x 25x^2 x 7x
= 22 x 25x (cube) (7 gets cancelled)
But it is given that volume = 550 cm cube
So, 22 x 25x (cube) = 550
x (cube) = 550 / 22 x 25
x(cube) = 1 ( as 22 x 25=550 and 550 is both in nm and dm)
x = 3√1
x = 1
so radius = 5x = 5 x 1 cm = 5cm (Ans.)
If the diameter of a metallic sphere is 6 cm, it is melted and a wire of diameter 0·2 cm is drawn, then the length of the wire made shall be- a)24 m
- b)28 m
- c)32 m
- d)36 m
Correct answer is option 'D'. Can you explain this answer?
If the diameter of a metallic sphere is 6 cm, it is melted and a wire of diameter 0·2 cm is drawn, then the length of the wire made shall be
a)
24 m
b)
28 m
c)
32 m
d)
36 m
|
|
Anita Menon answered |
We have
Diameter of metallic sphere =6cm
Radius of metallic sphere =3cm
Also we have
Diameter of cross-section of cylindrical wire=0.2cm
∴ Radius of cross-section fo cylindrical wire=0.1cm
Let the length of the wire be h cm
Since the metallic sphere is converted into a cylindrical shaped wire of length h cm
Volume of the metal used in wire= Volume of the sphere
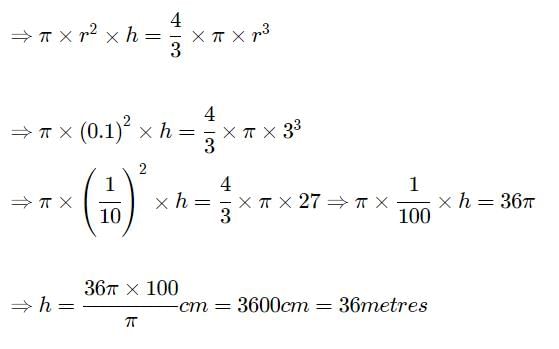
Diameter of metallic sphere =6cm
Radius of metallic sphere =3cm
Also we have
Diameter of cross-section of cylindrical wire=0.2cm
∴ Radius of cross-section fo cylindrical wire=0.1cm
Let the length of the wire be h cm
Since the metallic sphere is converted into a cylindrical shaped wire of length h cm
Volume of the metal used in wire= Volume of the sphere
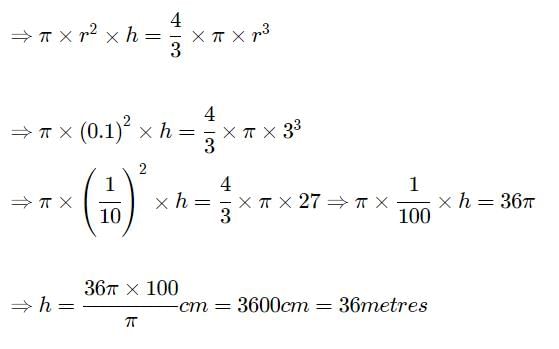
The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is- a)9.7 cm3
- b)77.6 cm3
- c)58.2 cm3
- d)19.4 cm3
Correct answer is option 'D'. Can you explain this answer?
The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
a)
9.7 cm3
b)
77.6 cm3
c)
58.2 cm3
d)
19.4 cm3
|
Rajeev Malik answered |
The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is 19.404 cm^3.
Edge of the cube = 4.2 cm
i.e 2r = 4.2
r = 4.2/2 = 2.1 cm
h = 4.2 cm
Volume of the cone = 1/3 * pi * r^2 * h
=> 1/3 * 22/7 * 2.1 * 2.1 * 4.2
=> 19.404 cm^3
Hence, the volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is 19.404 cm^3.
A hemisphere of lead of radius 9 cm is cast into a right circular cone of height 72 cm. The radius of the base of cone is- a)5.4 cm
- b)4.5 cm
- c)3 cm
- d)6 cm
Correct answer is option 'B'. Can you explain this answer?
A hemisphere of lead of radius 9 cm is cast into a right circular cone of height 72 cm. The radius of the base of cone is
a)
5.4 cm
b)
4.5 cm
c)
3 cm
d)
6 cm
|
|
Arun Sharma answered |
Given,
Radius of hemisphere = (R) = 9 cm
Height of cone = 72 cm
Let radius of cone = r cm
We know that,
Volume of hemisphere = volume of cone
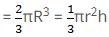
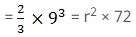
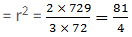
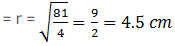
Radius of base of cone = 4.5 cm.
Radius of hemisphere = (R) = 9 cm
Height of cone = 72 cm
Let radius of cone = r cm
We know that,
Volume of hemisphere = volume of cone
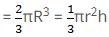
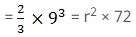
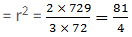
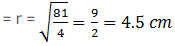
Radius of base of cone = 4.5 cm.
A solid iron rectangular block of dimensions 4.4 m, 2.6 m and 1 m is melted and cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. The length of the pipe will be- a)130 m
- b)102 m
- c)112 m
- d)120 m
Correct answer is option 'C'. Can you explain this answer?
A solid iron rectangular block of dimensions 4.4 m, 2.6 m and 1 m is melted and cast into a hollow cylindrical pipe of internal radius 30 cm and thickness 5 cm. The length of the pipe will be
a)
130 m
b)
102 m
c)
112 m
d)
120 m
|
Naina Sharma answered |
Given that:
Internal radius r=30 cm
Thickness w=5 cm
External radius R=30+5=35 cm
Thickness w=5 cm
External radius R=30+5=35 cm
Let the length of pipe be h.
Here,
The volume of cuboid = Volume of a hollow cylinder
440×260×100=π(R2–r2)h
⇒440×260×100=π(352–302)h
⇒440×260×100=π(325)h
⇒h=11204
The length of the pipe h=11204 cm=112.04 m
In a shower 10 cm of rain fall. The volume of water that falls on 1.5 hectares of ground is :- a)1500 m3
- b)1400 m3
- c)1200 m3
- d)1000 m3
Correct answer is option 'A'. Can you explain this answer?
In a shower 10 cm of rain fall. The volume of water that falls on 1.5 hectares of ground is :
a)
1500 m3
b)
1400 m3
c)
1200 m3
d)
1000 m3
|
|
Priyanshu Intelligent answered |
1 hectare = 10,000 m cube .
1.5 hectare = 15 , 000 m cube .
Height = 10 cm = 0.1 m.
Since, Volume = Area * Height
V = 15000 * 0.1 meter cube
V = 1500 meter cube .
Hence , option A is correct answer .
1.5 hectare = 15 , 000 m cube .
Height = 10 cm = 0.1 m.
Since, Volume = Area * Height
V = 15000 * 0.1 meter cube
V = 1500 meter cube .
Hence , option A is correct answer .
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is- a)64 : 27
- b)16 : 9
- c)16 : 27
- d)27 : 64
Correct answer is option 'A'. Can you explain this answer?
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is
a)
64 : 27
b)
16 : 9
c)
16 : 27
d)
27 : 64
|
|
Ananya Das answered |
Let r1 and r2 be the radius of the two spheres respectively. Therefore. the ratio of their volumes.
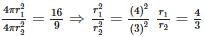
Now, ratio of thier volumes,
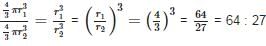
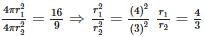
Now, ratio of thier volumes,
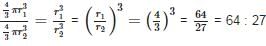
If the curved surface area of a right circular cone is 12320 cm2 and its base-radius is 56 cm, then its height is (Takeπ = 22/7)- a)42 cm
- b)36 cm
- c)48 cm
- d)52 cm
Correct answer is option 'A'. Can you explain this answer?
If the curved surface area of a right circular cone is 12320 cm2 and its base-radius is 56 cm, then its height is (Takeπ = 22/7)
a)
42 cm
b)
36 cm
c)
48 cm
d)
52 cm
|
Gayatri bajaj answered |
Π = 22/7)
We know that the curved surface area (CSA) of a cone is given by:
CSA = πrl
where r is the base radius of the cone, l is the slant height of the cone and π = 22/7.
We are given that the base radius is 56 cm and the CSA is 12320 cm². Let us first find the slant height:
12320 = (22/7) x 56 x l
l = (12320 x 7) / (22 x 56)
l = 140 cm
Now, we can use the Pythagorean theorem to find the height of the cone:
h² = l² - r²
h² = 140² - 56²
h² = 19136
h = √19136
h = 138.4 cm (approx)
Therefore, the height of the cone is approximately 138.4 cm.
We know that the curved surface area (CSA) of a cone is given by:
CSA = πrl
where r is the base radius of the cone, l is the slant height of the cone and π = 22/7.
We are given that the base radius is 56 cm and the CSA is 12320 cm². Let us first find the slant height:
12320 = (22/7) x 56 x l
l = (12320 x 7) / (22 x 56)
l = 140 cm
Now, we can use the Pythagorean theorem to find the height of the cone:
h² = l² - r²
h² = 140² - 56²
h² = 19136
h = √19136
h = 138.4 cm (approx)
Therefore, the height of the cone is approximately 138.4 cm.
A frustum of a right circular cone is of height 16 cm with radii of its ends as 8 cm and 20 cm. The volume of the frustum is- a)3328 π cm3
- b)3228 π cm3
- c)3240 π cm3
- d)3340 π cm3
Correct answer is option 'A'. Can you explain this answer?
A frustum of a right circular cone is of height 16 cm with radii of its ends as 8 cm and 20 cm. The volume of the frustum is
a)
3328 π cm3
b)
3228 π cm3
c)
3240 π cm3
d)
3340 π cm3
|
|
Priyanshu Intelligent answered |
🏅 Volume = 1/3 π * 16 [ (20*20) + (8*8) + 20*8]
= 1/3 π * 16 [400+64+160]
= 1/3 π * 16 * 624 )
= 1/3 * 9984 π
= 3328 π cm3.
Option a) is the correct answer.
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. The internal diameter of the shell is:- a)6√19 cm
- b)619 cm
- c)6(19)1/4 cm
- d)6(19)1/3 cm
Correct answer is option 'D'. Can you explain this answer?
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. The internal diameter of the shell is:
a)
6√19 cm
b)
619 cm
c)
6(19)1/4 cm
d)
6(19)1/3 cm
|
|
Cat Warior answered |
D
The total surface area of a solid hemisphere of radius 3·5 m is covered with canvas at the rate of Rs. 20 per m2. The total cost to cover the hemisphere is (Take π = 227)- a)Rs. 2210
- b)Rs. 2310
- c)Rs. 2320
- d)Rs. 2420
Correct answer is option 'B'. Can you explain this answer?
The total surface area of a solid hemisphere of radius 3·5 m is covered with canvas at the rate of Rs. 20 per m2. The total cost to cover the hemisphere is (Take π = 227)
a)
Rs. 2210
b)
Rs. 2310
c)
Rs. 2320
d)
Rs. 2420
|
|
Ananya Das answered |
Total Surface Area of a hemisphere of radius 'r' =3πr2
Hence, total surface area of this hemisphere =3×22/7×3.5×3.5=115.5sqm
∴ cost of covering the hemisphere with canvas at the rate of Rs. 20 per m2=115.5×20=Rs2310
Hence, total surface area of this hemisphere =3×22/7×3.5×3.5=115.5sqm
∴ cost of covering the hemisphere with canvas at the rate of Rs. 20 per m2=115.5×20=Rs2310
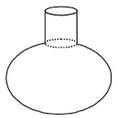
A container is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the sphere is 24 cm and the total height of the container is 16 cm. Its capacity is- a)5390.60 cm3
- b)5100 cm3
- c)5400 cm3
- d)5425.92 cm3
Correct answer is option 'D'. Can you explain this answer?
A container is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the sphere is 24 cm and the total height of the container is 16 cm. Its capacity is
a)
5390.60 cm3
b)
5100 cm3
c)
5400 cm3
d)
5425.92 cm3
|
Meghana shah answered |
To find the capacity of the container, we need to calculate the volume of the hemispherical bowl and the volume of the cylinder separately, and then add them together.
Given:
Diameter of the sphere = 24 cm
Total height of the container = 16 cm
**Calculating the Volume of the Hemispherical Bowl:**
The radius of the sphere (r) can be calculated by dividing the diameter by 2.
r = 24 cm / 2 = 12 cm
The volume of a hemisphere is given by the formula:
V_hemisphere = (2/3) * π * r^3
Substituting the value of r, we get:
V_hemisphere = (2/3) * π * 12^3
Calculating this value, we find:
V_hemisphere ≈ 3617.92 cm^3
**Calculating the Volume of the Cylinder:**
The height of the cylinder can be calculated by subtracting the radius of the sphere from the total height of the container.
Height of the cylinder = Total height of the container - Radius of the sphere
Height of the cylinder = 16 cm - 12 cm = 4 cm
The radius of the cylinder is the same as the radius of the sphere, which is 12 cm.
The volume of a cylinder is given by the formula:
V_cylinder = π * r^2 * h
Substituting the values of r and h, we get:
V_cylinder = π * 12^2 * 4
Calculating this value, we find:
V_cylinder ≈ 1809.28 cm^3
**Calculating the Total Capacity:**
The total capacity of the container is the sum of the volume of the hemisphere and the volume of the cylinder.
Total capacity = V_hemisphere + V_cylinder
Total capacity ≈ 3617.92 cm^3 + 1809.28 cm^3
Calculating this value, we find:
Total capacity ≈ 5427.20 cm^3
Rounding off to two decimal places, we get:
Total capacity ≈ 5425.92 cm^3
Therefore, the correct answer is option D) 5425.92 cm^3.
Given:
Diameter of the sphere = 24 cm
Total height of the container = 16 cm
**Calculating the Volume of the Hemispherical Bowl:**
The radius of the sphere (r) can be calculated by dividing the diameter by 2.
r = 24 cm / 2 = 12 cm
The volume of a hemisphere is given by the formula:
V_hemisphere = (2/3) * π * r^3
Substituting the value of r, we get:
V_hemisphere = (2/3) * π * 12^3
Calculating this value, we find:
V_hemisphere ≈ 3617.92 cm^3
**Calculating the Volume of the Cylinder:**
The height of the cylinder can be calculated by subtracting the radius of the sphere from the total height of the container.
Height of the cylinder = Total height of the container - Radius of the sphere
Height of the cylinder = 16 cm - 12 cm = 4 cm
The radius of the cylinder is the same as the radius of the sphere, which is 12 cm.
The volume of a cylinder is given by the formula:
V_cylinder = π * r^2 * h
Substituting the values of r and h, we get:
V_cylinder = π * 12^2 * 4
Calculating this value, we find:
V_cylinder ≈ 1809.28 cm^3
**Calculating the Total Capacity:**
The total capacity of the container is the sum of the volume of the hemisphere and the volume of the cylinder.
Total capacity = V_hemisphere + V_cylinder
Total capacity ≈ 3617.92 cm^3 + 1809.28 cm^3
Calculating this value, we find:
Total capacity ≈ 5427.20 cm^3
Rounding off to two decimal places, we get:
Total capacity ≈ 5425.92 cm^3
Therefore, the correct answer is option D) 5425.92 cm^3.
The edge of the cube whose volume is 1728cm is- a)17cm
- b)12cm
- c)18cm
- d)72cm
Correct answer is option 'B'. Can you explain this answer?
The edge of the cube whose volume is 1728cm is
a)
17cm
b)
12cm
c)
18cm
d)
72cm
|
Sagarika Nair answered |
Given : Volume of cube = 1728 cm
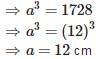
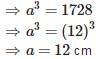
If the radius and slant height of a cone are in the ratio 4 : 7 and its curved surface area is 792 cm2, then its radius is (Take π = 22/7)- a)10 cm
- b)8 cm
- c)12 cm
- d)9 cm
Correct answer is option 'C'. Can you explain this answer?
If the radius and slant height of a cone are in the ratio 4 : 7 and its curved surface area is 792 cm2, then its radius is (Take π = 22/7)
a)
10 cm
b)
8 cm
c)
12 cm
d)
9 cm
|
|
Amol srinivasan answered |
Let the radius of the cone be 4x and the slant height be 7x.
The curved surface area of a cone is given by the formula A = πrl, where r is the radius and l is the slant height.
Plugging in the given values, we have:
792 = π(4x)(7x)
792 = 28πx^2
Dividing both sides of the equation by 28π:
792/(28π) = x^2
9 = x^2
Taking the square root of both sides:
x = 3
Therefore, the radius of the cone is 4x = 4(3) = 12 cm.
The curved surface area of a cone is given by the formula A = πrl, where r is the radius and l is the slant height.
Plugging in the given values, we have:
792 = π(4x)(7x)
792 = 28πx^2
Dividing both sides of the equation by 28π:
792/(28π) = x^2
9 = x^2
Taking the square root of both sides:
x = 3
Therefore, the radius of the cone is 4x = 4(3) = 12 cm.
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Surface Area and Volumes" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths) Q. If the volume of a cube is 1728 cm3, the length of its edge is equal to- a)12 cm
- b)14 cm
- c)16 cm
- d)24 cm
Correct answer is option 'A'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Surface Area and Volumes" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
Q. If the volume of a cube is 1728 cm3, the length of its edge is equal to
a)
12 cm
b)
14 cm
c)
16 cm
d)
24 cm
|
Vikram Kapoor answered |
Volume of the cube=a3=1728cm3
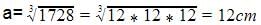
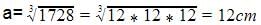
How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm.- a)64
- b)512
- c)8
- d)256
Correct answer is option 'B'. Can you explain this answer?
How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm.
a)
64
b)
512
c)
8
d)
256
|
|
Nikhila garg answered |
Solution:
Given, radius of solid sphere of lead = 8 cm
Radius of each ball = 1 cm
Let's assume that we can make n balls from the solid sphere of lead.
Then, the volume of the solid sphere of lead = sum of volumes of n balls
Volume of solid sphere of lead = 4/3π(8)^3 cubic cm
Volume of each ball = 4/3π(1)^3 cubic cm
Volume of n balls = n × 4/3π cubic cm
As we know that volume of solid sphere of lead = volume of n balls
4/3π(8)^3 = n × 4/3π(1)^3
n = (4/3π(8)^3)/(4/3π(1)^3)
n = (2^9)/(1^9) = 512
Therefore, the number of balls that can be made from a solid sphere of lead of radius 8 cm is 512.
Given, radius of solid sphere of lead = 8 cm
Radius of each ball = 1 cm
Let's assume that we can make n balls from the solid sphere of lead.
Then, the volume of the solid sphere of lead = sum of volumes of n balls
Volume of solid sphere of lead = 4/3π(8)^3 cubic cm
Volume of each ball = 4/3π(1)^3 cubic cm
Volume of n balls = n × 4/3π cubic cm
As we know that volume of solid sphere of lead = volume of n balls
4/3π(8)^3 = n × 4/3π(1)^3
n = (4/3π(8)^3)/(4/3π(1)^3)
n = (2^9)/(1^9) = 512
Therefore, the number of balls that can be made from a solid sphere of lead of radius 8 cm is 512.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is - a)4.2
- b)2.1
- c)8.1
- d)1.05
Correct answer is option 'B'. Can you explain this answer?
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
a)
4.2
b)
2.1
c)
8.1
d)
1.05
|
Akash Mehta answered |
Diameter of cone= edge of cube
Radius= edge of cube/2
=4.2/2
=2.1cm
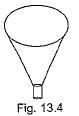
A cylindrical pencil sharpened at one edge is the combination of- a)a hemisphere and a cylinder
- b)a cone and a hemisphere
- c)a cone and a cylinder
- d)a frustum of a cone and a cylinder
Correct answer is option 'C'. Can you explain this answer?
A cylindrical pencil sharpened at one edge is the combination of
a)
a hemisphere and a cylinder
b)
a cone and a hemisphere
c)
a cone and a cylinder
d)
a frustum of a cone and a cylinder
|
Sahana Basu answered |
A cylindrical pencil sharpened at one edge is the combination of a cone and a cylinder.
A cone and a cylinder have their heights in the ratio 4: 5 and their diameters are in the ratio 3: 2. The ratio of their volumes will be- a)6: 7
- b)4: 3
- c)3: 5
- d)5: 3
Correct answer is option 'C'. Can you explain this answer?
A cone and a cylinder have their heights in the ratio 4: 5 and their diameters are in the ratio 3: 2. The ratio of their volumes will be
a)
6: 7
b)
4: 3
c)
3: 5
d)
5: 3
|
|
Ananya Das answered |
Height of cone =4x
Height of cylinder=5x
Diameter of cone=3y
Diameter of cylinder=2y
Volume of cone=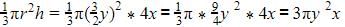
Volume of cylinder= πr2h=y2*5x
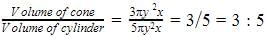
Height of cylinder=5x
Diameter of cone=3y
Diameter of cylinder=2y
Volume of cone=
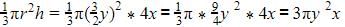Volume of cylinder= πr2h=y2*5x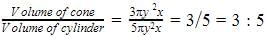 A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is- a)0.36 cm3
- b)0.35 cm3
- c)0.34 cm3
- d)0.33 cm3
Correct answer is option 'A'. Can you explain this answer?
A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is
a)
0.36 cm3
b)
0.35 cm3
c)
0.34 cm3
d)
0.33 cm3
|
Kds Coaching answered |
A cubical ice cream brick of edge 22 cm is to be distributed among some children by filling ice cream cones of radius 2 cm and height 7 cm upto its brim. How many children will get the ice cream cones?- a)163
- b)263
- c)363
- d)463
Correct answer is option 'C'. Can you explain this answer?
A cubical ice cream brick of edge 22 cm is to be distributed among some children by filling ice cream cones of radius 2 cm and height 7 cm upto its brim. How many children will get the ice cream cones?
a)
163
b)
263
c)
363
d)
463
|
|
Nature Lover answered |
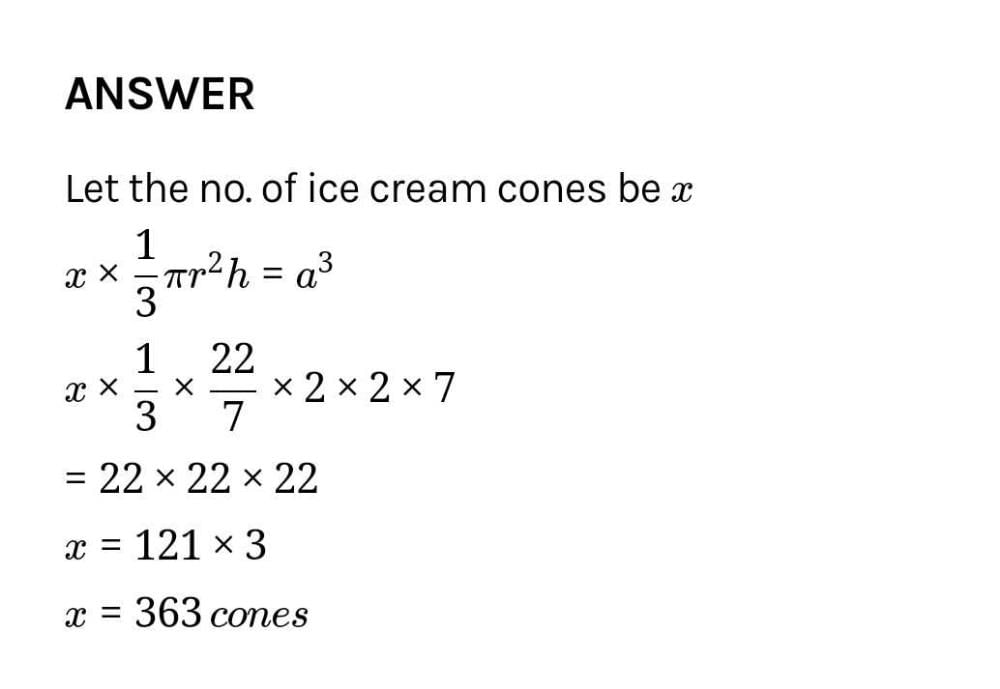
A cylinder, a cone and a hemisphere are of equal base and have the same height. The ratio of their volumes is
- a)4: 5: 7
- b)3: 2: 1
- c)1: 2:3
- d)3: 1: 2
Correct answer is option 'D'. Can you explain this answer?
A cylinder, a cone and a hemisphere are of equal base and have the same height. The ratio of their volumes is
a)
4: 5: 7
b)
3: 2: 1
c)
1: 2:3
d)
3: 1: 2
|
Abhishek Kumar Pandey answered |
According to me, Option D is not the right answer.....
option B is the right answer.
I am sorry because I couldn't able to attach the solution...
solution:
let r be the radius and h be the height.
so, ratio of volume of cylinder,cone& hemisphere=
πr²h: 1/3πr²h:2/3πr³
(since h=r)
=> πr³:1/3πr³:2/3πr³
=>1:1/3:2/3
=>3:1:2
your explanation.
If the radius of the base and the height of a right circular cone are respectively 21 cm and 28 cm, then the curved surface area of the cone is (Take π = 22/7)- a)3696 cm2
- b)2310 cm2
- c)2550 cm2
- d)2410 cm2
Correct answer is option 'B'. Can you explain this answer?
If the radius of the base and the height of a right circular cone are respectively 21 cm and 28 cm, then the curved surface area of the cone is (Take π = 22/7)
a)
3696 cm2
b)
2310 cm2
c)
2550 cm2
d)
2410 cm2
|
|
Abhishek Sharma answered |
For a cone, l=h^2+rr^2 whole root , where h is the height.
Hence, l=28^2+212^2 whole root
l=35 cm
Curved surface area of a cone =πrl where r is the radius of the cone and l is the slant height.
Hence, curved surface area of this cone =722×21×35=2310cm^2
Hence, l=28^2+212^2 whole root
l=35 cm
Curved surface area of a cone =πrl where r is the radius of the cone and l is the slant height.
Hence, curved surface area of this cone =722×21×35=2310cm^2
A toy is in the form of a cone mounted on a hemisphere with same radius. The diameter of the base of the conical portion is 6 cm and its height is 4 cm. The surface area of the toy is- a)36 π cm2
- b)33 π cm2
- c)35 π cm2
- d)24 π cm2
Correct answer is option 'B'. Can you explain this answer?
A toy is in the form of a cone mounted on a hemisphere with same radius. The diameter of the base of the conical portion is 6 cm and its height is 4 cm. The surface area of the toy is
a)
36 π cm2
b)
33 π cm2
c)
35 π cm2
d)
24 π cm2
|
|
Aarav murthy answered |
First, we need to find the radius of the hemisphere and the slant height of the cone.
The diameter of the base of the conical portion is 6cm, so the radius is 3cm.
To find the slant height of the cone, we can use the Pythagorean theorem. The height is 4cm and the radius is 3cm, so:
slant height = √(4^2 + 3^2) = 5cm
Now we can calculate the surface area of the toy. The surface area of the cone is:
πrℓ = π(3)(5) = 15π
The surface area of the hemisphere is:
2πr^2 = 2π(3^2) = 18π
Therefore, the total surface area of the toy is:
15π + 18π = 33π
So the answer is (b) 33π cm2.
The diameter of the base of the conical portion is 6cm, so the radius is 3cm.
To find the slant height of the cone, we can use the Pythagorean theorem. The height is 4cm and the radius is 3cm, so:
slant height = √(4^2 + 3^2) = 5cm
Now we can calculate the surface area of the toy. The surface area of the cone is:
πrℓ = π(3)(5) = 15π
The surface area of the hemisphere is:
2πr^2 = 2π(3^2) = 18π
Therefore, the total surface area of the toy is:
15π + 18π = 33π
So the answer is (b) 33π cm2.
A cylinder and a cone are of same base radius and of same height. The ratio of the volume of cylinder to that of the cone is:- a)1:2
- b)2:3
- c)3:1
- d)1:3
Correct answer is option 'C'. Can you explain this answer?
A cylinder and a cone are of same base radius and of same height. The ratio of the volume of cylinder to that of the cone is:
a)
1:2
b)
2:3
c)
3:1
d)
1:3
|
Moumita Joshi answered |
Introduction:
The question states that a cylinder and a cone have the same base radius and height. We are required to find the ratio of the volume of the cylinder to the volume of the cone.
Formula for the volume of a cylinder:
The volume of a cylinder is given by the formula Vcylinder = πr²h, where r is the base radius and h is the height.
Formula for the volume of a cone:
The volume of a cone is given by the formula Vcone = (1/3)πr²h, where r is the base radius and h is the height.
Calculating the volumes:
Let's assume the base radius of both the cylinder and the cone is 'r' and the height is 'h'. Using these values, we can calculate the volumes of both shapes.
Volume of the cylinder: Vcylinder = πr²h
Volume of the cone: Vcone = (1/3)πr²h
Ratio of the volumes:
To find the ratio of the volumes, we divide the volume of the cylinder by the volume of the cone.
Ratio = Vcylinder / Vcone
Ratio = (πr²h) / ((1/3)πr²h)
Ratio = 3
Conclusion:
The ratio of the volume of the cylinder to the volume of the cone is 3:1.
The question states that a cylinder and a cone have the same base radius and height. We are required to find the ratio of the volume of the cylinder to the volume of the cone.
Formula for the volume of a cylinder:
The volume of a cylinder is given by the formula Vcylinder = πr²h, where r is the base radius and h is the height.
Formula for the volume of a cone:
The volume of a cone is given by the formula Vcone = (1/3)πr²h, where r is the base radius and h is the height.
Calculating the volumes:
Let's assume the base radius of both the cylinder and the cone is 'r' and the height is 'h'. Using these values, we can calculate the volumes of both shapes.
Volume of the cylinder: Vcylinder = πr²h
Volume of the cone: Vcone = (1/3)πr²h
Ratio of the volumes:
To find the ratio of the volumes, we divide the volume of the cylinder by the volume of the cone.
Ratio = Vcylinder / Vcone
Ratio = (πr²h) / ((1/3)πr²h)
Ratio = 3
Conclusion:
The ratio of the volume of the cylinder to the volume of the cone is 3:1.
A cylinder, a cone and a hemisphere have equal base and height. Find the ratio of their volumes- a)1:1:1
- b)2:3:1
- c)3 :1 :2
- d)1:2:3
Correct answer is option 'C'. Can you explain this answer?
A cylinder, a cone and a hemisphere have equal base and height. Find the ratio of their volumes
a)
1:1:1
b)
2:3:1
c)
3 :1 :2
d)
1:2:3
|
|
Nandini jain answered |
**Given**
- A cylinder, a cone, and a hemisphere have equal base and height.
**To Find**
- The ratio of their volumes.
**Solution**
Let's assume the height and base radius of each shape to be 'h' and 'r', respectively.
**Volume of a Cylinder**
The volume of a cylinder is given by the formula:
Vcylinder = πr^2h
**Volume of a Cone**
The volume of a cone is given by the formula:
Vcone = (1/3)πr^2h
**Volume of a Hemisphere**
The volume of a hemisphere is given by the formula:
Vhemisphere = (2/3)πr^3
**Given Conditions**
- The base radius and height of the cylinder, cone, and hemisphere are equal.
- So, r = h for all three shapes.
**Substituting Values**
Substituting r = h in the volume formulas for each shape, we get:
Vcylinder = πr^2h = πh^2h = πh^3
Vcone = (1/3)πr^2h = (1/3)πh^2h = (1/3)πh^3
Vhemisphere = (2/3)πr^3 = (2/3)πh^3
**Comparing Volumes**
The ratio of the volumes of the cylinder, cone, and hemisphere can be found by dividing each volume by the volume of the cylinder (since the cylinder has the largest volume):
Ratio = (Vcylinder : Vcone : Vhemisphere) / Vcylinder
= (πh^3 : (1/3)πh^3 : (2/3)πh^3) / πh^3
= 1 : (1/3) : (2/3)
= 3 : 1 : 2
Therefore, the ratio of their volumes is 3 : 1 : 2. The correct answer is option 'C'.
- A cylinder, a cone, and a hemisphere have equal base and height.
**To Find**
- The ratio of their volumes.
**Solution**
Let's assume the height and base radius of each shape to be 'h' and 'r', respectively.
**Volume of a Cylinder**
The volume of a cylinder is given by the formula:
Vcylinder = πr^2h
**Volume of a Cone**
The volume of a cone is given by the formula:
Vcone = (1/3)πr^2h
**Volume of a Hemisphere**
The volume of a hemisphere is given by the formula:
Vhemisphere = (2/3)πr^3
**Given Conditions**
- The base radius and height of the cylinder, cone, and hemisphere are equal.
- So, r = h for all three shapes.
**Substituting Values**
Substituting r = h in the volume formulas for each shape, we get:
Vcylinder = πr^2h = πh^2h = πh^3
Vcone = (1/3)πr^2h = (1/3)πh^2h = (1/3)πh^3
Vhemisphere = (2/3)πr^3 = (2/3)πh^3
**Comparing Volumes**
The ratio of the volumes of the cylinder, cone, and hemisphere can be found by dividing each volume by the volume of the cylinder (since the cylinder has the largest volume):
Ratio = (Vcylinder : Vcone : Vhemisphere) / Vcylinder
= (πh^3 : (1/3)πh^3 : (2/3)πh^3) / πh^3
= 1 : (1/3) : (2/3)
= 3 : 1 : 2
Therefore, the ratio of their volumes is 3 : 1 : 2. The correct answer is option 'C'.
The diameters of the top and bottom of a bucket are 40 cm and 20 cm respectively. If the depth of the bucket is 12 cm then its volume will be- a)8000 cm3
- b)8800 cm3
- c)9000 cm3
- d)4400 cm3
Correct answer is option 'B'. Can you explain this answer?
The diameters of the top and bottom of a bucket are 40 cm and 20 cm respectively. If the depth of the bucket is 12 cm then its volume will be
a)
8000 cm3
b)
8800 cm3
c)
9000 cm3
d)
4400 cm3
|
|
Sonam dasgupta answered |
Volume = 1/3πh(R² + r² + R*r)
= 1/3*3.14*1.2*(2² + 1² + 2*1)
= 1/3*3.14*1.2*7
= 26.376/3
Volume = 8.792 cu dm ~= 8800 cm3
Two cubes each of 10 cm edge are joined end to end. The surface area of the resulting cuboid is- a)1200 cm2
- b)1000 cm2
- c)800 cm2
- d)1400 cm2
Correct answer is option 'B'. Can you explain this answer?
Two cubes each of 10 cm edge are joined end to end. The surface area of the resulting cuboid is
a)
1200 cm2
b)
1000 cm2
c)
800 cm2
d)
1400 cm2
|
|
Amit Kumar answered |
The length of the resulting cuboid=2 x 10 cm = 20 cm
Its width= 10 cm and its height = 10 cm
i.e. l=20cm, b=10cm, h=10 cm
∴The total surface area of the resulting cuboid
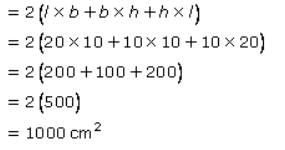
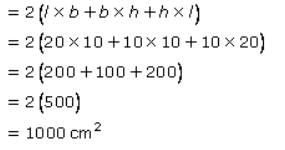
The inner dimensions of a closed box are 12cm, 10cm and 8cm. If the thickness of the wood is 1cm, then the capacity f the box is- a)1920 cu.cm
- b)480 cu.cm
- c)960 cu.cm
- d)1200 cu.cm
Correct answer is option 'C'. Can you explain this answer?
The inner dimensions of a closed box are 12cm, 10cm and 8cm. If the thickness of the wood is 1cm, then the capacity f the box is
a)
1920 cu.cm
b)
480 cu.cm
c)
960 cu.cm
d)
1200 cu.cm
|
Divya Choudhary answered |
Given: l = 12 cm, b = 10 cm and h = 8 cm
∴ Capacity of a closed box = lbh = 12 x 10 x 8 = 960 cm. cm
Capacity of box of thickness 1 cm = 960/1 = 960 cu. cm
∴ Capacity of a closed box = lbh = 12 x 10 x 8 = 960 cm. cm
Capacity of box of thickness 1 cm = 960/1 = 960 cu. cm
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the a hemisphere is 3.5 cm and height of cone outside the hemisphere is 5 cm, find the volume of the water left in the tub.- a)200 cm3
- b)600 cm3
- c)550 cm3
- d)616 cm3
Correct answer is option 'D'. Can you explain this answer?
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the a hemisphere is 3.5 cm and height of cone outside the hemisphere is 5 cm, find the volume of the water left in the tub.
a)
200 cm3
b)
600 cm3
c)
550 cm3
d)
616 cm3
|
Rajeev Chavan answered |
Given:
Radius of cylindrical tub, r = 5 cm
Length of cylindrical tub, l = 9.8 cm
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
To find: Volume of the water left in the tub
Approach:
First, we find the total volume of the cylindrical tub.
Then, we find the volume of the solid (cone mounted on a hemisphere) that is immersed in the tub.
Finally, we subtract the volume of the solid from the total volume of the tub to get the volume of the water left in the tub.
Calculation:
1. Volume of the cylindrical tub
Given,
Radius of the cylindrical tub, r = 5 cm
Length of the cylindrical tub, l = 9.8 cm
The formula for the volume of a cylinder is:
V_cylinder = πr^2l
Substituting the given values, we get:
V_cylinder = π(5)^2(9.8) = 245π cm^3
2. Volume of the solid (cone mounted on a hemisphere)
Given,
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
The solid consists of a cone mounted on a hemisphere. We can find the volume of the solid by adding the volumes of the cone and the hemisphere.
The formula for the volume of a cone is:
V_cone = 1/3πr^2h
Substituting the given values, we get:
V_cone = 1/3π(3.5)^2(5) = 61.25π/3 cm^3
The formula for the volume of a hemisphere is:
V_hemisphere = 2/3πR^3
Substituting the given values, we get:
V_hemisphere = 2/3π(3.5)^3 = 42.875π/3 cm^3
Therefore, the volume of the solid is:
V_solid = V_cone + V_hemisphere = 61.25π/3 + 42.875π/3 = 104.125π/3 cm^3
3. Volume of the water left in the tub
The volume of the water left in the tub is the total volume of the cylindrical tub minus the volume of the solid that is immersed in the tub.
V_water = V_cylinder - V_solid
V_water = 245π - 104.125π/3
V_water = 735/3π - 104.125/3π
V_water = (735 - 104.125)/3π
V_water = 216.875/3π cm^3
V_water = 216.875/3 × 3.14
V_water = 616.06 cm^3
Therefore, the volume of the water left in the tub is 616.06 cm^3 (approximately).
Hence, the correct option is (d) 616 cm^3.
Radius of cylindrical tub, r = 5 cm
Length of cylindrical tub, l = 9.8 cm
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
To find: Volume of the water left in the tub
Approach:
First, we find the total volume of the cylindrical tub.
Then, we find the volume of the solid (cone mounted on a hemisphere) that is immersed in the tub.
Finally, we subtract the volume of the solid from the total volume of the tub to get the volume of the water left in the tub.
Calculation:
1. Volume of the cylindrical tub
Given,
Radius of the cylindrical tub, r = 5 cm
Length of the cylindrical tub, l = 9.8 cm
The formula for the volume of a cylinder is:
V_cylinder = πr^2l
Substituting the given values, we get:
V_cylinder = π(5)^2(9.8) = 245π cm^3
2. Volume of the solid (cone mounted on a hemisphere)
Given,
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
The solid consists of a cone mounted on a hemisphere. We can find the volume of the solid by adding the volumes of the cone and the hemisphere.
The formula for the volume of a cone is:
V_cone = 1/3πr^2h
Substituting the given values, we get:
V_cone = 1/3π(3.5)^2(5) = 61.25π/3 cm^3
The formula for the volume of a hemisphere is:
V_hemisphere = 2/3πR^3
Substituting the given values, we get:
V_hemisphere = 2/3π(3.5)^3 = 42.875π/3 cm^3
Therefore, the volume of the solid is:
V_solid = V_cone + V_hemisphere = 61.25π/3 + 42.875π/3 = 104.125π/3 cm^3
3. Volume of the water left in the tub
The volume of the water left in the tub is the total volume of the cylindrical tub minus the volume of the solid that is immersed in the tub.
V_water = V_cylinder - V_solid
V_water = 245π - 104.125π/3
V_water = 735/3π - 104.125/3π
V_water = (735 - 104.125)/3π
V_water = 216.875/3π cm^3
V_water = 216.875/3 × 3.14
V_water = 616.06 cm^3
Therefore, the volume of the water left in the tub is 616.06 cm^3 (approximately).
Hence, the correct option is (d) 616 cm^3.
Chapter doubts & questions for Surface Area and Volumes - Online MCQ Tests for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Surface Area and Volumes - Online MCQ Tests for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup