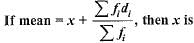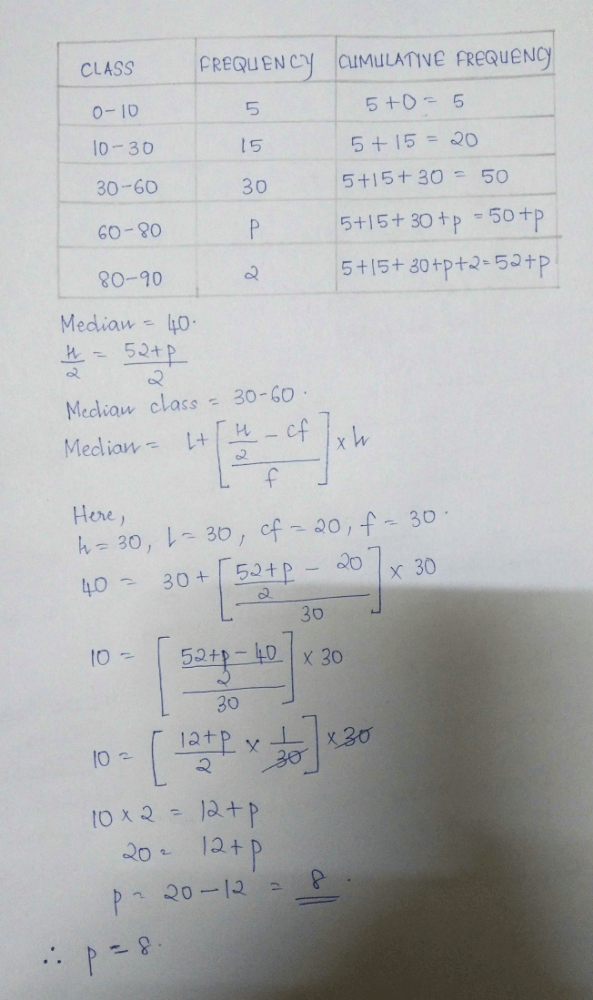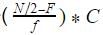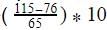All Exams >
Class 10 >
Online MCQ Tests for Class 10 >
All Questions
All questions of Statistics for Class 10 Exam
The wickets taken by a bowler in 10 cricket matches are 2, 6, 4, 5, 0, 3, 1, 3, 2, 3. The mode of the data is- a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
The wickets taken by a bowler in 10 cricket matches are 2, 6, 4, 5, 0, 3, 1, 3, 2, 3. The mode of the data is
a)
1
b)
2
c)
3
d)
4
|
|
Ananya Das answered |
Mode is the most frequently occurring observation. Since it's not a grouped data the frequency is the occurrence of only one observation , So the highest no. of frequency is 3 . So the modal age is 3.
Find out the mode of the following data:
- a)450
- b)400
- c)600
- d)478
Correct answer is option 'A'. Can you explain this answer?
Find out the mode of the following data:
a)
450
b)
400
c)
600
d)
478

|
Rohini Seth answered |
The mode of a set of data values is the value that appears most often .So mode is the most occurrence of observation.
Converting the distribution in continuous grouped and applying the formula
Mode=
Modal class is 400-500
Where L=lower limit of the modal class =400
f1= modal class frequency=32
f2 = just after the modal class frequency=20
f0 = just previous the modal class frequency=20
C = Class size=100
Mode=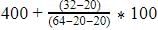
=400+50=450
Converting the distribution in continuous grouped and applying the formula
Mode=

Modal class is 400-500
Where L=lower limit of the modal class =400
f1= modal class frequency=32
f2 = just after the modal class frequency=20
f0 = just previous the modal class frequency=20
C = Class size=100
Mode=
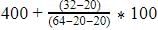
=400+50=450
The mean of all the factors of 24 is- a)7.5
- b)24
- c)7
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The mean of all the factors of 24 is
a)
7.5
b)
24
c)
7
d)
none of these

|
EduRev Class 10 answered |
To find the mean of all the factors of 24:
- List the factors of 24: 1, 2, 3, 4, 6, 8, 12, 24.
- Sum the factors: (1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60).
- Count the factors: There are 8 factors.
- Calculate the mean: Sum of the factors/ number of the factors = 60/8 = 7.5
Thus, the mean of all the factors is 7.5. The correct answer is A: 7.5.
- List the factors of 24: 1, 2, 3, 4, 6, 8, 12, 24.
- Sum the factors: (1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60).
- Count the factors: There are 8 factors.
- Calculate the mean: Sum of the factors/ number of the factors = 60/8 = 7.5
Thus, the mean of all the factors is 7.5. The correct answer is A: 7.5.
The marks obtained by 9 students in Mathematics are 59, 46, 30, 23, 27, 44, 52, 40 and 29. The median of the data is- a)30
- b)29
- c)35
- d)40
Correct answer is option 'D'. Can you explain this answer?
The marks obtained by 9 students in Mathematics are 59, 46, 30, 23, 27, 44, 52, 40 and 29. The median of the data is
a)
30
b)
29
c)
35
d)
40
|
|
Kiran Mehta answered |
Median is the middle value of the observations. So Median cannot be obtained when the observations are not in order. So first we have to arrange in ascending order.
59, 46, 30, 23, 27, 44, 52, 40 and 29
Gives- 23,27,29,30,40,44,46,52,59
Since the no. of observations is odd

59, 46, 30, 23, 27, 44, 52, 40 and 29
Gives- 23,27,29,30,40,44,46,52,59
Since the no. of observations is odd

The measure of central tendency that can be obtained graphically is- a)mean
- b)median
- c)mode
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The measure of central tendency that can be obtained graphically is
a)
mean
b)
median
c)
mode
d)
none of these

|
Smriti Tripathi answered |
I think its Median option(b)
The
median is a
simple measure of central tendency. To find the
median, we arrange the observations in order from smallest to largest value. If there is an odd number of observations, the
median is the middle value. If there is an even number of observations, the
median is the average of the two middle value
The mean of 1, 2, 3, 4 …n is given by- a)
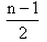
- b)n/2
- c)

- d)

Correct answer is option 'D'. Can you explain this answer?
The mean of 1, 2, 3, 4 …n is given by
a)
b)
n/2
c)
d)
|
|
Krishna Iyer answered |
⇒ We have the sequence, 1,2,3.......n
⇒ This is an AP, with the initial term a=1 and the common difference d=1.
∴ The sum of n terms of an AP is given by,
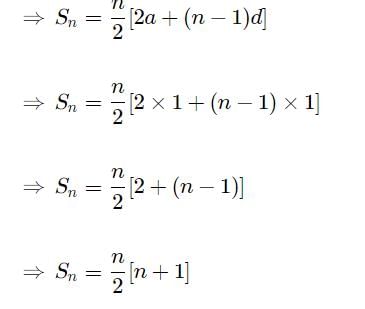
→ Arithmetic mean of n numbers a1,a2,a3,a4,...an is given by the formula
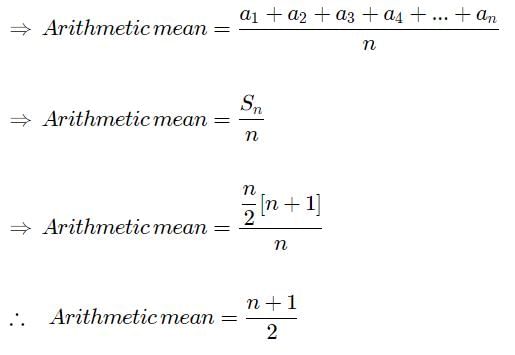
⇒ This is an AP, with the initial term a=1 and the common difference d=1.
∴ The sum of n terms of an AP is given by,
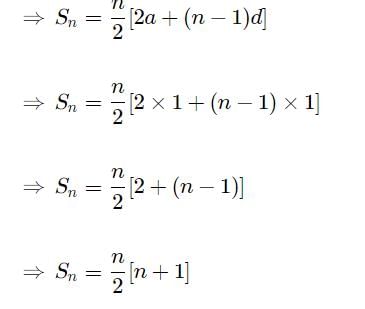
→ Arithmetic mean of n numbers a1,a2,a3,a4,...an is given by the formula
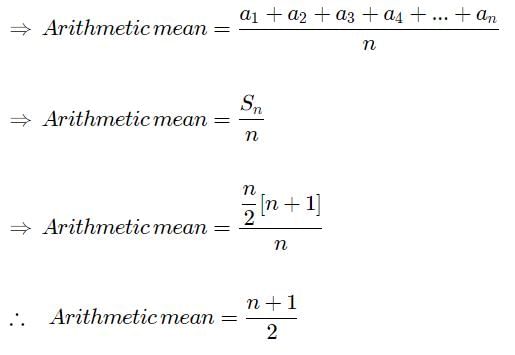
The mean of the first 10 natural numbers is- a)5
- b)6
- c)4.5
- d)5.5
Correct answer is option 'D'. Can you explain this answer?
The mean of the first 10 natural numbers is
a)
5
b)
6
c)
4.5
d)
5.5
|
|
Pooja Shah answered |
The first 10 natural numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10.
Mean = Sum of Observations/Total No of Observations
Mean = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 ÷ 10
Mean = 55/10
Mean = 5.5
Mean = Sum of Observations/Total No of Observations
Mean = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 ÷ 10
Mean = 55/10
Mean = 5.5
 What is the mode of the given data?
What is the mode of the given data?- a)24
- b)21
- c)22
- d)25
Correct answer is option 'A'. Can you explain this answer?
What is the mode of the given data?
a)
24
b)
21
c)
22
d)
25

|
Skyhigh Academy answered |
Mode= 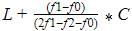
Where L=lower limit of the modal class =20
f1= modal class frequency.=27
f2 = just after the modal class frequency.=21
f0 = just previous the modal class frequency=23
C = Class size=10
Mode=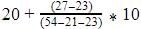
=20+4=24
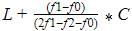
Where L=lower limit of the modal class =20
f1= modal class frequency.=27
f2 = just after the modal class frequency.=21
f0 = just previous the modal class frequency=23
C = Class size=10
Mode=
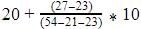
=20+4=24
The arithmetic mean of a set of 40 values is 65. If each of the 40 values is increased by 5, what will be the mean of the set of new values:- a)50
- b)60
- c)70
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The arithmetic mean of a set of 40 values is 65. If each of the 40 values is increased by 5, what will be the mean of the set of new values:
a)
50
b)
60
c)
70
d)
none of these
|
|
Arun Sharma answered |
We have mean = 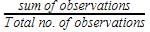
Mean =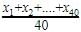
Now each value is increased by 5
Mean =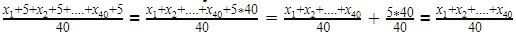
+5=65+5=70
Hence the mean is 70
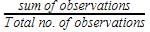
Mean =
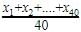
Now each value is increased by 5
Mean =
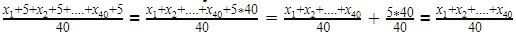
+5=65+5=70
Hence the mean is 70
The mean of the first 10 prime numbers is- a)12.9
- b)1.29
- c)129
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The mean of the first 10 prime numbers is
a)
12.9
b)
1.29
c)
129
d)
none of these

|
Let's Tute answered |
Step-by-step explanation:mean=2+3+5+7+11+13+17+19+23+29/10
Mean=129/10
Mean=12.9
If mean = (3 median - mode). k, then the value of k is- a)1
- b)2
- c)1/2
- d)3/2
Correct answer is option 'C'. Can you explain this answer?
If mean = (3 median - mode). k, then the value of k is
a)
1
b)
2
c)
1/2
d)
3/2
|
|
Kiran Mehta answered |
∵ Mode = 3 median - 2 mean
⇒ 2 mean = 3 m edian - mode

⇒ 2 mean = 3 m edian - mode

The age of 18 students of a class is reported below. Their modal age is 10, 17, 14, 10, 11, 12, 12, 13, 17, 13, 14, 14, 15, 16, 17, 15, 17, 16- a)22 years
- b)17 years
- c)14 years
- d)16 years
Correct answer is option 'B'. Can you explain this answer?
The age of 18 students of a class is reported below. Their modal age is 10, 17, 14, 10, 11, 12, 12, 13, 17, 13, 14, 14, 15, 16, 17, 15, 17, 16
a)
22 years
b)
17 years
c)
14 years
d)
16 years
|
|
Gaurav Kumar answered |
Mode is the highest number of times an observation occurs, which means the number that appears most frequently in a set. So modal age is the age which occurs maximum number of times. It is evident that 17 occurs most of the times. So, modal age is 17 years.
The mean of 15 numbers is 25. If each number is multiplied by 4, mean of the new numbers is- a)100
- b)40
- c)10
- d)60
Correct answer is option 'A'. Can you explain this answer?
The mean of 15 numbers is 25. If each number is multiplied by 4, mean of the new numbers is
a)
100
b)
40
c)
10
d)
60
|
|
Anmol Das answered |
Answer:
100
Step-by-step explanation:
mean=25
every number is multiplied by 4,
then 4 is common
Therefore, 25x4=100
The mean and median of same data are 24 and 26 respectively. The value of mode is :- a)26
- b)23
- c)25
- d)30
Correct answer is option 'D'. Can you explain this answer?
The mean and median of same data are 24 and 26 respectively. The value of mode is :
a)
26
b)
23
c)
25
d)
30
|
|
Neha Patel answered |
3 median = mode + 2 mean
3 * 26 = mode + 2 * 24
78 - 48 = mode
mode = 30
The marks obtained by 9 students in Mathematics are 59, 46, 31, 23, 27, 44, 52, 40 and 29. The mean of the data is- a)37
- b)38
- c)39
- d)40
Correct answer is option 'C'. Can you explain this answer?
The marks obtained by 9 students in Mathematics are 59, 46, 31, 23, 27, 44, 52, 40 and 29. The mean of the data is
a)
37
b)
38
c)
39
d)
40
|
|
Avinash Patel answered |
The mean is the average of the numbers.
So, Mean =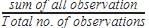
Mean= 351/9=39
351/9=39
So, Mean =
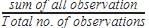
Mean=
 351/9=39
351/9=39The mean of five numbers is 28. If one of the numbers is excluded, the mean gets reduced by 2. The excluded number is- a)45
- b)36
- c)30
- d)25
Correct answer is option 'B'. Can you explain this answer?
The mean of five numbers is 28. If one of the numbers is excluded, the mean gets reduced by 2. The excluded number is
a)
45
b)
36
c)
30
d)
25
|
|
Vikas Kumar answered |
Mean of 5 nos.= 28
Therefore, sum of the 5 nos. = 28 * 5 = 140
The the no. exclude by 'x'.
New sum of 4 nos.= 140 - x
New mean = 28- 2 = 26
Therefore, (140 - x ) / 4 = 26
=> 140 - x = 104
=> x = 36
ANSWER= 36
In a data, if l = 40, h = 15, f1=7, f0=3, f2=6, then the mode is- a)52
- b)62
- c)72
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
In a data, if l = 40, h = 15, f1=7, f0=3, f2=6, then the mode is
a)
52
b)
62
c)
72
d)
none of these
|
|
Vivek Rana answered |
Mode=L+ 
Where L=lower limit of the modal class =40
f1= modal class frequency.=7
f2 = just after the modal class frequency.=6
f0 = just previous the modal class frequency=3
C = Class size=15
Mode=40+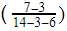 * 15 = 40 + 12 = 52
* 15 = 40 + 12 = 52

Where L=lower limit of the modal class =40
f1= modal class frequency.=7
f2 = just after the modal class frequency.=6
f0 = just previous the modal class frequency=3
C = Class size=15
Mode=40+
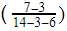 * 15 = 40 + 12 = 52
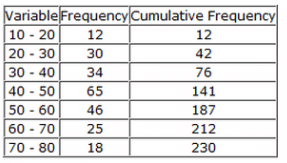
* 15 = 40 + 12 = 52The median of the given data is 46 and the total number of items is 230.
Using the formula Mode = 3 Median – 2 Mean, the mean will be- a)44
- b)43
- c)44.5
- d)45.9
Correct answer is option 'D'. Can you explain this answer?
The median of the given data is 46 and the total number of items is 230.

Using the formula Mode = 3 Median – 2 Mean, the mean will be
Using the formula Mode = 3 Median – 2 Mean, the mean will be
a)
44
b)
43
c)
44.5
d)
45.9
|
|
Ananya Das answered |
To find Mode
Mode=L+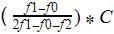
Where L=lower limit of the modal class = 40
f1 = modal class frequency.= 65
f2 = just after the modal class frequency.=46
f0 = just previous the modal class frequency=34
C = Class size=10
Mode =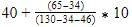
=46.2
Mode = 3 Median – 2 Mean
46.2 =3*46-2Mean
2Mean=138-46.2=91.8
Mean=91.8/2=45.9
Mode=L+
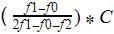
Where L=lower limit of the modal class = 40
f1 = modal class frequency.= 65
f2 = just after the modal class frequency.=46
f0 = just previous the modal class frequency=34
C = Class size=10
Mode =
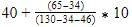
=46.2
Mode = 3 Median – 2 Mean
46.2 =3*46-2Mean
2Mean=138-46.2=91.8
Mean=91.8/2=45.9
If the median of the following data is 166.79, then the mean and mode are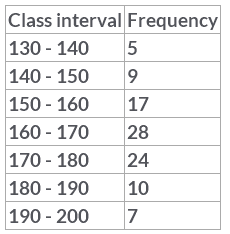
- a)Mode = 167.3, Mean = 168.03
- b)Mode = 160.9 Mean = 167
- c)Mode = 161.9 Mean = 168
- d)Mode = 152.9 Mean = 166.73
Correct answer is option 'A'. Can you explain this answer?
If the median of the following data is 166.79, then the mean and mode are
a)
Mode = 167.3, Mean = 168.03
b)
Mode = 160.9 Mean = 167
c)
Mode = 161.9 Mean = 168
d)
Mode = 152.9 Mean = 166.73
|
|
Amit Kumar answered |
We have
Mode=L+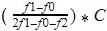
Where L=lower limit of the modal class =160
f1= modal class frequency.=28
f2 = just after the modal class frequency.=24
f0 = just previous the modal class frequency=17
C = Class size=10
Mode=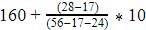
=167.3
Mode = 3 Median – 2 Mean
Mean=(3*166.79-167.3)/2=168.03
Mode=L+
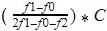
Where L=lower limit of the modal class =160
f1= modal class frequency.=28
f2 = just after the modal class frequency.=24
f0 = just previous the modal class frequency=17
C = Class size=10
Mode=
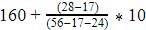
=167.3
Mode = 3 Median – 2 Mean
Mean=(3*166.79-167.3)/2=168.03
The mean of the following data 12, 22, 32,.......n2 is –- a)(n+1)(2n+1)/6
- b)n(n – 1)(2n+1)/6
- c)n(n+1)(2n – 1)/6
- d)n(n – 1)(2n – 1)/6
Correct answer is option 'A'. Can you explain this answer?
The mean of the following data 12, 22, 32,.......n2 is –
a)
(n+1)(2n+1)/6
b)
n(n – 1)(2n+1)/6
c)
n(n+1)(2n – 1)/6
d)
n(n – 1)(2n – 1)/6
|
|
Lighτ Yαmɪ answered |
Sum of Series 1²+2²+3²+….+n² = n(n+1)(2n+1)/6
[as, (1+2+3+4+…..n) = n(n+1) / 2
Using the identity: a^3 -b^3 = (a-b)(a² +ab +b²)
We get, x^3 -(x-1)^3 = 3x² -3x +1 , by putting x = 1,2,3…n
We get,
1^3 - 0^3 = 3×1² - 3×1 + 1
2^3 -1^3 = 3×2² - 3×2 +1
3^3 - 2^3 = 3×3² - 3×3 +1
…..
n^3 - (n-1)^3 = 3*n² - 3n +1
By adding LHS up to x=3
1^3–0^3 + 2^3–1^3 + 3^3–2^3 = 3^3 -0^3
So by adding LHS up to x= n
We get, n^3 - 0^3 …….. LHS
Now by adding RHS =
3( 1²+2²+3² +…n²) - 3( 1+2+3+….n) + n
=3(1²+2²+3²+..n²) = n^3 +3(1+2+3+…n) -n
=(1² +2²+3²+..n²) = 1/3 [n^3 +(3 n(n+1)/2) - n]
=(1²+2² +3² +..n²) = 1/3 [ (2n^3 +3n²+3n - 2n) /2 ]
= (1²+2²+3²+..n²) = ( 2n^3 +3n² +n) /6
=n (n+1)(2n+1) /6]
mean=sum/number of terms
=n(n+1)(2n+1)/6×n
=(n+1) (2n+1) /6
Hence, option A is correct
[as, (1+2+3+4+…..n) = n(n+1) / 2
Using the identity: a^3 -b^3 = (a-b)(a² +ab +b²)
We get, x^3 -(x-1)^3 = 3x² -3x +1 , by putting x = 1,2,3…n
We get,
1^3 - 0^3 = 3×1² - 3×1 + 1
2^3 -1^3 = 3×2² - 3×2 +1
3^3 - 2^3 = 3×3² - 3×3 +1
…..
n^3 - (n-1)^3 = 3*n² - 3n +1
By adding LHS up to x=3
1^3–0^3 + 2^3–1^3 + 3^3–2^3 = 3^3 -0^3
So by adding LHS up to x= n
We get, n^3 - 0^3 …….. LHS
Now by adding RHS =
3( 1²+2²+3² +…n²) - 3( 1+2+3+….n) + n
=3(1²+2²+3²+..n²) = n^3 +3(1+2+3+…n) -n
=(1² +2²+3²+..n²) = 1/3 [n^3 +(3 n(n+1)/2) - n]
=(1²+2² +3² +..n²) = 1/3 [ (2n^3 +3n²+3n - 2n) /2 ]
= (1²+2²+3²+..n²) = ( 2n^3 +3n² +n) /6
=n (n+1)(2n+1) /6]
mean=sum/number of terms
=n(n+1)(2n+1)/6×n
=(n+1) (2n+1) /6
Hence, option A is correct
In a data, if l = 60, h = 15, f1 = 16, f0 = 6, f2 = 6, then the mode is- a)60
- b)72
- c)67.5
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
In a data, if l = 60, h = 15, f1 = 16, f0 = 6, f2 = 6, then the mode is
a)
60
b)
72
c)
67.5
d)
none of these
|
|
Shreya Shajilal answered |
Mode=l+(f1-f0/2f1-f0-f2)×h
=60+(16-6/2×16-6-6)×15
=60+(10/20)×15
=60+(1/2)×15
=60+15/2
=60+7.5
=67.5.
Therefore the mode is 67.5.
=60+(16-6/2×16-6-6)×15
=60+(10/20)×15
=60+(1/2)×15
=60+15/2
=60+7.5
=67.5.
Therefore the mode is 67.5.
The mean and the median of a distribution are 45.9 and 46 respectively. The mode will be- a)45
- b)47
- c)48
- d)46.2
Correct answer is option 'D'. Can you explain this answer?
The mean and the median of a distribution are 45.9 and 46 respectively. The mode will be
a)
45
b)
47
c)
48
d)
46.2

|
Bye Bye answered |
Given, mean=45.9 and median=46
to find:- mode
as we know,
3median= 2mean+mode
3(46)=2(45.9)+mode
mode=138-91.8
mode=46.2
so correct answer is
(d)46.2
to find:- mode
as we know,
3median= 2mean+mode
3(46)=2(45.9)+mode
mode=138-91.8
mode=46.2
so correct answer is
(d)46.2
The following table gives the marks obtained by 80 students in a selection test:

The median marks is- a)34.3
- b)45.5
- c)20
- d)28.5
Correct answer is option 'A'. Can you explain this answer?
The following table gives the marks obtained by 80 students in a selection test:

The median marks is
The median marks is
a)
34.3
b)
45.5
c)
20
d)
28.5
|
|
Subset Academy answered |
Median = 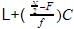
First change the table into continuous data.
Middle of the frequencies=40 which will lie in 30-40. So
L=30
N/2=80/2=40
F=27
f=30
c=10
Median =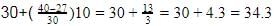
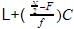
First change the table into continuous data.
Middle of the frequencies=40 which will lie in 30-40. So
L=30
N/2=80/2=40
F=27
f=30
c=10
Median =
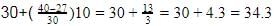
The median of first 10 prime numbers is- a)11
- b)12
- c)13
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The median of first 10 prime numbers is
a)
11
b)
12
c)
13
d)
none of these
|
|
Gaurav Kumar answered |
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. So 10 prime numbers are: 2,3,5,7,11,13,17,19,23,29
Since the number of terms are even ,
Median =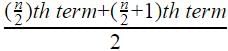
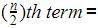 10/2=5th term=11
10/2=5th term=11
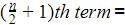 10/2 +1=6th term=13
10/2 +1=6th term=13
Median =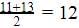
Since the number of terms are even ,
Median =
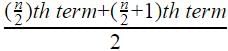
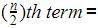 10/2=5th term=11
10/2=5th term=11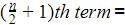 10/2 +1=6th term=13
10/2 +1=6th term=13Median =
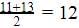
The mean of the following data is: 45, 35, 20, 15, 25, 40- a)15
- b)25
- c)30
- d)35
Correct answer is option 'C'. Can you explain this answer?
The mean of the following data is: 45, 35, 20, 15, 25, 40
a)
15
b)
25
c)
30
d)
35
|
|
Pankaj verma answered |
Mean of Data Set
To find the mean of a data set, we add up all the numbers in the set and then divide by the total number of values in the set.
Calculation
To find the mean of the given data set, we need to add up all the numbers in the set and then divide by the total number of values in the set:
Mean = (45 + 35 + 20 + 15 + 25 + 40) / 6
Mean = 180 / 6
Mean = 30
Therefore, the mean of the given data set is 30. The correct answer is option C.
To find the mean of a data set, we add up all the numbers in the set and then divide by the total number of values in the set.
Calculation
To find the mean of the given data set, we need to add up all the numbers in the set and then divide by the total number of values in the set:
Mean = (45 + 35 + 20 + 15 + 25 + 40) / 6
Mean = 180 / 6
Mean = 30
Therefore, the mean of the given data set is 30. The correct answer is option C.
Mode is not affected by- a)Maximum value
- b)Minimum value
- c)Extreme values
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Mode is not affected by
a)
Maximum value
b)
Minimum value
c)
Extreme values
d)
All of the above
|
|
Himaja Ammu answered |
Yaa.....mode is not affected by any of them
The mean of following distribution is –

- a)18.50
- b)18.05
- c)18.15
- d)18.25
Correct answer is option 'B'. Can you explain this answer?
The mean of following distribution is –
a)
18.50
b)
18.05
c)
18.15
d)
18.25
|
|
Ræjû Bhæï answered |
B option sahi hi n.. Bss isme khuss raho.. Aur explain chaiye toh subh ko fir milenge abhi sone ja rha hu.
The marks obtained by 9 students in Mathematics are 59, 46, 31, 23, 27, 40, 52, 35 and 29. The mean of the data is- a)23
- b)30
- c)38
- d)41
Correct answer is option 'C'. Can you explain this answer?
The marks obtained by 9 students in Mathematics are 59, 46, 31, 23, 27, 40, 52, 35 and 29. The mean of the data is
a)
23
b)
30
c)
38
d)
41
|
|
Pooja Shah answered |
The mean is the average of the numbers.
So, Mean =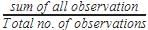
Mean=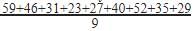 =342/9=38
=342/9=38
So, Mean =
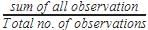
Mean=
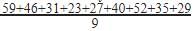 =342/9=38
=342/9=38Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Statistics" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths) Q. Which of the following is a measure of central tendency?- a)Frequency
- b)Cumulative frequency
- c)Mean
- d)Class limit
Correct answer is option 'C'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Statistics" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
Q. Which of the following is a measure of central tendency?
a)
Frequency
b)
Cumulative frequency
c)
Mean
d)
Class limit
|
|
Rahul Kapoor answered |
There are three main measures of central tendency: the mode, the median and the mean. Each of these measures describes a different indication of the typical or central value in the distribution. The mode is the most commonly occurring value in a distribution.
The mean of the first 10 multiples of 6 is- a)3.3
- b)33
- c)34
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The mean of the first 10 multiples of 6 is
a)
3.3
b)
33
c)
34
d)
none of these
|
|
Komal nayar answered |
Mean of First 10 Multiples of 6
To find the mean of the first 10 multiples of 6, we need to add the first 10 multiples of 6 and divide by 10.
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
Addition: 6 + 12 + 18 + 24 + 30 + 36 + 42 + 48 + 54 + 60 = 330
Mean: 330/10 = 33
Therefore, the correct answer is option B, 33.
To find the mean of the first 10 multiples of 6, we need to add the first 10 multiples of 6 and divide by 10.
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
Addition: 6 + 12 + 18 + 24 + 30 + 36 + 42 + 48 + 54 + 60 = 330
Mean: 330/10 = 33
Therefore, the correct answer is option B, 33.
If median of 20 observations is 50 and mode is also 50, then the mean is- a)45
- b)55
- c)50
- d)49
Correct answer is option 'C'. Can you explain this answer?
If median of 20 observations is 50 and mode is also 50, then the mean is
a)
45
b)
55
c)
50
d)
49

|
Ria Madan answered |
3Median =2Mean+Mode
3(50) = 2Mean+ 50
150-50=2Mean
100=2Mean
Mean=100/2
=50
Gende the mean is also 50
Hope it helps
3(50) = 2Mean+ 50
150-50=2Mean
100=2Mean
Mean=100/2
=50
Gende the mean is also 50
Hope it helps
Which of the following is not a measure of central tendency?- a)Standard deviation.
- b)Median
- c)Mode
- d)Mean
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a measure of central tendency?
a)
Standard deviation.
b)
Median
c)
Mode
d)
Mean

|
Priya Kumari answered |
Standard deviation are not central tendency
central tendency
!
!
!
!
3median = 2Mean + Mode
central tendency
!
!
!
!
3median = 2Mean + Mode
Mode is not affected by- a)Maximum value
- b)Minimum value
- c)Extreme values
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Mode is not affected by
a)
Maximum value
b)
Minimum value
c)
Extreme values
d)
All of the above

|
Anika Singh answered |
Mode is the measure which counts for the maximum no. Of frequency of a number. So for eg. I have 2,36,3,4,3.
So the mode is 3..the maximum value or minimum value doesn't matter
The mean of a data set with 12 observations is calculated as 19.25. If one more value is included in the data, then for the new data with 13 observations, mean becomes 20. Value of this 13th observation is- a)28
- b)29
- c)31
- d)30
Correct answer is option 'B'. Can you explain this answer?
The mean of a data set with 12 observations is calculated as 19.25. If one more value is included in the data, then for the new data with 13 observations, mean becomes 20. Value of this 13th observation is
a)
28
b)
29
c)
31
d)
30
|
|
Anita Menon answered |
Suppose be all twelevth terms = x
Mean = Terms / Observation
19 . 25 = x / 12
x = 19.25 × 12
x = 231 .00
Now let thirteenth term will be y
Mean = 20
So, 20 = x + y / 13
20 = 231 + y / 13
20 × 13 = 231 + x
260 = 231 + x
260 - 231 = x
29 = x
Mean = Terms / Observation
19 . 25 = x / 12
x = 19.25 × 12
x = 231 .00
Now let thirteenth term will be y
Mean = 20
So, 20 = x + y / 13
20 = 231 + y / 13
20 × 13 = 231 + x
260 = 231 + x
260 - 231 = x
29 = x
For a symmetrical distribution, which is correct- a)Mean > Mode > Median
- b)Mode = Mean+ Median/2
- c)Mean < Mode < Median
- d)Mean = Median = Mode
Correct answer is option 'D'. Can you explain this answer?
For a symmetrical distribution, which is correct
a)
Mean > Mode > Median
b)
Mode = Mean+ Median/2
c)
Mean < Mode < Median
d)
Mean = Median = Mode
|
|
Anjana Khatri answered |
Symmetrical distribution occurs when the values of variables occur at regular frequencies and the mean, median and mode occur at the same point. In graph form, symmetrical distribution often appears as a bell curve. If a line were drawn dissecting the middle of the graph, it would show two sides that mirror each other.
The class mark of the class 15.5 - 20.5
- a)15.5
- b)20.5
- c)18
- d)5
Correct answer is option 'C'. Can you explain this answer?
The class mark of the class 15.5 - 20.5
a)
15.5
b)
20.5
c)
18
d)
5

|
Crafty Classes answered |
class mark= (upper limit+lower limit)/2
= (15.5+20.5)/2
=36/2
=18
= (15.5+20.5)/2
=36/2
=18
The lower limit of the modal class of the following data is:
- a)10
- b)20
- c)30
- d)50
Correct answer is option 'B'. Can you explain this answer?
The lower limit of the modal class of the following data is:
a)
10
b)
20
c)
30
d)
50
|
|
Raghav Bansal answered |
Modal class is the interval which has the highest frequency ie, which occur most of the times.Here highest frequency is 13 in the class interval 20-30. So lower limit of the class interval is 20.
Which of the following is true –- a)Mode = 3Median + 2Mean
- b)Median = Mode +3/2[Mean – Median]
- c)Mean = Mode + 3/2[Median – Mode]
- d)Median = Mode + 3/2[Median + Mode]
Correct answer is option 'C'. Can you explain this answer?
Which of the following is true –
a)
Mode = 3Median + 2Mean
b)
Median = Mode +3/2[Mean – Median]
c)
Mean = Mode + 3/2[Median – Mode]
d)
Median = Mode + 3/2[Median + Mode]
|
|
Amit Sharma answered |
Mean = Mode + 3/2 [Median – Mode]
Mean= Mode+3/2 Median-3/2Mode
2 Mean=2 Mode+3 Median-3 Mode
3 Median=2 Mean + Mode
So C is the correct answer.
Mean= Mode+3/2 Median-3/2Mode
2 Mean=2 Mode+3 Median-3 Mode
3 Median=2 Mean + Mode
So C is the correct answer.
The mean of the marks obtained by 7 students in a group is 226. If the marks obtained by six of them are 340, 180, 260, 56, 275, 307, then the marks obtained by the seventh student are- a)200
- b)125
- c)174
- d)164
Correct answer is option 'D'. Can you explain this answer?
The mean of the marks obtained by 7 students in a group is 226. If the marks obtained by six of them are 340, 180, 260, 56, 275, 307, then the marks obtained by the seventh student are
a)
200
b)
125
c)
174
d)
164
|
|
Deepak trivedi answered |
Let's start by finding the sum of the marks obtained by the six students:
Sum of marks = 340 + 180 + 260 + 56 + 275 + 307 = 1418
We can then use the formula for the mean to find the total marks obtained by all seven students:
Mean = (Total marks) / (Number of students)
226 = (Total marks) / 7
Total marks = 1582
Finally, we can find the marks obtained by the seventh student by subtracting the sum of the marks obtained by the six students from the total marks obtained by all seven students:
Marks obtained by seventh student = Total marks - Sum of marks
Marks obtained by seventh student = 1582 - 1418
Marks obtained by seventh student = 164
Therefore, the answer is (d) 164.
Sum of marks = 340 + 180 + 260 + 56 + 275 + 307 = 1418
We can then use the formula for the mean to find the total marks obtained by all seven students:
Mean = (Total marks) / (Number of students)
226 = (Total marks) / 7
Total marks = 1582
Finally, we can find the marks obtained by the seventh student by subtracting the sum of the marks obtained by the six students from the total marks obtained by all seven students:
Marks obtained by seventh student = Total marks - Sum of marks
Marks obtained by seventh student = 1582 - 1418
Marks obtained by seventh student = 164
Therefore, the answer is (d) 164.
Mode and mean of a data are 12k and 15k. Median of the data is- a)12k
- b)14k
- c)15k
- d)16k
Correct answer is option 'B'. Can you explain this answer?
Mode and mean of a data are 12k and 15k. Median of the data is
a)
12k
b)
14k
c)
15k
d)
16k
|
|
Amit Kumar answered |
Here's the solution to your question:
If two values are given in the below formula than we can use the formula if one is given than we cannot use the formula
3median = 2mean+mode
3median = 2(15k)+12k
3median = 30k+12k
3median = 42k
median = 42k/3
median = 14k
You can understand all the concepts of Class 10 mathematics through the link:
The class marks of the class 18-22 is- a)4
- b)18
- c)22
- d)20
Correct answer is option 'D'. Can you explain this answer?
The class marks of the class 18-22 is
a)
4
b)
18
c)
22
d)
20
|
|
Harshit Agrawal answered |
We know that ,
Class Mark = upper limit + lower limit /2
--->. Class Mark = 22 + 18/2
--->. Class Mark = 40/2
--->. Class Mark = 20
Hence , option D is correct.
Class Mark = upper limit + lower limit /2
--->. Class Mark = 22 + 18/2
--->. Class Mark = 40/2
--->. Class Mark = 20
Hence , option D is correct.
The mean of the first 10 natural odd numbers is- a)9
- b)10
- c)11
- d)12
Correct answer is option 'B'. Can you explain this answer?
The mean of the first 10 natural odd numbers is
a)
9
b)
10
c)
11
d)
12
|
|
Ananya Das answered |
Natural numbers start from 1
First ten natural odd numbers=1,3,5,7,9,11,13,15,17,19
Mean =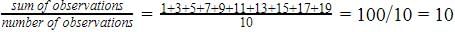
So mean is 10.
First ten natural odd numbers=1,3,5,7,9,11,13,15,17,19
Mean =
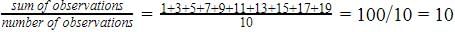
So mean is 10.
Chapter doubts & questions for Statistics - Online MCQ Tests for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Statistics - Online MCQ Tests for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Related Class 10 Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily