All Exams >
Class 6 >
Online MCQ Tests for Class 6 >
All Questions
All questions of Mensuration for Class 6 Exam
The side of a square is 6 cm. If its side is doubled, then its new perimeter is- a)48 cm
- b)36 cm
- c)60 cm
- d)24 cm
Correct answer is option 'A'. Can you explain this answer?
The side of a square is 6 cm. If its side is doubled, then its new perimeter is
a)
48 cm
b)
36 cm
c)
60 cm
d)
24 cm
|
|
Devika Basak answered |
To find the new perimeter of a square when its side is doubled, we need to first calculate the new side length of the square after doubling its original side length.
Given that the original side length of the square is 6 cm, we can find the new side length by multiplying the original side length by 2.
New side length = 6 cm * 2 = 12 cm
Now that we have the new side length, we can calculate the new perimeter of the square by multiplying the new side length by 4 (since a square has four equal sides).
New perimeter = 12 cm * 4 = 48 cm
Therefore, the correct answer is option A) 48 cm.
Given that the original side length of the square is 6 cm, we can find the new side length by multiplying the original side length by 2.
New side length = 6 cm * 2 = 12 cm
Now that we have the new side length, we can calculate the new perimeter of the square by multiplying the new side length by 4 (since a square has four equal sides).
New perimeter = 12 cm * 4 = 48 cm
Therefore, the correct answer is option A) 48 cm.
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Mensuration, Class 6, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic. Q. The length and breadth of a rectangle are 40 cm and 10 cm respectively. Its perimeter is- a)140 cm
- b)160 cm
- c)80 cm
- d)120 cm
Correct answer is option 'C'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Mensuration, Class 6, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q. The length and breadth of a rectangle are 40 cm and 10 cm respectively. Its perimeter is
a)
140 cm
b)
160 cm
c)
80 cm
d)
120 cm

|
Swara Mukherjee answered |
Area of rectangle = 400 cm^2
400 =
side^2
side = 20 cm
perimeter of square = 4 side
= 80 cm
If the area of a square is 64 cm2, then its perimeter is
- a)32 cm
- b)24 cm
- c)16 cm
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If the area of a square is 64 cm2, then its perimeter is
a)
32 cm
b)
24 cm
c)
16 cm
d)
None of these

|
Gayatri Chavan answered |
The correct option is A 32 cm
Given:
Area of the square =64 cm2
We know, area of a square = side × side
⇒64=(side)2
∴ Side of the square = 8 cm
Perimeter of the square =4×side
=4×8
=32 cm
Therefore, perimeter of the square = 32 cm
Given:
Area of the square =64 cm2
We know, area of a square = side × side
⇒64=(side)2
∴ Side of the square = 8 cm
Perimeter of the square =4×side
=4×8
=32 cm
Therefore, perimeter of the square = 32 cm
Area of a rectangle = ________- a)(length + breadth)
- b)(length/breadth)
- c)(length × breadth)
- d)(length - breadth)
Correct answer is option 'C'. Can you explain this answer?
Area of a rectangle = ________
a)
(length + breadth)
b)
(length/breadth)
c)
(length × breadth)
d)
(length - breadth)
|
|
Mansi Yadav answered |
• Perimeter of Rectangle = 2 × ( L + B )
• Area of Rectangle = L × B
• Area of Rectangle = L × B
Find the area of square whose perimeter is 48cm- a)144 cm2
- b)4 m2
- c)1 m
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the area of square whose perimeter is 48cm
a)
144 cm2
b)
4 m2
c)
1 m
d)
None of these
|
|
Suhana Jha answered |
perimeter = 4*S
length of each side = 48/4=12
area = 12*12 =
144 cm
2
please upvote if this helps you !
What is the perimeter of a square of side s units?
- a)4s units
- b)S4 units
- c)4 + s units
- d)s × s units
Correct answer is option 'A'. Can you explain this answer?
What is the perimeter of a square of side s units?
a)
4s units
b)
S4 units
c)
4 + s units
d)
s × s units
|
|
Sania Arju answered |
Here 's' is a variable. The formula of getting the perimeter of a square is 4× side length. You imagine that you have a square and its 1 side length is s unit, so the answer will be 4×s= 4s units.
The perimeter of a rectangle is 170 m and its length is 50 m. What is its breadth?
- a)80 m
- b)35 m
- c)55 m
- d)60 m
Correct answer is option 'B'. Can you explain this answer?
The perimeter of a rectangle is 170 m and its length is 50 m. What is its breadth?
a)
80 m
b)
35 m
c)
55 m
d)
60 m

|
EduRev Class 6 answered |
2(l+b) = 170
2(50+b) = 170
50 + b = 170/2 = 85
b = 85−50 = 35m
2(50+b) = 170
50 + b = 170/2 = 85
b = 85−50 = 35m
Which figure encloses more area: a square of side 2 cm ; a rectangle of side 3 cm and 2 cm ;An equilateral triangle of side 4 cm?- a)rectangle
- b)square
- c)equilateral triangle
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Which figure encloses more area: a square of side 2 cm ; a rectangle of side 3 cm and 2 cm ;An equilateral triangle of side 4 cm?
a)
rectangle
b)
square
c)
equilateral triangle
d)
None of these

|
Tamana Jindal answered |
Area of square =side ×side 2×2 4cm
area of rectangle=l×b so 3×2=6cm2
area of equilateral triangle=4×3=12cm2
so option c is correct
area of rectangle=l×b so 3×2=6cm2
area of equilateral triangle=4×3=12cm2
so option c is correct
The side of a square is 12 m. Its perimeter is- a)36 m
- b)24 m
- c)48 m
- d)144 m
Correct answer is option 'C'. Can you explain this answer?
The side of a square is 12 m. Its perimeter is
a)
36 m
b)
24 m
c)
48 m
d)
144 m
|
|
Anita Menon answered |
Perimeter of square is 4 X side
thus 4 X 12 = 48 m
The side of a square is 8 cm. If its side is doubled, then its new perimeter is- a)48 cm
- b)32 cm
- c)40 cm
- d)64 cm
Correct answer is option 'D'. Can you explain this answer?
The side of a square is 8 cm. If its side is doubled, then its new perimeter is
a)
48 cm
b)
32 cm
c)
40 cm
d)
64 cm
|
|
Akash Tiwari answered |
Given:
- The side of the square is 8 cm.
To find:
- The new perimeter when the side is doubled.
Calculation:
1. The perimeter of a square is given by the formula: P = 4s, where s is the length of a side.
2. The given square has a side length of 8 cm, so its initial perimeter is P = 4(8) = 32 cm.
3. When the side length is doubled, the new side length becomes 2 * 8 = 16 cm.
4. The new perimeter is then given by P = 4(16) = 64 cm.
Answer:
The new perimeter of the square, when its side is doubled, is 64 cm. Therefore, the correct answer is option D.
Perimeter of a rectangle = _________ × (length + breadth)- a)2
- b)5
- c)4
- d)3
Correct answer is option 'A'. Can you explain this answer?
Perimeter of a rectangle = _________ × (length + breadth)
a)
2
b)
5
c)
4
d)
3
|
|
Hansraj Bhadane answered |
The formula for the perimeter of a rectangle is
2 × length + breadth.
2 × length + breadth.
The perimeter of a square is 728 cm. Find the measure of its side.- a)81 cm
- b)182m
- c)128cm
- d)182cm
Correct answer is option 'D'. Can you explain this answer?
The perimeter of a square is 728 cm. Find the measure of its side.
a)
81 cm
b)
182m
c)
128cm
d)
182cm

|
Gayatri Chavan answered |
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square.
We know that all the sides of a square are equal.
Perimeter of a Square
Perimeter of the square ABCD
= AB + BC + CD + AD
= 2 cm + 2 cm + 2 cm + 2 cm
= (2 x 4) cm
= 8 cm
Perimeter of a square is 4 times of s side.
Perimeter of a square = 4 x length of a side.
The perimeter of a square is 100 cm. Its side is- a)50 cm
- b)25 cm
- c)20 cm
- d)10 cm
Correct answer is option 'B'. Can you explain this answer?
The perimeter of a square is 100 cm. Its side is
a)
50 cm
b)
25 cm
c)
20 cm
d)
10 cm
|
|
Shilpa Shah answered |
Given, Perimeter of the square = 100 cm
Let the side of the square be 'a' cm.
Perimeter of square = 4 × Side
So, 4 × a = 100
Simplifying the above equation, we get:
a = 25 cm
Therefore, the side of the square is 25 cm.
Hence, option B is the correct answer.
Let the side of the square be 'a' cm.
Perimeter of square = 4 × Side
So, 4 × a = 100
Simplifying the above equation, we get:
a = 25 cm
Therefore, the side of the square is 25 cm.
Hence, option B is the correct answer.
A farmer has a rectangular field of length and breadth 240 m and 180 m respectively. He wants to fence it with 3 rounds of rope. What is the total length of rope he must use?- a)2700 m
- b)2520 m
- c)2400 m
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A farmer has a rectangular field of length and breadth 240 m and 180 m respectively. He wants to fence it with 3 rounds of rope. What is the total length of rope he must use?
a)
2700 m
b)
2520 m
c)
2400 m
d)
None of these

|
Keshav Garg answered |
Answer is 2520m option B
Find the area of a square plot of side 7 m.- a)28 m2
- b)49 m
- c)49 m2
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Find the area of a square plot of side 7 m.
a)
28 m2
b)
49 m
c)
49 m2
d)
None of these
|
|
NANDNI answered |
49m².
side of square = 7m
area of square= side × side
= 7 × 7.
49m²
side of square = 7m
area of square= side × side
= 7 × 7.
49m²
Perimeter of a square = ________ × length of a side- a)4
- b)3
- c)2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Perimeter of a square = ________ × length of a side
a)
4
b)
3
c)
2
d)
None of these
|
|
Priyanka Sharma answered |
To find the perimeter of a square, we need to multiply the length of one side by 4, as all sides of a square are equal in length.
The formula for the perimeter of a square is:
Perimeter = 4 * Length of a side
Step-by-step solution:
1. Identify the formula for the perimeter of a square: Perimeter = 4 * Length of a side.
2. The question states that the length of a side is multiplied by the perimeter to find the perimeter of a square.
3. We need to choose the option that correctly represents the formula for finding the perimeter of a square.
4. Option A: 4. This option correctly represents the formula for the perimeter of a square, as it shows that the perimeter is equal to 4 times the length of a side.
5. Option B: 3. This option does not represent the correct formula for finding the perimeter of a square. It is incorrect.
6. Option C: 2. This option does not represent the correct formula for finding the perimeter of a square. It is incorrect.
7. Option D: None of these. This option does not represent the correct formula for finding the perimeter of a square. It is incorrect.
8. Therefore, the correct answer is option A: 4.
Answer: A. 4
In a square shaped park, whose side measures 28 m, a rectangular pond is located at the centre with dimensions 3 m and 2 m. What is the area of the park excluding the pond?- a)784 sq. m
- b)6 sq. m
- c)778 sq. m
- d)708 sq. m
Correct answer is option 'C'. Can you explain this answer?
In a square shaped park, whose side measures 28 m, a rectangular pond is located at the centre with dimensions 3 m and 2 m. What is the area of the park excluding the pond?
a)
784 sq. m
b)
6 sq. m
c)
778 sq. m
d)
708 sq. m
|
|
Bhaskar Gupta answered |
Area of pond = 3m × 2m = 6 sq m
Area of park = 28 × 28
= 784 sq m
Area of the park excluding the pond
= 784-6
= 778 sq m
Area of park = 28 × 28
= 784 sq m
Area of the park excluding the pond
= 784-6
= 778 sq m
The area of a rectangle is 96 cm2. If the breadth of the rectangle is 8 cm, find its perimeter. - a)5 cm
- b)40 cm
- c)6 cm
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The area of a rectangle is 96 cm2. If the breadth of the rectangle is 8 cm, find its perimeter.
a)
5 cm
b)
40 cm
c)
6 cm
d)
None of these
|
|
Sudha Menon answered |
Area of rectangle = L×B
96 = L×8
L = 96/8
Length of rectangle = 12cm
Perimeter of rectangle = 2×(l+b)
= 2× (12+8)
= 2×20
Perimeter of rectangle =40 cm
96 = L×8
L = 96/8
Length of rectangle = 12cm
Perimeter of rectangle = 2×(l+b)
= 2× (12+8)
= 2×20
Perimeter of rectangle =40 cm
Samuel wanted to erect some vertical stones along the boundary of his plot at a distance of 10 m each. If the length of the plot is 30 m and the breadth is 15 m how many stones are required?- a)450
- b)45
- c)9
- d)10
Correct answer is option 'C'. Can you explain this answer?
Samuel wanted to erect some vertical stones along the boundary of his plot at a distance of 10 m each. If the length of the plot is 30 m and the breadth is 15 m how many stones are required?
a)
450
b)
45
c)
9
d)
10
|
|
Anoushka gupta answered |
Perimeter of plot = 2(l+b) = 2(30+15) = 90m
Distance between two stones = 10m
Therefore, number of stones = 90/10 = 9
How many sq. cm make a sq. m?- a)100
- b)1000
- c)10000
- d)10
Correct answer is option 'C'. Can you explain this answer?
How many sq. cm make a sq. m?
a)
100
b)
1000
c)
10000
d)
10

|
Sagar Mehra answered |
1 sq. m = 10,000 sq. cm
Find the perimeter of a regular pentagon with each side measuring 3 cm.- a)12 cm
- b)9 cm
- c)6 cm
- d)15 cm
Correct answer is option 'D'. Can you explain this answer?
Find the perimeter of a regular pentagon with each side measuring 3 cm.
a)
12 cm
b)
9 cm
c)
6 cm
d)
15 cm
|
|
Suhana Jha answered |
sides of pentagon = 5
perimeter = 3*S
= 3*5 = 15
please upvote answer if it helps you !
What is the perimeter of an equilateral triangle of side a units?- a)2a + b units
- b)3a units
- c)a + b + c units
- d)a + 2b units
Correct answer is option 'B'. Can you explain this answer?
What is the perimeter of an equilateral triangle of side a units?
a)
2a + b units
b)
3a units
c)
a + b + c units
d)
a + 2b units
|
|
Himaja Ammu answered |
Perimeter of an equilateral triangle =a+a+a=3a
If the perimeter of a square is 44 cm, then its area is- a)121 cm2
- b)121 cm
- c)33 cm2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If the perimeter of a square is 44 cm, then its area is
a)
121 cm2
b)
121 cm
c)
33 cm2
d)
None of these
|
|
Shadow 😇🤍 answered |
Given, Perimeter of square =44 cm
We know perimeter of square =4a
where ′a′ is side of square
4a÷44=11
Area of square = 44 x 44
Area = 121 cm2
Area will be 121 cm²
We know perimeter of square =4a
where ′a′ is side of square
4a÷44=11
Area of square = 44 x 44
Area = 121 cm2
Area will be 121 cm²
The area of a rectangle is 630 sq. cm and its breadth is 15 cm. What is its length?- a)40 cm
- b)60 cm
- c)42 cm
- d)35 cm
Correct answer is option 'C'. Can you explain this answer?
The area of a rectangle is 630 sq. cm and its breadth is 15 cm. What is its length?
a)
40 cm
b)
60 cm
c)
42 cm
d)
35 cm
|
|
Shubham Gupta answered |
length x breadth = 630
length = 630/breadth
= 630/15
length = 42 cm
Find the area of a rectangle whose length is 11 cm and breadth is 4 cm.- a)36 sq. cm
- b)44 sq. cm
- c)52 sq. cm
- d)60 sq. cm
Correct answer is option 'B'. Can you explain this answer?
Find the area of a rectangle whose length is 11 cm and breadth is 4 cm.
a)
36 sq. cm
b)
44 sq. cm
c)
52 sq. cm
d)
60 sq. cm

|
Vp Classes answered |
The area of a rectangle is calculated using the formula:
Area=Length×Breadth
Substitute the given values:
Area=11×4=44 sq. cm
Meera went to a park 150 m long and 80 m wide. She took one complete round on its boundary. What is the distance covered by her?- a)230 m
- b)460 m
- c)300 m
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Meera went to a park 150 m long and 80 m wide. She took one complete round on its boundary. What is the distance covered by her?
a)
230 m
b)
460 m
c)
300 m
d)
None of these
|
|
Deepak Majumdar answered |
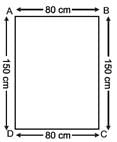
Let ABCD is a park whose lengths are BC, AD and widths are AB, CD, respectively. Hence, AB = CD = 80 m. and BC = DA = 150m Now, the sum of the lengths of four sides
=AB + BC + CD + DA
= 80 m + 150 m + 80 m + 150 m
= (80 + 150 + 80 + 150) m
=460 m
Perimeter of the park = sum of the lengths of four sides of the park = 460 m
Hence, distance covered by Meera is 460 m.
A table top is covered with 25 squares of equal size. The side of the square is 3 cm. What is the area of the table top?- a)300 sq. cm
- b)225 cm
- c)225 sq. cm
- d)300 cm
Correct answer is option 'C'. Can you explain this answer?
A table top is covered with 25 squares of equal size. The side of the square is 3 cm. What is the area of the table top?
a)
300 sq. cm
b)
225 cm
c)
225 sq. cm
d)
300 cm

|
Subham Verma answered |
Area of square
= s × s
= 3×3 = 9 sq. cm
Area of 25 squares
= 25 × 9
= 225 sq.cm
= s × s
= 3×3 = 9 sq. cm
Area of 25 squares
= 25 × 9
= 225 sq.cm
A wooden plank measures 6 m in length and 3 m in breadth. If five such wooden planks are arranged in order, what is the area occupied by them?- a)18 sq. m
- b)90 sq. m
- c)5 sq. m
- d)95 sq. m
Correct answer is option 'B'. Can you explain this answer?
A wooden plank measures 6 m in length and 3 m in breadth. If five such wooden planks are arranged in order, what is the area occupied by them?
a)
18 sq. m
b)
90 sq. m
c)
5 sq. m
d)
95 sq. m
|
|
Debolina Shah answered |
The area occupied by the wooden planks can be calculated by multiplying the length and breadth of the arrangement. Given that each wooden plank measures 6 m in length and 3 m in breadth, we can determine the area occupied by five such wooden planks arranged in order as follows:
1. Calculate the area of a single wooden plank:
- Length = 6 m
- Breadth = 3 m
- Area = Length x Breadth = 6 m x 3 m = 18 sq. m
2. Determine the total area occupied by five wooden planks:
- As we have five wooden planks arranged in order, the total area would be the sum of the areas of each individual plank.
- Total area = 18 sq. m (area of a single plank) x 5 (number of planks) = 90 sq. m
Therefore, the area occupied by five wooden planks arranged in order is 90 square meters.
So, the correct answer is option B: 90 sq. m.
1. Calculate the area of a single wooden plank:
- Length = 6 m
- Breadth = 3 m
- Area = Length x Breadth = 6 m x 3 m = 18 sq. m
2. Determine the total area occupied by five wooden planks:
- As we have five wooden planks arranged in order, the total area would be the sum of the areas of each individual plank.
- Total area = 18 sq. m (area of a single plank) x 5 (number of planks) = 90 sq. m
Therefore, the area occupied by five wooden planks arranged in order is 90 square meters.
So, the correct answer is option B: 90 sq. m.
80 students of the same height stand with both hands stretched all along the sides of a rectangular garden, each student covering a length of 1.75 m. What is the perimeter of the garden?
- a)1400 m
- b)140 m
- c)14 m
- d)1400 km
Correct answer is option 'B'. Can you explain this answer?
80 students of the same height stand with both hands stretched all along the sides of a rectangular garden, each student covering a length of 1.75 m. What is the perimeter of the garden?
a)
1400 m
b)
140 m
c)
14 m
d)
1400 km

|
Deepika Basu answered |
Perimeter of garden= covering made by the 80 students
80 × 1.75 m = 140 m
80 × 1.75 m = 140 m
An isosceles triangle has a measure of p units for its equal sides and q units for its unequal side. What is its perimeter?- a)2 (p + q) units
- b)2p + q units
- c)2q + p units
- d)2 (q + p) units
Correct answer is option 'B'. Can you explain this answer?
An isosceles triangle has a measure of p units for its equal sides and q units for its unequal side. What is its perimeter?
a)
2 (p + q) units
b)
2p + q units
c)
2q + p units
d)
2 (q + p) units
|
|
Nabanita Khanna answered |
Explanation:
An isosceles triangle is a triangle with two equal sides. Let's call the measure of the equal sides as "p" units and the measure of the unequal side as "q" units.
Perimeter of a triangle:
The perimeter of any polygon is the sum of the lengths of all its sides. In the case of a triangle, the perimeter is the sum of the lengths of all three sides.
Calculating the perimeter of the isosceles triangle:
The isosceles triangle has two equal sides, each measuring "p" units, and one unequal side measuring "q" units.
To calculate the perimeter, we need to add up the lengths of all three sides.
Perimeter = p + p + q
Simplifying the expression, we get:
Perimeter = 2p + q
Therefore, the correct answer is option B: 2p + q units.
An isosceles triangle is a triangle with two equal sides. Let's call the measure of the equal sides as "p" units and the measure of the unequal side as "q" units.
Perimeter of a triangle:
The perimeter of any polygon is the sum of the lengths of all its sides. In the case of a triangle, the perimeter is the sum of the lengths of all three sides.
Calculating the perimeter of the isosceles triangle:
The isosceles triangle has two equal sides, each measuring "p" units, and one unequal side measuring "q" units.
To calculate the perimeter, we need to add up the lengths of all three sides.
Perimeter = p + p + q
Simplifying the expression, we get:
Perimeter = 2p + q
Therefore, the correct answer is option B: 2p + q units.
If the perimeter of a square is 16 cm, then its area is- a)16 cm2
- b)12 cm2
- c)10 cm2
- d)15 cm2
Correct answer is option 'A'. Can you explain this answer?
If the perimeter of a square is 16 cm, then its area is
a)
16 cm2
b)
12 cm2
c)
10 cm2
d)
15 cm2
|
|
Manasa Saha answered |
Understanding the Perimeter of a Square
The perimeter of a square is the total distance around it. For a square, the perimeter can be calculated using the formula:
- Perimeter = 4 × side length
Given that the perimeter is 16 cm, we can find the side length:
- 4 × side length = 16 cm
- Side length = 16 cm / 4
- Side length = 4 cm
Calculating the Area of the Square
The area of a square measures the space contained within it. The formula for the area is:
- Area = side length × side length
Now, substituting the side length we found:
- Area = 4 cm × 4 cm
- Area = 16 cm²
Conclusion
Thus, the area of the square, when the perimeter is 16 cm, is:
- Answer: 16 cm²
This matches option 'A'.
Key Takeaway
- Perimeter = 4 × side length
- Area = side length × side length
- Side length from perimeter = 4 cm
- Area calculated = 16 cm²
Understanding these concepts helps in solving similar problems easily!
The perimeter of a square is the total distance around it. For a square, the perimeter can be calculated using the formula:
- Perimeter = 4 × side length
Given that the perimeter is 16 cm, we can find the side length:
- 4 × side length = 16 cm
- Side length = 16 cm / 4
- Side length = 4 cm
Calculating the Area of the Square
The area of a square measures the space contained within it. The formula for the area is:
- Area = side length × side length
Now, substituting the side length we found:
- Area = 4 cm × 4 cm
- Area = 16 cm²
Conclusion
Thus, the area of the square, when the perimeter is 16 cm, is:
- Answer: 16 cm²
This matches option 'A'.
Key Takeaway
- Perimeter = 4 × side length
- Area = side length × side length
- Side length from perimeter = 4 cm
- Area calculated = 16 cm²
Understanding these concepts helps in solving similar problems easily!
On a wall of dimensions 10.5 m long and 8.5 m wide, a square shaped wall poster is stuck at the centre whose side measure is 2.5 m. If the remaining part of the wall is to be painted with pink colour costing Rs. 12 per sq. m, how much does it cost?- a)Rs. 89.25
- b)Rs. 996
- c)Rs. 830
- d)Rs. 12
Correct answer is option 'B'. Can you explain this answer?
On a wall of dimensions 10.5 m long and 8.5 m wide, a square shaped wall poster is stuck at the centre whose side measure is 2.5 m. If the remaining part of the wall is to be painted with pink colour costing Rs. 12 per sq. m, how much does it cost?
a)
Rs. 89.25
b)
Rs. 996
c)
Rs. 830
d)
Rs. 12
|
|
Devika Basak answered |
Calculation:
To find the area of the remaining part of the wall that needs to be painted, we first need to calculate the area of the square wall poster and then subtract it from the total area of the wall.
Area of the square wall poster:
Given side of the square = 2.5 m
Area of a square = side x side
Area of the square wall poster = 2.5 x 2.5 = 6.25 sq. m
Total area of the wall:
Length of the wall = 10.5 m
Width of the wall = 8.5 m
Total area of the wall = Length x Width
Total area of the wall = 10.5 x 8.5 = 89.25 sq. m
Remaining area to be painted:
Remaining area = Total area of the wall - Area of the square wall poster
Remaining area = 89.25 - 6.25 = 83 sq. m
Cost of painting the remaining area:
Cost per sq. m = Rs. 12
Total cost = Cost per sq. m x Remaining area
Total cost = 12 x 83 = Rs. 996
Therefore, the cost of painting the remaining part of the wall with pink color is Rs. 996. Hence, the correct answer is option B.
To find the area of the remaining part of the wall that needs to be painted, we first need to calculate the area of the square wall poster and then subtract it from the total area of the wall.
Area of the square wall poster:
Given side of the square = 2.5 m
Area of a square = side x side
Area of the square wall poster = 2.5 x 2.5 = 6.25 sq. m
Total area of the wall:
Length of the wall = 10.5 m
Width of the wall = 8.5 m
Total area of the wall = Length x Width
Total area of the wall = 10.5 x 8.5 = 89.25 sq. m
Remaining area to be painted:
Remaining area = Total area of the wall - Area of the square wall poster
Remaining area = 89.25 - 6.25 = 83 sq. m
Cost of painting the remaining area:
Cost per sq. m = Rs. 12
Total cost = Cost per sq. m x Remaining area
Total cost = 12 x 83 = Rs. 996
Therefore, the cost of painting the remaining part of the wall with pink color is Rs. 996. Hence, the correct answer is option B.
Find the perimeter of an isosceles triangle with equal sides 8 cm each and third side 6 cm.- a)20 cm
- b)22 cm
- c)14 cm
- d)16 cm
Correct answer is option 'B'. Can you explain this answer?
Find the perimeter of an isosceles triangle with equal sides 8 cm each and third side 6 cm.
a)
20 cm
b)
22 cm
c)
14 cm
d)
16 cm
|
|
Nishtha Mukherjee answered |
Given,
Equal sides of an isosceles triangle = 8 cm each
Third side = 6 cm
To find: Perimeter of the triangle
Explanation:
The perimeter of a triangle is the sum of the lengths of all its sides.
In an isosceles triangle, two sides are equal in length.
Therefore, the perimeter of an isosceles triangle with equal sides of length 8 cm each and the third side of length 6 cm can be calculated as follows:
Perimeter = Sum of all sides
Perimeter = 8 cm + 8 cm + 6 cm
Perimeter = 22 cm
Therefore, the perimeter of the given isosceles triangle is 22 cm.
Hence, the correct answer is option B.
Equal sides of an isosceles triangle = 8 cm each
Third side = 6 cm
To find: Perimeter of the triangle
Explanation:
The perimeter of a triangle is the sum of the lengths of all its sides.
In an isosceles triangle, two sides are equal in length.
Therefore, the perimeter of an isosceles triangle with equal sides of length 8 cm each and the third side of length 6 cm can be calculated as follows:
Perimeter = Sum of all sides
Perimeter = 8 cm + 8 cm + 6 cm
Perimeter = 22 cm
Therefore, the perimeter of the given isosceles triangle is 22 cm.
Hence, the correct answer is option B.
The length of a rectangle is 150 cm. If its breadth is 1 m, then its perimeter is- a)300 cm
- b)250 cm
- c)5 m
- d)2 m
Correct answer is option 'C'. Can you explain this answer?
The length of a rectangle is 150 cm. If its breadth is 1 m, then its perimeter is
a)
300 cm
b)
250 cm
c)
5 m
d)
2 m
|
|
Ananya Das answered |
Understanding Rectangle Dimensions
To find the perimeter of a rectangle, we need to know its length and breadth. In this case:
- Length: 150 cm
- Breadth: 1 m
Unit Conversion
Before calculating the perimeter, we must ensure both dimensions are in the same unit.
- Convert the breadth from meters to centimeters:
- 1 m = 100 cm
- Therefore, the breadth is 100 cm.
Calculating the Perimeter
The formula for calculating the perimeter (P) of a rectangle is:
P = 2 * (Length + Breadth)
Now substituting the values:
- Length = 150 cm
- Breadth = 100 cm
Substituting Values
- P = 2 * (150 cm + 100 cm)
- P = 2 * (250 cm)
- P = 500 cm
Converting Perimeter to Meters
The perimeter in centimeters is 500 cm. To convert this to meters:
- 500 cm = 5 m
Conclusion
Thus, the perimeter of the rectangle is 5 m, making the correct answer option 'C'.
To find the perimeter of a rectangle, we need to know its length and breadth. In this case:
- Length: 150 cm
- Breadth: 1 m
Unit Conversion
Before calculating the perimeter, we must ensure both dimensions are in the same unit.
- Convert the breadth from meters to centimeters:
- 1 m = 100 cm
- Therefore, the breadth is 100 cm.
Calculating the Perimeter
The formula for calculating the perimeter (P) of a rectangle is:
P = 2 * (Length + Breadth)
Now substituting the values:
- Length = 150 cm
- Breadth = 100 cm
Substituting Values
- P = 2 * (150 cm + 100 cm)
- P = 2 * (250 cm)
- P = 500 cm
Converting Perimeter to Meters
The perimeter in centimeters is 500 cm. To convert this to meters:
- 500 cm = 5 m
Conclusion
Thus, the perimeter of the rectangle is 5 m, making the correct answer option 'C'.
What is the area of the given figure? 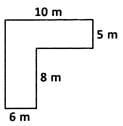
- a)2400 sq. m
- b)48 sq. m
- c)50 sq. m
- d)98 sq. m
Correct answer is option 'D'. Can you explain this answer?
What is the area of the given figure?

a)
2400 sq. m
b)
48 sq. m
c)
50 sq. m
d)
98 sq. m

|
Get Idea answered |
10×5 = 50sq.m
6×8=48 sq. m
∴ The required area = 50 + 48 = 98 sq. m
6×8=48 sq. m
∴ The required area = 50 + 48 = 98 sq. m
The side of a square is 8 cm. Its area is- a)12 cm2
- b)16 cm2
- c)81 cm2
- d)64 cm2
Correct answer is option 'D'. Can you explain this answer?
The side of a square is 8 cm. Its area is
a)
12 cm2
b)
16 cm2
c)
81 cm2
d)
64 cm2

|
Get Idea answered |
To find the area of a square, we need to square the length of one of its sides.
Given:
Side of the square = 8 cm
To find the area of the square, we can use the formula:
Area = side * side
Substituting the given value, we have:
Area = 8 cm * 8 cm
Calculating the area, we get:
Area = 64 cm²
Therefore, the area of the square is 64 cm².
Answer: D. 64 cm²
Given:
Side of the square = 8 cm
To find the area of the square, we can use the formula:
Area = side * side
Substituting the given value, we have:
Area = 8 cm * 8 cm
Calculating the area, we get:
Area = 64 cm²
Therefore, the area of the square is 64 cm².
Answer: D. 64 cm²
If the area of rectangle increases from 2 cm2 to 4 cm2 the perimeter will- a)decreases
- b)increases
- c)remain same
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If the area of rectangle increases from 2 cm2 to 4 cm2 the perimeter will
a)
decreases
b)
increases
c)
remain same
d)
None of these

|
Get Idea answered |
To solve this problem, we need to understand the relationship between the area and perimeter of a rectangle.
1. Area of a rectangle:
- The area is calculated using the formula: Area = length × width.
2. Perimeter of a rectangle:
- The perimeter is calculated using the formula: Perimeter = 2 × (length + width).
3. Relationship between area and perimeter:
- If the area increases, it indicates that either the length or width, or both, have increased.
- Possible scenarios include:
- If only the length increases while the width stays the same, the perimeter will increase.
- If only the width increases while the length stays the same, the perimeter will increase.
- If both dimensions increase, the perimeter will also increase.
4. Applying the concepts to the given problem:
- The area of the rectangle increases from 2 cm² to 4 cm², indicating an increase in either length or width.
- In all scenarios, the perimeter will increase.
Therefore, we conclude that the perimeter will increase when the area of the rectangle increases from 2 cm² to 4 cm².
What is the amount of surface enclosed by a closed figure called?- a)Volume
- b)Area
- c)Space
- d)Perimeter
Correct answer is option 'B'. Can you explain this answer?
What is the amount of surface enclosed by a closed figure called?
a)
Volume
b)
Area
c)
Space
d)
Perimeter
|
|
Swara Chakraborty answered |
**Area: The Amount of Surface Enclosed by a Closed Figure**
**Introduction**
When we talk about a closed figure, we are referring to a shape that has no openings or holes in it. Examples of closed figures include circles, squares, rectangles, triangles, and many more. The amount of surface enclosed by these closed figures is called the area. It is a fundamental concept in geometry and represents the two-dimensional space within the boundaries of the shape.
**Definition of Area**
The area of a closed figure is the measure of the surface enclosed by its boundaries. It is expressed in square units, such as square centimeters (cm²), square inches (in²), or square meters (m²). The area provides information about the size of a shape, and it helps us compare and analyze different figures.
**Calculation of Area**
The method to calculate the area varies depending on the shape of the closed figure. Here are some formulas commonly used to find the area of different shapes:
1. Square: The area of a square is given by the formula A = side × side, where A represents the area and side represents the length of one side of the square.
2. Rectangle: The area of a rectangle is calculated as A = length × width, where A is the area, length is the length of the rectangle, and width is the width of the rectangle.
3. Circle: The area of a circle is determined using the formula A = πr², where A represents the area, π (pi) is a mathematical constant approximately equal to 3.14159, and r is the radius of the circle.
4. Triangle: The area of a triangle can be found using the formula A = ½ × base × height, where A is the area, base is the length of the base of the triangle, and height is the perpendicular distance from the base to the opposite vertex.
**Importance of Area**
Understanding the concept of area is crucial in various real-life scenarios. For instance:
1. Construction: Architects and builders need to calculate the area of rooms, floors, and land to plan and estimate resources accurately.
2. Agriculture: Farmers need to determine the area of their fields to manage irrigation, fertilizers, and crop yield.
3. Art and Design: Artists and designers consider the area of different elements to create visually appealing compositions.
4. Geometry and Mathematics: Area is a fundamental concept in geometry and plays a significant role in solving problems involving shapes and figures.
In conclusion, the amount of surface enclosed by a closed figure is referred to as the area. It is a measure of the two-dimensional space within the boundaries of a shape. The calculation of area varies depending on the shape, and it is expressed in square units. Understanding the concept of area is essential in various practical applications and mathematical contexts.
**Introduction**
When we talk about a closed figure, we are referring to a shape that has no openings or holes in it. Examples of closed figures include circles, squares, rectangles, triangles, and many more. The amount of surface enclosed by these closed figures is called the area. It is a fundamental concept in geometry and represents the two-dimensional space within the boundaries of the shape.
**Definition of Area**
The area of a closed figure is the measure of the surface enclosed by its boundaries. It is expressed in square units, such as square centimeters (cm²), square inches (in²), or square meters (m²). The area provides information about the size of a shape, and it helps us compare and analyze different figures.
**Calculation of Area**
The method to calculate the area varies depending on the shape of the closed figure. Here are some formulas commonly used to find the area of different shapes:
1. Square: The area of a square is given by the formula A = side × side, where A represents the area and side represents the length of one side of the square.
2. Rectangle: The area of a rectangle is calculated as A = length × width, where A is the area, length is the length of the rectangle, and width is the width of the rectangle.
3. Circle: The area of a circle is determined using the formula A = πr², where A represents the area, π (pi) is a mathematical constant approximately equal to 3.14159, and r is the radius of the circle.
4. Triangle: The area of a triangle can be found using the formula A = ½ × base × height, where A is the area, base is the length of the base of the triangle, and height is the perpendicular distance from the base to the opposite vertex.
**Importance of Area**
Understanding the concept of area is crucial in various real-life scenarios. For instance:
1. Construction: Architects and builders need to calculate the area of rooms, floors, and land to plan and estimate resources accurately.
2. Agriculture: Farmers need to determine the area of their fields to manage irrigation, fertilizers, and crop yield.
3. Art and Design: Artists and designers consider the area of different elements to create visually appealing compositions.
4. Geometry and Mathematics: Area is a fundamental concept in geometry and plays a significant role in solving problems involving shapes and figures.
In conclusion, the amount of surface enclosed by a closed figure is referred to as the area. It is a measure of the two-dimensional space within the boundaries of a shape. The calculation of area varies depending on the shape, and it is expressed in square units. Understanding the concept of area is essential in various practical applications and mathematical contexts.
The length and breadth of a rectangle are 3.2 m and 150 cm. What is its area?- a)48 sq cm
- b)4.8 cm
- c)4.8 sq m
- d)48 cm
Correct answer is option 'C'. Can you explain this answer?
The length and breadth of a rectangle are 3.2 m and 150 cm. What is its area?
a)
48 sq cm
b)
4.8 cm
c)
4.8 sq m
d)
48 cm

|
Get Idea answered |
We know that,
Area=l∗b
l=3.2m
b=1.5m
l×b = 3.2×1.5 =4.80 sq m
b=1.5m
l×b = 3.2×1.5 =4.80 sq m
The length and breadth of a rectangular plot are 900 m and 700 m respectively. If three rounds of fence is fixed around the field at the cost of Rs. 8 per metre, what is the total amount spent?- a)Rs. 768
- b)Rs. 7680
- c)Rs. 76,800
- d)Rs. 768,000
Correct answer is option 'C'. Can you explain this answer?
The length and breadth of a rectangular plot are 900 m and 700 m respectively. If three rounds of fence is fixed around the field at the cost of Rs. 8 per metre, what is the total amount spent?
a)
Rs. 768
b)
Rs. 7680
c)
Rs. 76,800
d)
Rs. 768,000

|
Get Idea answered |
Solution:
- Length of the rectangular plot: 900 m
- Breadth of the rectangular plot: 700 m
- Calculate the perimeter:
- Perimeter = 2 × (Length + Breadth)
- Perimeter = 2 × (900 m + 700 m) = 2 × 1600 m = 3200 m
- For three rounds of fencing:
- Total perimeter for 3 rounds = 3 × 3200 m = 9600 m
- Calculate the total cost:
- Cost per metre = Rs. 8
- Total amount spent = 9600 m × Rs. 8 = Rs. 76,800
Chapter doubts & questions for Mensuration - Online MCQ Tests for Class 6 2025 is part of Class 6 exam preparation. The chapters have been prepared according to the Class 6 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mensuration - Online MCQ Tests for Class 6 in English & Hindi are available as part of Class 6 exam.
Download more important topics, notes, lectures and mock test series for Class 6 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily