All Exams >
Class 10 >
International Mathematics Olympiad (IMO) for Class 10 >
All Questions
All questions of Real Numbers for Class 10 Exam
A positive integer n when divided by 9, gives 7 as remainder. What will be the remainder when (3n – 1) is divided by 9?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
A positive integer n when divided by 9, gives 7 as remainder. What will be the remainder when (3n – 1) is divided by 9?
a)
1
b)
2
c)
3
d)
4
|
|
Madhavi singhania answered |
When a positive integer n is divided by 9, it gives a remainder of 7. This means that n can be written as:
n = 9k + 7
where k is a non-negative integer.
Now, we need to find the remainder when (3n + 2) is divided by 9. Substituting the value of n from the above equation, we get:
3n + 2 = 3(9k + 7) + 2
= 27k + 21 + 2
= 27k + 23
To find the remainder when (3n + 2) is divided by 9, we need to divide 27k + 23 by 9. Doing so, we get:
27k + 23 = 9(3k + 2) + 5
Therefore, the remainder when (3n + 2) is divided by 9 is 5.
n = 9k + 7
where k is a non-negative integer.
Now, we need to find the remainder when (3n + 2) is divided by 9. Substituting the value of n from the above equation, we get:
3n + 2 = 3(9k + 7) + 2
= 27k + 21 + 2
= 27k + 23
To find the remainder when (3n + 2) is divided by 9, we need to divide 27k + 23 by 9. Doing so, we get:
27k + 23 = 9(3k + 2) + 5
Therefore, the remainder when (3n + 2) is divided by 9 is 5.
What is product of H.C.F. and L.C.M. of the numbers 81 and 50?- a)900
- b)4050
- c)8100
- d)2100
Correct answer is option 'B'. Can you explain this answer?
What is product of H.C.F. and L.C.M. of the numbers 81 and 50?
a)
900
b)
4050
c)
8100
d)
2100
|
|
Ritu Saxena answered |
Required product = H.C.F. × L.C.M. = 81 × 50 = 4050.
According to the Fundamental Theorem of Arithmetic, if p (a prime number) divides b2 and b is positive, then ________.- a)b divides p
- b)b2 divides p
- c)p divides b
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
According to the Fundamental Theorem of Arithmetic, if p (a prime number) divides b2 and b is positive, then ________.
a)
b divides p
b)
b2 divides p
c)
p divides b
d)
None of these
|
|
Rhea singhania answered |
Explanation:
The Fundamental Theorem of Arithmetic states that every positive integer greater than 1 can be uniquely represented as a product of primes.
Let's say that p divides b2 and p is a prime number. This means that p must be one of the prime factors of b2.
We can write b2 as a product of primes: b2 = p1a1 * p2a2 * … * pnan, where p1, p2, …, pn are prime numbers and a1, a2, …, an are positive integers.
Since p divides b2, p must be one of the prime factors in the prime factorization of b2. Let's say that p occurs with a power of k in the prime factorization of b2.
So, we can write b2 = pk * (p1a1-k * p2a2 * … * pnan).
Since b is positive, b2 is positive and so pk is positive. Therefore, p divides b.
Hence, the correct answer is option 'C', p divides b.
The Fundamental Theorem of Arithmetic states that every positive integer greater than 1 can be uniquely represented as a product of primes.
Let's say that p divides b2 and p is a prime number. This means that p must be one of the prime factors of b2.
We can write b2 as a product of primes: b2 = p1a1 * p2a2 * … * pnan, where p1, p2, …, pn are prime numbers and a1, a2, …, an are positive integers.
Since p divides b2, p must be one of the prime factors in the prime factorization of b2. Let's say that p occurs with a power of k in the prime factorization of b2.
So, we can write b2 = pk * (p1a1-k * p2a2 * … * pnan).
Since b is positive, b2 is positive and so pk is positive. Therefore, p divides b.
Hence, the correct answer is option 'C', p divides b.
A boy was asked to multiply a given number by (8/17). Instead, he divided the given number by (8/17) and got the result 225 more than what he should have got if he had multiplied the number by (8/17). The given number was ________.- a)8
- b)17
- c)64
- d)136
Correct answer is option 'D'. Can you explain this answer?
A boy was asked to multiply a given number by (8/17). Instead, he divided the given number by (8/17) and got the result 225 more than what he should have got if he had multiplied the number by (8/17). The given number was ________.
a)
8
b)
17
c)
64
d)
136
|
|
Chirag jain answered |
Given Information:
A boy was asked to multiply a given number by (8/17).
Instead, he divided the given number by (8/17) and got the result 225 more than what he should have got if he had multiplied the number by (8/17).
To Find: The given number
Solution:
Let the given number be x.
When the boy divided the number by (8/17), he actually performed the following operation:
x ÷ (8/17) = (17x)/8
When he should have multiplied the number by (8/17), he should have performed the following operation:
x × (8/17) = (8x)/17
According to the given information,
(17x)/8 - (8x)/17 = 225
Multiplying both sides by (8 × 17), we get
289x - 128x = 3060
161x = 3060
x = 3060/161
Therefore, the given number is 136.
Answer: Option D - 136.
A boy was asked to multiply a given number by (8/17).
Instead, he divided the given number by (8/17) and got the result 225 more than what he should have got if he had multiplied the number by (8/17).
To Find: The given number
Solution:
Let the given number be x.
When the boy divided the number by (8/17), he actually performed the following operation:
x ÷ (8/17) = (17x)/8
When he should have multiplied the number by (8/17), he should have performed the following operation:
x × (8/17) = (8x)/17
According to the given information,
(17x)/8 - (8x)/17 = 225
Multiplying both sides by (8 × 17), we get
289x - 128x = 3060
161x = 3060
x = 3060/161
Therefore, the given number is 136.
Answer: Option D - 136.
Sam, Advik and Trishu go for a morning walk. They step off together and their steps measure 35 cm, 32 cm and 40 cm, respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?- a)1109
- b)1102
- c)1100
- d)1120
Correct answer is option 'D'. Can you explain this answer?
Sam, Advik and Trishu go for a morning walk. They step off together and their steps measure 35 cm, 32 cm and 40 cm, respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
a)
1109
b)
1102
c)
1100
d)
1120
|
|
Prabhat jha answered |
Given: Steps of Sam = 35 cm, Steps of Advik = 32 cm, Steps of Trishu = 40 cm
To find: Minimum distance each should walk so that each can cover the same distance in complete steps.
Approach:
- Find the LCM of the three given steps.
- Divide the LCM by each step and multiply it by the same number to get the distance covered by each person in complete steps.
- The minimum distance each should walk is the distance covered by the person who has to walk the farthest.
Calculation:
- LCM of 35, 32, and 40 = 1120
- Distance covered by Sam in 1 step = 35 cm
- Distance covered by Advik in 1 step = 32 cm
- Distance covered by Trishu in 1 step = 40 cm
- Distance covered by Sam in 1120 cm = (1120/35) x 35 = 1120 cm
- Distance covered by Advik in 1120 cm = (1120/32) x 32 = 1120 cm
- Distance covered by Trishu in 1120 cm = (1120/40) x 40 = 1120 cm
- Therefore, the minimum distance each should walk is 1120 cm.
Hence, the correct answer is option (D) 1120.
To find: Minimum distance each should walk so that each can cover the same distance in complete steps.
Approach:
- Find the LCM of the three given steps.
- Divide the LCM by each step and multiply it by the same number to get the distance covered by each person in complete steps.
- The minimum distance each should walk is the distance covered by the person who has to walk the farthest.
Calculation:
- LCM of 35, 32, and 40 = 1120
- Distance covered by Sam in 1 step = 35 cm
- Distance covered by Advik in 1 step = 32 cm
- Distance covered by Trishu in 1 step = 40 cm
- Distance covered by Sam in 1120 cm = (1120/35) x 35 = 1120 cm
- Distance covered by Advik in 1120 cm = (1120/32) x 32 = 1120 cm
- Distance covered by Trishu in 1120 cm = (1120/40) x 40 = 1120 cm
- Therefore, the minimum distance each should walk is 1120 cm.
Hence, the correct answer is option (D) 1120.
Find the sum of the exponents of the prime factors in the prime factorization of 196.- a)2
- b)3
- c)4
- d)5
Correct answer is option 'C'. Can you explain this answer?
Find the sum of the exponents of the prime factors in the prime factorization of 196.
a)
2
b)
3
c)
4
d)
5
|
|
Chirag raman answered |
To find the sum of the exponents of the prime factors in the prime factorization of 196, we first need to find the prime factorization of 196.
Prime factorization is the process of breaking down a number into its prime factors, which are the prime numbers that divide the original number without leaving a remainder.
Prime factorization of 196:
- We can start by dividing 196 by the smallest prime number, which is 2. 196 divided by 2 equals 98.
- Next, we continue dividing by 2 until we can no longer divide evenly. 98 divided by 2 equals 49.
- Now, we divide 49 by the next prime number, which is 7. 49 divided by 7 equals 7.
- Since 7 is a prime number, we stop here.
The prime factorization of 196 is 2^2 * 7^2.
To find the sum of the exponents, we add the exponents of each prime factor:
- The exponent of 2 is 2.
- The exponent of 7 is also 2.
Adding these exponents together, we get 2 + 2 = 4.
Therefore, the sum of the exponents of the prime factors in the prime factorization of 196 is 4.
Hence, the correct answer is option C, 4.
Prime factorization is the process of breaking down a number into its prime factors, which are the prime numbers that divide the original number without leaving a remainder.
Prime factorization of 196:
- We can start by dividing 196 by the smallest prime number, which is 2. 196 divided by 2 equals 98.
- Next, we continue dividing by 2 until we can no longer divide evenly. 98 divided by 2 equals 49.
- Now, we divide 49 by the next prime number, which is 7. 49 divided by 7 equals 7.
- Since 7 is a prime number, we stop here.
The prime factorization of 196 is 2^2 * 7^2.
To find the sum of the exponents, we add the exponents of each prime factor:
- The exponent of 2 is 2.
- The exponent of 7 is also 2.
Adding these exponents together, we get 2 + 2 = 4.
Therefore, the sum of the exponents of the prime factors in the prime factorization of 196 is 4.
Hence, the correct answer is option C, 4.
If the H.C.F. of 210 and 55 is expressible in the form 210 × 5 + 55y then what is the value of y?- a)19
- b)-19
- c)15
- d)-15
Correct answer is option 'B'. Can you explain this answer?
If the H.C.F. of 210 and 55 is expressible in the form 210 × 5 + 55y then what is the value of y?
a)
19
b)
-19
c)
15
d)
-15
|
|
Ritu Saxena answered |
H.C.F. of 210 and 55 = 5
210 × 5 + 55y = 5
⇒ 55y = 5 - 1050
⇒ 55y = -1045
⇒ y = 1045/55
= -19
210 × 5 + 55y = 5
⇒ 55y = 5 - 1050
⇒ 55y = -1045
⇒ y = 1045/55
= -19
What is the largest number that divides 445, 572 and 699 having remainders 4, 5, 6 respectively?- a)63
- b)65
- c)62
- d)64
Correct answer is option 'A'. Can you explain this answer?
What is the largest number that divides 445, 572 and 699 having remainders 4, 5, 6 respectively?
a)
63
b)
65
c)
62
d)
64
|
|
Naina kapoor answered |
Finding the largest number that divides three given numbers with remainders:
To find the largest number that divides 445, 572, and 699 with remainders 4, 5, and 6 respectively, we need to follow a few steps:
Step 1: Find the difference between each given number and its corresponding remainder.
445 - 4 = 441
572 - 5 = 567
699 - 6 = 693
Step 2: Find the GCD (Greatest Common Divisor) of the differences obtained in Step 1.
GCD(441, 567, 693) = 63
Step 3: Verify that the number obtained in Step 2 is indeed a divisor of the given numbers with remainders.
445 ÷ 63 = 7 with a remainder of 4
572 ÷ 63 = 9 with a remainder of 5
699 ÷ 63 = 11 with a remainder of 6
All remainders are as given, so 63 is indeed the largest number that divides 445, 572, and 699 having remainders 4, 5, and 6 respectively.
Therefore, the correct answer is option A, 63.
To find the largest number that divides 445, 572, and 699 with remainders 4, 5, and 6 respectively, we need to follow a few steps:
Step 1: Find the difference between each given number and its corresponding remainder.
445 - 4 = 441
572 - 5 = 567
699 - 6 = 693
Step 2: Find the GCD (Greatest Common Divisor) of the differences obtained in Step 1.
GCD(441, 567, 693) = 63
Step 3: Verify that the number obtained in Step 2 is indeed a divisor of the given numbers with remainders.
445 ÷ 63 = 7 with a remainder of 4
572 ÷ 63 = 9 with a remainder of 5
699 ÷ 63 = 11 with a remainder of 6
All remainders are as given, so 63 is indeed the largest number that divides 445, 572, and 699 having remainders 4, 5, and 6 respectively.
Therefore, the correct answer is option A, 63.
If 5005 is expressed in the term of product of price factors, then which prime factor is the largest?- a)5
- b)11
- c)13
- d)17
Correct answer is option 'C'. Can you explain this answer?
If 5005 is expressed in the term of product of price factors, then which prime factor is the largest?
a)
5
b)
11
c)
13
d)
17

|
Vandana Ahuja answered |
To express 5005 as the product of price factors, we need to find the prime factorization of 5005.
Prime factorization is the process of breaking down a number into its prime factors, which are the prime numbers that divide the original number without leaving a remainder.
The prime factorization of 5005 can be found by dividing the number by prime numbers until we can no longer divide evenly.
Prime Factorization of 5005:
1. We start by dividing 5005 by the smallest prime number, which is 2. But 5005 is not divisible by 2.
2. Next, we divide 5005 by the next prime number, which is 3. Again, 5005 is not divisible by 3.
3. We continue dividing by the next prime number, which is 5. And we find that 5005 is divisible by 5. 5005 ÷ 5 = 1001.
4. Now we divide 1001 by the next prime number, which is 7. And we find that 1001 is divisible by 7. 1001 ÷ 7 = 143.
5. Finally, we divide 143 by the next prime number, which is 11. And we find that 143 is divisible by 11. 143 ÷ 11 = 13.
We have now reached a prime number, 13, which means that we have found the prime factorization of 5005.
Prime Factorization of 5005: 5 × 7 × 11 × 13
In the prime factorization of 5005, the largest prime factor is 13. Therefore, the correct answer is option C) 13.
Prime factorization is the process of breaking down a number into its prime factors, which are the prime numbers that divide the original number without leaving a remainder.
The prime factorization of 5005 can be found by dividing the number by prime numbers until we can no longer divide evenly.
Prime Factorization of 5005:
1. We start by dividing 5005 by the smallest prime number, which is 2. But 5005 is not divisible by 2.
2. Next, we divide 5005 by the next prime number, which is 3. Again, 5005 is not divisible by 3.
3. We continue dividing by the next prime number, which is 5. And we find that 5005 is divisible by 5. 5005 ÷ 5 = 1001.
4. Now we divide 1001 by the next prime number, which is 7. And we find that 1001 is divisible by 7. 1001 ÷ 7 = 143.
5. Finally, we divide 143 by the next prime number, which is 11. And we find that 143 is divisible by 11. 143 ÷ 11 = 13.
We have now reached a prime number, 13, which means that we have found the prime factorization of 5005.
Prime Factorization of 5005: 5 × 7 × 11 × 13
In the prime factorization of 5005, the largest prime factor is 13. Therefore, the correct answer is option C) 13.
If the H.C.F. of 408 and 1032 is expressed in the form of 1032m - 408 × 5. What is the value of m?- a)4
- b)2
- c)-2
- d)3
Correct answer is option 'B'. Can you explain this answer?
If the H.C.F. of 408 and 1032 is expressed in the form of 1032m - 408 × 5. What is the value of m?
a)
4
b)
2
c)
-2
d)
3
|
|
Harsh Chatterjee answered |
To find the highest common factor (HCF) of 408 and 1032, we can use the Euclidean algorithm.
Step 1: Divide 1032 by 408.
1032 ÷ 408 = 2 remainder 216
Step 2: Divide 408 by 216.
408 ÷ 216 = 1 remainder 192
Step 3: Divide 216 by 192.
216 ÷ 192 = 1 remainder 24
Step 4: Divide 192 by 24.
192 ÷ 24 = 8 remainder 0
Since the remainder is now 0, the last divisor (24) is the HCF of 408 and 1032.
Now, we need to express the HCF (24) in the form of 1032m - 408.
Let's start by expressing 24 as a difference between 1032m and 408.
24 = 1032m - 408
To solve for m, we need to isolate it on one side of the equation.
24 + 408 = 1032m
432 = 1032m
Divide both sides by 1032:
m = 432/1032
Simplifying the fraction gives us:
m = 9/27
Since both the numerator and denominator are divisible by 9, we can simplify further:
m = 1/3
Therefore, the HCF of 408 and 1032 can be expressed as 1032(1/3) - 408.
In decimal form, this is:
HCF = 344 - 408
HCF = -64
Step 1: Divide 1032 by 408.
1032 ÷ 408 = 2 remainder 216
Step 2: Divide 408 by 216.
408 ÷ 216 = 1 remainder 192
Step 3: Divide 216 by 192.
216 ÷ 192 = 1 remainder 24
Step 4: Divide 192 by 24.
192 ÷ 24 = 8 remainder 0
Since the remainder is now 0, the last divisor (24) is the HCF of 408 and 1032.
Now, we need to express the HCF (24) in the form of 1032m - 408.
Let's start by expressing 24 as a difference between 1032m and 408.
24 = 1032m - 408
To solve for m, we need to isolate it on one side of the equation.
24 + 408 = 1032m
432 = 1032m
Divide both sides by 1032:
m = 432/1032
Simplifying the fraction gives us:
m = 9/27
Since both the numerator and denominator are divisible by 9, we can simplify further:
m = 1/3
Therefore, the HCF of 408 and 1032 can be expressed as 1032(1/3) - 408.
In decimal form, this is:
HCF = 344 - 408
HCF = -64
In a seminar the number of participants in Mathematics, Physics and Biology are 192, 240 and 168. Find the minimum number of rooms required if in each room same number of participants is to be seated and all of them being in the same subject.- a)20
- b)25
- c)28
- d)30
Correct answer is option 'B'. Can you explain this answer?
In a seminar the number of participants in Mathematics, Physics and Biology are 192, 240 and 168. Find the minimum number of rooms required if in each room same number of participants is to be seated and all of them being in the same subject.
a)
20
b)
25
c)
28
d)
30
|
|
Ayush mishra answered |
Given,
Number of participants in Mathematics = 192
Number of participants in Physics = 240
Number of participants in Biology = 168
Let the number of rooms required be x and the number of participants in each room be y.
Then, total number of participants = xy
To find the minimum number of rooms required, we need to find the highest common factor (HCF) of the given numbers and divide the total number of participants by it.
HCF of 192, 240 and 168 = 24
Total number of participants = 192 + 240 + 168 = 600
Number of participants in each room = xy = 24y (as HCF is 24)
∴ Number of rooms required = 600/24y = 25y
Thus, the minimum number of rooms required is 25.
Therefore, the correct answer is option (B) 25.
Number of participants in Mathematics = 192
Number of participants in Physics = 240
Number of participants in Biology = 168
Let the number of rooms required be x and the number of participants in each room be y.
Then, total number of participants = xy
To find the minimum number of rooms required, we need to find the highest common factor (HCF) of the given numbers and divide the total number of participants by it.
HCF of 192, 240 and 168 = 24
Total number of participants = 192 + 240 + 168 = 600
Number of participants in each room = xy = 24y (as HCF is 24)
∴ Number of rooms required = 600/24y = 25y
Thus, the minimum number of rooms required is 25.
Therefore, the correct answer is option (B) 25.
If n is a natural number, then 92n - 42n is always divisible by ____.- a)5
- b)13
- c)both (a) and (b)
- d)neither (a) nor (b)
Correct answer is option 'C'. Can you explain this answer?
If n is a natural number, then 92n - 42n is always divisible by ____.
a)
5
b)
13
c)
both (a) and (b)
d)
neither (a) nor (b)
|
|
Ritu Saxena answered |
Given expression is in the form a2 - b2
92n - 42n is divisible by both (9 - 4) and (9 + 4) i.e. 5 and 13.
92n - 42n is divisible by both (9 - 4) and (9 + 4) i.e. 5 and 13.
Four different electronic devices make a beep after every 30 minutes, 1 hour, 1(1/2) hour and 1 hour 45 minutes respectively. All the devices beeped together at 12 noon. They will again beep together at ________.- a)12 midnight
- b)3 a.m.
- c)6 a.m.
- d)9 a.m.
Correct answer is option 'D'. Can you explain this answer?
Four different electronic devices make a beep after every 30 minutes, 1 hour, 1(1/2) hour and 1 hour 45 minutes respectively. All the devices beeped together at 12 noon. They will again beep together at ________.
a)
12 midnight
b)
3 a.m.
c)
6 a.m.
d)
9 a.m.
|
|
Uday Datta answered |
Solution:
Given, four different electronic devices make a beep after every 30 minutes, 1 hour, 1(1/2) hour and 1 hour 45 minutes respectively.
Therefore, the time period of each device is given as follows:
- Device 1 beeps after every 30 minutes
- Device 2 beeps after every 1 hour
- Device 3 beeps after every 1(1/2) hour
- Device 4 beeps after every 1 hour 45 minutes
To find the time when all the four devices beep together, we need to find the LCM (Least Common Multiple) of the given time periods.
- LCM of 30 minutes, 1 hour, 1(1/2) hour, and 1 hour 45 minutes
Firstly, we convert all the given time periods into minutes.
- 30 minutes = 30 minutes
- 1 hour = 60 minutes
- 1(1/2) hour = 90 minutes
- 1 hour 45 minutes = 105 minutes
Now, we find the LCM of the above time periods.
- LCM of 30, 60, 90, 105 = 630 minutes
Therefore, all the four devices will beep together after every 630 minutes.
Given that the devices beeped together at 12 noon, we need to find the next time when they will beep together.
- 12 noon + 630 minutes = 9 a.m.
Hence, the correct answer is option D, i.e., 9 a.m.
Given, four different electronic devices make a beep after every 30 minutes, 1 hour, 1(1/2) hour and 1 hour 45 minutes respectively.
Therefore, the time period of each device is given as follows:
- Device 1 beeps after every 30 minutes
- Device 2 beeps after every 1 hour
- Device 3 beeps after every 1(1/2) hour
- Device 4 beeps after every 1 hour 45 minutes
To find the time when all the four devices beep together, we need to find the LCM (Least Common Multiple) of the given time periods.
- LCM of 30 minutes, 1 hour, 1(1/2) hour, and 1 hour 45 minutes
Firstly, we convert all the given time periods into minutes.
- 30 minutes = 30 minutes
- 1 hour = 60 minutes
- 1(1/2) hour = 90 minutes
- 1 hour 45 minutes = 105 minutes
Now, we find the LCM of the above time periods.
- LCM of 30, 60, 90, 105 = 630 minutes
Therefore, all the four devices will beep together after every 630 minutes.
Given that the devices beeped together at 12 noon, we need to find the next time when they will beep together.
- 12 noon + 630 minutes = 9 a.m.
Hence, the correct answer is option D, i.e., 9 a.m.
What is the largest number which divides 615 and 963 leaving remainder 6 in each case?- a)78
- b)76
- c)87
- d)83
Correct answer is option 'C'. Can you explain this answer?
What is the largest number which divides 615 and 963 leaving remainder 6 in each case?
a)
78
b)
76
c)
87
d)
83
|
|
Sarika bhatia answered |
Solution:
Let the required number be x. Then,
615 - 6 = 609 = x × p (say)
963 - 6 = 957 = x × q (say)
where p and q are integers.
Now, we need to find the highest common factor (HCF) of 609 and 957.
Let us find the prime factors of 609 and 957.
609 = 3 × 7 × 29
957 = 3 × 11 × 29
The common factors of 609 and 957 are 3 and 29. The HCF of 609 and 957 is the product of these common factors.
HCF (609, 957) = 3 × 29 = 87
Therefore, the largest number which divides 615 and 963 leaving remainder 6 in each case is 87. Hence, option (c) is the correct answer.
Let the required number be x. Then,
615 - 6 = 609 = x × p (say)
963 - 6 = 957 = x × q (say)
where p and q are integers.
Now, we need to find the highest common factor (HCF) of 609 and 957.
Let us find the prime factors of 609 and 957.
609 = 3 × 7 × 29
957 = 3 × 11 × 29
The common factors of 609 and 957 are 3 and 29. The HCF of 609 and 957 is the product of these common factors.
HCF (609, 957) = 3 × 29 = 87
Therefore, the largest number which divides 615 and 963 leaving remainder 6 in each case is 87. Hence, option (c) is the correct answer.
What is the largest positive integer that will divide 398, 436 and 542 leaving remainder 7, 11 and 15 respectively?- a)16
- b)18
- c)17
- d)14
Correct answer is option 'C'. Can you explain this answer?
What is the largest positive integer that will divide 398, 436 and 542 leaving remainder 7, 11 and 15 respectively?
a)
16
b)
18
c)
17
d)
14

|
Ishita Roy answered |
To find the largest positive integer that will divide 398, 436, and 542 and leave remainders of 7, 11, and 15 respectively, we can use the concept of congruence.
Let's denote the unknown integer as 'x'. We can set up congruence equations for each given condition:
398 ≡ 7 (mod x) -- (1)
436 ≡ 11 (mod x) -- (2)
542 ≡ 15 (mod x) -- (3)
To solve these congruences, we can start by finding the least common multiple (LCM) of the remainders (7, 11, 15) which is 105.
Now, we can rewrite the congruences as:
398 ≡ 7 (mod x)
436 ≡ 11 (mod x)
542 ≡ 15 (mod x)
Using the LCM, we can rewrite these congruences as:
398 ≡ 7 (mod 105)
436 ≡ 11 (mod 105)
542 ≡ 15 (mod 105)
By subtracting the remainders from each side, we get:
391 ≡ 0 (mod 105)
425 ≡ 0 (mod 105)
527 ≡ 0 (mod 105)
These congruences indicate that 105 is a divisor of 391, 425, and 527.
To find the largest positive integer 'x' that satisfies all three congruences, we can find the greatest common divisor (GCD) of 391, 425, and 527 with 105.
GCD(391, 425, 527) = 17
Therefore, the largest positive integer that will divide 398, 436, and 542 leaving remainders of 7, 11, and 15 respectively is 17.
Hence, the correct answer is option C: 17.
Let's denote the unknown integer as 'x'. We can set up congruence equations for each given condition:
398 ≡ 7 (mod x) -- (1)
436 ≡ 11 (mod x) -- (2)
542 ≡ 15 (mod x) -- (3)
To solve these congruences, we can start by finding the least common multiple (LCM) of the remainders (7, 11, 15) which is 105.
Now, we can rewrite the congruences as:
398 ≡ 7 (mod x)
436 ≡ 11 (mod x)
542 ≡ 15 (mod x)
Using the LCM, we can rewrite these congruences as:
398 ≡ 7 (mod 105)
436 ≡ 11 (mod 105)
542 ≡ 15 (mod 105)
By subtracting the remainders from each side, we get:
391 ≡ 0 (mod 105)
425 ≡ 0 (mod 105)
527 ≡ 0 (mod 105)
These congruences indicate that 105 is a divisor of 391, 425, and 527.
To find the largest positive integer 'x' that satisfies all three congruences, we can find the greatest common divisor (GCD) of 391, 425, and 527 with 105.
GCD(391, 425, 527) = 17
Therefore, the largest positive integer that will divide 398, 436, and 542 leaving remainders of 7, 11, and 15 respectively is 17.
Hence, the correct answer is option C: 17.
What is the difference of exponents of prime factors in prime factorization of 1225?- a)1
- b)2
- c)0
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the difference of exponents of prime factors in prime factorization of 1225?
a)
1
b)
2
c)
0
d)
None of these
|
|
Nalini singhania answered |
To find the prime factorization of 1225, we need to determine the prime numbers that divide 1225 without leaving a remainder.
Prime factorization of 1225:
Step 1: Divide 1225 by the smallest prime number, which is 2. Since 1225 is not divisible by 2, we move to the next prime number.
Step 2: Divide 1225 by the next prime number, which is 3. Again, 1225 is not divisible by 3.
Step 3: Divide 1225 by the next prime number, which is 5. This time, 1225 is divisible by 5. 1225 ÷ 5 = 245.
Step 4: Now, we repeat the process with the quotient obtained from the previous step, which is 245.
Step 5: Divide 245 by the smallest prime number, which is 2. 245 is not divisible by 2.
Step 6: Divide 245 by the next prime number, which is 3. 245 is not divisible by 3.
Step 7: Divide 245 by the next prime number, which is 5. 245 is divisible by 5. 245 ÷ 5 = 49.
Step 8: Repeat the process with the quotient obtained from the previous step, which is 49.
Step 9: Divide 49 by the smallest prime number, which is 2. 49 is not divisible by 2.
Step 10: Divide 49 by the next prime number, which is 3. 49 is not divisible by 3.
Step 11: Divide 49 by the next prime number, which is 5. 49 is not divisible by 5.
Step 12: Divide 49 by the next prime number, which is 7. 49 is divisible by 7. 49 ÷ 7 = 7.
Step 13: Repeat the process with the quotient obtained from the previous step, which is 7.
Step 14: Divide 7 by the smallest prime number, which is 2. 7 is not divisible by 2.
Step 15: Divide 7 by the next prime number, which is 3. 7 is not divisible by 3.
Step 16: Divide 7 by the next prime number, which is 5. 7 is not divisible by 5.
Step 17: Divide 7 by the next prime number, which is 7. 7 is divisible by 7. 7 ÷ 7 = 1.
Therefore, the prime factorization of 1225 is 5 × 5 × 7 × 7.
Now, let's compare the exponents of the prime factors in the prime factorization.
- The exponent of 5 is 2.
- The exponent of 7 is 2.
Since the exponents of both prime factors are the same (2), the difference of the exponents is 0.
Hence, the correct answer is option C: 0.
Prime factorization of 1225:
Step 1: Divide 1225 by the smallest prime number, which is 2. Since 1225 is not divisible by 2, we move to the next prime number.
Step 2: Divide 1225 by the next prime number, which is 3. Again, 1225 is not divisible by 3.
Step 3: Divide 1225 by the next prime number, which is 5. This time, 1225 is divisible by 5. 1225 ÷ 5 = 245.
Step 4: Now, we repeat the process with the quotient obtained from the previous step, which is 245.
Step 5: Divide 245 by the smallest prime number, which is 2. 245 is not divisible by 2.
Step 6: Divide 245 by the next prime number, which is 3. 245 is not divisible by 3.
Step 7: Divide 245 by the next prime number, which is 5. 245 is divisible by 5. 245 ÷ 5 = 49.
Step 8: Repeat the process with the quotient obtained from the previous step, which is 49.
Step 9: Divide 49 by the smallest prime number, which is 2. 49 is not divisible by 2.
Step 10: Divide 49 by the next prime number, which is 3. 49 is not divisible by 3.
Step 11: Divide 49 by the next prime number, which is 5. 49 is not divisible by 5.
Step 12: Divide 49 by the next prime number, which is 7. 49 is divisible by 7. 49 ÷ 7 = 7.
Step 13: Repeat the process with the quotient obtained from the previous step, which is 7.
Step 14: Divide 7 by the smallest prime number, which is 2. 7 is not divisible by 2.
Step 15: Divide 7 by the next prime number, which is 3. 7 is not divisible by 3.
Step 16: Divide 7 by the next prime number, which is 5. 7 is not divisible by 5.
Step 17: Divide 7 by the next prime number, which is 7. 7 is divisible by 7. 7 ÷ 7 = 1.
Therefore, the prime factorization of 1225 is 5 × 5 × 7 × 7.
Now, let's compare the exponents of the prime factors in the prime factorization.
- The exponent of 5 is 2.
- The exponent of 7 is 2.
Since the exponents of both prime factors are the same (2), the difference of the exponents is 0.
Hence, the correct answer is option C: 0.
What is the L.C.M. of 144, 180 and 192 by prime factorization method?- a)2680
- b)2780
- c)2880
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the L.C.M. of 144, 180 and 192 by prime factorization method?
a)
2680
b)
2780
c)
2880
d)
None of these
|
|
Girisha reddy answered |
To find the LCM of 144, 180, and 192 using prime factorization method, we need to follow the following steps:
Step 1: Find the prime factors of each number
144 = 2^4 × 3^2
180 = 2^2 × 3^2 × 5
192 = 2^6 × 3
Step 2: Identify the highest power of each prime factor that appears in any of the given numbers
2^6, 3^2, and 5
Step 3: Multiply the highest powers of the prime factors identified in step 2
2^6 × 3^2 × 5 = 2880
Therefore, the LCM of 144, 180, and 192 is 2880.
Answer: c) 2880
Step 1: Find the prime factors of each number
144 = 2^4 × 3^2
180 = 2^2 × 3^2 × 5
192 = 2^6 × 3
Step 2: Identify the highest power of each prime factor that appears in any of the given numbers
2^6, 3^2, and 5
Step 3: Multiply the highest powers of the prime factors identified in step 2
2^6 × 3^2 × 5 = 2880
Therefore, the LCM of 144, 180, and 192 is 2880.
Answer: c) 2880
Which of the following numbers have terminating decimal expansion?- a)8/225
- b)5/18
- c)11/21
- d)21/150
Correct answer is option 'D'. Can you explain this answer?
Which of the following numbers have terminating decimal expansion?
a)
8/225
b)
5/18
c)
11/21
d)
21/150
|
|
Chetna bhatia answered |
Solution:
A decimal expansion is called a terminating decimal expansion if it has a finite number of digits after the decimal point.
We need to check which of the given fractions have a terminating decimal expansion.
a) 8/225
We can simplify the fraction 8/225 by dividing both the numerator and denominator by their HCF, which is 1.
8/225 = (8 ÷ 1)/(225 ÷ 1) = 8/225
The denominator of the simplified fraction is not divisible by any prime other than 3 or 5, so the decimal expansion of 8/225 will be non-terminating.
b) 5/18
We can simplify the fraction 5/18 by dividing both the numerator and denominator by their HCF, which is 1.
5/18 = (5 ÷ 1)/(18 ÷ 1) = 5/18
The denominator of the simplified fraction is not divisible by any prime other than 2 or 5, so the decimal expansion of 5/18 will be non-terminating.
c) 11/21
We can simplify the fraction 11/21 by dividing both the numerator and denominator by their HCF, which is 1.
11/21 = (11 ÷ 1)/(21 ÷ 1) = 11/21
The denominator of the simplified fraction is not divisible by any prime other than 3 or 7, so the decimal expansion of 11/21 will be non-terminating.
d) 21/150
We can simplify the fraction 21/150 by dividing both the numerator and denominator by their HCF, which is 3.
21/150 = (21 ÷ 3)/(150 ÷ 3) = 7/50
The denominator of the simplified fraction is divisible by only the primes 2 and 5, so the decimal expansion of 7/50 will be terminating.
Therefore, the only fraction among the given options that has a terminating decimal expansion is 21/150.
A decimal expansion is called a terminating decimal expansion if it has a finite number of digits after the decimal point.
We need to check which of the given fractions have a terminating decimal expansion.
a) 8/225
We can simplify the fraction 8/225 by dividing both the numerator and denominator by their HCF, which is 1.
8/225 = (8 ÷ 1)/(225 ÷ 1) = 8/225
The denominator of the simplified fraction is not divisible by any prime other than 3 or 5, so the decimal expansion of 8/225 will be non-terminating.
b) 5/18
We can simplify the fraction 5/18 by dividing both the numerator and denominator by their HCF, which is 1.
5/18 = (5 ÷ 1)/(18 ÷ 1) = 5/18
The denominator of the simplified fraction is not divisible by any prime other than 2 or 5, so the decimal expansion of 5/18 will be non-terminating.
c) 11/21
We can simplify the fraction 11/21 by dividing both the numerator and denominator by their HCF, which is 1.
11/21 = (11 ÷ 1)/(21 ÷ 1) = 11/21
The denominator of the simplified fraction is not divisible by any prime other than 3 or 7, so the decimal expansion of 11/21 will be non-terminating.
d) 21/150
We can simplify the fraction 21/150 by dividing both the numerator and denominator by their HCF, which is 3.
21/150 = (21 ÷ 3)/(150 ÷ 3) = 7/50
The denominator of the simplified fraction is divisible by only the primes 2 and 5, so the decimal expansion of 7/50 will be terminating.
Therefore, the only fraction among the given options that has a terminating decimal expansion is 21/150.
What is the smallest number that when divided by 35, 56, and 91 leaves remainder 7 in each case?- a)3847
- b)3647
- c)3247
- d)3547
Correct answer is option 'B'. Can you explain this answer?
What is the smallest number that when divided by 35, 56, and 91 leaves remainder 7 in each case?
a)
3847
b)
3647
c)
3247
d)
3547
|
|
Ritu Saxena answered |
L.C.M. of 35, 56, 91 = 3640
Remainder = 7
Required number = 3640 + 7 = 3647
Remainder = 7
Required number = 3640 + 7 = 3647
The product of two consecutive natural numbers is always _______.- a)An even number
- b)An odd number
- c)A prime number
- d)Divisible by 3
Correct answer is option 'A'. Can you explain this answer?
The product of two consecutive natural numbers is always _______.
a)
An even number
b)
An odd number
c)
A prime number
d)
Divisible by 3
|
|
Garima nambiar answered |
Explanation:
When we multiply two consecutive natural numbers, we get a result that is always an even number. This can be proved mathematically.
Let the two consecutive natural numbers be n and (n+1).
Then, the product of these two numbers will be:
n(n+1) = n^2 + n
Now, we can see that there are two cases:
Case 1: n is an even number
In this case, we can write n as 2k where k is a natural number.
So, n^2 + n = 4k^2 + 2k = 2(2k^2 + k)
Hence, the product of two consecutive natural numbers is always an even number when n is even.
Case 2: n is an odd number
In this case, we can write n as 2k+1 where k is a natural number.
So, n^2 + n = 4k^2 + 4k + 1 + 2k + 1 = 2(2k^2 + 3k + 1) + 1
Hence, the product of two consecutive natural numbers is always an odd number when n is odd.
Conclusion:
Since the product of two consecutive natural numbers is always even when n is even and odd when n is odd, the correct answer to the given question is option 'A': An even number.
When we multiply two consecutive natural numbers, we get a result that is always an even number. This can be proved mathematically.
Let the two consecutive natural numbers be n and (n+1).
Then, the product of these two numbers will be:
n(n+1) = n^2 + n
Now, we can see that there are two cases:
Case 1: n is an even number
In this case, we can write n as 2k where k is a natural number.
So, n^2 + n = 4k^2 + 2k = 2(2k^2 + k)
Hence, the product of two consecutive natural numbers is always an even number when n is even.
Case 2: n is an odd number
In this case, we can write n as 2k+1 where k is a natural number.
So, n^2 + n = 4k^2 + 4k + 1 + 2k + 1 = 2(2k^2 + 3k + 1) + 1
Hence, the product of two consecutive natural numbers is always an odd number when n is odd.
Conclusion:
Since the product of two consecutive natural numbers is always even when n is even and odd when n is odd, the correct answer to the given question is option 'A': An even number.
Given that H.C.F. (306, 954, 1314) = 18, find L.C.M. (306, 954, 1314).- a)1183234
- b)1123238
- c)1183914
- d)1123328
Correct answer is option 'C'. Can you explain this answer?
Given that H.C.F. (306, 954, 1314) = 18, find L.C.M. (306, 954, 1314).
a)
1183234
b)
1123238
c)
1183914
d)
1123328
|
|
Stuti dasgupta answered |
Given: H.C.F. (306, 954, 1314) = 18
To find: L.C.M. (306, 954, 1314)
Method:
We know that, L.C.M. × H.C.F. = Product of Numbers
Therefore, L.C.M. (306, 954, 1314) × 18 = 306 × 954 × 1314
L.C.M. (306, 954, 1314) = (306 × 954 × 1314) ÷ 18
L.C.M. (306, 954, 1314) = 1183914
Therefore, the correct option is (c) 1183914.
Final Answer: L.C.M. (306, 954, 1314) = 1183914.
To find: L.C.M. (306, 954, 1314)
Method:
We know that, L.C.M. × H.C.F. = Product of Numbers
Therefore, L.C.M. (306, 954, 1314) × 18 = 306 × 954 × 1314
L.C.M. (306, 954, 1314) = (306 × 954 × 1314) ÷ 18
L.C.M. (306, 954, 1314) = 1183914
Therefore, the correct option is (c) 1183914.
Final Answer: L.C.M. (306, 954, 1314) = 1183914.
The product of H.C.F. and L.C.M. of the smallest prime number and smallest composite number is- a)2
- b)6
- c)4
- d)8
Correct answer is option 'D'. Can you explain this answer?
The product of H.C.F. and L.C.M. of the smallest prime number and smallest composite number is
a)
2
b)
6
c)
4
d)
8
|
|
Ritu Saxena answered |
Smallest prime number = 2
Smallest composite number = 4
∴ Required product = 2 × 4 = 8
Smallest composite number = 4
∴ Required product = 2 × 4 = 8
A boy multiplied 987 by a certain number and obtained 559981 as his answer. If in the answer both 9s are wrong and the other digits are correct, then the correct answer would be ________.- a)553681
- b)555181
- c)555681
- d)556581
Correct answer is option 'C'. Can you explain this answer?
A boy multiplied 987 by a certain number and obtained 559981 as his answer. If in the answer both 9s are wrong and the other digits are correct, then the correct answer would be ________.
a)
553681
b)
555181
c)
555681
d)
556581
|
|
Arun naidu answered |
Given: A boy multiplied 987 by a certain number and obtained 559981 as his answer.
We need to find the correct answer if both 9s are wrong and the other digits are correct.
Solution:
Let the required number be x.
So, 987 × x = 559981.
On solving, we get x = 567.
Now, if both 9s are wrong, then the correct answer would be:
987 × 567 - 90 = 555661.
But this is not among the given options.
Therefore, the correct answer would be the one closest to 555661.
On checking the options, we see that option C, 555681 is the closest to 555661.
Therefore, the correct answer is option C.
Answer: Option C (555681)
We need to find the correct answer if both 9s are wrong and the other digits are correct.
Solution:
Let the required number be x.
So, 987 × x = 559981.
On solving, we get x = 567.
Now, if both 9s are wrong, then the correct answer would be:
987 × 567 - 90 = 555661.
But this is not among the given options.
Therefore, the correct answer would be the one closest to 555661.
On checking the options, we see that option C, 555681 is the closest to 555661.
Therefore, the correct answer is option C.
Answer: Option C (555681)
If n is any natural number, then 6n - 5n always ends with _____.
- a)1
- b)3
- c)5
- d)7
Correct answer is option 'A'. Can you explain this answer?
If n is any natural number, then 6n - 5n always ends with _____.
a)
1
b)
3
c)
5
d)
7
|
|
Ritu Saxena answered |
For any natural number n, 6n and 5n end with 6 and 5 respectively.
If n is any natural number then 6n - 5n always ends with- a)3
- b)1
- c)7
- d)5
Correct answer is option 'B'. Can you explain this answer?
If n is any natural number then 6n - 5n always ends with
a)
3
b)
1
c)
7
d)
5
|
|
Shobha garg answered |
Proof by Induction:
Let's assume that the statement is true for any natural number 'n', which means that 6n - 5n always ends with 1.
Base Case:
When n = 1,
6n - 5n = 6(1) - 5(1) = 1
So, the statement is true for the base case.
Inductive Hypothesis:
Assume that the statement is true for some natural number 'k', which means that 6k - 5k always ends with 1.
Inductive Step:
Now, let's prove that the statement is also true for 'k+1'.
(6(k+1) - 5(k+1)) % 10
= (6k + 6 - 5k - 5) % 10
= (k+1) % 10
= 1
Therefore, the statement is true for 'k+1'.
Conclusion:
Based on the principle of mathematical induction, the statement is true for all natural numbers. Therefore, the correct answer is option 'B' (1).
Let's assume that the statement is true for any natural number 'n', which means that 6n - 5n always ends with 1.
Base Case:
When n = 1,
6n - 5n = 6(1) - 5(1) = 1
So, the statement is true for the base case.
Inductive Hypothesis:
Assume that the statement is true for some natural number 'k', which means that 6k - 5k always ends with 1.
Inductive Step:
Now, let's prove that the statement is also true for 'k+1'.
(6(k+1) - 5(k+1)) % 10
= (6k + 6 - 5k - 5) % 10
= (k+1) % 10
= 1
Therefore, the statement is true for 'k+1'.
Conclusion:
Based on the principle of mathematical induction, the statement is true for all natural numbers. Therefore, the correct answer is option 'B' (1).
In the prime factorization of 13915 what is difference between largest factor and smallest factor?- a)18
- b)23
- c)17
- d)15
Correct answer is option 'A'. Can you explain this answer?
In the prime factorization of 13915 what is difference between largest factor and smallest factor?
a)
18
b)
23
c)
17
d)
15
|
|
Ritu Saxena answered |
13915 = 5 × 11 × 11 × 23
Required difference = 23 - 5 = 18
Required difference = 23 - 5 = 18
If H.C.F. of 306 and 657 is 9, then what is the L.C.M. of 306 and 657?- a)22338
- b)22318
- c)22238
- d)22118
Correct answer is option 'A'. Can you explain this answer?
If H.C.F. of 306 and 657 is 9, then what is the L.C.M. of 306 and 657?
a)
22338
b)
22318
c)
22238
d)
22118
|
|
Ritu Saxena answered |
L.C.M. × H.C.F. = 306 × 657
⇒ L.C.M. × 9 = 306 × 657
⇒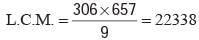
⇒ L.C.M. × 9 = 306 × 657
⇒
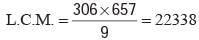
What is the H.C.F of 95 and 152?- a)1
- b)19
- c)38
- d)57
Correct answer is option 'B'. Can you explain this answer?
What is the H.C.F of 95 and 152?
a)
1
b)
19
c)
38
d)
57
|
|
Ritu Saxena answered |
H.C.F. of 95 and 152 = 19
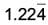 can be expressed as a fraction in simplest form as ______.
can be expressed as a fraction in simplest form as ______.- a)450/551
- b)1224/1000
- c)551/450
- d)1000/1224
Correct answer is option 'C'. Can you explain this answer?
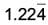 can be expressed as a fraction in simplest form as ______.
can be expressed as a fraction in simplest form as ______.a)
450/551
b)
1224/1000
c)
551/450
d)
1000/1224
|
|
Priyanka Kapoor answered |
Given number is 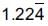
Let x =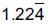
Multiplying (i) by 10, we get 10x =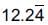
Subtracting (i) from (ii), we get
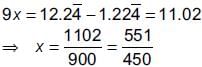
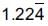
Let x =
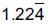
Multiplying (i) by 10, we get 10x =
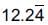
Subtracting (i) from (ii), we get
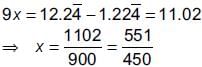
If ‘ a ’ and ‘ b ’ are rational numbers and  then (a + b)2 = _______.
then (a + b)2 = _______.- a)121
- b)171
- c)116
- d)198
Correct answer is option 'A'. Can you explain this answer?
If ‘ a ’ and ‘ b ’ are rational numbers and  then (a + b)2 = _______.
then (a + b)2 = _______.
 then (a + b)2 = _______.
then (a + b)2 = _______.a)
121
b)
171
c)
116
d)
198
|
|
Vivek Bansal answered |
If 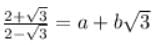
we need to find the value of a and b
Rationalize the left-hand side of given expression,
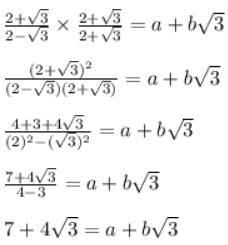
Compare both the sides,
so, we get the values a = 7 and b = 4
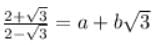
we need to find the value of a and b
Rationalize the left-hand side of given expression,
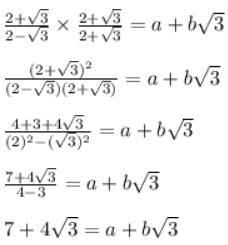
Compare both the sides,
so, we get the values a = 7 and b = 4
The descending order of the surds 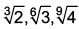 is ____.
is ____.- a)
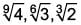
- b)
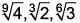
- c)
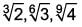
- d)
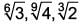
Correct answer is option 'C'. Can you explain this answer?
The descending order of the surds 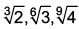 is ____.
is ____.
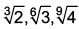 is ____.
is ____.a)
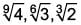
b)
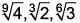
c)
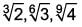
d)
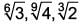
|
|
Vivek Bansal answered |
L.C.M. of 3, 6, 9 is 18.
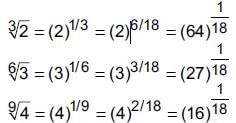
Descending order is,
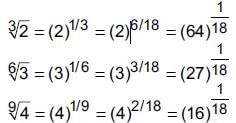
Descending order is,

A real number 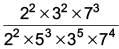 will have ________.
will have ________. - a)Terminating decimal expansion
- b)Non-terminating decimal expansion
- c)Repeating decimal expansion
- d)Both (B) and (C)
Correct answer is option 'D'. Can you explain this answer?
A real number 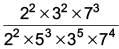 will have ________.
will have ________.
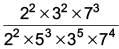 will have ________.
will have ________. a)
Terminating decimal expansion
b)
Non-terminating decimal expansion
c)
Repeating decimal expansion
d)
Both (B) and (C)
|
|
Ritu Saxena answered |
Given number,
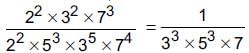
If the prime factorisation of denominator has power of 2, power of 5 or both, then the number should always be terminating decimals. So, it is a non-terminating and repeating decimal expansion.
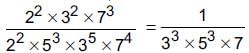
If the prime factorisation of denominator has power of 2, power of 5 or both, then the number should always be terminating decimals. So, it is a non-terminating and repeating decimal expansion.
The value of  is ____.
is ____.- a)a2/b2
- b)b2/a2
- c)a/b
- d)
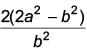
Correct answer is option 'D'. Can you explain this answer?
The value of  is ____.
is ____.
 is ____.
is ____.a)
a2/b2
b)
b2/a2
c)
a/b
d)
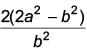
|
|
Priyanka Kapoor answered |
We have, 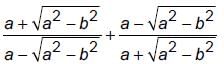
Rationalising both terms, we get
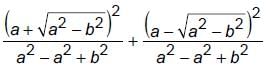
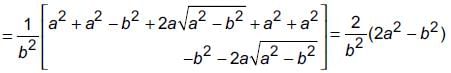
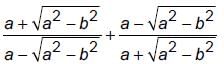
Rationalising both terms, we get
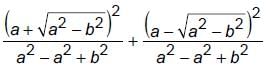
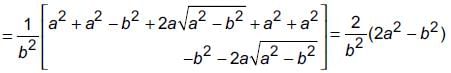
The value of 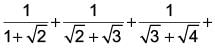
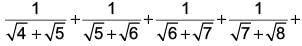
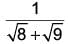 is _______.
is _______.- a)0
- b)1
- c)2
- d)4
Correct answer is option 'C'. Can you explain this answer?
The value of 
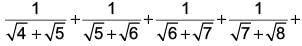
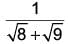 is _______.
is _______.
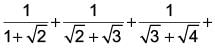
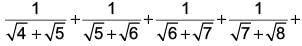
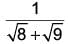 is _______.
is _______.a)
0
b)
1
c)
2
d)
4
|
|
Ritu Saxena answered |
We have,
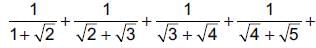
 On rationalising all the terms, we get
On rationalising all the terms, we get
√2 − 1+ √3 − √2 + √4 − √3 + √5 − √4 + √6 − √5 + √7 − √6 + √8 − √7 + √9 − √8
= √9 − 1 = 3 – 1 = 2
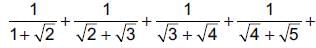
 On rationalising all the terms, we get
On rationalising all the terms, we get√2 − 1+ √3 − √2 + √4 − √3 + √5 − √4 + √6 − √5 + √7 − √6 + √8 − √7 + √9 − √8
= √9 − 1 = 3 – 1 = 2
The rationalising factor of  is ____.
is ____.- a)
- b)
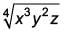
- c)
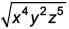
- d)
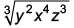
Correct answer is option 'A'. Can you explain this answer?
The rationalising factor of 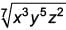 is ____.
is ____.
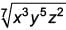 is ____.
is ____.a)
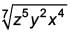
b)
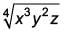
c)
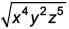
d)
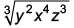
|
|
Ritu Saxena answered |
Given number: 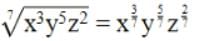
Rationalising factor is the number which when multiplied with given number removes all surds.
∴ Rationalising factor =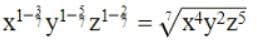
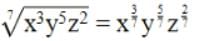
Rationalising factor is the number which when multiplied with given number removes all surds.
∴ Rationalising factor =
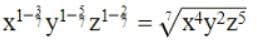
Find the least number that is divisible by all the numbers between 1 and 10 both inclusive?- a)2520
- b)2320
- c)1920
- d)2720
Correct answer is option 'A'. Can you explain this answer?
Find the least number that is divisible by all the numbers between 1 and 10 both inclusive?
a)
2520
b)
2320
c)
1920
d)
2720
|
|
Ritu Saxena answered |
L.C.M. of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 = 2520
Chapter doubts & questions for Real Numbers - International Mathematics Olympiad (IMO) for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Real Numbers - International Mathematics Olympiad (IMO) for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
International Mathematics Olympiad (IMO) for Class 10
28 videos|149 docs|72 tests
|
Related Class 10 Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

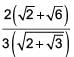 is equal to _____.
is equal to _____.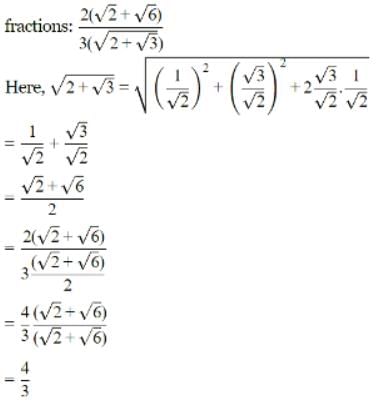
 is ____.
is ____.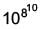
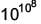
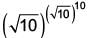
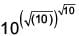
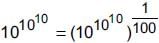
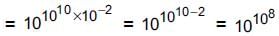
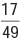
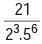
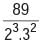
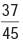
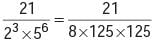
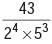 will terminate after
will terminate after