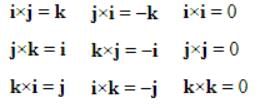All Exams >
JEE >
Mathematics CUET UG Mock Test Series 2026 >
All Questions
All questions of Chapter 10 - Vectors for JEE Exam
The area of triangle whose adjacent sides are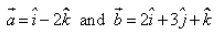 is :
is :- a)√70/2 sq. units
- b)9√2 /2 sq. units
- c)3√3 /2 sq. units
- d)2√3 /2 sq. units
Correct answer is option 'A'. Can you explain this answer?
The area of triangle whose adjacent sides are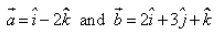 is :
is :
a)
√70/2 sq. units
b)
9√2 /2 sq. units
c)
3√3 /2 sq. units
d)
2√3 /2 sq. units
|
|
Suresh Iyer answered |
Area of triangle = ½(a * b)
a = (1, 0, -2) b = (2, 3, 1)
= i(0 + 6) + j(-4 - 1) + k(3 - 0)
= 6i - 5j + 3k
|a * b| = (36 + 25 + 9)½
|a * b| = (70)½
Area of triangle = ½(a * b)
= [(70)½]/2
a = (1, 0, -2) b = (2, 3, 1)
= i(0 + 6) + j(-4 - 1) + k(3 - 0)
= 6i - 5j + 3k
|a * b| = (36 + 25 + 9)½
|a * b| = (70)½
Area of triangle = ½(a * b)
= [(70)½]/2
A vector of magnitude 14 units, which is parallel to the vector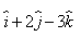
- a)
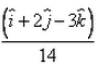
- b)
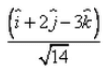
- c)
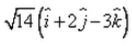
- d)
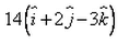
Correct answer is option 'C'. Can you explain this answer?
A vector of magnitude 14 units, which is parallel to the vector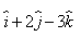
a)
b)
c)
d)

|
EduRev JEE answered |
Given vector = i + 2j - 3k
Magnitude = √12 + 22 + (-3)2 = √14
Unit vector in direction of resultant = (i + 2j - 3k) / √14
Vector of magnitude 14 unit in direction of resultant,
⇒ 14[ (i + 2j - 3k) / √14 ]
⇒ √14(i + 2j - 3k)
Magnitude = √12 + 22 + (-3)2 = √14
Unit vector in direction of resultant = (i + 2j - 3k) / √14
Vector of magnitude 14 unit in direction of resultant,
⇒ 14[ (i + 2j - 3k) / √14 ]
⇒ √14(i + 2j - 3k)
If a, b, c and d are the position vectors of the points A, B, C and D such that a + c = b + d, then ABCD is a- a)Trapezium
- b)Rectangle
- c)Square
- d)Parallelogram
Correct answer is option 'D'. Can you explain this answer?
If a, b, c and d are the position vectors of the points A, B, C and D such that a + c = b + d, then ABCD is a
a)
Trapezium
b)
Rectangle
c)
Square
d)
Parallelogram
|
|
Tejas Verma answered |
Given:
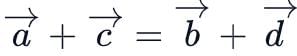
If we divide both sides with 2 we get,

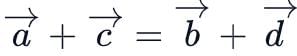
If we divide both sides with 2 we get,

⇒ Mid pt. of AC = Mid. pt. of BD
∴ ABCD is a parallelogram.
∴ ABCD is a parallelogram.
If 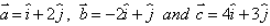 and
and 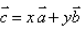 , then the value of scalars x and y are:
, then the value of scalars x and y are:- a)x = 1 and y = -2
- b)x = -2 and y = 1
- c)x = 2 and y = -1
- d)x = 2 and y = 1
Correct answer is option 'C'. Can you explain this answer?
If 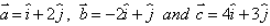 and
and 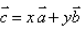 , then the value of scalars x and y are:
, then the value of scalars x and y are:
a)
x = 1 and y = -2
b)
x = -2 and y = 1
c)
x = 2 and y = -1
d)
x = 2 and y = 1

|
Sushil Kumar answered |
Given, a = i + 2j
b = -2i + j
c = 4i +3j
Also, c = xa +yb
Now putting the values in above equation,
4i + 3j = x(i + 2j) + y(-2i +j)
⇒ xi + 2xj - 2yi + yj
⇒ (x-2y)i + (2x+y)j
We get,
x - 2y = 4
2x + y = 3
After solving,
x = 2
y = -1
b = -2i + j
c = 4i +3j
Also, c = xa +yb
Now putting the values in above equation,
4i + 3j = x(i + 2j) + y(-2i +j)
⇒ xi + 2xj - 2yi + yj
⇒ (x-2y)i + (2x+y)j
We get,
x - 2y = 4
2x + y = 3
After solving,
x = 2
y = -1
If a and b are the position vectors of two points A and B and C is a point on AB produced such that AC = 3AB, then position vector of C will be- a)3b – 2a
- b)3a – b
- c)3a – 2b
- d)3b – a
Correct answer is option 'A'. Can you explain this answer?
If a and b are the position vectors of two points A and B and C is a point on AB produced such that AC = 3AB, then position vector of C will be
a)
3b – 2a
b)
3a – b
c)
3a – 2b
d)
3b – a
|
|
Snehal Choudhary answered |
AC = 3AB
(c - a)= 3(b - a). (c - a)
= 3b -3a
c= 3b--2a
Unit vectors along the axes OX, OY and OZ are denoted by - a)

- b)
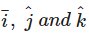
- c)

- d)
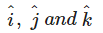
Correct answer is option 'D'. Can you explain this answer?
Unit vectors along the axes OX, OY and OZ are denoted by
a)
b)
c)
d)
|
|
Krishna Iyer answered |
The unit vector in the direction of 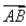 , where A and B are the points (2, – 3, 7) and (1, 3, – 4) is:
, where A and B are the points (2, – 3, 7) and (1, 3, – 4) is:- a)
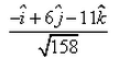
- b)
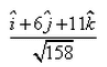
- c)
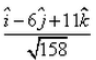
- d)
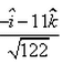
Correct answer is option 'A'. Can you explain this answer?
The unit vector in the direction of 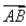 , where A and B are the points (2, – 3, 7) and (1, 3, – 4) is:
, where A and B are the points (2, – 3, 7) and (1, 3, – 4) is:
a)
b)
c)
d)

|
Sushil Kumar answered |
Given, Point A (2,-3,7)
Point B (1,3,-4)
Let vector in the direction of AB be C.
∴ C = B - A
⇒ (1,3,-4) - (2,-3,7)
⇒ ( 1-2 , 3+3 , -4-7 )
⇒ (-1,6,-11)
⇒ -1i + 6j -11k
Magnitude of vector C
|C| = √(-1)2 + 62 + (-11)2
⇒ √1+36+121
⇒ √158
Magnitude of vector C
|C| = √(-1)2 + 62 + (-11)2
⇒ √1+36+121
⇒ √158
Unit vector = (Vector)/(Magnitude of vector)
Unit vector C = (C vector)/(Magnitude of C vector) = (-1i + 6j -11k)/√158
Unit vector C = (C vector)/(Magnitude of C vector) = (-1i + 6j -11k)/√158
The points with position vectors 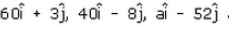 are collinear vectors, Value of a =
are collinear vectors, Value of a =- a)-20
- b)20
- c)-40
- d)40
Correct answer is option 'C'. Can you explain this answer?
The points with position vectors 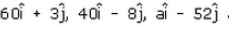 are collinear vectors, Value of a =
are collinear vectors, Value of a =
a)
-20
b)
20
c)
-40
d)
40
|
|
Om Desai answered |
Position vector A = 60i+3j
Position vector B = 40i-8j
Position vector C = aj-52j
Now, find vector AB and BC
AB = -20i-11j
BC= (a-40)i-44j
To be collinear, angle between the vector AB and BC made by the given position vectors should be 0 or 180 degree.
That’s why the cross product of the vectors should be zero
ABXBC=(-20i-11j)X(a-40)i-44j
0i+0j+(880+11(a-40))=0
a-40= -80
a=-40
Therefore, a should be -40 to be the given positions vectors collinear.
Position vector B = 40i-8j
Position vector C = aj-52j
Now, find vector AB and BC
AB = -20i-11j
BC= (a-40)i-44j
To be collinear, angle between the vector AB and BC made by the given position vectors should be 0 or 180 degree.
That’s why the cross product of the vectors should be zero
ABXBC=(-20i-11j)X(a-40)i-44j
0i+0j+(880+11(a-40))=0
a-40= -80
a=-40
Therefore, a should be -40 to be the given positions vectors collinear.
The value of 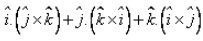 is:
is:- a)0
- b)3
- c)1/3
- d)1
Correct answer is option 'B'. Can you explain this answer?
The value of 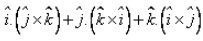 is:
is:
a)
0
b)
3
c)
1/3
d)
1

|
Sahil Soni answered |
Cross multiply in maths take place in cycle like i》j》k i×j=k j×k=i k×i=j but j×i=-k k×j=-i i×k=-j and dotmultiply takes place as i.i=1j.j=1K.K=1BUTI.J=0J.K=0k.i=0so the correct answer is b
What is the additive identity of a vector?- a)zero vector
- b)Negative of the vector
- c)unit vector
- d)The vector itself
Correct answer is option 'A'. Can you explain this answer?
What is the additive identity of a vector?
a)
zero vector
b)
Negative of the vector
c)
unit vector
d)
The vector itself
|
|
Nandini Iyer answered |
In the Additive Identity of vectors, the additive identity is zero vector 0.
For any vector V additive identity is defined as,
0 + V = V and V + 0 = V
For any vector V additive identity is defined as,
0 + V = V and V + 0 = V
For any two vectors a and b, we always have
- a)|a – b| ≥ |a| – |b|
- b)|a + b| ≤ |a| + |b|
- c)|a + b| ≤ |a| – |b|
- d)|a – b| = |a + b|
Correct answer is option 'B'. Can you explain this answer?
For any two vectors a and b, we always have
a)
|a – b| ≥ |a| – |b|
b)
|a + b| ≤ |a| + |b|
c)
|a + b| ≤ |a| – |b|
d)
|a – b| = |a + b|
|
|
Nandini Iyer answered |
|a + b|2 = |a|2 + |b|2 + 2|a||b|.cosθ
|a|2 + |b|2 = |a|2 + |b|2 + 2|a| + |b| ∵ −1 ⩽ cosθ ⩽ 1
⇒ 2|a||b|.cosθ ⩽ 2|a||b|
So, |a + b|2 ⩽ (|a| + |b|
⇒ |a + b| ≤ |a| + |b|
This is also known as Triangle Inequality of vectors.
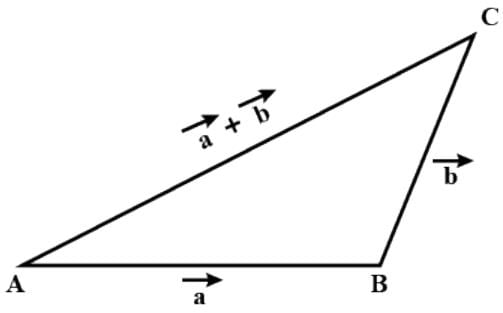
|a|2 + |b|2 = |a|2 + |b|2 + 2|a| + |b| ∵ −1 ⩽ cosθ ⩽ 1
⇒ 2|a||b|.cosθ ⩽ 2|a||b|
So, |a + b|2 ⩽ (|a| + |b|
)2
⇒ |a + b| ≤ |a| + |b|
This is also known as Triangle Inequality of vectors.

ABCD is a parallelogram. If coordinates of A,B,C are (2,3), (1,4) and (0, -2). Coordinates of D =- a)(-1,3)
- b)(1,-3)
- c)(1,3)
- d)(-1,-3)
Correct answer is option 'B'. Can you explain this answer?
ABCD is a parallelogram. If coordinates of A,B,C are (2,3), (1,4) and (0, -2). Coordinates of D =
a)
(-1,3)
b)
(1,-3)
c)
(1,3)
d)
(-1,-3)
|
|
Naina Bansal answered |
Here's a generic way to solve problems like this.
The angles α, β, γ made by the vector with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector
with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector are:
are: - a)cos α, cos β, cos γ
- b)sin α, sin β, sin γ
- c)180° - α, 180° - β, 180° γ
- d)tan α, tan β, tan γ
Correct answer is option 'A'. Can you explain this answer?
The angles α, β, γ made by the vector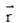 with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector
with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector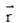 are:
are:
a)
cos α, cos β, cos γ
b)
sin α, sin β, sin γ
c)
180° - α, 180° - β, 180° γ
d)
tan α, tan β, tan γ
|
|
Sarita Yadav answered |
Direction Cosines for angle α, β, γ are:
cos α, cos β, cos γ
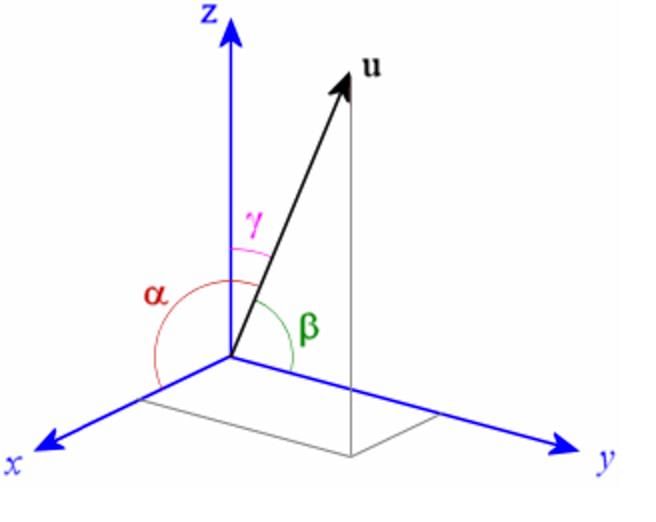
cos α, cos β, cos γ

If 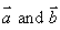 are two vectors, such that
are two vectors, such that 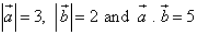 , then
, then 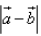 = ……
= ……- a)3
- b)√7
- c)√5
- d)√3
Correct answer is option 'D'. Can you explain this answer?
If 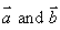 are two vectors, such that
are two vectors, such that 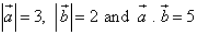 , then
, then 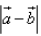 = ……
= ……
a)
3
b)
√7
c)
√5
d)
√3
|
|
Neha Sharma answered |
|a - b|2 = |a|2 + |b|2 - 2|a||b|
|a - b|2 = (3)2 + (2)2 - 2(5)
|a - b|2 = 9 + 4 - 10
|a - b|2 = 3
|a - b| = (3)½.
|a - b|2 = (3)2 + (2)2 - 2(5)
|a - b|2 = 9 + 4 - 10
|a - b|2 = 3
|a - b| = (3)½.
If the magnitude of the position vector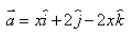 is 7, the value of x is:
is 7, the value of x is:- a)±1
- b)±5
- c)±3
- d)±2
Correct answer is option 'C'. Can you explain this answer?
If the magnitude of the position vector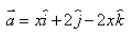 is 7, the value of x is:
is 7, the value of x is:
a)
±1
b)
±5
c)
±3
d)
±2

|
Shiksha Academy answered |
|a| = (x2 + 22 + (2x)2)1/2
7 = (x2 + 22 + (2x)2)1/2
⇒ 49 = x2 + 22 + 4x2
⇒ 49 = 4 + 5x2
⇒ 5x2 = 45
⇒ x2 = 9
x = ±3
Coinitial Vectors are- a)Two or more vectors having the same final point
- b)Two or more pseudo vectors having the same initial point
- c)Two or more force vectors having the same initial point
- d)Two or more vectors having the same initial point
Correct answer is option 'D'. Can you explain this answer?
Coinitial Vectors are
a)
Two or more vectors having the same final point
b)
Two or more pseudo vectors having the same initial point
c)
Two or more force vectors having the same initial point
d)
Two or more vectors having the same initial point

|
Bhavana Dey answered |
Two vectors whose initial point is same are called co- initial vectors
A vector whose initial and terminal points coincide, is called- a)zero vector
- b)unit vector
- c)equal vectors
- d)coterminus vectors
Correct answer is option 'A'. Can you explain this answer?
A vector whose initial and terminal points coincide, is called
a)
zero vector
b)
unit vector
c)
equal vectors
d)
coterminus vectors
|
|
Nandini Patel answered |
Zero Vector Or Null Vector – A vector whose initia... morel and terminal points coincide is known as zero vector.Unit Vector
If a unit vector  makes angles
makes angles 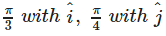 and an acute angle θ with
and an acute angle θ with 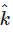 , then the components of
, then the components of 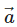 are
are- a)
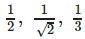
- b)
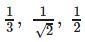
- c)
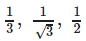
- d)
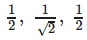
Correct answer is option 'D'. Can you explain this answer?
If a unit vector 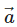 makes angles
makes angles 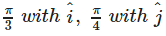 and an acute angle θ with
and an acute angle θ with 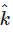 , then the components of
, then the components of 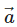 are
are
a)
b)
c)
d)
|
|
Riya Banerjee answered |
Let 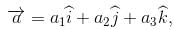 It is given that left|
It is given that left| 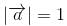 , then ,
, then ,
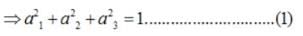
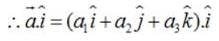

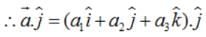
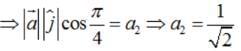
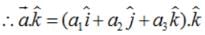
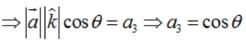
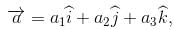 It is given that left|
It is given that left| 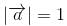 , then ,
, then , 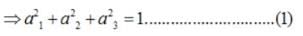
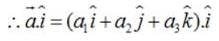

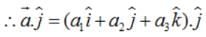
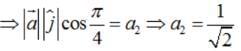
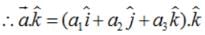
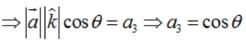
Putting these values in (1) , we get :

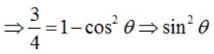

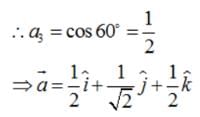
The vector joining the points A(2, – 3, 1) and B(1, – 2, – 5) directed from B to A is:- a)
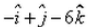
- b)
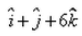
- c)
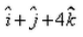
- d)
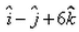
Correct answer is option 'D'. Can you explain this answer?
The vector joining the points A(2, – 3, 1) and B(1, – 2, – 5) directed from B to A is:
a)
b)
c)
d)

|
Siddhant Kumar answered |
The vector goes from B to A means that its initial coordinates is at B and final at A.
so the vector BA will be [ (2-1)i + (-3+2) j + (1+5)k ] = i-j+6k.
so the vector BA will be [ (2-1)i + (-3+2) j + (1+5)k ] = i-j+6k.
The distance between the point (2, 3, 1) and (–1, 2, – 3) is:
- a)√26 units
- b)5 units
- c)√20 units
- d)4 units
Correct answer is option 'A'. Can you explain this answer?
The distance between the point (2, 3, 1) and (–1, 2, – 3) is:
a)
√26 units
b)
5 units
c)
√20 units
d)
4 units
|
|
Giriraj Gupta answered |
Use the distance formula
distance=root of [ (x1-x2)^2+(y1-y2)^2+(z1-z2)^2]
distance=root of [ (x1-x2)^2+(y1-y2)^2+(z1-z2)^2]
If 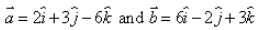 , then
, then- a)
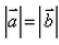
- b)
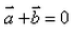
- c)

- d)
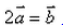
Correct answer is option 'A'. Can you explain this answer?
If 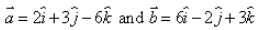 , then
, then
a)
b)
c)
d)
|
|
Lavanya Menon answered |
a = 2i + 3j - 6k
|a| = √4+9+36 = √49 = 7
b = 6i - 2j + 3k
|b| = √36+4+9 = √49 = 7
|a| = |b|
Hence, option A is correct.
|a| = √4+9+36 = √49 = 7
b = 6i - 2j + 3k
|b| = √36+4+9 = √49 = 7
|a| = |b|
Hence, option A is correct.
The position vectors of the end points of diameter of a circle are  and
and  , then the position vector of the centre of the circle is:
, then the position vector of the centre of the circle is:- a)
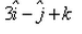
- b)
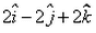
- c)
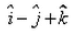
- d)

Correct answer is option 'D'. Can you explain this answer?
The position vectors of the end points of diameter of a circle are 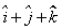 and
and 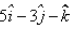 , then the position vector of the centre of the circle is:
, then the position vector of the centre of the circle is:
a)
b)
c)
d)
|
|
Om Desai answered |
{(1+5)î +(1-3)j + (1-1)k} / 2
= {6i - 2j + 0k}/2
= 3i - j
= {6i - 2j + 0k}/2
= 3i - j
If  are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors
are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors  are collinear.
are collinear. - a)1
- b)2
- c)-1
- d)-2
Correct answer is option 'B'. Can you explain this answer?
If  are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors
are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors  are collinear.
are collinear.
a)
1
b)
2
c)
-1
d)
-2
|
|
Neha Sharma answered |
Given a = (-1,1) and b = (m,-2)
Given that above two vectors are collinear, so they are parallel
⇒ -1/m = 1/-2
⇒ m = 2
Given that above two vectors are collinear, so they are parallel
⇒ -1/m = 1/-2
⇒ m = 2
For what values of x and y, the vectors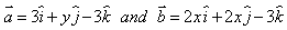 are equal?
are equal?- a)
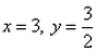
- b)x = 3, y = 6
- c)
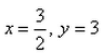
- d)x = 6, y = 3
Correct answer is option 'C'. Can you explain this answer?
For what values of x and y, the vectors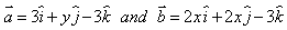 are equal?
are equal?
a)
b)
x = 3, y = 6
c)
d)
x = 6, y = 3

|
Satyam Sriraj answered |
For equal vector
2x=3
and 2x=y
now
solve it.
2x=3
and 2x=y
now
solve it.
The direction of zero vector.- a)Is towards the origin
- b)Is towards a fixed point
- c)Does not exist
- d)Is indeterminate
Correct answer is option 'D'. Can you explain this answer?
The direction of zero vector.
a)
Is towards the origin
b)
Is towards a fixed point
c)
Does not exist
d)
Is indeterminate

|
Supriya Senapati answered |
Zero vector is the unit vector having zero length ,hence the direction is undefined
Direction: Read the following text and answer the following questions on the basis of the same:Solar Panels have to be installed carefully so that the tilt of the roof, and the direction to the sun, produce the largest possible electrical power in the solar panels. A surveyor uses his instrument to determine the coordinates of the four corners of a roof where solar panels are to be mounted. In the picture , suppose the points are labelled counter clockwise from the roof corner nearest to the camera in units of meters P1(6, 8, 4), P2(21, 8, 4), P3(21, 16, 10) and P4(6, 16, 10)Q. What is the magnitude of
A surveyor uses his instrument to determine the coordinates of the four corners of a roof where solar panels are to be mounted. In the picture , suppose the points are labelled counter clockwise from the roof corner nearest to the camera in units of meters P1(6, 8, 4), P2(21, 8, 4), P3(21, 16, 10) and P4(6, 16, 10)Q. What is the magnitude of 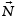 and in what units?
and in what units?- a)100
- b)150
- c)50
- d)90
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Solar Panels have to be installed carefully so that the tilt of the roof, and the direction to the sun, produce the largest possible electrical power in the solar panels.

A surveyor uses his instrument to determine the coordinates of the four corners of a roof where solar panels are to be mounted. In the picture , suppose the points are labelled counter clockwise from the roof corner nearest to the camera in units of meters P1(6, 8, 4), P2(21, 8, 4), P3(21, 16, 10) and P4(6, 16, 10)
Q. What is the magnitude of 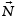 and in what units?
and in what units?
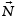 and in what units?
and in what units?a)
100
b)
150
c)
50
d)
90
|
|
Anjali Sharma answered |
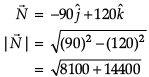
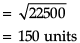
Vectors A and BareCollinear- a)if they are in the same line
- b)if they are have equal magnitude
- c)if the direction cosines of one are negatives of the other
- d)if they are parallel to the same lineirrespective of their magnitudes and directions.
Correct answer is option 'D'. Can you explain this answer?
Vectors A and BareCollinear
a)
if they are in the same line
b)
if they are have equal magnitude
c)
if the direction cosines of one are negatives of the other
d)
if they are parallel to the same lineirrespective of their magnitudes and directions.

|
Nishanth Verma answered |
Two vectors A and B are said to be collinear , if they are parallel to the same line irrespective of their magnitudes and directions.
इनमें से कौन-सा क्षेत्र प्रागैतिहासिक शैल कला चित्रों की मेजबानी के लिए प्रसिद्ध हैं?
1. मध्य प्रदेश की विंध्य पर्वतमाला
2. उत्तर प्रदेश का कैमूरियन विस्तार
उपरोक्त में से कौन सा/से सही हैं?
- a)केवल 1
- b)केवल 2
- c)दोनों 1 और 2
- d)इनमे से कोई भी नहीं
Correct answer is option 'C'. Can you explain this answer?
इनमें से कौन-सा क्षेत्र प्रागैतिहासिक शैल कला चित्रों की मेजबानी के लिए प्रसिद्ध हैं?
1. मध्य प्रदेश की विंध्य पर्वतमाला
2. उत्तर प्रदेश का कैमूरियन विस्तार
2. उत्तर प्रदेश का कैमूरियन विस्तार
उपरोक्त में से कौन सा/से सही हैं?
a)
केवल 1
b)
केवल 2
c)
दोनों 1 और 2
d)
इनमे से कोई भी नहीं
|
|
Amit Sharma answered |
- मध्य प्रदेश के विंध्य पर्वतमाला और उत्तर प्रदेश में उनके कैमूरियन विस्तार से सबसे समृद्ध चित्रों की सूचना मिली है। ये पर्वत श्रृंखलाएं पुरापाषाण और मध्यपाषाणकालीन अवशेषों से परिपूर्ण हैं। 9000 ईसा पूर्व में पाषाण युग की संस्कृति में एक मध्यवर्ती चरण शुरू हुआ, जिसे मेसोलिथिक युग कहा जाता है।
- मध्य प्रदेश, उत्तर प्रदेश, आंध्र प्रदेश, कामतका और बिहार के कई जिलों की गुफाओं में शैल चित्रों के अवशेष हैं।
- उत्तराखंड में कुमाऊं की पहाड़ियां भी शैल चित्रों के लिए जानी जाती हैं।
Any vector in an arbitrary direction can be replaced by two or three vectors - a)Perpendicular to each other and have the original vector as their resultant
- b)Parallel to each other and have the original vector as their resultant
- c)Arbitrary vectors which have original vectors as their resultant
- d)It is impossible to resolve a vector
Correct answer is option 'C'. Can you explain this answer?
Any vector in an arbitrary direction can be replaced by two or three vectors
a)
Perpendicular to each other and have the original vector as their resultant
b)
Parallel to each other and have the original vector as their resultant
c)
Arbitrary vectors which have original vectors as their resultant
d)
It is impossible to resolve a vector
|
|
Varun Kapoor answered |
If we slide a vector parallel to its position it will be the same as before. Any vector in an arbitrary direction can always be replaced by two (or three) arbitrary vectors which have the original vector as their resultant.
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice asAssertion (A): The area of parallelogram with diagonals 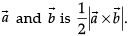 Reason (R): If
Reason (R): If 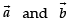 represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating
represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating 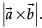
- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false but R is True
Correct answer is option 'C'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): The area of parallelogram with diagonals 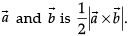
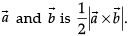
Reason (R): If 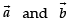 represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating
represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating 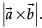
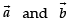 represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating
represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating 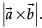
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false but R is True
|
|
Anjali Sharma answered |
If 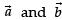 represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating
represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating 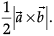
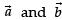 represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating
represent the adjacent sides of a triangle, then the area of triangle can be obtained by evaluating 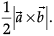
Unit Vector is- a)A vector whose direction angle γ is unity
- b)A vector whose magnitude is unity
- c)A vector whose direction angle α is unity
- d)A vector whose direction angle β is unity
Correct answer is option 'B'. Can you explain this answer?
Unit Vector is
a)
A vector whose direction angle γ is unity
b)
A vector whose magnitude is unity
c)
A vector whose direction angle α is unity
d)
A vector whose direction angle β is unity

|
Amrita Sarkar answered |
The vector whose magnitude is always 1 or unity is called a Unit Vector.
Show that the points A(1, – 2, – 8), B (5, 0, – 2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.- a)2 :1
- b)3 :2
- c)2 :4
- d)2 : 3
Correct answer is option 'D'. Can you explain this answer?
Show that the points A(1, – 2, – 8), B (5, 0, – 2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
a)
2 :1
b)
3 :2
c)
2 :4
d)
2 : 3

|
Lekshmi Basu answered |
Therefore , AB and BC are parallel, but point B is common , so points , A,B,C are collinear. As
भारतीय उपमहाद्वीप में मेसोलिथिक युग से लौह युग तक के प्रमुख पुरातात्विक स्थलों पर विचार करें। वर्तमान भारत में उनके संबंधित क्षेत्रों के साथ उनका मिलान करें:1. कोल्डिहवा : मध्य प्रदेश2. मेहरगढ़: हरियाणा3. पय्यमपल्ली: तमिलनाडुनीचे दिए गए कोड का उपयोग करके सही उत्तर चुनें।- a)केवल 1 और 2
- b)केवल 3
- c)2 और 3 ही
- d)1 ही
Correct answer is option 'B'. Can you explain this answer?
भारतीय उपमहाद्वीप में मेसोलिथिक युग से लौह युग तक के प्रमुख पुरातात्विक स्थलों पर विचार करें। वर्तमान भारत में उनके संबंधित क्षेत्रों के साथ उनका मिलान करें:
1. कोल्डिहवा : मध्य प्रदेश
2. मेहरगढ़: हरियाणा
3. पय्यमपल्ली: तमिलनाडु
नीचे दिए गए कोड का उपयोग करके सही उत्तर चुनें।
a)
केवल 1 और 2
b)
केवल 3
c)
2 और 3 ही
d)
1 ही
|
|
Kuldeep Rajput answered |
2
A point from a vector starts is called …… and where it ends is called its ……- a)terminal point, end point.
- b)initial point, terminal point
- c)Origin, end point
- d)initial point, end point
Correct answer is option 'B'. Can you explain this answer?
A point from a vector starts is called …… and where it ends is called its ……
a)
terminal point, end point.
b)
initial point, terminal point
c)
Origin, end point
d)
initial point, end point
|
|
Gauri Rane answered |
A vector is a specific quantity drawn as a line segment with an arrowhead at one end. It has an initial point, where it begins, and a terminal point, where it ends. A vector is defined by its magnitude, or the length of the line, and its direction, indicated by an arrowhead at the terminal point.
Direction: Read the following text and answer the following questions on the basis of the same:A class XII student appearing for a competitive examination was asked to attempt the following questions.Let 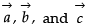 be three non zero vectors.Q.
be three non zero vectors.Q. 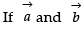 are unit vectors and θ be the angle between them then
are unit vectors and θ be the angle between them then 
- a)sin θ/2
- b)2sin θ/2
- c)2cos θ/2
- d)cos θ/2
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A class XII student appearing for a competitive examination was asked to attempt the following questions.
Let 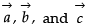 be three non zero vectors.
be three non zero vectors.
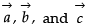 be three non zero vectors.
be three non zero vectors.Q. 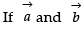 are unit vectors and θ be the angle between them then
are unit vectors and θ be the angle between them then 
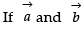 are unit vectors and θ be the angle between them then
are unit vectors and θ be the angle between them then 
a)
sin θ/2
b)
2sin θ/2
c)
2cos θ/2
d)
cos θ/2
|
|
Swati Verma answered |
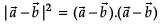
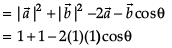
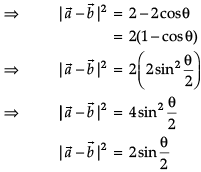
Direction: Read the following text and answer the following questions on the basis of the same:ABCD is a parallelogram whose adjacent sides are represented by the vectors 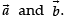 Three of its vertices are A(1, 2, 3), B(2, 0, 5) and D(–1, 4, 1).
Three of its vertices are A(1, 2, 3), B(2, 0, 5) and D(–1, 4, 1).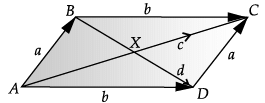 Q. The diagonal
Q. The diagonal 
- a)
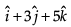
- b)
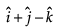
- c)
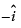
- d)

Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
ABCD is a parallelogram whose adjacent sides are represented by the vectors 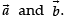 Three of its vertices are A(1, 2, 3), B(2, 0, 5) and D(–1, 4, 1).
Three of its vertices are A(1, 2, 3), B(2, 0, 5) and D(–1, 4, 1).
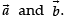 Three of its vertices are A(1, 2, 3), B(2, 0, 5) and D(–1, 4, 1).
Three of its vertices are A(1, 2, 3), B(2, 0, 5) and D(–1, 4, 1).
Q. The diagonal 

a)
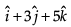
b)
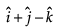
c)
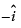
d)

|
|
Krishna Iyer answered |
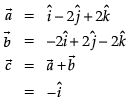
Can you explain the answer of this question below:If l, m and n are direction cosines of the position vector OP the coordinates of P are
- A:
lr, mr and nr
- B:
lr, m and nr
- C:
l, mr and nr
- D:
lr, mr and n
The answer is a.
If l, m and n are direction cosines of the position vector OP the coordinates of P are
lr, mr and nr
lr, m and nr
l, mr and nr
lr, mr and n

|
Shreya Gupta answered |
If l , m and n are the direction cosines of vector  then , the coordinates of point P are given by : lr ,mr and nr respectively.
then , the coordinates of point P are given by : lr ,mr and nr respectively.
Two or more vectors having the same initial point are called- a)co-terminus vectors.
- b)zero vectors
- c)co-initial vectors
- d)unit vectors
Correct answer is option 'C'. Can you explain this answer?
Two or more vectors having the same initial point are called
a)
co-terminus vectors.
b)
zero vectors
c)
co-initial vectors
d)
unit vectors
|
|
Naina Bansal answered |
Two or more vectors having the same initial point are called coinitial vector. Two or more vectors are said to be collinear,if they are parallel to the same line,irrespective of their magnitudes and directions.
Direction cosines- a)are cosines of Direction angles
- b)arecotangents of Direction angles
- c)are tangents of Direction angles
- d)aresines of Direction angles
Correct answer is option 'A'. Can you explain this answer?
Direction cosines
a)
are cosines of Direction angles
b)
arecotangents of Direction angles
c)
are tangents of Direction angles
d)
aresines of Direction angles

|
Sanaya Menon answered |
Cosines of the angles α,β,γ are called direction cosines.
Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).- a)

- b)
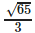
- c)
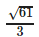
- d)
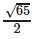
Correct answer is option 'A'. Can you explain this answer?
Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
a)
b)
c)
d)

|
Jatin Dasgupta answered |
Therefore , the area of triangle
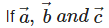 are any three vectors then the correct expression for distributivity of scalar product over addition is
are any three vectors then the correct expression for distributivity of scalar product over addition is- a)
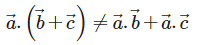
- b)
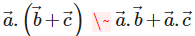
- c)
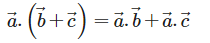
- d)
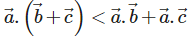
Correct answer is option 'C'. Can you explain this answer?
a)
b)
c)
d)

|
Sanaya Menon answered |
Chapter doubts & questions for Chapter 10 - Vectors - Mathematics CUET UG Mock Test Series 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 10 - Vectors - Mathematics CUET UG Mock Test Series 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily