All Exams >
CUET Commerce >
General Test Preparation for CUET UG >
All Questions
All questions of Calendars for CUET Commerce Exam
The maximum gap between two successive leap year is?- a)4
- b)8
- c)2
- d)1
Correct answer is option 'B'. Can you explain this answer?
The maximum gap between two successive leap year is?
a)
4
b)
8
c)
2
d)
1

|
Bhargavi Dey answered |
This can be illustrated with an example.
Ex: 1896 is a leap year.The next leap year comes in 1904 (1900 is not a leap year).
Explanation : The length of the solar year, however, is slightly less than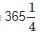 days-by about 11 minutes. To compensate for this discrepancy, the leap year is omitted three times every four hundred years.
days-by about 11 minutes. To compensate for this discrepancy, the leap year is omitted three times every four hundred years.
In other words, a century year cannot be a leap year unless it is divisible by 400. Thus 1700, 1800, and 1900 were not leap years, but 1600, 2000, and 2400 are leap years.
Ex: 1896 is a leap year.The next leap year comes in 1904 (1900 is not a leap year).
Explanation : The length of the solar year, however, is slightly less than
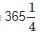 days-by about 11 minutes. To compensate for this discrepancy, the leap year is omitted three times every four hundred years.
days-by about 11 minutes. To compensate for this discrepancy, the leap year is omitted three times every four hundred years.In other words, a century year cannot be a leap year unless it is divisible by 400. Thus 1700, 1800, and 1900 were not leap years, but 1600, 2000, and 2400 are leap years.
What is the year next to 1990 which will have the same calendar as that of the year 1990?- a)1992
- b)2001
- c)1995
- d)1996
Correct answer is option 'B'. Can you explain this answer?
What is the year next to 1990 which will have the same calendar as that of the year 1990?
a)
1992
b)
2001
c)
1995
d)
1996

|
Saumya Bose answered |
For a year to have the same calendar with 1990 ,total odd days from 1990 should be 0. Take the year 1992 from the given choices.
Total odd days in the period 1990-1991 = 2 normal years
⇒ 2 x 1 = 2 odd daysTake the year 1995 from the given choices.
Number of odd days in the period 1990-1994 = 4 normal years + 1 leap year
⇒ 4 x 1 + 1 x 2 = 6 odd daysTake the year 1996 from the given choices.
Number of odd days in the period 1990-1995 = 5 normal years + 1 leap year
⇒ 5 x 1 + 1 x 2 = 7 odd days = 0 odd days
(As we can reduce multiples of 7 from odd days which will not change anything) Though number of odd days in the period 1990-1995 is 0, there is a catch here.
1990 is not a leap year whereas 1996 is a leap year.
Hence calendar for 1990 and 1996 will never be the same.Take the year 2001 from the given choices. Number of odd days in the period 1990-2000 = 8 normal years + 3 leap years
⇒ 8 x 1 + 3 x 2 = 14 odd days = 0 odd days
Also, both 1990 and 2001 are normal years.
Hence 1990 will have the same calendar as that of 2001
Total odd days in the period 1990-1991 = 2 normal years
⇒ 2 x 1 = 2 odd daysTake the year 1995 from the given choices.
Number of odd days in the period 1990-1994 = 4 normal years + 1 leap year
⇒ 4 x 1 + 1 x 2 = 6 odd daysTake the year 1996 from the given choices.
Number of odd days in the period 1990-1995 = 5 normal years + 1 leap year
⇒ 5 x 1 + 1 x 2 = 7 odd days = 0 odd days
(As we can reduce multiples of 7 from odd days which will not change anything) Though number of odd days in the period 1990-1995 is 0, there is a catch here.
1990 is not a leap year whereas 1996 is a leap year.
Hence calendar for 1990 and 1996 will never be the same.Take the year 2001 from the given choices. Number of odd days in the period 1990-2000 = 8 normal years + 3 leap years
⇒ 8 x 1 + 3 x 2 = 14 odd days = 0 odd days
Also, both 1990 and 2001 are normal years.
Hence 1990 will have the same calendar as that of 2001
What was day of the week on 21-September-1987?- a)Saturday
- b)Sunday
- c)Monday
- d)Tuesday
Correct answer is option 'C'. Can you explain this answer?
What was day of the week on 21-September-1987?
a)
Saturday
b)
Sunday
c)
Monday
d)
Tuesday
|
|
Sagar Sharma answered |
The day of the week on 21st September 1987 was Monday.
Explanation:
- **Finding the day of the week**: To determine the day of the week for a specific date like 21st September 1987, we can use the Zeller's Congruence formula. This formula calculates the day of the week for any given date in the Gregorian calendar.
- **Zeller's Congruence formula**: The formula is as follows:
\[ h = \left(q + \left\lfloor\frac{13(m+1)}{5}\right\rfloor + K + \left\lfloor\frac{K}{4}\right\rfloor + \left\lfloor\frac{J}{4}\right\rfloor - 2J\right) \mod 7 \]
where:
- h is the day of the week (0 = Saturday, 1 = Sunday, 2 = Monday, ..., 6 = Friday)
- q is the day of the month
- m is the month (3 = March, 4 = April, ..., 12 = December; January and February are counted as months 13 and 14 of the previous year)
- K is the year of the century (year % 100)
- J is the zero-based century (year / 100)
- **Plugging in the values**:
- For 21st September 1987, q = 21, m = 9, K = 87, J = 19 (as 1987 belongs to the 20th century)
- Calculating the value of h using the formula will give us the day of the week, which is Monday in this case.
Therefore, the day of the week on 21st September 1987 was Monday.
Explanation:
- **Finding the day of the week**: To determine the day of the week for a specific date like 21st September 1987, we can use the Zeller's Congruence formula. This formula calculates the day of the week for any given date in the Gregorian calendar.
- **Zeller's Congruence formula**: The formula is as follows:
\[ h = \left(q + \left\lfloor\frac{13(m+1)}{5}\right\rfloor + K + \left\lfloor\frac{K}{4}\right\rfloor + \left\lfloor\frac{J}{4}\right\rfloor - 2J\right) \mod 7 \]
where:
- h is the day of the week (0 = Saturday, 1 = Sunday, 2 = Monday, ..., 6 = Friday)
- q is the day of the month
- m is the month (3 = March, 4 = April, ..., 12 = December; January and February are counted as months 13 and 14 of the previous year)
- K is the year of the century (year % 100)
- J is the zero-based century (year / 100)
- **Plugging in the values**:
- For 21st September 1987, q = 21, m = 9, K = 87, J = 19 (as 1987 belongs to the 20th century)
- Calculating the value of h using the formula will give us the day of the week, which is Monday in this case.
Therefore, the day of the week on 21st September 1987 was Monday.
What was the day of the week on 26-January-1950?- a)Monday
- b)Sunday
- c)Thursday
- d)Wednesday
Correct answer is option 'C'. Can you explain this answer?
What was the day of the week on 26-January-1950?
a)
Monday
b)
Sunday
c)
Thursday
d)
Wednesday

|
Charvi Sen answered |
Formula : (Date + Month code + No.of years + No.of leap year + Century code)/7
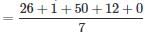
=84/7
=5
=Thursday
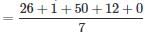
=84/7
=5
=Thursday
How many leap years does 100 years have?- a)25
- b)24
- c)4
- d)26
Correct answer is option 'B'. Can you explain this answer?
How many leap years does 100 years have?
a)
25
b)
24
c)
4
d)
26

|
Rithika Iyer answered |
Given year is divided by 4, and the quotient gives the number of leap years.
Here, 100%4 = 25
But, as 100 is not a leap year ⇒ 25 - 1 = 24 leap years.
Here, 100%4 = 25
But, as 100 is not a leap year ⇒ 25 - 1 = 24 leap years.
There are twenty people working in an office. The first group of five works between 8.00 A.M. and 2.00 P.M. The second group of ten works between 10.00 A.M. and 4.00 P.M. And the third group of five works between 12 noon and 6.00 P.M. There are three computers in the office which all the employees frequently use. During which of the following hours the computers are likely to be used most ?- a)10.00 A.M. – 12 noon
- b)12 noon – 2.00 P.M.
- c)1.00 P.M. – 3.00 P.M.
- d)2.00 P.M. – 4.00 P.M.
Correct answer is option 'B'. Can you explain this answer?
There are twenty people working in an office. The first group of five works between 8.00 A.M. and 2.00 P.M. The second group of ten works between 10.00 A.M. and 4.00 P.M. And the third group of five works between 12 noon and 6.00 P.M. There are three computers in the office which all the employees frequently use. During which of the following hours the computers are likely to be used most ?
a)
10.00 A.M. – 12 noon
b)
12 noon – 2.00 P.M.
c)
1.00 P.M. – 3.00 P.M.
d)
2.00 P.M. – 4.00 P.M.
|
|
Stuti Basak answered |
The computers are likely to be used most during the hours when the second group of ten people are working, between 10.00 A.M. and 4.00 P.M. This is because there are more people working during this time compared to the other time periods.
If it was Saturday on 17th November, 1962, what will be the day on 22nd November, 1964?- a)Monday
- b)Tuesday
- c)Wednesday
- d)Sunday
Correct answer is option 'D'. Can you explain this answer?
If it was Saturday on 17th November, 1962, what will be the day on 22nd November, 1964?
a)
Monday
b)
Tuesday
c)
Wednesday
d)
Sunday
|
|
Vivek Bansal answered |
In 1962, on 17th November it is Saturday. So, in 1963, 17th November will be Sunday and in 1964, 17th November should be Monday but as it is leap year so it will be Tuesday. On 22nd November, 1963 therefore, will be Sunday.
If Feb 12th,1986 falls on Wednesday then Jan 1st,1987 falls on which day?- a)Wednesday
- b)Tuesday
- c)Thursday
- d)Friday
Correct answer is option 'C'. Can you explain this answer?
If Feb 12th,1986 falls on Wednesday then Jan 1st,1987 falls on which day?
a)
Wednesday
b)
Tuesday
c)
Thursday
d)
Friday
|
|
Aarav Sharma answered |
Given:
Feb 12th,1986 falls on Wednesday
To find:
Jan 1st,1987 falls on which day?
Explanation:
We need to count the number of days between Feb 12th,1986 and Jan 1st,1987.
Number of days in Feb 1986 = 28
Number of days in Mar 1986 = 31
Number of days in Apr 1986 = 30
Number of days in May 1986 = 31
Number of days in Jun 1986 = 30
Number of days in Jul 1986 = 31
Number of days in Aug 1986 = 31
Number of days in Sep 1986 = 30
Number of days in Oct 1986 = 31
Number of days in Nov 1986 = 30
Number of days in Dec 1986 = 31
Number of days in Jan 1987 = 31
Total number of days between Feb 12th,1986 and Jan 1st,1987 = 31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 31 + 30 + 31 = 365
Since there are 365 days between Feb 12th,1986 and Jan 1st,1987, Jan 1st,1987 will be one day ahead of Feb 12th,1986.
As Feb 12th,1986 falls on Wednesday, Jan 1st,1987 will be one day ahead, i.e., Thursday.
Therefore, the answer is option (c) Thursday.
Feb 12th,1986 falls on Wednesday
To find:
Jan 1st,1987 falls on which day?
Explanation:
We need to count the number of days between Feb 12th,1986 and Jan 1st,1987.
Number of days in Feb 1986 = 28
Number of days in Mar 1986 = 31
Number of days in Apr 1986 = 30
Number of days in May 1986 = 31
Number of days in Jun 1986 = 30
Number of days in Jul 1986 = 31
Number of days in Aug 1986 = 31
Number of days in Sep 1986 = 30
Number of days in Oct 1986 = 31
Number of days in Nov 1986 = 30
Number of days in Dec 1986 = 31
Number of days in Jan 1987 = 31
Total number of days between Feb 12th,1986 and Jan 1st,1987 = 31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 31 + 30 + 31 = 365
Since there are 365 days between Feb 12th,1986 and Jan 1st,1987, Jan 1st,1987 will be one day ahead of Feb 12th,1986.
As Feb 12th,1986 falls on Wednesday, Jan 1st,1987 will be one day ahead, i.e., Thursday.
Therefore, the answer is option (c) Thursday.
Find the day of the week on 26 January, 1995.- a)Tuesday
- b)Friday
- c)Wednesday
- d)Thursday
Correct answer is option 'D'. Can you explain this answer?
Find the day of the week on 26 January, 1995.
a)
Tuesday
b)
Friday
c)
Wednesday
d)
Thursday
|
|
Sarthak Chaudhary answered |
Calculating the Day of the Week
To determine the day of the week for 26 January 1995, we can use the Zeller's Congruence formula or a simpler method based on known reference dates.
Step-by-Step Method
1. Identify the Reference Year
- January 1, 1995, is known to be a Sunday.
2. Count the Days from the Reference Date
- January has 31 days. Since we're calculating for January 26, we need to find out how many days have passed since January 1.
- From January 1 to January 26, there are 25 days.
3. Calculate the Day of the Week
- Start from Sunday (0):
- Sunday (0) + 25 days = 25.
- Now, divide 25 by 7 (since there are 7 days in a week):
- 25 ÷ 7 = 3 weeks and 4 days.
- This means we move 4 days forward from Sunday.
4. Identify the Resulting Day
- Counting 4 days from Sunday:
- Monday (1), Tuesday (2), Wednesday (3), Thursday (4).
Therefore, January 26, 1995, falls on a Thursday.
Conclusion
- The correct answer is D) Thursday.
- This method can be applied to any date to find the corresponding day of the week efficiently.
To determine the day of the week for 26 January 1995, we can use the Zeller's Congruence formula or a simpler method based on known reference dates.
Step-by-Step Method
1. Identify the Reference Year
- January 1, 1995, is known to be a Sunday.
2. Count the Days from the Reference Date
- January has 31 days. Since we're calculating for January 26, we need to find out how many days have passed since January 1.
- From January 1 to January 26, there are 25 days.
3. Calculate the Day of the Week
- Start from Sunday (0):
- Sunday (0) + 25 days = 25.
- Now, divide 25 by 7 (since there are 7 days in a week):
- 25 ÷ 7 = 3 weeks and 4 days.
- This means we move 4 days forward from Sunday.
4. Identify the Resulting Day
- Counting 4 days from Sunday:
- Monday (1), Tuesday (2), Wednesday (3), Thursday (4).
Therefore, January 26, 1995, falls on a Thursday.
Conclusion
- The correct answer is D) Thursday.
- This method can be applied to any date to find the corresponding day of the week efficiently.
If February 1, 1996 is Wednesday, what day is March 10, 1996 ?- a)Monday
- b)Sunday
- c)Saturday
- d)Friday
Correct answer is option 'C'. Can you explain this answer?
If February 1, 1996 is Wednesday, what day is March 10, 1996 ?
a)
Monday
b)
Sunday
c)
Saturday
d)
Friday
|
|
Vivek Bansal answered |
Feb 1, 1996 is Wednesday, and February will be a leap year therefore it will have 29 days.
So, Feb 8, Feb 15, Feb 22, February 29 and Mar 7 will be Wednesday. Therefore, March 10 will be Saturday.
So, Feb 8, Feb 15, Feb 22, February 29 and Mar 7 will be Wednesday. Therefore, March 10 will be Saturday.
If the day before yesterday was Thursday, when will Sunday be?- a)Today
- b)Tomorrow
- c)Two days after today
- d)Day after tomorrow
Correct answer is option 'B'. Can you explain this answer?
If the day before yesterday was Thursday, when will Sunday be?
a)
Today
b)
Tomorrow
c)
Two days after today
d)
Day after tomorrow

|
Bhargavi Dey answered |
Day before yesterday was Thursday
⇒ Yesterday was a Friday
⇒ Today is a Saturday
⇒ Tomorrow is a Sunday
⇒ Yesterday was a Friday
⇒ Today is a Saturday
⇒ Tomorrow is a Sunday
How many odd days are there from 13th May, 2005 to 19th August 2005 (both inclusive)?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
How many odd days are there from 13th May, 2005 to 19th August 2005 (both inclusive)?
a)
1
b)
2
c)
3
d)
4

|
Bhargavi Dey answered |
Here we have to count the number days from 13th May, 2005 to 18rd August 2005 ( both inclusive)
From 13th to 31st May = 19 days
In June = 30 days
In July = 31 days
From 1st to 19th April = 19 days
Total number of days = 19 + 30 + 31 + 19 = 99 days
The number of odd days are = 14 x 7 + 1 = 99
So there is 1 odd day in the given period
From 13th to 31st May = 19 days
In June = 30 days
In July = 31 days
From 1st to 19th April = 19 days
Total number of days = 19 + 30 + 31 + 19 = 99 days
The number of odd days are = 14 x 7 + 1 = 99
So there is 1 odd day in the given period
The year next to 2005 will have the same calendar as that of the year 2005?- a)2016
- b)2022
- c)2011
- d)None
Correct answer is option 'C'. Can you explain this answer?
The year next to 2005 will have the same calendar as that of the year 2005?
a)
2016
b)
2022
c)
2011
d)
None

|
Devanshi Dey answered |
NOTE :
Repetition of leap year ⇒ Add + 28 to the Given Year.
Repetition of non leap year
Step 1 : Add + 11 to the Given Year. If Result is a leap year, Go to step 2.
Step 2: Add + 6 to the Given Year.
Solution :
Given Year is 2005, Which is a non leap year.
Step 1 : Add + 11 to the given year (i.e 2005 + 11) = 2016, Which is a leap year.
Step 2 : Add + 6 to the given year (i.e 2005 + 6) = 2011
Therefore, The calendar for the year 2005 will be same for the year 2011
Repetition of leap year ⇒ Add + 28 to the Given Year.
Repetition of non leap year
Step 1 : Add + 11 to the Given Year. If Result is a leap year, Go to step 2.
Step 2: Add + 6 to the Given Year.
Solution :
Given Year is 2005, Which is a non leap year.
Step 1 : Add + 11 to the given year (i.e 2005 + 11) = 2016, Which is a leap year.
Step 2 : Add + 6 to the given year (i.e 2005 + 6) = 2011
Therefore, The calendar for the year 2005 will be same for the year 2011
Find the number of odd days in 126 years.- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
Find the number of odd days in 126 years.
a)
1
b)
2
c)
3
d)
4
|
|
Aarav Sharma answered |
Solution:
First, we need to understand what odd days mean.
Odd days are the days that are left over when we divide the total number of days by 7. For example, if we have 22 days, then there are 3 odd days (21 days can be divided by 7 evenly, but there is 1 day left over).
Now, let's find the number of odd days in 126 years.
- One year has 365 days (except for leap years, which have 366 days).
- To find the number of odd days in 126 years, we need to multiply 126 by 365.
126 x 365 = 45,990
- Now, we need to divide 45,990 by 7 to find the number of odd days.
45,990 ÷ 7 = 6,570 with a remainder of 6
- The quotient tells us that there are 6,570 groups of 7 days in 45,990 days.
- The remainder tells us that there are 6 odd days left over.
Therefore, there are 6 odd days in 126 years.
Answer: Option B (2)
First, we need to understand what odd days mean.
Odd days are the days that are left over when we divide the total number of days by 7. For example, if we have 22 days, then there are 3 odd days (21 days can be divided by 7 evenly, but there is 1 day left over).
Now, let's find the number of odd days in 126 years.
- One year has 365 days (except for leap years, which have 366 days).
- To find the number of odd days in 126 years, we need to multiply 126 by 365.
126 x 365 = 45,990
- Now, we need to divide 45,990 by 7 to find the number of odd days.
45,990 ÷ 7 = 6,570 with a remainder of 6
- The quotient tells us that there are 6,570 groups of 7 days in 45,990 days.
- The remainder tells us that there are 6 odd days left over.
Therefore, there are 6 odd days in 126 years.
Answer: Option B (2)
On what dates of July. 2004 did Monday fall?- a)6th, 10th, 21th, 30th
- b)12th, 7th, 19th, 28th
- c) 5th, 10th, 24th, 17th
- d)5th, 12th, 19th, 26th
Correct answer is option 'D'. Can you explain this answer?
On what dates of July. 2004 did Monday fall?
a)
6th, 10th, 21th, 30th
b)
12th, 7th, 19th, 28th
c)
5th, 10th, 24th, 17th
d)
5th, 12th, 19th, 26th

|
Ujwal Sengupta answered |
Let us find the day on 1st July, 2004.
2000 years have 0 odd day. 3 ordinary years have 3 odd days.
Jan. Feb. March April May June July
31 + 29 + 31 + 30 + 31 + 30 + 1
= 183 days
= (26 weeks + 1 day)
Total number of odd days = (0 + 3 + 1) odd days = 4 odd days.
∴ 1st July 2004 was 'Thursday'
Thus, 1st Monday in July 2004 as on 5th July. Hence, during July 2004, Monday fell on 5th, 12th, 19th and 26th.
2000 years have 0 odd day. 3 ordinary years have 3 odd days.
Jan. Feb. March April May June July
31 + 29 + 31 + 30 + 31 + 30 + 1
= 183 days
= (26 weeks + 1 day)
Total number of odd days = (0 + 3 + 1) odd days = 4 odd days.
∴ 1st July 2004 was 'Thursday'
Thus, 1st Monday in July 2004 as on 5th July. Hence, during July 2004, Monday fell on 5th, 12th, 19th and 26th.
How many leap years do 300 years have?- a)75
- b)74
- c)72
- d)73
Correct answer is option 'C'. Can you explain this answer?
How many leap years do 300 years have?
a)
75
b)
74
c)
72
d)
73

|
Neha Das answered |
Given year is divided by 4, and the quotient gives the number of leap years.
Here, 300%4 = 75.
But, as 100, 200 and 300 are not leap years ⇒ 75 - 3 = 72 leap years.
Here, 300%4 = 75.
But, as 100, 200 and 300 are not leap years ⇒ 75 - 3 = 72 leap years.
Today is Thursday. The day after 59 days will be?- a)Sunday
- b)Monday
- c)Tuesday
- d)Wednesday
Correct answer is option 'A'. Can you explain this answer?
Today is Thursday. The day after 59 days will be?
a)
Sunday
b)
Monday
c)
Tuesday
d)
Wednesday

|
Rithika Iyer answered |
59 days = 8 weeks 3 days = 3 odd days
Hence if today is Thursday, After 59 days, it will be
= (Thursday + 3 odd days)
= Sunday
Hence if today is Thursday, After 59 days, it will be
= (Thursday + 3 odd days)
= Sunday
The train for Lucknow leaves every two and a half hours from New Delhi railway station. An announcement was made at the station that the train for Lucknow had left 40 minutes ago and the next train will leave at 18.00 hrs. At what time was the announcement made?- a)15.30 hrs
- b)17.10 hrs
- c)16.00 hrs
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The train for Lucknow leaves every two and a half hours from New Delhi railway station. An announcement was made at the station that the train for Lucknow had left 40 minutes ago and the next train will leave at 18.00 hrs. At what time was the announcement made?
a)
15.30 hrs
b)
17.10 hrs
c)
16.00 hrs
d)
None of these
|
|
Anirban Choudhury answered |
Analysis:
To solve this problem, we need to determine the time at which the announcement was made. We are given that the train for Lucknow leaves every two and a half hours from New Delhi railway station. We are also given that the train had left 40 minutes ago and the next train will leave at 18.00 hrs.
Solution:
Let's break down the problem step by step to find the answer.
Step 1: Determine the time difference between two consecutive trains.
We are given that the train for Lucknow leaves every two and a half hours. This means that there is a time gap of 2.5 hours between two consecutive trains.
Step 2: Calculate the time when the next train will leave.
We are given that the next train will leave at 18.00 hrs. Since the time gap between two consecutive trains is 2.5 hours, we can add 2.5 hours to 18.00 hrs to find the departure time of the next train.
18.00 hrs + 2.5 hrs = 20.30 hrs
Step 3: Determine the time at which the announcement was made.
We are given that the train for Lucknow had left 40 minutes ago. We need to subtract 40 minutes from the departure time of the next train to find the time at which the announcement was made.
20.30 hrs - 40 minutes = 19.50 hrs
Therefore, the announcement was made at 19.50 hrs.
Conclusion:
The announcement was made at 19.50 hrs. Hence, the correct answer is option 'D' (None of these).
To solve this problem, we need to determine the time at which the announcement was made. We are given that the train for Lucknow leaves every two and a half hours from New Delhi railway station. We are also given that the train had left 40 minutes ago and the next train will leave at 18.00 hrs.
Solution:
Let's break down the problem step by step to find the answer.
Step 1: Determine the time difference between two consecutive trains.
We are given that the train for Lucknow leaves every two and a half hours. This means that there is a time gap of 2.5 hours between two consecutive trains.
Step 2: Calculate the time when the next train will leave.
We are given that the next train will leave at 18.00 hrs. Since the time gap between two consecutive trains is 2.5 hours, we can add 2.5 hours to 18.00 hrs to find the departure time of the next train.
18.00 hrs + 2.5 hrs = 20.30 hrs
Step 3: Determine the time at which the announcement was made.
We are given that the train for Lucknow had left 40 minutes ago. We need to subtract 40 minutes from the departure time of the next train to find the time at which the announcement was made.
20.30 hrs - 40 minutes = 19.50 hrs
Therefore, the announcement was made at 19.50 hrs.
Conclusion:
The announcement was made at 19.50 hrs. Hence, the correct answer is option 'D' (None of these).
Today is Thursday. What day of the week it was 30 days?- a)Sunday
- b)Monday
- c)Tuesday
- d)Wednesday
Correct answer is option 'C'. Can you explain this answer?
Today is Thursday. What day of the week it was 30 days?
a)
Sunday
b)
Monday
c)
Tuesday
d)
Wednesday

|
Milan Kulkarni answered |
30 days = 4 x 7 + 2 = 2 odd days
The day is 2 days before Thursday i.e Tuesday
The day is 2 days before Thursday i.e Tuesday
How many times are the hands of a clock perpendicular in a day?- a)42
- b)48
- c)44
- d)46
Correct answer is option 'C'. Can you explain this answer?
How many times are the hands of a clock perpendicular in a day?
a)
42
b)
48
c)
44
d)
46
|
|
Isha Ahuja answered |
Understanding Clock Hands
In a 12-hour period, the minute and hour hands of a clock are perpendicular to each other multiple times. To analyze how many times this occurs in a day, let’s break it down.
Frequency of Perpendicular Positions
- The hands of a clock are perpendicular when they form a right angle (90 degrees).
- In one hour, the hands of the clock are perpendicular twice, except during specific hours.
Exceptions in Hourly Intervals
- The two exceptions occur between 2:00-3:00 and 8:00-9:00:
- Between 2:00 and 3:00, the hands are perpendicular once.
- Between 8:00 and 9:00, the same occurs.
Calculating Perpendicular Occurrences
- In a 12-hour cycle:
- Normally, there are 2 occurrences of perpendicular hands for each hour: 12 hours x 2 = 24.
- However, due to the exceptions noted above, we subtract 2 occurrences (one for each exception).
- Final Calculation:
- Total in 12 hours = 24 - 2 = 22 times.
Extending to a Full Day
- Since a full day consists of two 12-hour cycles:
- Total in 24 hours = 22 x 2 = 44 times.
Conclusion
Thus, the hands of a clock are perpendicular 44 times in a day. Therefore, the correct answer is option 'C'.
In a 12-hour period, the minute and hour hands of a clock are perpendicular to each other multiple times. To analyze how many times this occurs in a day, let’s break it down.
Frequency of Perpendicular Positions
- The hands of a clock are perpendicular when they form a right angle (90 degrees).
- In one hour, the hands of the clock are perpendicular twice, except during specific hours.
Exceptions in Hourly Intervals
- The two exceptions occur between 2:00-3:00 and 8:00-9:00:
- Between 2:00 and 3:00, the hands are perpendicular once.
- Between 8:00 and 9:00, the same occurs.
Calculating Perpendicular Occurrences
- In a 12-hour cycle:
- Normally, there are 2 occurrences of perpendicular hands for each hour: 12 hours x 2 = 24.
- However, due to the exceptions noted above, we subtract 2 occurrences (one for each exception).
- Final Calculation:
- Total in 12 hours = 24 - 2 = 22 times.
Extending to a Full Day
- Since a full day consists of two 12-hour cycles:
- Total in 24 hours = 22 x 2 = 44 times.
Conclusion
Thus, the hands of a clock are perpendicular 44 times in a day. Therefore, the correct answer is option 'C'.
At what time between 2 and 3 O’ clock the hands of clock will make an angle of 1600 ?- a)20 minutes past 2
- b)30 minutes past 2
- c)40 minutes past 2
- d)50 minutes past 2
Correct answer is option 'C'. Can you explain this answer?
At what time between 2 and 3 O’ clock the hands of clock will make an angle of 1600 ?
a)
20 minutes past 2
b)
30 minutes past 2
c)
40 minutes past 2
d)
50 minutes past 2
|
|
Sravya Kumar answered |
Understanding Clock Angles
To determine the angle between the hands of a clock, we can use the formula:
- Angle = |(30*Hour - (11/2)*Minutes)|
Here, "Hour" is the hour hand position, and "Minutes" is the minute hand position.
Calculating the Positions
1. Hour Hand Position:
- At 2:00, the hour hand is at 60 degrees (2 hours * 30 degrees/hour).
- For every minute, the hour hand moves 0.5 degrees (30 degrees/60 minutes).
- So, if 'm' is the number of minutes past 2:00, the hour hand's position is:
Hour Position = 60 + 0.5m
2. Minute Hand Position:
- The minute hand moves 6 degrees per minute (360 degrees/60 minutes).
- Therefore, the minute hand's position is:
Minute Position = 6m
Setting Up the Equation
We want the angle between the two hands to be 160 degrees. Thus, we set up the equation:
- |(60 + 0.5m) - (6m)| = 160
This simplifies to two cases:
1. Case 1:
60 + 0.5m - 6m = 160
- This leads to:
- -5.5m = 100
- m = -100/5.5 (not applicable)
2. Case 2:
60 + 0.5m - 6m = -160
- This simplifies to:
- -5.5m = -220
- m = 220/5.5 = 40
Conclusion
Therefore, the hands of the clock will make an angle of 160 degrees at 40 minutes past 2. Hence, the correct answer is option 'C' - 40 minutes past 2.
To determine the angle between the hands of a clock, we can use the formula:
- Angle = |(30*Hour - (11/2)*Minutes)|
Here, "Hour" is the hour hand position, and "Minutes" is the minute hand position.
Calculating the Positions
1. Hour Hand Position:
- At 2:00, the hour hand is at 60 degrees (2 hours * 30 degrees/hour).
- For every minute, the hour hand moves 0.5 degrees (30 degrees/60 minutes).
- So, if 'm' is the number of minutes past 2:00, the hour hand's position is:
Hour Position = 60 + 0.5m
2. Minute Hand Position:
- The minute hand moves 6 degrees per minute (360 degrees/60 minutes).
- Therefore, the minute hand's position is:
Minute Position = 6m
Setting Up the Equation
We want the angle between the two hands to be 160 degrees. Thus, we set up the equation:
- |(60 + 0.5m) - (6m)| = 160
This simplifies to two cases:
1. Case 1:
60 + 0.5m - 6m = 160
- This leads to:
- -5.5m = 100
- m = -100/5.5 (not applicable)
2. Case 2:
60 + 0.5m - 6m = -160
- This simplifies to:
- -5.5m = -220
- m = 220/5.5 = 40
Conclusion
Therefore, the hands of the clock will make an angle of 160 degrees at 40 minutes past 2. Hence, the correct answer is option 'C' - 40 minutes past 2.
1.12.91 is the first Sunday. Which is the fourth Tuesday of December 91?- a)20.12.91
- b)22.12.91
- c)24.12.91
- d)25.12.91
Correct answer is option 'C'. Can you explain this answer?
1.12.91 is the first Sunday. Which is the fourth Tuesday of December 91?
a)
20.12.91
b)
22.12.91
c)
24.12.91
d)
25.12.91

|
Atharva Chawla answered |
Given that 1.12.91 is the first Sunday
Hence we can assume that 3.12.91 is the first Tuesday
If we add 7 days to 3.12.91, we will get second Tuesday
If we add 14 days to 3.12.91, we will get third Tuesday
If we add 21 days to 3.12.91, we will get fourth Tuesday
⇒ Fourth Tuesday = (3.12.91 + 21 days) = 24.12.91
Hence we can assume that 3.12.91 is the first Tuesday
If we add 7 days to 3.12.91, we will get second Tuesday
If we add 14 days to 3.12.91, we will get third Tuesday
If we add 21 days to 3.12.91, we will get fourth Tuesday
⇒ Fourth Tuesday = (3.12.91 + 21 days) = 24.12.91
Which two months in a year have the same calendar?- a)October, December
- b)April, November
- c)June, October
- d)April, July
Correct answer is option 'D'. Can you explain this answer?
Which two months in a year have the same calendar?
a)
October, December
b)
April, November
c)
June, October
d)
April, July

|
Avik Kapoor answered |
If the period between the two months is divisible by 7, then that two months will have the same calendar.
(a). Oct + Nov = 31 + 30 = 61 (not divisible by 7)
(b). Apr + May + Jun + Jul + Aug + Sep + Oct = 30 + 31 + 30 + 31 + 31 + 30 + 31 = 214 (not divisible by 7)
(c). Jun + July + Aug + Sep = 30 + 31 + 31 + 30 = 122 (not divisible by 7)
(d). Apr + May + June = 30 + 31 + 30 = 91 (divisible by 7)
Hence, April and July months will have the same calendar.
(a). Oct + Nov = 31 + 30 = 61 (not divisible by 7)
(b). Apr + May + Jun + Jul + Aug + Sep + Oct = 30 + 31 + 30 + 31 + 31 + 30 + 31 = 214 (not divisible by 7)
(c). Jun + July + Aug + Sep = 30 + 31 + 31 + 30 = 122 (not divisible by 7)
(d). Apr + May + June = 30 + 31 + 30 = 91 (divisible by 7)
Hence, April and July months will have the same calendar.
If the seventh day of month is three days earlier than Friday, what day will it be one the nineteenth day of the month?- a)Sunday
- b)Monday
- c)Wednesday
- d)Friday
Correct answer is option 'A'. Can you explain this answer?
If the seventh day of month is three days earlier than Friday, what day will it be one the nineteenth day of the month?
a)
Sunday
b)
Monday
c)
Wednesday
d)
Friday
|
|
Rishabh Singh answered |
Understanding the Problem
To solve the problem, we first need to establish the day of the week for the 7th of the month.
Identifying the Day of the 7th
- The problem states that the 7th day of the month is three days earlier than Friday.
- Counting backwards from Friday:
- Thursday (1 day earlier)
- Wednesday (2 days earlier)
- Tuesday (3 days earlier)
Thus, the 7th day of the month is a Tuesday.
Finding the Day on the 19th
Now, we need to determine what day it will be on the 19th day of the month.
- The difference between the 19th and the 7th is 12 days (19 - 7 = 12).
- We need to find out what day it is 12 days after Tuesday.
Counting the Days
- Starting from Tuesday:
- Wednesday (1 day)
- Thursday (2 days)
- Friday (3 days)
- Saturday (4 days)
- Sunday (5 days)
- Monday (6 days)
- Tuesday (7 days)
- Wednesday (8 days)
- Thursday (9 days)
- Friday (10 days)
- Saturday (11 days)
- Sunday (12 days)
Thus, 12 days after Tuesday is Sunday.
Conclusion
The day on the 19th of the month will be Sunday, which corresponds to option 'A'.
To solve the problem, we first need to establish the day of the week for the 7th of the month.
Identifying the Day of the 7th
- The problem states that the 7th day of the month is three days earlier than Friday.
- Counting backwards from Friday:
- Thursday (1 day earlier)
- Wednesday (2 days earlier)
- Tuesday (3 days earlier)
Thus, the 7th day of the month is a Tuesday.
Finding the Day on the 19th
Now, we need to determine what day it will be on the 19th day of the month.
- The difference between the 19th and the 7th is 12 days (19 - 7 = 12).
- We need to find out what day it is 12 days after Tuesday.
Counting the Days
- Starting from Tuesday:
- Wednesday (1 day)
- Thursday (2 days)
- Friday (3 days)
- Saturday (4 days)
- Sunday (5 days)
- Monday (6 days)
- Tuesday (7 days)
- Wednesday (8 days)
- Thursday (9 days)
- Friday (10 days)
- Saturday (11 days)
- Sunday (12 days)
Thus, 12 days after Tuesday is Sunday.
Conclusion
The day on the 19th of the month will be Sunday, which corresponds to option 'A'.
Ajay left home for the bus stop 15 minutes earlier than usual. It takes 10 minutes to reach the stop. He reached the stop at 8.40 a.m. What time does he usually leave home for the bus stop?- a)8.30 a.m.
- b)8.45 a.m.
- c)8.55 a.m.
- d)Data inadequate
Correct answer is option 'B'. Can you explain this answer?
Ajay left home for the bus stop 15 minutes earlier than usual. It takes 10 minutes to reach the stop. He reached the stop at 8.40 a.m. What time does he usually leave home for the bus stop?
a)
8.30 a.m.
b)
8.45 a.m.
c)
8.55 a.m.
d)
Data inadequate
|
|
Vivek Bansal answered |
Clearly, Ajay left home 10 minutes before 8.40 a.m. i.e., at 8.30 a.m. But it was 15 minutes earlier than usual. So, he usually leaves for the stop at 8.45 a.m.
Which two months in a year have the same calendar?- a)June, October
- b)April, November
- c)April, July
- d)October, December
Correct answer is option 'C'. Can you explain this answer?
Which two months in a year have the same calendar?
a)
June, October
b)
April, November
c)
April, July
d)
October, December
|
|
Vivek Bansal answered |
Two months will have the same calender if the period between them is divisible by 7.
Now,
(a) June + July + Aug. + Sep.
= 30 + 31 + 31 + 30
= 122 (not divisible by 7)
(b) Apr. + May + June + July + Aug. + Sep. + Oct. = 30 + 31 + 30 + 31 + 31 +30 + 31
= 213 (not divisible by 7)
(c) Apr. + May + June
= 30 + 31 + 30
= 91 (divisible by 7)
(d) October + November
= 31 + 30 = 61 (not divisible by 7)
Now,
(a) June + July + Aug. + Sep.
= 30 + 31 + 31 + 30
= 122 (not divisible by 7)
(b) Apr. + May + June + July + Aug. + Sep. + Oct. = 30 + 31 + 30 + 31 + 31 +30 + 31
= 213 (not divisible by 7)
(c) Apr. + May + June
= 30 + 31 + 30
= 91 (divisible by 7)
(d) October + November
= 31 + 30 = 61 (not divisible by 7)
What was the day on 15th august 1947 ?- a)Friday
- b)Saturday
- c)Sunday
- d)Thursday
Correct answer is option 'A'. Can you explain this answer?
What was the day on 15th august 1947 ?
a)
Friday
b)
Saturday
c)
Sunday
d)
Thursday

|
Advait Chawla answered |
15th Aug, 1947 = (1946 years + Period from 1.1.1947 to 15.8.1947)
Odd days in 1600 years = 0
Odd days in 300 years = 1
46 years
= (35 ordinary years + 11 leap years)
= (35 x 1 + 11 x 2)
= 57 (8 weeks + 1 day)
= 1 odd day
Jan. Feb. Mar. Apr. May. Jun. Jul. Aug
( 31 + 28 + 31 + 30 + 31 + 30 + 31 + 15 )
= 227 days
= (32 weeks + 3 days)
= 3 odd days
Total number of odd days = (0 + 1 + 1 + 3) = 5 odd days
Hence, as the number of odd days = 5, given day is Friday.
Odd days in 1600 years = 0
Odd days in 300 years = 1
46 years
= (35 ordinary years + 11 leap years)
= (35 x 1 + 11 x 2)
= 57 (8 weeks + 1 day)
= 1 odd day
Jan. Feb. Mar. Apr. May. Jun. Jul. Aug
( 31 + 28 + 31 + 30 + 31 + 30 + 31 + 15 )
= 227 days
= (32 weeks + 3 days)
= 3 odd days
Total number of odd days = (0 + 1 + 1 + 3) = 5 odd days
Hence, as the number of odd days = 5, given day is Friday.
Are the years 900 and 1000 leap years?- a)Yes
- b)No
- c)Can’t say
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Are the years 900 and 1000 leap years?
a)
Yes
b)
No
c)
Can’t say
d)
None of these
|
|
Avi Mehra answered |
Understanding Leap Years
Leap years are determined by specific rules in the Gregorian calendar. The rules are as follows:
Evaluating the Year 900
To determine if 900 is a leap year:
Evaluating the Year 1000
Now, let's assess the year 1000:
Conclusion
Based on the rules of leap years, both 900 and 1000 are not leap years. Thus, the correct answer is option 'B' - No.
Leap years are determined by specific rules in the Gregorian calendar. The rules are as follows:
- A year is a leap year if it is divisible by 4.
- However, if the year is divisible by 100, it is not a leap year, unless it is also divisible by 400.
Evaluating the Year 900
To determine if 900 is a leap year:
- 900 is divisible by 4 (900 ÷ 4 = 225).
- 900 is also divisible by 100 (900 ÷ 100 = 9).
- Since it is divisible by 100 but not by 400 (900 ÷ 400 = 2.25, not an integer), it does not qualify as a leap year.
Evaluating the Year 1000
Now, let's assess the year 1000:
- 1000 is divisible by 4 (1000 ÷ 4 = 250).
- 1000 is divisible by 100 (1000 ÷ 100 = 10).
- However, it is not divisible by 400 (1000 ÷ 400 = 2.5, not an integer), so it is not a leap year either.
Conclusion
Based on the rules of leap years, both 900 and 1000 are not leap years. Thus, the correct answer is option 'B' - No.
Karan was born on Saturday 22nd March 1982. On what day of the week was he 14 years 7 months and 8 days of age?- a)Sunday
- b)Tuesday
- c)Wednesday
- d)Monday
Correct answer is option 'C'. Can you explain this answer?
Karan was born on Saturday 22nd March 1982. On what day of the week was he 14 years 7 months and 8 days of age?
a)
Sunday
b)
Tuesday
c)
Wednesday
d)
Monday
|
|
Gitanjali Roy answered |
Understanding Karan's Birth Date
Karan was born on Saturday, March 22, 1982. To determine the day of the week when he turned 14 years, 7 months, and 8 days old, we need to add this duration to his birth date.
Calculating the Age
- 14 Years:
March 22, 1982 + 14 years = March 22, 1996
- 7 Months:
March 22, 1996 + 7 months = October 22, 1996
- 8 Days:
October 22, 1996 + 8 days = October 30, 1996
Now we find that Karan was 14 years, 7 months, and 8 days old on October 30, 1996.
Determining the Day of the Week
To find the day of the week for October 30, 1996, we can use the known day of the week from his birth date and calculate forward.
Steps to Calculate the Day
- Days from March 22 to October 30:
- March 22 to March 31: 9 days
- April: 30 days
- May: 31 days
- June: 30 days
- July: 31 days
- August: 31 days
- September: 30 days
- October 1 to October 30: 30 days
Total days = 9 + 30 + 31 + 30 + 31 + 31 + 30 + 30 = 21 + 31 + 30 + 31 + 30 = 251 days
Calculating the Weekday
- Finding the Weekday:
- Start from Saturday (March 22, 1982)
- 251 days % 7 = 6 days
- Counting forward from Saturday:
- Saturday (0)
- Sunday (1)
- Monday (2)
- Tuesday (3)
- Wednesday (4)
- Thursday (5)
- Friday (6)
- Saturday (7)
Thus, October 30, 1996, was a Wednesday.
Final Answer
Therefore, Karan was 14 years, 7 months, and 8 days old on a Wednesday. Hence, the correct answer is option 'C'.
Karan was born on Saturday, March 22, 1982. To determine the day of the week when he turned 14 years, 7 months, and 8 days old, we need to add this duration to his birth date.
Calculating the Age
- 14 Years:
March 22, 1982 + 14 years = March 22, 1996
- 7 Months:
March 22, 1996 + 7 months = October 22, 1996
- 8 Days:
October 22, 1996 + 8 days = October 30, 1996
Now we find that Karan was 14 years, 7 months, and 8 days old on October 30, 1996.
Determining the Day of the Week
To find the day of the week for October 30, 1996, we can use the known day of the week from his birth date and calculate forward.
Steps to Calculate the Day
- Days from March 22 to October 30:
- March 22 to March 31: 9 days
- April: 30 days
- May: 31 days
- June: 30 days
- July: 31 days
- August: 31 days
- September: 30 days
- October 1 to October 30: 30 days
Total days = 9 + 30 + 31 + 30 + 31 + 31 + 30 + 30 = 21 + 31 + 30 + 31 + 30 = 251 days
Calculating the Weekday
- Finding the Weekday:
- Start from Saturday (March 22, 1982)
- 251 days % 7 = 6 days
- Counting forward from Saturday:
- Saturday (0)
- Sunday (1)
- Monday (2)
- Tuesday (3)
- Wednesday (4)
- Thursday (5)
- Friday (6)
- Saturday (7)
Thus, October 30, 1996, was a Wednesday.
Final Answer
Therefore, Karan was 14 years, 7 months, and 8 days old on a Wednesday. Hence, the correct answer is option 'C'.
A watch, which gains uniformly, is 3 minutes slow at noon on Monday and is 3 minutes 48 seconds fast at 2 p.m. on the following Monday. What time was it correct?- a)2 p.m. on Tuesday
- b)2 p.m. on Wednesday
- c)3 p.m. on Thursday
- d)1 p.m. on Friday.
Correct answer is option 'C'. Can you explain this answer?
A watch, which gains uniformly, is 3 minutes slow at noon on Monday and is 3 minutes 48 seconds fast at 2 p.m. on the following Monday. What time was it correct?
a)
2 p.m. on Tuesday
b)
2 p.m. on Wednesday
c)
3 p.m. on Thursday
d)
1 p.m. on Friday.

|
Varun Singh answered |
Understanding the Watch's Gain
To solve the problem, we need to calculate the total time elapsed and the watch's uniform rate of gaining time.
Time Analysis
- The watch is 3 minutes slow at noon on Monday.
- It becomes 3 minutes 48 seconds fast at 2 p.m. the following Monday.
- The time period from the first Monday to the next Monday is 7 days (or 168 hours).
Converting Time Gains
- The total time gained by the watch:
- From being 3 minutes slow to being 3 minutes 48 seconds fast:
- Total gain = 3 minutes + 3 minutes 48 seconds = 6 minutes 48 seconds.
- Converting 48 seconds into minutes gives us: 48/60 = 0.8 minutes.
- Therefore, total gain = 6.8 minutes.
Calculating the Gain Rate
- Gain per minute = Total gain / Total time in minutes.
- Total time in minutes = 168 hours * 60 minutes/hour = 10,080 minutes.
- Gain rate = 6.8 minutes / 10,080 minutes = 0.000674 minutes gained per minute.
Finding the Correct Time
To find when the watch was correct, we must determine how long it takes for it to gain 3 minutes from being slow.
- Since the watch gains time uniformly, we can calculate the time when it was correct:
- Time to gain back the 3 minutes = 3 minutes / (0.000674 minutes gained per minute) ≈ 4442 minutes.
Converting Minutes to Days
- 4442 minutes = 74 hours and 2 minutes.
- From noon on Monday, adding 74 hours takes us to:
- 48 hours = 2 p.m. Wednesday.
- An additional 26 hours = 3 p.m. Thursday.
Conclusion
The watch was correct at 3 p.m. on Thursday, thus confirming that option 'C' is correct.
To solve the problem, we need to calculate the total time elapsed and the watch's uniform rate of gaining time.
Time Analysis
- The watch is 3 minutes slow at noon on Monday.
- It becomes 3 minutes 48 seconds fast at 2 p.m. the following Monday.
- The time period from the first Monday to the next Monday is 7 days (or 168 hours).
Converting Time Gains
- The total time gained by the watch:
- From being 3 minutes slow to being 3 minutes 48 seconds fast:
- Total gain = 3 minutes + 3 minutes 48 seconds = 6 minutes 48 seconds.
- Converting 48 seconds into minutes gives us: 48/60 = 0.8 minutes.
- Therefore, total gain = 6.8 minutes.
Calculating the Gain Rate
- Gain per minute = Total gain / Total time in minutes.
- Total time in minutes = 168 hours * 60 minutes/hour = 10,080 minutes.
- Gain rate = 6.8 minutes / 10,080 minutes = 0.000674 minutes gained per minute.
Finding the Correct Time
To find when the watch was correct, we must determine how long it takes for it to gain 3 minutes from being slow.
- Since the watch gains time uniformly, we can calculate the time when it was correct:
- Time to gain back the 3 minutes = 3 minutes / (0.000674 minutes gained per minute) ≈ 4442 minutes.
Converting Minutes to Days
- 4442 minutes = 74 hours and 2 minutes.
- From noon on Monday, adding 74 hours takes us to:
- 48 hours = 2 p.m. Wednesday.
- An additional 26 hours = 3 p.m. Thursday.
Conclusion
The watch was correct at 3 p.m. on Thursday, thus confirming that option 'C' is correct.
What was the day of the week on, 16th July, 1776?- a)Tuesday
- b)Wednesday
- c)Monday
- d)Saturday
Correct answer is option 'A'. Can you explain this answer?
What was the day of the week on, 16th July, 1776?
a)
Tuesday
b)
Wednesday
c)
Monday
d)
Saturday

|
Neha Das answered |
16th July, 1776 = (1775 years + Period from 1st Jan, 1776 to 16th July, 1776)
Counting of odd days :
1600 years have 0 odd day
100 years have 5 odd days
75 years = (18 leap years + 57 ordinary years)
= [(18 x 2) + (57 x 1)]
= 93 (13 weeks + 2 days)
= 2 odd days
1775 years have (0 + 5 + 2) odd days = 7 odd days = 0 odd day
Jan Feb Mar Apr May Jun Jul
31 + 29 + 31 + 30 + 31 + 30 + 16
= 198 days
= (28 weeks + 2 days)
Total number of odd days = (0 + 2) = 2
Required day was 'Tuesday'.
Counting of odd days :
1600 years have 0 odd day
100 years have 5 odd days
75 years = (18 leap years + 57 ordinary years)
= [(18 x 2) + (57 x 1)]
= 93 (13 weeks + 2 days)
= 2 odd days
1775 years have (0 + 5 + 2) odd days = 7 odd days = 0 odd day
Jan Feb Mar Apr May Jun Jul
31 + 29 + 31 + 30 + 31 + 30 + 16
= 198 days
= (28 weeks + 2 days)
Total number of odd days = (0 + 2) = 2
Required day was 'Tuesday'.
If the day before yesterday was Saturday, what day will fall on the day after tomorrow?- a)Friday
- b)Thursday
- c)Wednesday
- d)Tuesday
Correct answer is option 'C'. Can you explain this answer?
If the day before yesterday was Saturday, what day will fall on the day after tomorrow?
a)
Friday
b)
Thursday
c)
Wednesday
d)
Tuesday
|
|
Vivek Bansal answered |
If day before yesterday was Saturday, that means today is Monday. Therefore, day after tomorrow will be Wednesday.
The priest told the devotee, “The temple bell is rung at regular intervals of 45 minutes. The last bell was rung five minutes ago. The next bell is due to be rung at 7.45 a.m. “At what time did the priest give this information to the devotee?- a)7.40 a.m.
- b)7.05 a.m.
- c)6.55 a.m.
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The priest told the devotee, “The temple bell is rung at regular intervals of 45 minutes. The last bell was rung five minutes ago. The next bell is due to be rung at 7.45 a.m. “At what time did the priest give this information to the devotee?
a)
7.40 a.m.
b)
7.05 a.m.
c)
6.55 a.m.
d)
None of these
|
|
Vivek Bansal answered |
Clearly, the last bell rung 45 minutes before 7.45 a.m. i.e. at 7.00 a.m. But it happened five minutes before gave the information to the devotee. So, the information was given at 7.05 a.m.
Sangeeta remembers that her father’s birthday was certainly after eight but before thirteenth of December. Her sister Natasha remembers that their father’s birthday was definitely after ninth but before fourteenth of December. On which date of December was their father’s birthday?- a)10th
- b)11th
- c)12th
- d)Data inadequate
Correct answer is option 'D'. Can you explain this answer?
Sangeeta remembers that her father’s birthday was certainly after eight but before thirteenth of December. Her sister Natasha remembers that their father’s birthday was definitely after ninth but before fourteenth of December. On which date of December was their father’s birthday?
a)
10th
b)
11th
c)
12th
d)
Data inadequate
|
|
Anshul Saini answered |
Analysis of Sangeeta's Statement
- Sangeeta recalls that her father’s birthday is after the 8th of December and before the 13th.
- This means possible dates are: 9th, 10th, 11th, and 12th of December.
Analysis of Natasha's Statement
- Natasha remembers that their father’s birthday is after the 9th of December and before the 14th.
- This narrows down the possible dates to: 10th, 11th, 12th, and 13th of December.
Finding the Overlap
- To find a common date that fits both sisters' memories:
- From Sangeeta: Possible dates are 9th, 10th, 11th, 12th.
- From Natasha: Possible dates are 10th, 11th, 12th, 13th.
- The overlapping dates from both statements are: 10th, 11th, and 12th.
Conclusion: Data Inadequate
- Although we have overlapping dates of 10th, 11th, and 12th, both sisters do not provide definitive information to pinpoint the exact date.
- Therefore, it is impossible to determine a unique date for their father's birthday based only on the information given.
Final Answer
- The correct option is D) Data inadequate.
- Sangeeta recalls that her father’s birthday is after the 8th of December and before the 13th.
- This means possible dates are: 9th, 10th, 11th, and 12th of December.
Analysis of Natasha's Statement
- Natasha remembers that their father’s birthday is after the 9th of December and before the 14th.
- This narrows down the possible dates to: 10th, 11th, 12th, and 13th of December.
Finding the Overlap
- To find a common date that fits both sisters' memories:
- From Sangeeta: Possible dates are 9th, 10th, 11th, 12th.
- From Natasha: Possible dates are 10th, 11th, 12th, 13th.
- The overlapping dates from both statements are: 10th, 11th, and 12th.
Conclusion: Data Inadequate
- Although we have overlapping dates of 10th, 11th, and 12th, both sisters do not provide definitive information to pinpoint the exact date.
- Therefore, it is impossible to determine a unique date for their father's birthday based only on the information given.
Final Answer
- The correct option is D) Data inadequate.
Chapter doubts & questions for Calendars - General Test Preparation for CUET UG 2025 is part of CUET Commerce exam preparation. The chapters have been prepared according to the CUET Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CUET Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Calendars - General Test Preparation for CUET UG in English & Hindi are available as part of CUET Commerce exam.
Download more important topics, notes, lectures and mock test series for CUET Commerce Exam by signing up for free.
General Test Preparation for CUET UG
164 videos|628 docs|1136 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup











