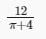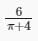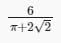All Exams >
CUET Commerce >
General Test Preparation for CUET UG >
All Questions
All questions of Geometry for CUET Commerce Exam
A rectangular enclosure 40 m x 36 m has a horse tethered to a corner with a rope of 14 m in length. What is the ratio of the respective areas it can graze, if it is outside the enclosure and if it is inside the enclosure?- a)2
- b)2:3
- c)1:4
- d)3:1
Correct answer is option 'D'. Can you explain this answer?
A rectangular enclosure 40 m x 36 m has a horse tethered to a corner with a rope of 14 m in length. What is the ratio of the respective areas it can graze, if it is outside the enclosure and if it is inside the enclosure?
a)
2
b)
2:3
c)
1:4
d)
3:1
|
Talent Skill Learning answered |
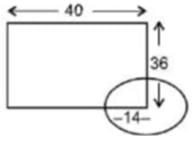
- Imagine a circle on the corner of the rectangle.
- 3 quarters of the circle lie outside the rectangle and 1 quarter lies inside.
- Hence, Required ratio = 3 : 1
Four horses are tethered at four comers of a square plot of side 14 m so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m2 at the centre. Find the ungrazed area.- a)42 m2
- b)22 m2
- c)84 m2
- d)168 m2
Correct answer is option 'B'. Can you explain this answer?
Four horses are tethered at four comers of a square plot of side 14 m so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m2 at the centre. Find the ungrazed area.
a)
42 m2
b)
22 m2
c)
84 m2
d)
168 m2
|
Preeti Khanna answered |
Total area of plot = 14 * 14 = 196m2
Horses can graze in quarter circle of radius = 7m
Grazed area = 4 * (pie r2)/4 = 154 m2
Area of plot when horses cannot reach = (196 - 154) = 42m2
Ungrazed area = 42 - 20 = 22m2
Horses can graze in quarter circle of radius = 7m
Grazed area = 4 * (pie r2)/4 = 154 m2
Area of plot when horses cannot reach = (196 - 154) = 42m2
Ungrazed area = 42 - 20 = 22m2
In the given figure, AB and CD are two chords of a circle intersecting at O. If AO = 4 cm and OB = 6 cm and OC = 3 cm. Find OD.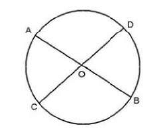
- a)4 cm
- b)6 cm
- c)8 cm
- d)10 cm
Correct answer is option 'C'. Can you explain this answer?
In the given figure, AB and CD are two chords of a circle intersecting at O. If AO = 4 cm and OB = 6 cm and OC = 3 cm. Find OD.
a)
4 cm
b)
6 cm
c)
8 cm
d)
10 cm
|
Pathways Academy answered |
By the rule of chords, cutting externally, we get:
(9 + 6) * 6 = (5 + x) * 5
90 = 25 + 5x
5x = 65
x = 13 cm
90 = 25 + 5x
5x = 65
x = 13 cm
A cyclic quadrilateral is such that two of its adjacent angles are divisible by 6 and 10 respectively. One of the remaining angles will necessarily be divisible by:
- a)3
- b)4
- c)8
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
A cyclic quadrilateral is such that two of its adjacent angles are divisible by 6 and 10 respectively. One of the remaining angles will necessarily be divisible by:
a)
3
b)
4
c)
8
d)
None of these
|
Palak Bose answered |
We know that the sum of the opposite angles of a cyclic quadrilateral is 180 degrees. Let the four angles be A, B, C, and D, with A and B being the angles divisible by 6 and 10, respectively.
Since A is divisible by 6 and B is divisible by 10, we know that A = 6m and B = 10n for some integers m and n.
Now, consider the opposite angles. Since the sum of opposite angles is 180 degrees, we have:
C = 180 - B = 180 - 10n
D = 180 - A = 180 - 6m
We want to find which of the given options the angles C or D are necessarily divisible by. Let's examine each option:
1. 3: Since B is divisible by 10, it is possible that B is divisible by 5 but not 3 (e.g. B = 10). In this case, C = 180 - B would not be divisible by 3. Also, A is divisible by 6, so A is always divisible by 3, which means D = 180 - A would never be divisible by 3. So, this option is incorrect.
2. 4: Since A is divisible by 6, it is possible that A is divisible by 2 but not 4 (e.g. A = 6). In this case, D = 180 - A would not be divisible by 4. Also, B is divisible by 10, so B is always divisible by 2, which means C = 180 - B would never be divisible by 4. So, this option is also incorrect.
3. 8: If A is divisible by 6, then it can be even or odd multiples of 6 (e.g. A = 6, 12, 18, ...). D will be 180 - A, which means D can be both even and odd (e.g. D = 180 - 6 = 174, D = 180 - 12 = 168, D = 180 - 18 = 162, ...). Since D can be both even and odd, it is not necessarily divisible by 8. Similarly, C can also be both even and odd, so it is not necessarily divisible by 8. Thus, this option is also incorrect.
4. None of these: Since none of the previous options work, the correct answer is None of these.
So, the correct answer is option 4: None of these.
Since A is divisible by 6 and B is divisible by 10, we know that A = 6m and B = 10n for some integers m and n.
Now, consider the opposite angles. Since the sum of opposite angles is 180 degrees, we have:
C = 180 - B = 180 - 10n
D = 180 - A = 180 - 6m
We want to find which of the given options the angles C or D are necessarily divisible by. Let's examine each option:
1. 3: Since B is divisible by 10, it is possible that B is divisible by 5 but not 3 (e.g. B = 10). In this case, C = 180 - B would not be divisible by 3. Also, A is divisible by 6, so A is always divisible by 3, which means D = 180 - A would never be divisible by 3. So, this option is incorrect.
2. 4: Since A is divisible by 6, it is possible that A is divisible by 2 but not 4 (e.g. A = 6). In this case, D = 180 - A would not be divisible by 4. Also, B is divisible by 10, so B is always divisible by 2, which means C = 180 - B would never be divisible by 4. So, this option is also incorrect.
3. 8: If A is divisible by 6, then it can be even or odd multiples of 6 (e.g. A = 6, 12, 18, ...). D will be 180 - A, which means D can be both even and odd (e.g. D = 180 - 6 = 174, D = 180 - 12 = 168, D = 180 - 18 = 162, ...). Since D can be both even and odd, it is not necessarily divisible by 8. Similarly, C can also be both even and odd, so it is not necessarily divisible by 8. Thus, this option is also incorrect.
4. None of these: Since none of the previous options work, the correct answer is None of these.
So, the correct answer is option 4: None of these.
The ratio of the sides of Δ ABC is 1:2:4. What is the ratio of the altitudes drawn onto these sides?- a)4:2:1
- b)1:2:4
- c)1:4:16
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The ratio of the sides of Δ ABC is 1:2:4. What is the ratio of the altitudes drawn onto these sides?
a)
4:2:1
b)
1:2:4
c)
1:4:16
d)
None of these
|
Aakash Giery answered |
Sum of any two sides should be greater than third side.
here 1+2=3 is not less than 4 ,
1+2<4 ,so="" triangle="" is="" not="" possible.="" ,so="" triangle="" is="" not="">
here 1+2=3 is not less than 4 ,
1+2<4 ,so="" triangle="" is="" not="" possible.="" ,so="" triangle="" is="" not="">
.
Find the value of x in the given figure.
- a)16 cm
- b)7 cm
- c)12 cm
- d)9 cm
Correct answer is option 'D'. Can you explain this answer?
Find the value of x in the given figure.
a)
16 cm
b)
7 cm
c)
12 cm
d)
9 cm
|
Pooja Sen answered |
Isosceles trapezium is always cyclic The sum of opposite angles of a cyclic quadrilateral is 180°
Read the passage below and solve the questions based on it The area of a square is equal lo the area of a rectangle. Moreover, the perimeter of the square is also equal to the perimeter of the rectangle,Q.The length of the rectangle is equal to the:a)Breadth of the rectangleb)Side of the squarec)Cannot be determinedd)Both [1] and [2]Correct answer is option 'D'. Can you explain this answer?
|
Nikita Singh answered |
This is possible only when both the length and breadth of the rectangle are equal to the side of the square.
The volume of two spheres are in the ratio 27 : 125. The ratio of their surface area is?- a)25 : 9
- b)27 : 11
- c)11 : 27
- d)9 : 25
Correct answer is option 'D'. Can you explain this answer?
The volume of two spheres are in the ratio 27 : 125. The ratio of their surface area is?
a)
25 : 9
b)
27 : 11
c)
11 : 27
d)
9 : 25
|
Sagar Sharma answered |
Understanding the Volume and Surface Area of Spheres
The problem states that the volumes of two spheres are in the ratio 27:125. To find the ratio of their surface areas, we need to understand the relationships between the two.
Volume of a Sphere
- The formula for the volume (V) of a sphere is given by V = (4/3)πr^3, where r is the radius.
- If the volumes of two spheres are in the ratio 27:125, we can express this as:
- V1/V2 = 27/125
Finding the Ratio of Radii
- Since volumes are proportional to the cube of the radii, we have:
- (r1^3)/(r2^3) = 27/125
- Taking the cube root on both sides gives us:
- r1/r2 = (27^(1/3))/(125^(1/3)) = 3/5
Surface Area of a Sphere
- The formula for the surface area (A) of a sphere is A = 4πr^2.
- Now, to find the ratio of the surface areas of the two spheres, we have:
- A1/A2 = (4πr1^2)/(4πr2^2) = (r1^2)/(r2^2)
Calculating the Surface Area Ratio
- Substituting the ratio of the radii:
- r1/r2 = 3/5
- Therefore, (r1^2)/(r2^2) = (3^2)/(5^2) = 9/25
Final Answer
- The ratio of the surface areas of the two spheres is 9:25, which corresponds to option 'D'.
The problem states that the volumes of two spheres are in the ratio 27:125. To find the ratio of their surface areas, we need to understand the relationships between the two.
Volume of a Sphere
- The formula for the volume (V) of a sphere is given by V = (4/3)πr^3, where r is the radius.
- If the volumes of two spheres are in the ratio 27:125, we can express this as:
- V1/V2 = 27/125
Finding the Ratio of Radii
- Since volumes are proportional to the cube of the radii, we have:
- (r1^3)/(r2^3) = 27/125
- Taking the cube root on both sides gives us:
- r1/r2 = (27^(1/3))/(125^(1/3)) = 3/5
Surface Area of a Sphere
- The formula for the surface area (A) of a sphere is A = 4πr^2.
- Now, to find the ratio of the surface areas of the two spheres, we have:
- A1/A2 = (4πr1^2)/(4πr2^2) = (r1^2)/(r2^2)
Calculating the Surface Area Ratio
- Substituting the ratio of the radii:
- r1/r2 = 3/5
- Therefore, (r1^2)/(r2^2) = (3^2)/(5^2) = 9/25
Final Answer
- The ratio of the surface areas of the two spheres is 9:25, which corresponds to option 'D'.
Two circles of an equal radii are drawn, without any overlap, in a semicircle of radius 2 cm. If these are the largest possible circles that the semicircle can accommodate, what is the radius (in cm) of each of the circles?a)0.414b)0.828c)0.172d)0.586Correct answer is option 'B'. Can you explain this answer?
|
Naveen Unni answered |
The dimensions of a rectangular box are in the ratio of 1:2:4 and the difference between the costs of covering it with the cloth and a sheet at the rate of Rs 20 and Rs 20.5 per sq m respectively is Rs 126. Find the dimensions of the box.- a)2 m, 6 m, 9 m
- b)6 m, 12 m, 24 m
- c)1 m, 2 m, 4 m
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The dimensions of a rectangular box are in the ratio of 1:2:4 and the difference between the costs of covering it with the cloth and a sheet at the rate of Rs 20 and Rs 20.5 per sq m respectively is Rs 126. Find the dimensions of the box.
a)
2 m, 6 m, 9 m
b)
6 m, 12 m, 24 m
c)
1 m, 2 m, 4 m
d)
None of these
|
Debanshi Rane answered |
A pond 100 m in diameter is surrounded by a circular grass walk-way 2 m wide. How many square metres of grass is the on the walk-way?- a)98 π
- b)100 π
- c)204 π
- d)202 π
Correct answer is option 'C'. Can you explain this answer?
A pond 100 m in diameter is surrounded by a circular grass walk-way 2 m wide. How many square metres of grass is the on the walk-way?
a)
98 π
b)
100 π
c)
204 π
d)
202 π
|
|
Aarav Sharma answered |
The radius of the pond is 100/2 = <100 =50="">>50 m.
The radius of the grass walkway is 50+2 = <50+2=52>>52 m.
The area of the grass walkway is pi*(52^2 - 50^2) = pi*(2704 - 2500) = pi*204
≈ 204*pi
≈ 204*3.14
≈ <204*3.14=640.56>>640.56 m^2.
So, the answer is a) 640.
The radius of the grass walkway is 50+2 = <50+2=52>>52 m.
The area of the grass walkway is pi*(52^2 - 50^2) = pi*(2704 - 2500) = pi*204
≈ 204*pi
≈ 204*3.14
≈ <204*3.14=640.56>>640.56 m^2.
So, the answer is a) 640.
In the given figure, AD is the bisector of ∠BAC, AB = 6 cm, AC = 5 cm and BD = 3 cm. Find DC. It is given that ∠ABD = ∠ACD.
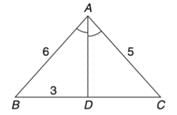
- a)11.3 cm
- b)4 cm
- c)3.5 cm
- d)2.5 cm
Correct answer is option 'D'. Can you explain this answer?
In the given figure, AD is the bisector of ∠BAC, AB = 6 cm, AC = 5 cm and BD = 3 cm. Find DC. It is given that ∠ABD = ∠ACD.
a)
11.3 cm
b)
4 cm
c)
3.5 cm
d)
2.5 cm
|
|
Pooja Shah answered |
We know that the internal bisector of angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
Hence:
Hence:
In triangle ABD and ACD
Angle BAD = CAD (Given AD is the bisector)
Angle ABD = ACD (GIven)
there fore they are similar (AAA Property)
AB/BD = AC/CD
6/3 = 5/CD
CD = 2.5 cm
6/3 = 5/CD
CD = 2.5 cm
Two sides of a triangle are 4 and 5. Then, for the area of the triangle, which one of the following bounds is the sharpest?- a)<10.
- b)≤ 10.
- c)< 8.
- d)> 5.
Correct answer is option 'B'. Can you explain this answer?
Two sides of a triangle are 4 and 5. Then, for the area of the triangle, which one of the following bounds is the sharpest?
a)
<10.
b)
≤ 10.
c)
< 8.
d)
> 5.
|
|
Prerna Choudhary answered |
Let AB = 4 and BC = 5 and AB is perpendicular to BC
then Area = 1/2 AB . AC = 1/2 . 4.5 = 10
In the given figure, straight line AB and CD intersect at O. IF ∠δ =3∠v, then ∠v = ?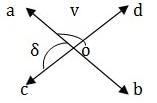
- a)40⁰
- b)50⁰
- c)55⁰
- d)45⁰
Correct answer is option 'D'. Can you explain this answer?
In the given figure, straight line AB and CD intersect at O. IF ∠δ =3∠v, then ∠v = ?
a)
40⁰
b)
50⁰
c)
55⁰
d)
45⁰
|
Meera Kapoor answered |
COD is a straight line
∴ ∠δ + ∠v =180⁰ ⇒ 3v +v =180 ⇒ 4v = 180 ⇒ v =45⁰.
∴ ∠δ + ∠v =180⁰ ⇒ 3v +v =180 ⇒ 4v = 180 ⇒ v =45⁰.
PQRS is trapezium, in which PQ is parallel to RS, and PQ = 3 (RS). The diagonal of the trapezium intersect each other at X, then the ratio of Δ PXQ and ARXS is- a)6:1
- b)3:1
- c)9:1
- d)7:1
Correct answer is option 'C'. Can you explain this answer?
PQRS is trapezium, in which PQ is parallel to RS, and PQ = 3 (RS). The diagonal of the trapezium intersect each other at X, then the ratio of Δ PXQ and ARXS is
a)
6:1
b)
3:1
c)
9:1
d)
7:1
|
|
Aarav Sharma answered |
Given: PQRS is a trapezium with PQ || RS and PQ = 3RS. The diagonals of the trapezium intersect at X.
To find: The ratio of the areas of triangles PXQ and RXS.
Solution:
Step 1: Draw a rough figure of the trapezium PQRS and mark the given information.
Step 2: Draw the diagonals PR and QS which intersect at X.
Step 3: Divide the trapezium into two triangles PXQ and RXS by drawing a line parallel to PQ through point S.
Step 4: Now we need to find the ratio of the areas of triangles PXQ and RXS.
Step 5: Let the height of the trapezium be h.
Step 6: We know that PQ = 3RS. Let RS = x. Then PQ = 3x.
Step 7: The area of trapezium PQRS = (1/2)h(PQ + RS) = (1/2)h(3x + x) = 2hx.
Step 8: Using the area of a triangle formula, the area of triangle RXS = (1/2)xh and the area of triangle PXQ = (1/2)(3x)h = (3/2)xh.
Step 9: Therefore, the ratio of the areas of triangles PXQ and RXS = (3/2)xh / (1/2)xh = 3:1.
Step 10: Hence, the correct option is (c) 9:1.
Final Answer: The ratio of the areas of triangles PXQ and RXS is 9:1.
To find: The ratio of the areas of triangles PXQ and RXS.
Solution:
Step 1: Draw a rough figure of the trapezium PQRS and mark the given information.
Step 2: Draw the diagonals PR and QS which intersect at X.
Step 3: Divide the trapezium into two triangles PXQ and RXS by drawing a line parallel to PQ through point S.
Step 4: Now we need to find the ratio of the areas of triangles PXQ and RXS.
Step 5: Let the height of the trapezium be h.
Step 6: We know that PQ = 3RS. Let RS = x. Then PQ = 3x.
Step 7: The area of trapezium PQRS = (1/2)h(PQ + RS) = (1/2)h(3x + x) = 2hx.
Step 8: Using the area of a triangle formula, the area of triangle RXS = (1/2)xh and the area of triangle PXQ = (1/2)(3x)h = (3/2)xh.
Step 9: Therefore, the ratio of the areas of triangles PXQ and RXS = (3/2)xh / (1/2)xh = 3:1.
Step 10: Hence, the correct option is (c) 9:1.
Final Answer: The ratio of the areas of triangles PXQ and RXS is 9:1.
What is the area of the triangle in which two of its medians 9 cm and 12 cm long intersect at the right angles?- a)72
- b)60
- c)56
- d)48
Correct answer is option 'A'. Can you explain this answer?
What is the area of the triangle in which two of its medians 9 cm and 12 cm long intersect at the right angles?
a)
72
b)
60
c)
56
d)
48
|
|
Aarav Sharma answered |
Given: Two medians of a triangle are 9 cm and 12 cm long and they intersect at right angles.
To find: The area of the triangle.
Solution:
Let ABC be the given triangle and D and E be the midpoints of AB and AC respectively. Let F be the intersection point of medians AD and CE.
Let AF = 9 and CF = 12. Then, BD = AD = 9 and CE = AE = 12.
We know that the medians of a triangle divide it into six equal parts. Therefore, the area of triangle ABC is four times the area of triangle AFE.
Area of triangle AFE = (1/2) * AF * CE = (1/2) * 9 * 12 = 54 sq. cm.
Therefore, the area of triangle ABC = 4 * 54 = 216 sq. cm.
Hence, the correct option is (a) 72.
To find: The area of the triangle.
Solution:
Let ABC be the given triangle and D and E be the midpoints of AB and AC respectively. Let F be the intersection point of medians AD and CE.
Let AF = 9 and CF = 12. Then, BD = AD = 9 and CE = AE = 12.
We know that the medians of a triangle divide it into six equal parts. Therefore, the area of triangle ABC is four times the area of triangle AFE.
Area of triangle AFE = (1/2) * AF * CE = (1/2) * 9 * 12 = 54 sq. cm.
Therefore, the area of triangle ABC = 4 * 54 = 216 sq. cm.
Hence, the correct option is (a) 72.
= 100°, find 
.
AB is the diameter of the circle and ∠PAB=40∘
what is the value of ∠PCA?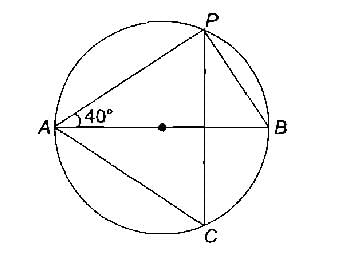
- a)50∘
- b)55°
- c)70°
- d)45°
Correct answer is option 'A'. Can you explain this answer?
AB is the diameter of the circle and ∠PAB=40∘
what is the value of ∠PCA?
what is the value of ∠PCA?
a)
50∘
b)
55°
c)
70°
d)
45°
|
KS Coaching Center answered |
- In △PAB⇒ ∠PAB=40o [ Given ]⇒ ∠BPA=90o [ angle inscribed in a semi-circle ]⇒ ∠PAB+∠PBA+∠BPA=180o∴ 40o+∠PBA+90o=180o∴ ∠PBA=180o−130o∴ ∠PBA=50o⇒ ∠PBA=∠PCA=50o [ angles inscribed in a same arc PA ]∴ ∠PCA=50o
What is the area of the triangle below?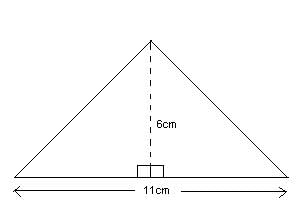
- a)22 cm2
- b)33 cm2
- c)44 cm2
- d)50 cm2
Correct answer is option 'B'. Can you explain this answer?
What is the area of the triangle below?
a)
22 cm2
b)
33 cm2
c)
44 cm2
d)
50 cm2
|
|
Pritam Saha answered |
The area of a triangle may be found by using the formula, A=1/2bh, where brepresents the base and h represents the height. Thus, the area may be written as A=1/2(11)(6), or A = 33. The area of the triangle is 33 cm'.
Chapter doubts & questions for Geometry - General Test Preparation for CUET UG 2025 is part of CUET Commerce exam preparation. The chapters have been prepared according to the CUET Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CUET Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Geometry - General Test Preparation for CUET UG in English & Hindi are available as part of CUET Commerce exam.
Download more important topics, notes, lectures and mock test series for CUET Commerce Exam by signing up for free.
General Test Preparation for CUET UG
164 videos|628 docs|1137 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup