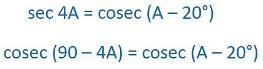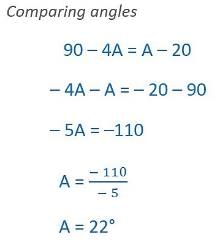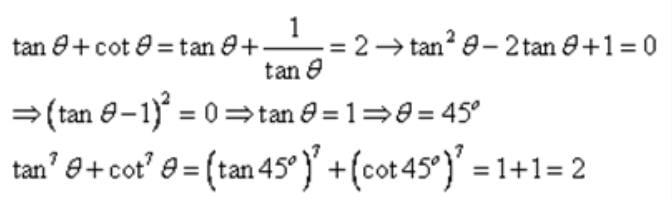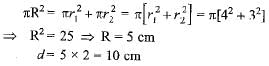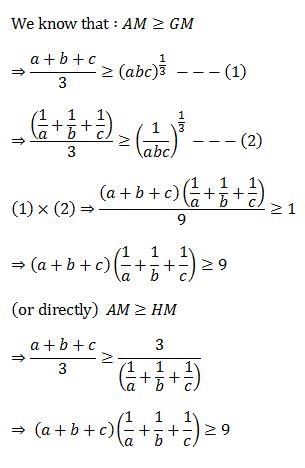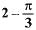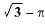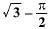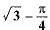All Exams >
Class 10 >
NTSE for Class 10 >
All Questions
All questions of Mathematics for Class 10 Exam
The probability of getting an even number, when a die is thrown once, is:- a)1/6
- b)1/2
- c)1/3
- d)5/6
Correct answer is option 'B'. Can you explain this answer?
The probability of getting an even number, when a die is thrown once, is:
a)
1/6
b)
1/2
c)
1/3
d)
5/6
|
Pooja Shah answered |
If we throw a die once, then possible outcomes (s), are
S = { 1, 2, 3, 4, 5, 6 }
⇒ n(E) = 6
(i) Let E be the favourable outcomes of getting an even number, then
E = { 2, 4, 6 }
⇒ n(S) = 3
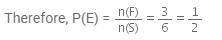
S = { 1, 2, 3, 4, 5, 6 }
⇒ n(E) = 6
(i) Let E be the favourable outcomes of getting an even number, then
E = { 2, 4, 6 }
⇒ n(S) = 3
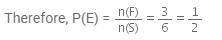
Solve 9x2 = 36- a)±2
- b)±6
- c)±4
- d)2
Correct answer is option 'A'. Can you explain this answer?
Solve 9x2 = 36
a)
±2
b)
±6
c)
±4
d)
2
|
Nilanjan Shah answered |
Solution:
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
To solve this equation, we need to isolate the variable x.
Given equation is 9x2 = 36
Step 1: Divide both sides by 9
9x2/9 = 36/9
Step 2: Simplify
x2 = 4
Step 3: Take square root on both sides
√(x2) = √4
Step 4: Simplify
x = ±2
Therefore, the solution of the given equation 9x2 = 36 is x = ±2.
Explanation:
The given equation is a quadratic equation in which we need to find the value of x. To solve the equation, we need to isolate the variable x by following the steps mentioned above. We divided both sides by 9 to simplify the equation. After simplification, we got x2 = 4 which means x can be either positive or negative 2. We took the square root of both sides and simplified the equation to get the final solution x = ±2.
If tan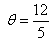 
, then 
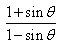is equal to- a)24
- b)12/13
- c)25
- d)9
Correct answer is option 'C'. Can you explain this answer?
If tan 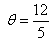, then 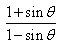is equal to
, then is equal toa)
24
b)
12/13
c)
25
d)
9
|
Vp Classes answered |
tanθ = 12/5
so sinθ = 12/13
so
(1 + 12/13)/(1-12/13)
= 25/1 = 25
If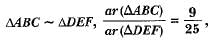 
BC = 21 cm, then EF is equal to- a)9 cm
- b)6 cm
- c)35 cm
- d)25 cm
Correct answer is option 'C'. Can you explain this answer?
If 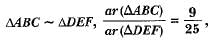BC = 21 cm, then EF is equal to
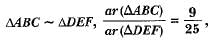BC = 21 cm, then EF is equal toa)
9 cm
b)
6 cm
c)
35 cm
d)
25 cm
|
Imk Pathshala answered |
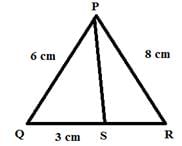
Since, PS is the angle bisector of angle QPR
So, by angle bisector theorem,
QS/SR = PQ/PR
⇒ 3/SR = 6/8
⇒ SR = (3 X 8)/6 cm = 4 cm
Two coins are tossed together. The probability of getting head on both the coins is- a)1/4
- b)3/4
- c)0
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Two coins are tossed together. The probability of getting head on both the coins is
a)
1/4
b)
3/4
c)
0
d)
1/2
|
Krishna Iyer answered |
The sample space for the event is : (H,H) (T,H) (H,T) (T,T)
Therefore total outcomes= 4
Therefore total outcomes= 4
Probability = 1/4
It is given that ar(ΔABC) = 81 square units and ar(ΔDEF) = 64 square units. If ΔABC ~ ΔDEF, then- a)AB/DE = 81/64
- b)
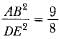
- c)AB/DE = 9/8
- d)AB = 81 units, DE = 64 units
Correct answer is option 'C'. Can you explain this answer?
It is given that ar(ΔABC) = 81 square units and ar(ΔDEF) = 64 square units. If ΔABC ~ ΔDEF, then
a)
AB/DE = 81/64
b)
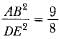
c)
AB/DE = 9/8
d)
AB = 81 units, DE = 64 units
|
|
Imk Pathshala answered |
In triangle ACB and ADC
∠A=∠A
∠ACB = ∠CDA
Therefore triangle ACB and ADC are similar,
Hence
AC/AD = AB/AC
AC2 = AD X AB
82 = 3 x AB
⇒ AB = 64/3
This implies,
BD = 64/3 – AD
⇒ BD = 55/3
∠A=∠A
∠ACB = ∠CDA
Therefore triangle ACB and ADC are similar,
Hence
AC/AD = AB/AC
AC2 = AD X AB
82 = 3 x AB
⇒ AB = 64/3
This implies,
BD = 64/3 – AD
⇒ BD = 55/3
If a digit is chosen at random from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 then the probability that it is odd is
- a) 1/9
- b) 5/9
- c) 4/9
- d) 2/3
Correct answer is option 'B'. Can you explain this answer?
If a digit is chosen at random from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 then the probability that it is odd is
a)
1/9b)
5/9c)
4/9d)
2/3
|
Nisha Choudhury answered |
The even numbers out of these are= 2, 4, 6, 8
No. of even numbers = 4
Total numbers = 9
So probability of choosing an odd number will be
= No. of odd numbers/Total numbers
= 5 / 9
Similarly probability of choosing an even number will be
= No. of even numbers/Total numbers
= 4 / 9
If a letter of English alphabet is chosen at random, then the probability that the letter is a consonant is:- a)11/13
- b)5/26
- c)10/13
- d)21/26
Correct answer is option 'D'. Can you explain this answer?
If a letter of English alphabet is chosen at random, then the probability that the letter is a consonant is:
a)
11/13
b)
5/26
c)
10/13
d)
21/26
|
|
Naina Sharma answered |
The probability that the letter is a consonant = (26 - 5)/26 = 21/26.
Which geometric figures are always similar?- a)Circles
- b)Circles and all regular polygons
- c)Circles and triangles
- d)Regular polygons
Correct answer is option 'B'. Can you explain this answer?
Which geometric figures are always similar?
a)
Circles
b)
Circles and all regular polygons
c)
Circles and triangles
d)
Regular polygons
|
|
Raghav Bansal answered |
It can be found that circles map one onto another.So they are similar figures. A regular polygon is a polygon which has the same sides and equal measures of angles. So they are also similar.
Can you explain the answer of this question below:If 7sin2x + 3cos2x = 4 then , secx + cosecx =- A:
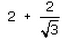
- B:
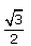
- C:
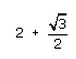
- D:
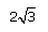
The answer is a.
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
A:
B:
C:
D:
|
Gunjan Lakhani answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=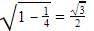
Sec x= 1/cos x=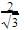
Cosec x + sec x=2+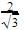
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
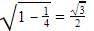
Sec x= 1/cos x=
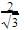
Cosec x + sec x=2+
In triangle ABC, if AB = 6√3 cm, AC = 12 cm and BC cm, then ∠B is - a)120°
- b)60°
- c)90°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
In triangle ABC, if AB = 6√3 cm, AC = 12 cm and BC cm, then ∠B is
a)
120°
b)
60°
c)
90°
d)
45°
|
Gaurav Kumar answered |
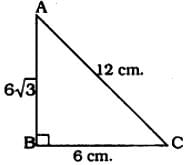
Here largest side is 12 cm.
If the square of the hypotenuse is equal to the square of the other two sides, then it is a right-angled triangle.
If the square of the hypotenuse is equal to the square of the other two sides, then it is a right-angled triangle.
∴ c2 = a2 + b2
AC2 = AB2 + BC2
(12)2 = (63)2 + (6)2
44 = 36 × 3 + 36
144 = 108 + 36
144 = 144
∴ ∆ABC is a right angled triangle and angle opposite to hypotenuse, ∠B = 90°.
The pair of linear equations x + y + 10 = 0 and x + y – 7 = 0 has:- a)One solution
- b)Infinitely many solutions
- c)No solutions
- d)Two solutions
Correct answer is option 'C'. Can you explain this answer?
The pair of linear equations x + y + 10 = 0 and x + y – 7 = 0 has:
a)
One solution
b)
Infinitely many solutions
c)
No solutions
d)
Two solutions
|
|
Gaurav Kumar answered |
We have a1, a2 the coefficients of x2,b1 and b2 coefficients of x and c1 and c2 the constant terms.
So,
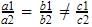a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.
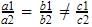So,a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations. The value of tan1°.tan2°.tan3°………. tan89° is :- a)2
- b)1
- c)1/2
- d)0
Correct answer is option 'B'. Can you explain this answer?
The value of tan1°.tan2°.tan3°………. tan89° is :
a)
2
b)
1
c)
1/2
d)
0
|
Meera Rana answered |
tan 1.tan 2.tan 3...tan (90 - 3 ).tan ( 90 - 2 ).tan ( 90 - 1)
=tan 1.tan 2 .tan 3...cot 3.cot 2.cot 1
=tan 1.cot 1.tan 2.cot 2.tan 3.cot 3 ... tan 89.cot 89
1 x 1 x 1 x 1 x ... x 1 =1
=tan 1.tan 2 .tan 3...cot 3.cot 2.cot 1
=tan 1.cot 1.tan 2.cot 2.tan 3.cot 3 ... tan 89.cot 89
1 x 1 x 1 x 1 x ... x 1 =1
A card is drawn from a well-shuffled deck of 52 playing cards. The probability that the card will not be an ace card is
a)12/13b)1/4c)3/4d)1/13Correct answer is option 'A'. Can you explain this answer?
|
Ananya Das answered |
Total no. of outcomes=52
No. of ace cards=4
No. of non-ace cards=48
Probability of getting a non-ace card = No. of favourable outcomes / total no. of outcomes
=48/52=12/13
No. of ace cards=4
No. of non-ace cards=48
Probability of getting a non-ace card = No. of favourable outcomes / total no. of outcomes
=48/52=12/13
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then- a)R1 + R2 = R
- b)R1 + R2 > R
- c)R1 + R2 < R
- d)nothing definite can be said about the relation among R1, R2 and R
Correct answer is option 'A'. Can you explain this answer?
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then
a)
R1 + R2 = R
b)
R1 + R2 > R
c)
R1 + R2 < R
d)
nothing definite can be said about the relation among R1, R2 and R
|
|
Pooja Shah answered |
2π R1 + 2πR2 = 2πR
⇒ R1 + R2 = R.
⇒ R1 + R2 = R.
The probability of an event that is certain to happen is- a)2
- b)1
- c)0
- d)-1
Correct answer is option 'B'. Can you explain this answer?
The probability of an event that is certain to happen is
a)
2
b)
1
c)
0
d)
-1
|
|
Ananya Das answered |
The probability of an event is a number describing the chance that the event will happen. An event that is certain to happen has a probability of 1. An event that cannot possibly happen has a probability of zero. If there is a chance that an event will happen, then its probability is between zero and 1.
Examples of Events:
- tossing a coin and it landing on heads
- tossing a coin and it landing on tails
- rolling a '3' on a die
- rolling a number > 4 on a die
- it rains two days in a row
- drawing a card from the suit of clubs
- guessing a certain number between 000 and 999 (lottery)
If the probability of winning a game is 0.995, then the probability of losing is- a)0.05
- b)1
- c)0.005
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
If the probability of winning a game is 0.995, then the probability of losing is
a)
0.05
b)
1
c)
0.005
d)
None of the above
|
Sun Ray Institute answered |
Let P(winning the game)=0.995
Since the probability of two complimentary event sums to 1 so-
P(not winning the game) + P(winning the game )=1
=P(losing it )=1-P(winning the game )
=1-0.995=0.005
ΔABC ~ ΔPQR, ∠B = 50° and ∠C = 70° then ∠P is equal to- a)50°
- b)60°
- c)40°
- d)70°
Correct answer is option 'B'. Can you explain this answer?
ΔABC ~ ΔPQR, ∠B = 50° and ∠C = 70° then ∠P is equal to
a)
50°
b)
60°
c)
40°
d)
70°
|
|
Radha Iyer answered |
Similar triangles have corresponding angles equal. So Angle Q=Angle B = 50° and Angle R = Angle C = 70° . So by angle sum property, Angle P+Angle Q +Angle R = 180°
Angle P=180° - 50° - 70° = 60°
Angle P=180° - 50° - 70° = 60°
If TP and TQ are two tangents to a circle with centre O so that angle POQ = 110° then angle PTQ is equal to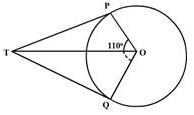
- a)600
- b)800
- c)700
- d)900
Correct answer is option 'C'. Can you explain this answer?
If TP and TQ are two tangents to a circle with centre O so that angle POQ = 110° then angle PTQ is equal to
a)
600
b)
800
c)
700
d)
900
|
|
Krishna Iyer answered |
We know that the sum of angle made by two tangents joined by an exterior point and the angle made at the centre of the circle is equal to 180 degrees
So, Angle POQ + Angle PTQ = 180
110 + Angle PTQ = 180
Angle PTQ = 180- 110 = 70 degrees
So, Angle POQ + Angle PTQ = 180
110 + Angle PTQ = 180
Angle PTQ = 180- 110 = 70 degrees
A circle can pass through
- a)2 collinear points
- b)3 collinear points
- c)4 collinear points
- d)4 collinear points
Correct answer is option 'A'. Can you explain this answer?
A circle can pass through
a)
2 collinear points
b)
3 collinear points
c)
4 collinear points
d)
4 collinear points
|
|
Krishna Iyer answered |
The answer can be 2 collinear points as well. We have three collinear points. Join one point to the other two points and then draw the perpendicular bisector for both the lines
Join the perpendicular bisectors. The point is the centre of the circle. And a circle can be formed then. Also two points can form a circle as the two points joines becomes a diameter.
Join the perpendicular bisectors. The point is the centre of the circle. And a circle can be formed then. Also two points can form a circle as the two points joines becomes a diameter.
Option D : The number of circles which can pass through three given non-collinear points is exactly one.
So, A is the correct Option
Which of the following cannot be the probability of an event?- a)0.7
- b)15%
- c)2/3
- d)-1.5
Correct answer is option 'D'. Can you explain this answer?
Which of the following cannot be the probability of an event?
a)
0.7
b)
15%
c)
2/3
d)
-1.5
|
|
Rohan Kapoor answered |
D cannot be a probability as it has negative value
The probability of getting a prime number in single throw of a dice is:- a)Zero
- b)1/2
- c)1/4
- d)1/3
Correct answer is option 'B'. Can you explain this answer?
The probability of getting a prime number in single throw of a dice is:
a)
Zero
b)
1/2
c)
1/4
d)
1/3
|
|
Krishna Iyer answered |
Given, A dice is thrown once. So,
Total number of outcomes (n) = 6
Number of prime numbers = {2, 3,5}
So, Favorable number of outcomes (m) = 3
Thus, probability of getting a prime number = m/n = 3/6 = 1/2
The pair of equations 3x + 4y = k, 9x + 12y = 6 has infinitely many solutions if –- a)k = 2
- b)k = 6
- c)k = 6
- d)k = 3
Correct answer is option 'A'. Can you explain this answer?
The pair of equations 3x + 4y = k, 9x + 12y = 6 has infinitely many solutions if –
a)
k = 2
b)
k = 6
c)
k = 6
d)
k = 3
|
|
Naina Sharma answered |
An equation has infinitely many solutions when the lines are coincident.
The lines are coincident when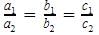
So 3x + 4y = k, 9x + 12y = 6 are coincident when
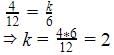
The lines are coincident when
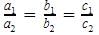
So 3x + 4y = k, 9x + 12y = 6 are coincident when
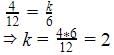
If the area of a circle is 154 cm2, then its perimeter is- a)11cm
- b)22 cm
- c)44 cm
- d)55 cm
Correct answer is option 'C'. Can you explain this answer?
If the area of a circle is 154 cm2, then its perimeter is
a)
11cm
b)
22 cm
c)
44 cm
d)
55 cm
|
Vivek Rana answered |
Given area of circle=154
⇒area of circle=πr²
=22/7 ×7×7.
=154
so radius of the circle=7cm
perimeter of circle=2πr
=2 ×22/7×7
=44cm
⇒perimeter of the circle=44 cm.
⇒area of circle=πr²
=22/7 ×7×7.
=154
so radius of the circle=7cm
perimeter of circle=2πr
=2 ×22/7×7
=44cm
⇒perimeter of the circle=44 cm.
Find out the mode of the following data:
- a)450
- b)400
- c)600
- d)478
Correct answer is option 'A'. Can you explain this answer?
Find out the mode of the following data:
a)
450
b)
400
c)
600
d)
478
|
Rohini Seth answered |
The mode of a set of data values is the value that appears most often .So mode is the most occurrence of observation.
Converting the distribution in continuous grouped and applying the formula
Mode=
Modal class is 400-500
Where L=lower limit of the modal class =400
f1= modal class frequency=32
f2 = just after the modal class frequency=20
f0 = just previous the modal class frequency=20
C = Class size=100
Mode=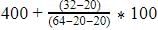
=400+50=450
Converting the distribution in continuous grouped and applying the formula
Mode=
Modal class is 400-500
Where L=lower limit of the modal class =400
f1= modal class frequency=32
f2 = just after the modal class frequency=20
f0 = just previous the modal class frequency=20
C = Class size=100
Mode=
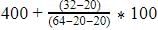
=400+50=450
Write the general form of a quadratic polynomia- a)ax2 + bx + c where a, b and c are real numbers
- b)ax2 + bx + c=0
- c)ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
- d)ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
Correct answer is option 'C'. Can you explain this answer?
Write the general form of a quadratic polynomia
a)
ax2 + bx + c where a, b and c are real numbers
b)
ax2 + bx + c=0
c)
ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
d)
ax2 + bx + c or bx + ax2 + c or c+ bx + ax2
|
|
Krishna Iyer answered |
If the coefficient of x2 is zero , then the equation is not a quadratic equation , its a linear equation. So its necessary condition for the quadratic equation.
Which of the following in not a quadratic equation:- a)(x – 2)2 + 1 = 2x – 3
- b)(x + 2)2 = x3 – 4
- c)x(2x + 3) = x2 + 1
- d)x(x + 1) + 8 = (x + 2) (x – 2)
Correct answer is option 'D'. Can you explain this answer?
Which of the following in not a quadratic equation:
a)
(x – 2)2 + 1 = 2x – 3
b)
(x + 2)2 = x3 – 4
c)
x(2x + 3) = x2 + 1
d)
x(x + 1) + 8 = (x + 2) (x – 2)
|
Rahul Kumar answered |
Option (B) and (D) , both are the correct answers. We have x(x + 1) + 8 = (x + 2) (x – 2)
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
=x2 + x + 8 = x2 - 4
= x = -12, which is not a quadratic equation
Also, in (B) (x + 2)2 = x3 – 4
=x2 +4x + 4=x3 - 4, which is a cubic equation
Which of the following is not a solution of pair of equations 3x – 2y = 4 and 6x – 4y = 8?- a)x = 5, y = 3
- b)x = 2, y = 1
- c)x = 6, y = 7
- d)x = 4, y = 4
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a solution of pair of equations 3x – 2y = 4 and 6x – 4y = 8?
a)
x = 5, y = 3
b)
x = 2, y = 1
c)
x = 6, y = 7
d)
x = 4, y = 4
|
|
Vikram Kapoor answered |
3x – 2y = 4 and 6x – 4y = 8
Putting x=5 and y=3
LHS=3(5)-2(3)
15-6=9
RHS=4
LHS ≠ RHS
Also,
6(5)-4(3)=30-12=18 ≠ 8
Putting x=5 and y=3
LHS=3(5)-2(3)
15-6=9
RHS=4
LHS ≠ RHS
Also,
6(5)-4(3)=30-12=18 ≠ 8
Six years hence a man's age will be three times the age of his son and three years ago he was nine times as old as his son. The present age of the man is –- a)28 years
- b)30 years
- c)32 years
- d)34 years
Correct answer is option 'B'. Can you explain this answer?
Six years hence a man's age will be three times the age of his son and three years ago he was nine times as old as his son. The present age of the man is –
a)
28 years
b)
30 years
c)
32 years
d)
34 years
|
Dr Manju Sen answered |
Let the present age of man is x and of son is y.
Six years hence,
Man’s age =x+6
Son’s age=y+6
Man’s age is 3 times son’s age
x+6=3(y+6)
x+6=3y+18
x=3y+12 …...1
Three years ago,
Man’s age =x-3
Son’s age=y-3
Man’s age was 9 times as of son
x-3=9(y-3)
x-3=9y-27
x=9y-24 ….2
From 1 and 2
3y+12=9y-24
6y=36
y=6
x=3*6+12=18+12=30 years
Six years hence,
Man’s age =x+6
Son’s age=y+6
Man’s age is 3 times son’s age
x+6=3(y+6)
x+6=3y+18
x=3y+12 …...1
Three years ago,
Man’s age =x-3
Son’s age=y-3
Man’s age was 9 times as of son
x-3=9(y-3)
x-3=9y-27
x=9y-24 ….2
From 1 and 2
3y+12=9y-24
6y=36
y=6
x=3*6+12=18+12=30 years
The value of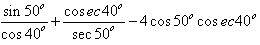 
is- a)2
- b)0
- c)4
- d)-2
Correct answer is option 'D'. Can you explain this answer?
The value of 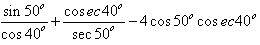is
isa)
2
b)
0
c)
4
d)
-2
|
|
Krishna Iyer answered |
we know sin(90 - a) = cos(a)
cos(90 - a) = sin(a)
sin(a) = 1/cosec(a)
sec(a) = 1/cos(a)
cos40 = cos(90-50) = sin50
cosec40 = cosec(90-50) = sec50
so our expression becomes
sin50/sin50 + sec50/sec50 - 4cos50 / sin40
= 1 + 1 - 4(1) since cos50 = sin40
= -2
The probability that a leap year has 53 Sundays is- a)3/7
- b)2/7
- c)4/7
- d)1/7
Correct answer is option 'B'. Can you explain this answer?
The probability that a leap year has 53 Sundays is
a)
3/7
b)
2/7
c)
4/7
d)
1/7
|
|
Ananya Das answered |
There are 366 days in a leap year, i.e, 1 more than a normal year.
Now, 52 weeks make up 344 days (52 x 7 = 344)
That means that we already have 52 sundays for sure.
That means that we already have 52 sundays for sure.
Then, we are left with 2 days. Now, these days can be any from a pair of- mon-tues,tues-wed,wed-thurs,thurs-fri,fri-sat,sat-sun,sun-mon. Here favourable cases are sat-sun and sun-mon i.e, 2 cases and total number of cases is 7.
So, Probability=number of favourable cases/Total number of cases.
Therefore, Probability= 2/7.
If the length of a shadow cast by a pole is √3 times the length of the pole, then the angle of elevation of the sun is- a)45°
- b)60°
- c)30°
- d)90°
Correct answer is option 'C'. Can you explain this answer?
If the length of a shadow cast by a pole is √3 times the length of the pole, then the angle of elevation of the sun is
a)
45°
b)
60°
c)
30°
d)
90°
|
|
Anjana Khatri answered |
Consider the height of tower be h
∴ height of shadow =√3h .
In a triangle ABC,
tan ∠ACB = h / √3h
tan ∠ACB = 1 / √3
∠ACB = 30degree.
Therefore, angle of elevation is 30degree .
If the probability of winning a game is 0.3, then the probability of losing it is:- a)0.3
- b)0.7
- c)0.2
- d)0.5
Correct answer is option 'B'. Can you explain this answer?
If the probability of winning a game is 0.3, then the probability of losing it is:
a)
0.3
b)
0.7
c)
0.2
d)
0.5
|
|
Amit Sharma answered |
Let the probability of losing the game be x
We know that sum of the the sum of probabilities is equal to 1
So
0.3+x=1
x=0.7
We know that sum of the the sum of probabilities is equal to 1
So
0.3+x=1
x=0.7
Can you explain the answer of this question below: If 4 is a root of the equation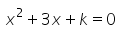 
, then k is
- A:
-28
- B:
-12
- C:
12
- D:
28
The answer is a.
If 4 is a root of the equation , then k is
-28
-12
12
28
|
|
Vp Classes answered |
4 is the solution , this means that if we put x=4 we get 0. So putting x=4 in the equation x2+3x+k=0 we get 42+3*4+k=0
16+12+k=0 ⇒ k=-28
16+12+k=0 ⇒ k=-28
Solve for x : 6x2 + 40 = 31x- a)
- b)
- c)0,8/3
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Solve for x : 6x2 + 40 = 31x
a)
b)
c)
0,8/3
d)
None of the above
|
|
Nirmal Kumar answered |
6x²-31x+40=0,
a=6,
b=-31,
c=40,
by quadratic formula-->
x=-b±√b²-4ac/2a,
by putting the values of a,b and c, we get,
x=-(-31)±√(-31)²-4(6)(40)/2(6),
=31±√961-960/12,
=31±√1/12,
=31±1/12,
x=30/12or ,32/12,
x=5/2 or, 8/3,
hence , option B is correct
a=6,
b=-31,
c=40,
by quadratic formula-->
x=-b±√b²-4ac/2a,
by putting the values of a,b and c, we get,
x=-(-31)±√(-31)²-4(6)(40)/2(6),
=31±√961-960/12,
=31±√1/12,
=31±1/12,
x=30/12or ,32/12,
x=5/2 or, 8/3,
hence , option B is correct
The probability that a randomly chosen number from one to twelve is a divisor of twelve is- a)1/6
- b)1/12
- c)1/2
- d)1/4
Correct answer is option 'D'. Can you explain this answer?
The probability that a randomly chosen number from one to twelve is a divisor of twelve is
a)
1/6
b)
1/12
c)
1/2
d)
1/4
|
Coachify answered |
We have the numbers from 1 to 12. Total possible outcomes = 12 Now, divisors of 12 : 1, 2, 3, 4, 6 and 12 Number of divisors of 12 = 6 Number of favourable outcomes = 6
Required probability
Required probability
Chapter doubts & questions for Mathematics - NTSE for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mathematics - NTSE for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
NTSE for Class 10
338 docs|163 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily