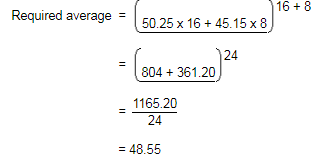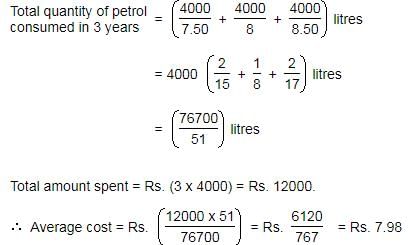All Exams >
SSC MTS / SSC GD >
Numerical Aptitude for SSC Exams >
All Questions
All questions of Averages for SSC MTS / SSC GD Exam
Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?
- a)82
- b)81
- c)81.5
- d)84.5
Correct answer is option 'C'. Can you explain this answer?
Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?
a)
82
b)
81
c)
81.5
d)
84.5

|
Nipun Tuteja answered |
Avg speed of train = 2xy/x+y
⇒ [2(84)(56)]/(84+56)
⇒ [2(84)(56)]/140
= 67.2km/hr
⇒ [2(84)(56)]/(84+56)
⇒ [2(84)(56)]/140
= 67.2km/hr
There are 7 members in a family whose average age is 25 years. Ram who is 12 years old is the second youngest in the family. Find the average age of the family in years just before Ram was born?
- a)15.167
- b)18.2
- c)13
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
There are 7 members in a family whose average age is 25 years. Ram who is 12 years old is the second youngest in the family. Find the average age of the family in years just before Ram was born?
a)
15.167
b)
18.2
c)
13
d)
Cannot be determined
|
|
Rajeev Kumar answered |
In order to find the average age of the family before Ram was born, we need to know the age of the youngest member of the family.
Since, we do not know the age of the youngest member, we can not calculate the total age of the family before Ram was born.
Hence, we can not calculate the answer with the given conditions.
Since, we do not know the age of the youngest member, we can not calculate the total age of the family before Ram was born.
Hence, we can not calculate the answer with the given conditions.
Thus, D is the right choice.
The average marks of a class of 48 students is 35. Of them, two score zero, of the rest, the first 30 scored an average of 40, the next fourteen scored an average of 20. If the remaining two scored equal marks, what are their individual marks?- a)80
- b)75
- c)90
- d)100
Correct answer is option 'D'. Can you explain this answer?
The average marks of a class of 48 students is 35. Of them, two score zero, of the rest, the first 30 scored an average of 40, the next fourteen scored an average of 20. If the remaining two scored equal marks, what are their individual marks?
a)
80
b)
75
c)
90
d)
100
|
|
Garima Shah answered |
The average price of a share is the average of 5 readings taken at regular intervals in a day. The index price is taken by a weighted arithmetic average price of a class A and class B stock. The respective weights are 1.1 and 0.9 for the two kinds of stocks. If the five readings of a class A stock were 19, 26, 31, 35, 39 and for a class B stock the readings were 7, 8, 17, 20, 23 then what was the index price that day?- a)46.5
- b)25
- c)23.25
- d)45
Correct answer is option 'C'. Can you explain this answer?
The average price of a share is the average of 5 readings taken at regular intervals in a day. The index price is taken by a weighted arithmetic average price of a class A and class B stock. The respective weights are 1.1 and 0.9 for the two kinds of stocks. If the five readings of a class A stock were 19, 26, 31, 35, 39 and for a class B stock the readings were 7, 8, 17, 20, 23 then what was the index price that day?
a)
46.5
b)
25
c)
23.25
d)
45
|
|
Kavya Saxena answered |
Can you explain the answer of this question below:The average of 20 numbers is zero. Of them, How many of them may be greater than zero , at the most?
- A:1
- B:20
- C:0
- D:19
The answer is D.

|
Ishita Das answered |
Average of 20 numbers = 0.
 Sum of 20 numbers (0 x 20) = 0.
Sum of 20 numbers (0 x 20) = 0.It is quite possible that 19 of these numbers may be positive and if their sum is a then 20th number is (-a).
Can you explain the answer of this question below: A car owner buys diesel at Rs.7.50, Rs. 8 and Rs. 8.50 per litre for three successive years. What approximately is the average cost per litre of diesel if he spends Rs. 4000 each year?
- A:Rs. 8
- B:Rs. 7.98
- C:Rs. 6.2
- D:Rs. 8.1
The answer is B.

|
Ishani Rane answered |
Average cost per litre of petrol = Total amount / Total quantity of petrol
Re. 4000 is spent each year, so total amount spent = 3 * Rs. 4000 = Rs. 12,000
Total quantity of petrol consumed in 3 years = (4000/7.50) + (4000/8) + (4000/8.50) litres
= 533.3 + 500 + 470.6 = 1505
Average cost = Total amount / Total quantity
= 12000/1504 = 7.98
To find quickly, you can take cube root of (7.50 * 8 * 8.50), and it will be slightly less than 8.
The correct option is B.
A, B, C, D and E are five consecutive integers and the average of these five numbers is less than 1/4th of A. Then A is
- a)Negative
- b) Positive
- c)Even
- d)Data Sufficient
Correct answer is option 'A'. Can you explain this answer?
A, B, C, D and E are five consecutive integers and the average of these five numbers is less than 1/4th of A. Then A is
a)
Negative
b)
Positive
c)
Even
d)
Data Sufficient
|
|
Preeti Khanna answered |

As a is less than a negative number, so 'a' is also a negative number. Hence option C is correct.
A library has an average of 510 visitors on Sundays and 240 on other days. What is the average number of visitors per day in a month of 30 days beginning with a Sunday?
- a)290
- b)304
- c)285
- d)270
Correct answer is option 'C'. Can you explain this answer?
a)
290
b)
304
c)
285
d)
270

|
Ishani Rane answered |
Since the month begins with a Sunday, to there will be five Sundays in the month.
Required average = [510 x 5 + 240 x 25] 30
= 8550/30
= 285
A batsman makes a score of 87 runs in the 17th inning and thus increases his averages by 3. What is his average after 17th inning?
- a)39
- b)35
- c)42
- d)40.5
Correct answer is option 'A'. Can you explain this answer?
a)
39
b)
35
c)
42
d)
40.5

|
Manoj Ghosh answered |
Let the average after 17 innings = x
Total runs scored in 17 innings = 17x
then average after 16 innings = (x-3)
Total runs scored in 16 innings = 16(x-3)
We know that Total runs scored in 16 innings + 87 = Total runs scored in 17 innings
=> 16(x-3) + 87 = 17x
=> 16x - 48 + 87 = 17x
=> x = 39
I went to a hotel along with 12 friends. I paid Rs 145 and all the others paid an equal amount. In the end, we did some calculations and found that the average sum paid by all of us was Rs 5 more than what was originally paid by each of my friends. How much money did each of my friends pay?- a)Rs 120
- b)Rs 100
- c)Rs 80
- d)Rs 70
Correct answer is 'C'. Can you explain this answer?
I went to a hotel along with 12 friends. I paid Rs 145 and all the others paid an equal amount. In the end, we did some calculations and found that the average sum paid by all of us was Rs 5 more than what was originally paid by each of my friends. How much money did each of my friends pay?
a)
Rs 120
b)
Rs 100
c)
Rs 80
d)
Rs 70
|
|
Bhavana Choudhary answered |
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?- a)6.25
- b)5.5
- c)7.4
- d)5
Correct answer is 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?
a)
6.25
b)
5.5
c)
7.4
d)
5

|
Ishani Rane answered |
For the 1st 10 overs the score will be 10*3.2=32so the remaining score is 282-32=250remaining overs = 40so the run rate 250/40=6.25ans is 6.25
If the average marks of three batches of 55, 60 and 45 students respectively is 50, 55, 60, what is the average marks of all the students?
- a)53.23
- b)54.68
- c)51.33
- d)50
Correct answer is 'B'. Can you explain this answer?
a)
53.23
b)
54.68
c)
51.33
d)
50

|
Manoj Ghosh answered |
Total marks of first batch(55) is= 55*50=2750
Total marks of second batch (60) is= 60*55=3300
Total marks of third batch(45)= 45*60=2700
Total marks of second batch= 2750+3300+2700 = 8750
Total number of Students= 55+60+45 =160
Avg= 8750/160= 54.68
The average monthly income of P and Q is Rs. 5050. The average monthly income of Q and R is Rs. 6250 and the average monthly income of P and R is Rs. 5200. The monthly income of P is:
- a)3500
- b)4000
- c)4050
- d)5000
Correct answer is 'B'. Can you explain this answer?
a)
3500
b)
4000
c)
4050
d)
5000

|
Arya Roy answered |
Let monthly income of A = a
monthly income of B = b
monthly income of C = c
a + b = 2 * 5050 .... (Equation 1)
b + c = 2 * 6250 .... (Equation 2)
a + c = 2 * 5200 .... (Equation 3)
(Equation 1) + (Equation 3) - (Equation 2)
= a + b + a + c - (b + c) = (2 * 5050) + (2 * 5200) - (2 * 6250)
= 2a = 2(5050 + 5200 - 6250)
= a = 4000
i.e., Monthly income of A = 4000
The average number of runs scored by Virat Kohli in four matches is 48. In the fifth match, Kohli scores some runs such that his average now becomes 60. In the 6th innings he scores 12 runs more than his fifth innings and now the average of his last five innings becomes 78. How many runs did he score in his first innings? (He does not remain not out in any of the innings)- a)30
- b)50
- c)70
- d)90
Correct answer is option 'A'. Can you explain this answer?
The average number of runs scored by Virat Kohli in four matches is 48. In the fifth match, Kohli scores some runs such that his average now becomes 60. In the 6th innings he scores 12 runs more than his fifth innings and now the average of his last five innings becomes 78. How many runs did he score in his first innings? (He does not remain not out in any of the innings)
a)
30
b)
50
c)
70
d)
90

|
Quantronics answered |
Runs scored by Kohli in first 4 innings = 48*4 = 192
Average of 5 innings is 60, so total runs scored after 5 innings = 60*5 = 300
Hence runs scored by Kohli in fifth inning = 300 – 192 = 108
It is given that in 6th innings he scores 12 runs more than this, so he must score 120 in the sixth inning. Hence total runs scored in 6 innings = 300+120 = 420
Now average of last five innings is 78, so runs scored in last innings = 390
Hence runs scored in first inning = 420 – 390 = 30.
Average of 5 innings is 60, so total runs scored after 5 innings = 60*5 = 300
Hence runs scored by Kohli in fifth inning = 300 – 192 = 108
It is given that in 6th innings he scores 12 runs more than this, so he must score 120 in the sixth inning. Hence total runs scored in 6 innings = 300+120 = 420
Now average of last five innings is 78, so runs scored in last innings = 390
Hence runs scored in first inning = 420 – 390 = 30.
The captain of a cricket team of 11 members is 26 years old and the wicket keeper is 3 years older. If the ages of these two are excluded, the average age of the remaining players is one year less than the average age of the whole team. Find out the average age of the team.
- a)23 years
- b)20 years
- c)24 years
- d)21 years
Correct answer is option 'A'. Can you explain this answer?
a)
23 years
b)
20 years
c)
24 years
d)
21 years

|
Pallabi Deshpande answered |
Number of members in the team = 11
Let the average age of of the team = x
=> Sum of the ages of all the 11 members of the team / 11 = x
=> Sum of the ages of all the 11 members of the team = 11 x
Age of the captain = 26
Age of the wicket keeper = 26 + 3 = 29
Sum of the ages of 9 members of the team excluding captain and wicket keeper
= 11x − 26 − 29 =11x − 55
Average age of 9 members of the team excluding captain and wicket keeper
= 11x−55 / 9
Given that
11x−55 / 9 =(x−1)
⇒11x−55=9(x−1)
⇒11x−55=9x−9
⇒2x=46
⇒x = 46/2 = 23 years
A student's marks were wrongly entered as 83 instead of 63. Due to that, the average marks for the class got increased by 1/2. What is the number of students in the class?- a)45
- b)40
- c)35
- d)30
Correct answer is option 'B'. Can you explain this answer?
A student's marks were wrongly entered as 83 instead of 63. Due to that, the average marks for the class got increased by 1/2. What is the number of students in the class?
a)
45
b)
40
c)
35
d)
30
|
|
Aarav Sharma answered |
To solve this problem, we can use the concept of average age and find the number of men in the group.
Let's assume there are 'x' men in the group.
First, we can find the sum of the ages of all the men in the group before the replacement. Since the average age is the sum of all ages divided by the number of men, we have:
Sum of ages before replacement = Average age before replacement * Number of men
Next, we need to find the sum of ages after the replacement. We know that when the person aged 26 years is replaced by a new person aged 56 years, the average age of the group increases by 6 years. Therefore, the new average age is the average age before replacement plus 6:
New average age = Average age before replacement + 6
We can now find the sum of ages after the replacement using the new average age:
Sum of ages after replacement = New average age * Number of men
Since the sum of ages after the replacement is greater than the sum of ages before the replacement by the age of the replaced person, we have:
Sum of ages after replacement = Sum of ages before replacement + Age of replaced person
Now we can equate the two equations and solve for 'x', the number of men in the group:
New average age * Number of men = Average age before replacement * Number of men + Age of replaced person
Substituting the values given in the problem, we have:
(Average age before replacement + 6) * x = Average age before replacement * x + 26
Simplifying the equation, we get:
6x = 26
Dividing both sides by 6, we find:
x = 26/6
x ≈ 4.33
Since the number of men in the group cannot be a fraction, we can round up to the nearest whole number. Therefore, there are 5 men in the group.
Hence, the correct answer is option B.
Let's assume there are 'x' men in the group.
First, we can find the sum of the ages of all the men in the group before the replacement. Since the average age is the sum of all ages divided by the number of men, we have:
Sum of ages before replacement = Average age before replacement * Number of men
Next, we need to find the sum of ages after the replacement. We know that when the person aged 26 years is replaced by a new person aged 56 years, the average age of the group increases by 6 years. Therefore, the new average age is the average age before replacement plus 6:
New average age = Average age before replacement + 6
We can now find the sum of ages after the replacement using the new average age:
Sum of ages after replacement = New average age * Number of men
Since the sum of ages after the replacement is greater than the sum of ages before the replacement by the age of the replaced person, we have:
Sum of ages after replacement = Sum of ages before replacement + Age of replaced person
Now we can equate the two equations and solve for 'x', the number of men in the group:
New average age * Number of men = Average age before replacement * Number of men + Age of replaced person
Substituting the values given in the problem, we have:
(Average age before replacement + 6) * x = Average age before replacement * x + 26
Simplifying the equation, we get:
6x = 26
Dividing both sides by 6, we find:
x = 26/6
x ≈ 4.33
Since the number of men in the group cannot be a fraction, we can round up to the nearest whole number. Therefore, there are 5 men in the group.
Hence, the correct answer is option B.
The average age of husband, wife and their child 3 years ago was 27 years and that of wife and the child 5 years ago was 20 years. What is the present age of the husband?
- a)40
- b)32
- c)28
- d)30
Correct answer is option 'A'. Can you explain this answer?
a)
40
b)
32
c)
28
d)
30

|
Arya Roy answered |
Sum of the present ages of husband, wife and child = (27 x 3 + 3 x 3) years = 90 years.
Sum of the present ages of wife and child (20 x 2 + 5 x 2) years = 50 years.
Husband's present age = (90 - 50) years = 40 years.
There are two divisions A and B of a class, consisting of 36 and 44 students respectively. If the average weight of divisions A is 40 kg and that of division b is 35 kg. What is the average weight of the whole class?
- a)38.25
- b)37.25
- c)38.5
- d)37
Correct answer is option 'B'. Can you explain this answer?
a)
38.25
b)
37.25
c)
38.5
d)
37

|
Ishani Rane answered |
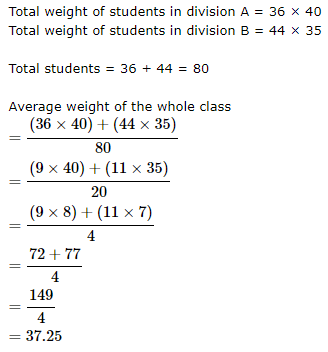
The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, what is the weight of B?- a)31 kg
- b)28 kg
- c)32 kg
- d)30 kg
Correct answer is option 'A'. Can you explain this answer?
The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, what is the weight of B?
a)
31 kg
b)
28 kg
c)
32 kg
d)
30 kg
|
|
Kavya Saxena answered |
Let A, B, C represent their respective weights. Then, we have:
A + B + C = (45 x 3) = 135 .... (i)
A + B = (40 x 2) = 80 .... (ii)
B + C = (43 x 2) = 86 ....(iii)
Adding (ii) and (iii), we get: A + 2B + C = 166 .... (iv)
Subtracting (i) from (iv), we get : B = 31.
 B's weight = 31 kg.
B's weight = 31 kg.One collective farm got an average harvest of 21 tons of wheat and another collective farm that had 12 acres of land less given to wheat, got 25 tons from a hectare. As a result, the second farm harvested 300 tons of wheat more than the first. How many tons of wheat did each farm harvest?
- a)3150, 3450
- b)3250, 3550
- c)2150, 2450
- d)3350, 3150
Correct answer is option 'A'. Can you explain this answer?
One collective farm got an average harvest of 21 tons of wheat and another collective farm that had 12 acres of land less given to wheat, got 25 tons from a hectare. As a result, the second farm harvested 300 tons of wheat more than the first. How many tons of wheat did each farm harvest?
a)
3150, 3450
b)
3250, 3550
c)
2150, 2450
d)
3350, 3150

|
Dhruv Mehra answered |
Let's solve the problem again step by step, ensuring accuracy:
- Let the area of the first farm be AAA acres.
- Therefore, the area of the second farm is A−12A - 12A−12 acres.
Given that:
- The first farm gets an average harvest of 21 tons of wheat per acre.
- The second farm gets an average harvest of 25 tons of wheat per acre.
- The second farm harvested 300 tons more wheat than the first.
Set up the equations:
- The total harvest of the first farm: 21A21A21A tons
- The total harvest of the second farm: 25(A−12)25(A - 12)25(A−12) tons
- The difference in harvest: 25(A−12)−21A=30025(A - 12) - 21A = 30025(A−12)−21A=300
Solve the equation: 25A−300−21A=30025A - 300 - 21A = 30025A−300−21A=300 4A−300=3004A - 300 = 3004A−300=300 4A=6004A = 6004A=600 A=150A = 150A=150
The area of the first farm is 150 acres, and the area of the second farm is 150−12=138150 - 12 = 138150−12=138 acres.
Calculate the total harvest for each farm:
- The first farm: 21×150=315021 \times 150 = 315021×150=3150 tons
- The second farm: 25×138=345025 \times 138 = 345025×138=3450 tons
The correct answer is:
- 3150, 3450
The average weight of a class of 10 students is increased by 2 kg when one student of 30kg left and another student joined. After a few months, this new student left and another student joined whose weight was 10 less than the student who left now. What is the difference between the final and initial averages?
- a)11
- b)1
- c)111
- d)121
Correct answer is option 'B'. Can you explain this answer?
The average weight of a class of 10 students is increased by 2 kg when one student of 30kg left and another student joined. After a few months, this new student left and another student joined whose weight was 10 less than the student who left now. What is the difference between the final and initial averages?
a)
11
b)
1
c)
111
d)
121
|
|
Rajeev Kumar answered |
Change in total weight of 10 students = difference in weight of the student who joined and the student
=> weigth of first student who left = 30 + (10×2) = 50
weight of the student who joined last = 50 – 10 = 40...
Thus change in average weight = (40 – 30)/10 = 1...
Thus change in average weight = (40 – 30)/10 = 1...
Read the following passage and answer the following question that follows.
Aman, Binod, Charan, Dharam and Ehsaan are the members of the same family. Each and everyone loves one another very much. Their birthdays are in different months and on different dates. Aman remembers that his birthday is between 25th and 30th, of Binod it is between 20th and 25th, of Charan it is between 10th and 20th, of Dharam it is between 5th and 10th and of Ehsaan it is between 1st and 5th of the month. The sum of the date of birth is defined as the addition of the date and the month, for example 12th January will be written as 12/1 and will add to a sum of the date of 13. (Between 25th and 30th includes 25 and 30).
If the dates of birth, of four of them are prime numbers, then find the maximum average of the sum of their dates of birth?
- a)29
- b)23
- c)28
- d)27.2
Correct answer is option 'D'. Can you explain this answer?
Read the following passage and answer the following question that follows.
Aman, Binod, Charan, Dharam and Ehsaan are the members of the same family. Each and everyone loves one another very much. Their birthdays are in different months and on different dates. Aman remembers that his birthday is between 25th and 30th, of Binod it is between 20th and 25th, of Charan it is between 10th and 20th, of Dharam it is between 5th and 10th and of Ehsaan it is between 1st and 5th of the month. The sum of the date of birth is defined as the addition of the date and the month, for example 12th January will be written as 12/1 and will add to a sum of the date of 13. (Between 25th and 30th includes 25 and 30).
If the dates of birth, of four of them are prime numbers, then find the maximum average of the sum of their dates of birth?
a)
29
b)
23
c)
28
d)
27.2
|
|
Alok Verma answered |
It is given that the date of births of four of them are prime numbers
For the average to be maximum, the dates we need to choose must be closest to the maximum dates
Therefore, the four prime dates are 29th, 23th, 19 and 5th
Sum of the date of birth = 29+23+19+10+5+12+11+10+9+8 =136
Average = 136/5 = 27.2
The maximum average when the birth dates of four of them are prime numbers is 27.2
The average of 20 numbers is zero. Of them, How many of them may be greater than zero , at the most?
- a)1
- b)20
- c)0
- d)19
Correct answer is 'D'. Can you explain this answer?
a)
1
b)
20
c)
0
d)
19

|
Priyanka Datta answered |
Average of 20 numbers = 0.
 Sum of 20 numbers (0 x 20) = 0.
Sum of 20 numbers (0 x 20) = 0.It is quite possible that 19 of these numbers may be positive and if their sum is a then 20th number is (-a).
Ram was born 30 years after his father was born and Ram's sister was born 25 years after Ram’s mother was born. The average age of the Ram family is 26.25 years right now. Ram's sister will get married 4 years from now and will leave the family. Then the sum of age of the family will be 107 years. What is the age of Ram's father?
- a)30 year
- b)35 year
- c)40 year
- d)45 years
Correct answer is option 'D'. Can you explain this answer?
Ram was born 30 years after his father was born and Ram's sister was born 25 years after Ram’s mother was born. The average age of the Ram family is 26.25 years right now. Ram's sister will get married 4 years from now and will leave the family. Then the sum of age of the family will be 107 years. What is the age of Ram's father?
a)
30 year
b)
35 year
c)
40 year
d)
45 years

|
Shilpa Nambiar answered |
Let the present age of father be x and mother be y
∴ Ram age = (x – 30)
And Ram’s sister = (y – 25)
We know that
Average = Sum of all/total number of terms
⇒ 26.25 = Sum of all/4
Sum of their ages will be = 105
∴ x + y + (x - 30) + (y – 25) = 105
⇒ x + y = 80 ----(i)
After four years their total ages will be (excluding daughter age)
∴ (x + 4) + (y + 4) + (x – 30) + 4 = 107
⇒ 2x + y = 125 ----(ii)
By solving equation (i) and (ii) we get
⇒ x = 45 and y = 35
∴ The age of Ram’s father will be 45 years
In 2001 there were 6 members in Barney’s family and their average age was 28 years. He got married between 2001 and 2004 and in 2004 there was an addition of a child in his family. In 2006, the average age of his family was 32 years. What is the present age (in 2006) of Barney’s wife (in years) is:- a)61
- b)57
- c)59
- d)56
Correct answer is option 'D'. Can you explain this answer?
In 2001 there were 6 members in Barney’s family and their average age was 28 years. He got married between 2001 and 2004 and in 2004 there was an addition of a child in his family. In 2006, the average age of his family was 32 years. What is the present age (in 2006) of Barney’s wife (in years) is:
a)
61
b)
57
c)
59
d)
56
|
|
Aarav Sharma answered |
& Friends. The main characters were:
1. Barney - a purple anthropomorphic Tyrannosaurus rex who is the main protagonist and host of the show.
2. Baby Bop - a green Triceratops who is one of Barney's best friends. She is known for her love of music and dancing.
3. BJ - a yellow Protoceratops who is another of Barney's best friends. He is known for his love of sports and games.
4. Riff - a brown Hadrosaur who is a new character introduced in 2006. He is known for his love of music and playing the guitar.
5. Tosha - a human girl who is one of Barney's human friends. She is known for her love of singing and dancing.
6. Min - another human girl who is also one of Barney's human friends. She is known for her love of art and drawing.
1. Barney - a purple anthropomorphic Tyrannosaurus rex who is the main protagonist and host of the show.
2. Baby Bop - a green Triceratops who is one of Barney's best friends. She is known for her love of music and dancing.
3. BJ - a yellow Protoceratops who is another of Barney's best friends. He is known for his love of sports and games.
4. Riff - a brown Hadrosaur who is a new character introduced in 2006. He is known for his love of music and playing the guitar.
5. Tosha - a human girl who is one of Barney's human friends. She is known for her love of singing and dancing.
6. Min - another human girl who is also one of Barney's human friends. She is known for her love of art and drawing.
The average age of a class of 30 students and a teacher reduces by 0.5 years if we exclude the teacher. If the initial average is 14 years, find the age of the class teacher.
- a)27 years
- b)28 years
- c)29 years
- d)30 years
Correct answer is option 'C'. Can you explain this answer?
The average age of a class of 30 students and a teacher reduces by 0.5 years if we exclude the teacher. If the initial average is 14 years, find the age of the class teacher.
a)
27 years
b)
28 years
c)
29 years
d)
30 years

|
Bank Exams India answered |
Let the age of the teacher be T.
The initial total age of the class (including the teacher) is (30+1)*14 = 434 years.
If we exclude the teacher, the total age of the 30 students is 30*(14-0.5) = 405 years.
So the teacher's age, T, must be:
434 - 405 = 29 years
Therefore, the age of the class teacher is 29 years.
Read the passage below and solve the questions based on it.
The average score of a batsman for a certain number of innings was 21 75 per inning. He played 3 innings more and scored 28. 34 and 37 runs respectively, thus increasing his average by 1.25.Q. How many innings in all did he play?- a)35
- b)60
- c)30
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Read the passage below and solve the questions based on it.
The average score of a batsman for a certain number of innings was 21 75 per inning. He played 3 innings more and scored 28. 34 and 37 runs respectively, thus increasing his average by 1.25.
The average score of a batsman for a certain number of innings was 21 75 per inning. He played 3 innings more and scored 28. 34 and 37 runs respectively, thus increasing his average by 1.25.
Q. How many innings in all did he play?
a)
35
b)
60
c)
30
d)
None of these
|
|
Rajeev Kumar answered |
Let number of innings be x
average of the first (x-3) innings = 21.75
Total of the first (x-3) innings = 21.75(x-3)
Total of the first (x-3) innings = 21.75(x-3)
Average of the x innings = (21.75+1.125) = 22.875
Total of the x innings = 22.875x
Total of the x innings = 22.875x
21.75(x-3) + 28+34+37= 22.875x
21.75(x-3) + 99 = 22.875x
21.75x - 65.25 + 99 = 22.875x
1.125x = 33.75
x = 30
21.75(x-3) + 99 = 22.875x
21.75x - 65.25 + 99 = 22.875x
1.125x = 33.75
x = 30
60 litres of a 75% solution of wine is taken into a laboratory. 4 litres of the solution is flushed and 4 litres of water is added to compensate the loss. Then 5 litres of the solution is flushed again and 5 litres of water is added. Again 6 litres of the solution is flushed and 6 litres of water is added. The final concentration of wine in the solution is- a)255%
- b)57.75%
- c)60.25%
- d)59%
Correct answer is option 'B'. Can you explain this answer?
60 litres of a 75% solution of wine is taken into a laboratory. 4 litres of the solution is flushed and 4 litres of water is added to compensate the loss. Then 5 litres of the solution is flushed again and 5 litres of water is added. Again 6 litres of the solution is flushed and 6 litres of water is added. The final concentration of wine in the solution is
a)
255%
b)
57.75%
c)
60.25%
d)
59%

|
Arindam Mehta answered |
Initial Concentration of wine = 75% Concentration of wine after 1st flushing
The average mark of a class of n students is 64. When eight new students with an average mark of 73 join the class, the new average of the entire class is a whole number. Find the number of students now in the class, given that n lies between 25 and 60.- a)44
- b)32
- c)36
- d)72
Correct answer is option 'C'. Can you explain this answer?
The average mark of a class of n students is 64. When eight new students with an average mark of 73 join the class, the new average of the entire class is a whole number. Find the number of students now in the class, given that n lies between 25 and 60.
a)
44
b)
32
c)
36
d)
72

|
Arya Roy answered |
Let ‘x’ be the increase in the average

For ‘x’ to be a whole number 72 (= 9 * 8) should be divisible by (n + 8)
From the choices it can be said that 36 and 72 are two such factors. But 72 does not lie within the range.
∴ number of students in class are 36.
A student needed to find the arithmetic mean of the numbers 3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14 and x. He found the mean to be 12. What is the value of x?
- a)12
- b)5
- c)7
- d)9
Correct answer is option 'C'. Can you explain this answer?
a)
12
b)
5
c)
7
d)
9

|
Arya Roy answered |
Mean = Sum / Total count
12 = (3+11+7+9+15+13+8+19+17+21+14+x) / 12
12*12 = 137 + x
144 = 137 + x
x = 144 - 137
x = 7
Read the following and answer the questions that follow. If 5 people are transferred from E to R and another independent set of 5 people are transferred back from R to E, then after this operation (Assume that the set transferred from R to E contains none from the set of students that came to R from E)For question 3, what could be the minimum value of the average of class R?- a)25
- b)24.2
- c)22.4
- d)23
Correct answer is option 'C'. Can you explain this answer?
Read the following and answer the questions that follow.
If 5 people are transferred from E to R and another independent set of 5 people are transferred back from R to E, then after this operation (Assume that the set transferred from R to E contains none from the set of students that came to R from E)
For question 3, what could be the minimum value of the average of class R?
a)
25
b)
24.2
c)
22.4
d)
23
|
|
Preeti Khanna answered |
For the minimum possible value of R we will need the E to R transfer to be the lowest possible value while the R to E transfer must have the highest possible value.
Thus, E to R transfer -> 18* 5 while R to E transfer will be 31*5. Hence the answer is 22.4.
The average weight of the books carried by Kuku to school is 1.5 kg and 2.5 kg is the average weight of the exercise books. If Kuku is carrying only text books and exercise books in the ratio of 3:4, what is the total weight of his school bag? (Ignore any other weights such as that of school bag, stationary etc.)- a)10.5 kg
- b)1 kg
- c)6 kg
- d)Data insufficient
Correct answer is option 'D'. Can you explain this answer?
The average weight of the books carried by Kuku to school is 1.5 kg and 2.5 kg is the average weight of the exercise books. If Kuku is carrying only text books and exercise books in the ratio of 3:4, what is the total weight of his school bag? (Ignore any other weights such as that of school bag, stationary etc.)
a)
10.5 kg
b)
1 kg
c)
6 kg
d)
Data insufficient
|
|
Ravi Singh answered |
No data regarding the numbers of books is given, hence we cannot determine the weight of school bag. Hence, (d)
A grocer has a sale of Rs. 6435, Rs. 6927, Rs. 6855, Rs. 7230 and Rs. 6562 for 5 consecutive months. How much sale must he have in the sixth month so that he gets an average sale of Rs. 6500?
- a)4800
- b)4991
- c)5004
- d)5000
Correct answer is option 'B'. Can you explain this answer?
a)
4800
b)
4991
c)
5004
d)
5000

|
Pallabi Deshpande answered |
Total sale for 5 months = Rs. (6435 + 6927 + 6855 + 7230 + 6562) = Rs. 34009.
Required sale = Rs. [ (6500 x 6) - 34009 ]
= Rs.(39000 - 34009)
= Rs.4991.
The average age of a family of 5 members is 20 years. If the age of the youngest member is 10 years, what was the average age of the family at the birth of the youngest member?- a)12.50
- b)15.25
- c)21.25
- d)18.75
Correct answer is option 'D'. Can you explain this answer?
The average age of a family of 5 members is 20 years. If the age of the youngest member is 10 years, what was the average age of the family at the birth of the youngest member?
a)
12.50
b)
15.25
c)
21.25
d)
18.75
|
|
Rajeev Kumar answered |
At present the total age of the family = 5 × 20 =100
The total age of the family at the time of the birth of the youngest member,
= 100 - 10 - (10 × 4)
= 50
Therefore, average age of the family at the time of birth of the youngest member,
= 50/4 =12.5
The total age of the family at the time of the birth of the youngest member,
= 100 - 10 - (10 × 4)
= 50
Therefore, average age of the family at the time of birth of the youngest member,
= 50/4 =12.5
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?- a)6.25
- b)5.5
- c)7.4
- d)5
Correct answer is option 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Average" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. In the first 10 overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?
a)
6.25
b)
5.5
c)
7.4
d)
5

|
Arya Roy answered |
Runs scored in the first 10 overs = 10 * 3.2 = 32
Total runs = 282
Remaining runs to be scored = 282 - 32 = 250
Remaining overs = 40
Run rate needed =250/40 = 6.25
Read the following:There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes,answer the questions that follow:A Æ Highest score 22, Lowest score 18B Æ Highest score 31, Lowest score 23C Æ Highest score 33, Lowest score 26In a transfer of 5 students from B to CWhich of these can be said about the average score of B?- a)Increases if C decreases
- b)Decreases if C increases
- c)Increases if A decreases
- d)Decreases if B increases
Correct answer is option 'B'. Can you explain this answer?
Read the following:
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes,
answer the questions that follow:
A Æ Highest score 22, Lowest score 18
B Æ Highest score 31, Lowest score 23
C Æ Highest score 33, Lowest score 26
In a transfer of 5 students from B to C
Which of these can be said about the average score of B?
a)
Increases if C decreases
b)
Decreases if C increases
c)
Increases if A decreases
d)
Decreases if B increases
|
|
Aarav Sharma answered |
- Class A has a total of 400 marks
- Class B has a total of 625 marks
- Class C has a total of 900 marks
B - If all three classes are combined, what is the total number of students and the overall average marks?
The total number of students is 75 (20+25+30). To find the overall average marks, we need to first find the total marks of all three classes combined, which is 400 + 625 + 900 = 1925. Then, we divide this total by the total number of students, which is 75. So, the overall average marks is 1925/75 = 25.67 (rounded to two decimal places).
C - If a student has scored 30 marks in each class, what is the student's overall average marks?
To find the overall average marks of a student who has scored 30 marks in each class, we need to find the total marks earned by the student and divide it by the total number of classes. The student has scored a total of 30 x 3 = 90 marks overall. The total number of classes is 3. So, the overall average marks of the student is 90/3 = 30.
- Class B has a total of 625 marks
- Class C has a total of 900 marks
B - If all three classes are combined, what is the total number of students and the overall average marks?
The total number of students is 75 (20+25+30). To find the overall average marks, we need to first find the total marks of all three classes combined, which is 400 + 625 + 900 = 1925. Then, we divide this total by the total number of students, which is 75. So, the overall average marks is 1925/75 = 25.67 (rounded to two decimal places).
C - If a student has scored 30 marks in each class, what is the student's overall average marks?
To find the overall average marks of a student who has scored 30 marks in each class, we need to find the total marks earned by the student and divide it by the total number of classes. The student has scored a total of 30 x 3 = 90 marks overall. The total number of classes is 3. So, the overall average marks of the student is 90/3 = 30.
A family consists of two grandparents, two parents and three grandchildren. The average age of the grandparents is 67 years, that of the parents is 35 years and that of the grandchildren is 6 years. The average age of the family is
- a)32 2/7 years
- b)31 5/7 years
- c)28 1/7 years
- d)30 5/7 years
Correct answer is option 'B'. Can you explain this answer?
a)
32 2/7 years
b)
31 5/7 years
c)
28 1/7 years
d)
30 5/7 years

|
Ishani Rane answered |
Total age of the grandparents = 67 * 2
Total age of the parents = 35 * 2
Total age of the grandchildren = 6 * 3
Average age of the family
= (67 *2 ) + (35*2) + (6*2) / 7
= 134 + 70 + 18 / 7
= 22/7
= 31 5/7
There are 20 students in Mr Rahul Ghosh’s class. He conducts an examination out of 100 and then arranged the marks in an ascending order. He found Chandan, the topper of the class, had slipped to the tenth position. When he was adding the scores of the last 11 students the average was 64 and that of the top 10 was 67. If the average marks obtained by all the students of his class was 65, how many marks did Chandan score?- a)64
- b)67
- c)74
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
There are 20 students in Mr Rahul Ghosh’s class. He conducts an examination out of 100 and then arranged the marks in an ascending order. He found Chandan, the topper of the class, had slipped to the tenth position. When he was adding the scores of the last 11 students the average was 64 and that of the top 10 was 67. If the average marks obtained by all the students of his class was 65, how many marks did Chandan score?
a)
64
b)
67
c)
74
d)
Cannot be determined

|
Arindam Mehta answered |
Score of Chandan = 64 x 11 + 10 x 67 - 20 x 65 = 704 + 670 - 1300
= 1374 -1300 = 74
= 1374 -1300 = 74
The average of 20 numbers is zero. Of them, How many of them may be greater than zero , at the most?
- a)1
- b)20
- c)0
- d)19
Correct answer is option 'D'. Can you explain this answer?
a)
1
b)
20
c)
0
d)
19
|
|
Sagar Sharma answered |
Problem:
The average of 20 numbers is zero. How many of them may be greater than zero, at the most?
Solution:
To find the maximum number of numbers that can be greater than zero, we need to understand the concept of average and the properties of numbers.
Understanding the Average:
The average of a set of numbers is found by summing all the numbers in the set and then dividing the sum by the total number of numbers.
Properties of Numbers:
1. The sum of positive numbers is always greater than zero.
2. The sum of negative numbers is always less than zero.
3. The sum of positive and negative numbers can be zero if the sum of positive numbers equals the sum of negative numbers.
Explanation:
Given that the average of 20 numbers is zero, we can conclude that the sum of these 20 numbers is also zero.
Let's assume that there are 'x' numbers greater than zero and 'y' numbers less than or equal to zero.
Since the sum of these 20 numbers is zero, we can write the equation:
(x * positive number) + (y * non-positive number) = 0
To maximize the number of numbers greater than zero, we need to minimize the number of non-positive numbers. The smallest non-positive number is zero. Therefore, we can rewrite the equation as:
(x * positive number) + (y * 0) = 0
Simplifying the equation, we get:
x * positive number = 0
In order for this equation to be true, the value of 'x' must be zero. This means that there can be zero numbers greater than zero in the set of 20 numbers.
Therefore, the maximum number of numbers that can be greater than zero is 0.
Hence, the correct answer is option 'C' - 0.
The average of 20 numbers is zero. How many of them may be greater than zero, at the most?
Solution:
To find the maximum number of numbers that can be greater than zero, we need to understand the concept of average and the properties of numbers.
Understanding the Average:
The average of a set of numbers is found by summing all the numbers in the set and then dividing the sum by the total number of numbers.
Properties of Numbers:
1. The sum of positive numbers is always greater than zero.
2. The sum of negative numbers is always less than zero.
3. The sum of positive and negative numbers can be zero if the sum of positive numbers equals the sum of negative numbers.
Explanation:
Given that the average of 20 numbers is zero, we can conclude that the sum of these 20 numbers is also zero.
Let's assume that there are 'x' numbers greater than zero and 'y' numbers less than or equal to zero.
Since the sum of these 20 numbers is zero, we can write the equation:
(x * positive number) + (y * non-positive number) = 0
To maximize the number of numbers greater than zero, we need to minimize the number of non-positive numbers. The smallest non-positive number is zero. Therefore, we can rewrite the equation as:
(x * positive number) + (y * 0) = 0
Simplifying the equation, we get:
x * positive number = 0
In order for this equation to be true, the value of 'x' must be zero. This means that there can be zero numbers greater than zero in the set of 20 numbers.
Therefore, the maximum number of numbers that can be greater than zero is 0.
Hence, the correct answer is option 'C' - 0.
Read the following and answer the questions that follow.If 5 people are transferred from E to R and another independent set of 5 people are transferred back from R to E, then after this operation (Assume that the set transferred from R to E contains none from the set of students that came to R from E)What could be the maximum possible average achieved by class E at the end of the operation?- a)25.2
- b)23.25
- c)26
- d)23.75
Correct answer is option 'B'. Can you explain this answer?
Read the following and answer the questions that follow.
If 5 people are transferred from E to R and another independent set of 5 people are transferred back from R to E, then after this operation (Assume that the set transferred from R to E contains none from the set of students that came to R from E)
What could be the maximum possible average achieved by class E at the end of the operation?
a)
25.2
b)
23.25
c)
26
d)
23.75
|
|
Rajeev Kumar answered |
The maximum value for E will happen in the case of Q4. Then the increment for group E is:
31* 5 – 18 * 5 = 5 * (31 – 18) = 65.
Thus the maximum possible value is 465 / 20 = 23.25.
31* 5 – 18 * 5 = 5 * (31 – 18) = 65.
Thus the maximum possible value is 465 / 20 = 23.25.
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes, answer the questions that follow:
A - Highest score 22, Lowest score 18
B - Highest score 31, Lowest score 23
C - Highest score 33, Lowest score 26
If five students are transferred from A to B. What will happen to the average score of B?
- a)Definitely increase
- b)Cannot Say
- c)Remain constant
- d)Definitely decrease
Correct answer is option 'D'. Can you explain this answer?
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes, answer the questions that follow:
A - Highest score 22, Lowest score 18
B - Highest score 31, Lowest score 23
C - Highest score 33, Lowest score 26
If five students are transferred from A to B. What will happen to the average score of B?
a)
Definitely increase
b)
Cannot Say
c)
Remain constant
d)
Definitely decrease
|
|
Aarav Sharma answered |
- The highest marks in class A is 40 and the lowest marks is 10.
- The range of marks in class B is 20.
- The mode of marks in class C is 30.
B
- The total marks obtained by all students in class B is 1250.
- The median marks in class B is 25.
C
- The highest marks in class C is 50.
- The lowest marks in class C is 10.
- The mean marks in class C is 30.
- The range of marks in class B is 20.
- The mode of marks in class C is 30.
B
- The total marks obtained by all students in class B is 1250.
- The median marks in class B is 25.
C
- The highest marks in class C is 50.
- The lowest marks in class C is 10.
- The mean marks in class C is 30.
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes, answer the questions that follow:A Æ Highest score 22, Lowest score 18B Æ Highest score 31, Lowest score 23C Æ Highest score 33, Lowest score 26If five students are transferred from A to B.What will happen to the average score of B?- a)Definitely increase
- b)Definitely decrease
- c)Remain constant
- d)Cannot say
Correct answer is option 'B'. Can you explain this answer?
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes, answer the questions that follow:
A Æ Highest score 22, Lowest score 18
B Æ Highest score 31, Lowest score 23
C Æ Highest score 33, Lowest score 26
If five students are transferred from A to B.
What will happen to the average score of B?
a)
Definitely increase
b)
Definitely decrease
c)
Remain constant
d)
Cannot say
|
|
Rajeev Kumar answered |
Definitely decrease, since the highest marks in Class A is less than the lowest marks in Class B.
So, the correct answer is B
The average rainfall for the first 3 days out of five days was recorded to be 0.45 inches. The rainfall on the last two days was in the ratio 2:3. The average of five days was 0.40 inches. What was the rainfall on the last day?- a)0.45 inches
- b)0.39 inches
- c)0.35 inches
- d)0.30 inches
Correct answer is option 'B'. Can you explain this answer?
The average rainfall for the first 3 days out of five days was recorded to be 0.45 inches. The rainfall on the last two days was in the ratio 2:3. The average of five days was 0.40 inches. What was the rainfall on the last day?
a)
0.45 inches
b)
0.39 inches
c)
0.35 inches
d)
0.30 inches

|
Ishaan Shah answered |
A vessel contains a mixture of two liquids A and B in the ratio of 7:5. When 9 litres of the mixture is taken out and the vessel is filled with B, the ratio of A and B is now 7:9. How many litres of liquid A was there in the vessel initially?- a)24 litres
- b)21 litres
- c)18 litres
- d)27 litres
Correct answer is option 'B'. Can you explain this answer?
A vessel contains a mixture of two liquids A and B in the ratio of 7:5. When 9 litres of the mixture is taken out and the vessel is filled with B, the ratio of A and B is now 7:9. How many litres of liquid A was there in the vessel initially?
a)
24 litres
b)
21 litres
c)
18 litres
d)
27 litres

|
Arindam Mehta answered |
Let 7x and 5x volume of liquids A and Liquid B are present in vessel then,
Hence, 7.3 = 211 liquid A was present.
The weight of a metal piece as calculated by the average of 7 different experiments is 53.735 gm. The average of the first three experiments is 54.005 gm, of the fourth is 0.004 gm greater than the fifth, while the average of the sixth and seventh experiment was 0.010 gm less than the average of the first three. Find the weight of the body obtained by the fourth experiment.
- a)49.353 gm
- b)51.712 gm
- c)54.512 gm
- d)53.072 gm
Correct answer is option 'D'. Can you explain this answer?
The weight of a metal piece as calculated by the average of 7 different experiments is 53.735 gm. The average of the first three experiments is 54.005 gm, of the fourth is 0.004 gm greater than the fifth, while the average of the sixth and seventh experiment was 0.010 gm less than the average of the first three. Find the weight of the body obtained by the fourth experiment.
a)
49.353 gm
b)
51.712 gm
c)
54.512 gm
d)
53.072 gm

|
Amrutha Joshi answered |
Chapter doubts & questions for Averages - Numerical Aptitude for SSC Exams 2025 is part of SSC MTS / SSC GD exam preparation. The chapters have been prepared according to the SSC MTS / SSC GD exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC MTS / SSC GD 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Averages - Numerical Aptitude for SSC Exams in English & Hindi are available as part of SSC MTS / SSC GD exam.
Download more important topics, notes, lectures and mock test series for SSC MTS / SSC GD Exam by signing up for free.
Numerical Aptitude for SSC Exams
172 videos|87 docs|127 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup