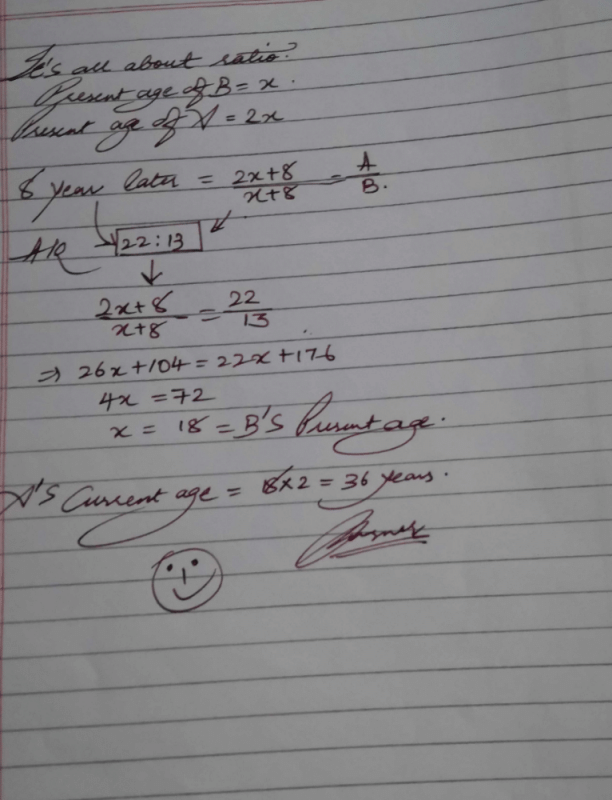All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of Problem on Ages for CDS Exam
The age of father 10 years ago was thrice the age of his son. Ten years hence, father’s age will be twice that of his son. The ratio of their present ages is- a)5:2
- b)7:3
- c)9:2
- d)13:4
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The age of father 10 years ago was thrice the age of his son. Ten years hence, father’s age will be twice that of his son. The ratio of their present ages is
a)
5:2
b)
7:3
c)
9:2
d)
13:4
e)
None of these
|
Future Foundation Institute answered |
The correct option ia B.
Let the ages of father and son 10 years ago be 3x and x years respectively.
Then, (3x + 10) + 10 = 2[(x + 10) + 10]
⇒ 3x + 20 = 2x + 40
⇒ x = 20
∴ Required ratio
= (3x + 10) : (x + 10)
= 70 : 30
= 7 : 3
Let the ages of father and son 10 years ago be 3x and x years respectively.
Then, (3x + 10) + 10 = 2[(x + 10) + 10]
⇒ 3x + 20 = 2x + 40
⇒ x = 20
∴ Required ratio
= (3x + 10) : (x + 10)
= 70 : 30
= 7 : 3
The ratio between the present ages of Ravi and Vinay is 7:15 respectively. Two years from now Vinay’s age will be twice that of Ravi’s age. What was the difference between their ages 5 years ago.- a)13 years
- b)16 years
- c)11 years
- d)18 years
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio between the present ages of Ravi and Vinay is 7:15 respectively. Two years from now Vinay’s age will be twice that of Ravi’s age. What was the difference between their ages 5 years ago.
a)
13 years
b)
16 years
c)
11 years
d)
18 years
e)
None of these
|
Aspire Academy answered |
The correct option is B.
Let the present age of Ravi be 7x and that of Vinay be 15x.
After 2 yrs , Ravi age = 7x+2
Vinay age = 15x+2.
Acc. to ques,
15x+2 = 2 (7x+2)
15x+2 = 14x+4
x = 2.
Five yrs ago,
Ravi age = 7x-5 => 7*2 - 5 = 9 yrs
Vinay age = 15x - 5 = 15*2 - 5 = 25 yrs.
Difference = 25 - 9 = 16 years
Let the present age of Ravi be 7x and that of Vinay be 15x.
After 2 yrs , Ravi age = 7x+2
Vinay age = 15x+2.
Acc. to ques,
15x+2 = 2 (7x+2)
15x+2 = 14x+4
x = 2.
Five yrs ago,
Ravi age = 7x-5 => 7*2 - 5 = 9 yrs
Vinay age = 15x - 5 = 15*2 - 5 = 25 yrs.
Difference = 25 - 9 = 16 years
A father said to his son, "I was as old as you now at the time of your birth". If the father's age is 38 years now, the son's age five years back was:
- a)14 years
- b)19 years
- c)33 years
- d)38 years
Correct answer is option 'A'. Can you explain this answer?
A father said to his son, "I was as old as you now at the time of your birth". If the father's age is 38 years now, the son's age five years back was:
a)
14 years
b)
19 years
c)
33 years
d)
38 years
|
Target Study Academy answered |
Let the son's present age be x years. Then, (38 - x) = x
2x = 38. x = 19.
Son's age 5 years back (19 - 5) = 14 years.The ratio of the age of a man and his wife is 4 : 3 . At the time of marriage the ratio was 5 : 3 and After 4 years this ratio will become 9 : 7 . How many years ago were they married?- a)8 years
- b)10 years
- c)11 years
- d)12 years
- e)13 years
Correct answer is option 'D'. Can you explain this answer?
The ratio of the age of a man and his wife is 4 : 3 . At the time of marriage the ratio was 5 : 3 and After 4 years this ratio will become 9 : 7 . How many years ago were they married?
a)
8 years
b)
10 years
c)
11 years
d)
12 years
e)
13 years
|
Meera Rana answered |
Let the present age of the man and his wife be 4 x and 3 x respectively.
After 4 years this ratio will become 9 : 7 ⇒ ( 4 x + 4 ) : ( 3 x + 4 ) = 9 : 7
⇒ 7 ( 4 x + 4 ) = 9 ( 3 x + 4 )
⇒ 28 x + 28 = 27 x + 36
⇒ x = 8
⇒ 7 ( 4 x + 4 ) = 9 ( 3 x + 4 )
⇒ 28 x + 28 = 27 x + 36
⇒ x = 8
Present age of the man = 4 x = 4 × 8 = 32
Present age of his wife = 3 x = 3 × 8 = 24
Assume that they got married before t years. Then,
( 32 − t ) : ( 24 − t ) = 5 : 3
⇒ 3 ( 32 − t ) = 5 ( 24 − t )
⇒ 96 − 3 t = 120 − 5 t
⇒ 2 t = 24
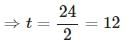
Present age of his wife = 3 x = 3 × 8 = 24
Assume that they got married before t years. Then,
( 32 − t ) : ( 24 − t ) = 5 : 3
⇒ 3 ( 32 − t ) = 5 ( 24 − t )
⇒ 96 − 3 t = 120 − 5 t
⇒ 2 t = 24
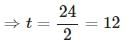
Six years ago, the ratio of the ages of Vimal and Saroj was 6 : 5 . Four years hence, the ratio of their ages will be 11 : 10 . What is Saroj's age at present?- a)18
- b)17
- c)16
- d)15
- e)19
Correct answer is option 'C'. Can you explain this answer?
Six years ago, the ratio of the ages of Vimal and Saroj was 6 : 5 . Four years hence, the ratio of their ages will be 11 : 10 . What is Saroj's age at present?
a)
18
b)
17
c)
16
d)
15
e)
19
|
Harmanjot Singh answered |
Given that, six years ago, the ratio of the ages of Vimal and Saroj = 6 : 5
Hence we can assume that age of Vimal six years ago = 6x
age of Saroj six years ago = 5x
After 4 years, the ratio of their ages = 11 : 10
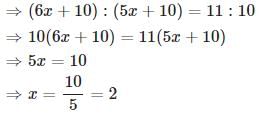
Saroj's present age
Hence we can assume that age of Vimal six years ago = 6x
age of Saroj six years ago = 5x
After 4 years, the ratio of their ages = 11 : 10
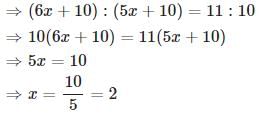
Saroj's present age
= ( 5x + 6 ) = 5 x 2 + 6 = 16
The ratio between the present ages of P and Q is 6:7. If Q is four years older than P, what will be the ratio of the ages of P and Q after 4 years?
- a)3:4
- b)3:5
- c)4:3
- d)Data inadequate
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
The ratio between the present ages of P and Q is 6:7. If Q is four years older than P, what will be the ratio of the ages of P and Q after 4 years?
a)
3:4
b)
3:5
c)
4:3
d)
Data inadequate
e)
None of these
|
Aishwarya Rajput answered |
P:Q = 6:7 i.e P/Q = 6/7 => 7P = 6Q--------1
Given that Q = P + 4 (put in 1)
7P = 6(P + 4)
So, P = 24 and Q = P+4 i.e 28years
After 4 years, P+4 i.e 24+4= 28yrs
And Q = 28 +4 = 32years
The ratio we get is 7:8
Six years ago, the ratio of the ages of Kunal and Sagar was 6 : 5. Four years hence, the ratio of their ages will be 11 : 10. What is Sagar's age at present?- a)16 years
- b)18 years
- c)20 years
- d)Can not be determined
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Six years ago, the ratio of the ages of Kunal and Sagar was 6 : 5. Four years hence, the ratio of their ages will be 11 : 10. What is Sagar's age at present?
a)
16 years
b)
18 years
c)
20 years
d)
Can not be determined
e)
None of these
|
Kavya Saxena answered |
Let the ages of Kunal and Sagar 6 years ago be 6x and 5x years respectively.
The total age of A and B is 12 years more than the total age of B and C. C is how many years younger than A?- a)12 years
- b)24 years
- c)C is elder than A
- d)Data inadequate
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The total age of A and B is 12 years more than the total age of B and C. C is how many years younger than A?
a)
12 years
b)
24 years
c)
C is elder than A
d)
Data inadequate
e)
None of these
|
Glance Learning Institute answered |
The correct option is A.
Given that A+B = 12 + B + C
⇒ A – C = 12 + B – B = 12
⇒ C is younger than A by 12 years
Given that A+B = 12 + B + C
⇒ A – C = 12 + B – B = 12
⇒ C is younger than A by 12 years
In a family the average age of the father and mother is 38 years, whereas the average age of father, mother and only daughter is 28 years. The age of daughters is- a)5 years
- b)6 years
- c)8 years
- d)10 years
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In a family the average age of the father and mother is 38 years, whereas the average age of father, mother and only daughter is 28 years. The age of daughters is
a)
5 years
b)
6 years
c)
8 years
d)
10 years
e)
None of these
|
Anaya Patel answered |
The correct option is C.
Let father's age be x, mother's age be y and daughter's age be z.
(x+y)/2 = 38
x+y = 76
(x+y+z)/3 = 28
(76+z)/3 = 28
76+z = 84
z = 8 years
Let father's age be x, mother's age be y and daughter's age be z.
(x+y)/2 = 38
x+y = 76
(x+y+z)/3 = 28
(76+z)/3 = 28
76+z = 84
z = 8 years
Ayesha’s father was 38 year of age when she was born. Her mother was 36 years old when her brother, four years younger to her, was born, What was the age of Ayesha’s father and mother respectively when her brother was born.- a)32 years, 23 years
- b)32 years, 29 years
- c)35 years, 29 years
- d)35 years, 33 years
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Ayesha’s father was 38 year of age when she was born. Her mother was 36 years old when her brother, four years younger to her, was born, What was the age of Ayesha’s father and mother respectively when her brother was born.
a)
32 years, 23 years
b)
32 years, 29 years
c)
35 years, 29 years
d)
35 years, 33 years
e)
None of these
|
Dia Mehta answered |
Mother's age when Ayesha's brother was born = 36 years.
Father's age when Ayesha's brother was born = (38 + 4) years = 42 years.
Required difference = (42 - 36) years = 6 years.If 6 years are subtracted from the present age of Ajay and the remainder is divided by 18 , then the present age of Rahul is obtained. If Rahul is 2 years younger to Denis whose age is 5 years, then what is Ajay's present age?- a)50 years
- b)60 years
- c)55 years
- d)62 years
- e)58 years
Correct answer is option 'B'. Can you explain this answer?
If 6 years are subtracted from the present age of Ajay and the remainder is divided by 18 , then the present age of Rahul is obtained. If Rahul is 2 years younger to Denis whose age is 5 years, then what is Ajay's present age?
a)
50 years
b)
60 years
c)
55 years
d)
62 years
e)
58 years
|
|
Aarav Sharma answered |
Given:
- Ajay's present age is x
- When 6 years are subtracted from x and the remainder is divided by 18, Rahul's age is obtained.
- Rahul is 2 years younger than Denis, whose age is 5 years.
To find:
Ajay's present age
Solution:
1. When 6 years are subtracted from Ajay's present age, we get (x-6).
2. When (x-6) is divided by 18, we get Rahul's present age.
- (x-6)/18 = Rahul's present age
3. Denis is 2 years older than Rahul.
- Denis's age = Rahul's age + 2
- Denis's age = (x-6)/18 + 2
4. Denis's age is given as 5 years.
- (x-6)/18 + 2 = 5
- (x-6)/18 = 3
- x-6 = 54 (Taking LCM of 18 and 3 as 18)
- x = 60
Therefore, Ajay's present age is 60 years. (Option B)
- Ajay's present age is x
- When 6 years are subtracted from x and the remainder is divided by 18, Rahul's age is obtained.
- Rahul is 2 years younger than Denis, whose age is 5 years.
To find:
Ajay's present age
Solution:
1. When 6 years are subtracted from Ajay's present age, we get (x-6).
2. When (x-6) is divided by 18, we get Rahul's present age.
- (x-6)/18 = Rahul's present age
3. Denis is 2 years older than Rahul.
- Denis's age = Rahul's age + 2
- Denis's age = (x-6)/18 + 2
4. Denis's age is given as 5 years.
- (x-6)/18 + 2 = 5
- (x-6)/18 = 3
- x-6 = 54 (Taking LCM of 18 and 3 as 18)
- x = 60
Therefore, Ajay's present age is 60 years. (Option B)
The average age of a man and his son is 54 years. The ratio of their ages is 23: 13. What will be the ratio of their ages after 6 years.
- a)10:7
- b)5:3
- c)4:3
- d)3:2
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The average age of a man and his son is 54 years. The ratio of their ages is 23: 13. What will be the ratio of their ages after 6 years.
a)
10:7
b)
5:3
c)
4:3
d)
3:2
e)
None of these
|
Vertex Academy answered |
To find the ratio of their ages after 6 years:
- Let the current ages be 23x and 13x.
avg age =sum/2
sum = avg age x 2
sum = 54x2 =108
- Their sum is 36x (23x + 13x = 36x), and this equals 108 years.
- So, 36x = 108 years, thus x = 3.
- After 6 years, their ages will be 23(3) + 6 = 75 and 13(3) + 6 = 45.
- The ratio of their ages after 6 years is 75:45, which simplifies to 5:3.
- This simplifies further to 5:3, which is the correct answer (Option B).
- Let the current ages be 23x and 13x.
avg age =sum/2
sum = avg age x 2
sum = 54x2 =108
- Their sum is 36x (23x + 13x = 36x), and this equals 108 years.
- So, 36x = 108 years, thus x = 3.
- After 6 years, their ages will be 23(3) + 6 = 75 and 13(3) + 6 = 45.
- The ratio of their ages after 6 years is 75:45, which simplifies to 5:3.
- This simplifies further to 5:3, which is the correct answer (Option B).
If 6 years are subtracted from the present age of Gagan and the remainder is divided by 18,then the present age of his grandson Anup is obtained. If Anup is 2 years younger to Madan whose age is 5 years,then what is Gagan's present age?- a)48 years
- b)60 years
- c)84 years
- d)96 years
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If 6 years are subtracted from the present age of Gagan and the remainder is divided by 18,then the present age of his grandson Anup is obtained. If Anup is 2 years younger to Madan whose age is 5 years,then what is Gagan's present age?
a)
48 years
b)
60 years
c)
84 years
d)
96 years
e)
None of these
|
|
Anaya Patel answered |
The correct option is B.
Let gagan's age be "x".
anup's age = (x-6)/18
madan's age=5 therefore anup's age =3
btp,
(x-6)/18=3
so x=60
Let gagan's age be "x".
anup's age = (x-6)/18
madan's age=5 therefore anup's age =3
btp,
(x-6)/18=3
so x=60
The ratio between the present age of Radha and Seema is 5:4. Four years ago Seema’s age was 24 years. What will be the age of Radha after 5 years.- a)39 years
- b)40 years
- c)32 years
- d)35 years
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio between the present age of Radha and Seema is 5:4. Four years ago Seema’s age was 24 years. What will be the age of Radha after 5 years.
a)
39 years
b)
40 years
c)
32 years
d)
35 years
e)
None of these
|
Anannya Reddy answered |
Radha and seema present age =5x, 4x
4years ago seema age =24
so 4x-4=24
4x=28
x=7 so present age of radha=35 seema =28
so 5years after =35+5=40 so B is the answer
4years ago seema age =24
so 4x-4=24
4x=28
x=7 so present age of radha=35 seema =28
so 5years after =35+5=40 so B is the answer
Ayesha's father was 38 years of age when she was born while her mother was 36 years old when her brother four years younger to her was born. What is the difference between the ages of her parents?- a)2 years
- b)4 years
- c)6 years
- d)8 years
Correct answer is option 'C'. Can you explain this answer?
Ayesha's father was 38 years of age when she was born while her mother was 36 years old when her brother four years younger to her was born. What is the difference between the ages of her parents?
a)
2 years
b)
4 years
c)
6 years
d)
8 years
|
|
Anaya Patel answered |
Mother's age when Ayesha's brother was born = 36 years.
Father's age when Ayesha's brother was born = (38 + 4) years = 42 years.
Required difference = (42 - 36) years = 6 years.Father is aged three times more than his son Ronit. After 8 years, he would be two and a half times of Ronit's age. After further 8 years, how many times would he be of Ronit's age?- a)2 times
- b)
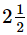times - c)
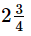times - d)3 times
Correct answer is option 'A'. Can you explain this answer?
Father is aged three times more than his son Ronit. After 8 years, he would be two and a half times of Ronit's age. After further 8 years, how many times would he be of Ronit's age?
a)
2 times
b)
timesc)
timesd)
3 times
|
Preeti Khanna answered |
Let Ronit's present age be x years. Then, father's present age =(x + 3x) years = 4x years.
The ratio between the present ages of Radha and Seema is 5:7. After 8 years Radha’s age will be 28 years. What was Seema’s age 5 years ago.- a)21 years
- b)24 years
- c)28 years
- d)22 years
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
The ratio between the present ages of Radha and Seema is 5:7. After 8 years Radha’s age will be 28 years. What was Seema’s age 5 years ago.
a)
21 years
b)
24 years
c)
28 years
d)
22 years
e)
None of these
|
|
Anaya Patel answered |
The correct option is E.
Let the present age of Radha be 5x So 8 yrs back , i.e, at present she is 20.
this means 5x = 20 => x = 4
Then Seema 's age = 7x = 7*4 = 28yrs.
Five yrs ago , her age was 28 - 5 = 23yrs.
Let the present age of Radha be 5x So 8 yrs back , i.e, at present she is 20.
this means 5x = 20 => x = 4
Then Seema 's age = 7x = 7*4 = 28yrs.
Five yrs ago , her age was 28 - 5 = 23yrs.
On Teacher’s Day, 4800 sweets were to be equally distributed among a certain number of children. But on that particular day 100 children were absent. Hence, each child got four sweets extra. How many children were originally supposed to be there?- a)300
- b)400
- c)540
- d) 500
- e)None of these .
Correct answer is option 'B'. Can you explain this answer?
On Teacher’s Day, 4800 sweets were to be equally distributed among a certain number of children. But on that particular day 100 children were absent. Hence, each child got four sweets extra. How many children were originally supposed to be there?
a)
300
b)
400
c)
540
d)
500
e)
None of these .
|
Tanvi Dey answered |
Let the original number of children be x.
∴ 4800/x-100 - 4800/x = 4
=> 4800((x-x+100)/(x(x-100))) = 4
=> x(x-100) = 1200 * 100
=> x(x-100) = 400(400-100)
=> x = 400
Present ages of Sameer and Anand are in the ratio of 5 : 4 respectively. Three years hence, the ratio of their ages will become 11 : 9 respectively. What is Anand's present age in years?- a)27
- b)24
- c)40
- d)Cannot be determined
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Present ages of Sameer and Anand are in the ratio of 5 : 4 respectively. Three years hence, the ratio of their ages will become 11 : 9 respectively. What is Anand's present age in years?
a)
27
b)
24
c)
40
d)
Cannot be determined
e)
None of these
|
Yash Patel answered |
Let the present ages of Sameer and Anand be 5x years and 4x years respectively.
Two years ago the ratio of ages of A and B was 5:7. Two years hence the ratio of their ages will be 7:9. What is the present age of B.
- a)16 years
- b)14.5 years
- c)12 years
- d)15 years
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Two years ago the ratio of ages of A and B was 5:7. Two years hence the ratio of their ages will be 7:9. What is the present age of B.
a)
16 years
b)
14.5 years
c)
12 years
d)
15 years
e)
None of these
|
|
Aarav Sharma answered |
Given:
The ratio of ages of A and B two years ago = 5:7
The ratio of their ages two years hence = 7:9
To find: Present age of B
Solution:
Let the present ages of A and B be A and B respectively.
According to the given condition,
(A-2)/(B-2) = 5/7 ----(1)
(A+2)/(B+2) = 7/9 ----(2)
Solving the above equations, we get:
A = 22
B = 28
Therefore, the present age of B is 28 years.
Answer: (a) 16 years
The ratio of ages of A and B two years ago = 5:7
The ratio of their ages two years hence = 7:9
To find: Present age of B
Solution:
Let the present ages of A and B be A and B respectively.
According to the given condition,
(A-2)/(B-2) = 5/7 ----(1)
(A+2)/(B+2) = 7/9 ----(2)
Solving the above equations, we get:
A = 22
B = 28
Therefore, the present age of B is 28 years.
Answer: (a) 16 years
The average age of a man and his two twin sons is 30 years. The ratio of the ages of father and one of his sons is 5:2. What is the father’s age- a)50 years
- b)30 years
- c)45 years
- d)20 years
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The average age of a man and his two twin sons is 30 years. The ratio of the ages of father and one of his sons is 5:2. What is the father’s age
a)
50 years
b)
30 years
c)
45 years
d)
20 years
e)
None of these
|
|
Aishwarya Rajput answered |
Let father's age be M and age of twins be 2x
(M + 2x)/3 = 30
M + 2x = 90------------(1)
M/x = 5/2
2M = 5x---------------(2)
Multiply (1) with 2
We get, 2M + 4x = 180--------------(3)
Putting (2) in (3)
5x+4x = 180 => 9x = 180x = 20. [his children are twins so 2x = 40]Since M + 2x = 90M = 90 -40 = 50years
(M + 2x)/3 = 30
M + 2x = 90------------(1)
M/x = 5/2
2M = 5x---------------(2)
Multiply (1) with 2
We get, 2M + 4x = 180--------------(3)
Putting (2) in (3)
5x+4x = 180 => 9x = 180x = 20. [his children are twins so 2x = 40]Since M + 2x = 90M = 90 -40 = 50years
At present, the ratio between the ages of Arun and Deepak is 4 : 3. After 6 years, Arun's age will be 26 years. What is the age of Deepak at present ?- a)12 years
- b)15 years
- c)19 and half
- d)21 years
Correct answer is option 'B'. Can you explain this answer?
At present, the ratio between the ages of Arun and Deepak is 4 : 3. After 6 years, Arun's age will be 26 years. What is the age of Deepak at present ?
a)
12 years
b)
15 years
c)
19 and half
d)
21 years
|
|
Anaya Patel answered |
Let the present ages of Arun and Deepak be 4x years and 3x years respectively. Then,
4x + 6 = 26 
4x = 20
4x = 20x = 5.
Deepak's age = 3x = 15 years.The sum of the present ages of a father and his son is 60 years. Six years ago, father's age was five times the age of the son. After 6 years, son's age will be:- a)12 years
- b)14 years
- c)18 years
- d)20 years
Correct answer is option 'D'. Can you explain this answer?
The sum of the present ages of a father and his son is 60 years. Six years ago, father's age was five times the age of the son. After 6 years, son's age will be:
a)
12 years
b)
14 years
c)
18 years
d)
20 years
|
|
Aarav Sharma answered |
The Problem:
The sum of the present ages of a father and his son is 60 years. Six years ago, the father's age was five times the age of the son. After 6 years, what will be the son's age?
Given Information:
- The present sum of the father and son's ages is 60 years.
- Six years ago, the father's age was five times the age of the son.
Let's solve the problem step by step:
Step 1: Define Variables
Let's assume the present age of the son is 'x' years.
Therefore, the present age of the father will be (60 - x) years.
Step 2: Translate the Given Information into Equations
According to the problem, six years ago, the father's age was five times the age of the son.
So, six years ago, the father's age would be (60 - x - 6) years, and the son's age would be (x - 6) years.
Step 3: Set up Equations
According to the given information, the father's age six years ago was five times the son's age six years ago.
Therefore, we can set up the equation: (60 - x - 6) = 5(x - 6).
Step 4: Solve the Equation
Let's solve the equation we set up in the previous step:
(60 - x - 6) = 5(x - 6)
54 - x = 5x - 30
4x = 84
x = 21
Step 5: Find the Son's Age After 6 Years
To find the son's age after 6 years, we need to add 6 to the current age of the son.
Son's age after 6 years = 21 + 6 = 27 years.
Conclusion:
After 6 years, the son's age will be 27 years. Therefore, the correct answer is option 'D' (20 years).
The sum of the present ages of a father and his son is 60 years. Six years ago, the father's age was five times the age of the son. After 6 years, what will be the son's age?
Given Information:
- The present sum of the father and son's ages is 60 years.
- Six years ago, the father's age was five times the age of the son.
Let's solve the problem step by step:
Step 1: Define Variables
Let's assume the present age of the son is 'x' years.
Therefore, the present age of the father will be (60 - x) years.
Step 2: Translate the Given Information into Equations
According to the problem, six years ago, the father's age was five times the age of the son.
So, six years ago, the father's age would be (60 - x - 6) years, and the son's age would be (x - 6) years.
Step 3: Set up Equations
According to the given information, the father's age six years ago was five times the son's age six years ago.
Therefore, we can set up the equation: (60 - x - 6) = 5(x - 6).
Step 4: Solve the Equation
Let's solve the equation we set up in the previous step:
(60 - x - 6) = 5(x - 6)
54 - x = 5x - 30
4x = 84
x = 21
Step 5: Find the Son's Age After 6 Years
To find the son's age after 6 years, we need to add 6 to the current age of the son.
Son's age after 6 years = 21 + 6 = 27 years.
Conclusion:
After 6 years, the son's age will be 27 years. Therefore, the correct answer is option 'D' (20 years).
Q is as much younger than R as he is older than T. If the sum of the ages of R and T is 50 years, what is definitely the difference between R and Q's age?- a)1 year
- b)2 years
- c)25 years
- d)Data inadequate
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Q is as much younger than R as he is older than T. If the sum of the ages of R and T is 50 years, what is definitely the difference between R and Q's age?
a)
1 year
b)
2 years
c)
25 years
d)
Data inadequate
e)
None of these
|
|
Aarav Sharma answered |
Given Information:
- Q is as much younger than R as he is older than T.
- The sum of the ages of R and T is 50 years.
To find:
- The definite difference between R and Q's age.
Let's assume Q's age as x years.
According to the given information, the age difference between Q and R is the same as the age difference between Q and T.
Age difference between Q and R: x - T
Age difference between Q and T: R - x
According to the given information, the sum of R and T's ages is 50 years.
Therefore, we can write the equation:
R + T = 50
Solving the Equations:
From the equation R + T = 50, we can express T in terms of R:
T = 50 - R
Substituting the value of T in the equation R - x = x - T, we get:
R - x = x - (50 - R)
R - x = x + R - 50
2R - 50 = 2x
2R = 2x + 50
R = x + 25
The difference between R and Q's age is given by:
Difference = R - Q
Substituting the values of R and Q, we get:
Difference = (x + 25) - x
Difference = 25
Therefore, the definite difference between R and Q's age is 25 years.
- Q is as much younger than R as he is older than T.
- The sum of the ages of R and T is 50 years.
To find:
- The definite difference between R and Q's age.
Let's assume Q's age as x years.
According to the given information, the age difference between Q and R is the same as the age difference between Q and T.
Age difference between Q and R: x - T
Age difference between Q and T: R - x
According to the given information, the sum of R and T's ages is 50 years.
Therefore, we can write the equation:
R + T = 50
Solving the Equations:
From the equation R + T = 50, we can express T in terms of R:
T = 50 - R
Substituting the value of T in the equation R - x = x - T, we get:
R - x = x - (50 - R)
R - x = x + R - 50
2R - 50 = 2x
2R = 2x + 50
R = x + 25
The difference between R and Q's age is given by:
Difference = R - Q
Substituting the values of R and Q, we get:
Difference = (x + 25) - x
Difference = 25
Therefore, the definite difference between R and Q's age is 25 years.
A father said to his son, “At the time of your birth, I was as old as you are at present”. If father’s age is 38 years now the sons age 5 years back was- a)14 years
- b)19 years
- c)33 years
- d)38 years
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A father said to his son, “At the time of your birth, I was as old as you are at present”. If father’s age is 38 years now the sons age 5 years back was
a)
14 years
b)
19 years
c)
33 years
d)
38 years
e)
None of these
|
|
Prani Garg answered |
HERE IS YOUR ANSWER.
Let the present age of son= x
At the time of birth of son,father age = x
So after x yrs i.e. at present age of father= 38
38=x+x
x= 38÷2= 19
So the present age of son is 19
Age of son before 5 yrs= 19-5= 14 yrs.
HOPE IT HELPS.
Let the present age of son= x
At the time of birth of son,father age = x
So after x yrs i.e. at present age of father= 38
38=x+x
x= 38÷2= 19
So the present age of son is 19
Age of son before 5 yrs= 19-5= 14 yrs.
HOPE IT HELPS.
The age of father 10 years ago was thrice the age of his son. Ten years hence, father's age will be twice that of his son. The ratio of their present ages is:- a)5 : 2
- b)7 : 3
- c)9 : 2
- d)13 : 4
Correct answer is option 'B'. Can you explain this answer?
The age of father 10 years ago was thrice the age of his son. Ten years hence, father's age will be twice that of his son. The ratio of their present ages is:
a)
5 : 2
b)
7 : 3
c)
9 : 2
d)
13 : 4
|
Sagar Sharma answered |
Given Information:
- 10 years ago, the father's age was thrice the age of his son.
- 10 years hence, the father's age will be twice that of his son.
Let's Solve the Problem:
Let the present age of the son be S and the present age of the father be F.
- According to the first condition, 10 years ago:
F - 10 = 3(S - 10) (Father's age 10 years ago was thrice his son's age)
F - 10 = 3S - 30
F = 3S - 20
- According to the second condition, 10 years hence:
F + 10 = 2(S + 10) (Father's age 10 years hence will be twice his son's age)
F + 10 = 2S + 20
F = 2S + 10
- Equating the two expressions for F:
3S - 20 = 2S + 10
S = 30
- Substituting S = 30 into F = 2S + 10:
F = 2(30) + 10
F = 70
Therefore, the present ages of the father and son are 70 and 30 respectively.
Ratio of their present ages:
70:30
7:3
Therefore, the ratio of their present ages is 7:3.
Present age of X and Y are in the ratio 5:6 respectively. Seven years hence this ratio will become 6:7 respectively. Wat is X’s present age?- a)35
- b)42
- c)49
- d)Cannot be determined
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Present age of X and Y are in the ratio 5:6 respectively. Seven years hence this ratio will become 6:7 respectively. Wat is X’s present age?
a)
35
b)
42
c)
49
d)
Cannot be determined
e)
None of these
|
Shivu D B answered |
Let
X present age is 5a---(1)
Y present age is 6a
After 7 years
5a+7/6a+7=6/7
cross multiply
So
7(5a+7)=6(6a+7)
35a+49=36a+42
a=7--(2)
substitute (2) in (1)
X present age is 5(7)= 35
X present age is 5a---(1)
Y present age is 6a
After 7 years
5a+7/6a+7=6/7
cross multiply
So
7(5a+7)=6(6a+7)
35a+49=36a+42
a=7--(2)
substitute (2) in (1)
X present age is 5(7)= 35
A is two years older than B who is twice as old as C. If the total of the ages of A, B and C be 27, the how old is B?- a)7
- b)8
- c)9
- d)10
- e)11
Correct answer is option 'D'. Can you explain this answer?
A is two years older than B who is twice as old as C. If the total of the ages of A, B and C be 27, the how old is B?
a)
7
b)
8
c)
9
d)
10
e)
11
|
Nikita Singh answered |
Let C's age be x years. Then, B's age = 2x years. A's age = (2x + 2) years.
(2x + 2) + 2x + x = 27
5x = 25
x = 5.Hence, B's age = 2x = 10 years.
At present, the ratio between the ages of Shekhar and Shobha is 4 : 3 . After 6 years, Shekhar's age will be 26 years. Find out the age of Shobha at present?- a)15 years
- b)14 years
- c)13 years
- d)12 years
- e)11 years
Correct answer is option 'A'. Can you explain this answer?
At present, the ratio between the ages of Shekhar and Shobha is 4 : 3 . After 6 years, Shekhar's age will be 26 years. Find out the age of Shobha at present?
a)
15 years
b)
14 years
c)
13 years
d)
12 years
e)
11 years
|
Mihir Nambiar answered |
After 6 years, Shekhar's age will be 26 years
Therefore, Present age of Shekhar = 26 − 6 = 20
Let present age of Shobha = x
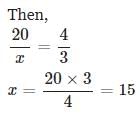
Therefore, Present age of Shekhar = 26 − 6 = 20
Let present age of Shobha = x
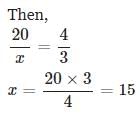
The product of the ages of Syam and Sunil is 240 . If twice the age of Sunil is more than Syam's age by 4 years, what is Sunil's age?- a)16
- b)14
- c)12
- d)10
- e)8
Correct answer is option 'C'. Can you explain this answer?
The product of the ages of Syam and Sunil is 240 . If twice the age of Sunil is more than Syam's age by 4 years, what is Sunil's age?
a)
16
b)
14
c)
12
d)
10
e)
8
|
Pallavi Sharma answered |
Let age of Sunil = x
and age of Syam = y
xy = 240 ⋯ ( 1 )
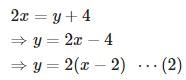
Substituting equation ( 2 ) in equation ( 1 ) . We get
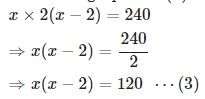
We got a quadratic equation to solve.
Always time is precious and objective tests measure not only how accurate you are but also how fast you are. We can solve this quadratic equation in the traditional way. But it is more easy to substitute the values given in the choices in the quadratic equation (equation 3 ) and see which choice satisfy the equation.
Here, option A is 10 . If we substitute that value in the quadratic equation, x ( x − 2 ) = 10 × 8 which is not equal to 120
Now try option B which is 12 . If we substitute that value in the quadratic equation, x ( x − 2 ) = 12 × 10 = 120 . See, we got that x = 12
Hence Sunil's age = 12
(Or else, we can solve the quadratic equation by factorization as,
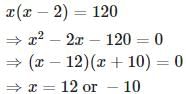
Since x is age and cannot be negative, x = 12
Or by using quadratic formula as
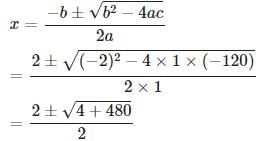
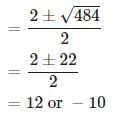
Since age is positive, x = 12
and age of Syam = y
xy = 240 ⋯ ( 1 )
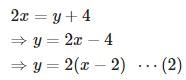
Substituting equation ( 2 ) in equation ( 1 ) . We get
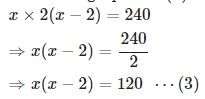
We got a quadratic equation to solve.
Always time is precious and objective tests measure not only how accurate you are but also how fast you are. We can solve this quadratic equation in the traditional way. But it is more easy to substitute the values given in the choices in the quadratic equation (equation 3 ) and see which choice satisfy the equation.
Here, option A is 10 . If we substitute that value in the quadratic equation, x ( x − 2 ) = 10 × 8 which is not equal to 120
Now try option B which is 12 . If we substitute that value in the quadratic equation, x ( x − 2 ) = 12 × 10 = 120 . See, we got that x = 12
Hence Sunil's age = 12
(Or else, we can solve the quadratic equation by factorization as,
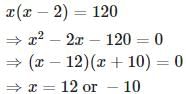
Since x is age and cannot be negative, x = 12
Or by using quadratic formula as
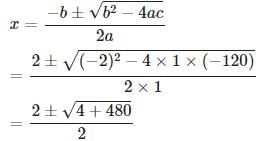
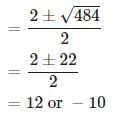
Since age is positive, x = 12
Sandeep's age after six years will be three-seventh of his father's age. Ten years ago the ratio of their ages was 1 : 5 . What is Sandeep's father's age at present?- a)30 years
- b)40 years
- c)50 years
- d)60 years
- e)65 years
Correct answer is option 'C'. Can you explain this answer?
Sandeep's age after six years will be three-seventh of his father's age. Ten years ago the ratio of their ages was 1 : 5 . What is Sandeep's father's age at present?
a)
30 years
b)
40 years
c)
50 years
d)
60 years
e)
65 years
|
|
Sahana Mehta answered |
Let the age of Sandeep and his father before 10 years be x and 5 x respectively.
Given that Sandeep's age after six years will be three-seventh of his father's age
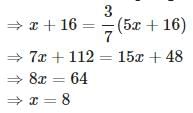
Sandeep's father's present age
= 5 x + 10 = 5 × 8 + 10 = 50
Given that Sandeep's age after six years will be three-seventh of his father's age
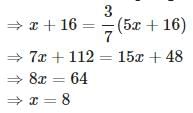
Sandeep's father's present age
= 5 x + 10 = 5 × 8 + 10 = 50
The present ages of three persons in proportions 4 : 7 : 9. Eight years ago, the sum of their ages was 56. Find their present ages (in years).- a)8, 20, 28
- b)16, 28, 36
- c)20, 35, 45
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The present ages of three persons in proportions 4 : 7 : 9. Eight years ago, the sum of their ages was 56. Find their present ages (in years).
a)
8, 20, 28
b)
16, 28, 36
c)
20, 35, 45
d)
None of these
|
Ravi Singh answered |
Let their present ages be 4x, 7x and 9x years respectively.
Then, (4x - 8) + (7x - 8) + (9x - 8) = 56
20x = 80
x = 4.
Their present ages are 4x = 16 years, 7x = 28 years and 9x = 36 years respectively.5 years ago the ratio of the age of A to that of B was 7 : 6. 20 years hence, the ratio of the age of A to that of B will be 22 : 21. What is the sum of their current ages?- a)30 years
- b)31.67 years
- c)33.33 years
- d)36 years
Correct answer is option 'B'. Can you explain this answer?
5 years ago the ratio of the age of A to that of B was 7 : 6. 20 years hence, the ratio of the age of A to that of B will be 22 : 21. What is the sum of their current ages?
a)
30 years
b)
31.67 years
c)
33.33 years
d)
36 years
|
EduRev SSC CGL answered |
Let the age of A 5 years ago = 7x
The age of B 5 years ago = 6x
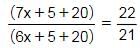
147x + 525 = 132x + 550
15x = 25
So the answer = (7x + 5 + 6x + 5) = 13x + 10
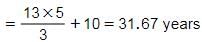
Hence, Option B is correct.
The age of B 5 years ago = 6x
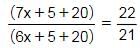
147x + 525 = 132x + 550
15x = 25
So the answer = (7x + 5 + 6x + 5) = 13x + 10
Hence, Option B is correct.
The ages of two persons differ by 16 years. 6 years ago, the elder one was 3 times as old as the younger one. What are their present ages of the elder person?- a)10
- b)20
- c)30
- d)40
- e)50
Correct answer is option 'C'. Can you explain this answer?
The ages of two persons differ by 16 years. 6 years ago, the elder one was 3 times as old as the younger one. What are their present ages of the elder person?
a)
10
b)
20
c)
30
d)
40
e)
50
|
|
Abhishek Choudhury answered |
Let present age of the elder person = x and
present age of the younger person = x − 16
present age of the younger person = x − 16
My brother is 3 years elder to me. My father was 28 years of age when my sister was born while my mother was 26 years of age when I was born. If my sister was 4 years of age when my brother was born, then what was the age of my father when my brother was born?- a)35 years
- b)34 years
- c)33 years
- d)32 years
- e)31 years
Correct answer is option 'D'. Can you explain this answer?
My brother is 3 years elder to me. My father was 28 years of age when my sister was born while my mother was 26 years of age when I was born. If my sister was 4 years of age when my brother was born, then what was the age of my father when my brother was born?
a)
35 years
b)
34 years
c)
33 years
d)
32 years
e)
31 years
|
|
Arka Basu answered |
Let my age = x
Then
My brother's age = x + 3
My mother's age = x + 26
My sister's age = ( x + 3 ) + 4 = x + 7 My father's age = ( x + 7 ) + 28 = x + 35
Age of my father when my brother was born = x + 35 − ( x + 3 ) = 32
Then
My brother's age = x + 3
My mother's age = x + 26
My sister's age = ( x + 3 ) + 4 = x + 7 My father's age = ( x + 7 ) + 28 = x + 35
Age of my father when my brother was born = x + 35 − ( x + 3 ) = 32
The present ages of A,B and C are in proportions 4 : 7 : 9 . Eight years ago, the sum of their ages was 56 . What are their present ages (in years)?- a)16 , 30 , 38
- b)16 , 30 , 40
- c)16 , 28 , 40
- d)16 , 28 , 36
- e)Insufficient data
Correct answer is option 'D'. Can you explain this answer?
The present ages of A,B and C are in proportions 4 : 7 : 9 . Eight years ago, the sum of their ages was 56 . What are their present ages (in years)?
a)
16 , 30 , 38
b)
16 , 30 , 40
c)
16 , 28 , 40
d)
16 , 28 , 36
e)
Insufficient data
|
|
Chirag Sen answered |
Let present age of A,B and C be 4 x , 7 x and 9 x respectively.
(4x−8)+(7x−8)+(9x−8)=56
⇒20x=80
⇒x=4
Hence present age of A, B and C are
4 × 4 , 7 × 4 and 9 × 4 respectively.
i.e., 16 , 28 and 36 respectively.
(4x−8)+(7x−8)+(9x−8)=56
⇒20x=80
⇒x=4
Hence present age of A, B and C are
4 × 4 , 7 × 4 and 9 × 4 respectively.
i.e., 16 , 28 and 36 respectively.
The average age of A, B, C and D is 20 years and their ages are in Arithmetic progression. If the youngest among them is 15 years old, what is the age of the oldest one?- a)15 years
- b)20 years
- c)21 years
- d)25 years
Correct answer is option 'D'. Can you explain this answer?
The average age of A, B, C and D is 20 years and their ages are in Arithmetic progression. If the youngest among them is 15 years old, what is the age of the oldest one?
a)
15 years
b)
20 years
c)
21 years
d)
25 years
|
G.K Academy answered |
Since their ages are in Arithmetic progression, the average age of the youngest and oldest must be 20 years.
15 + The age of the oldest one = 20 × 2
The age of the oldest one = 40 – 15 = 25 years
Hence, Option D is correct.
15 + The age of the oldest one = 20 × 2
The age of the oldest one = 40 – 15 = 25 years
Hence, Option D is correct.
The ratio of the ages of A, B and C is 2 : 3 : 5 respectively. The age of A is what percentage of the difference between the ages of B and C?- a)60
- b)75
- c)80
- d)100
Correct answer is option 'D'. Can you explain this answer?
The ratio of the ages of A, B and C is 2 : 3 : 5 respectively. The age of A is what percentage of the difference between the ages of B and C?
a)
60
b)
75
c)
80
d)
100
|
Ishaan Roy answered |
Understanding the Age Ratio
The ages of A, B, and C are in the ratio 2 : 3 : 5. This means we can represent their ages as:
- Age of A = 2x
- Age of B = 3x
- Age of C = 5x
Here, 'x' is a common multiplier for their ages.
Calculating the Difference Between Ages of B and C
To find the difference between the ages of B and C:
- Difference between ages of B and C = Age of C - Age of B
- Difference = 5x - 3x = 2x
Calculating Age of A as a Percentage of the Difference
Next, we need to find what percentage the age of A is of the difference calculated above:
- Age of A = 2x
- Difference = 2x
Now, we can calculate the percentage:
\[
\text{Percentage} = \left( \frac{\text{Age of A}}{\text{Difference}} \right) \times 100
\]
Substituting the values:
\[
\text{Percentage} = \left( \frac{2x}{2x} \right) \times 100 = 1 \times 100 = 100\%
\]
Conclusion
The age of A is 100% of the difference between the ages of B and C. Therefore, the correct answer is option 'D'.
This demonstrates how the ratio of their ages directly correlates to the percentage calculation based on the differences in their ages.
The ages of A, B, and C are in the ratio 2 : 3 : 5. This means we can represent their ages as:
- Age of A = 2x
- Age of B = 3x
- Age of C = 5x
Here, 'x' is a common multiplier for their ages.
Calculating the Difference Between Ages of B and C
To find the difference between the ages of B and C:
- Difference between ages of B and C = Age of C - Age of B
- Difference = 5x - 3x = 2x
Calculating Age of A as a Percentage of the Difference
Next, we need to find what percentage the age of A is of the difference calculated above:
- Age of A = 2x
- Difference = 2x
Now, we can calculate the percentage:
\[
\text{Percentage} = \left( \frac{\text{Age of A}}{\text{Difference}} \right) \times 100
\]
Substituting the values:
\[
\text{Percentage} = \left( \frac{2x}{2x} \right) \times 100 = 1 \times 100 = 100\%
\]
Conclusion
The age of A is 100% of the difference between the ages of B and C. Therefore, the correct answer is option 'D'.
This demonstrates how the ratio of their ages directly correlates to the percentage calculation based on the differences in their ages.
Sachin's age after 15 years will be 5 times his age 5 years back. Find out the present age of Sachin?- a)10 years
- b)11 years
- c)12 years
- d)13 years
- e)14 years
Correct answer is option 'A'. Can you explain this answer?
Sachin's age after 15 years will be 5 times his age 5 years back. Find out the present age of Sachin?
a)
10 years
b)
11 years
c)
12 years
d)
13 years
e)
14 years
|
|
Gitanjali Kumar answered |
Let present age of Sachin = x . Then,
( x + 15 ) = 5 ( x − 5 )
⇒ 4 x = 40
⇒ x = 10
( x + 15 ) = 5 ( x − 5 )
⇒ 4 x = 40
⇒ x = 10
The sum of ages of 5 children born at the intervals of 3 years each is 50 years. What is the age of the youngest child?- a)4 years
- b)8 years
- c)10 years
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The sum of ages of 5 children born at the intervals of 3 years each is 50 years. What is the age of the youngest child?
a)
4 years
b)
8 years
c)
10 years
d)
None of these
|
|
Target Study Academy answered |
Let the ages of children be x, (x + 3), (x + 6), (x + 9) and (x + 12) years.
Then, x + (x + 3) + (x + 6) + (x + 9) + (x + 12) = 50
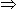5x = 20
x = 4.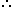
Age of the youngest child = x = 4 years.The total age of A and B is 12 years more than the total age of B and C. C is how many year younger than A?- a)10
- b)11
- c)12
- d)13
- e)14
Correct answer is option 'C'. Can you explain this answer?
The total age of A and B is 12 years more than the total age of B and C. C is how many year younger than A?
a)
10
b)
11
c)
12
d)
13
e)
14
|
|
Manasa Kulkarni answered |
Given that, A + B = 12 + B + C
⇒ A - C = 12
Therefore, C is younger than A by 12 years
One year ago, the ratio of Sooraj's and Vimal's age was 6 : 7 respectively. Four years hence, this ratio would become 7 : 8 . How old is Vimal?- a)32
- b)34
- c)36
- d)38
- e)40
Correct answer is option 'C'. Can you explain this answer?
One year ago, the ratio of Sooraj's and Vimal's age was 6 : 7 respectively. Four years hence, this ratio would become 7 : 8 . How old is Vimal?
a)
32
b)
34
c)
36
d)
38
e)
40
|
|
Sandeep Mehra answered |
Let the age of Sooraj and Vimal, 1 year ago, be 6 x and 7 x respectively.
Given that, four years hence, this ratio would become 7 : 8
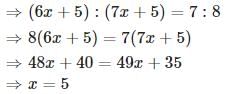
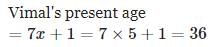
Given that, four years hence, this ratio would become 7 : 8
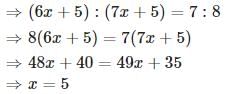
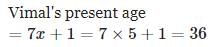
A is as much younger than B and he is older than C. If the sum of the ages of B and C is 50 years, what is definitely the difference between B and A's age?- a)Data inadequate
- b)3 years
- c)2 years
- d)5 years
- e)4 years
Correct answer is option 'A'. Can you explain this answer?
A is as much younger than B and he is older than C. If the sum of the ages of B and C is 50 years, what is definitely the difference between B and A's age?
a)
Data inadequate
b)
3 years
c)
2 years
d)
5 years
e)
4 years
|
|
Prateek Gupta answered |
Age of C < Age of A < Age of B
Given that sum of the ages of B and C is 50 years.
Now we need to find out (B's age - A's age). But this cannot be determined with the given data.
Sobha's father was 38 years of age when she was born while her mother was 36 years old when her brother four years younger to her was born. What is the difference between the ages of her parents?- a)6 years
- b)5 years
- c)4 years
- d)3 years
- e)7 years
Correct answer is option 'A'. Can you explain this answer?
Sobha's father was 38 years of age when she was born while her mother was 36 years old when her brother four years younger to her was born. What is the difference between the ages of her parents?
a)
6 years
b)
5 years
c)
4 years
d)
3 years
e)
7 years
|
|
Sonal Banerjee answered |
Let Sobha's age = x and
her brother's age = x − 4
Sobha's father's age = x + 38
Sobha's mother's age = ( x − 4 ) + 36 = x + 32
Sobha's father's age - Sobha's mother's age
=(x+38)−(x+32)=6
her brother's age = x − 4
Sobha's father's age = x + 38
Sobha's mother's age = ( x − 4 ) + 36 = x + 32
Sobha's father's age - Sobha's mother's age
=(x+38)−(x+32)=6
The age of father 10 years ago was thrice the age of his son. Ten years hence, father's age will be twice that of his son. What is the ratio of their present ages?- a)7 : 3
- b)3 : 7
- c)9 : 4
- d)4 : 9
- e)7: 4
Correct answer is option 'A'. Can you explain this answer?
The age of father 10 years ago was thrice the age of his son. Ten years hence, father's age will be twice that of his son. What is the ratio of their present ages?
a)
7 : 3
b)
3 : 7
c)
9 : 4
d)
4 : 9
e)
7: 4
|
|
Sagar Sharma answered |
Given:
- Age of the father 10 years ago was thrice the age of his son.
- Age of the father 10 years hence will be twice that of his son.
To find:
The ratio of their present ages.
Solution:
Let's assume the present age of the son as 'x' years.
Therefore, the present age of the father will be '3x' years.
10 years ago:
Son's age = x - 10
Father's age = 3x - 10
According to the given condition, the age of the father 10 years ago was thrice the age of his son.
So, we have the equation:
3x - 10 = 3(x - 10)
3x - 10 = 3x - 30
3x - 3x = -30 + 10
0 = -20
This equation does not hold true, which means our assumption is incorrect.
Let's assume the present age of the father as 'y' years.
Therefore, the present age of the son will be 'y/3' years.
10 years ago:
Son's age = y/3 - 10
Father's age = y - 10
According to the given condition, the age of the father 10 years ago was thrice the age of his son.
So, we have the equation:
y - 10 = 3(y/3 - 10)
y - 10 = y - 30
y - y = -30 + 10
0 = -20
This equation does not hold true, which means our assumption is incorrect.
Let's assume the present age of the son as 'a' years.
Therefore, the present age of the father will be '2a' years.
10 years ago:
Son's age = a - 10
Father's age = 2a - 10
According to the given condition, the age of the father 10 years ago was thrice the age of his son.
So, we have the equation:
2a - 10 = 3(a - 10)
2a - 10 = 3a - 30
2a - 3a = -30 + 10
-a = -20
a = 20
Therefore, the present age of the son is 20 years.
And the present age of the father is 2a = 2 * 20 = 40 years.
Ratio of their present ages:
Son's age : Father's age
20 : 40
Simplifying the ratio by dividing both terms by 20, we get:
1 : 2
Therefore, the ratio of their present ages is 1 : 2, which is equivalent to 7 : 14.
Hence, option A is the correct answer.
- Age of the father 10 years ago was thrice the age of his son.
- Age of the father 10 years hence will be twice that of his son.
To find:
The ratio of their present ages.
Solution:
Let's assume the present age of the son as 'x' years.
Therefore, the present age of the father will be '3x' years.
10 years ago:
Son's age = x - 10
Father's age = 3x - 10
According to the given condition, the age of the father 10 years ago was thrice the age of his son.
So, we have the equation:
3x - 10 = 3(x - 10)
3x - 10 = 3x - 30
3x - 3x = -30 + 10
0 = -20
This equation does not hold true, which means our assumption is incorrect.
Let's assume the present age of the father as 'y' years.
Therefore, the present age of the son will be 'y/3' years.
10 years ago:
Son's age = y/3 - 10
Father's age = y - 10
According to the given condition, the age of the father 10 years ago was thrice the age of his son.
So, we have the equation:
y - 10 = 3(y/3 - 10)
y - 10 = y - 30
y - y = -30 + 10
0 = -20
This equation does not hold true, which means our assumption is incorrect.
Let's assume the present age of the son as 'a' years.
Therefore, the present age of the father will be '2a' years.
10 years ago:
Son's age = a - 10
Father's age = 2a - 10
According to the given condition, the age of the father 10 years ago was thrice the age of his son.
So, we have the equation:
2a - 10 = 3(a - 10)
2a - 10 = 3a - 30
2a - 3a = -30 + 10
-a = -20
a = 20
Therefore, the present age of the son is 20 years.
And the present age of the father is 2a = 2 * 20 = 40 years.
Ratio of their present ages:
Son's age : Father's age
20 : 40
Simplifying the ratio by dividing both terms by 20, we get:
1 : 2
Therefore, the ratio of their present ages is 1 : 2, which is equivalent to 7 : 14.
Hence, option A is the correct answer.
Kiran is younger than Bineesh by 7 years and their ages are in the respective ratio of 7 : 9. How old is Kiran?- a)25
- b)24.5
- c)24
- d)23.5
- e)25.5
Correct answer is option 'B'. Can you explain this answer?
Kiran is younger than Bineesh by 7 years and their ages are in the respective ratio of 7 : 9. How old is Kiran?
a)
25
b)
24.5
c)
24
d)
23.5
e)
25.5
|
|
Aarav Sharma answered |
Given, Kiran is younger than Bineesh by 7 years.
Let Kiran's age be x and Bineesh's age be y.
Then, y = x + 7 (as Kiran is younger by 7 years)
Their ages are in the respective ratio of 7:9.
Therefore, x:y = 7:9
We can express y in terms of x as follows:
x:y = 7:9
x:(x+7) = 7:9
9x = 7x + 63
2x = 63
x = 31.5
Therefore, Kiran's age is 31.5 years.
The answer given in the options is in decimal form, so we need to round off the answer to the nearest half.
31.5 is between 31 and 32, so the nearest half is 31.5 itself.
Hence, the correct answer is option (b) 24.5.
Let Kiran's age be x and Bineesh's age be y.
Then, y = x + 7 (as Kiran is younger by 7 years)
Their ages are in the respective ratio of 7:9.
Therefore, x:y = 7:9
We can express y in terms of x as follows:
x:y = 7:9
x:(x+7) = 7:9
9x = 7x + 63
2x = 63
x = 31.5
Therefore, Kiran's age is 31.5 years.
The answer given in the options is in decimal form, so we need to round off the answer to the nearest half.
31.5 is between 31 and 32, so the nearest half is 31.5 itself.
Hence, the correct answer is option (b) 24.5.
The sum of the present ages of a son and his father is 60 years. Six years ago, father's age was five times the age of the son. After 6 years, what will be son's age?- a)23 years
- b)22 years
- c)21 years
- d)20 years
- e)24 years
Correct answer is option 'D'. Can you explain this answer?
The sum of the present ages of a son and his father is 60 years. Six years ago, father's age was five times the age of the son. After 6 years, what will be son's age?
a)
23 years
b)
22 years
c)
21 years
d)
20 years
e)
24 years
|
|
Prateek Gupta answered |
Let the present age of the son = x Then, present age of the father = ( 60 − x ) Six years ago father's age was 5 times the age of the son
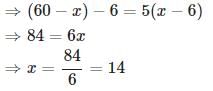
Son's age after 6 years = x + 6 = 14 + 6 = 20
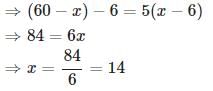
Son's age after 6 years = x + 6 = 14 + 6 = 20
Chapter doubts & questions for Problem on Ages - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Problem on Ages - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup