All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of Time and Work for CDS Exam
Charlie and Alan run a race between points A and B, 5 km apart. Charlie starts at 9 a.m. from A at a speed of 5 km/hr, reaches B, and returns to A at the same speed. Alan starts at 9:45 a.m. from A at a speed of 10 km/hr, reaches B and comes back to A at the same speed. At what time do Charlie and Alan first meet each other?
- a)10 a.m.
- b)10:20 a.m.
- c)10:10 a.m
- d)10:30 a.m.
Correct answer is option 'C'. Can you explain this answer?
Charlie and Alan run a race between points A and B, 5 km apart. Charlie starts at 9 a.m. from A at a speed of 5 km/hr, reaches B, and returns to A at the same speed. Alan starts at 9:45 a.m. from A at a speed of 10 km/hr, reaches B and comes back to A at the same speed. At what time do Charlie and Alan first meet each other?
a)
10 a.m.
b)
10:20 a.m.
c)
10:10 a.m
d)
10:30 a.m.
|
|
Madhujya Chutia answered |
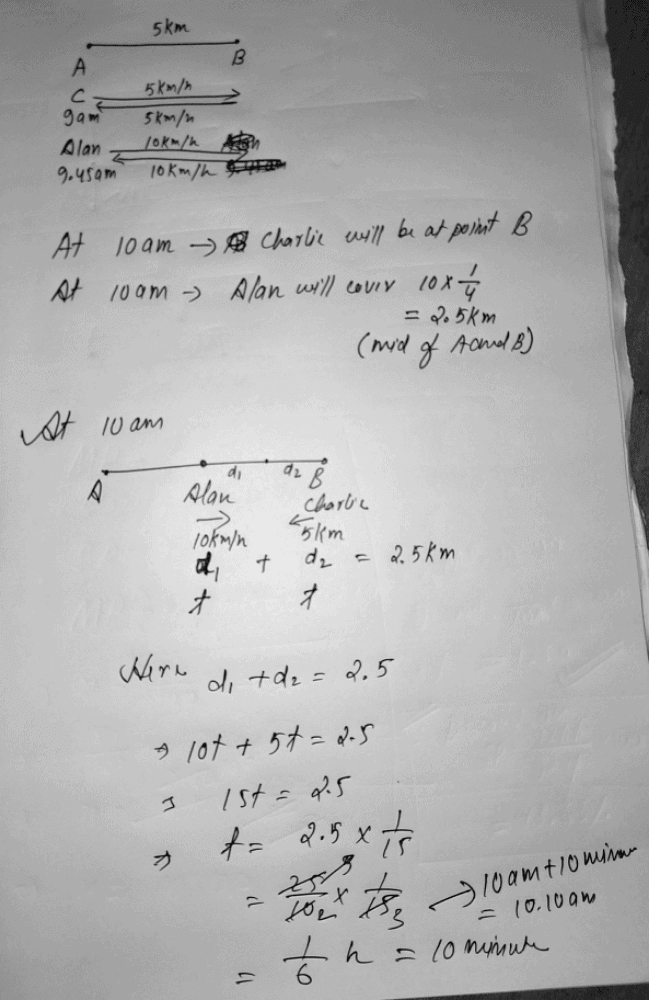
A can type 100 letters in 5 minutes. B and C typing together can type 50 letters in 2 minutes. If all of them working together then can type 90 letters in how many minutes?
- a)2 minutes
- b)4 minutes
- c)5 minutes
- d)10 minutes
- e)None
Correct answer is option 'A'. Can you explain this answer?
A can type 100 letters in 5 minutes. B and C typing together can type 50 letters in 2 minutes. If all of them working together then can type 90 letters in how many minutes?
a)
2 minutes
b)
4 minutes
c)
5 minutes
d)
10 minutes
e)
None
|
|
Aisha Gupta answered |
(1/5+1/4)
20/9*90/100 = 2
20/9*90/100 = 2
P can do a work in the same time in which Q and R together can do it. If P and Q work together, the work can be completed in 10 days. R alone needs 50 days to complete the same work. then Q alone can do it in
- a)30 days
- b)25 days
- c)20 days
- d)15 days
Correct answer is option 'B'. Can you explain this answer?
a)
30 days
b)
25 days
c)
20 days
d)
15 days

|
Future Foundation Institute answered |
Let distance between the two places = d km
Let total time taken by faster horse = t hr
⇒ Total time taken by slower horse = (t + 5) hr,
Let total time taken by faster horse = t hr
⇒ Total time taken by slower horse = (t + 5) hr,
Therefore,
speed of the faster horse = d/t km/hr
speed of the slower horse = d/(t + 5) km/hr
The two horses meet each other in 3 hour 20 min i.e. in 3(1/3) hr = 10/3 hr
In this time, total distance travelled by both the horses together is d.
speed of the faster horse = d/t km/hr
speed of the slower horse = d/(t + 5) km/hr
The two horses meet each other in 3 hour 20 min i.e. in 3(1/3) hr = 10/3 hr
In this time, total distance travelled by both the horses together is d.
∴ d/(t+5) * 10/3 + d/t * 10/3 = d
⇒ 10/(3(t+5)) + 10/3t = 1
⇒ 10t + 10(t+5) = 3t(t+5)
⇒ 20t + 50 = 3t2 + 15t
⇒ 3t2 − 5t − 50 = 0
⇒ 3t2 + 10t − 15t − 50 = 0
⇒ t(3t + 10) − 5(3t + 10) = 0
⇒ (3t + 10)(t − 5) = 0
⇒ t = 5 (ignoring -ve value)
⇒ 10/(3(t+5)) + 10/3t = 1
⇒ 10t + 10(t+5) = 3t(t+5)
⇒ 20t + 50 = 3t2 + 15t
⇒ 3t2 − 5t − 50 = 0
⇒ 3t2 + 10t − 15t − 50 = 0
⇒ t(3t + 10) − 5(3t + 10) = 0
⇒ (3t + 10)(t − 5) = 0
⇒ t = 5 (ignoring -ve value)
Thus, Total time taken by slower horse = 5 + 5 = 10 hr
So Option B is correct
A can do a piece of work in 21days. B is 50% more efficient than A. C is twice efficient than B. A started the work alone and worked for some days and left the work then B and C joined together and completed the work in 2 days. Then how many days does A worked alone?
- a)7 Days
- b)12 Days
- c)14 Days
- d)21 Days
- e)None
Correct answer is option 'B'. Can you explain this answer?
A can do a piece of work in 21days. B is 50% more efficient than A. C is twice efficient than B. A started the work alone and worked for some days and left the work then B and C joined together and completed the work in 2 days. Then how many days does A worked alone?
a)
7 Days
b)
12 Days
c)
14 Days
d)
21 Days
e)
None

|
Machine Experts answered |
A = 21 B = 14 C =7
x/21+2*(1/14+1/7) = 1
x = 12.
x/21+2*(1/14+1/7) = 1
x = 12.
7 Indian and 4 American finish a job in 6 days. 7 African and 3 American finish the same job in 8 days. The efficiency of each person of a particular nationality is same but different from others. One Indian One American and One African will complete the work in:- a)10 days
- b)12 days
- c)24 days
- d)36 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
7 Indian and 4 American finish a job in 6 days. 7 African and 3 American finish the same job in 8 days. The efficiency of each person of a particular nationality is same but different from others. One Indian One American and One African will complete the work in:
a)
10 days
b)
12 days
c)
24 days
d)
36 days
e)
None of these
|
|
Anaya Patel answered |
7I + 4Am = 1/6
7Af + 4Am = 1/8
7I + 7Af + 7Am = 7/24
1I + 1Af + 1Am = 1/24
One Indian One American and One African will complete the work in – 24 days.
7Af + 4Am = 1/8
7I + 7Af + 7Am = 7/24
1I + 1Af + 1Am = 1/24
One Indian One American and One African will complete the work in – 24 days.
Sheldon had to cover a distance of 60 km. However, he started 6 minutes later than his scheduled time and raced at a speed 1 km/h higher than his originally planned speed and reached the finish at the time he would reach it if he began to race strictly at the appointed time and raced with the assumed speed. Find the speed at which he travelled during the journey described.
- a)25 km/h
- b)10 km/h
- c)6 km/h
- d)15 km/h
Correct answer is option 'A'. Can you explain this answer?
Sheldon had to cover a distance of 60 km. However, he started 6 minutes later than his scheduled time and raced at a speed 1 km/h higher than his originally planned speed and reached the finish at the time he would reach it if he began to race strictly at the appointed time and raced with the assumed speed. Find the speed at which he travelled during the journey described.
a)
25 km/h
b)
10 km/h
c)
6 km/h
d)
15 km/h

|
Asf Institute answered |
Solve this question through options.
⇒ For instance, if he travelled at 25 km/h, his original speed would have been 24 km/h.
⇒ The time difference can be seen to be 6 minutes in this case = 60 / 24 – 60 / 25 = 0.1 hrs = 6 mins
⇒ For instance, if he travelled at 25 km/h, his original speed would have been 24 km/h.
⇒ The time difference can be seen to be 6 minutes in this case = 60 / 24 – 60 / 25 = 0.1 hrs = 6 mins
Thus, 25 km/h is the correct answer.
So Option A is correct
P is able to do a piece of work in 15 days and Q can do the same work in 20 days. If they can work together for 4 days, what is the fraction of work left?- a)8/15
- b)7/15
- c)11/15
- d)2/11
Correct answer is option 'A'. Can you explain this answer?
a)
8/15
b)
7/15
c)
11/15
d)
2/11
|
|
Academic Studio answered |
Since P to R is double the distance of P to Q,
Therefore, it is evident that the time taken from P to R and back would be double the time taken from P to Q and back (i.e. double of 6.5 hours = 13 hours).
Therefore, it is evident that the time taken from P to R and back would be double the time taken from P to Q and back (i.e. double of 6.5 hours = 13 hours).
Since going from P to R takes 9 hours, coming back from R to P would take 4 hours i.e. 13- 9 = 4
So Option A is correct
A alone can complete a work in 5 days more than A+B together and B alone can complete a work in 45 days more than A+B together. Then in how many days A and B together can complete the work?- a)16 days
- b)21 days
- c)15 days
- d)20 days
- e)25 days
Correct answer is option 'C'. Can you explain this answer?
A alone can complete a work in 5 days more than A+B together and B alone can complete a work in 45 days more than A+B together. Then in how many days A and B together can complete the work?
a)
16 days
b)
21 days
c)
15 days
d)
20 days
e)
25 days

|
Target Study Academy answered |
Shortcut = √5×45 = 15
OR
Let (A+B) can do in x days, so
1/(x+5) + 1/(x+45) = 1/x
Solve, x2 = 225, x = 15
OR
Let (A+B) can do in x days, so
1/(x+5) + 1/(x+45) = 1/x
Solve, x2 = 225, x = 15
Arun can do a piece of work in 40 days, but Bala can do the same work in 5 days less, than Arun, when working alone. Arun and Bala both started the work together but Bala left after some days and Arun finished the remaining work in 30 days with half of his efficiency but he did the work with Bala with his complete efficiency. For how many days they had worked together?- a)25/3 days
- b)31/3 days
- c)35/3 days
- d)38/3 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Arun can do a piece of work in 40 days, but Bala can do the same work in 5 days less, than Arun, when working alone. Arun and Bala both started the work together but Bala left after some days and Arun finished the remaining work in 30 days with half of his efficiency but he did the work with Bala with his complete efficiency. For how many days they had worked together?
a)
25/3 days
b)
31/3 days
c)
35/3 days
d)
38/3 days
e)
None of these
|
|
Anaya Patel answered |
1 day work of Arun and Bala = 1/40 + 1/35 = 15/280
Arun finished the remaining work in 30 days = 30 * 1/40 * 2 = 3/8
Remaining work done by Arun and Bala = 5/8
Worked together = (5/8)/(15/280) = 35/3 days.
Arun finished the remaining work in 30 days = 30 * 1/40 * 2 = 3/8
Remaining work done by Arun and Bala = 5/8
Worked together = (5/8)/(15/280) = 35/3 days.
20 men can complete a piece of work in 14 days. 7 men started the work and after 20 days, 7 more men joined the work. In how many days the remaining work will be completed?- a)18 days
- b)20 days
- c)8 days
- d)12 days
- e)10 days
Correct answer is option 'E'. Can you explain this answer?
20 men can complete a piece of work in 14 days. 7 men started the work and after 20 days, 7 more men joined the work. In how many days the remaining work will be completed?
a)
18 days
b)
20 days
c)
8 days
d)
12 days
e)
10 days

|
Bank Exams India answered |
Let (7+7) complete remaining work in x days.
So 20*14 = 7*20 + 14*x
x = 10 days
So 20*14 = 7*20 + 14*x
x = 10 days
Machine P can print one lakh books in 8 hours. Machine Q can print the same number of books in 10 hours while machine R can print the same in 12 hours. All the machines started printing at 9 A.M. Machine P is stopped at 11 A.M. and the remaining two machines complete work. Approximately at what time will the printing of one lakh books be completed?
- a)3 pm
- b)2 pm
- c)1:00 pm
- d)11 am
Correct answer is option 'C'. Can you explain this answer?
a)
3 pm
b)
2 pm
c)
1:00 pm
d)
11 am
|
|
Kiran Mehta answered |
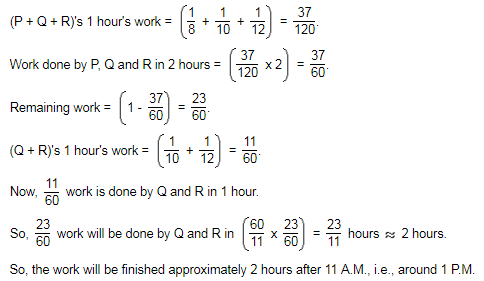
If 20 women and 10 boys can reap a field in 30 days, then in how many days 15 women and 30 boys will reap the field. It is given that work done by 4 women is equal to work done by 3 boys.
- a)210/11 days
- b)200/9 days
- c)200/11 days
- d)210/13 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If 20 women and 10 boys can reap a field in 30 days, then in how many days 15 women and 30 boys will reap the field. It is given that work done by 4 women is equal to work done by 3 boys.
a)
210/11 days
b)
200/9 days
c)
200/11 days
d)
210/13 days
e)
None of these
|
|
Preeti Khanna answered |
It is given that 4w = 3b
20w + 10b = 30 days
20w + 40/3w = 30
100/3w = 30
20w + 10b = 30 days
20w + 40/3w = 30
100/3w = 30
15w + 30b = x
15w+ 40w = x
55w = x
15w+ 40w = x
55w = x
100/3*30 = 55*x
x= 200/11
x= 200/11
To complete a work, A takes 50% more time than B. If together they take 18 days to complete the work, how much time shall B take to do it?- a)30 days
- b)35 days
- c)40 days
- d)45 days
Correct answer is option 'A'. Can you explain this answer?
To complete a work, A takes 50% more time than B. If together they take 18 days to complete the work, how much time shall B take to do it?
a)
30 days
b)
35 days
c)
40 days
d)
45 days
|
|
Rajesh Khatri answered |
We have,
B = 3/2*A
→
A = 2/3*B
One day's work, (A+B) = 1/18
(2/3*B+B) = 1/18
5/3*B = 1/18
One day's work of B = 3/90
B alone can complete the work in,
= 90/3
= 30 days.
A and B together can do a piece of work in 24 days, which B and C together can do it in 32 days. After A has been working at it for 10 days and B for 14 days, C finishes it in 26 days. In how many days C alone will do the work?- a)32
- b)36
- c)44
- d)48
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A and B together can do a piece of work in 24 days, which B and C together can do it in 32 days. After A has been working at it for 10 days and B for 14 days, C finishes it in 26 days. In how many days C alone will do the work?
a)
32
b)
36
c)
44
d)
48
e)
None of these
|
|
Anaya Patel answered |
Correct Answer :- d
Explanation : Work done by (A+B)'s in 1 day = 24
work done by (B+C)'s in 1 day = 32
Let C does a work in x days
Then work done by C in a day = 1/x
According to the question
A's 10 day's work + B's 14 day's work + C's 26 day's work = 1
10A + 14B + 26C = 1 ;
10A + 10B + 4B + 4C + 22C = 1 ;
10(A + B ) + 4( B + C ) + 22C = 1 ;
10( 1/24 ) + 4( 1/32 ) + 22C = 1 ;
10/24 + 4/32 + 22C = 1 ;
13/24 + 22C = 1 ;
22C = 1 - 13/24 ;
22C = 11/24 ;
2C = 1/24 ;
C = 1/48 ;
Therefore , C alone takes 48 days to finish the job.
2 men and 3 women can together complete a piece of work in 4 days and 3 men and 2 women together can complete work in 3 days. In how many days 10 women will complete this work?- a)9 days
- b)6 days
- c)7 days
- d)12 days
- e)10 days
Correct answer is option 'B'. Can you explain this answer?
2 men and 3 women can together complete a piece of work in 4 days and 3 men and 2 women together can complete work in 3 days. In how many days 10 women will complete this work?
a)
9 days
b)
6 days
c)
7 days
d)
12 days
e)
10 days

|
Divey Sethi answered |
2m + 3w = 4, 3m + 2w = 3
So 4(2m + 3w) = 3(3m + 2w)
8m + 12w = 9m + 6w
6w = 1m
Given 2m + 3w = 4, so 2*(6w) + 3w = 4, so 15 women in 4 days, so 10 women in (15*4)/10 = 6 days
So 4(2m + 3w) = 3(3m + 2w)
8m + 12w = 9m + 6w
6w = 1m
Given 2m + 3w = 4, so 2*(6w) + 3w = 4, so 15 women in 4 days, so 10 women in (15*4)/10 = 6 days
A factory produces nuts and bolts. A machine in it produces only nuts while another produces only bolts. The machine producing only nuts produces 500 nuts per minute and need to be cleared for 10 minutes after production of 2000 nuts. The machine producing only bolts produces 600 bolts per minute and needs to be cleared for 15 minutes after production of 3000 bolts. Find the minimum time required to produce 6000 pairs of bolts and nuts if both machines are operated simultaneously.- a)32 minutes
- b)20 minutes
- c)25 minutes
- d)40 minutes
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A factory produces nuts and bolts. A machine in it produces only nuts while another produces only bolts. The machine producing only nuts produces 500 nuts per minute and need to be cleared for 10 minutes after production of 2000 nuts. The machine producing only bolts produces 600 bolts per minute and needs to be cleared for 15 minutes after production of 3000 bolts. Find the minimum time required to produce 6000 pairs of bolts and nuts if both machines are operated simultaneously.
a)
32 minutes
b)
20 minutes
c)
25 minutes
d)
40 minutes
e)
None of these
|
|
Preeti Khanna answered |
2000 nuts are produced in 14 minutes (10 minutes break and 500 nuts per minutes so 4 minutes to produce 2000 nuts ), for next 2000 nuts it will take 14 minutes more, and for more two thousand it will take 4 minutes more, so total time = 32 minutes
similarly, 6000 bolts are produced in 20 + 5 = 25 minutes
so minimum time required is 32 minutes
similarly, 6000 bolts are produced in 20 + 5 = 25 minutes
so minimum time required is 32 minutes
A and B alone can do a piece of wok in 8 and 18 days respectively. In how many days the work will be completed if they both work on alternate days starting with B?
- a)
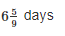
- b)5 days
- c)
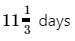
- d)
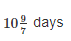
- e)
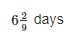
Correct answer is option 'C'. Can you explain this answer?
A and B alone can do a piece of wok in 8 and 18 days respectively. In how many days the work will be completed if they both work on alternate days starting with B?
a)
b)
5 days
c)
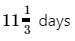
d)
e)

|
Machine Experts answered |
A = 8 days, B = 18 days
Total work = LCM(8,18) = 72
So efficiency of A = 72/8 = 9, efficiency of B = 72/18 = 4
2 days work of (A+B) = 9+4 = 13
2*5(10) days work of (A+B) = 9+4 = 13*5 = 65
So remaining work = 72-65 = 7
Now A’s turn on 6th day, he will do remaining work(7) in 7/9 day
So total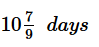
Total work = LCM(8,18) = 72
So efficiency of A = 72/8 = 9, efficiency of B = 72/18 = 4
2 days work of (A+B) = 9+4 = 13
2*5(10) days work of (A+B) = 9+4 = 13*5 = 65
So remaining work = 72-65 = 7
Now A’s turn on 6th day, he will do remaining work(7) in 7/9 day
So total
P can finish a work in 18 days. Q can finish the same work in 15 days. Q worked for 10 days and left the job. how many days does P alone need to finish the remaining work?
- a)8
- b)5
- c)4
- d)6
Correct answer is option 'D'. Can you explain this answer?
a)
8
b)
5
c)
4
d)
6

|
Spectrum Coaching Institute answered |
Initial distance = 25 dog leaps
Per-minute dog makes 5 dog leaps and cat makes 6 cat leaps = 3 dog leaps
⇒ Relative speed = 2 dog leaps / minutes
⇒ An initial distance of 25 dog leaps would get covered in 12.5 minutes.
Per-minute dog makes 5 dog leaps and cat makes 6 cat leaps = 3 dog leaps
⇒ Relative speed = 2 dog leaps / minutes
⇒ An initial distance of 25 dog leaps would get covered in 12.5 minutes.
So Option D is correct
Sekar, Pradeep and Sandeep can do a piece of work in 15 days. After all the three worked for 2 days, sekar left. Pradeep and Sandeep worked for 10 more days and Pradeep left. Sandeep worked for another 40 days and completed the work. In how many days can sekar alone complete the work if sandeep can complete it in 75 days?- a)25 days
- b)20 days
- c)30 days
- d)35 days
- e)15 days
Correct answer is option 'C'. Can you explain this answer?
Sekar, Pradeep and Sandeep can do a piece of work in 15 days. After all the three worked for 2 days, sekar left. Pradeep and Sandeep worked for 10 more days and Pradeep left. Sandeep worked for another 40 days and completed the work. In how many days can sekar alone complete the work if sandeep can complete it in 75 days?
a)
25 days
b)
20 days
c)
30 days
d)
35 days
e)
15 days

|
Bank Exams India answered |
Assume the total work to be 600 units. (LCM of all the numbers) Then Sandeep’s 1 day work = 8 units.
All three’s 1 day work = 40 units.All work together in the first 2 days
Work done in the first 2 days = 40 × 2 = 80 units
Sandeep alone works during the last 40 days
Work done in the last 40 days = 40 × 8 = 320 units
Remaining work = 600 – (320 + 80) = 200 units
This work is done by pradeep and sandeep in 10 days.
Pradeep and Sandeep together’s 1 day work = 20 units
Sekar’s 1 day work = All three 1 day work – Pradeep and Sandeep together’s 1 day
work = 40 units – 20 units = 20 units
Sekar can do the work of 600 units in 30 days.
All three’s 1 day work = 40 units.All work together in the first 2 days
Work done in the first 2 days = 40 × 2 = 80 units
Sandeep alone works during the last 40 days
Work done in the last 40 days = 40 × 8 = 320 units
Remaining work = 600 – (320 + 80) = 200 units
This work is done by pradeep and sandeep in 10 days.
Pradeep and Sandeep together’s 1 day work = 20 units
Sekar’s 1 day work = All three 1 day work – Pradeep and Sandeep together’s 1 day
work = 40 units – 20 units = 20 units
Sekar can do the work of 600 units in 30 days.
Arun can do a certain work in the same time in which Bipasha and Rahul together can do it. If Arun and Bipasha together could do it in 10 days and Rahul alone in 50 days, then Bipasha alone could do it in:- a)15 days
- b)20 days
- c)25 days
- d)30 days
- e)35 days
Correct answer is option 'C'. Can you explain this answer?
Arun can do a certain work in the same time in which Bipasha and Rahul together can do it. If Arun and Bipasha together could do it in 10 days and Rahul alone in 50 days, then Bipasha alone could do it in:
a)
15 days
b)
20 days
c)
25 days
d)
30 days
e)
35 days
|
|
Kavya Saxena answered |
Arun, Bipasha and rahul’s 1 day work = 1/10 + 1/50 = 6/50 = 3/25
Arun’s 1 day work = Bipasha + Rahul ‘s 1 day work
2*(Arun’s 1 day work) = 3/25
Arun’s 1 day work = 3/50
Bipasha’s 1 day work = 1/10 – 3/50 = 2/50 = 1/25
Arun’s 1 day work = Bipasha + Rahul ‘s 1 day work
2*(Arun’s 1 day work) = 3/25
Arun’s 1 day work = 3/50
Bipasha’s 1 day work = 1/10 – 3/50 = 2/50 = 1/25
If P and Q work together, they will complete a job in 7.5 days. However, if P works alone and completes half the job and then Q takes over and completes the remaining half alone, they will be able to complete the job in 20 days. How long will Q alone take to do the job if P is more efficient than Q?- a)20 days
- b)30 days
- c)40 days
- d)10 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If P and Q work together, they will complete a job in 7.5 days. However, if P works alone and completes half the job and then Q takes over and completes the remaining half alone, they will be able to complete the job in 20 days. How long will Q alone take to do the job if P is more efficient than Q?
a)
20 days
b)
30 days
c)
40 days
d)
10 days
e)
None of these

|
Naroj Boda answered |
1/P + 1/Q = 2/15 from first line. Now, let P take x days and Q takes y days to complete half the work respectively.
x/P = 1/2, x = P/2 similarly y/Q = 1/2, y = Q/2
so, x +y = 20 i.e. P/2 + Q/2 = 20, P +Q = 40
solve both equation, u will get Q = 30 days
x/P = 1/2, x = P/2 similarly y/Q = 1/2, y = Q/2
so, x +y = 20 i.e. P/2 + Q/2 = 20, P +Q = 40
solve both equation, u will get Q = 30 days
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?- a)30
- b)35
- c)40
- d)45
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?
a)
30
b)
35
c)
40
d)
45
e)
None of these

|
KS Coaching Center answered |
suppose Initially X men get employed. Half work is done in 30 days it means full work will be done by X men in 60 days. Now,
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
P and Q together can complete a job in 90days, Q and R takes 60 days to complete the same work and P and R will take 45 days to complete the same work. How much time will P, Q and R will take to complete the work together.- a)40 days
- b)42 days
- c)36 days
- d)44 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
P and Q together can complete a job in 90days, Q and R takes 60 days to complete the same work and P and R will take 45 days to complete the same work. How much time will P, Q and R will take to complete the work together.
a)
40 days
b)
42 days
c)
36 days
d)
44 days
e)
None of these

|
Bank Exams India answered |
(1/90 + 1/60 + 1/45)*1/2 = (1/P +1/Q + 1/R) = 1/40
so 40 days
so 40 days
Chetan is thrice as efficient as Mamta and together they can finish a piece of work in 60 days. Mamta will take how many days to finish this work alone?- a)80
- b)160
- c)240
- d)320
Correct answer is option 'C'. Can you explain this answer?
Chetan is thrice as efficient as Mamta and together they can finish a piece of work in 60 days. Mamta will take how many days to finish this work alone?
a)
80
b)
160
c)
240
d)
320
|
|
Ritika Choudhury answered |
- Chetan is thrice as efficient as Mamta.
- Let, Mamta takes 3x days and Chetan takes x days to complete the work.
- ∴ 1/x + 1/3x = 1/60 ⇒ x = 80.
- ∴ Mamta will take 80 × 3 = 240 days to complete the work.
If P can do 1/3 of the work in 5 days and Q can do 1/4 of the work in 6 days, then how much money will Q get if they were paid a total of 390 rupee?- a)120
- b)150
- c)170
- d)190
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If P can do 1/3 of the work in 5 days and Q can do 1/4 of the work in 6 days, then how much money will Q get if they were paid a total of 390 rupee?
a)
120
b)
150
c)
170
d)
190
e)
None of these

|
Bank Exams India answered |
sol = P can alone complete the whole work in 15 days and Q can complete the same work alone in 24 days. So ratio of work done by them 1/15: 1/24 i.e. 8: 5
Q get = (5/13)*390 = 150
Q get = (5/13)*390 = 150
Efficiency of A is 25% more then B and B takes 25 days to complete a piece of work. A started a work alone and then B joined her 5 days before actual completion of the work. For how many days A worked alone?- a)9
- b)11
- c)10
- d)25
- e)12
Correct answer is option 'B'. Can you explain this answer?
Efficiency of A is 25% more then B and B takes 25 days to complete a piece of work. A started a work alone and then B joined her 5 days before actual completion of the work. For how many days A worked alone?
a)
9
b)
11
c)
10
d)
25
e)
12

|
KS Coaching Center answered |
Efficiency (A : B) = 5 : 4
Number of days(A : B) = 4x : 5x = 4x : 25
∴ Number of days required by A to finish the work alone = 4x
= 4 x 5 = 20.
A and B work together for last 5 days = 5 x 9 = 45%
Efficiency of A = 5% and B’s efficiency = 4%
∴ No. of days taken by A to complete 55% work = 55/5 = 11days
Number of days(A : B) = 4x : 5x = 4x : 25
∴ Number of days required by A to finish the work alone = 4x
= 4 x 5 = 20.
A and B work together for last 5 days = 5 x 9 = 45%
Efficiency of A = 5% and B’s efficiency = 4%
∴ No. of days taken by A to complete 55% work = 55/5 = 11days
6 men and 8 women can complete a work in 10 days. 26 men and 48 women can finish the same work in 2 days. 15 men and 20 women can do the same work in - days.
- a)4 days
- b)6 days
- c)2 days
- d)8 days
Correct answer is option 'A'. Can you explain this answer?
a)
4 days
b)
6 days
c)
2 days
d)
8 days
|
|
Vikas Choudhury answered |
Let work done by 1 man in 1 day = m and work done by 1 woman in 1 day = b
Work done by 6 men and 8 women in 1 day = 1/10
=> 6m + 8b = 1/10
=> 60m + 80b = 1 (1)
Work done by 26 men and 48 women in 1 day = 1/2
=> 26m + 48b =1/2
=> 52m + 96b = 1 (2)
Solving equation 1 and equation 2. We get m = 1/100 and b = 1/200
Work done by 15 men and 20 women in 1 day
= 15/100 + 20/200 =1/4
=> Time taken by 15 men and 20 women in doing the work = 4 days
The ratio of efficiency of Arun is to Chitra is 5:3. The ratio of number of days taken by Bala is to Chitra is 2:3. Arun takes 6 days less than Chitra, when Arun and Chitra complete the work individually. Bala and Chitra started the work and left after 2 days. The number of days taken by Arun to finish the remaining work is?- a)4 days
- b)5 days
- c)6 days
- d)9 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The ratio of efficiency of Arun is to Chitra is 5:3. The ratio of number of days taken by Bala is to Chitra is 2:3. Arun takes 6 days less than Chitra, when Arun and Chitra complete the work individually. Bala and Chitra started the work and left after 2 days. The number of days taken by Arun to finish the remaining work is?
a)
4 days
b)
5 days
c)
6 days
d)
9 days
e)
None of these
|
|
Anaya Patel answered |
Ratio of number of days = 9:10:15
Work done By B and C in first two days = 2*1/6 = 1/3
Rest of the work = 2/3
Number of days = (2/3)/(1/9) = 6 days
Work done By B and C in first two days = 2*1/6 = 1/3
Rest of the work = 2/3
Number of days = (2/3)/(1/9) = 6 days
A Contractor employed a certain number of workers to finish constructing a building in a certain scheduled time. Some time later, when a part of work had been completed, he realized that the work would get delayed by half of the scheduled time, so he at once doubled the no of workers and thus he managed to finish the building on the scheduled time. How much work he had been completed, before increasing the number of workers?- a)200/3%
- b)100/3%
- c)300/3%
- d)Can’t be determined
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A Contractor employed a certain number of workers to finish constructing a building in a certain scheduled time. Some time later, when a part of work had been completed, he realized that the work would get delayed by half of the scheduled time, so he at once doubled the no of workers and thus he managed to finish the building on the scheduled time. How much work he had been completed, before increasing the number of workers?
a)
200/3%
b)
100/3%
c)
300/3%
d)
Can’t be determined
e)
None of these

|
KS Coaching Center answered |
D * x +(100- D) * 2x= 150x
⇒ D = 50 days
work done in 50 days = 50x
Total work = 150x
50x/150x * 100 = 100/3
⇒ D = 50 days
work done in 50 days = 50x
Total work = 150x
50x/150x * 100 = 100/3
Among four persons Anuj, Bhim, Carl and Dinesh. Anuj takes thrice as much time as Bhim to complete a piece of work. Bhim takes thrice as much time as Carl and Carl takes thrice as much time as Dinesh to complete the same work. If all together they take 3 days to complete the work. Find the time taken by Bhim alone to complete the work alone.- a)20 days
- b)30 days
- c)40 days
- d)50 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Among four persons Anuj, Bhim, Carl and Dinesh. Anuj takes thrice as much time as Bhim to complete a piece of work. Bhim takes thrice as much time as Carl and Carl takes thrice as much time as Dinesh to complete the same work. If all together they take 3 days to complete the work. Find the time taken by Bhim alone to complete the work alone.
a)
20 days
b)
30 days
c)
40 days
d)
50 days
e)
None of these
|
|
Faizan Khan answered |
Let Bhim takes x days alone to complete the job, so Anuj will take 3x days, Carl will take x/3 days and Dinesh will take x/9 days to complete the work alone
1/3x + 1/x + 3/x + 9/x = 1/3
Solve for x
1/3x + 1/x + 3/x + 9/x = 1/3
Solve for x
P is 20 % more efficient than Q, how much time will they working together take to complete a job which P alone could have done in 20 days ?- a)9 days
- b)11 days
- c)17 days
- d)22 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
P is 20 % more efficient than Q, how much time will they working together take to complete a job which P alone could have done in 20 days ?
a)
9 days
b)
11 days
c)
17 days
d)
22 days
e)
None of these

|
KS Coaching Center answered |
P : Q = 100 : 120
10/12 = 20/x
12/10 = x/20
X = 24
Q = 1/24 or 20*120/100 = 24
P+Q = 1/20 + 1/24
= 24+20/480 = 44/480 = 10.91 = 11 days
10/12 = 20/x
12/10 = x/20
X = 24
Q = 1/24 or 20*120/100 = 24
P+Q = 1/20 + 1/24
= 24+20/480 = 44/480 = 10.91 = 11 days
A can do a piece of work in 60days working 14 hours. B has the same efficiency as of A. A and B started working together. A works 5,6,7 and 8 hours respectively on first four days and repeats the cycle again. Then B has to work how many hours daily if they together completed the work in 80 days?
- a)1 Hour
- b)2 Hours
- c)3 Hours
- d)4 Hours
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A can do a piece of work in 60days working 14 hours. B has the same efficiency as of A. A and B started working together. A works 5,6,7 and 8 hours respectively on first four days and repeats the cycle again. Then B has to work how many hours daily if they together completed the work in 80 days?
a)
1 Hour
b)
2 Hours
c)
3 Hours
d)
4 Hours
e)
None of these

|
Arya Roy answered |



A piece of work is to be completed in 100days, 11 Men are employed to do the work it is found that after 50 days only 1/3 rd work is completed. Now additionally how many more Men are to be employed to work to finish the work in time?- a)5
- b)6
- c)7
- d)11
- e)None
Correct answer is option 'D'. Can you explain this answer?
A piece of work is to be completed in 100days, 11 Men are employed to do the work it is found that after 50 days only 1/3 rd work is completed. Now additionally how many more Men are to be employed to work to finish the work in time?
a)
5
b)
6
c)
7
d)
11
e)
None
|
|
Aisha Gupta answered |
11*50/1/3 = (11+x)*50/2/3
X = 11
X = 11
If P can do a work in 6 days and Q can do the same work in 8 days. If R who can do the same work in 12 days, joins them, then the work will be completed in how many days?- a)7/3 days
- b)8/3 days
- c)10/3 days
- d)11/3 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If P can do a work in 6 days and Q can do the same work in 8 days. If R who can do the same work in 12 days, joins them, then the work will be completed in how many days?
a)
7/3 days
b)
8/3 days
c)
10/3 days
d)
11/3 days
e)
None of these
|
|
Faizan Khan answered |
1/6 + 1/8 + 1/12 = 1/d.
D = 8/3 days
D = 8/3 days
Ravi can do a piece of work in 16 days. Rakesh can do the same work in 64/5 days, while Geeta can do it in 32 days. All of them started to work together but Ravi leaves after 4 days. Rakesh leaves the job 3 days before the completion of the work. How long would the work last?- a)6 days
- b)9 days
- c)18 days
- d)5 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Ravi can do a piece of work in 16 days. Rakesh can do the same work in 64/5 days, while Geeta can do it in 32 days. All of them started to work together but Ravi leaves after 4 days. Rakesh leaves the job 3 days before the completion of the work. How long would the work last?
a)
6 days
b)
9 days
c)
18 days
d)
5 days
e)
None of these
|
|
Kavya Saxena answered |
Let the work lasted for x days,
Ravi’s 4 day’s work + Rakesh (x – 3) day’s work + Geeta’s x day’s work = 1
⇒ (4/16) + (x – 3) / (64/5) + x/32 = 1
⇒ 5(x – 3)/64 + x/32 = 1 – 1/4
⇒ [5(x – 3) + 2x] / 64 = 3/4
⇒ 7x – 15 = 48
∴ x = (48 + 15)/7 = 63/7 = 9 days
Ravi’s 4 day’s work + Rakesh (x – 3) day’s work + Geeta’s x day’s work = 1
⇒ (4/16) + (x – 3) / (64/5) + x/32 = 1
⇒ 5(x – 3)/64 + x/32 = 1 – 1/4
⇒ [5(x – 3) + 2x] / 64 = 3/4
⇒ 7x – 15 = 48
∴ x = (48 + 15)/7 = 63/7 = 9 days
Angel can do a piece of work in 10 days, Balu in 15 days. They work together for 5 days, the rest of the work is finished by Chitra in two more days. If they get Rs. 6000 as wages for the whole work, what are the daily wages of Angel, Bala and Chitra respectively?- a)200, 250, 300
- b)300, 200, 250
- c)600, 400, 200
- d)600, 400, 500
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Angel can do a piece of work in 10 days, Balu in 15 days. They work together for 5 days, the rest of the work is finished by Chitra in two more days. If they get Rs. 6000 as wages for the whole work, what are the daily wages of Angel, Bala and Chitra respectively?
a)
200, 250, 300
b)
300, 200, 250
c)
600, 400, 200
d)
600, 400, 500
e)
None of these

|
Bank Exams India answered |
Angel’s 5 days work = 50%
Balu’s 5 days work = 33.33%
Chitra’s 2 days work = 16.66%
[100- (50+33.33)]
Ratio of work of Angel, Balu and Chitra = 3: 2: 1
Angel’s total share = Rs. 3000
Balu’s total share = Rs. 2000
Chitra’s total share = Rs. 1000
Angel’s one day’s wage = Rs.600
Balu’s one day’s wage = Rs.400
Chitra’s one day’s wage = Rs.500
Balu’s 5 days work = 33.33%
Chitra’s 2 days work = 16.66%
[100- (50+33.33)]
Ratio of work of Angel, Balu and Chitra = 3: 2: 1
Angel’s total share = Rs. 3000
Balu’s total share = Rs. 2000
Chitra’s total share = Rs. 1000
Angel’s one day’s wage = Rs.600
Balu’s one day’s wage = Rs.400
Chitra’s one day’s wage = Rs.500
Working together Bala and Chitra take 50% more number of days than Angel, Bala and Chitra together take and Angel and Bala working together, take 8/3 more number of days than Angel, Bala and Chitra take together. If Angel, Bala and Chitra all have worked together till the completion of the work and Bala has received Rs.120 out of total earnings of Rs. 480 then in how many days did Angel, Bala and Chitra together complete the whole work?- a)2 days
- b)4 days
- c)6 days
- d)8 days
- e)5 days
Correct answer is option 'E'. Can you explain this answer?
Working together Bala and Chitra take 50% more number of days than Angel, Bala and Chitra together take and Angel and Bala working together, take 8/3 more number of days than Angel, Bala and Chitra take together. If Angel, Bala and Chitra all have worked together till the completion of the work and Bala has received Rs.120 out of total earnings of Rs. 480 then in how many days did Angel, Bala and Chitra together complete the whole work?
a)
2 days
b)
4 days
c)
6 days
d)
8 days
e)
5 days

|
Future Foundation Institute answered |
The days ratio of (Angel + Bala + Chitra) : (Bala + Chitra) = X:3X/2 = 2X:3x;
Efficiency ratio = 3X:2X
Efficiency of Angel = x.
(480/3X) = Rs.160
Amount received by Bala = Rs.120 & Chitra = 200
160:120:200 =4:3:5
1/4:1/3:1/5= 15:20:12;
(1/15+1/12+1/20)*Y = 1
Y = 5 days
Efficiency ratio = 3X:2X
Efficiency of Angel = x.
(480/3X) = Rs.160
Amount received by Bala = Rs.120 & Chitra = 200
160:120:200 =4:3:5
1/4:1/3:1/5= 15:20:12;
(1/15+1/12+1/20)*Y = 1
Y = 5 days
A, B and C can alone complete a work in 10, 12 and 15 days respectively. All started the work but B left the work 3 days before completion. How much work was then done by A and B together in the total work?- a)2/3
- b)3/4
- c)1/3
- d)3/5
- e)2/5
Correct answer is option 'A'. Can you explain this answer?
A, B and C can alone complete a work in 10, 12 and 15 days respectively. All started the work but B left the work 3 days before completion. How much work was then done by A and B together in the total work?
a)
2/3
b)
3/4
c)
1/3
d)
3/5
e)
2/5
|
|
Aarav Sharma answered |
Given information:
A can complete the work in 10 days.
B can complete the work in 12 days.
C can complete the work in 15 days.
B left the work 3 days before completion.
To find:
How much work was then done by A and B together in the total work?
Solution:
To solve this problem, we need to understand the concept of work done per day.
Let's assume that the total work to be done is 60 units (considering the LCM of 10, 12, and 15).
Work done by A per day:
A can complete the work in 10 days, so the work done by A per day is 60/10 = 6 units.
Work done by B per day:
B can complete the work in 12 days, so the work done by B per day is 60/12 = 5 units.
Work done by C per day:
C can complete the work in 15 days, so the work done by C per day is 60/15 = 4 units.
Now, let's calculate the total work done by A, B, and C in the given time frame.
Work done by A in the given time:
Since A is working continuously until the completion of the work, the work done by A in the given time is 6 units/day * (10-3) days = 6 * 7 = 42 units.
Work done by B in the given time:
B left the work 3 days before completion, so the work done by B in the given time is 5 units/day * 3 days = 15 units.
Total work done by A and B together:
The total work done by A and B together in the given time is 42 units + 15 units = 57 units.
Calculating the fraction of work done:
To find the fraction of work done by A and B together, we need to divide the total work done by A and B by the total work done.
Fraction of work done by A and B = (57 units) / (60 units) = 19/20 = 0.95
This can be simplified to 2/3.
Therefore, the answer is option 'A' (2/3).
A can complete the work in 10 days.
B can complete the work in 12 days.
C can complete the work in 15 days.
B left the work 3 days before completion.
To find:
How much work was then done by A and B together in the total work?
Solution:
To solve this problem, we need to understand the concept of work done per day.
Let's assume that the total work to be done is 60 units (considering the LCM of 10, 12, and 15).
Work done by A per day:
A can complete the work in 10 days, so the work done by A per day is 60/10 = 6 units.
Work done by B per day:
B can complete the work in 12 days, so the work done by B per day is 60/12 = 5 units.
Work done by C per day:
C can complete the work in 15 days, so the work done by C per day is 60/15 = 4 units.
Now, let's calculate the total work done by A, B, and C in the given time frame.
Work done by A in the given time:
Since A is working continuously until the completion of the work, the work done by A in the given time is 6 units/day * (10-3) days = 6 * 7 = 42 units.
Work done by B in the given time:
B left the work 3 days before completion, so the work done by B in the given time is 5 units/day * 3 days = 15 units.
Total work done by A and B together:
The total work done by A and B together in the given time is 42 units + 15 units = 57 units.
Calculating the fraction of work done:
To find the fraction of work done by A and B together, we need to divide the total work done by A and B by the total work done.
Fraction of work done by A and B = (57 units) / (60 units) = 19/20 = 0.95
This can be simplified to 2/3.
Therefore, the answer is option 'A' (2/3).
50 men could complete a work in 200 days. They worked together for 150 days, after that due to bad weather the work is stopped for 25 days. How many more workers should be employed so as to complete the work in time?- a)25
- b)35
- c)50
- d)60
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
50 men could complete a work in 200 days. They worked together for 150 days, after that due to bad weather the work is stopped for 25 days. How many more workers should be employed so as to complete the work in time?
a)
25
b)
35
c)
50
d)
60
e)
None of these
|
|
Yash Patel answered |
Let additional workers be P,
(50*150)/(50*200) = 3/4 of the work is already completed and now only 1/4 of the work is to be done. So,
1/4 = ((50 + P) * 25)/50*200, solve for p, we get P = 50
(50*150)/(50*200) = 3/4 of the work is already completed and now only 1/4 of the work is to be done. So,
1/4 = ((50 + P) * 25)/50*200, solve for p, we get P = 50
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?- a)30
- b)35
- c)40
- d)45
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?
a)
30
b)
35
c)
40
d)
45
e)
None of these
|
|
Faizan Khan answered |
suppose Initially X men get employed. Half work is done in 30 days it means full work will be done by X men in 60 days. Now,
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
A does half as much work as B does in one sixth of the time. If together they take 20 days to complete the work, then what is the time taken by A to complete the work independently.- a)80/3 days
- b)100/3 days
- c)60/3 days
- d)140/3 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A does half as much work as B does in one sixth of the time. If together they take 20 days to complete the work, then what is the time taken by A to complete the work independently.
a)
80/3 days
b)
100/3 days
c)
60/3 days
d)
140/3 days
e)
None of these
|
|
Faizan Khan answered |
Let B complete the work in X days so in one day work done by B is 1/x
as A do half work in one-sixth of the time so A will complete work in 2*x/6 = x/3 days
One day work of A and B i.e. 3/x + 1/x = 1/20. So we get x = 80
So time taken by A alone = 80/3 days
as A do half work in one-sixth of the time so A will complete work in 2*x/6 = x/3 days
One day work of A and B i.e. 3/x + 1/x = 1/20. So we get x = 80
So time taken by A alone = 80/3 days
Nakul and Ram are working on aproduction company. Nakul takes 6 hours to make 32 products, while Ram takes 5 hours to make 40 products. How much time will they take, working together to make 110 products?- a)8 hours
- b)8 hours 15 minutes
- c)9 hours
- d)8 hours 25 minutes
- e)9 hours 15 minutes
Correct answer is option 'B'. Can you explain this answer?
Nakul and Ram are working on aproduction company. Nakul takes 6 hours to make 32 products, while Ram takes 5 hours to make 40 products. How much time will they take, working together to make 110 products?
a)
8 hours
b)
8 hours 15 minutes
c)
9 hours
d)
8 hours 25 minutes
e)
9 hours 15 minutes
|
|
Nikita Singh answered |
Number of products made by Nakul in 1 hour = 32/6 = 16/3
Number of products made by Ram in 1 hour = 40/5 = 8
Number of products made by both in 1 hour = 16/3 + 8 = 40/3
Time taken by both to make 110 products = 110* 3/40 = 8 ¼ hrs
Number of products made by Ram in 1 hour = 40/5 = 8
Number of products made by both in 1 hour = 16/3 + 8 = 40/3
Time taken by both to make 110 products = 110* 3/40 = 8 ¼ hrs
Ram and shyam can do a piece of work in 5 and 7 days respectively. They start working alternatively starting from shyam, then in how many days the work is completed- a)5.(3/7) days
- b)6.(5/7) days
- c)7.(5/6) days
- d)5.(6/7) days
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Ram and shyam can do a piece of work in 5 and 7 days respectively. They start working alternatively starting from shyam, then in how many days the work is completed
a)
5.(3/7) days
b)
6.(5/7) days
c)
7.(5/6) days
d)
5.(6/7) days
e)
None of these
|
|
Alok Verma answered |
1/7 + 1/5 = 12/35 this much work is completed in 2 days.
So 24/35 will be completed in 4 days
In the next day, 29/35 work get completed in 5 days, so remaining work will be completed by Ram in 6/7 days
So 24/35 will be completed in 4 days
In the next day, 29/35 work get completed in 5 days, so remaining work will be completed by Ram in 6/7 days
A does half as much work as B does in one sixth of the time. If together they take 20 days to complete the work, then what is the time taken by B to complete the work independently.- a)80 days
- b)100 days
- c)120 days
- d)140 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A does half as much work as B does in one sixth of the time. If together they take 20 days to complete the work, then what is the time taken by B to complete the work independently.
a)
80 days
b)
100 days
c)
120 days
d)
140 days
e)
None of these
|
|
Ravi Singh answered |
Let B take X days to complete the work then in one –sixth of the time i.e. x/6 days. Now A do half work as done by B so A will take twice the time i.e. 2*x/6 = x/3 to complete the job alone
So 1/x + 3/x = 1/20, x = 80 days
So 1/x + 3/x = 1/20, x = 80 days
P takes 6 days less than Q to finish the work individually. If P and Q working together complete the work in 4 days, then how many days are required by Q to complete the work alone ?- a)7 days
- b)10 days
- c)5 days
- d)12 days
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
P takes 6 days less than Q to finish the work individually. If P and Q working together complete the work in 4 days, then how many days are required by Q to complete the work alone ?
a)
7 days
b)
10 days
c)
5 days
d)
12 days
e)
None of these
|
|
Nikita Singh answered |
= 1/6 + 1/12
= 2+1/12 =3/12 = 1/4
= 2+1/12 =3/12 = 1/4
A can do a work in 32 days. P who is 60 percent more efficient than A. Find how much time they will take together to do the same work?- a)150/13 days
- b)160/13 days
- c)170/3 days
- d)190/3 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A can do a work in 32 days. P who is 60 percent more efficient than A. Find how much time they will take together to do the same work?
a)
150/13 days
b)
160/13 days
c)
170/3 days
d)
190/3 days
e)
None of these
|
|
Kavya Saxena answered |
A’s one day work = 1/32 so P one day work = (160/100)*1/32 = 1/20, so P will take 20 days to complete the work.
So Both A and P will take = (32*20)/52 = 160/13 days
So Both A and P will take = (32*20)/52 = 160/13 days
A certain number of men take 45 days to complete a work. If there are 10 men less then they will take 60 days to complete the work. Find the original number of men.- a)30
- b)40
- c)50
- d)60
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A certain number of men take 45 days to complete a work. If there are 10 men less then they will take 60 days to complete the work. Find the original number of men.
a)
30
b)
40
c)
50
d)
60
e)
None of these
|
|
Aarav Sharma answered |
Let initially there are X men. Then x*45 = (x-10)*60. So we get x = 40
4 women and 5 men working together can do 3 times the work done by 2 women and one man together. Calculate the work of a man to that of woman.- a)1:2
- b)2:1
- c)1:1
- d)3:2
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
4 women and 5 men working together can do 3 times the work done by 2 women and one man together. Calculate the work of a man to that of woman.
a)
1:2
b)
2:1
c)
1:1
d)
3:2
e)
None of these
|
|
Rajeev Kumar answered |
4w + 5m = 3*(2w + m)
i.e. 2w = 2m
so ratio of work done by man to woman is 1:1
i.e. 2w = 2m
so ratio of work done by man to woman is 1:1
Sruthi, Swetha and Swati together can cut 216 Apples of the same size in 3 hours. Number of Apples cut by Sruthi in 9 hours is same as the number of Apples cut by Swati in 7 hours. In one hour, Swati can cut as many Apples more than Swetha as Swetha can cut more than Sruthi.Then the number of Apples cut by Swetha in one hour?
- a)21
- b)24
- c)27
- d)29
- e)None
Correct answer is option 'B'. Can you explain this answer?
Sruthi, Swetha and Swati together can cut 216 Apples of the same size in 3 hours. Number of Apples cut by Sruthi in 9 hours is same as the number of Apples cut by Swati in 7 hours. In one hour, Swati can cut as many Apples more than Swetha as Swetha can cut more than Sruthi.Then the number of Apples cut by Swetha in one hour?
a)
21
b)
24
c)
27
d)
29
e)
None
|
|
Aruna Singh answered |
Let's denote:
- Sruthi's efficiency as 'S' apples/hour
- Swetha's efficiency as 'W' apples/hour
- Swati's efficiency as 'T' apples/hour
Given information:
- S * 9 = T * 7 => S = (7/9)T
- T - W = W - S => T = 2W - S
Total work done in 3 hours:
- (S + W + T) * 3 = 216
- S + W + T = 72
Substituting S and T in terms of W:
- (7/9)T + W + 2W - (7/9)T = 72
- 3W = 72
- W = 24
Therefore, Swetha can cut 24 apples in one hour.
So, the correct answer is option B: 24.
(x-2) person can do a work in x days and (x+7) person can do 75% of the same work in (x-10)days. Then in how many days can (x+10) person finish the work?- a)27 days
- b)12 days
- c)25 days
- d)18 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
(x-2) person can do a work in x days and (x+7) person can do 75% of the same work in (x-10)days. Then in how many days can (x+10) person finish the work?
a)
27 days
b)
12 days
c)
25 days
d)
18 days
e)
None of these
|
|
Aisha Gupta answered |
3/4 * (x-2)x = (x+7)(x-10)
x – 6x – 280 = 0
x = 20; x = -14
(x-2)x = 18 * 20 = 360
360 = 30 * y
y = 12 days
x – 6x – 280 = 0
x = 20; x = -14
(x-2)x = 18 * 20 = 360
360 = 30 * y
y = 12 days
Chapter doubts & questions for Time and Work - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Time and Work - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









