All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of Square Roots & Cube Roots for CDS Exam
How many natural numbers lie between 92 and 102?
a) 36
b) 27
c) 9
d) 18
Correct answer is option 'D'. Can you explain this answer?
|
|
Sohini Das answered |
Between 92 and 102
Here, n = 9 and n + 1 = 10
∴ Natural number between 92 and 102 are (2 × n) or 2 x 9, i.e. 18.
Here, n = 9 and n + 1 = 10
∴ Natural number between 92 and 102 are (2 × n) or 2 x 9, i.e. 18.
Which of the following is a perfect square number?
- a)222222
- b)23453
- c)1681
- d)1057
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a perfect square number?
a)
222222
b)
23453
c)
1681
d)
1057

|
Shashwat Singh answered |
The answer is 1681 because it is the only number which has it's last digit as a number which a perfect square can have . 9×9=81 the last digit is 1.
Find the perfect square number between 30 and 40.
- a)36
- b)49
- c)25
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Find the perfect square number between 30 and 40.
a)
36
b)
49
c)
25
d)
none of these
|
|
Amita Verma answered |
Since, 1 x 1 = 1
2 x 2 = 4
3 x 3 = 9
4 x 4 = 16
5 x 5 = 25
6 x 6 = 36
7 x 7 = 49
Thus, 36 is a perfact square number between 30 and 40.
Which of the following would end with digit 1?- a)1232
- b)1612
- c)772
- d)822
Correct answer is 'B'. Can you explain this answer?
Which of the following would end with digit 1?
a)
1232
b)
1612
c)
772
d)
822

|
Sneha Singh answered |
Option B is correct because the unit digit of 161 is 1 and if unit digit of any digit ends with 1 the its square will also end with 1.
The square of 23 is :
- a)529
- b)526
- c)461
- d)429
Correct answer is option 'A'. Can you explain this answer?
The square of 23 is :
a)
529
b)
526
c)
461
d)
429
|
|
Amit Sharma answered |
Yes the correct option is A because..... 23×23=529.....
How many numbers lie between square of 12 and 13?
- a)21
- b)23
- c)22
- d)24
Correct answer is option 'D'. Can you explain this answer?
How many numbers lie between square of 12 and 13?
a)
21
b)
23
c)
22
d)
24

|
Gunjan Lakhani answered |
The number of non square numbers
between n² and ( n + 1 )² is 2n
Here,
n = 12,
n + 1 = 13
Therefore ,
Number of natural numbers lie
between 12² and 13² = 2 × 12
= 24
between n² and ( n + 1 )² is 2n
Here,
n = 12,
n + 1 = 13
Therefore ,
Number of natural numbers lie
between 12² and 13² = 2 × 12
= 24
What will be the number of zeros in the square of 400 ?
- a)5
- b)1
- c)3
- d)4
Correct answer is option 'D'. Can you explain this answer?
What will be the number of zeros in the square of 400 ?
a)
5
b)
1
c)
3
d)
4
|
|
Priyanka Sharma answered |
Square of 400 = 160000
Therefore, the number of zeroes is 4
The square root of 169 is
- a)13
- b)1.3
- c)-1.3
- d)13/10
Correct answer is option 'A'. Can you explain this answer?
The square root of 169 is
a)
13
b)
1.3
c)
-1.3
d)
13/10
|
|
Shubham Sharma answered |
13 is the square root of 169.
Without doing any calculation, find the numbers which are surely perfect squares.- a)441
- b)408
- c)153
- d)257
Correct answer is option 'A'. Can you explain this answer?
Without doing any calculation, find the numbers which are surely perfect squares.
a)
441
b)
408
c)
153
d)
257

|
KS Coaching Center answered |
The perfect squares have 0,1,2,4,5,6 or 9 at their units place.
Therefore153,257 and 408 are surely not perfect squares.
Therefore153,257 and 408 are surely not perfect squares.
The square of which of the following would be even number?
- a)2826
- b)7779
- c)1057
- d)131
Correct answer is option 'A'. Can you explain this answer?
The square of which of the following would be even number?
a)
2826
b)
7779
c)
1057
d)
131

|
EduRev Class 8 answered |
Since the square of an odd natural number is odd and that of an even number is an even number.
∴ (i) The square of 431 is an odd number
(∵ 431 is an odd number)
(ii) The square of 2826 is an even nnumber.
(∵ 2826 is an even number)
(iii) The square of 7779 is an odd number
(∵ 7779 is an odd number)
(iv) The square of 131 is an odd nnumber.
(∵ 82004 is an odd number)
Without adding, find the sum. 1 + 3 + 5 + 7 + 9 + 11 + 13
- a)36
- b)49
- c)25
- d)19
Correct answer is option 'B'. Can you explain this answer?
Without adding, find the sum. 1 + 3 + 5 + 7 + 9 + 11 + 13
a)
36
b)
49
c)
25
d)
19

|
Zzz answered |
We have to just add that how many odd no. are ther... moree then we have to take out
Which smallest number should be added to 80 so as to make it a perfect square ?
- a)2
- b)3
- c)1
- d)4
Correct answer is option 'C'. Can you explain this answer?
Which smallest number should be added to 80 so as to make it a perfect square ?
a)
2
b)
3
c)
1
d)
4

|
Target Study Academy answered |
The smallest number to be added to 80 so as to obtain a perfect square number is 1.
80+1=81 and the square root of 81 is 9,so 81 becomes a perfect square.
Without adding, find the sum. 1 + 3 + 5 + 7 + 9- a)16
- b)36
- c)9
- d)25
Correct answer is option 'D'. Can you explain this answer?
Without adding, find the sum. 1 + 3 + 5 + 7 + 9
a)
16
b)
36
c)
9
d)
25

|
Lakesway Classes answered |
Here, we have to find the sum of first five odd natural numbers.
Therefore, 1 + 3 + 5 + 7 + 9 = (5)2 = 25
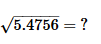
- a)2.24
- b)1.24
- c)1.34
- d)2.34
Correct answer is option 'D'. Can you explain this answer?
a)
2.24
b)
1.24
c)
1.34
d)
2.34

|
Pathways Academy answered |
(5.4756)1/2 = 2.34
Can you explain the answer of this question below: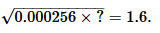
- A:
0.1
- B:
10
- C:
10000
- D:
1000
The answer is C.
0.1
10
10000
1000
|
|
Juhi Desai answered |
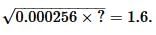
Squaring both side,
⇒ 0.000256 x a = 2.56
⇒ a = 2.56/0.000256
⇒ a = 10000
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Square Root and Cube Root" under Logical Reasoning and Data Interpretative. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.Q.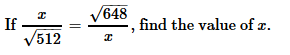
- a)24
- b)12
- c)48
- d)36
Correct answer is 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Square Root and Cube Root" under Logical Reasoning and Data Interpretative. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q.
a)
24
b)
12
c)
48
d)
36

|
Shalini Kumar answered |
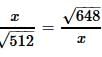
⇒ x2 = √331776
⇒ x2 = 576
⇒ x = √576
⇒ x = 24
Without adding, find the sum of 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
- a)100
- b)64
- c)49
- d)81
Correct answer is option 'A'. Can you explain this answer?
Without adding, find the sum of 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
a)
100
b)
64
c)
49
d)
81

|
Target Study Academy answered |
Total consecutive odd numbers = 10
Thus n = 10
Therefore sum = n × n
= 10× 10 = 100
Which of the following is a perfect square ?
- a)45
- b)81
- c)18
- d)54
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a perfect square ?
a)
45
b)
81
c)
18
d)
54
|
|
Pooja Shah answered |
81 is the square of 9..... 9 × 9 = 81
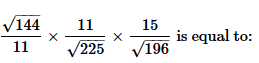
- a)0.85
- b)0.72
- c)2.8
- d)0.4
Correct answer is option 'A'. Can you explain this answer?
a)
0.85
b)
0.72
c)
2.8
d)
0.4

|
Pioneer Academy answered |
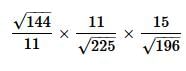
= (12/11) x (11/15) x (15/14)
= 12/14
= 0.85
The perfect square number between 30 and 40 is :
- a)35
- b)39
- c)36
- d)32
Correct answer is option 'C'. Can you explain this answer?
The perfect square number between 30 and 40 is :
a)
35
b)
39
c)
36
d)
32
|
|
Ananya Das answered |
Since 35,32,39 are not perfect squares . hence the only perfect square between 30 and 40 is 36
What is the least perfect square which is divisible by 2, 4 and 6?
- a)36
- b)64
- c)16
- d)18
Correct answer is option 'A'. Can you explain this answer?
What is the least perfect square which is divisible by 2, 4 and 6?
a)
36
b)
64
c)
16
d)
18
|
|
Preeti Khanna answered |
LCM of 2,4,6= 2×1×2×3=12
Least perfect square which is a multiple of 12 is 36.
Least perfect square which is a multiple of 12 is 36.
Which least number should be subtracted from 629 so as to get a perfect square ?
- a)4
- b)5
- c)6
- d)3
Correct answer is option 'A'. Can you explain this answer?
Which least number should be subtracted from 629 so as to get a perfect square ?
a)
4
b)
5
c)
6
d)
3
|
|
Preeti Khanna answered |
If we subtract 4 from the given number, then it becomes 625.
625 is a square of 25.
Hence, the answer is 4
Which is the smallest three-digit perfect square?
- a)100
- b)101
- c)121
- d)144
Correct answer is option 'A'. Can you explain this answer?
Which is the smallest three-digit perfect square?
a)
100
b)
101
c)
121
d)
144
|
|
Shivika Kumari answered |
Yes as the the smallest 3 digit no. is 100 and it is the square of 10 so also a perfect square.
Which is the greatest 4-digit perfect square?
- a)9999
- b)9990
- c)9800
- d)9801
Correct answer is option 'D'. Can you explain this answer?
Which is the greatest 4-digit perfect square?
a)
9999
b)
9990
c)
9800
d)
9801
|
|
Ananya Das answered |
By division method we find the root of 9999 and we get the remainder 198.So subtracting 198 from 9999 we get 9801 as the greatest 4-digit perfect square.
How many non square numbers lie between 112 and 122?
- a)21
- b)23
- c)22
- d) 20
Correct answer is option 'C'. Can you explain this answer?
How many non square numbers lie between 112 and 122?
a)
21
b)
23
c)
22
d)
20

|
EduRev Class 8 answered |
Between 112 and 122
Here, n = 11 and n + 1 = 12
∴ Natural numbers between 112 and 122 are (2 × n) or 2 × 11, i.e. 22.
What could be the possible “one’s digit” of the square root of 625?
- a)5
- b)0
- c)4
- d)8
Correct answer is option 'A'. Can you explain this answer?
What could be the possible “one’s digit” of the square root of 625?
a)
5
b)
0
c)
4
d)
8
|
|
Pooja Shah answered |
625 is square root of 25 and one's digit of 25 is 5
Find the least square number (perfect square) which is exactly divisible by each of the numbers 6, 9, 12a)36b)65c)81d)49Correct answer is option 'A'. Can you explain this answer?
|
|
Prachi Sangwan answered |
It should be 36, 24 is not a perfect square!
Which is the smallest 4-digit perfect square?
- a)1024
- b)1025
- c)1000
- d)1016
Correct answer is option 'A'. Can you explain this answer?
Which is the smallest 4-digit perfect square?
a)
1024
b)
1025
c)
1000
d)
1016

|
Randhir Singh answered |
No, the correct answer is a 1024
The square root of 16641 is- a)129
- b)121
- c)211
- d)229
Correct answer is option 'A'. Can you explain this answer?
The square root of 16641 is
a)
129
b)
121
c)
211
d)
229
|
|
Nikita Singh answered |
Step 1:
- We now need to obtain the digital root of the number. Here's how you do it:
- Split the number up and add each digit together:
1 + 6 + 6 + 4 + 1 = 18 - If the answer is more than one digit, you would add each digit of the answer together again:
1 + 8 = 9 - What is the digital root of number 16,641?
Answer: 9
Step 2:
- So now we know the digital root of 16,641 is 9. Is 9 in the list of digital roots that are always a square root (1, 4, 7 or 9)?
- Answer: YES, 9 is in the list of digital roots that are always perfect squares. We can conclude that 16,641 could be a perfect square!
Factoring
- OK, so now we know that 16,641 could be a perfect square. We have to find the factors of the number to be sure.
- Here are all of the factors of 16,641:
(1 x 16,641) (3 x 5,547) (9 x 1,849) (43 x 387) (129 x 129)
Hence the answer is 129.
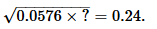
- a)10
- b)1
- c)0.1
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
a)
10
b)
1
c)
0.1
d)
None of these

|
BT Educators answered |
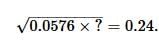
Squaring both side,
⇒ 0.0576 x a = 0.0576
⇒ a = 1
Find the least number that must be subtracted from 5607 so as to get a perfect square.- a)130
- b)135
- c)131
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Find the least number that must be subtracted from 5607 so as to get a perfect square.
a)
130
b)
135
c)
131
d)
none of these

|
Sounak Sengupta answered |
Square of 75 is 5625
square of 74 is 5476
so use must get 5476
5607 - x is 5476
x is 131
square root of 5476 is 74
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Squares and Square Roots, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.Q.Which of the following is a perfect square number?- a)222222
- b)23453
- c)1681
- d)1057
Correct answer is 'C'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Squares and Square Roots, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
Which of the following is a perfect square number?
a)
222222
b)
23453
c)
1681
d)
1057

|
Sanjana Bose answered |
A number is a perfect square (or a square number) if its square root is an integer; that is to say, it is the product of an integer with itself. Here, the square root of 1681 is 41.
Therefore, the square root of 1681 is an integer, and as a consequence 1681 is a perfect square.
As a consequence, 41 is the square root of 1681.
What will be the number of digits in the square root of 25600?
- a)3
- b)2
- c)5
- d)4
Correct answer is option 'A'. Can you explain this answer?
What will be the number of digits in the square root of 25600?
a)
3
b)
2
c)
5
d)
4
|
|
Preeti Khanna answered |
The square root of 25600 is 160. Hence, number of digits is 3.
By which smallest number 48 must be divided so as to make it a perfect square ?
- a)2
- b)3
- c)6
- d)4
Correct answer is option 'B'. Can you explain this answer?
By which smallest number 48 must be divided so as to make it a perfect square ?
a)
2
b)
3
c)
6
d)
4
|
|
Anita Menon answered |
By Prime factorisation, we have 48=2*2*2*2*3. We have two pairs of 2 but no pair of 3. Hence 48 must be divided by 3 to make it a perfect square.
Can you explain the answer of this question below: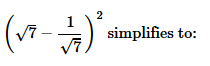
- A:

- B:
7/36
- C:
36/7
- D:
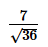
The answer is c.
7/36
36/7
|
|
Meera Rana answered |

► Using identity, (a-b)2 = a2 + b2 - 2ab
► Here a = √7 and b = 1/√7

= (√7)2 + (1/√7)2 - 2. √7.1/√7
= 7 + 1/7 - 2
= 5 + 1/7
= 36/7
What will be the number of digits in the square root of 1296?
- a)2
- b)3
- c)1
- d)4
Correct answer is option 'A'. Can you explain this answer?
What will be the number of digits in the square root of 1296?
a)
2
b)
3
c)
1
d)
4
|
|
Preeti Khanna answered |
The square root of 1296 is 36.
Hence, number of digits os 2
The least perfect square, which is divisible by each of 21, 36 and 66 is:- a)213444
- b)214344
- c)214434
- d)231444
Correct answer is option 'A'. Can you explain this answer?
The least perfect square, which is divisible by each of 21, 36 and 66 is:
a)
213444
b)
214344
c)
214434
d)
231444

|
Ishani Rane answered |
L.C.M of 21,36,66=2772
Now, 2772=2*2*3*3*7*11
Hence to make it a perfect square , it must be multiplied by 7*11
∴ The required number is 2^2*3^3*7^2*11^2
= 213444
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of plants in each row.
- a)55
- b)65
- c)45
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of plants in each row.
a)
55
b)
65
c)
45
d)
none of these
|
|
Rajeev Kumar answered |
Let the number of rows be x
Thus, the each row contains x plants.
The total number of plants in the garden = number of rows × number of plants in each rows
Thus,
2025=x×x
=>x2 =2025
=>x= 3×3×3×3×5×5
=3×3×5
=45
Thus, there are 45 rows and each row contains 45 plants.
Thus, the each row contains x plants.
The total number of plants in the garden = number of rows × number of plants in each rows
Thus,
2025=x×x
=>x2 =2025
=>x= 3×3×3×3×5×5
=3×3×5
=45
Thus, there are 45 rows and each row contains 45 plants.
Sum of squares of two numbers is 145. If square root of one number is 3, find the other number.
- a)136
- b)9
- c)64
- d)8
Correct answer is option 'D'. Can you explain this answer?
Sum of squares of two numbers is 145. If square root of one number is 3, find the other number.
a)
136
b)
9
c)
64
d)
8

|
Saksham Maitri answered |
?= (8.97)²-(8.01)² ?= 16.98×0.96 ?=16..... so the answer is 16( d)
What is the length of the diagonal of a rectangle having dimensions 3 cm and 4 cm?
- a)5
- b)7
- c)1
- d)4
Correct answer is option 'A'. Can you explain this answer?
What is the length of the diagonal of a rectangle having dimensions 3 cm and 4 cm?
a)
5
b)
7
c)
1
d)
4

|
EduRev Class 8 answered |
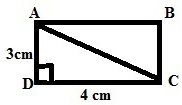
Here let us consider ABCD is a rectangle given in the figure.
AD = 3 cm (Breadth)
DC = 4 cm (Length)
To Find:
AC (Diagonal)
We know that, Triangle ADC is a right triangle, right angled at D. So by using Pythagorus Theorem
Length^2 + Breadth^2 = Hypotenuse^2 (diagonal)
DC^2 + AD^2 = AC^2
=> 4^2 + 3^2 = AC^2
=> 16 + 9 = AC^2
=> 25 = AC^2
=> AC = √25 = 5
Therefore the length of the diagonal AC is 5 cm.
In a right angle triangle ABC, right angled at B, AB = 6cm, BC = 8cm ,then AC = ____ .
- a)10
- b)12
- c)21
- d)14
Correct answer is option 'A'. Can you explain this answer?
In a right angle triangle ABC, right angled at B, AB = 6cm, BC = 8cm ,then AC = ____ .
a)
10
b)
12
c)
21
d)
14
|
|
Aarav Sharma answered |
Given information:
- In a right-angled triangle ABC, angle B is right-angled.
- AB = 6 cm, BC = 8 cm.
To find: AC.
We can use the Pythagorean theorem to solve this problem. The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Applying the Pythagorean theorem, we have:
AC^2 = AB^2 + BC^2
Substituting the given values, we get:
AC^2 = 6^2 + 8^2
AC^2 = 36 + 64
AC^2 = 100
Taking the square root of both sides, we get:
AC = √100
AC = 10
Hence, the length of side AC is 10 cm.
Answer: a) 10 cm.
- In a right-angled triangle ABC, angle B is right-angled.
- AB = 6 cm, BC = 8 cm.
To find: AC.
We can use the Pythagorean theorem to solve this problem. The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Applying the Pythagorean theorem, we have:
AC^2 = AB^2 + BC^2
Substituting the given values, we get:
AC^2 = 6^2 + 8^2
AC^2 = 36 + 64
AC^2 = 100
Taking the square root of both sides, we get:
AC = √100
AC = 10
Hence, the length of side AC is 10 cm.
Answer: a) 10 cm.
Chapter doubts & questions for Square Roots & Cube Roots - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Square Roots & Cube Roots - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

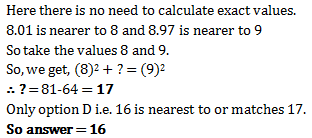

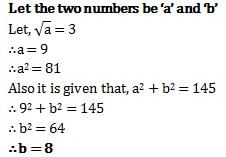
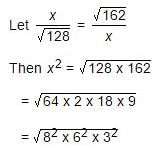
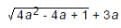 is:
is: