All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of Statistics for CDS Exam
If scores of 10 students in a class are arranged in the table (shown below), then what is the Range of their scores? 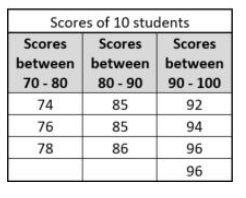
- a)16
- b)18
- c)20
- d)22
- e)24
Correct answer is option 'D'. Can you explain this answer?
If scores of 10 students in a class are arranged in the table (shown below), then what is the Range of their scores?
a)
16
b)
18
c)
20
d)
22
e)
24
|
|
Anaya Patel answered |
The difference between the highest and lowest observations in a given data is called its Range.
Score of 10 students in ascending order = 74, 76, 78, 85, 85, 86, 92, 94, 96, 96
Then the difference between the highest and lowest value will be 96 - 74
Range = 22
The average (arithmetic mean) of the prime numbers that lie between 10 and 20 is how much greater than the average of the
prime numbers that lie between 1 and 10?- a)10.25
- b)10.75
- c)11
- d)11.25
- e)11.75
Correct answer is option 'B'. Can you explain this answer?
The average (arithmetic mean) of the prime numbers that lie between 10 and 20 is how much greater than the average of the
prime numbers that lie between 1 and 10?
prime numbers that lie between 1 and 10?
a)
10.25
b)
10.75
c)
11
d)
11.25
e)
11.75
|
|
Aditya Kumar answered |
Given:
2 sets of Prime Numbers – let’s call them Sets A and B:
- Set A = {2, 3, 5, 7}
- Set B = {11, 13, 17, 19}
To find: Difference between Average(Set B) and Average (Set A)
- That is, Average(Set B) – Average (Set A)
Approach:
- In order to find the answer, we need to know the values of Average(Set A), Average(Set B)
- Since we know all the elements in each of Set A and B, we will be easily able to find the required averages.
Working out:
Correct Answer – Option B
If scores of 10 students in a class are arranged in the table (shown below), then what is the Median of their scores?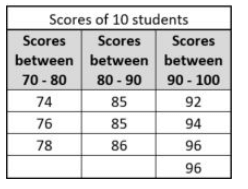
- a)84
- b)84.5
- c)85
- d)85.5
- e)86
Correct answer is option 'D'. Can you explain this answer?
If scores of 10 students in a class are arranged in the table (shown below), then what is the Median of their scores?
a)
84
b)
84.5
c)
85
d)
85.5
e)
86

|
Bank Exams India answered |
Score of 10 students in ascending order = 74, 76, 78, 85, 85, 86, 92, 94, 96, 96
Since number of observations is even, the median is given by finding the average or mean of the two middle most observations.
So, median = (85 + 86)/2
Median = 85.5
When positive integer y is added to each of the first n non-negative integers, which of the following statements is true?
I. If the median of the resulting numbers is 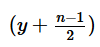 then n is oddII. The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
then n is oddII. The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
When positive integer y is added to each of the first n non-negative integers, which of the following statements is true?
I. If the median of the resulting numbers is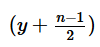 then n is odd
then n is odd
I. If the median of the resulting numbers is
II. The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above

|
Naroj Boda answered |
Given:
- The list of first n non-negative integers: {0, 1, 2, 3, . . . , n – 1}
- Positive integer y is added to each integer in this list: {0 + y, 1 + y, 2 + y, . . . n – 1 + y}
- = {y, y + 1, y + 2, . . . , y + n – 1}
To Find: Which of the 3 statements is/are true?
Approach:
- Since these 3 statements deal with:
- Mean of the first n positive integers
- Mean of the resulting numbers
- And, Median of the resulting numbers,
We will first find the expressions for these 3 quantities.
2. Then, we’ll evaluate the 3 statements one by one to determine which is/are true for all values of y and n
Working out:
- Finding the expressions for the 3 quantities featured in Statements I – III
- Finding Mean of the first n positive integers
- Sum of first n positive integers =
- So, the mean of the first n positive integers =
- (n+2/2)
- Sum of first n positive integers =
- Finding Mean of the first n positive integers
- Finding Mean of the Resulting Numbers
- The resulting numbers are: {y, y + 1, y + 2, . . . , y + n – 1}
- These numbers form an increasing arithmetic sequence of n terms.
- First term of the sequence = y
- Last term of the sequence = y + n -1
- So, the sum of these numbers =
- These numbers form an increasing arithmetic sequence of n terms.
- The resulting numbers are: {y, y + 1, y + 2, . . . , y + n – 1}
- Finding Median of the Resulting Numbers
- The resulting numbers are: {y, y + 1, y + 2, . . . , y + n – 1}
- The total number of elements in this set is (y + n – 1) – y + 1 = n
- These numbers form an increasing arithmetic sequence of n terms.
- Now, in an ordered list that has:
- An even number of elements (say 4 elements), the median of the list is equal to the average of the middle 2 elements of the list
- An odd number of elements (Say 5 elements), the median of the list is equal to the middle element in the list
- Case 1: If n is odd,
- Then, Median = the middle element in the list of resulting numbers
- The first term in the list is y + 0 and the last term is y +(n – 1)
- So, the Median =
- (Note: If the above expression for the Median is not intuitive to you, you can arrive at it by taking a few easy values of n. For example:
- If n = 3, the list is {y, y + 1, y + 2}. So, the median = y + 1
- If n = 5, the list is {y, y + 1. y + 2, y + 3, y + 4}. So, the median = y + 2
- Similarly, if n = 7, the list goes from y to y + 6 and the median = y + 3
- From these examples, the pattern for how the value of Median changes with n becomes easy to see)
- Case 2: If n is even,
- This means, the median of the list is equal to the
- This means, the median of the list is equal to the
- Evaluating Statement I
- If the median of the resulting numbers is
then n is odd
- In our calculation of the Median of the Resulting Numbers, observe that the median is always equal to
, whether n is even or odd.
- Therefore, Statement I is not correct
- If the median of the resulting numbers is
- Evaluating Statement II
- The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
- From our calculations of the Mean and Median of the Resulting Numbers, we see that:
- Mean of the Resulting numbers =
- Median =
- Mean of the Resulting numbers =
- From our calculations of the Mean and Median of the Resulting Numbers, we see that:
- So, Statement II is indeed true.
- The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
- Evaluating Statement III
- The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
- From our calculations above, we see that:
- Mean of the Resulting numbers =
- Mean of the first n positive integers
- Mean of the Resulting numbers =
- Note that
is not equal to
. Therefore, it is wrong to say that Mean of the Resulting Numbers is y units greater than the Mean of the first n positive integers.
- So, Statement III is not true.
- Getting to the answer
- Of the 3 statements, we see that only Statement II is true.
Looking at the answer choices, we see that the correct answer is Option B
From January to October, the revenue of a textile manufacturing plant averaged 20,000 USD per month. What average monthly revenue in USD was required in November and December, if the plant had a goal to achieve 330,000 USD in revenue by the end of the calendar year? - a)65000
- b)75000
- c)80000
- d)100000
- e)110000
Correct answer is option 'A'. Can you explain this answer?
From January to October, the revenue of a textile manufacturing plant averaged 20,000 USD per month. What average monthly revenue in USD was required in November and December, if the plant had a goal to achieve 330,000 USD in revenue by the end of the calendar year?
a)
65000
b)
75000
c)
80000
d)
100000
e)
110000

|
Sravya Joshi answered |
Step 1: Question statement and Inferences
We are given that the average revenue for a textile manufacturing plant was 20,000 USD per month from January till October. The plant wanted to achieve a total revenue of 330,000 USD by the end of the year.
We have to find the average revenue that the plant must achieve in November and December to meet its total targeted revenue.
Let’s say the monthly revenues for the plant are M1, M2, M3 ….. M12.
Now, we don’t know the individual values of the monthly revenues. But we do know that the average monthly revenue for the first ten months is USD 20,000. Thus,
Hence,
M1 + M2 + M3 …. + M10 = 200,000 ………… (1)
The targeted revenue for the year is USD 330,000. Thus,
M1 + M2 + M3 …. + M11 + M12 = 330,000 ………… (2)
Step 2: Finding required values
The question wants us to find the average monthly revenue for November and December. Let’s say the average monthly revenue for these two months is X. Thus,
That is, M11 + M12 = 2X ………… (3)
Substituting values from Equations 1 and 3 in Equation 2:
200,000 + 2X = 330,000
2X = 130,000
X = 65,000
So, the average monthly revenue for the months of November and December is 65,000 USD.
Answer: Option (A)
Set X is given by {a, 2a, 3a, 4a, 5a} where ‘a’ is a positive integer. If element ‘a’ in Set X is replaced by ‘b’ and b < a, then which of the following must be true?I.Mean would not change.II.Median would not change.III. Standard deviation would not change- a)I only
- b)II only
- c)III only
- d)Both I and II
- e)Both II and III
Correct answer is option 'B'. Can you explain this answer?
Set X is given by {a, 2a, 3a, 4a, 5a} where ‘a’ is a positive integer. If element ‘a’ in Set X is replaced by ‘b’ and b < a, then which of the following must be true?
I.Mean would not change.
II.Median would not change.
III. Standard deviation would not change
a)
I only
b)
II only
c)
III only
d)
Both I and II
e)
Both II and III

|
Krithika Datta answered |
Solution:
Given, Set X = {a, 2a, 3a, 4a, 5a}
If element a in Set X is replaced by b and b < a,="" then="" the="" set="" becomes="" {b,="" 2b,="" 3b,="" 4b,="" />
To find out which of the given options is true, we need to calculate the mean, median, and standard deviation of both sets and compare them.
Mean:
Mean of Set X = (a + 2a + 3a + 4a + 5a)/5 = 3a
Mean of {b, 2b, 3b, 4b, 5b} = (b + 2b + 3b + 4b + 5b)/5 = 3b
Since a > b, the mean of the second set is less than the mean of the first set. Therefore, option I is not true.
Median:
Median of Set X = 3a
Median of {b, 2b, 3b, 4b, 5b} = 3b
Since the median of both sets is the third element, which is 3a and 3b respectively, the median does not change. Therefore, option II is true.
Standard deviation:
Standard deviation of Set X can be calculated as follows:
σ = √[(1/5) * {(a - 3a)² + (2a - 3a)² + (3a - 3a)² + (4a - 3a)² + (5a - 3a)²}]
= √[(1/5) * {4a² + a² + a² + 4a² + 16a²}]
= √(26a²/5)
Standard deviation of {b, 2b, 3b, 4b, 5b} can be calculated as follows:
σ = √[(1/5) * {(b - 3b)² + (2b - 3b)² + (3b - 3b)² + (4b - 3b)² + (5b - 3b)²}]
= √[(1/5) * {4b² + b² + b² + 4b² + 16b²}]
= √(26b²/5)
Since a > b, the standard deviation of the first set is greater than the standard deviation of the second set. Therefore, option III is not true.
Hence, the correct answer is option II only.
Given, Set X = {a, 2a, 3a, 4a, 5a}
If element a in Set X is replaced by b and b < a,="" then="" the="" set="" becomes="" {b,="" 2b,="" 3b,="" 4b,="" />
To find out which of the given options is true, we need to calculate the mean, median, and standard deviation of both sets and compare them.
Mean:
Mean of Set X = (a + 2a + 3a + 4a + 5a)/5 = 3a
Mean of {b, 2b, 3b, 4b, 5b} = (b + 2b + 3b + 4b + 5b)/5 = 3b
Since a > b, the mean of the second set is less than the mean of the first set. Therefore, option I is not true.
Median:
Median of Set X = 3a
Median of {b, 2b, 3b, 4b, 5b} = 3b
Since the median of both sets is the third element, which is 3a and 3b respectively, the median does not change. Therefore, option II is true.
Standard deviation:
Standard deviation of Set X can be calculated as follows:
σ = √[(1/5) * {(a - 3a)² + (2a - 3a)² + (3a - 3a)² + (4a - 3a)² + (5a - 3a)²}]
= √[(1/5) * {4a² + a² + a² + 4a² + 16a²}]
= √(26a²/5)
Standard deviation of {b, 2b, 3b, 4b, 5b} can be calculated as follows:
σ = √[(1/5) * {(b - 3b)² + (2b - 3b)² + (3b - 3b)² + (4b - 3b)² + (5b - 3b)²}]
= √[(1/5) * {4b² + b² + b² + 4b² + 16b²}]
= √(26b²/5)
Since a > b, the standard deviation of the first set is greater than the standard deviation of the second set. Therefore, option III is not true.
Hence, the correct answer is option II only.
What is x, if the average of five numbers, x, 6, 3, 15 and 12 is equal to the median?(1) 6 < x < 12(2) x is median of the five numbers- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
What is x, if the average of five numbers, x, 6, 3, 15 and 12 is equal to the median?
(1) 6 < x < 12
(2) x is median of the five numbers
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Sravya Joshi answered |
Steps 1 & 2: Understand Question and Draw Inferences
Arithmetic mean is same as median
- As there are five elements, median must be one of them
Step 3: Analyze Statement 1
6<x<12
- As x is less than two numbers (12, 15) and greater than the other two (3, 6), it must be the median
- x is the average of all the numbers
It is given that the mean is same as the median
- (3+6+12+15+x)/5 = x
- 3+6+12+15+x = 5x
- 4x = 36
- x = 9
Therefore statement 1 is sufficient.
Step 4: Analyze Statement 2
x is median of the five numbers
It is given that the mean is same as the median
- (3+6+12+15+x)/5 = x
- 3+6+12+15+x = 5x
- 4x = 36
- x = 9
Therefore statement 2 is sufficient.
Step 5: Analyze Both Statements Together (if needed)
We get a unique answer in step 3 and step 4, so this step is not required
Answer: Option (D)
Set P consists of 10 positive integers arranged in order of increasing magnitude. The difference between any two successive
terms of the set is 4. If the two largest terms of the set are removed, what is the decrease in the average(arithmetic mean) of
the set?- a)0
- b)2
- c)4
- d)6
- e)8
Correct answer is option 'C'. Can you explain this answer?
Set P consists of 10 positive integers arranged in order of increasing magnitude. The difference between any two successive
terms of the set is 4. If the two largest terms of the set are removed, what is the decrease in the average(arithmetic mean) of
the set?
terms of the set is 4. If the two largest terms of the set are removed, what is the decrease in the average(arithmetic mean) of
the set?
a)
0
b)
2
c)
4
d)
6
e)
8

|
Rutuja Banerjee answered |
Given:
- Set P is an arithmetic sequence with common difference(d) = 4 and number of terms(n) = 10
- Let the first term be a.
- So, the other 9 terms = {a+d, a+2d, ……a+9d}
- (a+9d) and (a+8d) are removed
To Find: Decrease in the average of the set after removal of (a+9d) and (a+8d)
Approach:
- To calculate the decrease in the average of the sequence, we need to calculate the average of the sequences before and after removal of the terms (a+9d) and (a+8d)
- Calculating Average of the original set P
- As we know all the terms of the set P in terms of a, we can calculate the sum of all the terms in set P using the sum of an arithmetic sequence formula.
- Once, we know the sum of an arithmetic sequence P, we can calculate the average of the arithmetic sequence by dividing the sum by the number of terms(i.e. 10)
- As we know all the terms of the set P in terms of a, we can calculate the sum of all the terms in set P using the sum of an arithmetic sequence formula.
- Calculating Average of set P after removal of (a+9d) and (a+8d)
- The new sum of the arithmetic sequence can be calculated by subtracting the sum of (a+9d) and (a+8d) from the original sum of the arithmetic sequence
- The new average can then be calculated by dividing the new sum by the remaining terms in the sequence(i.e. 8)
- The new sum of the arithmetic sequence can be calculated by subtracting the sum of (a+9d) and (a+8d) from the original sum of the arithmetic sequence
Working out:
- Calculating Average of the original set P
- Sum of the 10
Hence, the average decreased by 4 units.
Answer : C
If a, b and c are positive integers, what is the average (arithmetic mean) of a and c?
1. The average of a + b and 4 is 6
2. The average of a + c and b is 18- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If a, b and c are positive integers, what is the average (arithmetic mean) of a and c?
1. The average of a + b and 4 is 6
2. The average of a + c and b is 18
1. The average of a + b and 4 is 6
2. The average of a + c and b is 18
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Sanskriti Ahuja answered |
Step 1 & 2: Understand Question and Draw Inference
Given: Integers a, b, c > 0
To find: (a+c) /2
To find: (a+c) /2
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘The average of a + b and 4 is 6’
- This equation doesn’t indicate to us the value of a + c
- So, Statement 1 is not sufficient to answer the question
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘The average of a + c and b is 18’
- We need to find the value of a + c. However, the above equation gives us the value of a + b + c
- Multiple values of a + c will satisfy this equation
- For example, a + c = 35 and b = 1 or a + c = 34 and b = 2 etc.
- Multiple values of a + c will satisfy this equation
- Therefore, Statement 2 alone is not sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: a + b = 8
- From Statement 2: a + b + c = 36
- Combining the 2 statements: c = 36 – 8 = 28
- However, we do not yet know the value of a
- So, we are still unable to find the value of a + c
So, even the 2 statements together are not sufficient to answer the question
Answer: Option E
In an inter-state Mathematics Olympiad, the distribution of the scores obtained by the participating students is symmetric about
the mean m. 68 percent of the distribution lies within one standard deviation d of the mean and 95 percent of the distribution lies
within 2 standard deviations of the mean. If there were 70 students who scored more than Ricky, 428 students who scored less than Ricky and none that scored equal to him, his score must lie between- a)m - 2d and m – d
- b)m - d and m
- c)m and m + d
- d)m + d and m + 2d
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
In an inter-state Mathematics Olympiad, the distribution of the scores obtained by the participating students is symmetric about
the mean m. 68 percent of the distribution lies within one standard deviation d of the mean and 95 percent of the distribution lies
within 2 standard deviations of the mean. If there were 70 students who scored more than Ricky, 428 students who scored less than Ricky and none that scored equal to him, his score must lie between
the mean m. 68 percent of the distribution lies within one standard deviation d of the mean and 95 percent of the distribution lies
within 2 standard deviations of the mean. If there were 70 students who scored more than Ricky, 428 students who scored less than Ricky and none that scored equal to him, his score must lie between
a)
m - 2d and m – d
b)
m - d and m
c)
m and m + d
d)
m + d and m + 2d
e)
None of the above

|
Aditya Sharma answered |
Given:
- 70 students scored more than Ricky
- 428 students scored less than Ricky
- None scored equal to Ricky
- Number of students = 70 + 428 + 1 = 499
- When arranged in ascending order, Ricky’s score would be at 429 place.
- Mean score = m
- Standard deviation of the scores = d
To Find:: The range in which Ricky’s score should lie
Approach:
- As the options are given in terms of m and d, we first need to understand the distribution curve.
- The above distribution is symmetric about the mean m
- 68% of the distribution lies within 1 standard deviation, the distribution would have 68% / 2 = 34 of data sets on either sides of the mean.
- Similarly, 95% of the distribution lies within 2 standard deviation, the distribution would have 95 % / 2 = 47.5 % of data sets on either sides of the mean.
- Since we know the position of Ricky’s score and we know the number of students who appeared in the Olympiad, we can calculate the number of students between consecutive standard deviations of the mean score.
Working out:
- Since, 499 students appeared in the Olympiad, the mean score would lie at position 250
- So, number of students whose score lies within 1 standard deviation = 68% of 500 = 340
- So, number of students whose score is between m and m+d = 340 / 2 = 170 i.e. position of scores of students who lie between m and m + d will be between 250 and (250+170) = 420
- We need not bother with scores of students whose position is less than 250, as we are concerned about the position of student who is at 429th place.
- As Ricky’s score is at 429 place, his score does not lie between m and m+ d. Let’s see if he lies between m + d and m + 2d.
- Number of students whose score lie within 2 standard deviations = 95% of 500 = 475
- Number of students whose score lie between m and m + 2d = 475/2 = 237
- So, number of students whose score lie between m + d and m + 2d = 237– 170 = 67
- So, the position of students whose score lie between m + d and m + 2d will be between 420 and 420 + 67 = 487
- As Ricky’s score lies at a position of 429, his score would lie between m + d and m + 2d
Answer : D
S is standard deviation of a, b, and c, if a constant C is added to all the three digits, the new standard deviation will be?- a)S
- b)S*C
- c)S*3C
- d)S+C
- e)S+3C
Correct answer is option 'A'. Can you explain this answer?
S is standard deviation of a, b, and c, if a constant C is added to all the three digits, the new standard deviation will be?
a)
S
b)
S*C
c)
S*3C
d)
S+C
e)
S+3C

|
Mihir Ghoshal answered |
Finding standard deviation of {a, b, c}
Step 1
Let Mean of {a,b,c} = {a + b + c}/3 = M
Step 2
Distances of each point from the mean:
- a-M
- b-M
- c-M
Step 3
Squared Distance from Mean
- = (a -M)2 + (b-M)2 + (c -M)2
Step 4
- Average = {(a -M)2 + (b-M)2 + (c -M)2} /3
Step 5
- Standard Deviation = √ {(a -M)2 + (b-M)2 + (c -M)2} /√ 3 = S
Finding standard deviation of {a+C, b+C, c+C}
Remember: The standard deviation of a set remains the same even if a constant is added to all the elements of the set
So the standard deviation of this set should be S.
Alternatively you can calculate the standard deviation of this set as shown below by following same step by step method.
Step 1
Mean of {a+C, b+C, c+C} = (a + b + c )/3 + C = M + C
Step 2
Distances of each point from the mean:
- a+C – M-C = a – M
- b+C -M-C = b-M
- c+C – M-C = c-M
Step 3
Squared Distance from Mean
- = (a -M)2 + (b-M)2 + (c -M)2
Step 4
- Average = {(a -M)2 + (b-M)2 + (c -M)2} /3
Step 5
Standard Deviation = √ {(a -M)2 + (b-M)2 + (c -M)2} /√ 3 = S
Answer: Option (A)
In triangle ABC (not shown), is the range of the angles of the triangle greater than 90o?
(1) The median angle of triangle ABC is 70o
(2) The difference between the two larger angles of triangle ABC
is 10o- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
Correct answer is option 'B'. Can you explain this answer?
In triangle ABC (not shown), is the range of the angles of the triangle greater than 90o?
(1) The median angle of triangle ABC is 70o
(2) The difference between the two larger angles of triangle ABC
is 10o
(1) The median angle of triangle ABC is 70o
(2) The difference between the two larger angles of triangle ABC
is 10o
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
answer the question asked, and additional data specific to the problem are needed

|
Prateek Gupta answered |
Step 1 & 2: Understand Question and Draw Inference
Given: A triangle ABC
- Let the angles of the triangle be x, y, z in increasing order of magnitude.
- We know x + y + z = 180o . . . (1)
To find: Is z – x > 90o ?
Step 3 : Analyze Statement 1 independent
(1) The median angle of triangle ABC is 70o.
But we do not know if x < 10o . So, Statement 1 alone is not sufficient.
Step 4 : Analyze Statement 2 independent
(2) The difference between the two larger angles of triangle ABC is 10o
But we do not know if 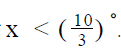 So, Statement 2 alone is not sufficient.
So, Statement 2 alone is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: y = 70
- From Statement 2: z – y = 10
- By combining these two equations, we’ll get a unique value of z
- From (1), we’ll get a unique value of x
Since we now know the values of x, y and z, we’ll be able to answer the question on the range of the angles.
The two statements together are sufficient to answer the question.
The two statements together are sufficient to answer the question.
Answer: Option C
Arrange the following sets in the order of the increasing magnitude of their mean to standard deviation ratio.
I. {50, 60, 70, 80}
II. {35, 40, 45, 50}
III. {90, 110, 130, 150}- a)I < II < III
- b)II < III < I
- c)II < I < III
- d)III < I < II
- e)III < II < I
Correct answer is option 'D'. Can you explain this answer?
Arrange the following sets in the order of the increasing magnitude of their mean to standard deviation ratio.
I. {50, 60, 70, 80}
II. {35, 40, 45, 50}
III. {90, 110, 130, 150}
I. {50, 60, 70, 80}
II. {35, 40, 45, 50}
III. {90, 110, 130, 150}
a)
I < II < III
b)
II < III < I
c)
II < I < III
d)
III < I < II
e)
III < II < I

|
Sanskriti Ahuja answered |
Given:
- {50, 60, 70, 80}
- {35, 40, 45, 50}
- {90, 110, 130, 150}
To Find: Arrange the sets in increasing order of the (Mean / Standard deviation) ratio.
Approach:
- Let’s assume the mean of set-I be m and standard deviation be d.
- We would try to express the terms of the other two sets in terms of set-I for establishing a relation between the standard deviations and the means of the set
- Also, we will use the following properties of standard deviation to calculate the standard deviation of the other sets in terms of d:
- If all the numbers of a set are multiplied or divided by the same constant x, the standard deviation is also multiplied or divided by |x| respectively.
- If all the numbers of a set are increased or decreased by the same constant x, the standard deviation of the set does not change.
Working out:
- Set-I: {50, 60, 70, 80}
- Assuming the mean of set {50, 60, 70, 80} as m and standard deviation be d
- Ratio = m/d………(1)
- Set-II: {35, 40, 45, 50}
- {50, 60, 70, 80} → Dividing all the terms of the set by 2, results in the standard deviation of d/2 and mean of m/2 . The set becomes = {25, 30, 35, 40}
- Adding 10 to all the numbers of the set {25, 30, 35, 40} does not change its standard deviation but increases its mean by 10. The set becomes = {35, 40, 45, 50}
- Hence, the set {35, 40, 45, 50} has a standard deviation of d/2 and mean of
- Set-III: {90, 110, 130, 150}
- {50, 60, 70, 80}→ Multiplying all the terms of the set by 2, results in standard deviation of 2d and mean of 2m. The set becomes = { 100, 120, 140, 160}
- Subtracting 10 from all the terms of the set {100, 120, 140, 160} does not change its standard deviation but decreases the mean by 10. The set becomes = {90, 110, 130, 150}
- Hence, the set {90, 110, 130, 150} has a standard deviation of 2d and mean of 2m – 10
- Comparing (1), (2) and (3), we can arrange the sets in the ratio of mean to standard deviation as
a. III < I < II
Answer : D
A, B, C, D, E, and F are six consecutive positive odd integers in increasing order. What is the value of the median of these six integers?(1) The sum of the two smallest integers is greater than the largest integer by 13 (2) The average (arithmetic mean) of these integers is 26- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
A, B, C, D, E, and F are six consecutive positive odd integers in increasing order. What is the value of the median of these six integers?
(1) The sum of the two smallest integers is greater than the largest integer by 13
(2) The average (arithmetic mean) of these integers is 26
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Mihir Ghoshal answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given six consecutive positive odd integers. We have to find the median of this set of integers.
Since the integers are consecutive odd integers, they can be represented with the help of a positive integer n, as follows:
A = 2*n + 1
B = 2*n + 3
C = 2*n + 5
D = 2*n + 7
E = 2*n + 9
F = 2*n + 11
Now, we know that, for a series in increasing order, the median is the middle number in case of odd number of integers and the average of the middle two numbers in case of even number of integers.
Since there are even number (6) of integers in this series, the median will be the average of the 3rd and 4th number:
Thus, in order to find the value of the median, we need to know the value of n. So, the question becomes “what is the value of n?”
Step 3: Analyze Statement 1
The sum of the two smallest integers is greater than the largest integer by 13 ?
Now, the two smallest integers in the sequence are 2n+1 and 2n+3 and their sum = 4n+4
The largest integer in the sequence is 2n+11.
Per statement (1), the difference between these two should be 13. So,
(4n+4) – (2n+11) = 13
2n-7 = 13
2n = 20
Thus, n =10.
Now, since we have found the value of n, we can find the median.
Hence, statement (1) is sufficient to find a unique value of the median.
Step 4: Analyze Statement 2
The average (arithmetic mean) of these integers is 26
Thus:
Now, since we have found the value of n, we can find the median.
Hence, statement (2) is sufficient to find a unique value of the median
Step 5: Analyze Both Statements Together (if needed)
Since statement (1) and (2) alone are sufficient to answer the question, we don’t need to perform this step.
Answer: Option (D)
Set X consists of 10 integers and has median of 20 and a range of 20. What is the value of the greatest possible integer that can be present in the set?- a)32
- b)37
- c)40
- d)43
- e)50
Correct answer is option 'C'. Can you explain this answer?
Set X consists of 10 integers and has median of 20 and a range of 20. What is the value of the greatest possible integer that can be present in the set?
a)
32
b)
37
c)
40
d)
43
e)
50

|
Sravya Joshi answered |
Given: Median and Range
To Find: The greatest possible number
Let the lowest number be P and the greatest number be Q
Given:
- Range = 20
- Q – P = 20
- Q = 20 + P
Here we expressed Q (the highest value) in terms of P (the lowest value).
Therefore by finding the max value of P, we can find the max value of Q.
Now we know that the median = 20
- So, the greatest value which P can take = 20
- This means that at least 6 numbers in the given set of 10 numbers will have the same value of 20. This ways, when the 10 numbers are arranged in an ascending order, the median will be equal to half the sum of the 5th and 6th term. And so, will be equal to 20. The 7th, 8th and 9th terms (when the 10 numbers are arranged in an ascending order) can take any value between 20 and 40. The 10th term will be 40.
- That is, Q = 40
- Thus, the greatest integer that can be present in this set is 40.
Remember -The difference between any two numbers in a set cannot be greater than the range.
Answer: Option (C)
While debugging a piece of software, an engineer records the number of bugs he finds each day. If the number of bugs found by the engineer reduces by x with each passing day, what is the standard deviation of the number of bugs found by the engineer during the last 7 days?
(1) The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7
days is 24.
(2) The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'A'. Can you explain this answer?
While debugging a piece of software, an engineer records the number of bugs he finds each day. If the number of bugs found by the engineer reduces by x with each passing day, what is the standard deviation of the number of bugs found by the engineer during the last 7 days?
(1) The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7
days is 24.
(2) The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24
(1) The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7
days is 24.
(2) The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Rutuja Banerjee answered |
Step 1 & 2: Understand Question and Draw Inference
- Let the number of bugs the engineer found on day 1 = a
- Number of bugs he found on day 2 = a-x
- Number of bugs he found on day 3 = a- x- x = a - 2x
- Number of bugs he found on day n = a - (n-1)x
- Thus the number of bugs found by the engineer is a decreasing Arithmetic Progression.
To Find: standard deviation of the number of bugs found during the last 7 days
- To find the standard deviation of a set, we need to know the following:
- Number of data points in the set
- We are given the number of days = 7
- Number of data points in the set
- Distance of each data point of the set from the mean of the set
- We are given the difference between the bugs found on consecutive days = x
- If we know the value of x, we can find the distance of each data point from its mean.
- So, we need to know the value of x to calculate the standard deviation
Step 3 : Analyze Statement 1 independent
- The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7 days is 24.
- Maximum number of bugs found = (Number of bugs found on day 1) = a
- Minimum number of bugs found = (Number of bugs found on day 7) = a – 6x
- a - (a - 6x) = 24
- x = 6
Sufficient to answer
Step 4 : Analyze Statement 2 independent
2. The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24
- Total number of bugs found in during the last 7 days = a + (a –x) +(a-2x) +……(a-6x) = 7a –21x
- Average number of bugs found =
- a - 3x = 24
1 equation 2 variablesà cannot find a unique value of x.
Insufficient to answer
Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
Since, we have a unique answer from step- 3, this step is not required.
Answer: A
Answer: A
List A: 20, 4, 8, x
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?(1) The range of the numbers in List A is equal to the range of the numbers in List B(2) The median of the numbers in List A is equal to the median of the numbers in List B.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
List A: 20, 4, 8, x
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?
(1) The range of the numbers in List A is equal to the range of the numbers in List B
(2) The median of the numbers in List A is equal to the median of the numbers in List B.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
answer the question asked, and additional data specific to the problem are needed.

|
Rutuja Banerjee answered |
Step 1 & 2: Understand Question and Draw Inference
Given:
- List A: 4, 8, 20, x (don’t know the value of x, other numbers arranged in ascending order)
- List B: -4, 3, 6, 8, 12 (numbers arranged in ascending order)
To find: x = ?
Step 3 : Analyze Statement 1 independent
(1) The range of the numbers in List A is equal to the range of the numbers in List B
- Range of List B = 12 – (-4 ) = 12 + 4 = 16
- So, Range of List A = 16
- (Greatest number of List A) – (Smallest number of List A) = 16
- In List A, difference between 20 and 4 is 16
- This means, Greatest number of List A = 20
- And, Smallest number of List A = 4
- This means, 4 ≤ x ≤ 20
Not sufficient to find a unique value of x.
Step 4 : Analyze Statement 2 independent
(2) The median of the numbers in List A is equal to the median of the numbers
in List B.
in List B.
- Median of List B = 6
- So, Median of List A = 6
- In List A, possible arrangements of the 4 elements in ascending order and the corresponding medians:
- Thus, from Statement 2, we infer that x ≤ 4
Not sufficient to find a unique value of x
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: 4 ≤ x ≤ 20
- From Statement 2: x ≤ 4
- combing the 2 statements: x = 4Combin
Thus, the two statements together are sufficient to find a unique value of x
Answer: Option C
Answer: Option C
What is the mean of an increasing sequence of 10 consecutive integers?(1) The mean of the first 7 integers is 7.(2) The mean of the last 7 integers is 10.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
What is the mean of an increasing sequence of 10 consecutive integers?
(1) The mean of the first 7 integers is 7.
(2) The mean of the last 7 integers is 10.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Sravya Joshi answered |
Step 1 & 2 – Understand the question and draw inferences from the question statement.
We have to find the mean of an increasing sequence of 10 consecutive integers
Let the integers be a, a+ 1, a+ 2, a+ 3, a+ 4, a+ 5, a+ 6, a+ 7, a+ 8 and a+ 9, where a is the lowest integer:
Sum of the 10 consecutive integers
= a+ a+ 1 + a+ 2 + a+ 3 +a+ 4 +a+ 5 + a+ 6 +a+ 7 +a+ 8 +a+ 9
= 10a + 45
Mean of {a1, …..a1 + 9} = (10a+45)/10
If we can find the value of a, we can find the mean.
Step 3 – Analyze Statement 1 Independently
Statement 1 – The mean of the first 7 integers is 7
We Inferred: first seven integers are: a, a+ 1, a+ 2, a+ 3, a+ 4, a+ 5, a+ 6
Their Sum
= a+ a+ 1 + a+ 2 + a+ 3 +a+ 4 +a+ 5 + a+ 6
= 7a + 21
Mean of {a1, ….., a1 + 7} = (7a +21)/7 = a + 3
Given Mean = 7
- a + 3 = 7
- a = 7 -3 = 4
Statement 1 is independently sufficient to arrive at a unique answer.
Step 4 – Analyze Statement 2 Independently
Statement 2 -The mean of the last 7 integers is 10.
We Inferred: last seven integers are: a+ 3, a+ 4, a+ 5, a+ 6, a+ 7, a+ 8, a+ 9
Their Sum
= a+ 3 + a+ 4 + a+ 5 +a+ 6 +a+ 7 + a+ 8 +a+ 9
= 7a + 42
Mean of {a1,….., a1 + 7} = (7a +42)/7 = a + 6
Given Mean = 10
- a + 6 = 10
- a = 10 -6 = 4
Statement 2 is independently sufficient to arrive at a unique answer.
Step 5 – Analyze Both Statements Together
We get a unique value in Step 3 and Step 4
Statement (1) and (2) are independently sufficient to arrive at a unique answer.
Answer: Option (D)
Some milk was added to each of the 5 cans. If standard deviation of the quantity of milk in the 5 cans at the beginning was 3.5 liters, what was the standard deviation of the quantity of milk in the 5 cans at the end?(1) In each can, 20% of existing amount of milk was added.(2) The average volume of milk in the cans at the end was 25 liters.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?
Some milk was added to each of the 5 cans. If standard deviation of the quantity of milk in the 5 cans at the beginning was 3.5 liters, what was the standard deviation of the quantity of milk in the 5 cans at the end?
(1) In each can, 20% of existing amount of milk was added.
(2) The average volume of milk in the cans at the end was 25 liters.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Amrutha Jain answered |
Step 1 & 2 – Understand the question and draw inferences from the question statement.
To Find: We have to find the standard deviation of the volume of milk in 5 cans after some was added to each of the cans.
Given: Standard Deviation of the 5 cans of milk in the beginning is 3.5 liters.
Let the quantity of milk in 5 cans be a, b, c, d and e.
Finding standard deviation of {a, b, c, d, e}
Step 1
Mean of {a,b,c, d, e} = {a + b + c + d + e}/5 = M
Step 2
Distances of each point from the mean:
- a-M
- b-M
- c-M
- d-M
- e-M
Step 3
Squared Distance from Mean
- = (a -M)2 + (b-M)2 + (c -M)2 + (d -M)2 + (e -M)2
Step 4
Average = {(a -M)2 + (b-M)2 + (c -M)2 + (d -M)2 + (e -M)2} /5
Step 5
- Standard Deviation = √ [{(a -M)2 + (b-M)2 + (c -M)2 + (d -M)2 + (e -M)2} / 5] = 3.5
Step 3 – Analyze Statement 1 Independently
Statement 1 – In each can, 20% of the existing quantity of milk was added
The amount of milk be a+20%a, b+20%b, c+20%c, d+20%d, e+20%e
Remember: If all the elements of a set are increased by the x%, the standard deviation of the set also increases by the x%.
So the standard deviation of this set will increase by 20%
New S = 3.5 + 20% *3.5 = Unique number
Alternatively you can calculate the standard deviation of this set as shown below by following same step by step method.
Set = { a+20%a, b+20%b, c+20%c, d+20%d, e+20%e }
Step 1
- Sum of {a+20%a, b+20%b, c+20%c, d+20%d, e+20%e}
- = (1.2)(a + b + c + d + e)
- Mean of {a+20%a, b+20%b, c+20%c, d+20%d, e+20%e}
- = (1.2)(a + b + c + d + e)/5 = 1.2 M
Step 2
Distances of each point from the mean:
- 1.2 (a –M)
- 1.2 (b-M)
- 1.2(c-M)
- 1.2(d-M)
- 1.2(e-M)
Step 3
Squared Distance from Mean
- = 1.22 [(a -M)2 + (b-M)2 + (c -M)2 + (d -M)2 + (e -M)2 ]
Step 4
- Average = 1.22{(a -M)2 + (b-M)2 + (c -M)2 + (d -M)2 + (e -M)2} /5
Step 5
- Standard Deviation = 1.2 √ [{(a -M)2 + (b-M)2 + (c -M)2 + (d -M)2 + (e -M)2} / 5]
- = 1.2 *3.5 = 3.5 + 20% *3.5
- = Unique value
Statement (1) is independently sufficient to arrive at a unique answer.
Step 4 – Analyze Statement 2 Independently
Statement 2 -The average quantity of milk in the cans at the end was 25 liters
We do not know how the quantity changed in each of the cans.
Thus, the information given in statement (2) is not sufficient to arrive at a unique solution.
Step 5 – Analyze Both Statements Together
We get a unique value in Step 3.
Statement (1) independently is sufficient to arrive at a unique answer
Answer: Option (A)
Set P contains 3 distinct positive integers: A, B and C. Is the average (arithmetic mean) of set P divisible by 3?
(1) The sum of A×104 , B×102 and C is divisible by 9
(2) The product of the range of Set P and the median of Set P is 18.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'A'. Can you explain this answer?
Set P contains 3 distinct positive integers: A, B and C. Is the average (arithmetic mean) of set P divisible by 3?
(1) The sum of A×104 , B×102 and C is divisible by 9
(2) The product of the range of Set P and the median of Set P is 18.
(1) The sum of A×104 , B×102 and C is divisible by 9
(2) The product of the range of Set P and the median of Set P is 18.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Aditya Sharma answered |
Step 1 & 2: Understand Question and Draw Inference
Given:
- Set P = {A, B, C} where A, B and C are distinct positive integers
- Average of Set P =
To find: Is 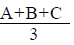 divisible by 3?
divisible by 3?
- If A + B + C divisible by 9?
- Is =
an integer?
- Let A = 9m + a, where a is the remainder that A leaves with 9. So a lies between 0 and 8, inclusive
- Similarly let B = 9n + b
- And let C = 9p + c
- So, the question is to find: Is
an integer?
- Is
an integer?
- Since m + n + p is an integer, the question simplifies to find: is
Step 3 : Analyze Statement 1 independent
- So, the number 10,000a + 100b +c is divisible by 9
- By applying the divisibility rule of 9, we can say that the sum of the digits of the number 10,000a + 100b +c is divisible by 9
- Since a, b and c are each single-digit integers that lie between 0 and 8, inclusive, the number 10,000a + 100b +c is of the form a00b0c (that is, a is the ten-thousands digit of this number, b is the hundreds digit and c is the units digit).
- So, the sum of digits of 10,000a +100b+c (=a00b0c) = a+b+c
- So, a+b+c is divisible by 9
- So,
is an integer
Sufficient.
Step 4 : Analyze Statement 2 independent
- The product of the range of Set P and the median of Set P is 18.
- (Range of Set P)*(Median of Set P) = 18
- Since Set P contains only integers, Range of Set P is an integer
- Since Set P contains an odd number of integers, Median of Set P is equal to the middle integer when A, B and C are arranged in ascending order. Thus, Median of Set P is an integer as well.
- Thus, the product of 2 integers is 18
- The number of ways to express 18 as a product of 2 integers:
- Case 1: 18 = 18*1
- Either Range = 18 and Median = 1
- Not possible – A, B and C are distinct, positive integers. So, minimum value of an integer in Set P is 1. The second integer in Set P cannot also be 1. So, Median cannot be 1
- Or Range = 1 and Median = 18
- Not possible – A, B and C are distinct integers. So, the minimum possible value of Range is 2 (happens if A, B and C are consecutive integers)
- Either Range = 18 and Median = 1
- Case 2: 18 = 9*2
- Either Range = 9 and Median = 2
- This means, Set P = {1, 2, 10}
- A + B + C = 1 + 2 +10 = 13, which is not divisible by 9.
- So, the answer to the question is NO
- Or Range = 2 and Median = 9
- This means, Set P = {8, 9, 10}
- A + B + C = 8 + 9 + 10 = 27, which is divisible by 9
- So, the answer to the question is YES
- Either Range = 9 and Median = 2
- Case 3: 18 = 6*3
- Since we’ve already seen that Case 2 leads to conflicting answers, we need not analyze Case 3.
- Case 1: 18 = 18*1
Thus, Statement 2 is not sufficient to provide a unique answer to the posed question.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 3, this step is not required.
Answer: Option A
Answer: Option A
A set X: {a1, a2, a3, a4, a5} with non-zero elements have mean M. What is the mean of the set Y: {a1 - 1, a2 - 2, a3 - 3, a4 + 5, a5 + 1}?- a)M - 3
- b)M - 2
- c)M - 1
- d)M
- e)M + 1
Correct answer is option 'D'. Can you explain this answer?
A set X: {a1, a2, a3, a4, a5} with non-zero elements have mean M. What is the mean of the set Y: {a1 - 1, a2 - 2, a3 - 3, a4 + 5, a5 + 1}?
a)
M - 3
b)
M - 2
c)
M - 1
d)
M
e)
M + 1

|
Dhruv Mehra answered |
In Set X: {a1,a2,a3,a4,a5a1,a2,a3,a4,a5}
• Mean of Set X with 5 elements = M
• Sum = Mean * Number of elements
• a1+a2+a3+a4+a5 = 5M --(1)
In Set Y: {a1−1, a2−2, a3−3, a4+5, a5+1}
• Sum of elements =(a1–1) + (a2-2) + (a3-3) + (a4+5) + (a5+1)
Rearranging, we get
• Sum =a1+a2+a3+a4+a5+(−1+−2+−3+5+1)
• Sum =a1+a2+a3+a4+a5+0=a1+a2+a3+a4+a5+0
• Sum = 5M From(1)
• Mean=(Sum)/(Number of elements)
• Mean =5M/5=5M/5
• Mean = M
The numbers in set P denote the distance of certain positive integers from -1 on the number line. The numbers in set Q denote
the distance of the same integers from 1 on the number line. Which of the following statements is true about the standard deviation of the sets P and Q?- a)Standard Deviation (P) = Standard Deviation (Q)
- b)Standard Deviation (P) = - Standard Deviation (Q)
- c)Standard Deviation (P) = Standard Deviation (Q) + 2
- d)Standard Deviation (P) = 2* Standard Deviation (Q)
- e)None of the above
Correct answer is option 'A'. Can you explain this answer?
The numbers in set P denote the distance of certain positive integers from -1 on the number line. The numbers in set Q denote
the distance of the same integers from 1 on the number line. Which of the following statements is true about the standard deviation of the sets P and Q?
the distance of the same integers from 1 on the number line. Which of the following statements is true about the standard deviation of the sets P and Q?
a)
Standard Deviation (P) = Standard Deviation (Q)
b)
Standard Deviation (P) = - Standard Deviation (Q)
c)
Standard Deviation (P) = Standard Deviation (Q) + 2
d)
Standard Deviation (P) = 2* Standard Deviation (Q)
e)
None of the above

|
Nandita Yadav answered |
Given:
- Let the integers be a, b, c, d, e….
- Set P = {Respective Distance of a, b, c, , d, e…. from -1}
- Set Q = {Respective Distance of a, b, c, d, e…from 1}
To Find: the statement, which is true about the standard deviation of sets P and Q
Approach:
- To find the relation between the standard deviation of sets P and Q, we would need to find the relation between the terms that are present in sets P and Q
- Terms in set P
- We know that distance of a number x from -1 on the number line can be written as |x –(-1)| = |x +1|
- We will use the above understanding to write down the terms of set P
- Terms in set Q
- We know that distance of a number x from 1 on the number line can be written as |x -1|
- We will use the above understanding to write down the terms of set Q
- Once we write down the terms of sets P and Q, we will find the relation between the terms of these 2 sets. Then, we'll use the standard properties of standard deviation to compare the standard deviation of sets P and Q.
Working out:
- Terms in set P
- Set P = {|a+1|, |b+1|, |c+1|…….}
- Terms in set Q
- Set Q = {|a-1|, |b-1|, |c-1|…….} = {|(a + 1) -2|, |(b+1) -2|, |(c+1) -2|……..}
- We can observe that if we subtract 2 from each of the terms of set P, we will get the terms of set Q.
- We know from the property of standard deviation that reducing all the terms of a set by the same constant does not change the standard deviation of the set.
- So, we can write Standard Deviation(P) = Standard Deviation(Q)
Answer : A
A merchant sold 32 antique items for $28800. If his profit margin was 20%, then his average cost per antique item was- a)$720
- b)$750
- c)$900
- d)$1080
- e)$1125
Correct answer is option 'B'. Can you explain this answer?
A merchant sold 32 antique items for $28800. If his profit margin was 20%, then his average cost per antique item was
a)
$720
b)
$750
c)
$900
d)
$1080
e)
$1125

|
Nilotpal Sen answered |
Given:
- Total Selling Price for 32 items = $28800
- Profit margin = 20%
To Find: Average cost per item
Approach:
- Average cost per item
- We know that the number of items is 32
- So, to answer the question, we need to know the total cost price of all items
2. We’re given the total selling price of all items as well as the profit margin. Using these 2 pieces of information together, we can find the total cost price of all 32 items
Working out:
Looking at the answer choices, we see that the correct answer is Option B
A group of 4 boys and 5 girls take a test. What is the average (arithmetic mean) score of the group in the test? - The average score of the boys is 23 points while the average score of the girls is 20 points
- If one of the girls had scored 6 points more, the average score of the group would have been 22
- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'D'. Can you explain this answer?
A group of 4 boys and 5 girls take a test. What is the average (arithmetic mean) score of the group in the test?
- The average score of the boys is 23 points while the average score of the girls is 20 points
- If one of the girls had scored 6 points more, the average score of the group would have been 22
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Sanskriti Ahuja answered |
Step 1 & 2: Understand Question and Draw Inference
Given: 4 boys and 5 girls take a test
To find: The Average score of the group
To find: The Average score of the group
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘The average score of the boys is 23 points while the average score of the girls is 20 points’
- Therefore, we will be able to find the value of the Average Score of the group
- Statement 1 is sufficient to answer the question
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘If one of the girls had scored 6 points more, the average score of the group would have been 22’
Let the girl who scored 6 points be the first girl (in the list of scores). So, her new score = G + 6
So, Statement 2 is sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in each of Steps 3 and 4, this step is not required
Answer: Option D
Answer: Option D
A set consists of n distinct integers arranged in the order of increasing magnitude. Is the median of the n integers equal to the
arithmetic mean of the n integers?
(1) The sum of any 3 successive integers of the set is divisible by 3
(2) The difference between any 2 successive integers of the set is 4- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'B'. Can you explain this answer?
A set consists of n distinct integers arranged in the order of increasing magnitude. Is the median of the n integers equal to the
arithmetic mean of the n integers?
(1) The sum of any 3 successive integers of the set is divisible by 3
(2) The difference between any 2 successive integers of the set is 4
arithmetic mean of the n integers?
(1) The sum of any 3 successive integers of the set is divisible by 3
(2) The difference between any 2 successive integers of the set is 4
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Sharmila Singh answered |
Step 1 & 2: Understand Question and Draw Inference
Given: A set of n distinct integers, arranged in the order of increasing magnitude
To find: Is Median = Mean?
The median is equal to the mean if:
To find: Is Median = Mean?
The median is equal to the mean if:
- Either the given sequence is an Arithmetic progression
- Or, It’s not an Arithmetic Progression but symmetric about a number.
- Like the set, {1, 2, 4, 6, 7}. This set is {4 – 3, 4 – 2, 4, 4 + 2, 4 + 3}, i.e. it is symmetric about 4.So, the sum of the terms = 4*5 And
- Like the set, {1, 2, 4, 6, 7}. This set is {4 – 3, 4 – 2, 4, 4 + 2, 4 + 3}, i.e. it is symmetric about 4.So, the sum of the terms = 4*5 And
Step 3 : Analyze Statement 1 independent
(1) The sum of any 3 successive integers of the set is divisible by 3
- Statement 1 is fulfilled by more than one cases:
- Case 1: The terms of the set are in arithmetic progression
- Example: 1, 2, 3, 4, 5
- In this case, as discussed in Step 1 and 2, Median = Mean (= 3 in the Example above)
- Case 2: The terms of the set are not in arithmetic progression
- For example, a set of the form: {3k + 0, 3k + l, 3k + 5, 3k + 12, 3k + 16} where k is an integer
- In this set,
- But Median = 3k + 5
- So, Median ≠ Mean
- Thus, Statement 1 doesn’t give us a unique answer to the asked question. So, this statement is not sufficient
Step 4 : Analyze Statement 2 independent
(2) The difference between any 2 successive integers of the set is 4
- Note that we are given that the integers are arranged in ascending order.
- So, combining this fact with Statement 2, we can write that the numbers are of the form: {m, m + 4, m + 8, m + 12, . . . , m + (n-1)*4}
- Thus, the given sequence is an Arithmetic Progression.
- Therefore, the median of the sequence will definitely be equal to the mean of the sequence.
So Statement 2 is sufficient.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 4, this step is not required
Answer: Option B
Answer: Option B
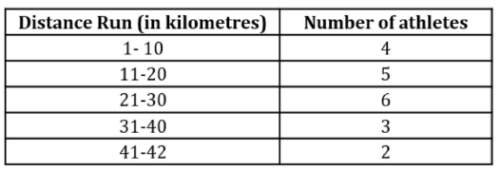 The table above shows the distribution of the distance, rounded to the nearest integer, run by 20 athletes in a marathon. Which of the
The table above shows the distribution of the distance, rounded to the nearest integer, run by 20 athletes in a marathon. Which of the
following cannot be the approximate average (arithmetic mean) distance run (in kilometres) by the athletes in the marathon?- a)18
- b)21
- c)24
- d)26
- e)28
Correct answer is option 'E'. Can you explain this answer?
The table above shows the distribution of the distance, rounded to the nearest integer, run by 20 athletes in a marathon. Which of the
following cannot be the approximate average (arithmetic mean) distance run (in kilometres) by the athletes in the marathon?
following cannot be the approximate average (arithmetic mean) distance run (in kilometres) by the athletes in the marathon?
a)
18
b)
21
c)
24
d)
26
e)
28

|
Nandita Yadav answered |
Given:
- Number of athletes = 20
- Table showing range of distances, rounded to the nearest integers, run by the athletes
To Find: The option that cannot be the average distance run by the athl
Approach:
- We need to look for a value that is outside the range of the average distance run by the 20 athletes.
- We know that the average distance would lie between the minimum possible average distance ran by the athletes and maximum possible average distance ran by the athletes
- So, for finding the range of the distances run, we need to find the maximum and minimum average distances run by the athletes.
- Once we know the maximum and minimum distance run, we can find the range of average distance run by dividing by the number of athletes.
- Maximum Average Distance
- The average distance ran by the athletes will be maximum when each athlete runs the maximum distance in a given range
- For example: In the range 1- 10 kilometers, each athlete should run 10 kilometers
- Maximum distance run = Sum of (maximum distance run in the range * number of athletes in the range)
- Maximum Average distance run =
- The average distance ran by the athletes will be maximum when each athlete runs the maximum distance in a given range
Working out:
- Minimum distance run = (4*1) + (5*11) +(6*21) + (3*31) +(2*41) = 4 + 55 +126 +93 +82 = 360
- Average of minimum distance run =
- Average of minimum distance run =
- Maximum distance run = (4 * 10) + ( 5 *20) +(6*30) + (3*40) +(2*42) = 40 + 100 + 180 +120 + 84 = 524 kilometres
- a. Average of maximum distance run =
- a. Average of maximum distance run =
- Hence the range of average distance run by the athletes can be from 18 to 26.2
- The only option that is outside the range is option E, 28 kilometres
Answer : E
Set P has n integers. What is the standard deviation of Set P?
(1) The range of Set P is equal to zero
(2) The mean of Set P is equal to the median of Set P- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
Correct answer is option 'A'. Can you explain this answer?
Set P has n integers. What is the standard deviation of Set P?
(1) The range of Set P is equal to zero
(2) The mean of Set P is equal to the median of Set P
(1) The range of Set P is equal to zero
(2) The mean of Set P is equal to the median of Set P
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
answer the question asked, and additional data specific to the problem are needed

|
Aditya Sharma answered |
Step 1 & 2: Understand Question and Draw Inference
- Set P→n integers
To Find: Standard Deviation (P)
Step 3 : Analyze Statement 1 independent
(1) The range of Set P is equal to zero
- Range = largest integer – smallest integer
- 0 = largest integer – smallest integer
- largest integer = smallest integer
- This tells us that:
- all the integers of set P are equal OR
- set P has only 1 element
In both the cases, the standard deviation is 0.
Sufficient to answer.
Sufficient to answer.
Step 4 : Analyze Statement 2 independent
(2) The mean of Set P is equal to the median of Set P
- As the mean of the set is equal to the median of the set, we can say that the set is symmetric about the mean and the median
- However, it does not tell us anything about the other terms of the set. So, we cannot say anything about the standard deviation of the set.
Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step- 3, this step is not required.
Answer : A
A is the average (arithmetic mean) of the first 7 multiples of 3 and B is the median of the first 3 multiples of positive integer n. If the
value of A2 – B2 is zero, what is the value of n?- a)3
- b)4
- c)5
- d)6
- e)7
Correct answer is option 'D'. Can you explain this answer?
A is the average (arithmetic mean) of the first 7 multiples of 3 and B is the median of the first 3 multiples of positive integer n. If the
value of A2 – B2 is zero, what is the value of n?
value of A2 – B2 is zero, what is the value of n?
a)
3
b)
4
c)
5
d)
6
e)
7

|
Nandita Yadav answered |
Given:
- A = Average of {3, 6, 9 . .. 21}
- B = Median of {n, 2n, 3n} where n is a positive integer
- So, B = 2n
- Since n is a positive integer, B must be a positive integer as well
- A2 - B2 =0
To Find: n =?
Approach:
- To find the value of n, we need to draft an equation in terms of n. From the given information, we can write n= B/2 So, to find n, we need to find the value of B
- We are given a relation between A2 and B2 . So, if we know the value of A, we can find the value of B
- We can find the value of A using the given information about A
Working out:
- Rejecting the negative value since we’ve inferred above that B is a positive integer
- So, B = 12
Looking at the answer choices, we see that the correct answer is Option D
Set A consists of 15 positive integers. Is the mean of set A equal to the median of set A?
(1) The integers in set A, when arranged in the order of increasing magnitude, are not evenly spaced
(2) If an integer x, which is equal to the mean of set A, is added to the set, the median of the set does not
change- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Set A consists of 15 positive integers. Is the mean of set A equal to the median of set A?
(1) The integers in set A, when arranged in the order of increasing magnitude, are not evenly spaced
(2) If an integer x, which is equal to the mean of set A, is added to the set, the median of the set does not
change
(1) The integers in set A, when arranged in the order of increasing magnitude, are not evenly spaced
(2) If an integer x, which is equal to the mean of set A, is added to the set, the median of the set does not
change
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Akshay Khanna answered |
Step 1 & 2: Understand Question and Draw Inference
- Set A has 15 positive integers
To Find: Is Mean (A) = Median (A)
Step 3 : Analyze Statement 1 independent
- The integers in set A, when arranged in the order of increasing magnitude, are not evenly spaced
- For an evenly spaced set, mean = median
- However, for a non-evenly spaced out, mean may or may not be equal to median. For example:
- {1, 2, 5, 8, 9}. Here mean = median = 5
- {1, 3, 6, 8, 22}. Here mean = 8 but median = 6
Insufficient to answer.
Step 4 : Analyze Statement 2 independent
2. If an integer x, which is equal to the mean of set A, is added to the set, the median of the set does not change
- When set A consists of 15 terms. Arranging them in ascending order, we have,
- Median = 8 term = let’s say y
- When set A consists of 16 terms, i.e. after the addition of a new term
- Median = Average of 8 and the 9 term = y(as the median did not change)
- 8th term + 9th term = 2y
- Now, let’s observe the position of the term y in the new set A
- If x < y
- Then y would become the 9 term of the new set A
- If x = y
- Then the 8th term and the 9th term both will be equal to y
- If x > y
- Then y would remain the 8 term of the new set A
- If x < y
- So, even after adding of the new term x, y (i.e. the 8 term of the original set A) would either be the 8 term or the 9 term in the new set A
- Hence, from the equation 8 term + 9 term = 2y, we can say that Either(8 term or 9 term) = y
- So, 8 term = 9 term = y
- For the above to hold true, following cases are possible:
- Case-I: mean = median = x .
- This is true for the case, when x = y
- If the same number is added, the mean and the median would not change
- Case-II: When median ≠ mean
- In this case the median ≠ mean and the median value is repeated more than once, such that addition of a new number results in the median being the average of the two repeated median values. For example: Set consisting of {3, 3, 3, 9, 9, 9, 9, 9, 9}. Mean = 7 and
median = 9
If 7 is added, Set = {3, 3, 3, 7, 9, 9, 9, 9, 9, 9}. Mean = 7 and
median = (9+9 ) /2 = 9
- In this case the median ≠ mean and the median value is repeated more than once, such that addition of a new number results in the median being the average of the two repeated median values. For example: Set consisting of {3, 3, 3, 9, 9, 9, 9, 9, 9}. Mean = 7 and
- So, the mean = median or the mean ≠ median Insufficient to answer
- Case-I: mean = median = x .
Step 5: Analyze Both Statements Together (if needed)
- Set A is not evenly spaced
- If an integer x, which is equal to the mean of set A, is added to the set, the median of the set does not change
Combining the two statements does not give us any extra information to answer the question.
Insufficient to answer.
Insufficient to answer.
Answer : E
List A contains 16 distinct odd integers and 9 distinct even integers such that the average (arithmetic mean) of List A is 13.84. If each odd integer is doubled in magnitude, what is the new average (arithmetic mean) of List A?
(1) The average (arithmetic mean) of the even integers in List A is 10
(2) Before each odd integer is doubled in magnitude, the smallest odd integer in List A is 1 and the largest odd integer in List A is
31.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'D'. Can you explain this answer?
List A contains 16 distinct odd integers and 9 distinct even integers such that the average (arithmetic mean) of List A is 13.84. If each odd integer is doubled in magnitude, what is the new average (arithmetic mean) of List A?
(1) The average (arithmetic mean) of the even integers in List A is 10
(2) Before each odd integer is doubled in magnitude, the smallest odd integer in List A is 1 and the largest odd integer in List A is
31.
(1) The average (arithmetic mean) of the even integers in List A is 10
(2) Before each odd integer is doubled in magnitude, the smallest odd integer in List A is 1 and the largest odd integer in List A is
31.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Mihir Ghoshal answered |
Step 1 & 2: Understand Question and Draw Inference
- List A has 16 distinct odd integers and 9 distinct even integers
- Total number of integers in List A = 16 + 9 = 25
- Average of List A = 13.84
- Sum of all integers in List A = 13.84 * 25 = 346
- Let the odd integers in List A be D1 , D2 , D3 . . .D16 Let the sum of these integers be D
- Let the Even integers be E , E , E . . . E . Let the sum of these
- integers be E.
- D + E = 346 . . . (1)
- When each odd number is doubled, the new sum of the odd numbers = 2D.
So, in order to answer this question, we need to know the value of D.
Step 3 : Analyze Statement 1 independent
(1) The average (arithmetic mean) of the even integers in List A is 10
Putting (2) in (1), we get the value of D.
So, Statement 1 alone is sufficient.
So, Statement 1 alone is sufficient.
Step 4 : Analyze Statement 2 independent
(2) Before each odd integer is doubled in magnitude, the smallest odd integer in
List A is 1 and the largest odd integer in List A is 31
List A is 1 and the largest odd integer in List A is 31
- D1 = 1
- D16 = 31
- Number of odd integers between 1 and 31, inclusive, is 16.
- This means, the 16 odd integers in List A are consecutive odd integers starting from 1 and ending at 31.
- Since we now know the values of the odd integers in List A, we can find their sum D.
So, Statement 2 alone is sufficient.
Step 5: Analyze Both Statements Together (if needed)
Since we get a unique answer in each of Steps 3 and 4, this step is not required
Answer: Option D
If the medians of the List A and List B are same, what is the value of k?List A: 2, 5, 7, 20List B: 2, 5, 7, 20, k- a)3
- b)4
- c)5
- d)6
- e)7
Correct answer is option 'D'. Can you explain this answer?
If the medians of the List A and List B are same, what is the value of k?
List A: 2, 5, 7, 20
List B: 2, 5, 7, 20, k
a)
3
b)
4
c)
5
d)
6
e)
7

|
Amrutha Jain answered |
Step 1: Question statement and Inferences
We need to find the median of List B and then compare the value of k
Step 2: Finding required values
Median of List A = (5+7)/2 = 6
Given: Median of List A = Median of List B
Therefore, Median of List B = 6
Step 3: Calculating the final answer
As there are five elements in List B, the median will be the middle number
As no element is equal to 6, k must be 6.
(Observe that 6 is exactly the middle number of List B).
Answer: Option (D)
Set A: {-11, 0, 0, 11}Set B: {2, 4, 6, 8}Set C: {50, 51, 52, 53}Set D: {12, 12, 12, 12}Which of the following sets have a maximum & minimum standard deviation respectively?- a)Max: A, Min: B
- b)Max: B, Min: C
- c)Max: C, Min: D
- d)Max: B, Min: D
- e)Max: A, Min: D
Correct answer is option 'E'. Can you explain this answer?
Set A: {-11, 0, 0, 11}
Set B: {2, 4, 6, 8}
Set C: {50, 51, 52, 53}
Set D: {12, 12, 12, 12}
Which of the following sets have a maximum & minimum standard deviation respectively?
a)
Max: A, Min: B
b)
Max: B, Min: C
c)
Max: C, Min: D
d)
Max: B, Min: D
e)
Max: A, Min: D

|
Bhavya Khanna answered |
To find the maximum and minimum standard deviation among the given sets, we need to calculate the standard deviation of each set and compare them.
Calculating Standard Deviation:
1. Set A: {-11, 0, 0, 11}
Mean = (-11+0+0+11)/4 = 0
Variance = [(0-(-11))^2 + (0-0)^2 + (0-0)^2 + (11-0)^2]/4
= [(121+0+0+121)]/4
= 60.5
Standard Deviation = √60.5 ≈ 7.78
2. Set B: {2, 4, 6, 8}
Mean = (2+4+6+8)/4 = 5
Variance = [(2-5)^2 + (4-5)^2 + (6-5)^2 + (8-5)^2]/4
= [9+1+1+9]/4
= 5
Standard Deviation = √5 ≈ 2.24
3. Set C: {50, 51, 52, 53}
Mean = (50+51+52+53)/4 = 51.5
Variance = [(50-51.5)^2 + (51-51.5)^2 + (52-51.5)^2 + (53-51.5)^2]/4
= [2.25+0.25+0.25+2.25]/4
= 1
Standard Deviation = √1 = 1
4. Set D: {12, 12, 12, 12}
Mean = (12+12+12+12)/4 = 12
Variance = [(12-12)^2 + (12-12)^2 + (12-12)^2 + (12-12)^2]/4
= 0
Standard Deviation = √0 = 0
Comparing Standard Deviations:
- The maximum standard deviation is in Set A, which is approximately 7.78.
- The minimum standard deviation is in Set D, which is 0.
Therefore, the correct answer is option E, which states that Set A has the maximum standard deviation and Set D has the minimum standard deviation.
Calculating Standard Deviation:
1. Set A: {-11, 0, 0, 11}
Mean = (-11+0+0+11)/4 = 0
Variance = [(0-(-11))^2 + (0-0)^2 + (0-0)^2 + (11-0)^2]/4
= [(121+0+0+121)]/4
= 60.5
Standard Deviation = √60.5 ≈ 7.78
2. Set B: {2, 4, 6, 8}
Mean = (2+4+6+8)/4 = 5
Variance = [(2-5)^2 + (4-5)^2 + (6-5)^2 + (8-5)^2]/4
= [9+1+1+9]/4
= 5
Standard Deviation = √5 ≈ 2.24
3. Set C: {50, 51, 52, 53}
Mean = (50+51+52+53)/4 = 51.5
Variance = [(50-51.5)^2 + (51-51.5)^2 + (52-51.5)^2 + (53-51.5)^2]/4
= [2.25+0.25+0.25+2.25]/4
= 1
Standard Deviation = √1 = 1
4. Set D: {12, 12, 12, 12}
Mean = (12+12+12+12)/4 = 12
Variance = [(12-12)^2 + (12-12)^2 + (12-12)^2 + (12-12)^2]/4
= 0
Standard Deviation = √0 = 0
Comparing Standard Deviations:
- The maximum standard deviation is in Set A, which is approximately 7.78.
- The minimum standard deviation is in Set D, which is 0.
Therefore, the correct answer is option E, which states that Set A has the maximum standard deviation and Set D has the minimum standard deviation.
10, 6, p, q, 11Given the above series of positive integers arranged in a random order, what is the value of p/q? (1) The average (arithmetic mean) of given numbers is 7 (2) p is the median of the given series - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
10, 6, p, q, 11
Given the above series of positive integers arranged in a random order, what is the value of p/q?
(1) The average (arithmetic mean) of given numbers is 7
(2) p is the median of the given series
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Amrutha Jain answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given that a series consist of 5 elements arranged in a random order. The numbers are 10, 6, p, q, and 11 where p and q are positive integers.
We have to find the value p/q. For that, we need to find the value of p and q.
Since there is no other information provided in the question, let’s move on to the analysis of statements 1 and 2.
Step 3: Analyze Statement 1
The average (arithmetic mean) of given numbers is 7
Now, the average of these numbers can be calculated as follows:
However, there are multiple options available for the values of p and q:
p = 7, q = 1 OR p = 1, q = 7
p = 6, q = 2 OR p = 2, q = 6
p = 5, q = 3 OR p = 3, q = 5
p = 4, q=4
Hence, statement 1 alone is not sufficient to answer the question.
Step 4: Analyze Statement 2
p is the median of the given series
The fact that p is the median of the series tells us only that if the numbers are arranged in ascending or descending order, the number p will come at the third place.
The following table lists all the possible arrangements and the corresponding values of (p,q) that are possible:
Thus, we see that there exist multiple sets of possible values of (p,q)
Hence, statement 2 alone is not sufficient to answer the question.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1,
p + q = 8
From Statement 2,
All the sets of (p,q) in the table above are possible
By combining both sets,
Let’s pick those sets from the table above for which p + q = 8
Such sets of (p, q) are:
(7,1), (6,2)
For the set (7,1), the value of p/q is 7
For the set (6,2), the value of p/q is 3
Thus, we don’t get a unique value of the ratio p/q.
Both statements combined are not sufficient to answer the question.
Answer: Option (E)
What is the standard deviation of {-3, -6, -5, -10} approximately equal to, if the standard deviation of {3, 6, 5, 10} is approximately equal to 2.5?- a)-5.0
- b)-2.5
- c)0
- d)2.5
- e)5.0
Correct answer is option 'D'. Can you explain this answer?
What is the standard deviation of {-3, -6, -5, -10} approximately equal to, if the standard deviation of {3, 6, 5, 10} is approximately equal to 2.5?
a)
-5.0
b)
-2.5
c)
0
d)
2.5
e)
5.0

|
Mihir Ghoshal answered |
Finding standard deviation of {-3, -6, -5, -10}
Step 1
Mean of {-3,-6,-5,-10} = {( -3) + (-6) + (-5) + (-10)}/4 = -6
Step 2
Distances of each point from the mean:
- -3 – (-6) = 3
- -6 – (-6) = 0
- -5 – (-6) = 1
- -10-(-6) = -4
Step 3
Squared Distance from Mean
- = (3)2 + (0)2 + (1)2 + (-4)2
- = 9 + 0 + 1 + 16 = 26
Step 4
- Average = 26/4 = 6.5
Step 5
- Standard Deviation = √6.5 ≌ 2.5
- Note that this Standard Deviation is the same as Standard deviation of {3, 6, 5, 10}.
Remember -The standard deviation of a set remains the same even if all the elements are multiplied by (-1)
Answer: Option (D)
A group of students was participating in a quizzing competition consisting of 3 rounds. A student had to clear the first round to move into the second round and so on till he cleared all the rounds. What was the median number of the rounds cleared by the students in the quiz?
(1) 20 percent of the students could not clear round 1 of the quiz
(2) 40 percent of the students could clear round 2 but could not clear round 3.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
Correct answer is option 'E'. Can you explain this answer?
A group of students was participating in a quizzing competition consisting of 3 rounds. A student had to clear the first round to move into the second round and so on till he cleared all the rounds. What was the median number of the rounds cleared by the students in the quiz?
(1) 20 percent of the students could not clear round 1 of the quiz
(2) 40 percent of the students could clear round 2 but could not clear round 3.
(1) 20 percent of the students could not clear round 1 of the quiz
(2) 40 percent of the students could clear round 2 but could not clear round 3.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
answer the question asked, and additional data specific to the
problem are needed

|
Rutuja Banerjee answered |
Step 1 & 2: Understand Question and Draw Inference
- Let the number of students be x
- Number of rounds in the quiz = 3
To Find: Median number of rounds cleared by the students
- Median = {0, 1, 2 or 3}
Step 3 : Analyze Statement 1 independent
- 20 percent of the students could not clear round 1 of the quiz.
- 0.2x could not clear round 1
- 0.8x cleared round 1
- Since more than half cleared the first round, we can be sure that Median is not equal to zero
- But we do not know how many of them cleared round 2 and round 3.So,
- Median may be 1, 2 or 3
Insufficient to find an answer.
Step 4 : Analyze Statement 2 independent
2. 40 percent of the students could clear round 2 but could not clear round 3.
- 0.4x could clear round 2 but not clear round 3
- All the students who cleared Round 2 must have cleared Round 1 first
- This means, we can be sure that at least 0.4x students definitely cleared Round 1
However, we do not know the number of students who cleared round 3 and the number of students who could not clear round 1
Insufficient to answer.
Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1, we inferred that 0.8x cleared round 1 and 0.2x didn’t
- From Statement 2, we know that 0.4x could clear round 2 but not clear round 3
Let there be a% of students who cleared round 1 and b% of students who cleared round 2
- a% ≥ 20%
- b% ≤ 100%
- From st-2 we know that b% - a% = 40%. Since we do not know the division of the rest 40% of the students, we will not have a unique value for the median. For example:
- If a% = 20% and b% = 60%, median = 2
- If a% = 60% and y% = 100%, median = 1
Insufficient to answer.
Answer: E
Answer: E
Chapter doubts & questions for Statistics - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Statistics - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









