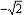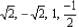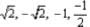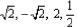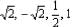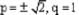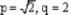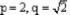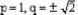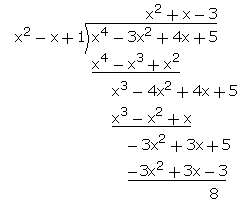All Exams >
CDS >
Elementary Mathematics for CDS >
All Questions
All questions of Theory of polynomials for CDS Exam
If one of the factors of x2 + x – 20 is (x + 5), then other factor is- a)(x – 4)
- b)(x – 5)
- c)(x – 6)
- d)(x – 7)
Correct answer is 'A'. Can you explain this answer?
If one of the factors of x2 + x – 20 is (x + 5), then other factor is
a)
(x – 4)
b)
(x – 5)
c)
(x – 6)
d)
(x – 7)
|
|
Arun Sharma answered |
Using mid-term splitting,
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
- a)6
- b)7
- c)8
- d)9
Correct answer is option 'A'. Can you explain this answer?
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
a)
6
b)
7
c)
8
d)
9
|
|
Zachary Foster answered |
Given α and β are the zeroes of the polynomial x2 − 5x + k
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
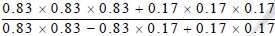 is equal to :-
is equal to :-
- a)1
- b)(0.83)3 + (0.17)3
- c)0
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
a)
1
b)
(0.83)3 + (0.17)3
c)
0
d)
None of these

|
Shalini Shahi answered |
Yes answer is 1. a=0.83 ,b=0.17 0.83×0.83×0.83 +0.17×0.17×0.17. / 0.83× 0.83+0.83× 0.17+0.17×0.17. = formula = a³+b³=( a+b)(a²-ab +b²) / a²-ab+ b² = cut the up and down a²-ab +b² = only a+b here ,add a+b =0.83+0.17= 1.00= 1, correct answer a) 1..
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =- a)2
- b)3
- c)1
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =
a)
2
b)
3
c)
1
d)
None of these
|
|
Pooja Shah answered |
If α and β are the zeros of the polynomial then
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
Now, comparing equation (i) and (ii),we get,
−(α + β) = 3
α + β = −3
−(α + β) = 3
α + β = −3
Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –- a)x2 – 5x – 14
- b)x2 – 10x – 14
- c)x2 – 5x + 14
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –
a)
x2 – 5x – 14
b)
x2 – 10x – 14
c)
x2 – 5x + 14
d)
None of these
|
|
Amit Kumar answered |
The quadratic equation is of the form x2 - (sum of zeros) x + (product of zeros)
=x2 - 5x - 14
=x2 - 5x - 14
If p(x) = x + 3, then p(x) + p(-x) is equal to- a)0
- b)3
- c)6
- d)2x
Correct answer is option 'C'. Can you explain this answer?
If p(x) = x + 3, then p(x) + p(-x) is equal to
a)
0
b)
3
c)
6
d)
2x

|
Sanjana answered |
we have , p(x) = x+3.........(1) Replacing x by -x ,we get p(-x)= -x+3 ............(2) adding the corresponding sides of (1)and (2),we get p(x)+p(-x) = 6
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :- a)5, 6
- b)- 5, - 6
- c)- 5, 6
- d)5, - 6
Correct answer is option 'C'. Can you explain this answer?
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :
a)
5, 6
b)
- 5, - 6
c)
- 5, 6
d)
5, - 6
|
|
Gaurav Kumar answered |
Zeros of the polynomials are the values which gives zero when their value is substituted in the polynomial
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
When the polynomial x3 + 3x2 + 3x + 1 is divided by x + 1, the remainder is :-- a)1
- b)8
- c)0
- d)- 6
Correct answer is option 'C'. Can you explain this answer?
When the polynomial x3 + 3x2 + 3x + 1 is divided by x + 1, the remainder is :-
a)
1
b)
8
c)
0
d)
- 6
|
|
Hansa Sharma answered |
The zero of x + 1 is –1
And by remainder theorem, when
p(x) = x3 + 3x2 + 3x + 1 is divided by x + 1, then remainder is p(–1).
∴ p(–1) = (–1)3 + 3 (–1)2 + 3(–1) + 1
= –1 + (3 × 1) + (–3) + 1
= –1 + 3 – 3 + 1
= 0
Thus, the required = 0
. Find the zeroes of the quadratic polynomial x2 +7x + 12- a)-2, -5
- b)-3, -4
- c)2, 5
- d)3, 4
Correct answer is option 'B'. Can you explain this answer?
. Find the zeroes of the quadratic polynomial x2 +7x + 12
a)
-2, -5
b)
-3, -4
c)
2, 5
d)
3, 4
|
|
Sneha Meena answered |
X2+7×+12
×2+4×+3×+12
×(×+4)+3(×+4)
×=-4,×=-3
×2+4×+3×+12
×(×+4)+3(×+4)
×=-4,×=-3
√2 is a polynomial of degree- a)1
- b)0
- c)2
- d)√2
Correct answer is option 'B'. Can you explain this answer?
√2 is a polynomial of degree
a)
1
b)
0
c)
2
d)
√2
|
|
Vivek Rana answered |
The highest power of the variable is known as the degree of the polynomial.
√2x^0 = √2
hence the degree of the polynomial is zero.
√2x^0 = √2
hence the degree of the polynomial is zero.
If the polynomial 2x3 – 3x2 + 2x – 4 is divided by x – 2, then the remainder is :-- a)- 4
- b)4
- c)-40
- d)2
Correct answer is option 'B'. Can you explain this answer?
If the polynomial 2x3 – 3x2 + 2x – 4 is divided by x – 2, then the remainder is :-
a)
- 4
b)
4
c)
-40
d)
2
|
|
Mahi Sharma answered |
3x2 - 5x + 7 is divided by x - 2, the remainder is:
To find the remainder, we can use the remainder theorem which states that if a polynomial f(x) is divided by x - a, the remainder is equal to f(a).
Therefore, if we substitute x = 2 in the given polynomial, we get:
2(2)3 - 3(2)2 - 5(2) + 7 = 16 - 12 - 10 + 7 = 1
Hence, the remainder when the polynomial 2x3 + 3x2 - 5x + 7 is divided by x - 2 is 1.
To find the remainder, we can use the remainder theorem which states that if a polynomial f(x) is divided by x - a, the remainder is equal to f(a).
Therefore, if we substitute x = 2 in the given polynomial, we get:
2(2)3 - 3(2)2 - 5(2) + 7 = 16 - 12 - 10 + 7 = 1
Hence, the remainder when the polynomial 2x3 + 3x2 - 5x + 7 is divided by x - 2 is 1.
(a – b)3 + (b – c)3 + (c – a)3 is equal to :-- a)3abc
- b)3a3b3c3
- c)3(a – b) (b – c) (c – a)
- d)[a – (b + c)]3
Correct answer is option 'C'. Can you explain this answer?
(a – b)3 + (b – c)3 + (c – a)3 is equal to :-
a)
3abc
b)
3a3b3c3
c)
3(a – b) (b – c) (c – a)
d)
[a – (b + c)]3

|
Indu Gupta answered |
Let x = (a – b), y = (b – c) and z = (c – a)
Consider, x + y + z = (a – b) + (b – c) + (c – a) = 0
⇒ x3 + y3 + z3 = 3xyz
That is (a – b)3 + (b – c)3 + (c – a)3 = 3(a – b)(b – c)(c – a)
Consider, x + y + z = (a – b) + (b – c) + (c – a) = 0
⇒ x3 + y3 + z3 = 3xyz
That is (a – b)3 + (b – c)3 + (c – a)3 = 3(a – b)(b – c)(c – a)
The quadratic polynomial whose sum of zeroes is 3 and the product of zeroes is –2 is :
- a)x2 + 3x – 2
- b)x2 – 2x + 3
- c)x2 – 3x + 2
- d)x2 – 3x – 2
Correct answer is option 'D'. Can you explain this answer?
The quadratic polynomial whose sum of zeroes is 3 and the product of zeroes is –2 is :
a)
x2 + 3x – 2
b)
x2 – 2x + 3
c)
x2 – 3x + 2
d)
x2 – 3x – 2
|
|
Meha nair answered |
Sum of zeros = 3/1
-b/a = 3/1 .....................(1)
-b/a = 3/1 .....................(1)
Product of zeros = -2/1
c/a = -2/1 ...................(2)
c/a = -2/1 ...................(2)
From equation (1) and (2)
a = 1
-b = 3, b = -3
c = -2
a = 1
-b = 3, b = -3
c = -2
The required quadratic equation is
ax2+b
= x2-3x-2
ax2+b
x
+c= x2-3x-2
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :- a) x2 + 3x – 2
- b)x2 – 2x + 3
- c)x2 – 3x + 2
- d)x2 – 3x – 2
Correct answer is 'C'. Can you explain this answer?
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :
a)
x2 + 3x – 2
b)
x2 – 2x + 3
c)
x2 – 3x + 2
d)
x2 – 3x – 2
|
|
Pooja Shah answered |
Sum of zeros = 3/1
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
The degree of the polynomial 4x4+0x3+0x5+5x+74x4+0x3+0x5+5x+7 is- a)4
- b)6
- c)7
- d)5
Correct answer is option 'A'. Can you explain this answer?
The degree of the polynomial 4x4+0x3+0x5+5x+74x4+0x3+0x5+5x+7 is
a)
4
b)
6
c)
7
d)
5
|
|
Vikram Khanna answered |
Degree of 4x4 + Ox3 + Ox5 + 5x + 7 is equal to the highest power of variable x. Here, the highest power of x is 4, Hence, the degree of a polynomial is 4.
The expanded form of (2x – 3y – z)2 is :-- a)4x2 + 9y2 + z2 – 6xy + 3yz – 2zx
- b)4x2 + 9y2 + z2 + 6xy + 6yz – 2zx
- c)4x2 + 9y2 + z2 – 12xy – 6yz – 4zx
- d)4x2 + 9y2 + z2 – 12xy + 6yz – 4zx
Correct answer is option 'D'. Can you explain this answer?
The expanded form of (2x – 3y – z)2 is :-
a)
4x2 + 9y2 + z2 – 6xy + 3yz – 2zx
b)
4x2 + 9y2 + z2 + 6xy + 6yz – 2zx
c)
4x2 + 9y2 + z2 – 12xy – 6yz – 4zx
d)
4x2 + 9y2 + z2 – 12xy + 6yz – 4zx
|
|
Sachi Menon answered |
The expanded form of (2x) is 2 times x, which can also be written as 2x. There is no further expansion needed as it is already in its simplest form.
Can you explain the answer of this question below:A polynomial of degree 5 in x has at most- A:5 terms
- B:4 terms
- C:6 terms
- D:10 terms
The answer is C.
A polynomial of degree 5 in x has at most
A:
5 terms
B:
4 terms
C:
6 terms
D:
10 terms
|
|
Dipika Chopra answered |
Explanation:
Polynomial is a mathematical expression that contains variables, constants and exponents, combined using arithmetic operations like addition, subtraction, multiplication and division.
Degree of a polynomial is the highest power of the variable in the polynomial.
For example, in the polynomial 2x^3 + 5x^2 - 7x + 4, the degree is 3.
A polynomial of degree 5 in x means that the highest power of x in the polynomial is 5.
Now, let's consider the number of terms in a polynomial of degree 5 in x.
A term in a polynomial is a product of a constant and one or more variables raised to some exponents.
For example, in the polynomial 2x^3 + 5x^2 - 7x + 4, the terms are 2x^3, 5x^2, -7x and 4.
The number of terms in a polynomial of degree 5 in x depends on the number of possible combinations of the variables and constants that can be multiplied together to obtain a term of degree 5.
To obtain a term of degree 5 in x, we can multiply x^5 by a constant, or we can multiply x^4 by x and a constant, or we can multiply x^3 by x^2 and a constant, and so on.
Thus, the number of possible terms in a polynomial of degree 5 in x is given by the sum of the binomial coefficients of the form (5 choose k), where k ranges from 0 to 5.
(5 choose 0) + (5 choose 1) + (5 choose 2) + (5 choose 3) + (5 choose 4) + (5 choose 5) = 1 + 5 + 10 + 10 + 5 + 1 = 32
Therefore, a polynomial of degree 5 in x can have at most 32 terms.
However, not all of these terms need to be present in the polynomial. Some of the terms may have a coefficient of 0, which means that they do not contribute to the polynomial.
For example, the polynomial x^5 + 2x^3 - x^2 - 3x + 4 has 5 terms, even though it is of degree 5 in x.
Thus, the correct answer is option 'C', which states that a polynomial of degree 5 in x has at most 6 terms.
Polynomial is a mathematical expression that contains variables, constants and exponents, combined using arithmetic operations like addition, subtraction, multiplication and division.
Degree of a polynomial is the highest power of the variable in the polynomial.
For example, in the polynomial 2x^3 + 5x^2 - 7x + 4, the degree is 3.
A polynomial of degree 5 in x means that the highest power of x in the polynomial is 5.
Now, let's consider the number of terms in a polynomial of degree 5 in x.
A term in a polynomial is a product of a constant and one or more variables raised to some exponents.
For example, in the polynomial 2x^3 + 5x^2 - 7x + 4, the terms are 2x^3, 5x^2, -7x and 4.
The number of terms in a polynomial of degree 5 in x depends on the number of possible combinations of the variables and constants that can be multiplied together to obtain a term of degree 5.
To obtain a term of degree 5 in x, we can multiply x^5 by a constant, or we can multiply x^4 by x and a constant, or we can multiply x^3 by x^2 and a constant, and so on.
Thus, the number of possible terms in a polynomial of degree 5 in x is given by the sum of the binomial coefficients of the form (5 choose k), where k ranges from 0 to 5.
(5 choose 0) + (5 choose 1) + (5 choose 2) + (5 choose 3) + (5 choose 4) + (5 choose 5) = 1 + 5 + 10 + 10 + 5 + 1 = 32
Therefore, a polynomial of degree 5 in x can have at most 32 terms.
However, not all of these terms need to be present in the polynomial. Some of the terms may have a coefficient of 0, which means that they do not contribute to the polynomial.
For example, the polynomial x^5 + 2x^3 - x^2 - 3x + 4 has 5 terms, even though it is of degree 5 in x.
Thus, the correct answer is option 'C', which states that a polynomial of degree 5 in x has at most 6 terms.
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =- a)- 2
- b)- 1
- c)1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =
a)
- 2
b)
- 1
c)
1
d)
None of these
|
|
Naina Sharma answered |
P(x) = 2x² + 5x + 1
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
Find a quadratic polynomial, the sum and product of whose zeroes are 
- a)4x2 - x + 1
- b)4x2 + x - 1
- c)4x2 + x + 1
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Find a quadratic polynomial, the sum and product of whose zeroes are 

a)
4x2 - x + 1
b)
4x2 + x - 1
c)
4x2 + x + 1
d)
none of these
|
|
Gaangailung Panmei answered |
Let B and Á be the roots of a quadratic equation ax* + bx + c, where * =2
B + Á = -b/a = -4/1 and
BÁ = c/a (given)
. ' . ax* + bx + c =x + b/ax + c/a
=x -(-b/a)x + c/a
=x -(-1/4) x +1/4 [ ' . ' -b/a = -1/4 ; c/a =1/4]
=x +1/4x + 1/4
=4x +x +1,, which is the reason to be cited.
. ' . Option ' C ' is the correct answer.
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Polynomials" are available for CBSE Class 9 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 9 Mathematics (Maths)Q A cubic polynomial is a polynomial with degree- a)1
- b)3
- c)0
- d)2
Correct answer is option 'B'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Polynomials" are available for CBSE Class 9 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 9 Mathematics (Maths)
Q A cubic polynomial is a polynomial with degree
a)
1
b)
3
c)
0
d)
2
|
|
Jyoti Kapoor answered |
A cubic polynomial is a polynomial of degree 3. A univariate cubic polynomial has the form f(x) = a3 x^3 + a2 x^2 + a1 x + a0. An equation involving a cubic polynomial is called a cubic equation. A closed-form solution known as the cubic formula exists for the solutions of an arbitrary cubic equation.
The value of k for which x – 1 is a factor of the polynomial 4x3+ 3x2 – 4x + k is :-- a)3
- b)0
- c)1
- d)- 3
Correct answer is option 'D'. Can you explain this answer?
The value of k for which x – 1 is a factor of the polynomial 4x3+ 3x2 – 4x + k is :-
a)
3
b)
0
c)
1
d)
- 3
|
|
Dhruv Banerjee answered |
Please provide more information or context for me to better understand your question.
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –- a)x2 + 2x + 3
- b)x2 – 5x + 3
- c)x2 + 5x + 3
- d)x2 + 3x – 5
Correct answer is option 'C'. Can you explain this answer?
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –
a)
x2 + 2x + 3
b)
x2 – 5x + 3
c)
x2 + 5x + 3
d)
x2 + 3x – 5
|
|
Bhaskar Dasgupta answered |
If α, β be the zeros of the quadratic polynomial ,then
(x−α)(x−β) is the quadratic polynomial.
Thus, (x−α)(x−β) is the polynomial.
=x^2−αx−βx+αβ
=x^2−x(α+β)+αβ(i)
(α+β)=−5αβ=3
Now putting the value of (α+β),αβ in equation (i) we get,
x^2−x(−5)+3
=x^2+5x+3
A linear polynomial :-- a)May have no zero
- b)May have one zero
- c)Has one and only one zero always
- d)May have more than one zero
Correct answer is option 'C'. Can you explain this answer?
A linear polynomial :-
a)
May have no zero
b)
May have one zero
c)
Has one and only one zero always
d)
May have more than one zero
|
|
Zara Khan answered |
Linear Polynomial and Zeroes
A linear polynomial is a polynomial of degree 1. It can be expressed in the form of ax + b, where a and b are constants and x is a variable.
Zeroes of a polynomial are the values of x for which the polynomial becomes zero.
Now, let's look at each option to understand which one is correct.
a) May have no zero
This statement is not true. All linear polynomials have exactly one zero.
b) May have one zero
This statement is partially true. A linear polynomial can only have one zero.
c) Has one and only one zero always
This statement is correct. A linear polynomial has exactly one zero.
d) May have more than one zero
This statement is incorrect. A linear polynomial cannot have more than one zero.
Conclusion
Therefore, option 'C' - Has one and only one zero always, is the correct answer. A linear polynomial always has exactly one zero.
A linear polynomial is a polynomial of degree 1. It can be expressed in the form of ax + b, where a and b are constants and x is a variable.
Zeroes of a polynomial are the values of x for which the polynomial becomes zero.
Now, let's look at each option to understand which one is correct.
a) May have no zero
This statement is not true. All linear polynomials have exactly one zero.
b) May have one zero
This statement is partially true. A linear polynomial can only have one zero.
c) Has one and only one zero always
This statement is correct. A linear polynomial has exactly one zero.
d) May have more than one zero
This statement is incorrect. A linear polynomial cannot have more than one zero.
Conclusion
Therefore, option 'C' - Has one and only one zero always, is the correct answer. A linear polynomial always has exactly one zero.
A polynomial of degree 5 in x has at most- a)5 terms
- b)4 terms
- c)6 terms
- d)10 terms
Correct answer is option 'C'. Can you explain this answer?
A polynomial of degree 5 in x has at most
a)
5 terms
b)
4 terms
c)
6 terms
d)
10 terms
|
|
Amit Sharma answered |
A polynomial of degree 5 is of the form p(x) = , where a, b, c, d, e, and f are real numbers and a ≠ 0.
, where a, b, c, d, e, and f are real numbers and a ≠ 0.
 , where a, b, c, d, e, and f are real numbers and a ≠ 0.
, where a, b, c, d, e, and f are real numbers and a ≠ 0.Thus, p(x) can have at most 6 terms and at least one term containing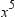 .
.
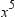 .
. The coefficient of x3 in the polynomial 5 + 2x + 3x2 – 7x3 is- a)5
- b)2
- c)7
- d)- 7
Correct answer is option 'D'. Can you explain this answer?
The coefficient of x3 in the polynomial 5 + 2x + 3x2 – 7x3 is
a)
5
b)
2
c)
7
d)
- 7
|
|
Avishi Iyer answered |
The coefficient of x^3 is 0 because there is no term with x^3 in the polynomial 5 + 2x + 3x^2.
Let p(x) = ax2 + bx + c be a quadratic polynomial. It can have at most –- a)One zero
- b)Two zeros
- c)Three zeros
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Let p(x) = ax2 + bx + c be a quadratic polynomial. It can have at most –
a)
One zero
b)
Two zeros
c)
Three zeros
d)
None of these
|
|
Uday Datta answered |
The polynomial ax^2+bx+c has three terms. The first one is ax^2, the second is bx, and the third is c.
The exponent of the first term is 2.
The exponent of the second term is 1 because bx=bx^1.
The exponent of the third term is 0 because c=cx^0.
Since the highest exponent is 2, therefore, the degree of ax^2+bx+c is 2.
Since, the degree of the polynomial is 2, hence, the polynomial ax^2+bx+c can have zero, one or two zeroes.
Hence, the polynomial ax^2+bx+c can have at most two zereos.
The value of m for which x – 2 is a factor of the polynomial x4 – x3 + 2x2 – mx + 4 is :-- a)10
- b)- 10
- c)4
- d)9
Correct answer is option 'A'. Can you explain this answer?
The value of m for which x – 2 is a factor of the polynomial x4 – x3 + 2x2 – mx + 4 is :-
a)
10
b)
- 10
c)
4
d)
9
|
|
Rhea Patel answered |
Please provide a complete question for me to assist you better.
The value of the polynomial 5x−4x2+3, when x = −1 is- a)-6
- b)-1
- c)1
- d)6
Correct answer is option 'A'. Can you explain this answer?
The value of the polynomial 5x−4x2+3, when x = −1 is
a)
-6
b)
-1
c)
1
d)
6

|
Sanchita Choudhury answered |
Let p (x) = 5x – 4x2 + 3 …(i)
On putting x = -1 in Eq. (i), we get
p(-1) = 5(-1) -4(-1)2 + 3= - 5 - 4 + 3 = -6
On putting x = -1 in Eq. (i), we get
p(-1) = 5(-1) -4(-1)2 + 3= - 5 - 4 + 3 = -6
The factors of 2x2 – 3x – 2 are :-- a)(2x – 1) (x + 2)
- b)(2x + 1) (x – 2)
- c)(x + 1) (x – 2)
- d)(x – 1) (x + 2)
Correct answer is option 'B'. Can you explain this answer?
The factors of 2x2 – 3x – 2 are :-
a)
(2x – 1) (x + 2)
b)
(2x + 1) (x – 2)
c)
(x + 1) (x – 2)
d)
(x – 1) (x + 2)
|
|
Swati Verma answered |
2x2 – 3x – 2
2x2 - 4x + x - 2 = 0
2x2(x-2) +1(x-2) = 0
(2x+1) (x-2)
x3 + y3 + z3 – 3xyz is :-- a)(x + y – z)
- b)(x – y + z)3
- c)(x + y + z) (x2 + y2 + z2 – xy – yz – zx)
- d)(x + y + z)3 – 3xyz
Correct answer is option 'C'. Can you explain this answer?
x3 + y3 + z3 – 3xyz is :-
a)
(x + y – z)
b)
(x – y + z)3
c)
(x + y + z) (x2 + y2 + z2 – xy – yz – zx)
d)
(x + y + z)3 – 3xyz

|
Kalyan Malik answered |
We know that x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx).
If x + y + z = 0, then x3 + y3 + z3 – 3xyz = 0 or x3 + y3 + z3 = 3xyz.
If x + y + z = 0, then x3 + y3 + z3 – 3xyz = 0 or x3 + y3 + z3 = 3xyz.
The degree of the zero polynomial is- a)any natural number
- b)not defined
- c)1
- d)0
Correct answer is option 'B'. Can you explain this answer?
The degree of the zero polynomial is
a)
any natural number
b)
not defined
c)
1
d)
0

|
Kalyan Malik answered |
The degree of zero polynomial is not defined, because, in zero polynomial, the coefficient of any variable is zero i.e., Ox2 or Ox5, etc. Hence, we cannot exactly determine the degree of the variable.
The value of k for which x + 1 is a factor of the polynomial x3 + x2 + x + k is :-- a)0
- b)2
- c)1
- d)-1
Correct answer is option 'C'. Can you explain this answer?
The value of k for which x + 1 is a factor of the polynomial x3 + x2 + x + k is :-
a)
0
b)
2
c)
1
d)
-1
|
|
Ishita Yadav answered |
Given polynomial is x³ - x² + x - k.
To check if x - 1 is a factor, we can check if the value of the polynomial is 0 when x = 1.
Substituting x = 1, we get:
1³ - 1² + 1 - k = 1 - 1 + 1 - k = 0 - k = -k
So, for x - 1 to be a factor, we need -k = 0, which means k = 0.
Therefore, option (a) is incorrect and the correct answer is option (c), k = 1.
To check if x - 1 is a factor, we can check if the value of the polynomial is 0 when x = 1.
Substituting x = 1, we get:
1³ - 1² + 1 - k = 1 - 1 + 1 - k = 0 - k = -k
So, for x - 1 to be a factor, we need -k = 0, which means k = 0.
Therefore, option (a) is incorrect and the correct answer is option (c), k = 1.
If x + 2 is a factor of x3 – 2ax2 + 16, then value of a is- a)3
- b)1
- c)4
- d)2
Correct answer is option 'B'. Can you explain this answer?
If x + 2 is a factor of x3 – 2ax2 + 16, then value of a is
a)
3
b)
1
c)
4
d)
2
|
|
Prachi Shah answered |
If x 2 is a factor of x^3, then x^3 can be written as (x 2) multiplied by some other polynomial. We can use polynomial long division or synthetic division to find this polynomial:
x^2
--------
x 2 | x^3 + 0x^2 + 0x + 0
-x^3 - 2x^2
---------
-2x^2 + 0x
-2x^2 - 4x
----------
4x + 0
Therefore, x^3 = (x 2)(x^2 - 2x + 4).
x^2
--------
x 2 | x^3 + 0x^2 + 0x + 0
-x^3 - 2x^2
---------
-2x^2 + 0x
-2x^2 - 4x
----------
4x + 0
Therefore, x^3 = (x 2)(x^2 - 2x + 4).
If 2 and (- 1/2) as the sum and product of its zeros respectively then the quadratic polynomial f(x) is –- a)x2 – 2x – 4
- b)4x2 – 2x + 1
- c)2x2 + 4x – 1
- d)2x2 – 4x – 1
Correct answer is option 'D'. Can you explain this answer?
If 2 and (- 1/2) as the sum and product of its zeros respectively then the quadratic polynomial f(x) is –
a)
x2 – 2x – 4
b)
4x2 – 2x + 1
c)
2x2 + 4x – 1
d)
2x2 – 4x – 1
|
|
Archana gupta answered |
Understanding Quadratic Polynomials
A quadratic polynomial can be expressed in the form f(x) = ax² + bx + c, where the zeros (roots) of the polynomial can be derived from its coefficients.
Given Conditions
- Sum of Zeros (α + β): 2
- Product of Zeros (αβ): -1/2
Using the Relationships
For a quadratic polynomial f(x) = ax² + bx + c:
- The sum of the zeros is given by -b/a.
- The product of the zeros is given by c/a.
Using the conditions:
1. Sum of Zeros:
- -b/a = 2
- Therefore, b = -2a
2. Product of Zeros:
- c/a = -1/2
- Therefore, c = -a/2
Forming the Polynomial
Substituting b and c into the polynomial form:
f(x) = ax² + (-2a)x + (-a/2)
To eliminate the fraction, multiply through by 2:
f(x) = 2ax² - 4ax - a
Assuming a = 1 for simplicity:
f(x) = 2x² - 4x - 1
Thus, the polynomial becomes:
Final Polynomial
- f(x) = 2x² - 4x - 1
This corresponds to option D.
Conclusion
The correct quadratic polynomial based on the provided sum and product of its zeros is:
- 2x² - 4x - 1 (Option D)
A quadratic polynomial can be expressed in the form f(x) = ax² + bx + c, where the zeros (roots) of the polynomial can be derived from its coefficients.
Given Conditions
- Sum of Zeros (α + β): 2
- Product of Zeros (αβ): -1/2
Using the Relationships
For a quadratic polynomial f(x) = ax² + bx + c:
- The sum of the zeros is given by -b/a.
- The product of the zeros is given by c/a.
Using the conditions:
1. Sum of Zeros:
- -b/a = 2
- Therefore, b = -2a
2. Product of Zeros:
- c/a = -1/2
- Therefore, c = -a/2
Forming the Polynomial
Substituting b and c into the polynomial form:
f(x) = ax² + (-2a)x + (-a/2)
To eliminate the fraction, multiply through by 2:
f(x) = 2ax² - 4ax - a
Assuming a = 1 for simplicity:
f(x) = 2x² - 4x - 1
Thus, the polynomial becomes:
Final Polynomial
- f(x) = 2x² - 4x - 1
This corresponds to option D.
Conclusion
The correct quadratic polynomial based on the provided sum and product of its zeros is:
- 2x² - 4x - 1 (Option D)
The quotient and remainder are x - 2 and -2x + 4 respectively. If the polynomial x3 - 3x2 + x + 2 is divided by g(x). Find g(x)- a)x2 + x + 1
- b)x2 - x - 1
- c)x2 - x + 1
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The quotient and remainder are x - 2 and -2x + 4 respectively. If the polynomial x3 - 3x2 + x + 2 is divided by g(x). Find g(x)
a)
x2 + x + 1
b)
x2 - x - 1
c)
x2 - x + 1
d)
none of these
|
|
Aman Joshi answered |
Given, quotient = x - 2 and remainder = -2x + 4.
So, we know that:
x³ - 3x² + x + 2 = g(x) * (x - 2) - 2x + 4
Let's simplify the right-hand side:
x³ - 3x² + x + 2 = g(x) * x - 2g(x) - 2x + 4
Now, let's rearrange the terms:
x³ - 3x² + x + 2 = g(x) * x - 2x - 2g(x) + 4
x³ - 3x² + x + 2 = (g(x) - 2) * x - 2g(x) + 4
Now, we can equate the coefficients of x², x, and the constant term on both sides to get a system of equations:
Coefficient of x²: -3 = g(x) - 2
Coefficient of x: 1 = g(x)
Constant term: 2 = -2g(x) + 4
Solving the system of equations, we get:
g(x) = 1
-3 = g(x) - 2 = -1
2 = -2g(x) + 4
g(x) = 1
Therefore, the polynomial g(x) is x² - x + 1, which is option C.
So, we know that:
x³ - 3x² + x + 2 = g(x) * (x - 2) - 2x + 4
Let's simplify the right-hand side:
x³ - 3x² + x + 2 = g(x) * x - 2g(x) - 2x + 4
Now, let's rearrange the terms:
x³ - 3x² + x + 2 = g(x) * x - 2x - 2g(x) + 4
x³ - 3x² + x + 2 = (g(x) - 2) * x - 2g(x) + 4
Now, we can equate the coefficients of x², x, and the constant term on both sides to get a system of equations:
Coefficient of x²: -3 = g(x) - 2
Coefficient of x: 1 = g(x)
Constant term: 2 = -2g(x) + 4
Solving the system of equations, we get:
g(x) = 1
-3 = g(x) - 2 = -1
2 = -2g(x) + 4
g(x) = 1
Therefore, the polynomial g(x) is x² - x + 1, which is option C.
The expanded form of (x + y + 2z)2 is :-- a)x2 + y2 + 4z2 + 2xy + 2yz + 2zx
- b)x2 + y2 + 4z2 + xy + 2yz + 2zx
- c)x2 + y2 + 4z2 + 2xy + 4yz + 4zx
- d)x2 + y2 + 4z2 + 2xy + 2yz + 4zx
Correct answer is option 'C'. Can you explain this answer?
The expanded form of (x + y + 2z)2 is :-
a)
x2 + y2 + 4z2 + 2xy + 2yz + 2zx
b)
x2 + y2 + 4z2 + xy + 2yz + 2zx
c)
x2 + y2 + 4z2 + 2xy + 4yz + 4zx
d)
x2 + y2 + 4z2 + 2xy + 2yz + 4zx
|
|
Megha Mishra answered |
Solution:
Given expression is (x y 2z)2
To expand the given expression, we can use the formula (a + b)2 = a2 + 2ab + b2.
Therefore, (x y 2z)2 = (x y 2z)(x y 2z)
Expanding the above expression using the distributive property, we get:
= x(x y 2z) + y(x y 2z) + 2z(x y 2z)
= x2 + xy + 2xz + yx + y2 + 2yz + 2zx + 2zy + 4z2
= x2 y2 4z2 2xy 4yz 4zx
Therefore, the expanded form of (x y 2z)2 is x2 y2 4z2 2xy 4yz 4zx, which is option 'C'.
Given expression is (x y 2z)2
To expand the given expression, we can use the formula (a + b)2 = a2 + 2ab + b2.
Therefore, (x y 2z)2 = (x y 2z)(x y 2z)
Expanding the above expression using the distributive property, we get:
= x(x y 2z) + y(x y 2z) + 2z(x y 2z)
= x2 + xy + 2xz + yx + y2 + 2yz + 2zx + 2zy + 4z2
= x2 y2 4z2 2xy 4yz 4zx
Therefore, the expanded form of (x y 2z)2 is x2 y2 4z2 2xy 4yz 4zx, which is option 'C'.
The expanded form of 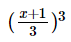 is :-
is :- - a)x3 +
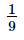 + 3x2 + 3x
+ 3x2 + 3x - b)x3 +
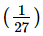 + x2 +
+ x2 + 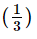 x
x - c)x3 +
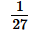 + 3x2 + x
+ 3x2 + x - d)x3 +
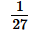 + 3x2 +
+ 3x2 + 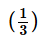 x
x
Correct answer is option 'B'. Can you explain this answer?
The expanded form of 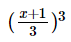 is :-
is :-
a)
x3 + 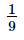 + 3x2 + 3x
+ 3x2 + 3x
b)
x3 + 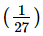 + x2 +
+ x2 + 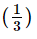 x
x
c)
x3 + 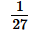 + 3x2 + x
+ 3x2 + x
d)
x3 + 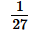 + 3x2 +
+ 3x2 + 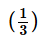 x
x
|
|
Anaya Gupta answered |
Expanded Form of (x 1/3)3
Explanation:
When we raise a binomial expression (a+b) to the power n, we expand it using the binomial theorem. The binomial theorem states that:
(a+b)n = nC0an + nC1an-1b + nC2an-2b2 + … + nCn-1abn-1 + nCnbn
where nCk is the binomial coefficient, given by nCk = n!/(k!(n-k)!), and ! denotes the factorial function.
Similarly, when we raise a monomial expression (axm) to the power n, we use the power rule of exponents, which states that:
(axm)n = anxm(n)
Therefore, to expand (x 1/3)3, we use the power rule of exponents, and get:
(x 1/3)3 = x3(1/3)3
Simplifying the expression, we get:
(x 1/3)3 = x3(1/27)
Therefore, the expanded form of (x 1/3)3 is option B:
x3 (1/27) x2 (1/3)x
Explanation:
When we raise a binomial expression (a+b) to the power n, we expand it using the binomial theorem. The binomial theorem states that:
(a+b)n = nC0an + nC1an-1b + nC2an-2b2 + … + nCn-1abn-1 + nCnbn
where nCk is the binomial coefficient, given by nCk = n!/(k!(n-k)!), and ! denotes the factorial function.
Similarly, when we raise a monomial expression (axm) to the power n, we use the power rule of exponents, which states that:
(axm)n = anxm(n)
Therefore, to expand (x 1/3)3, we use the power rule of exponents, and get:
(x 1/3)3 = x3(1/3)3
Simplifying the expression, we get:
(x 1/3)3 = x3(1/27)
Therefore, the expanded form of (x 1/3)3 is option B:
x3 (1/27) x2 (1/3)x
Chapter doubts & questions for Theory of polynomials - Elementary Mathematics for CDS 2025 is part of CDS exam preparation. The chapters have been prepared according to the CDS exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CDS 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Theory of polynomials - Elementary Mathematics for CDS in English & Hindi are available as part of CDS exam.
Download more important topics, notes, lectures and mock test series for CDS Exam by signing up for free.
Elementary Mathematics for CDS
174 videos|104 docs|134 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

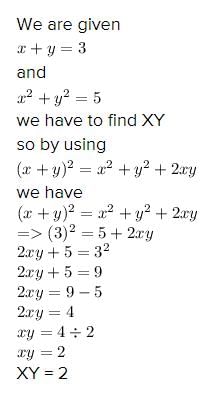
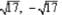
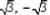
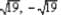

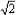 and
and