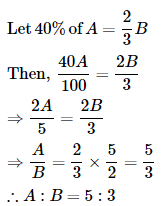All Exams >
RRB Group D / RPF Constable >
Mathematics for RRB Group D / RPF Constable >
All Questions
All questions of Ratio and Proportion for RRB Group D / RPF Constable Exam
In a mixture 60 litres, the ratio of milk and water 2 : 1. If this ratio is to be 1 : 2, then the quanity of water to be further added is:- a)20 litres
- b)30 litres
- c)40 litres
- d)60 litres
Correct answer is option 'D'. Can you explain this answer?
In a mixture 60 litres, the ratio of milk and water 2 : 1. If this ratio is to be 1 : 2, then the quanity of water to be further added is:
a)
20 litres
b)
30 litres
c)
40 litres
d)
60 litres
|
Mihir Sen answered |
Quantity of milk 
Quantity of water in it = (60 - 40) litres = 20 litres.
New ratio = 1 : 2
Let quantity of water to be added further be x litres
Then, milk : water
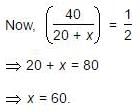
∴ Quantity of water to be added = 60 litres.
Quantity of water in it = (60 - 40) litres = 20 litres.
New ratio = 1 : 2
Let quantity of water to be added further be x litres
Then, milk : water
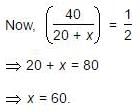
∴ Quantity of water to be added = 60 litres.
A and B together have Rs. 1210. If 
of A's amount is equal to 
of B's amount, how much amount does B have?
- a)Rs. 460
- b)Rs. 484
- c)Rs. 550
- d)Rs. 664
Correct answer is 'B'. Can you explain this answer?
A and B together have Rs. 1210. If of A's amount is equal to of B's amount, how much amount does B have?
of A's amount is equal to of B's amount, how much amount does B have?a)
Rs. 460
b)
Rs. 484
c)
Rs. 550
d)
Rs. 664
|
Manoj Ghosh answered |
A+B=1210(4/15)A=(2/5)B2A=3BTherefore, A=(3B)/2and substituting, (3B/2)+B=1210and hence, 5B=2420 => B=484 Rs.
The ratio of the income of A and B is 7 : 8, and the ratio of the income of B and C is 8 : 11, If the difference in the income earned by A and C is Rs. 800, then find the sum of income earned by all three of them.- a)Rs. 5200
- b)Rs. 4800
- c)Rs. 4000
- d)Rs. 3600
Correct answer is option 'A'. Can you explain this answer?
The ratio of the income of A and B is 7 : 8, and the ratio of the income of B and C is 8 : 11, If the difference in the income earned by A and C is Rs. 800, then find the sum of income earned by all three of them.
a)
Rs. 5200
b)
Rs. 4800
c)
Rs. 4000
d)
Rs. 3600
|
Kiran Reddy answered |
Given:
The ratio of the income of A and B = 7 : 8
The ratio of the income of B and C = 8 : 11
The difference in the income earned by A and C = Rs. 800
Calculation:
According to the question,
The ratio of the income of A and B = 7 : 8
The ratio of the income of B and C = 8 : 11
By combining the ratios, we get,
The ratio of the income of A, B and C = 7 : 8 : 11
Income of C = 11k
Income of A = 7k
The difference in the income earned by A and C = 11k - 7k = 4k
Again according to the question,
⇒ 4k = 800
⇒ k = 200
The income of A, B and C = 7k + 8k + 11k = 26k
Sum of income of A, B and C = 26 × 200 = Rs. 5200
Therefore, 'Rs. 5200' is the required answer.
Point mutation involves- a)Change in single base pair
- b)Deletion
- c)Insertion
- d)Duplication
Correct answer is option 'A'. Can you explain this answer?
Point mutation involves
a)
Change in single base pair
b)
Deletion
c)
Insertion
d)
Duplication
|
Honey answered |
Yes. it involves point mutation as in sickle call anaemia.
Seats for Mathematics, Physics and Biology in a school are in the ratio 5 : 7 : 8. There is a proposal to increase these seats by 40%, 50% and 75% respectively. What will be the ratio after increased seats?- a)2 : 3 : 4
- b)6 : 7 : 8
- c)6 : 8 : 9
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Seats for Mathematics, Physics and Biology in a school are in the ratio 5 : 7 : 8. There is a proposal to increase these seats by 40%, 50% and 75% respectively. What will be the ratio after increased seats?
a)
2 : 3 : 4
b)
6 : 7 : 8
c)
6 : 8 : 9
d)
None of these
|
Future Foundation Institute answered |
Let the incomes be 4x, 5x, 6x and the spending be 6y, 7y, 8y and savings are (4x–6y), (5x–7y) & (6x–8y)
Sheldon saves 1/4th of his income.
Sheldon saves 1/4th of his income.
Therefore:
⇒ 4x – 6y = 4x / 4
⇒ 4x – 6y = x
⇒ 3x = 6y
⇒ x / y = 2
∴ y = x / 2
⇒ 4x – 6y = x
⇒ 3x = 6y
⇒ x / y = 2
∴ y = x / 2
Ratio of Sheldon’s Leonard’s & Howard’s savings:
= 4x – 6y : 5x – 7y : 6x – 8y
= x : 5x – 7y : 6x – 8y
= x : 5x – 7x / 2 : 6x – 8x / 2
= x : 3x / 2 : 2x
= 2 : 3 : 4
= x : 5x – 7y : 6x – 8y
= x : 5x – 7x / 2 : 6x – 8x / 2
= x : 3x / 2 : 2x
= 2 : 3 : 4
The sum of three numbers is 98. If the ratio of the first to second is 2 :3 and that of the second to the third is 5 : 8, then the second number is:- a)20
- b)30
- c)48
- d)58
Correct answer is option 'B'. Can you explain this answer?
The sum of three numbers is 98. If the ratio of the first to second is 2 :3 and that of the second to the third is 5 : 8, then the second number is:
a)
20
b)
30
c)
48
d)
58
|
Aarav Sharma answered |
**Given Information:**
- The sum of three numbers is 98.
- The ratio of the first number to the second number is 2:3.
- The ratio of the second number to the third number is 5:8.
**Let's solve the problem step by step:**
**Step 1:**
Let's assume the three numbers as follows:
- The first number = 2x
- The second number = 3x
- The third number = 8y
**Step 2:**
According to the given information, the sum of the three numbers is 98. Therefore, we can write the equation as:
2x + 3x + 8y = 98
**Step 3:**
Simplifying the equation, we get:
5x + 8y = 98
**Step 4:**
Now, we need to find the values of x and y in order to find the second number.
**Step 5:**
According to the given information, the ratio of the second number to the third number is 5:8. Therefore, we can write the equation as:
3x/8y = 5/8
**Step 6:**
Cross-multiplying the equation, we get:
24x = 40y
**Step 7:**
Simplifying the equation, we get:
3x = 5y
**Step 8:**
Now, we have two equations:
5x + 8y = 98
3x = 5y
**Step 9:**
Substituting the value of 3x from the second equation into the first equation, we get:
5(5y/3) + 8y = 98
25y/3 + 8y = 98
(25y + 24y)/3 = 98
49y/3 = 98
49y = 294
y = 294/49
y = 6
**Step 10:**
Substituting the value of y into the second equation, we get:
3x = 5(6)
3x = 30
x = 30/3
x = 10
**Step 11:**
Now, we can find the second number:
The second number = 3x = 3 * 10 = 30
Therefore, the correct answer is option **B) 30**.
- The sum of three numbers is 98.
- The ratio of the first number to the second number is 2:3.
- The ratio of the second number to the third number is 5:8.
**Let's solve the problem step by step:**
**Step 1:**
Let's assume the three numbers as follows:
- The first number = 2x
- The second number = 3x
- The third number = 8y
**Step 2:**
According to the given information, the sum of the three numbers is 98. Therefore, we can write the equation as:
2x + 3x + 8y = 98
**Step 3:**
Simplifying the equation, we get:
5x + 8y = 98
**Step 4:**
Now, we need to find the values of x and y in order to find the second number.
**Step 5:**
According to the given information, the ratio of the second number to the third number is 5:8. Therefore, we can write the equation as:
3x/8y = 5/8
**Step 6:**
Cross-multiplying the equation, we get:
24x = 40y
**Step 7:**
Simplifying the equation, we get:
3x = 5y
**Step 8:**
Now, we have two equations:
5x + 8y = 98
3x = 5y
**Step 9:**
Substituting the value of 3x from the second equation into the first equation, we get:
5(5y/3) + 8y = 98
25y/3 + 8y = 98
(25y + 24y)/3 = 98
49y/3 = 98
49y = 294
y = 294/49
y = 6
**Step 10:**
Substituting the value of y into the second equation, we get:
3x = 5(6)
3x = 30
x = 30/3
x = 10
**Step 11:**
Now, we can find the second number:
The second number = 3x = 3 * 10 = 30
Therefore, the correct answer is option **B) 30**.
11 : b : 44 are in continued proportion. Find b.- a)4
- b)22
- c)44
- d)11
Correct answer is option 'B'. Can you explain this answer?
11 : b : 44 are in continued proportion. Find b.
a)
4
b)
22
c)
44
d)
11
|
|
Alok Verma answered |
We know that if a, b and c are in continued proportion then b2 = ac
b2 = 11.44
b2 = 484
b = 22
b2 = 11.44
b2 = 484
b = 22
The ratio of the number of boys and girls in a college is 7 : 8. If the percentage increase in the number of boys and girls be 20% and 10% respectively, what will be the new ratio?- a)8 : 9
- b)17 : 18
- c)21 : 22
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
The ratio of the number of boys and girls in a college is 7 : 8. If the percentage increase in the number of boys and girls be 20% and 10% respectively, what will be the new ratio?
a)
8 : 9
b)
17 : 18
c)
21 : 22
d)
Cannot be determined
|
Ravi Singh answered |
In a bag, there are coins of 25 p, 10 p and 5 p in the ratio of 1 : 2 : 3. If there is Rs. 30 in all, how many 5 p coins are there?- a)50
- b)100
- c)150
- d)200
Correct answer is option 'C'. Can you explain this answer?
In a bag, there are coins of 25 p, 10 p and 5 p in the ratio of 1 : 2 : 3. If there is Rs. 30 in all, how many 5 p coins are there?
a)
50
b)
100
c)
150
d)
200
|
Gowri Chakraborty answered |
Let x is the number of 25 paisa coins then 2x and 3x will be for 10 and 5 paisa coins.
Now 30 rupees equal to 30*100 paisa now total paisa equal to x*25+2x*10+3x*5=3000.
60x = 3000.
x = 50.
Now number 5 paisa coin is 3x equal to 3*50 = 150.
The monthly incomes of X and Y are in the ratio of 4:3 and their monthly expenses are in the ratio of 3:2. However, each saves Rs. 6,000 per month. What is their total monthly income?
- a)Rs. 28,000
- b)Rs. 42,000
- c)Rs. 56,000
- d)Rs. 84,000
Correct answer is option 'B'. Can you explain this answer?
The monthly incomes of X and Y are in the ratio of 4:3 and their monthly expenses are in the ratio of 3:2. However, each saves Rs. 6,000 per month. What is their total monthly income?
a)
Rs. 28,000
b)
Rs. 42,000
c)
Rs. 56,000
d)
Rs. 84,000
|
|
Kishan Darak answered |
Since expenses and Savings are correlated
Therefore income of:
X=6000×4=24000
Y=6000×3=18000
x+y =24000+18000=42000(that is option 'B' is the right answer
Therefore income of:
X=6000×4=24000
Y=6000×3=18000
x+y =24000+18000=42000(that is option 'B' is the right answer
Can you explain the answer of this question below:Two number are in the ratio 3 : 5. If 9 is subtracted from each, the new numbers are in the ratio 12 : 23. The smaller number is:
- A:
27
- B:
33
- C:
49
- D:
55
The answer is B.
Two number are in the ratio 3 : 5. If 9 is subtracted from each, the new numbers are in the ratio 12 : 23. The smaller number is:
27
33
49
55
|
Sagar Sharma answered |
Given:
The ratio of two numbers is 3:5
After subtracting 9 from each number, the new ratio is 12:23
Let's assume the two numbers in the original ratio are 3x and 5x.
Ratio of the new numbers:
(3x-9) : (5x-9) = 12 : 23
Cross-multiplying, we get:
12(5x-9) = 23(3x-9)
Simplifying the equation:
60x - 108 = 69x - 207
-9x = -99
x = 11
Finding the smaller number:
Smaller number = 3x = 3 * 11 = 33
Therefore, the smaller number is 33, which corresponds to option 'B'.
The ratio of two numbers is 3:5
After subtracting 9 from each number, the new ratio is 12:23
Let's assume the two numbers in the original ratio are 3x and 5x.
Ratio of the new numbers:
(3x-9) : (5x-9) = 12 : 23
Cross-multiplying, we get:
12(5x-9) = 23(3x-9)
Simplifying the equation:
60x - 108 = 69x - 207
-9x = -99
x = 11
Finding the smaller number:
Smaller number = 3x = 3 * 11 = 33
Therefore, the smaller number is 33, which corresponds to option 'B'.
If 4 : 8 : C are in continued proportion then find C?- a)16
- b)4
- c)36
- d)34
Correct answer is option 'A'. Can you explain this answer?
If 4 : 8 : C are in continued proportion then find C?
a)
16
b)
4
c)
36
d)
34
|
|
Aarav Sharma answered |
We know that if a, b and c are in continued proportion,
then b2 = ac
82 = 4.C
C = 64/4 = 16
then b2 = ac
82 = 4.C
C = 64/4 = 16
The salaries A, B, C are in the ratio 2 : 3 : 5. If the increments of 15%, 10% and 20% are allowed respectively in their salaries, then what will be new ratio of their salaries?- a)3 : 3 : 10
- b)10 : 11 : 20
- c)23 : 33 : 60
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
The salaries A, B, C are in the ratio 2 : 3 : 5. If the increments of 15%, 10% and 20% are allowed respectively in their salaries, then what will be new ratio of their salaries?
a)
3 : 3 : 10
b)
10 : 11 : 20
c)
23 : 33 : 60
d)
Cannot be determined
|
|
Kavya Saxena answered |
Salaries of Ravi and Sumit are in the ratio 2 : 3. If the 'salary of each' one of them is increased by Rs. 4000, the new ratio becomes 40 : 57. What is Sumit's present salary?
- a)Rs. 17,000
- b)Rs. 20,000
- c)Rs. 25,500
- d)Rs. 38,000
Correct answer is option 'D'. Can you explain this answer?
Salaries of Ravi and Sumit are in the ratio 2 : 3. If the 'salary of each' one of them is increased by Rs. 4000, the new ratio becomes 40 : 57. What is Sumit's present salary?
a)
Rs. 17,000
b)
Rs. 20,000
c)
Rs. 25,500
d)
Rs. 38,000
|
Sameer Rane answered |
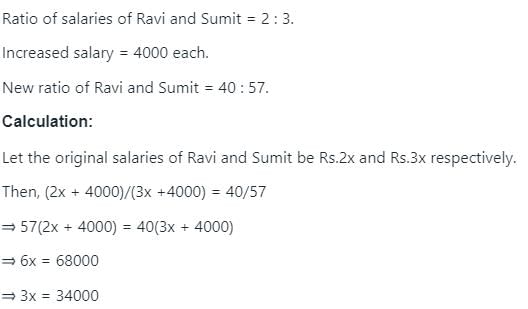
∴ Sumit's present salary = (3x + 4000) = Rs.(34000 + 4000) = Rs. 38000.
Find the ratio A : B : C : D : E if,
A : B = 4 : 5
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2- a)200 : 270 : 315 : 350 : 140
- b)120 : 270 : 315 : 350 : 140
- c) 216 : 270 : 315 : 350 : 140
- d)216 : 270 : 315 : 350 : 210
Correct answer is option 'C'. Can you explain this answer?
Find the ratio A : B : C : D : E if,
A : B = 4 : 5
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2
A : B = 4 : 5
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2
a)
200 : 270 : 315 : 350 : 140
b)
120 : 270 : 315 : 350 : 140
c)
216 : 270 : 315 : 350 : 140
d)
216 : 270 : 315 : 350 : 210
|
|
Rhea Reddy answered |
A : B = 4 : 5
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2
A : B : C : D : E = 4 x 6 x 9 x 5 : 5 x 6 x 9 x 5: 5 x 7 x 9 x 5: 5 x 7 x 10 x 5: 5 x 7 x 10 x 2
216 : 270 : 315 : 350 : 140
The required ratio A : B : C : D : E is 216 : 270 : 315 : 350 : 140
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2
A : B : C : D : E = 4 x 6 x 9 x 5 : 5 x 6 x 9 x 5: 5 x 7 x 9 x 5: 5 x 7 x 10 x 5: 5 x 7 x 10 x 2
216 : 270 : 315 : 350 : 140
The required ratio A : B : C : D : E is 216 : 270 : 315 : 350 : 140
In a library, the ratio of number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.- a) 312
- b) 321
- c) 936
- d) 1560
Correct answer is option 'A'. Can you explain this answer?
In a library, the ratio of number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.
a)
312
b)
321
c)
936
d)
1560
|
Ashwini Chatterjee answered |
**Given information:**
- The ratio of the number of story books to that of non-story books was 4:3.
- The total number of story books was 1248.
- When some more story books were bought, the ratio became 5:3.
**Let's solve the problem step by step:**
**Step 1: Calculate the number of non-story books**
- Since the ratio of story books to non-story books is 4:3, let's assume the number of story books as 4x and the number of non-story books as 3x.
- According to the given information, the total number of story books is 1248. So, we can write the equation as 4x = 1248.
- Solving the equation, we get x = 1248/4 = 312.
- Therefore, the number of non-story books is 3x = 3 * 312 = 936.
**Step 2: Calculate the number of story books after the purchase**
- After some more story books were bought, the ratio became 5:3. Let's assume the number of additional story books as y.
- Now, the total number of story books is 1248 + y, and the total number of non-story books is still 936.
- According to the new ratio, the equation can be written as (1248 + y)/936 = 5/3.
- Cross-multiplying, we get 3 * (1248 + y) = 5 * 936.
- Simplifying the equation, we have 3744 + 3y = 4680.
- Subtracting 3744 from both sides, we get 3y = 936.
- Dividing both sides by 3, we get y = 936/3 = 312.
**Step 3: Calculate the number of story books bought**
- The number of story books bought is given by the value of y, which we calculated as 312.
Therefore, the number of story books bought is 312.
Hence, the correct answer is option A) 312.
- The ratio of the number of story books to that of non-story books was 4:3.
- The total number of story books was 1248.
- When some more story books were bought, the ratio became 5:3.
**Let's solve the problem step by step:**
**Step 1: Calculate the number of non-story books**
- Since the ratio of story books to non-story books is 4:3, let's assume the number of story books as 4x and the number of non-story books as 3x.
- According to the given information, the total number of story books is 1248. So, we can write the equation as 4x = 1248.
- Solving the equation, we get x = 1248/4 = 312.
- Therefore, the number of non-story books is 3x = 3 * 312 = 936.
**Step 2: Calculate the number of story books after the purchase**
- After some more story books were bought, the ratio became 5:3. Let's assume the number of additional story books as y.
- Now, the total number of story books is 1248 + y, and the total number of non-story books is still 936.
- According to the new ratio, the equation can be written as (1248 + y)/936 = 5/3.
- Cross-multiplying, we get 3 * (1248 + y) = 5 * 936.
- Simplifying the equation, we have 3744 + 3y = 4680.
- Subtracting 3744 from both sides, we get 3y = 936.
- Dividing both sides by 3, we get y = 936/3 = 312.
**Step 3: Calculate the number of story books bought**
- The number of story books bought is given by the value of y, which we calculated as 312.
Therefore, the number of story books bought is 312.
Hence, the correct answer is option A) 312.
A sum of Rs. 12,384 is divided between A, B, C and D such that the ratio of the shares of A and B is 3 : 4, that of B and C is 5 : 6, and that of C and D is 8 : 9. What is the share of C ? - a)Rs. 2,880
- b)Rs. 3,888
- c)Rs. 3,456
- d)Rs. 2,160
Correct answer is option 'C'. Can you explain this answer?
A sum of Rs. 12,384 is divided between A, B, C and D such that the ratio of the shares of A and B is 3 : 4, that of B and C is 5 : 6, and that of C and D is 8 : 9. What is the share of C ?
a)
Rs. 2,880
b)
Rs. 3,888
c)
Rs. 3,456
d)
Rs. 2,160
|
Shilpa Choudhury answered |
Given:
A : B = 3 : 4
B : C = 5 : 6
C : D = 8 : 9
Sum to divided among them = Rs. 12,384
Concept used:
Ratio Proportion
Calculation:
A : B = 3 : 4 = 15 : 20
B : C = 5 : 6 = 20 : 24
C : D = 8 : 9 = 24 : 27
A : B : C : D = 15 : 20 : 24 : 27
Share of C = 24/(15 + 20 + 24 + 27) × 12384 = Rs. 3456
∴ The share of C is Rs. 3456.
If 0.75 : x :: 5 : 8, then x is equal to:- a)1.12
- b)1.2
- c)1.25
- d)1.30
Correct answer is option 'B'. Can you explain this answer?
If 0.75 : x :: 5 : 8, then x is equal to:
a)
1.12
b)
1.2
c)
1.25
d)
1.30
|
|
Aarav Sharma answered |
To find the value of "x" in the given proportion 0.75 : x :: 5 : 8, we can use the concept of cross-multiplication.
Step 1: Set up the proportion
0.75 : x :: 5 : 8
Step 2: Cross-multiply
0.75 * 8 = x * 5
Step 3: Solve for "x"
6 = 5x
Step 4: Divide both sides by 5
x = 6 / 5
Step 5: Simplify the fraction
x = 1.2
Therefore, the value of "x" in the proportion 0.75 : x :: 5 : 8 is equal to 1.2.
Summary:
To find the value of "x" in the given proportion, we set up the proportion and cross-multiply. Then we solve for "x" by dividing both sides of the equation. In this case, the value of "x" is equal to 1.2.
Step 1: Set up the proportion
0.75 : x :: 5 : 8
Step 2: Cross-multiply
0.75 * 8 = x * 5
Step 3: Solve for "x"
6 = 5x
Step 4: Divide both sides by 5
x = 6 / 5
Step 5: Simplify the fraction
x = 1.2
Therefore, the value of "x" in the proportion 0.75 : x :: 5 : 8 is equal to 1.2.
Summary:
To find the value of "x" in the given proportion, we set up the proportion and cross-multiply. Then we solve for "x" by dividing both sides of the equation. In this case, the value of "x" is equal to 1.2.
A sum of money is to be distributed among A, B, C, D in the proportion of 5 : 2 : 4 : 3. If C gets Rs. 1000 more than D, what is B's share?- a)Rs. 500
- b)Rs. 1500
- c)Rs. 2000
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A sum of money is to be distributed among A, B, C, D in the proportion of 5 : 2 : 4 : 3. If C gets Rs. 1000 more than D, what is B's share?
a)
Rs. 500
b)
Rs. 1500
c)
Rs. 2000
d)
None of these
|
|
Gowri Chakraborty answered |
Let the shares of A, B, C and D be Rs. 5x, Rs. 2x, Rs. 4x and Rs. 3x respectively.
Then, 4x - 3x = 1000
⇒ x = 1000.
∴ B's share = Rs. 2x = Rs. (2 x 1000) = Rs. 2000.
In a garrison of 3600 men, the provisions were sufficient for 20 days at the rate of 1.5 kg per man per day. If x more men joined, the provisions would be sufficient for 12 days at the rate of 2 kg per man per day. Find x.- a)600
- b)800
- c)900
- d)720
Correct answer is option 'C'. Can you explain this answer?
In a garrison of 3600 men, the provisions were sufficient for 20 days at the rate of 1.5 kg per man per day. If x more men joined, the provisions would be sufficient for 12 days at the rate of 2 kg per man per day. Find x.
a)
600
b)
800
c)
900
d)
720
|
|
Rhea Reddy answered |
Let x be the number of new men joined the garrison,
The total quantity of food is = 3600(20) (1.5) kg ----------1
Now the available food will be consumed by (3600+x) men
(3600+x) (12) (2) kg --------------2
1 = 2
Solving both the equations
3600(20) (1.5) = (3600+x) (12) (2)
108000 = 86400 + 24x
21600 = 24x
X = 900
900 more men joined the garrison.
The total quantity of food is = 3600(20) (1.5) kg ----------1
Now the available food will be consumed by (3600+x) men
(3600+x) (12) (2) kg --------------2
1 = 2
Solving both the equations
3600(20) (1.5) = (3600+x) (12) (2)
108000 = 86400 + 24x
21600 = 24x
X = 900
900 more men joined the garrison.
A bag has ₹ 785 in the denomination of ₹ 2, ₹ 5 and ₹ 10 coins. The coins are in the ratio of 6 : 9 : 10. How many coins of ₹ 5 are in the bag?- a)60
- b)12
- c)45
- d)24
Correct answer is option 'C'. Can you explain this answer?
A bag has ₹ 785 in the denomination of ₹ 2, ₹ 5 and ₹ 10 coins. The coins are in the ratio of 6 : 9 : 10. How many coins of ₹ 5 are in the bag?
a)
60
b)
12
c)
45
d)
24
|
|
Anjana Singh answered |
Given:
₹ 785 in the denomination of ₹ 2, ₹ 5 and ₹ 10 coins
The coins are in the ratio of 6 : 9 : 10
Calculation:
Let the number of coins of ₹ 2, ₹ 5 and ₹ 10 be 6x, 9x, and 10x respectively
⇒ (2 × 6x) + (5 × 9x) + (10 × 10x) = 785
⇒ 157x = 785
∴ x = 5
Number of coins of ₹ 5 = 9x = 9 × 5 = 45
∴ 45 coins of ₹ 5 are in the bag
₹ 785 in the denomination of ₹ 2, ₹ 5 and ₹ 10 coins
The coins are in the ratio of 6 : 9 : 10
Calculation:
Let the number of coins of ₹ 2, ₹ 5 and ₹ 10 be 6x, 9x, and 10x respectively
⇒ (2 × 6x) + (5 × 9x) + (10 × 10x) = 785
⇒ 157x = 785
∴ x = 5
Number of coins of ₹ 5 = 9x = 9 × 5 = 45
∴ 45 coins of ₹ 5 are in the bag
Chapter doubts & questions for Ratio and Proportion - Mathematics for RRB Group D / RPF Constable 2025 is part of RRB Group D / RPF Constable exam preparation. The chapters have been prepared according to the RRB Group D / RPF Constable exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for RRB Group D / RPF Constable 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Ratio and Proportion - Mathematics for RRB Group D / RPF Constable in English & Hindi are available as part of RRB Group D / RPF Constable exam.
Download more important topics, notes, lectures and mock test series for RRB Group D / RPF Constable Exam by signing up for free.
Mathematics for RRB Group D / RPF Constable
174 videos|94 docs|92 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup