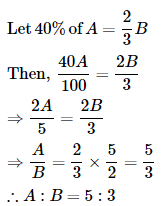All questions of Ratio and Proportion for Police Constable Exams Exam
In a mixture 60 litres, the ratio of milk and water 2 : 1. If this ratio is to be 1 : 2, then the quanity of water to be further added is:- a)20 litres
- b)30 litres
- c)40 litres
- d)60 litres
Correct answer is option 'D'. Can you explain this answer?
|
|
Mihir Sen answered |

Quantity of water in it = (60 - 40) litres = 20 litres.
New ratio = 1 : 2
Let quantity of water to be added further be x litres
Then, milk : water

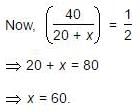
∴ Quantity of water to be added = 60 litres.
A and B together have Rs. 1210. If  of A's amount is equal to
of A's amount is equal to  of B's amount, how much amount does B have?
of B's amount, how much amount does B have?
- a)Rs. 460
- b)Rs. 484
- c)Rs. 550
- d)Rs. 664
Correct answer is 'B'. Can you explain this answer?
 of A's amount is equal to
of A's amount is equal to  of B's amount, how much amount does B have?
of B's amount, how much amount does B have?

|
Manoj Ghosh answered |
Can you explain the answer of this question below:According to the Boyle’s law, at a constant temperature, pressure of a definite mass of gas is inversely proportional to the volume. If the pressure is reduced by 20%, find the respective change in volume.
- A:
-33.33%
- B:
+25%
- C:
-25%
- D:
+33.33%
The answer is b.
According to the Boyle’s law, at a constant temperature, pressure of a definite mass of gas is inversely proportional to the volume. If the pressure is reduced by 20%, find the respective change in volume.
-33.33%
+25%
-25%
+33.33%
|
|
Ishan Chaudhary answered |
The ratio of the income of A and B is 7 : 8, and the ratio of the income of B and C is 8 : 11, If the difference in the income earned by A and C is Rs. 800, then find the sum of income earned by all three of them.- a)Rs. 5200
- b)Rs. 4800
- c)Rs. 4000
- d)Rs. 3600
Correct answer is option 'A'. Can you explain this answer?
|
|
Kiran Reddy answered |
Point mutation involves- a)Change in single base pair
- b)Deletion
- c)Insertion
- d)Duplication
Correct answer is option 'A'. Can you explain this answer?

|
Honey answered |
Seats for Mathematics, Physics and Biology in a school are in the ratio 5 : 7 : 8. There is a proposal to increase these seats by 40%, 50% and 75% respectively. What will be the ratio after increased seats?- a)2 : 3 : 4
- b)6 : 7 : 8
- c)6 : 8 : 9
- d)None of these
Correct answer is option 'A'. Can you explain this answer?

|
Future Foundation Institute answered |
Sheldon saves 1/4th of his income.
⇒ 4x – 6y = x
⇒ 3x = 6y
⇒ x / y = 2
∴ y = x / 2
= x : 5x – 7y : 6x – 8y
= x : 5x – 7x / 2 : 6x – 8x / 2
= x : 3x / 2 : 2x
= 2 : 3 : 4
Arun has a certain amount of money in the denomination of 1 rupee and 10 rupee notes . T he number of 1 rupee notes multiplied by the number of 10 rupee notes is equal to the total money (in rupees) that he has. What is the total number of ten rupee notes that he can have?- a)11
- b)13
- c)15
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
|
|
Dhruv Verma answered |
The sum of three numbers is 98. If the ratio of the first to second is 2 :3 and that of the second to the third is 5 : 8, then the second number is:- a)20
- b)30
- c)48
- d)58
Correct answer is option 'B'. Can you explain this answer?
|
|
Aarav Sharma answered |
- The sum of three numbers is 98.
- The ratio of the first number to the second number is 2:3.
- The ratio of the second number to the third number is 5:8.
**Let's solve the problem step by step:**
**Step 1:**
Let's assume the three numbers as follows:
- The first number = 2x
- The second number = 3x
- The third number = 8y
**Step 2:**
According to the given information, the sum of the three numbers is 98. Therefore, we can write the equation as:
2x + 3x + 8y = 98
**Step 3:**
Simplifying the equation, we get:
5x + 8y = 98
**Step 4:**
Now, we need to find the values of x and y in order to find the second number.
**Step 5:**
According to the given information, the ratio of the second number to the third number is 5:8. Therefore, we can write the equation as:
3x/8y = 5/8
**Step 6:**
Cross-multiplying the equation, we get:
24x = 40y
**Step 7:**
Simplifying the equation, we get:
3x = 5y
**Step 8:**
Now, we have two equations:
5x + 8y = 98
3x = 5y
**Step 9:**
Substituting the value of 3x from the second equation into the first equation, we get:
5(5y/3) + 8y = 98
25y/3 + 8y = 98
(25y + 24y)/3 = 98
49y/3 = 98
49y = 294
y = 294/49
y = 6
**Step 10:**
Substituting the value of y into the second equation, we get:
3x = 5(6)
3x = 30
x = 30/3
x = 10
**Step 11:**
Now, we can find the second number:
The second number = 3x = 3 * 10 = 30
Therefore, the correct answer is option **B) 30**.
The expenses of a hostel are partly fixed and partly variable with the number of boarders. When there are 50 boarders the charge is Rs. 48 per head and when there are 30 boarders the charge is Rs. 60 per head. Find the charges when there are 120 boarders?
- a)40
- b)32
- c)42
- d)37.5
Correct answer is option 'D'. Can you explain this answer?
|
|
Edu Impact answered |


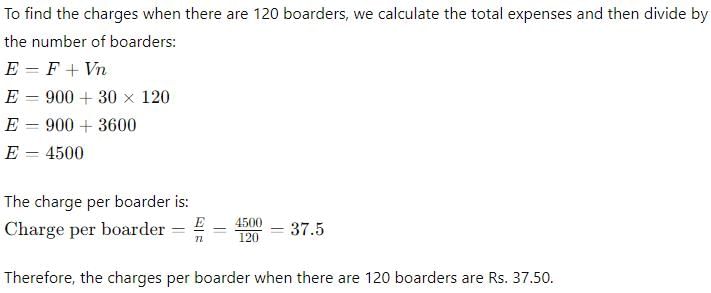
Price of each article of type P, Q, and R is Rs. 300, Rs. 180 and Rs. 120 respectively. Suresh buys articles of each type in the ratio 3:2:3 in Rs. 6480. How many articles of type Q did he purchase?- a)14
- b)20
- c)8
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?

|
Naroj Boda answered |
► Hence, the number of articles of type P, Q and R will be 3k, 2k and 3k respectively
► Also, Unit price of article x Number of articles = Total amount for the articles
∴ 300 x 3k + 180 x 2k + 120 x 3k = 6480
⇒ k = 4
∴ Number of articles of Type Q = 2k = 8
Two-fifth of Anil’s salary is equal of Bhuvan’s salary and seven -ninth of Bhuvan’s salary is equal to Chandra’s salary. The sum of the salary of all of them is Rs 770. Which of the following is the salary of each?- a)300, 225, 250
- b)500, 425, 375
- c)450, 180, 140
- d)520, 610, 475
Correct answer is option 'C'. Can you explain this answer?
|
|
Anaya Patel answered |
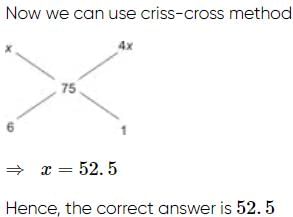
A metal trader buys 2 kinds of silver foils, the ratio of their prices being 1:4. He sells the alloy at Rs 90 per kg so that he can make a profit of 20%. If the ratio of their quantities present in a alloy is 6:1 respectively, find the purchase price of the foil present in lesser quantity.
- a)Rs 52.5
- b)Rs 55
- c)Rs 47.5
- d)Rs 45
Correct answer is option 'A'. Can you explain this answer?

|
Arya Roy answered |

Anand and Bhavana have a few one rupee, 50 paise and 25 paise coins each. The total amount with each of them is Rs 5. The number of coins of two of the three types of coins that Anand has are equal and same is the case for the coins that Bhavana has. If Anand has the maximum possible total number of coins, then find the maximum possible total number of coins that Bhavana can have given that she has fewer coins than Anand.- a)16
- b)12
- c)10
- d)9
Correct answer is option 'B'. Can you explain this answer?
|
|
Nandita Kaur answered |
11 : b : 44 are in continued proportion. Find b.- a)4
- b)22
- c)44
- d)11
Correct answer is option 'B'. Can you explain this answer?
|
|
Alok Verma answered |
b2 = 11.44
b2 = 484
b = 22
An alloy of manganese, tin and bronze contains 90% bronze, 7% manganese and 3% tin. A second alloy of bronze and tin is melted with the first and the mixture contains 85% of bronze, 5% of manganese and 10% of tin. What is the percentage of bronze in the second alloy?- a)67.5%
- b)72.5%
- c)77.5%
- d)82.5%
Correct answer is 'B'. Can you explain this answer?

|
Sameer Rane answered |
Can you explain the answer of this question below:The difference between the two positive numbers is 10 and the ratio between them is 5:3. Find the product of the two numbers.
- A:
375
- B:
325
- C:
275
- D:
125
The answer is a.
The difference between the two positive numbers is 10 and the ratio between them is 5:3. Find the product of the two numbers.
375
325
275
125

|
Subham Basu answered |
The average age of the students in a class of 50 is 13. The weight of each student is directly proportional to the height. A 165 cm tall student has a weight of 33 kg. The average weight of the class is:- a)33 kg
- b)39 kg
- c)36 kg
- d)Data insufficient
Correct answer is option 'B'. Can you explain this answer?

|
Sanyam Jain answered |
The ratio of the number of boys and girls in a college is 7 : 8. If the percentage increase in the number of boys and girls be 20% and 10% respectively, what will be the new ratio?- a)8 : 9
- b)17 : 18
- c)21 : 22
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
|
|
Ravi Singh answered |
In a bag, there are coins of 25 p, 10 p and 5 p in the ratio of 1 : 2 : 3. If there is Rs. 30 in all, how many 5 p coins are there?- a)50
- b)100
- c)150
- d)200
Correct answer is option 'C'. Can you explain this answer?

|
Gowri Chakraborty answered |
Can you explain the answer of this question below:A and B invest Rs 12,000 and Rs 16,000 respectively in a business. At the year-end, they share the profit in the ratio of 3:1. If A has invested his capital for the whole year, for how many months B has invested his capital?
- A:
4 months
- B:
3 months
- C:
6 months
- D:
8 months
The answer is b.
A and B invest Rs 12,000 and Rs 16,000 respectively in a business. At the year-end, they share the profit in the ratio of 3:1. If A has invested his capital for the whole year, for how many months B has invested his capital?
4 months
3 months
6 months
8 months
|
|
Saranya Kaur answered |
Gandhiji owns cows, some black and some white. He finds that 4 black cows and 3 white cows gave the same amount of milk in 5 days as 3 black cows and 5 white cows gave in 4 days. What is the ratio of milk given by a black cow in a day to that given by a white cow in a day?- a)8 : 5
- b)5 : 8
- c)3 : 5
- d)5 : 3
Correct answer is option 'B'. Can you explain this answer?

|
Janhavi Nambiar answered |
The sum of four numbers is 253. The ratio of the first number to the second number is 2:3. The ratio of the second number to the third number is 5:6. The ratio of the third number to the fourth number is 8:9. What is the average of the second number and the third number?- a)72
- b)132
- c)60
- d)66
Correct answer is option 'D'. Can you explain this answer?
|
|
Anaya Patel answered |
2nd no.= B , 3rd no.= C , 4th no. = D
A: B =2:3
A/B = 2/3
x/B =2/3
B= 3x/2
B:C=5:6
(3x/2)/ C= 5/6
C=( 6×3x)/2×5= 9x/5
C= 9x/5
C:D= 8:9
9x/5/ D = 8/9
D= (9x×9)/8×5= 81x/40
D= 81x/40
A+B+C+D= 253. (GIVEN)
x+ 3x/2+9x/5+81x/40
Lcm = 40
(40x+ 60x+ 72x+81x)/40= 253
253x= 253×40
X= (253×40)/253= 40
Ist no.(A)= X= 40
2no.(B)= 3x/2=( 3 × 40)/2= 60
3rd no.(C)= 9x/5 = (9×40)/5= 72
4th no.(D)= 81x/40=( 81×40/)/40= 81
Average of numbers= sum of observations/ total no.of observations
Average of 2nd no. & 3rd no.= (60+72)/2= 132/2= 66
The monthly incomes of X and Y are in the ratio of 4:3 and their monthly expenses are in the ratio of 3:2. However, each saves Rs. 6,000 per month. What is their total monthly income?
- a)Rs. 28,000
- b)Rs. 42,000
- c)Rs. 56,000
- d)Rs. 84,000
Correct answer is option 'B'. Can you explain this answer?
|
|
Kishan Darak answered |
Therefore income of:
X=6000×4=24000
Y=6000×3=18000
x+y =24000+18000=42000(that is option 'B' is the right answer
Four numbers in the ratio of 1:3:4:7 add up to give a sum of 75. Find the value of the biggest number.- a)42
- b)35
- c)49
- d)63
Correct answer is option 'B'. Can you explain this answer?
|
|
Kavya Saxena answered |
15x = 75
x = 75/15
x = 5
So, 1x = 1*5 = 5
3x = 3*5 = 15
4x = 4*5 = 20
7x = 7*5 = 35
Can you explain the answer of this question below:Two number are in the ratio 3 : 5. If 9 is subtracted from each, the new numbers are in the ratio 12 : 23. The smaller number is:
- A:
27
- B:
33
- C:
49
- D:
55
The answer is B.
Two number are in the ratio 3 : 5. If 9 is subtracted from each, the new numbers are in the ratio 12 : 23. The smaller number is:
27
33
49
55
|
|
Sagar Sharma answered |
The ratio of two numbers is 3:5
After subtracting 9 from each number, the new ratio is 12:23
Let's assume the two numbers in the original ratio are 3x and 5x.
Ratio of the new numbers:
(3x-9) : (5x-9) = 12 : 23
Cross-multiplying, we get:
12(5x-9) = 23(3x-9)
Simplifying the equation:
60x - 108 = 69x - 207
-9x = -99
x = 11
Finding the smaller number:
Smaller number = 3x = 3 * 11 = 33
Therefore, the smaller number is 33, which corresponds to option 'B'.
If 4 : 8 : C are in continued proportion then find C?- a)16
- b)4
- c)36
- d)34
Correct answer is option 'A'. Can you explain this answer?
|
|
Aarav Sharma answered |
then b2 = ac
82 = 4.C
C = 64/4 = 16
The total profit made by running a train between New Delhi to Lucknow consists of two parts: (i) a constant amount of Rs 24 lakh per trip and (ii) it varies as the square of the number of coaches attached to the engine that amounts to Rs 7P2, where P is the number of coaches attached to the engine in the trip. If the average profit per coach per trip should not fall below Rs 169 lakh, then what is the minimum number of coaches that have to be attached to the engine?
- a)23
- b)24
- c)25
- d)None of these
Correct answer is option 'B'. Can you explain this answer?

|
Nandita Tiwari answered |
which must be at least 169P
so now we get the equation
169P = 24L + 7P2 or 7P2- 169P + 24 = 0
on solving we get P = 24
Now go through the options.
In the famous Hawthorne studies by Elton Mayo, emplovecs of the organization were given the options of going to several places for entertainment. Onc-seventh of the employees preferred to go to the polo ground, a number equal to the square root of the remaining employees went to the museum. One-fifth of the remaining employees went to the fair. One-third of the remaining to the science exhibition and the rest to watch movie ASHOKA. which was running house full in the nearby theatre. The total number of employ ees who yvcnl to the polo ground and the museum is twice that of the employees who went to the fair.
Q.The entry tickets for museum, fair, exhibition and the movie were Rs 5, Rs 4, Rs 2 and Rs 25 respectively. How much money did the employees pay for all these on that Sunday?- a)Rs 275
- b)Rs 320
- c)Rs 388
- d)Rs 470
Correct answer is option 'D'. Can you explain this answer?
Q.The entry tickets for museum, fair, exhibition and the movie were Rs 5, Rs 4, Rs 2 and Rs 25 respectively. How much money did the employees pay for all these on that Sunday?
|
|
Rajeev Kumar answered |
The salaries A, B, C are in the ratio 2 : 3 : 5. If the increments of 15%, 10% and 20% are allowed respectively in their salaries, then what will be new ratio of their salaries?- a)3 : 3 : 10
- b)10 : 11 : 20
- c)23 : 33 : 60
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
|
|
Kavya Saxena answered |
Salaries of Ravi and Sumit are in the ratio 2 : 3. If the 'salary of each' one of them is increased by Rs. 4000, the new ratio becomes 40 : 57. What is Sumit's present salary?
- a)Rs. 17,000
- b)Rs. 20,000
- c)Rs. 25,500
- d)Rs. 38,000
Correct answer is option 'D'. Can you explain this answer?

|
Sameer Rane answered |
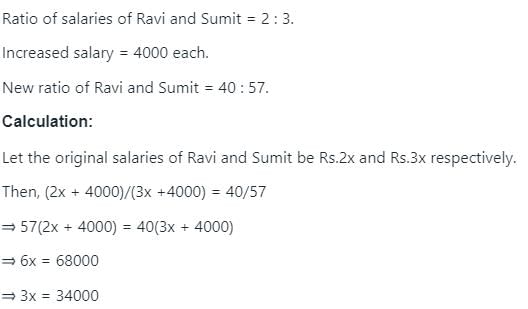
Bidhan is planning to buy a bike worth Rs 35,000, provided his brother agrees to lend him 3/2 times the money. Bidhan contributes and the financer provides 3 times the brother’s contribution. How much does Bidhan’s brother contribute?- a)5,000
- b)7,500
- c)10,000
- d)7,000
Correct answer is option 'B'. Can you explain this answer?
|
|
Nikita Singh answered |
Find the ratio A : B : C : D : E if,
A : B = 4 : 5
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2- a)200 : 270 : 315 : 350 : 140
- b)120 : 270 : 315 : 350 : 140
- c) 216 : 270 : 315 : 350 : 140
- d)216 : 270 : 315 : 350 : 210
Correct answer is option 'C'. Can you explain this answer?
A : B = 4 : 5
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2
|
|
Rhea Reddy answered |
B : C = 6 : 7
C : D = 9 : 10
D : E = 5 : 2
A : B : C : D : E = 4 x 6 x 9 x 5 : 5 x 6 x 9 x 5: 5 x 7 x 9 x 5: 5 x 7 x 10 x 5: 5 x 7 x 10 x 2
216 : 270 : 315 : 350 : 140
The required ratio A : B : C : D : E is 216 : 270 : 315 : 350 : 140
In a library, the ratio of number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.- a) 312
- b) 321
- c) 936
- d) 1560
Correct answer is option 'A'. Can you explain this answer?

|
Ashwini Chatterjee answered |
- The ratio of the number of story books to that of non-story books was 4:3.
- The total number of story books was 1248.
- When some more story books were bought, the ratio became 5:3.
**Let's solve the problem step by step:**
**Step 1: Calculate the number of non-story books**
- Since the ratio of story books to non-story books is 4:3, let's assume the number of story books as 4x and the number of non-story books as 3x.
- According to the given information, the total number of story books is 1248. So, we can write the equation as 4x = 1248.
- Solving the equation, we get x = 1248/4 = 312.
- Therefore, the number of non-story books is 3x = 3 * 312 = 936.
**Step 2: Calculate the number of story books after the purchase**
- After some more story books were bought, the ratio became 5:3. Let's assume the number of additional story books as y.
- Now, the total number of story books is 1248 + y, and the total number of non-story books is still 936.
- According to the new ratio, the equation can be written as (1248 + y)/936 = 5/3.
- Cross-multiplying, we get 3 * (1248 + y) = 5 * 936.
- Simplifying the equation, we have 3744 + 3y = 4680.
- Subtracting 3744 from both sides, we get 3y = 936.
- Dividing both sides by 3, we get y = 936/3 = 312.
**Step 3: Calculate the number of story books bought**
- The number of story books bought is given by the value of y, which we calculated as 312.
Therefore, the number of story books bought is 312.
Hence, the correct answer is option A) 312.
A sum of Rs. 12,384 is divided between A, B, C and D such that the ratio of the shares of A and B is 3 : 4, that of B and C is 5 : 6, and that of C and D is 8 : 9. What is the share of C ? - a)Rs. 2,880
- b)Rs. 3,888
- c)Rs. 3,456
- d)Rs. 2,160
Correct answer is option 'C'. Can you explain this answer?
|
|
Shilpa Choudhury answered |
If 0.75 : x :: 5 : 8, then x is equal to:- a)1.12
- b)1.2
- c)1.25
- d)1.30
Correct answer is option 'B'. Can you explain this answer?
|
|
Aarav Sharma answered |
Step 1: Set up the proportion
0.75 : x :: 5 : 8
Step 2: Cross-multiply
0.75 * 8 = x * 5
Step 3: Solve for "x"
6 = 5x
Step 4: Divide both sides by 5
x = 6 / 5
Step 5: Simplify the fraction
x = 1.2
Therefore, the value of "x" in the proportion 0.75 : x :: 5 : 8 is equal to 1.2.
Summary:
To find the value of "x" in the given proportion, we set up the proportion and cross-multiply. Then we solve for "x" by dividing both sides of the equation. In this case, the value of "x" is equal to 1.2.
The sum of the ages of the 4 members of Sinha family is 140 years. 5 years ago the ages of the 4 members Nishu, Vicky, Mrs Sinha and Mr Sinha were in the ratio of 2 : 3 : 7 : 8 . After how many years would Nishu be as old as the present age of his mother?- a)10yrs
- b)17yrs
- c)30 yrs
- d)32 yrs
Correct answer is option 'C'. Can you explain this answer?
|
|
Lavanya Menon answered |
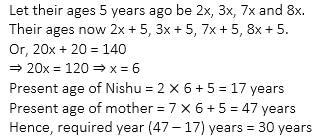
In an election, each voter may vote for two candidates. Half of the voters vote for A, but divide their votes between B, C and D in the ratio of 3:2:1. Of the remaining, half vote for B and divides their votes between C and D in the ratio of 2:1. Of the remaining, half vote for C and D and the remaining 840 do not vote for anyone. How many votes were received by A, B, C and D respectively?- a)3,360, 3,360, 3,080, 1,960
- b)3,360,3,360, 1,960,3,080
- c)3,450,3,210,4,120,1,210
- d)5,000, 5,000, 2,500, 1,250.
Correct answer is option 'A'. Can you explain this answer?

|
Harsh Jain answered |
A and B invested Rs 12,000 and Rs 18,000 respectively in a business for the whole year. At the year-end, there was a total profit of Rs 2,000. What is the share of A in the profit?- a)Rs 800
- b)Rs 1,200
- c)Rs 1,600
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
|
|
Advait Saini answered |
A and B have invested different amounts in a business:
- A's investment: Rs 12,000
- B's investment: Rs 18,000
Total Investment
- Total investment by both A and B = Rs 12,000 + Rs 18,000 = Rs 30,000
Profit Distribution
The total profit at the year-end is Rs 2,000. The profit is shared based on the ratio of their investments.
Calculating the Ratio
- A's investment = Rs 12,000
- B's investment = Rs 18,000
- Ratio of A’s investment to B’s investment = 12,000 : 18,000
To simplify:
- Divide both sides by 6
- A : B = 2 : 3
Finding A's Share in Profit
To determine A's share in the profit, we first calculate the total parts in the ratio. The total parts = 2 (for A) + 3 (for B) = 5 parts.
Next, we find out how much each part is worth:
- Value of each part = Total Profit / Total Parts = Rs 2,000 / 5 = Rs 400
Now, we can calculate A's share:
- A's share = 2 parts * Value of each part = 2 * Rs 400 = Rs 800
Conclusion
Thus, A's share in the profit is Rs 800, which corresponds to option 'A'.
Anil started a manufacturing unit with a certain amount of money. After a few months, Dheeraj became his partner, contributing three times of what Anil had contributed. At the end of the year, each was entitled to half the total profit. If Anil started the unit in January, then when did Dheeraj join as a partner?- a)August
- b)September
- c)July
- d)October
Correct answer is option 'B'. Can you explain this answer?

|
Shraddha Dasgupta answered |

In a fort there are 1600 soldiers fighting a battle against their enemy. On a particular day after their morning meal the balance provision inside the fort is only sufficient for 12 days at the rate of 1.2 kg per day. If by the evening 400 soldiers die then for how many days will the provision be sufficient for remaining men at the rate of 1.6 kg per day. (Assume soldiers eat either in morning or in evening).- a)10
- b)8
- c)18
- d)12
Correct answer is option 'D'. Can you explain this answer?
|
|
Aarav Sharma answered |
- Number of soldiers in the fort = 1600
- Provision available for 1 day = 1.2 kg
- Soldiers die in the evening and the remaining soldiers eat 1.6 kg per day
Calculation:
Total provision available in the fort = 1600 x 1.2 x 12 = 23,040 kg
After 400 soldiers die, the remaining soldiers = 1600 - 400 = 1200
The provision required for 1 day by 1200 soldiers = 1.6 x 1200 = 1920 kg
The total provision available after 400 soldiers die = 23,040 - (400 x 1.2) = 22,560 kg
The number of days this provision will last for 1200 soldiers = 22,560 / 1920 = 11.75 days
Since soldiers eat either in the morning or in the evening, we need to round off the answer to the lower integer value, i.e. 11 days.
Therefore, the answer is option 'D' - 12 days.
Chapter doubts & questions for Ratio and Proportion - Quantitative/Numerical Aptitude for Police Exams 2025 is part of Police Constable Exams exam preparation. The chapters have been prepared according to the Police Constable Exams exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Police Constable Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Quantitative/Numerical Aptitude for Police Exams
187 videos|112 docs|140 tests
|

Contact Support
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|