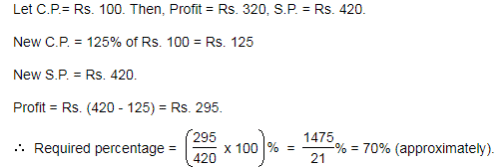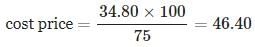All Exams >
GRE >
Quantitative Reasoning for GRE >
All Questions
All questions of Profit and Loss for GRE Exam
A sells a car to B at 10% loss. If B sells it for Rs. 54000 and gains 20%, the cost price of the car for A was
a)Rs. 25000
b)Rs. 50000
c)Rs. 37500
d)Rs. 60000
Correct answer is option 'B'. Can you explain this answer?
|
|
Gaurav Datta answered |
Selling price of the car = Rs.54,000
gain 20%
Friend's cost price of the car = Rs. 54000 x 100/120 = Rs.45,000
Now selling price of the car of the first owner Rs.45000
Loss 10%
Cost price of the car = 45000 x 100/90
= Rs.50,000
gain 20%
Friend's cost price of the car = Rs. 54000 x 100/120 = Rs.45,000
Now selling price of the car of the first owner Rs.45000
Loss 10%
Cost price of the car = 45000 x 100/90
= Rs.50,000
If a material is sold for Rs.34.80, there is a loss of 25%. Find out the cost price of the material?
- a)Rs.46.40
- b)Rs.44
- c)Rs.42
- d)Rs.47.20
Correct answer is option 'A'. Can you explain this answer?
If a material is sold for Rs.34.80, there is a loss of 25%. Find out the cost price of the material?
a)
Rs.46.40
b)
Rs.44
c)
Rs.42
d)
Rs.47.20

|
EduRev CAT answered |
The correct answer is A as
cost price
=34.80×100/75
=46.40
cost price
=34.80×100/75
=46.40
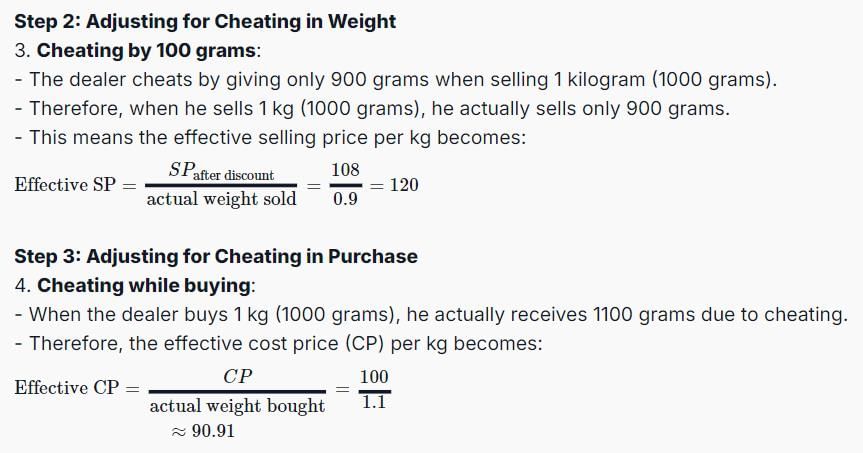
A dishonest dealer marks up the price of his goods by 20% and gives a discount of 10% to the customer. Besides, he also cheats both his supplier and his buyer by 100 grams while buying or selling 1 kilogram. Find the percentage profit earned by the shopkeeper.
- a)20%
- b)25%
- c)27.5%
- d)32%
Correct answer is option 'D'. Can you explain this answer?
A dishonest dealer marks up the price of his goods by 20% and gives a discount of 10% to the customer. Besides, he also cheats both his supplier and his buyer by 100 grams while buying or selling 1 kilogram. Find the percentage profit earned by the shopkeeper.
a)
20%
b)
25%
c)
27.5%
d)
32%

|
Arya Roy answered |


John buys an old scooter for Rs. 4700 and spends Rs. 800 on its repairs. If he sells the scooter for Rs. 5800, what is his gain percent ?
- a)12%
- b)10%
- c)4 + 4 / 7%
- d)5 + 5 / 11%
Correct answer is option 'D'. Can you explain this answer?
John buys an old scooter for Rs. 4700 and spends Rs. 800 on its repairs. If he sells the scooter for Rs. 5800, what is his gain percent ?
a)
12%
b)
10%
c)
4 + 4 / 7%
d)
5 + 5 / 11%
|
|
Milan Chaudhary answered |
Whenever we get this type of question, we should have formula in mind that,
Gain% = (gain/cost) x 100
Cost = 4700 + 800 = Rs. 5500
S.P. = Rs. 5800
Profit = 5800 - 5500 = 300
Gain% = (gain/cost) x 100
Cost = 4700 + 800 = Rs. 5500
S.P. = Rs. 5800
Profit = 5800 - 5500 = 300
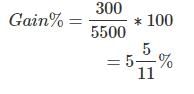
A man sells a TV set for Rs. 33000 and makes a profit of 10%. He sells another TV at a loss of 20%. If on the whole, he neither gains nor loses, find the selling price of the second TV set.
- a)Rs.15,000
- b)Rs.30,000
- c)Rs.12,000
- d)Rs.27,000
Correct answer is option 'C'. Can you explain this answer?
A man sells a TV set for Rs. 33000 and makes a profit of 10%. He sells another TV at a loss of 20%. If on the whole, he neither gains nor loses, find the selling price of the second TV set.
a)
Rs.15,000
b)
Rs.30,000
c)
Rs.12,000
d)
Rs.27,000
|
|
Aarav Sharma answered |
Given:
Selling price of first TV set = Rs. 33000
Profit earned on first TV set = 10%
To find: Selling price of the second TV set
Let's assume the cost price of the first TV set = x
Profit earned on the first TV set = 10%
Therefore, selling price of the first TV set = x + 0.1x = 1.1x
Selling price of the first TV set = Rs. 33000
So, 1.1x = 33000
x = 30000
Cost price of the second TV set = y
Loss incurred on the second TV set = 20%
Therefore, selling price of the second TV set = y - 0.2y = 0.8y
Now, let's assume that the man sells the second TV set at a selling price of z.
Total selling price of both the TV sets = 33000 + z
Total cost price of both the TV sets = 30000 + y
It is given that the man neither gains nor loses on the whole, i.e., total selling price = total cost price
33000 + z = 30000 + y + 0.8y
33000 + z = 38000 + 0.8y
z = 38000 - 0.8y
Substituting the value of z in the above equation, we get:
33000 + 38000 - 0.8y = 30000 + y
71000 - 0.8y = 30000 + y
71000 = 1.8y
y = 71000/1.8
y = 39444.44
Selling price of the second TV set = 0.8y = 0.8 x 39444.44 = Rs. 31555.56
Therefore, option (c) Rs. 27,000 is incorrect and the correct answer is option (a) Rs. 15,000.
Selling price of first TV set = Rs. 33000
Profit earned on first TV set = 10%
To find: Selling price of the second TV set
Let's assume the cost price of the first TV set = x
Profit earned on the first TV set = 10%
Therefore, selling price of the first TV set = x + 0.1x = 1.1x
Selling price of the first TV set = Rs. 33000
So, 1.1x = 33000
x = 30000
Cost price of the second TV set = y
Loss incurred on the second TV set = 20%
Therefore, selling price of the second TV set = y - 0.2y = 0.8y
Now, let's assume that the man sells the second TV set at a selling price of z.
Total selling price of both the TV sets = 33000 + z
Total cost price of both the TV sets = 30000 + y
It is given that the man neither gains nor loses on the whole, i.e., total selling price = total cost price
33000 + z = 30000 + y + 0.8y
33000 + z = 38000 + 0.8y
z = 38000 - 0.8y
Substituting the value of z in the above equation, we get:
33000 + 38000 - 0.8y = 30000 + y
71000 - 0.8y = 30000 + y
71000 = 1.8y
y = 71000/1.8
y = 39444.44
Selling price of the second TV set = 0.8y = 0.8 x 39444.44 = Rs. 31555.56
Therefore, option (c) Rs. 27,000 is incorrect and the correct answer is option (a) Rs. 15,000.
A shopkeeper offers two successive discounts of 20% each on a sweater and still makes a profit of 60%. By what percentage did
the shopkeeper mark-up the price of the sweater?- a)60%
- b)100%
- c)150%
- d)200%
- e)250%
Correct answer is option 'C'. Can you explain this answer?
A shopkeeper offers two successive discounts of 20% each on a sweater and still makes a profit of 60%. By what percentage did
the shopkeeper mark-up the price of the sweater?
the shopkeeper mark-up the price of the sweater?
a)
60%
b)
100%
c)
150%
d)
200%
e)
250%
|
|
Meera Rana answered |
Given:
- Successive discounts (d and d ) offered by the shopkeeper on a sweater
- d = 20%
- d = 20%
- Profit % of the shopkeeper = 60%
To Find: Mark-up% on the sweater?
Approach:
- So, in order to know the MarkUp %, we need to know either the ratio
or the values of Markup (the amount of markup) and the Cost Price. Since we are not given the dollar values of anything (like cost price, selling price, marked price, discount or profit), we will not be able to find the dollar values of MarkUp and Cost Price. So, we should try to find the ratio
- So, in order to know the MarkUp %, we need to know either the ratio
- So, in order to find the ratio we need to find the ratio
we need to fid the ratio
- So, in order to find the ratio we need to find the ratio
- We are given the discounts availed on the sweater. Using these discounts, we will be able to find the ratio of Marked Price and Selling Price of the sweater.
- Let’s assume the Marked Price to be x.
- So, Marked Price after applying discount d1 = x – d1 % of x
- Now, Marked Price after applying discount d2 = (x – d1% of x) – d2 % of (x – d1 % of x)
So, the selling price of the sweater = (x – d1 % of x) – d2 % of (x – d1 % of x) - So,
- Now, Marked Price after applying discount d2 = (x – d1% of x) – d2 % of (x – d1 % of x)
We are also given the profit % on the sweater. Using this, we will be able to find the ratio of Selling Price and Cost Price of the
sweater
sweater
Selling Price = Cost Price + Profit
Also, we know that
Also, we know that
Working out:
2. Calculating the Cost Price
a. Selling Price = 0.64x
b. Profit% = 60%
c. So, we can write 0.64x = CP + 60% of CP, which gives us CP = 0.4x
3. Calculating Mark-Up%
a. Hence, the price of sweater was marked up by = x – 0.4x = 0.6x. So, using (1), the mark-up5 can be given by
a. Selling Price = 0.64x
b. Profit% = 60%
c. So, we can write 0.64x = CP + 60% of CP, which gives us CP = 0.4x
3. Calculating Mark-Up%
a. Hence, the price of sweater was marked up by = x – 0.4x = 0.6x. So, using (1), the mark-up5 can be given by
Answer : C
E sold at table to R at a profit of 25%.R sold the same table to S for Rs. 90 thereby making a profit of 20%. Find the price at which E bought the table from Z if it is known that Z gained 25% in the transaction.
- a)Rs.80
- b)Rs.75
- c)Rs.90
- d)Rs.60
Correct answer is option 'D'. Can you explain this answer?
E sold at table to R at a profit of 25%.R sold the same table to S for Rs. 90 thereby making a profit of 20%. Find the price at which E bought the table from Z if it is known that Z gained 25% in the transaction.
a)
Rs.80
b)
Rs.75
c)
Rs.90
d)
Rs.60
|
|
Ritika Choudhury answered |
R sold the table at 20% profit at Rs. 90. Thus cost price would be given by: CPR X 1.2 = 90
R’s Cost price = Rs. 75.
We also know that E sold it to R at 25% profit. Thus,
E’s Cost price X 1.25 = 75
-> E’s cost price = 60.
R’s Cost price = Rs. 75.
We also know that E sold it to R at 25% profit. Thus,
E’s Cost price X 1.25 = 75
-> E’s cost price = 60.
On selling 17 balls at Rs. 720, there is a loss equal to the cost price of 5 balls. What is the cost price of a ball?
- a)Rs. 43
- b)Rs. 60
- c)Rs. 55
- d)Rs. 34
Correct answer is option 'B'. Can you explain this answer?
a)
Rs. 43
b)
Rs. 60
c)
Rs. 55
d)
Rs. 34
|
|
Alok Verma answered |
Let the cost price of a ball be Rs. x.
So, the CP of 17 balls is Rs. 17x.
The CP of 5 balls is Rs. 5x.
Since Loss = CP - SP
So, 5x = 17x - 720
On solving, we get
12 x = 720
that is, x = 60
So, the cost price of a ball is Rs. 60.
Murali purchased 20 dozens of toys at the rate of Rs. 375 per dozen. He sold each one of them at the rate of Rs. 33. Find out his profit percentage.- a)3.5
- b)5.6
- c)4.1
- d)3.4
Correct answer is 'B'. Can you explain this answer?
Murali purchased 20 dozens of toys at the rate of Rs. 375 per dozen. He sold each one of them at the rate of Rs. 33. Find out his profit percentage.
a)
3.5
b)
5.6
c)
4.1
d)
3.4

|
Gowri Chakraborty answered |
The cost price of 20 dozens of toys = 375*20 i.e per dozen 375= Rs 7500/-the selling price of one dozen toys = 12*33= Rs 396/-the selling price of 20 dozen toys = 396*20= Rs 7920/-gain=sp-cp = 7920-7500 =Rs.420/-gain%=(gain/cp)*100 = 420/7500*100 =5.6%
A vendor bought bananas at 6 for a rupee. How many for a rupee must he sell to gain 20%?
- a)3
- b)4
- c)5
- d)6
Correct answer is 'C'. Can you explain this answer?
a)
3
b)
4
c)
5
d)
6

|
Pallabi Deshpande answered |
Go through this doc which will help you understand the basic concepts of profit, loss, and discount for CAT exam.
A man sells an article at 10% above its cost price. If he had bought it at 15% less than what he paid for it and sold it for Rs. 33 less, he would have gained 10%. Find the cost price of the article.- a)Rs.400
- b)Rs.200
- c)Rs.325
- d)Rs.260
Correct answer is option 'B'. Can you explain this answer?
A man sells an article at 10% above its cost price. If he had bought it at 15% less than what he paid for it and sold it for Rs. 33 less, he would have gained 10%. Find the cost price of the article.
a)
Rs.400
b)
Rs.200
c)
Rs.325
d)
Rs.260

|
Surbhi Joshi answered |
Given:
Selling price = Cost price + 10% of cost price
Let the cost price be x
Selling price = 1.1x
To find:
Cost price of the article
Solution:
Let the original selling price be y
The cost price of the article if he had bought it at 15% less than what he paid for it = 0.85y
He sold it for Rs. 33 less, so the selling price = y - 33
He gained 10%
Selling price = Cost price + 10% of cost price
1.1x = 1.1(0.85y) + 0.1(0.85y)
1.1x = 0.935y + 0.085y
1.1x = 1.02y
y = 1.078x
Substituting the value of y in the equation y - 33 = 1.1(0.85y)
1.078x - 33 = 0.935y
1.078x - 33 = 0.935(1.078x)
1.078x - 33 = 1.00883x
0.06917x = 33
x = 33/0.06917
x = Rs. 476.86
Therefore, the cost price of the article is Rs. 476.86
But, the options given are not in decimals
So, the closest option to Rs. 476.86 is Rs. 200
Hence, the correct option is (B) Rs. 200.
Selling price = Cost price + 10% of cost price
Let the cost price be x
Selling price = 1.1x
To find:
Cost price of the article
Solution:
Let the original selling price be y
The cost price of the article if he had bought it at 15% less than what he paid for it = 0.85y
He sold it for Rs. 33 less, so the selling price = y - 33
He gained 10%
Selling price = Cost price + 10% of cost price
1.1x = 1.1(0.85y) + 0.1(0.85y)
1.1x = 0.935y + 0.085y
1.1x = 1.02y
y = 1.078x
Substituting the value of y in the equation y - 33 = 1.1(0.85y)
1.078x - 33 = 0.935y
1.078x - 33 = 0.935(1.078x)
1.078x - 33 = 1.00883x
0.06917x = 33
x = 33/0.06917
x = Rs. 476.86
Therefore, the cost price of the article is Rs. 476.86
But, the options given are not in decimals
So, the closest option to Rs. 476.86 is Rs. 200
Hence, the correct option is (B) Rs. 200.
A trader gives 12% additional discount on the discounted price, after giving an initial discount of 20% on the labeled price of an item. The final sale price of the item is Rs.704. Find out the labeled price?
- a)1000
- b)2000
- c)1200
- d)920
Correct answer is option 'A'. Can you explain this answer?
a)
1000
b)
2000
c)
1200
d)
920

|
Gowri Chakraborty answered |
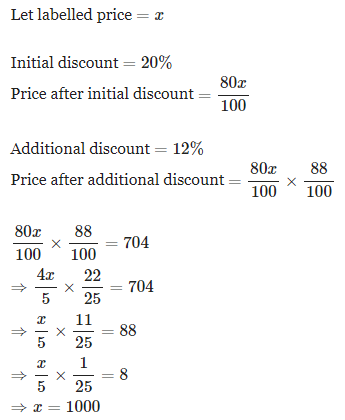
The cost price of 20 articles is the same as the selling price of x articles. If the profit is 25%, find out the value of x
- a)15
- b)25
- c)18
- d)16
Correct answer is 'D'. Can you explain this answer?
a)
15
b)
25
c)
18
d)
16

|
Sameer Rane answered |
Let C.P. of each article be Re. 1 C.P. of x articles = Rs. x.S.P. of x articles = Rs. 20.Profit = Rs. (20 - x).because [(20 - x)/x] x 100 = 25=> 2000 - 100x = 25x=> 125x = 2000 x = 16.
Product Y was sold after applying successive discounts of 20% and 30% on the list price (marked price). What is the list price of product Y if it was sold at $112?- a)180
- b)200
- c)224
- d)250
- e)300
Correct answer is option 'B'. Can you explain this answer?
Product Y was sold after applying successive discounts of 20% and 30% on the list price (marked price). What is the list price of product Y if it was sold at $112?
a)
180
b)
200
c)
224
d)
250
e)
300

|
Diode Electra answered |
Ok. let say the price without discount is X, and Y is the price with discount.
when the first discount's applied the price will be:
x - (x*20%) ===>> 0.8x
then apply the second discount
0.8x - (0.8x*30%) ===>> 0.56x (0.56 x is price with 20% and 30% discount)
then,
0.56x = y
x = y/0.56
x = 112*100:56
x = 200
when the first discount's applied the price will be:
x - (x*20%) ===>> 0.8x
then apply the second discount
0.8x - (0.8x*30%) ===>> 0.56x (0.56 x is price with 20% and 30% discount)
then,
0.56x = y
x = y/0.56
x = 112*100:56
x = 200
The marked price of an LCD television is 100% higher than the cost price. If it is sold at a price of $810 after applying two successive discounts of 10% each on the marked price, what is the cost price (in dollars) of LCD television?- a)450
- b)500
- c)750
- d)900
- e)1000
Correct answer is option 'B'. Can you explain this answer?
The marked price of an LCD television is 100% higher than the cost price. If it is sold at a price of $810 after applying two successive discounts of 10% each on the marked price, what is the cost price (in dollars) of LCD television?
a)
450
b)
500
c)
750
d)
900
e)
1000

|
Abhishek Kapoor answered |
Given information:
- Marked price = 100% higher than the cost price
- Two successive discounts of 10% each applied on the marked price
- Selling price = $810
Calculating the marked price:
Let the cost price be x.
Marked price = Cost price + 100% of cost price = x + x = 2x
Calculating the selling price after two discounts:
First discount: 10% of marked price = 0.1 * 2x = 0.2x
Price after first discount = Marked price - First discount = 2x - 0.2x = 1.8x
Second discount: 10% of price after first discount = 0.1 * 1.8x = 0.18x
Selling price = Price after first discount - Second discount = 1.8x - 0.18x = 1.62x
Given that selling price = $810, we have:
1.62x = 810
x = 810 / 1.62 = 500
Therefore, the cost price of the LCD television is $500 (option b).
- Marked price = 100% higher than the cost price
- Two successive discounts of 10% each applied on the marked price
- Selling price = $810
Calculating the marked price:
Let the cost price be x.
Marked price = Cost price + 100% of cost price = x + x = 2x
Calculating the selling price after two discounts:
First discount: 10% of marked price = 0.1 * 2x = 0.2x
Price after first discount = Marked price - First discount = 2x - 0.2x = 1.8x
Second discount: 10% of price after first discount = 0.1 * 1.8x = 0.18x
Selling price = Price after first discount - Second discount = 1.8x - 0.18x = 1.62x
Given that selling price = $810, we have:
1.62x = 810
x = 810 / 1.62 = 500
Therefore, the cost price of the LCD television is $500 (option b).
A light bulb manufacturer ships 10 boxes consisting of 100 light bulbs each to a retailer. The manufacturer bills the retailer at a rate of $10 per bulb with a condition that the defective light bulbs may be returned to the manufacturer for full refund. The probability of a light bulb in a box being defective is 20 percent. If the manufacturer makes a profit of 100 percent on each non-defective light bulb and he has to bear a return shipment cost of $2.5 per defective light bulb, which he treats as lost revenue, what is the profit percentage of the manufacture on the whole transaction?- a)30%
- b)33%
- c)45%
- d)50%
- e)60%
Correct answer is option 'D'. Can you explain this answer?
A light bulb manufacturer ships 10 boxes consisting of 100 light bulbs each to a retailer. The manufacturer bills the retailer at a rate of $10 per bulb with a condition that the defective light bulbs may be returned to the manufacturer for full refund. The probability of a light bulb in a box being defective is 20 percent. If the manufacturer makes a profit of 100 percent on each non-defective light bulb and he has to bear a return shipment cost of $2.5 per defective light bulb, which he treats as lost revenue, what is the profit percentage of the manufacture on the whole transaction?
a)
30%
b)
33%
c)
45%
d)
50%
e)
60%

|
Arya Yadav answered |
Given:
- Number of light bulbs in a box = 100
- Number of boxes shipped = 10
- So, Total light bulbs shipped = 10*100 = 1000
- Selling price of each non-defective light bulb = $10
- Profit % on each non-defective light bulb = 100%
- Probability(Defective Light Bulb) = 0.20
- Return shipment cost of each defective light bulb = $2.50
To Find: Total Profit % of the manufacturer?
Approach:
- So, to find the profit% of the manufacturer, we need to find the profit made by the manufacturer and the total cost incurred by the manufacturer
- Profit = Total net revenue – Total cost of all the light bulbs
- Thus we need to find the total net revenue and the total cost of all the light bulbs.
- For finding the total net revenue and the total cost of all the light bulbs, we need to find first the number of defective and non-defective light bulbs.
- Calculating number of Defective and Non-defective light bulbs
- As we know the total number of bulbs shipped and the probability of a bulb being defective, we can find the number of defective bulbs as Total defective light bulbs = Total light bulbs shipped
- Once, we find the number of defective light bulbs, we can find the number of non-defective light bulbs a Total non − defective light bulbs = Total light bulbs
- Total Net Revenue Calculation
a. Hence the total net revenue of the manufacturer can be calculated as
Total Net revenue=(Total revenue from non-defective light bulbs)- (Total lost revenue from defective light bulbs)
b. As we know the selling price of each non-defective light bulb and the number of non-defective light bulbs, we can calculate the total
revenue of the manufacturer from the non-defective light bulbs as
revenue of the manufacturer from the non-defective light bulbs as
Total Revenue from non − defective light bulbs
c. Also, the manufacturer has to recognise the shipment charges of the defective bulbs as lost revenue, it can be calculated as
4. Total Cost Calculation
- Total cost of all the light bulbs = Total light bulbs * Cost Price of each light bulb
- Please note here that we are calculating the cost price on total light bulbs as the transaction involves producing both the defective and non-defective light bulbs
- As we are given the selling price and profit % on each light bulb, we can calculate the cost price of each light bulb as
Selling Price = Cost Price + Profit ..............(1)
Also, we know that, 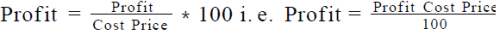
Working out:
1. Calculating number of Defective and Non-defective light bulbs
a. Total number of bulbs shipped = 1000
b. Total defective light bulbs = 0.2 * 1000 = 200
c. So, total non-defective light bulb = 1000 – 200 = 800
b. Total defective light bulbs = 0.2 * 1000 = 200
c. So, total non-defective light bulb = 1000 – 200 = 800
2. Total Net Revenue Calculation
a. Selling price of each non-defective light bulb = $10
b. Total revenue on the non-defective light bulbs = 800 * 10 = $8000
c. Lost revenue for each defective light bulb = $2.5
d. So, lost revenue for total defective bulbs = 2.5 * 200 = $500
e. Hence total net revenue = $(8000 – 500) = $7500
a. Selling price of each non-defective light bulb = $10
b. Total revenue on the non-defective light bulbs = 800 * 10 = $8000
c. Lost revenue for each defective light bulb = $2.5
d. So, lost revenue for total defective bulbs = 2.5 * 200 = $500
e. Hence total net revenue = $(8000 – 500) = $7500
3. Total Cost Calculation
a. Selling price of each non-defective light bulb = $10
b. Profit % on each non-defective light bulb = 100%
c. Cost price of each light bulb = $5
d. Total cost in producing all the light bulbs = 1000* 5 = $5000
a. Selling price of each non-defective light bulb = $10
b. Profit % on each non-defective light bulb = 100%
c. Cost price of each light bulb = $5
d. Total cost in producing all the light bulbs = 1000* 5 = $5000
4. Profit made = $(7500 – 5000) = $2500
5. Profit % = 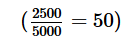 %
%
Hence the manufacturer made a profit of 50% on the whole transaction.
Hence the manufacturer made a profit of 50% on the whole transaction.
Answer : D
Sandy bought a share for $100. At what price should he sell the share to make a profit that is equal to 50 percent of the selling
price?- a)$125
- b)$150
- c)$175
- d)$200
- e)$250
Correct answer is option 'D'. Can you explain this answer?
Sandy bought a share for $100. At what price should he sell the share to make a profit that is equal to 50 percent of the selling
price?
price?
a)
$125
b)
$150
c)
$175
d)
$200
e)
$250

|
Arya Yadav answered |
Given:
- Cost Price of the share = $100
- Profit to be made = 50% of the selling price
- Let the selling price be S
To Find: Value of S?
Approach:
- We know that Selling Price = Cost Price + Profit
- As we know that Profit = 50% * Selling Price and we know the value of cost price we can calculate the value of the selling price using this equation.
Working out:
- S = Cost Price + 50% * S
- S = $100 + 0.5S
- 0.5S = $100
- S = $200
So, Sandy should sell the share at $200
Correct Option:D
A furniture dealer sold two chairs for $300 each. He made a profit of 25 percent on one of the chairs and a loss of 25 percent on theother. What was his overall loss or profit percentage on selling both the chairs?- a)Loss of about 7%
- b)Loss of about 6%
- c)No profit no loss
- d)Profit of about 6%
- e)Profit of about 7%
Correct answer is option 'B'. Can you explain this answer?
A furniture dealer sold two chairs for $300 each. He made a profit of 25 percent on one of the chairs and a loss of 25 percent on theother. What was his overall loss or profit percentage on selling both the chairs?
a)
Loss of about 7%
b)
Loss of about 6%
c)
No profit no loss
d)
Profit of about 6%
e)
Profit of about 7%

|
Jatin Kapoor answered |
Given:
- Chair-1 selling price = $300
- Profit% on selling chair-1 = 25%
- Chair-2 selling price = $300
- Loss% on selling chair-2 = 25%
To Find: Overall profit or loss% on selling both chairs?
Approach:
- Total profit or loss = Profit on chair-1 – Loss on chair 2
- Total cost price of the chairs = Cost Price of chair-1 + Cost Price of chair-2
2. The cost price of the chairs can be found out using the information given about the selling price and the profit% or loss%
3. Cost Price and profit on chair-1
- Selling Price = Cost Price + Profit……..(2)
As we know the selling price and the profit%, we can calculate the Cost price of chair-1. Once we know the cost price, we can calculate profit made on the chair using (2).
4. Cost Price and loss on chair-2
Selling Price = Cost Price - Loss……..(4)
Selling Price = Cost Price - Loss……..(4)
As we know the selling price and the loss%, we can calculate the Cost price of chair-2. Once we know the cost price, we can calculate loss made on the chair using (4).
5. Now, as we know the cost price of the chairs and profit or loss made on the chair, we can calculate the profit or loss% using (1)
5. Now, as we know the cost price of the chairs and profit or loss made on the chair, we can calculate the profit or loss% using (1)
Working out:
- Cost Price and profit on chair-1
a. Selling price of the chair = $300
b. Profit% on the chair = 25%
c. So, we can write
b. Profit% on the chair = 25%
c. So, we can write
2. Cost Price and loss on chair-2
a. Selling price of the chair = $300
b. Loss% on the chair = 25%
c. So, we can write
a. Selling price of the chair = $300
b. Loss% on the chair = 25%
c. So, we can write
3. As the loss made on chair-2 is greater than the profit made on chair-2, total
loss made = 100 – 60 = $40
loss made = 100 – 60 = $40
Hence, the shopkeeper made a loss of around 6% on the total transaction
Answer B
A retailer purchases an item at $700 per piece and sells it at a profit of 30 percent. To encourage the sale of the item in the holiday season, the retailer plans to offer at least two discount coupons to his loyal customers. At the same time, he wants to make sure that his profit margin does not fall below 10 percent. If the customers makes use of the discount coupons in an order which maximizes their discount, which of the following coupons should the retailer offer?I. $50 off
II. 8% off
III. 10% off- a)I and II only
- b)I and III only
- c)II and III only
- d)I, II and III
- e)None of the three coupons
Correct answer is option 'A'. Can you explain this answer?
A retailer purchases an item at $700 per piece and sells it at a profit of 30 percent. To encourage the sale of the item in the holiday season, the retailer plans to offer at least two discount coupons to his loyal customers. At the same time, he wants to make sure that his profit margin does not fall below 10 percent. If the customers makes use of the discount coupons in an order which maximizes their discount, which of the following coupons should the retailer offer?
I. $50 off
II. 8% off
III. 10% off
II. 8% off
III. 10% off
a)
I and II only
b)
I and III only
c)
II and III only
d)
I, II and III
e)
None of the three coupons

|
Nayanika Bajaj answered |
Given:
- Cost Price of the item, CP = $700
- Profit % before offering discounts = 30% (of CP)
- So, Profit = 30% of 700 = 210
- Therefore,
- Selling Price before offering discounts, SP = CP + Profit = = 700 + 210 = $910
- Minimum required Profit = 10%
- = 10% of 700 = $70
- 2 or more discount coupons are offered
- Discount coupons used in the order that maximizes the discount
To Find: Which of the given 3 discount coupons should the retailer offer?
Approach:
- To determine which discount coupons can be offered, we need to analyze the constraint on discount.
- The maximum discount allowed is one that leads to the minimum required profit (10%)
- So, we’ll calculate the value of the maximum discount allowed.
- Minimum Profit = (Minimum Required Profit %)*(CP)
- Profit = SP – CP
- So, Profit is minimum when SP is minimum
- So, Minimum SP = CP + (Minimum Profit)
- Now, SP = Marked Price – Discount
- So, SP is minimum when discount is maximum
- Therefore, (Maximum Discount) = (Marked Price) – (Minimum SP)
- Minimum Profit = (Minimum Required Profit %)*(CP)
- Next, we’ll evaluate all possible pairs that can be made from the given 3 discount coupons to determine the pairs in which the discount availed by using the discount coupons is greater than the maximum discount allowed. These are the pairs of discount coupons that cannot be offered by the retailer.
- Finally, by looking at the pairs of discount coupons that cannot be offered by the retailer, we’ll determine the discount coupons that cannot be offered by the retailer.
- For example, if pairs A-B and B-C cannot be offered but pair A-C can be offered, this means it is discount coupon B that should not be offered by the retailer.
Working out:
- Finding the maximum discount allowed
- As we have seen above, minimum profit = $70
- This is the case of maximum discount
- In the case of maximum discount, Selling Price = 700 + 70 = $770
- Whereas, the Selling Price beforre offering the disocunts = $910
- So, the maximum discount allowed = $910 - $770 = $140
- As we have seen above, minimum profit = $70
- So, we need to ensure that any combination of 2 coupons from among the 3 given doesn’t lead to a discount greater than $140
- Evaluating the possible combinations of given discount coupons
- 3 pairs are possible out of the 3 coupons- let’s discuss the discount in each:
- Case 1 : $ 50 off, 10% off
- Here, to maximize the discount, a person will avail the % discount first and then the cash discount.
- So the maximum discount that can be availed using these 2 coupons is: 10% of 910 + 50 = 91 + 50 = 141 dollars, which is greater than $140
- So, the retailer should not offer $50 off and 10% off coupons together because then customers will avail a discount greater than $140
- Case 2 : $ 50 off, 8% off
- Here again, to maximize the discount, a person will avail the % discount first and then the cash discount
- So, the Maximum discount that can be availed using these 2 coupons = 8% of 910 + 50 = 72.8 + 50 = $122.8, which is less than $140
- So, these 2 coupons together do not hurt the retailer’s minimum profit margin
- Case 3 : 10% off, 8% off
- In this case, the final Selling Price = 910$*(1 – 0.1)(1-0.08) = 910*0.9*0.92 = $753
- So, Discount availed = $910 – $753 = $157
- This is again greater than $140. So, this combination again cannot be offered.
- Getting to the answer
- Thus, we see that the following 2 combinations cannot be offered:
- $50 off, 10% off
- 10% off, 8% off
- But the following combination can be offered:
- $50 off, 8% off
- Thus, we see that the following 2 combinations cannot be offered:
- This means, the retailer should not offer the 10% off discount coupon. He can offer $50 off and 8% off discount coupons.
Looking at the answer choices, we see that the correct answer is Option A
A bicycle is sold after applying successive discounts of 10% and 20% on the list price at Shop A. The same is sold at a flat discount of 30% on the list price at Shop B. If the list price of bicycle is $200 for both Shop A and Shop B, what is the positive difference (if any) between the final prices of bicycles sold at Shop A and Shop B?- a)0
- b)4
- c)6
- d)9
- e)12
Correct answer is option 'B'. Can you explain this answer?
A bicycle is sold after applying successive discounts of 10% and 20% on the list price at Shop A. The same is sold at a flat discount of 30% on the list price at Shop B. If the list price of bicycle is $200 for both Shop A and Shop B, what is the positive difference (if any) between the final prices of bicycles sold at Shop A and Shop B?
a)
0
b)
4
c)
6
d)
9
e)
12

|
Diode Electra answered |
Let's say the original price is Y
shop A:
apply 10% discount, the price will be:
(1-10%)Y = 0.9Y
apply 20% discount, final price is:
0.9Y - (0.9Y*20%) = 0.72Y
Shop B:
price with 30% discount = (1 - 30%)Y = 0.7Y
so the difference,
0.72Y-0.7Y = 0.02Y
0.02Y = 0.02*200 = 4
shop A:
apply 10% discount, the price will be:
(1-10%)Y = 0.9Y
apply 20% discount, final price is:
0.9Y - (0.9Y*20%) = 0.72Y
Shop B:
price with 30% discount = (1 - 30%)Y = 0.7Y
so the difference,
0.72Y-0.7Y = 0.02Y
0.02Y = 0.02*200 = 4
If the maximum discount that a merchant who doesn’t want to sell an item at a loss can offer on that item is 20%, what will be the
profit percentage that the merchant makes if he sells the item at its marked price?- a)12.5%
- b)20%
- c)25%
- d)33%
- e)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
If the maximum discount that a merchant who doesn’t want to sell an item at a loss can offer on that item is 20%, what will be the
profit percentage that the merchant makes if he sells the item at its marked price?
profit percentage that the merchant makes if he sells the item at its marked price?
a)
12.5%
b)
20%
c)
25%
d)
33%
e)
Cannot be determined

|
Arya Yadav answered |
Given:
- Let Cost Price of the item be C, Marked Price be M and Selling Price be S
- Maximum discount for no loss = 20%
- This means, At 20% discount, the item is sold at Zero Profit, Zero Loss
- That is, At 20% discount, the discounted price of the item is equal to the Cost Price
- Maximum discount for no loss = 20%
To Find: % Profit if the item is sold at its Marked Price
Approach:
- So, to answer this question, we need to find the ratio M/C
- We are given one relation between M and C : At 20% discount on M, the discounted price is equal to the cost price. Using this relation, we’ll find the required ratio.
Working out:
- (Value of 20% Discount) = 20% of M = 0.2M
- This is the maximum discount that the merchant can offer without going into loss
- This means, at this point, his profit is zero (if the selling price was any lesser, he would make a loss)
- So, at this discount, his selling price is equal to his cost price
- Now, (Selling price at 20% discount on M) = M – (Value of 20% Discount) = M – 0.2M = 0.8M
- So, 0.8M = C
- So, Required % Profit
Looking at the answer choices, we see that the correct answer is Option C
When an item is sold for Rs. 18,700, the owner loses 15%. At what price should that plot be sold to get a gain of 15%?
- a)Rs. 25100
- b)Rs. 24200
- c)Rs. 25300
- d)Rs. 21200
Correct answer is option 'C'. Can you explain this answer?
a)
Rs. 25100
b)
Rs. 24200
c)
Rs. 25300
d)
Rs. 21200

|
Avi Shah answered |
First we find CP.
If SP is Rs. 85 then CP = Rs 100
If SP is Rs. 18,700, then
CP =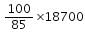 = Rs 22,000
= Rs 22,000
Now, if CP is Rs 100, then SP = Rs. 115
Thus, if CP is Rs. 22,000, then
SP =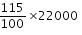 =Rs 25,300
=Rs 25,300
If SP is Rs. 85 then CP = Rs 100
If SP is Rs. 18,700, then
CP =
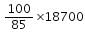 = Rs 22,000
= Rs 22,000Now, if CP is Rs 100, then SP = Rs. 115
Thus, if CP is Rs. 22,000, then
SP =
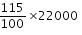 =Rs 25,300
=Rs 25,300A trader mixes 26 kg of rice at Rs. 20 per kg with 30 kg of rice of other variety at Rs. 36 per kg and sells the mixture at Rs. 30 per kg. What is his profit percentage?
- a)6%
- b)5%
- c)4%
- d)7%
Correct answer is option 'B'. Can you explain this answer?
A trader mixes 26 kg of rice at Rs. 20 per kg with 30 kg of rice of other variety at Rs. 36 per kg and sells the mixture at Rs. 30 per kg. What is his profit percentage?
a)
6%
b)
5%
c)
4%
d)
7%

|
Manoj Ghosh answered |
C.P. of 56 kg rice = Rs. (26 x 20 + 30 x 36) = Rs. (520 + 1080) = Rs. 1600.
S.P. of 56 kg rice = Rs. (56 x 30) = Rs. 1680.
Gain =(80/1600*100) % = 5%
A furniture dealer purchased 10 sofas for $500 each. If he sells all the sofas for no more than $600 each, what is the lowest price that he can sell any of the sofas to earn an average gross profit of $90 per sofa? - a)$470
- b)$480
- c)$490
- d)$500
- e)$510
Correct answer is option 'D'. Can you explain this answer?
A furniture dealer purchased 10 sofas for $500 each. If he sells all the sofas for no more than $600 each, what is the lowest price that he can sell any of the sofas to earn an average gross profit of $90 per sofa?
a)
$470
b)
$480
c)
$490
d)
$500
e)
$510

|
Kiran Nambiar answered |
To find the lowest price at which the dealer can sell any of the sofas and still earn an average gross profit of $90 per sofa, we need to consider the following:
1. Calculate the total cost of purchasing the 10 sofas:
Total Cost = Number of Sofas * Cost per Sofa
= 10 * $500
= $5000
2. Calculate the desired total revenue based on the average gross profit:
Total Revenue = Total Cost + Total Profit
= Total Cost + (Number of Sofas * Average Gross Profit)
= $5000 + (10 * $90)
= $5000 + $900
= $5900
3. Calculate the maximum revenue per sofa that the dealer can achieve:
Maximum Revenue per Sofa = Total Revenue / Number of Sofas
= $5900 / 10
= $590
4. Determine the lowest price the dealer can sell any of the sofas:
Lowest Price = Maximum Revenue per Sofa - Average Gross Profit
= $590 - $90
= $500
Therefore, the lowest price at which the dealer can sell any of the sofas and still earn an average gross profit of $90 per sofa is $500. So, the correct answer is option D.
1. Calculate the total cost of purchasing the 10 sofas:
Total Cost = Number of Sofas * Cost per Sofa
= 10 * $500
= $5000
2. Calculate the desired total revenue based on the average gross profit:
Total Revenue = Total Cost + Total Profit
= Total Cost + (Number of Sofas * Average Gross Profit)
= $5000 + (10 * $90)
= $5000 + $900
= $5900
3. Calculate the maximum revenue per sofa that the dealer can achieve:
Maximum Revenue per Sofa = Total Revenue / Number of Sofas
= $5900 / 10
= $590
4. Determine the lowest price the dealer can sell any of the sofas:
Lowest Price = Maximum Revenue per Sofa - Average Gross Profit
= $590 - $90
= $500
Therefore, the lowest price at which the dealer can sell any of the sofas and still earn an average gross profit of $90 per sofa is $500. So, the correct answer is option D.
The marked price of Brand A Milk is 50% higher than the cost price. If it is sold at a price of $2.7 after applying a discount of 10% on the marked price, what is the profit % in selling Brand A milk?- a)6%
- b)10.7%
- c)23.33%
- d)35%
- e)44%
Correct answer is option 'D'. Can you explain this answer?
The marked price of Brand A Milk is 50% higher than the cost price. If it is sold at a price of $2.7 after applying a discount of 10% on the marked price, what is the profit % in selling Brand A milk?
a)
6%
b)
10.7%
c)
23.33%
d)
35%
e)
44%

|
Ansh Khaneja answered |
90% of marked price = 2.7 $
marked price = 2.7/0.9 = 3 $
150% Cost price = Marked price
so 1.5 cost price = 3$
cost price = 3/1.5 = 2$
profit = Selling price -cost price = 2.7 - 2 = 0.7 $
profit percentage = (0.7/2)*100 = 35%
marked price = 2.7/0.9 = 3 $
150% Cost price = Marked price
so 1.5 cost price = 3$
cost price = 3/1.5 = 2$
profit = Selling price -cost price = 2.7 - 2 = 0.7 $
profit percentage = (0.7/2)*100 = 35%
Murali purchased 20 dozens of toys at the rate of Rs. 375 per dozen. He sold each one of them at the rate of Rs. 33. Find out his profit percentage.- a)3.5
- b)5.6
- c)4.1
- d)3.4
Correct answer is option 'B'. Can you explain this answer?
Murali purchased 20 dozens of toys at the rate of Rs. 375 per dozen. He sold each one of them at the rate of Rs. 33. Find out his profit percentage.
a)
3.5
b)
5.6
c)
4.1
d)
3.4

|
Arya Roy answered |
Cost Price of 1 toy = Rs.375/12 = Rs. 31.25
Selling Price of 1 toy = Rs. 33
So, Gain = Rs. (33 - 31.25) = Rs. 1.75
Profit % = [(1.75/31.25) x 100 ]% = 28/5 % = 5.6%
The marked price of a garment is 100% higher than the cost price. If it is sold at a price of $112 after applying successive discounts of 20% and 30% on the marked price, what is the profit (in dollars) obtained by selling the garment?- a)12
- b)32
- c)54
- d)88
- e)100
Correct answer is option 'A'. Can you explain this answer?
The marked price of a garment is 100% higher than the cost price. If it is sold at a price of $112 after applying successive discounts of 20% and 30% on the marked price, what is the profit (in dollars) obtained by selling the garment?
a)
12
b)
32
c)
54
d)
88
e)
100

|
Prashanth Rajan answered |
A
A shoe shop owner lists the price of a pair of shoes as the price at which he purchased the pair from the manufacturer plus a markup
which is equal to 40 percent of the selling price. After some time, he offers a discount on the shoes which is equal to 20 percent of
the selling price. Which of the following best represents the profit, as a percentage of the purchase price, which he earns on selling
the pair of shoes?- a)11%
- b)12%
- c)17%
- d)20%
- e)25%
Correct answer is option 'E'. Can you explain this answer?
A shoe shop owner lists the price of a pair of shoes as the price at which he purchased the pair from the manufacturer plus a markup
which is equal to 40 percent of the selling price. After some time, he offers a discount on the shoes which is equal to 20 percent of
the selling price. Which of the following best represents the profit, as a percentage of the purchase price, which he earns on selling
the pair of shoes?
which is equal to 40 percent of the selling price. After some time, he offers a discount on the shoes which is equal to 20 percent of
the selling price. Which of the following best represents the profit, as a percentage of the purchase price, which he earns on selling
the pair of shoes?
a)
11%
b)
12%
c)
17%
d)
20%
e)
25%

|
Sonal Banerjee answered |
Given:
- Let the cost price of a pair of shoes be C, the selling price be S and the marked price be M
- Discount offered = 20% of S = 0.2S
- Mark-up = 40% of S = 0.4S
- And, M = C + 40% of S
- M = C + 0.4S
To Find: Profit earned as a % of C
Approach:
- Required profit %
- So, to answer the question, we need to find the ratio S/C
- Now, we are given one equation that links M, C and S. In this equation, if we can substitute M in terms of C or S, we’ll get a linear equation that relates C and S, and so, from that equation, we’ll be able to find the required ratio.
- So, let’s now look at how we can express M in terms of S or C. We’re told the value of Discount in terms of S.
Using the fact that Discount = M – S, we will be able to express M in terms of S
Working out:
- Expressing M in terms of S
- Given: Discount = 0.2S
- So, M – S = 0.2S
- Therefore, M = 1.2S
- Finding the ratio S:C
- Given: M = C + 0.4S
Looking at the answer choices, we see that the correct answer is Option E
Sam bought a television set from a store at a discount of 10%. He sold the set to a friend at a further discount of 10%. What is the discount his friend got on the original list price of the television set?- a)12%
- b)19%
- c)20%
- d)22%
- e)25%
Correct answer is option 'B'. Can you explain this answer?
Sam bought a television set from a store at a discount of 10%. He sold the set to a friend at a further discount of 10%. What is the discount his friend got on the original list price of the television set?
a)
12%
b)
19%
c)
20%
d)
22%
e)
25%

|
Preitee Ranjan Pradhan answered |
-10-10+(100/100)=19%
An entrepreneur who is planning to set up a restaurant estimates that the monthly costs of running the restaurant will be given by the formula C = 15000 + 2000n + 5m, where C is in dollars, n is the number of employees at the restaurant and m is the number of orders received in the month. He plans to start the restaurant with only 2 employees and to hire 1 new employee each month. He estimates that the average order value at his restaurant will be $50 and that the number of orders per month will increase by 10% month on month. If the estimated number of orders the restaurant receives in the first month of its existence is 1000, then as per this model, after how many months of operation will the restaurant first achieve a profit margin of 20% or more?- a)1
- b)2
- c)3
- d)6
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
An entrepreneur who is planning to set up a restaurant estimates that the monthly costs of running the restaurant will be given by the formula C = 15000 + 2000n + 5m, where C is in dollars, n is the number of employees at the restaurant and m is the number of orders received in the month. He plans to start the restaurant with only 2 employees and to hire 1 new employee each month. He estimates that the average order value at his restaurant will be $50 and that the number of orders per month will increase by 10% month on month. If the estimated number of orders the restaurant receives in the first month of its existence is 1000, then as per this model, after how many months of operation will the restaurant first achieve a profit margin of 20% or more?
a)
1
b)
2
c)
3
d)
6
e)
Cannot be determined

|
Nayanika Bajaj answered |
Given:
- Monthly costs C = 15000 + 2000n + 5m, where
- n = number of employees
- m = number of orders
- Average order value = $50
- Month 1:
- n = 2
- m = 1000 (estimated)
- Month 2:
- n = 2 + 1 = 3
- m = 1.1*1000 (estimated)
- In general, for kth Month:
- n = 2 + (k – 1)
- m = (1.1) *1000
To Find: After how many months of operation is Profit ≥ 20%
Approach:
- We’re given the month-on-month growth trend for both n and m. So, we can find the value of n and m for all months of operation. We also know the Average order value and it is constant for all months of operation. So, starting from the 1 month, we’ll find the value of Monthly Profit % till we get to the month for which the Profit % is greater than or equal to 20%
Working out:
- Thus, we see that the profit for the 1 month itself is estimated, as per the given model, to be greater than 100%
- Therefore, we do not need to do the evaluations for any more months. The profit margin is (much) greater than 20% in Month 1 itself.
Looking at the answer choices, we see that the correct answer is Option A
The dealer of an electronic store discounted the price of a television and a microwave oven by the same percentage. On which of the two articles did the shopkeeper make a greater profit?
(1) The articles were marked up by the same percentage
(2) The amount of discount was same for both the articles- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'C'. Can you explain this answer?
The dealer of an electronic store discounted the price of a television and a microwave oven by the same percentage. On which of the two articles did the shopkeeper make a greater profit?
(1) The articles were marked up by the same percentage
(2) The amount of discount was same for both the articles
(1) The articles were marked up by the same percentage
(2) The amount of discount was same for both the articles
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Sahana Mehta answered |
Step 1 & 2: Understand Question and Draw Inference
- Let’s assume the cost price, selling price and marked price of the television be Ct, St and Mt respectively.
- Let’s assume the cost price, selling price and marked price of the microwave be Cm, Sm and Mm respectively
- Let the discount given be d%
Step 3 : Analyze Statement 1 independent
(1) The articles were marked up by the same percentage
- Let the markup% be m%.
- So, writing the markup on television and microwave oven in terms of m%, we get:
We do not know for sure if 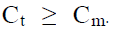 Insufficient to answer.
Insufficient to answer.
Step 4 : Analyze Statement 2 independent
(2) The amount of discount was same for both the articles
- Substituting in inequality (1), we have
We do not know for sure if 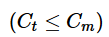 Insufficient to answer
Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
Combining both the statements, we have C = C . Hence, the only possible case is Pt = pm . Hence the shopkeeper made equal profit on both the items.
Sufficient to answer.
Sufficient to answer.
Answer : C
A certain motorcycle company manufactured and sold each of its 1,200 motorcycles during the last fiscal year. Did the company make a profit on the sales of motorcycles?(1) For each motorcycle sold, the company’s revenue was $10,000(2) The company’s expenses comprise a fixed expense of $2,000,000 per quarter and an additional $3,500 for each motorcycle.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
A certain motorcycle company manufactured and sold each of its 1,200 motorcycles during the last fiscal year. Did the company make a profit on the sales of motorcycles?
(1) For each motorcycle sold, the company’s revenue was $10,000
(2) The company’s expenses comprise a fixed expense of $2,000,000 per quarter and an additional $3,500 for each motorcycle.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Pranav Das answered |
Steps 1 & 2: Understand Question and Draw Inferences
The company manufactured and sold 1,200 motorcycles during its fiscal year. The question is whether it made a profit, so you need to know the revenue and expenses.
Step 3: Analyze Statement 1
(1) For each motorcycle sold, the company’s revenue was $10,000
Statement 1 tells you that the company’s revenue was $12,000,000 during its fiscal year. However, without knowing its expenses, you don’t know whether the company made a profit.
Statement 1 is not sufficient.
Step 4: Analyze Statement 2
(2) The company’s expenses comprise a fixed expense of $2,000,000 per quarter and an additional $3,500 for each motorcycle.
Statement 2 tells you that the company’s annual expenses were $8,000,000 fixed plus $4,200,000 ($3,500 × 1,200), for a total of $12,200,000. However, without knowing the revenue, you don’t know whether the company made a profit.
Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
Taken together, if the revenues were $12.0m and the expenses were $12.2m, you know that the company did not make a profit.
With these, you are able to answer the question, even though the answer is no.
Answer: Option (C)
Stuart paid $60 for purchasing a pair of identical chairs. He decided to sell the chairs at a price equal to the purchase price plus a markup that is 40 percent of the marked price, set by him. When he could not sell the chairs for one day, he discounted their marked price by 20 percent and quickly sold one chair. Worrying that he had underpriced the chairs, he raised the marked price of the remaining chair by 20 percent and sold it by the end of the day. What was his total profit or loss for the combined transactions?- a)10
- b)18
- c)28
- d)38
- e)48
Correct answer is option 'C'. Can you explain this answer?
Stuart paid $60 for purchasing a pair of identical chairs. He decided to sell the chairs at a price equal to the purchase price plus a markup that is 40 percent of the marked price, set by him. When he could not sell the chairs for one day, he discounted their marked price by 20 percent and quickly sold one chair. Worrying that he had underpriced the chairs, he raised the marked price of the remaining chair by 20 percent and sold it by the end of the day. What was his total profit or loss for the combined transactions?
a)
10
b)
18
c)
28
d)
38
e)
48

|
Palak Saha answered |
Step 1: Question statement and Inferences
Both chairs have the same cost price but different selling prices. We need to find the price at which each chair sells, in order to calculate the total profit made by selling the two chairs.
Step 2: Finding required values
Stuart purchased two chairs for $60
So, Cost price of one chair, CP = 60/2 = $30
Let the marked price of each chair be MP
MP = CP + Markup
Given: Markup = 40% of MP
So, MP = CP + 40% of MP
Or, 60% of MP = CP
60100MP=CPMP=10060×30=50
After 1 day, he discounted the marked price by 20%
So,new Marked Price=MP′=MP–20% of MP
=80 % of MP
MP′=40
He sold one chair at this price.
His profit on selling this chair = P1 = MP′ – CP
P1 = 40 – 30
P1 =$ 10
For the unsold chair,
He raised the marked price by 20%
New Marked Price = MP′′=MP′+20 of MP′
MP′′ = 120 of MP′
MP′′=$48
He sold the second chair at this price.
His profit on selling this chair
= P2 = MP′′–CP
P2 = 48 – 30
P2 = $18
Step 3: Calculating the final answer
Total profit earned on the sale of the two chairs
= P1 + P2 = $10 + $18 = $28
Looking at the answer choices, we see that Option C is correct
A manufacturer produces items at a fixed monthly cost of $2000 plus a variable cost of $100 per item. If he needs to sell N items to make a monthly profit of $50 per item, what is the value of N?
(1) Each item produced is sold for $200.
(2) If the fixed cost is not included in the cost and the manufacturer still sells N items at the same selling price, he will make a monthly profit of $100 per item.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked - d)EACH statement ALONE is sufficient to answer the question
asked - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
Correct answer is option 'D'. Can you explain this answer?
A manufacturer produces items at a fixed monthly cost of $2000 plus a variable cost of $100 per item. If he needs to sell N items to make a monthly profit of $50 per item, what is the value of N?
(1) Each item produced is sold for $200.
(2) If the fixed cost is not included in the cost and the manufacturer still sells N items at the same selling price, he will make a monthly profit of $100 per item.
(1) Each item produced is sold for $200.
(2) If the fixed cost is not included in the cost and the manufacturer still sells N items at the same selling price, he will make a monthly profit of $100 per item.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
d)
EACH statement ALONE is sufficient to answer the question
asked
asked
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
answer the question asked, and additional data specific to the
problem are needed

|
Jatin Kapoor answered |
Step 1 & 2: Understand Question and Draw Inference
Given:
- Fixed Cost = $2000
- Variable Cost = $100 per item
To find: N ( = Number of items to be sold to make a profit of $50 per item)
- Let the selling price each item be S dollar
- So, revenue generated by selling N items = N * S
- Cost of producing N items = N * 100 +$2000
- Profit on selling N items = N * S – (N * 100 +$2000)
- 50* N = N* S – ( N* 100 +$2000)
- So, we need to find the value of S
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘Each item produced is sold for $200
- So, S = $200
- As we know the value of S we can find the value of N.
Sufficient to answer
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘If the fixed cost is not included in the cost and the
manufacturer still sells N items at the same selling price, he will make a
monthly profit of $100 per item’
manufacturer still sells N items at the same selling price, he will make a
monthly profit of $100 per item’
- S = Variable Cost per item + $100
- S = $100 + $100 = $200
- As we know the value of S, we can calculate the value of N.
So, Statement 2 is sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Steps 3 and 4, this step is not required
Answer: Option D
Answer: Option D
For a manufacturer, the cost of producing x units is given the expression y +kx, where y and k are constants. If the manufacturer sells 100 units at $50 each, his per unit profit for these 100 units is equal to 64 percent of the selling price per unit and if he sells 250 units at $40 each, his per unit profit for these 250 units is equal to 70 percent of the selling price per unit. How much profit in dollars would the manufacturer make if he sold 50 units at $70 each?- a)1400
- b)1500
- c)2000
- d)2100
- e)2500
Correct answer is option 'D'. Can you explain this answer?
For a manufacturer, the cost of producing x units is given the expression y +kx, where y and k are constants. If the manufacturer sells 100 units at $50 each, his per unit profit for these 100 units is equal to 64 percent of the selling price per unit and if he sells 250 units at $40 each, his per unit profit for these 250 units is equal to 70 percent of the selling price per unit. How much profit in dollars would the manufacturer make if he sold 50 units at $70 each?
a)
1400
b)
1500
c)
2000
d)
2100
e)
2500

|
Jatin Kapoor answered |
Given:
- Cost of Producing x units = y +kx, where y and k are constants
- If number of units sold = 100
- Selling Price of each unit = $50
- Profit per unit = 64% of selling price per unit =64% of 50 =$32
- If number of units sold = 250
- Selling Price per unit = $40
- Profit per unit = 70% of the selling price per unit = 70% of 40 = $28
To Find: Profit made on selling 50 units at $70 each
Approach:
- Profit made on selling 50 units at $70 each = Total Selling price of 50 units – Total cost price of 50 units
- We are given the selling price per unit = $70. So, we can calculate the total selling price of 70 units
- Cost of producing 50 units = y +kx. We know x = 50. So, we need to find the value of y and k
- As we need to find the value of 2 variables, we would need 2 equations.
- Finding values of y and k
- We are given the selling price of each of the 100 units and the profit per unit made on selling these 100 units. So, using the formula
- Selling Price = Cost Price + Profit, we can find the cost price of 100 units.
- Also, we know that cost price of producing 100 units = y +100k…….(1)
- Similarly, we are given the selling price of each of the 250 units and the profit per unit made on selling these 250 units. So, using the formula
- Selling Price = Cost Price + Profit, we can find the cost price of 250 units.
- Also, we know that cost price of producing 250 units = y +250k…….(2)
- Thus, we have 2 equations through which we can find the values of y and k.
- Once, we know the values of k, we can find the cost price of producing 50 units, which can then be used to find the profit made on selling 50 units at $70 each.
Working out:
- Selling price of 100 units at $50 each = 100*50 = $5000
- Profit per unit = $32 (analysed in the Given section)
- Profit on 100 units = 100*32 = $320
- So, Cost price of 100 units = $5000 - $3200 = $1800
- As per the given formula for Cost Price, Cost of producing 100 units = y +100k
- Therefore, y+100k = $1800……..(1.1)
- Profit per unit = $32 (analysed in the Given section)
- Selling price of 250 units at $40 each = 250*40 = $1000
- Profit per unit = $28 (analysed in the Given section)
- i. Profit on 250 units = 250*28 = $7000
- So, Cost price of 250 units = $10000 - $7000 = $300
- As per the given formula of cos tprice, Cost of producing 250 units = y +250k
- Therefore, y + 250 - k = $3000……..(2.2)
- Profit per unit = $28 (analysed in the Given section)
- Solving equations (1.1) and (2.2), we have y = 1000 and k = 8
- So, cost of producing 50 units = y +50k = 1000 +50*8 = $1400
- Selling price of 50 units = 50*70 = $3500
- Hence, profit on selling 50 units at $70 each = $3500 - $1400 = $2100
Thus, the manufacturer made a profit of $2100 on selling 50 units at $70 each.
Answer : D
A shopkeeper buys two printers A and B. Had the shopkeeper paid the full price of both printers, they would have cost the same to him. However, he buys printer A with a down payment of 10 percent of the cost of printer A and printer B with a down payment of 20 percent of the cost of printer B and repays the remaining cost and the individual finance charges of the printers A and B over a period of time. The finance charges for printers A and B are equal to 40 percent of the remainder of the cost of printer A and y percent of the remainder of the cost of Printer B respectively. What should be the value of y so that the cost of buying the two printers is equal for the shopkeeper?- a)
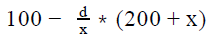
- b)
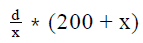
- c)
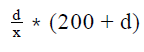
- d)

- e)
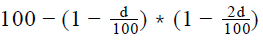
Correct answer is option 'B'. Can you explain this answer?
A shopkeeper buys two printers A and B. Had the shopkeeper paid the full price of both printers, they would have cost the same to him. However, he buys printer A with a down payment of 10 percent of the cost of printer A and printer B with a down payment of 20 percent of the cost of printer B and repays the remaining cost and the individual finance charges of the printers A and B over a period of time. The finance charges for printers A and B are equal to 40 percent of the remainder of the cost of printer A and y percent of the remainder of the cost of Printer B respectively. What should be the value of y so that the cost of buying the two printers is equal for the shopkeeper?
a)
b)
c)
d)
e)

|
Saumya Sharma answered |
Given:
- Marked price = x dollars
- First discount offered = d%
- Additional discount offered = 2d dollars
To Find: Single discount % equivalent to total discount given?
Approach:
- So, in order to find the Single Discount %, we need to know the Total Discount availed by the customer
- We know that
- (Selling Price) = (Marked Price) – (Total discount)
- So, (Total Discount) = (Marked Price) – (Selling Price)
- Therefore, once we know the Selling Price, we’ll be able to find the Total Discount.
- Now, we can calculate the selling price of the article by applying the discount% and the dollar discounts.
Working out:
3. So, we can write
Answer : B
If a man sells x oranges for a dollar, he loses 45 percent. By how much percentage should the man reduce his cost to make a profit
of 10 percent on selling 2x oranges in a dollar?- a)25%
- b)50%
- c)75%
- d)150%
- e)300%
Correct answer is option 'C'. Can you explain this answer?
If a man sells x oranges for a dollar, he loses 45 percent. By how much percentage should the man reduce his cost to make a profit
of 10 percent on selling 2x oranges in a dollar?
of 10 percent on selling 2x oranges in a dollar?
a)
25%
b)
50%
c)
75%
d)
150%
e)
300%

|
Aditya Gupta answered |
Given:
x oranges are sold for $1 at a loss of 45%
To Find: The percentage by which the cost should be reduced so that 2x oranges are sold for $1 at a profit of 10%
To Find: The percentage by which the cost should be reduced so that 2x oranges are sold for $1 at a profit of 10%
- ApproLet’s assume the cost price of x oranges when the man sells the x oranges for $1 and loses 45% be CP1 and the cost price of x oranges when he sells 2x oranges for $1 be CP2ach:
- So, the percentage by which the person should reduce his cost be
- So, the percentage by which the person should reduce his cost be
- Calculating CP1
a. Selling price of x oranges = $1
b. Loss% = 45%
c. Now, we know that Selling Price = Cost Price - Loss
f. As we know the selling price and the loss %, we can find the Cost Price of x oranges, i.e. CP1
2. Calculating CP2
a. Selling price of 2x oranges = $1
b. Profit% = 10%
c. Now, we know that Selling Price = Cost Price + Profit…..(3)
a. Selling price of 2x oranges = $1
b. Profit% = 10%
c. Now, we know that Selling Price = Cost Price + Profit…..(3)
So, we can find the Cost Price of 2x oranges.
g. Hence, we can find the cost price of x oranges i.e. CP2
g. Hence, we can find the cost price of x oranges i.e. CP2
Working out:
3. The percentage by which the man should decrease his price =
Thus the man should reduce his price by 75% to make a profit of 10% on selling 2x oranges for a dollar.
Answer C
The cost price of 20 articles is the same as the selling price of x articles. If the profit is 25%, find out the value of x
- a)15
- b)25
- c)18
- d)16
Correct answer is option 'D'. Can you explain this answer?
a)
15
b)
25
c)
18
d)
16

|
Dhruv Mehra answered |
Let the Cost Price of one article = Rs. 1
CP of x articles = Rs. x
CP of 20 articles = 20
Selling price of x articles = 20
Profit = 25% [Given]
⇒ (SP - CP) / CP = 25 / 100 = 1/4 ⇒ (20-x) / x = 1/4
⇒ 80−4x=x
⇒ 5x=80
⇒ x = 80/5 = 16
A local grocer purchased eggs at a cost of c dollars per dozen each morning and sold all of them by the day end at a cost of s dollars per dozen. He made a profit of 100% on the sale of eggs each day. One morning there was a minor accident at the grocer’s shop in which some of the eggs he had bought that morning broke and therefore, were rendered unsaleable. The grocer sold the remaining eggs at their usual selling price and made a profit of 50% on the sale of eggs that day. What percentage of the eggs bought by the grocer that morning broke in the accident?- a)25%
- b)33%
- c)50%
- d)67%
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
A local grocer purchased eggs at a cost of c dollars per dozen each morning and sold all of them by the day end at a cost of s dollars per dozen. He made a profit of 100% on the sale of eggs each day. One morning there was a minor accident at the grocer’s shop in which some of the eggs he had bought that morning broke and therefore, were rendered unsaleable. The grocer sold the remaining eggs at their usual selling price and made a profit of 50% on the sale of eggs that day. What percentage of the eggs bought by the grocer that morning broke in the accident?
a)
25%
b)
33%
c)
50%
d)
67%
e)
Cannot be determined

|
Disha Mehta answered |
Given:
- Cost price of eggs = c dollars per dozen
- Selling price of eggs = s dollars per dozen
- % profit = 100%
- This is the profit when all the eggs that were purchased get sold
- On the day of the accident,
- Let eggs bought = x dozen
- Eggs broken = b dozen
- So, eggs sold = x – b dozen
- % profit when b eggs broke, that is when only x – b dozen eggs get sold = 50%
To Find: % of eggs that broke = ?
Approach:
- We know the value of % profit with b dozen eggs broken. So, if we know the value of s/c then, by using the above equation, we’ll be able to get the ratio b/x
- We know the value of % profit when all the x eggs get sold. So, by equating the above expression to this value, we’ll be able to get the ratio s/c
Working out:
- Finding the ratio s/c
- The % profit when all the x eggs get sold is 100%
- Finding the ratio b/x
- % profit with b dozen eggs broken = 50%
Looking at the answer choices, we see that the correct answer is Option A
A craftsman sold his identical handcrafted items at a profit of 20 percent. Had he charged 20 percent more per item, his profit per
item would have been $9.6 more. What price did he charge, in dollars, for each item?- a)24
- b)28.8
- c)40
- d)48
- e)57.6
Correct answer is option 'D'. Can you explain this answer?
A craftsman sold his identical handcrafted items at a profit of 20 percent. Had he charged 20 percent more per item, his profit per
item would have been $9.6 more. What price did he charge, in dollars, for each item?
item would have been $9.6 more. What price did he charge, in dollars, for each item?
a)
24
b)
28.8
c)
40
d)
48
e)
57.6

|
Arya Yadav answered |
Given:
- Let the Cost Price of each item be C dollars and the selling price be S dollars
- If Selling Price is 20% more, profit per item is $9.6 more
To Find: S = ?
Approach:
- To find the value of S, we need to draft an equation in terms of S. We’re given the relation between Old Profit (when the selling price is S) and the New Profit (when the selling price is 20% greater than S). We’ll use this relation to draft an equation in terms of S.
Working out:
- New Selling Price = S + 20% of S = S + 0.2S = 1.2S
- New Profit = (Old Profit) + $9.6
- New profit = New SP – CP = 1.2S – C
- Old profit – Old SP – CP = S - C
- So, (1.2S – C) = (S – C) + 9.6
- 0.2S = 9.6
-
Looking at the answer choices, we see that the correct answer is Option D
A furniture retailer bought 100 identical chairs at a cost of $20 each. He sold some of the chairs within the first week for $35 each. In the second week, he sold all the remaining chairs for $30 each. If his total profit on the sale of the chairs was greater in the second week than in the first week, which of the following can be the number of chairs sold by the retailer in the second week?I. 30
II. 60
III. 80- a)I only
- b)II only
- c)III only
- d)I and II only
- e)II and III only
Correct answer is option 'C'. Can you explain this answer?
A furniture retailer bought 100 identical chairs at a cost of $20 each. He sold some of the chairs within the first week for $35 each. In the second week, he sold all the remaining chairs for $30 each. If his total profit on the sale of the chairs was greater in the second week than in the first week, which of the following can be the number of chairs sold by the retailer in the second week?
I. 30
II. 60
III. 80
II. 60
III. 80
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
II and III only

|
Arya Yadav answered |
Given:
- Number of chairs bought by retailer = 100
- Cost price of 1 chair = $20
- First Week
- Let the number of chairs sold in the first week be z.
- Selling price per chair = $35
- So, profit per chair = $35 - $20 = $15
- So, total profit on selling z chairs = $15z
- Second Week
- The number of chairs sold =100 – z
- Selling price per chair = $30
- So, profit per chair = $30 - $20 = $10
- So, total profit on selling 100 - z chairs = $10(100 – z) =$(1000-10z)
- Profit in 2nd week > Profit in 1st week
To Find: Which of the 3 values is/are possible for 100 –z?
Approach:
- To answer the question, we need to find the possible values of z
- We’ve already inferred above the profit of 1 and 2 weeks in terms of z.
We’re also given a relation between the profit of 1 and 2 weeks. We’ll use this relation to find the possible values of z.
Working out:
- Finding possible values of 100 –z
- Since z < 40, -z > -40
- So, 100-z > 100 – 40
- That is, number of chairs sold in the 2 week > 60
- Evaluating the 3 given values
- Of the 3 given values, the only value that is greater than 60 is the 3 value (80)
Looking at the answer choices, we see that the correct answer is Option C
A shopkeeper purchased 20 identical units of an item at a cost of $20 per unit. He sold some of the units at a price of $x per unit and the remaining units at $y per unit. What was his gross profit made by selling the 20 units of the item?
(1) The number of units sold at $x per unit was 12
(2) The total revenue generated by selling the 20 units was $880- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
Correct answer is option 'B'. Can you explain this answer?
A shopkeeper purchased 20 identical units of an item at a cost of $20 per unit. He sold some of the units at a price of $x per unit and the remaining units at $y per unit. What was his gross profit made by selling the 20 units of the item?
(1) The number of units sold at $x per unit was 12
(2) The total revenue generated by selling the 20 units was $880
(1) The number of units sold at $x per unit was 12
(2) The total revenue generated by selling the 20 units was $880
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
answer the question asked, and additional data specific to the
problem are needed

|
Sonal Banerjee answered |
Step 1 & 2: Understand Question and Draw Inference
Given:
- Total number of units = 20
- Cost price per unit = $20
- Let the number of items sold at $x per unit be a
- So, the number of items sold at $y per unit = 20 – a
To find: Gross Profit
- Gross Profit = (Total Revenue) – (Total Cost)
- = {ax + (20-a)*y } – 20*20
- So, in order to answer the question, we need to find the Total Revenue, and to find the Total Revenue, we need to know a, x and y
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘The number of units sold at $x per unit was 12’
- So, a = 12
- However, we do not yet know the value of x and y
- So, Statement 1 is not sufficient to find ‘Total Revenue’ and hence, to get to the answer
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘The total revenue generated by selling the 20 units was $880’
- Since we now know the value of ‘Total Revenue’, we can find Gross Profit
- So, Statement 2 is sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 4, this step is not required
Answer: Option B
Answer: Option B
Jamie purchased three items from a budget store. She received discounts of 40% on the marked price of item A, 20% on the marked price of item B and 10% on the marked price of item C. How much money did she save, in percent terms, by shopping at the budget store?(1) The marked price of item B is 75% of the marked price of item A and 200% more than the marked price of item C.(2) The marked price of item A is 400% of the marked price of item C.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?
Jamie purchased three items from a budget store. She received discounts of 40% on the marked price of item A, 20% on the marked price of item B and 10% on the marked price of item C. How much money did she save, in percent terms, by shopping at the budget store?
(1) The marked price of item B is 75% of the marked price of item A and 200% more than the marked price of item C.
(2) The marked price of item A is 400% of the marked price of item C.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Amar Chakraborty answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let the marked price of item A be a dollars,
The marked price of item B be b dollars, and
The marked price of item C be c dollars
So, had she not shopped at the budget store, she would have bought these three items at their marked price.
So, she would have spent a total of (a+b+c) dollars to buy these three items.
At the budget store,
Let the selling price of item A be a’
=> a’ = a – 40% of a = 0.6a
Let the selling price of item B be b’
=> b’ = b – 20% of b = 0.8b
Let the selling price of item C be c’
=> c’ = c – 10% of c = 0.9 c
So, the money actually paid by Jamie for the three items = (0.6a + 0.8b + 0.9c)
Money saved by her by shopping at the budget store = (Money she would have otherwise spent to buy these 3 items) – (Money she spent at the budget store to buy these three items)
=> Money saved = (a + b + c) – (0.6a + 0.8b + 0.9c)
=> Money saved = 0.4a + 0.2b + 0.1c
% Moneysaved=
% Moneysaved=
Thus, in order to find the % Money saved, we need to know the values of a, b and c.
Step 3: Analyze Statement 1 independently
Statement 1 states that:
The marked price of item B is 75% of the marked price of item A and 200% more than the marked price of item C
Also, 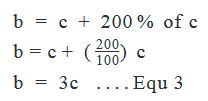
Substituting Equation 3 in Equation 2:
3c = 0.75 a
⇒ c = 0.25a ..... Equ 4
Substituting Equations 2 and 4 in Equation 1:
We see that if we divide the numerator and denominator by a, we will get a tangible number. We don’t need to actually solve this expression, since this is a DS question and not a PS question. But we do know that we will be able to get a unique value for % Money Saved.
Therefore, Statement 1 alone is sufficient to arrive at a unique answer.
Step 4: Analyse Statement 2 independently
Statement 2 states that:
The marked price of item A is 400% of the marked price of item C
=> a = 400% of c
=> a = 400/100 * c
=> a = 4c
However, Statement 2 gives us no idea of the value of b.
So, we will not be able to solve Equation 1 to determine a unique value of % Money Saved.
Therefore, Statement 2 is not sufficient.
Step 5: Analyse both statements together
This step is not required since we do get a unique solution in Step 3.
Correct answer = Option A.
Chapter doubts & questions for Profit and Loss - Quantitative Reasoning for GRE 2025 is part of GRE exam preparation. The chapters have been prepared according to the GRE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GRE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Profit and Loss - Quantitative Reasoning for GRE in English & Hindi are available as part of GRE exam.
Download more important topics, notes, lectures and mock test series for GRE Exam by signing up for free.
Quantitative Reasoning for GRE
124 videos|102 docs|108 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup