All Exams >
CTET & State TET >
Mathematics & Pedagogy Paper 2 for CTET & TET Exams >
All Questions
All questions of Construction for CTET & State TET Exam
What is the supplementary angle of 108°?- a)72°
- b)72.5°
- c)71.5°
- d)70°
Correct answer is option 'A'. Can you explain this answer?
What is the supplementary angle of 108°?
a)
72°
b)
72.5°
c)
71.5°
d)
70°
|
|
Zeenat Choudhary answered |
X + 108 = 180 (property of supplementry angle)
x = 180-108
x = 72
correct option is A(72)
x = 180-108
x = 72
correct option is A(72)
In Δ ABC if ∠B = ∠C = 300, which of the following is the longest side?- a)BC
- b)AC
- c)AB
- d)none
Correct answer is option 'A'. Can you explain this answer?
In Δ ABC if ∠B = ∠C = 300, which of the following is the longest side?
a)
BC
b)
AC
c)
AB
d)
none
|
|
Prateek Malik answered |
What do you need help with? Please provide more information.
Which of these triangles are possible to construct by knowing only its altitude?- a)Right angled triangle
- b)Equilateral triangle
- c)Isosceles triangle
- d)Any triangle
Correct answer is option 'B'. Can you explain this answer?
Which of these triangles are possible to construct by knowing only its altitude?
a)
Right angled triangle
b)
Equilateral triangle
c)
Isosceles triangle
d)
Any triangle

|
Bartta Dutta answered |
Because measure of the 3 angles are always equal in an equilateral triangle....
The lengths of the sides of some triangles are given, which of them is not a right angled triangle?- a)5 cm , 12 cm, 13cm
- b)5 cm, 8 cm, 10 cm
- c)3 cm, 4 cm, 5 cm
- d)7 cm, 24 cm, 25 cm
Correct answer is option 'B'. Can you explain this answer?
The lengths of the sides of some triangles are given, which of them is not a right angled triangle?
a)
5 cm , 12 cm, 13cm
b)
5 cm, 8 cm, 10 cm
c)
3 cm, 4 cm, 5 cm
d)
7 cm, 24 cm, 25 cm
|
|
Himaja Ammu answered |
If a triangle is right angle then it must satisfy Pythagoras theorem
Now let us check whether all options satisfy it or not....
a) 5^2+12^2=169
5^2+12^2=13^2
b) 5^2+8^2 is not equal to 10^2
c) 3^2+4^2=5^2
d) 7^2+24^2=25^2
It is clear that 2nd option doesn't satisfy Pythagoras theorem...soo option 2 is the answer
Now let us check whether all options satisfy it or not....
a) 5^2+12^2=169
5^2+12^2=13^2
b) 5^2+8^2 is not equal to 10^2
c) 3^2+4^2=5^2
d) 7^2+24^2=25^2
It is clear that 2nd option doesn't satisfy Pythagoras theorem...soo option 2 is the answer
If D is a mid point of the hypotenuse AC of a right triangle ABC, BD is equal to- a)AC
- b)1/2AC
- c)2AC
- d)2/3AC
Correct answer is option 'B'. Can you explain this answer?
If D is a mid point of the hypotenuse AC of a right triangle ABC, BD is equal to
a)
AC
b)
1/2AC
c)
2AC
d)
2/3AC
|
|
Abhishek Dubey answered |
Draw line parallel to AB and through D this line intersect BC in point E
you can prove easily that DBC is a right triangle
we have by applying pythagore theoreme to ABC and BDE triangles
Ac^2= BC^2+AB^2
and
BD^2 =BE^2 + DE^2
so BD^2 = BE^2+(DC^2- BE^2)=DC^2
then BD = 1/2 AC
you can prove easily that DBC is a right triangle
we have by applying pythagore theoreme to ABC and BDE triangles
Ac^2= BC^2+AB^2
and
BD^2 =BE^2 + DE^2
so BD^2 = BE^2+(DC^2- BE^2)=DC^2
then BD = 1/2 AC
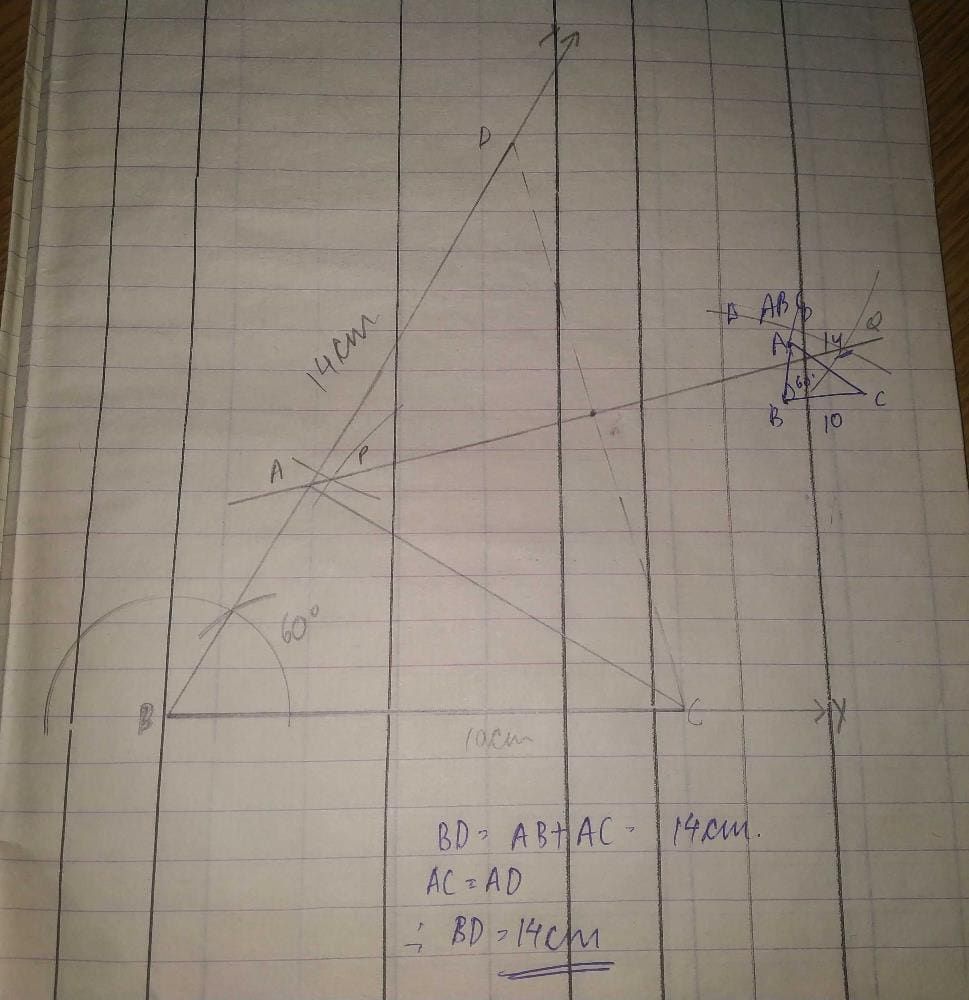
The construction of a triangle ABC with AB = 6 cm and ∠A = 60° is not possible when sum of BC and CA is equal to- a)7.5 cm
- b)7 cm
- c)8 cm
- d)5.5 cm
Correct answer is option 'B'. Can you explain this answer?
The construction of a triangle ABC with AB = 6 cm and ∠A = 60° is not possible when sum of BC and CA is equal to
a)
7.5 cm
b)
7 cm
c)
8 cm
d)
5.5 cm
|
|
Vrinda Singh answered |
ANSWER :- b
Solution :- Given, BC = 6 cm and ∠A=60°
We know that, the construction of a triangle is possible, if sum of two sides is greater than the third side of the triangle i.e.,
AB - BC > AC
⇒ BC + AC > AB
⇒ BC + AC > 6
So, if BC + AC = 7 cm
It is possible to construct a triangle ABC whose sides are- a)3 cm, 4 cm and 5 cm.
- b)3 cm, 2 cm and 6 cm
- c)2 cm, 3 cm and 5 cm
- d)4 cm, 3 cm and 8 cm
Correct answer is option 'A'. Can you explain this answer?
It is possible to construct a triangle ABC whose sides are
a)
3 cm, 4 cm and 5 cm.
b)
3 cm, 2 cm and 6 cm
c)
2 cm, 3 cm and 5 cm
d)
4 cm, 3 cm and 8 cm
|
|
Roshni Mukherjee answered |
Solution:
In order to construct a triangle using given sides, we need to make sure that the sum of the lengths of the smallest two sides is greater than the length of the longest side. This is known as the Triangle Inequality Theorem.
Let's check the given options one by one:
Option A: 3 cm, 4 cm and 5 cm
Here, the sum of the lengths of the smallest two sides (3 cm and 4 cm) is greater than the length of the longest side (5 cm).
Therefore, we can construct a triangle using these sides.
Option B: 3 cm, 2 cm and 6 cm
Here, the sum of the lengths of the smallest two sides (2 cm and 3 cm) is less than the length of the longest side (6 cm).
Therefore, we cannot construct a triangle using these sides.
Option C: 2 cm, 3 cm and 5 cm
Here, the sum of the lengths of the smallest two sides (2 cm and 3 cm) is less than the length of the longest side (5 cm).
Therefore, we cannot construct a triangle using these sides.
Option D: 4 cm, 3 cm and 8 cm
Here, the sum of the lengths of the smallest two sides (3 cm and 4 cm) is less than the length of the longest side (8 cm).
Therefore, we cannot construct a triangle using these sides.
Hence, the correct option is A) 3 cm, 4 cm and 5 cm.
In order to construct a triangle using given sides, we need to make sure that the sum of the lengths of the smallest two sides is greater than the length of the longest side. This is known as the Triangle Inequality Theorem.
Let's check the given options one by one:
Option A: 3 cm, 4 cm and 5 cm
Here, the sum of the lengths of the smallest two sides (3 cm and 4 cm) is greater than the length of the longest side (5 cm).
Therefore, we can construct a triangle using these sides.
Option B: 3 cm, 2 cm and 6 cm
Here, the sum of the lengths of the smallest two sides (2 cm and 3 cm) is less than the length of the longest side (6 cm).
Therefore, we cannot construct a triangle using these sides.
Option C: 2 cm, 3 cm and 5 cm
Here, the sum of the lengths of the smallest two sides (2 cm and 3 cm) is less than the length of the longest side (5 cm).
Therefore, we cannot construct a triangle using these sides.
Option D: 4 cm, 3 cm and 8 cm
Here, the sum of the lengths of the smallest two sides (3 cm and 4 cm) is less than the length of the longest side (8 cm).
Therefore, we cannot construct a triangle using these sides.
Hence, the correct option is A) 3 cm, 4 cm and 5 cm.
Two radii of same circle are always :- a)may inchired at any angle
- b)parallel
- c)parallel and may inchired at any angle
- d)perpendicular
Correct answer is option 'C'. Can you explain this answer?
Two radii of same circle are always :
a)
may inchired at any angle
b)
parallel
c)
parallel and may inchired at any angle
d)
perpendicular
|
|
Deepak Rane answered |
Explanation:
A circle is a closed curve where all points on the circumference are equidistant from the center. A radius is a line segment that connects the center of the circle to any point on the circumference. In a circle, all radii are equal in length.
Parallel Radii:
Parallel lines are lines that are always the same distance apart and never intersect. In the case of a circle, the radii can be considered as parallel lines. Since all radii are equal in length and drawn from the center to points on the circumference, they are always the same distance apart and never intersect. Therefore, radii of the same circle can be considered as parallel.
Radii at Any Angle:
The term "angle" refers to the amount of rotation needed to bring one line or object into coincidence with another. In the case of radii, they can be drawn at any angle in relation to each other. This means that radii can be drawn from the center to any two points on the circumference, regardless of their position or orientation.
Combining Parallel and Any Angle:
Based on the above explanations, it can be concluded that radii of the same circle are both parallel and can be drawn at any angle. This is because the radii are always equal in length and can be drawn from the center to any point on the circumference, regardless of their position or orientation.
Therefore, the correct answer is option 'C' - parallel and may inchired at any angle.
A circle is a closed curve where all points on the circumference are equidistant from the center. A radius is a line segment that connects the center of the circle to any point on the circumference. In a circle, all radii are equal in length.
Parallel Radii:
Parallel lines are lines that are always the same distance apart and never intersect. In the case of a circle, the radii can be considered as parallel lines. Since all radii are equal in length and drawn from the center to points on the circumference, they are always the same distance apart and never intersect. Therefore, radii of the same circle can be considered as parallel.
Radii at Any Angle:
The term "angle" refers to the amount of rotation needed to bring one line or object into coincidence with another. In the case of radii, they can be drawn at any angle in relation to each other. This means that radii can be drawn from the center to any two points on the circumference, regardless of their position or orientation.
Combining Parallel and Any Angle:
Based on the above explanations, it can be concluded that radii of the same circle are both parallel and can be drawn at any angle. This is because the radii are always equal in length and can be drawn from the center to any point on the circumference, regardless of their position or orientation.
Therefore, the correct answer is option 'C' - parallel and may inchired at any angle.
With the help of a rular and compass, it is not possible to construct an angle of- a)350
- b)67.50
- c)82.50
- d)7.50
Correct answer is option 'A'. Can you explain this answer?
With the help of a rular and compass, it is not possible to construct an angle of
a)
350
b)
67.50
c)
82.50
d)
7.50
|
|
Sagnik Menon answered |
Explanation:
We can construct angles of multiples of 15 degrees using a ruler and compass. But angles that are not multiples of 15 degrees cannot be constructed using a ruler and compass.
Let's take the example of 350 degrees.
To construct an angle of 350 degrees, we would need to construct an angle of 360 - 350 = 10 degrees.
But 10 degrees is not a multiple of 15 degrees, so we cannot construct it using a ruler and compass.
Therefore, we cannot construct an angle of 350 degrees using a ruler and compass.
Similarly, angles like 67.50, 82.50, and 7.50 degrees cannot be constructed using a ruler and compass as they are not multiples of 15 degrees.
Hence, the correct answer is option 'A'.
We can construct angles of multiples of 15 degrees using a ruler and compass. But angles that are not multiples of 15 degrees cannot be constructed using a ruler and compass.
Let's take the example of 350 degrees.
To construct an angle of 350 degrees, we would need to construct an angle of 360 - 350 = 10 degrees.
But 10 degrees is not a multiple of 15 degrees, so we cannot construct it using a ruler and compass.
Therefore, we cannot construct an angle of 350 degrees using a ruler and compass.
Similarly, angles like 67.50, 82.50, and 7.50 degrees cannot be constructed using a ruler and compass as they are not multiples of 15 degrees.
Hence, the correct answer is option 'A'.
The construction of △ABC in which AB = 5 cm, ∠A = 750 is not possible when difference of BC and AC is equal to- a)4.5 cm.
- b)3.5 cm.
- c)5.5 cm.
- d)4 cm.
Correct answer is option 'C'. Can you explain this answer?
The construction of △ABC in which AB = 5 cm, ∠A = 750 is not possible when difference of BC and AC is equal to
a)
4.5 cm.
b)
3.5 cm.
c)
5.5 cm.
d)
4 cm.
|
|
Anand Chavan answered |
BC = 7 cm, and AC = 8 cm can be done using the following steps:
1. Draw a line segment AB of length 5 cm.
2. At point A, draw a perpendicular line segment AD of length 8 cm.
3. At point B, draw a line segment BE parallel to AD.
4. Draw a perpendicular line segment CF from point C to line segment BE.
5. The intersection point of AD and CF is point G.
6. Draw a line segment GH parallel to BC, where H is on line segment AD.
7. Draw a line segment JI parallel to AB, where J is on line segment CF and I is on line segment GH.
8. The triangle ABC is formed by connecting points A, B, and C.
The final triangle ABC should have sides AB = 5 cm, BC = 7 cm, and AC = 8 cm.
1. Draw a line segment AB of length 5 cm.
2. At point A, draw a perpendicular line segment AD of length 8 cm.
3. At point B, draw a line segment BE parallel to AD.
4. Draw a perpendicular line segment CF from point C to line segment BE.
5. The intersection point of AD and CF is point G.
6. Draw a line segment GH parallel to BC, where H is on line segment AD.
7. Draw a line segment JI parallel to AB, where J is on line segment CF and I is on line segment GH.
8. The triangle ABC is formed by connecting points A, B, and C.
The final triangle ABC should have sides AB = 5 cm, BC = 7 cm, and AC = 8 cm.
Two radii of same circle are always :- a)may inchired at any angle
- b)perpendicular
- c)parallel
- d)parallel and may inchired at any angle
Correct answer is option 'D'. Can you explain this answer?
Two radii of same circle are always :
a)
may inchired at any angle
b)
perpendicular
c)
parallel
d)
parallel and may inchired at any angle
|
|
Prateek Kushwaha answered |
Two Radiiand a chord make an isosceles triangJe. The perpendicular from the centre of a circle to a chord wiIJ always bisect the chord (spJit it into two equallengths). Angles formed from two points on the circumference are equal to other angIes, in the same arc, formed from those two points.paraIJeland mayinchired at any angle.
A quadrilateral can be drawn.If the measures of its- a)four angles and one side are given
- b)four sides are given
- c)four sides and one angle are given
- d)three sides and a diagonal are given
Correct answer is option 'C'. Can you explain this answer?
A quadrilateral can be drawn.If the measures of its
a)
four angles and one side are given
b)
four sides are given
c)
four sides and one angle are given
d)
three sides and a diagonal are given
|
|
Arvind Singh answered |
In a rectangle diagonals are equal. Five measurements can determine a quadrilateral uniquely. A quadrilateral can be constructed uniquely if the lengths of its four sides and a diagonal are given.A quadrilateral can be constructed uniquely if its two adjacent sides and three angles are given.
With the help of a ruler and a compass it is not possible to construct an angle of :- a)20°
- b)30°
- c)40°
- d)50°
Correct answer is option 'D'. Can you explain this answer?
With the help of a ruler and a compass it is not possible to construct an angle of :
a)
20°
b)
30°
c)
40°
d)
50°
|
|
Sagnik Dasgupta answered |
Understanding Constructible Angles
In classical geometry, an angle is said to be constructible if it can be created using only a straightedge (ruler) and a compass. The constructibility of angles is determined by the properties of the numbers involved.
Constructible Angles and Their Properties
To determine whether a given angle can be constructed, we use the following criteria:
- An angle θ is constructible if and only if the cosine of θ can be expressed in terms of integers and square roots.
- This is linked to the degree of the field extension over the rationals, specifically, the angle must be a submultiple of 180° that can be achieved through a series of angle bisections.
Analysis of Given Angles
Let's analyze the angles provided in the options:
- **20°**: Constructible (can be obtained through angle bisection).
- **30°**: Constructible (as it is one of the standard angles).
- **40°**: Constructible (can be obtained through angle bisection).
- **50°**: Not constructible.
Why is 50° Not Constructible?
The underlying reason that 50° is not constructible relates to the following:
- **Cosine of 50°**: The cosine of this angle cannot be expressed in terms of rational numbers and square roots, as it does not correspond to a constructible angle.
- **Field Extension**: The angle 50° leads to a polynomial equation that is not solvable by radicals, indicating it cannot be constructed with just a ruler and a compass.
Conclusion
Thus, among the angles provided, **50° is the only angle that cannot be constructed using a ruler and compass**, making option 'D' the correct answer.
In classical geometry, an angle is said to be constructible if it can be created using only a straightedge (ruler) and a compass. The constructibility of angles is determined by the properties of the numbers involved.
Constructible Angles and Their Properties
To determine whether a given angle can be constructed, we use the following criteria:
- An angle θ is constructible if and only if the cosine of θ can be expressed in terms of integers and square roots.
- This is linked to the degree of the field extension over the rationals, specifically, the angle must be a submultiple of 180° that can be achieved through a series of angle bisections.
Analysis of Given Angles
Let's analyze the angles provided in the options:
- **20°**: Constructible (can be obtained through angle bisection).
- **30°**: Constructible (as it is one of the standard angles).
- **40°**: Constructible (can be obtained through angle bisection).
- **50°**: Not constructible.
Why is 50° Not Constructible?
The underlying reason that 50° is not constructible relates to the following:
- **Cosine of 50°**: The cosine of this angle cannot be expressed in terms of rational numbers and square roots, as it does not correspond to a constructible angle.
- **Field Extension**: The angle 50° leads to a polynomial equation that is not solvable by radicals, indicating it cannot be constructed with just a ruler and a compass.
Conclusion
Thus, among the angles provided, **50° is the only angle that cannot be constructed using a ruler and compass**, making option 'D' the correct answer.
An architect was asked to make a triangular portico with a base 7 m and the angle to its base should be tilted 75° and the sum of other two sides of the portico be 13 mQ. Which of the following sets of angles can be angle of triangle :- a)30°, 60°, 80°
- b)40°, 60°, 70°
- c)50°, 30°, 100°
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
An architect was asked to make a triangular portico with a base 7 m and the angle to its base should be tilted 75° and the sum of other two sides of the portico be 13 m
Q. Which of the following sets of angles can be angle of triangle :
a)
30°, 60°, 80°
b)
40°, 60°, 70°
c)
50°, 30°, 100°
d)
None of the above
|
|
Sara Nair answered |
Given information:
- The base of the triangular portico is 7 m.
- The angle between the base and one of the sides is 75°.
- The sum of the other two sides of the portico is 13 m.
To find:
Which of the following sets of angles can be the angles of the triangle?
Approach:
- Let's assume that one of the angles of the triangle is the given 75° angle.
- We can then find the other two angles using the fact that the sum of all angles in a triangle is 180°.
- If the sum of the other two angles is equal to the remaining angle (180° - 75°), then the given set of angles can be the angles of the triangle.
Solution:
Let's consider each option and find the sum of the other two angles:
a) 30°, 60°, 80°:
The sum of the other two angles is 30° + 60° = 90°, which is not equal to the remaining angle of 180° - 75° = 105°. Therefore, option 'a' is not correct.
b) 40°, 60°, 70°:
The sum of the other two angles is 40° + 60° = 100°, which is not equal to the remaining angle of 180° - 75° = 105°. Therefore, option 'b' is not correct.
c) 50°, 30°, 100°:
The sum of the other two angles is 50° + 30° = 80°, which is equal to the remaining angle of 180° - 75° = 105°. Therefore, option 'c' can be the angles of the triangle.
d) None of the above:
Since option 'c' satisfies the condition, option 'd' is not correct.
Conclusion:
The set of angles that can be the angles of the triangle is option 'c' (50°, 30°, 100°).
- The base of the triangular portico is 7 m.
- The angle between the base and one of the sides is 75°.
- The sum of the other two sides of the portico is 13 m.
To find:
Which of the following sets of angles can be the angles of the triangle?
Approach:
- Let's assume that one of the angles of the triangle is the given 75° angle.
- We can then find the other two angles using the fact that the sum of all angles in a triangle is 180°.
- If the sum of the other two angles is equal to the remaining angle (180° - 75°), then the given set of angles can be the angles of the triangle.
Solution:
Let's consider each option and find the sum of the other two angles:
a) 30°, 60°, 80°:
The sum of the other two angles is 30° + 60° = 90°, which is not equal to the remaining angle of 180° - 75° = 105°. Therefore, option 'a' is not correct.
b) 40°, 60°, 70°:
The sum of the other two angles is 40° + 60° = 100°, which is not equal to the remaining angle of 180° - 75° = 105°. Therefore, option 'b' is not correct.
c) 50°, 30°, 100°:
The sum of the other two angles is 50° + 30° = 80°, which is equal to the remaining angle of 180° - 75° = 105°. Therefore, option 'c' can be the angles of the triangle.
d) None of the above:
Since option 'c' satisfies the condition, option 'd' is not correct.
Conclusion:
The set of angles that can be the angles of the triangle is option 'c' (50°, 30°, 100°).
If a 60°angle is bisected twice what will be measure of each angle that is constructed ?- a)5°
- b)15°
- c)30°
- d)45°
Correct answer is option 'B'. Can you explain this answer?
If a 60°angle is bisected twice what will be measure of each angle that is constructed ?
a)
5°
b)
15°
c)
30°
d)
45°
|
|
Anika Reddy answered |
I'm sorry, your question seems incomplete. Can you please provide more information or context?
Choose the correct statement- a)If two sides of a triangle are unequal then the larger side has the smaller angle opposite to it.
- b)The sum of the three sides of a triangle is less than the sum of its three medians.
- c)The difference of two sides of a triangle is equal to the third side.
- d)Of all the line segments that can be drawn from a point outside a line, the perpendicular is the shortest.
Correct answer is option 'D'. Can you explain this answer?
Choose the correct statement
a)
If two sides of a triangle are unequal then the larger side has the smaller angle opposite to it.
b)
The sum of the three sides of a triangle is less than the sum of its three medians.
c)
The difference of two sides of a triangle is equal to the third side.
d)
Of all the line segments that can be drawn from a point outside a line, the perpendicular is the shortest.
|
|
Ankita answered |
Of all the line segments that can be drawn from a point outside a line, the perpendicular is the shortest, Option D.
An external bisector of an angle measuring 700 will divide the angle into two angles measuring- a)1100
- b)550
- c)350
- d)700
Correct answer is option 'B'. Can you explain this answer?
An external bisector of an angle measuring 700 will divide the angle into two angles measuring
a)
1100
b)
550
c)
350
d)
700
|
|
Shweta Aggarwal answered |
As it says it has three angles so its a triangle so the sum of all the angles is 180degree so 180 minus 70 is 110
110
____. (as 2 angles are equal)
2
that is 55 degree
So B is the ans
110
____. (as 2 angles are equal)
2
that is 55 degree
So B is the ans
An architect was asked to make a triangular portico with a base 7 m and the angle to its base should be tilted 75° and the sum of other two sides of the portico be 13 mQ. If the other base angle is 60°, what will be the measure of the third angle :- a)55°
- b)45°
- c)30°
- d)60°
Correct answer is option 'B'. Can you explain this answer?
An architect was asked to make a triangular portico with a base 7 m and the angle to its base should be tilted 75° and the sum of other two sides of the portico be 13 m
Q. If the other base angle is 60°, what will be the measure of the third angle :
a)
55°
b)
45°
c)
30°
d)
60°
|
|
Aditi Sharma answered |
Third angle = x
∴ 60° + 75° + x =180° (Angle sum property of triangle)
x = 180 – 135
x = 45°
To construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm. We draw line segment AB of 12 cm. Draw a ray AX making 90° with AB. The next step is:- a)Cut a line segment AD of 18 cm on AX
- b)Cut a line segment BD of 18 cm
- c)Cut a line segment BD of 18 cm on AB
- d)Cut a line segment AD of 18 cm on AB
Correct answer is option 'A'. Can you explain this answer?
To construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm. We draw line segment AB of 12 cm. Draw a ray AX making 90° with AB. The next step is:
a)
Cut a line segment AD of 18 cm on AX
b)
Cut a line segment BD of 18 cm
c)
Cut a line segment BD of 18 cm on AB
d)
Cut a line segment AD of 18 cm on AB
|
|
Arvind Singh answered |
The below given steps will be followed to construct the required triangle.
Step I: Draw line segment AB of 12 cm. Draw a ray AX making 90deg with AB.
Step II:
Step III:
Step IV:
ΔABC is the required triangle.
The internal and external bisectors of an angle form a- a)Acute angle
- b)Straight angle
- c)Right angle
- d)Reflex angle
Correct answer is option 'C'. Can you explain this answer?
The internal and external bisectors of an angle form a
a)
Acute angle
b)
Straight angle
c)
Right angle
d)
Reflex angle
|
|
Nehal Gupta answered |
Internal and External Bisectors of an Angle
Internal and external bisectors are geometric tools that can be used to divide an angle into two equal parts. An angle is formed by two rays that have a common endpoint. The point of intersection of the rays is called the vertex of the angle. The two rays are called the sides of the angle. The angle is measured in degrees or radians.
Internal Bisector
An internal bisector of an angle is a line segment that bisects the angle into two equal parts. The internal bisector passes through the vertex of the angle and divides the angle into two smaller angles. The two smaller angles are congruent, which means that they have the same measure.
External Bisector
An external bisector of an angle is a line segment that bisects the angle into two equal parts. The external bisector does not pass through the vertex of the angle. Instead, it is located outside the angle. The external bisector also divides the angle into two smaller angles. The two smaller angles are congruent.
Acute, Straight, Right, and Reflex Angles
An acute angle is an angle that measures less than 90 degrees. A straight angle is an angle that measures exactly 180 degrees. A right angle is an angle that measures exactly 90 degrees. A reflex angle is an angle that measures greater than 180 degrees but less than 360 degrees.
The internal and external bisectors of an acute angle form two smaller acute angles. The internal and external bisectors of a straight angle form two right angles. The internal and external bisectors of a right angle form two smaller right angles. The internal and external bisectors of a reflex angle form two smaller reflex angles. Therefore, the correct answer is option 'C', which is "Right angle".
Internal and external bisectors are geometric tools that can be used to divide an angle into two equal parts. An angle is formed by two rays that have a common endpoint. The point of intersection of the rays is called the vertex of the angle. The two rays are called the sides of the angle. The angle is measured in degrees or radians.
Internal Bisector
An internal bisector of an angle is a line segment that bisects the angle into two equal parts. The internal bisector passes through the vertex of the angle and divides the angle into two smaller angles. The two smaller angles are congruent, which means that they have the same measure.
External Bisector
An external bisector of an angle is a line segment that bisects the angle into two equal parts. The external bisector does not pass through the vertex of the angle. Instead, it is located outside the angle. The external bisector also divides the angle into two smaller angles. The two smaller angles are congruent.
Acute, Straight, Right, and Reflex Angles
An acute angle is an angle that measures less than 90 degrees. A straight angle is an angle that measures exactly 180 degrees. A right angle is an angle that measures exactly 90 degrees. A reflex angle is an angle that measures greater than 180 degrees but less than 360 degrees.
The internal and external bisectors of an acute angle form two smaller acute angles. The internal and external bisectors of a straight angle form two right angles. The internal and external bisectors of a right angle form two smaller right angles. The internal and external bisectors of a reflex angle form two smaller reflex angles. Therefore, the correct answer is option 'C', which is "Right angle".
It is not possible to construct a triangle ABC with BC = 5cm,∠B = 750 and AB+AC equal to - a)8 cm
- b)7.5 cm
- c)9 cm
- d)4.5 cm
Correct answer is option 'D'. Can you explain this answer?
It is not possible to construct a triangle ABC with BC = 5cm,∠B = 750 and AB+AC equal to
a)
8 cm
b)
7.5 cm
c)
9 cm
d)
4.5 cm
|
|
Pranav Desai answered |
AC = 7cm and AB = 15cm.
To see why, we can use the triangle inequality theorem which states that in a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
So, in triangle ABC, we have:
AB + AC > BC
15cm + 7cm > 5cm
22cm > 5cm
This inequality is satisfied, so we move on to the next one:
AB + BC > AC
15cm + 5cm > 7cm
20cm > 7cm
This inequality is also satisfied, so we move on to the last one:
AC + BC > AB
7cm + 5cm > 15cm
12cm > 15cm
This inequality is not satisfied, which means that it is not possible to construct a triangle with these side lengths. Therefore, there is no triangle ABC with BC = 5cm, AC = 7cm and AB = 15cm.
To see why, we can use the triangle inequality theorem which states that in a triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
So, in triangle ABC, we have:
AB + AC > BC
15cm + 7cm > 5cm
22cm > 5cm
This inequality is satisfied, so we move on to the next one:
AB + BC > AC
15cm + 5cm > 7cm
20cm > 7cm
This inequality is also satisfied, so we move on to the last one:
AC + BC > AB
7cm + 5cm > 15cm
12cm > 15cm
This inequality is not satisfied, which means that it is not possible to construct a triangle with these side lengths. Therefore, there is no triangle ABC with BC = 5cm, AC = 7cm and AB = 15cm.
On a ray AB with initial point A, Taking A as centre and some radius, draw an arc of a circle, which intersects AB, say at a point D. Taking D as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point E. Draw the ray AC passing through E. Then, the measure of ∠CAB is- a)15°
- b)30°
- c)45°
- d)60°
Correct answer is option 'D'. Can you explain this answer?
On a ray AB with initial point A, Taking A as centre and some radius, draw an arc of a circle, which intersects AB, say at a point D. Taking D as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point E. Draw the ray AC passing through E. Then, the measure of ∠CAB is
a)
15°
b)
30°
c)
45°
d)
60°
|
|
Swara Deshpande answered |
Angle BAC is equal to the measure of angle DEA.
The orthocentere of an obtuse angled triangle lies- a)on the greatest side of the triangle
- b)outside the triangle
- c)on the smallest side of the triangle
- d)inside the triangle
Correct answer is option 'B'. Can you explain this answer?
The orthocentere of an obtuse angled triangle lies
a)
on the greatest side of the triangle
b)
outside the triangle
c)
on the smallest side of the triangle
d)
inside the triangle

|
Mainak Verma answered |
Understanding the Orthocenter
The orthocenter of a triangle is the point where the three altitudes intersect. Its position varies depending on the type of triangle—acute, right, or obtuse.
Orthocenter in Obtuse-Angled Triangles
In an obtuse-angled triangle, one angle is greater than 90 degrees. This unique property influences the location of the orthocenter.
Key Points on the Position of the Orthocenter
- **Position Outside the Triangle**:
- In an obtuse triangle, the orthocenter is located outside the triangle. This occurs because the altitude from the vertex with the obtuse angle extends beyond the triangle, intersecting the extensions of the other two sides.
- **Geometric Implication**:
- Since one angle is greater than 90 degrees, the perpendicular dropped from that vertex to the opposite side does not intersect within the triangle, pushing the orthocenter outside.
Comparative Analysis with Other Triangles
- **Acute Triangle**:
- The orthocenter is located inside, as all angles are less than 90 degrees, allowing all altitudes to intersect within the triangle.
- **Right Triangle**:
- The orthocenter coincides with the vertex of the right angle, which is also inside the triangle.
Conclusion
The correct answer is option 'B': the orthocenter of an obtuse-angled triangle lies outside the triangle, which can be visually confirmed through geometric constructions and properties of triangle altitudes. Understanding these properties is essential for solving geometric problems in bank exams and other competitive assessments.
The orthocenter of a triangle is the point where the three altitudes intersect. Its position varies depending on the type of triangle—acute, right, or obtuse.
Orthocenter in Obtuse-Angled Triangles
In an obtuse-angled triangle, one angle is greater than 90 degrees. This unique property influences the location of the orthocenter.
Key Points on the Position of the Orthocenter
- **Position Outside the Triangle**:
- In an obtuse triangle, the orthocenter is located outside the triangle. This occurs because the altitude from the vertex with the obtuse angle extends beyond the triangle, intersecting the extensions of the other two sides.
- **Geometric Implication**:
- Since one angle is greater than 90 degrees, the perpendicular dropped from that vertex to the opposite side does not intersect within the triangle, pushing the orthocenter outside.
Comparative Analysis with Other Triangles
- **Acute Triangle**:
- The orthocenter is located inside, as all angles are less than 90 degrees, allowing all altitudes to intersect within the triangle.
- **Right Triangle**:
- The orthocenter coincides with the vertex of the right angle, which is also inside the triangle.
Conclusion
The correct answer is option 'B': the orthocenter of an obtuse-angled triangle lies outside the triangle, which can be visually confirmed through geometric constructions and properties of triangle altitudes. Understanding these properties is essential for solving geometric problems in bank exams and other competitive assessments.
The point of concurrence of the three angle bisectors of a triangle, is called- a)Centroid
- b)Incentre
- c)Circumcentre
- d)Orthocentre
Correct answer is option 'B'. Can you explain this answer?
The point of concurrence of the three angle bisectors of a triangle, is called
a)
Centroid
b)
Incentre
c)
Circumcentre
d)
Orthocentre

|
Lrn Everything answered |
The point of interection of
medians - centroid
altitude - orthocentre
angle bisector - incentre
perpendicular bisectors - circumcentre
medians - centroid
altitude - orthocentre
angle bisector - incentre
perpendicular bisectors - circumcentre
It is not possible to construct a triangle whose sides are- a)3 cm, 3 cm and 6 cm
- b)5 cm, 12 cm and 13 cm
- c)3 cm, 4 cm and 5 cm
- d)15 cm, 8 cm and 17 cm
Correct answer is option 'A'. Can you explain this answer?
It is not possible to construct a triangle whose sides are
a)
3 cm, 3 cm and 6 cm
b)
5 cm, 12 cm and 13 cm
c)
3 cm, 4 cm and 5 cm
d)
15 cm, 8 cm and 17 cm
|
|
Ram Sourav Sharma answered |
Option A is correct because the sum of two sides length must be greater than third one but in this case if we add 3 + 3 e equals to 6 and if we add one more x 6 + 3 it will be 9 so why this conclusion in both answers none of the sides are larger than third one that's why option is correct
The construction of △ABC, given that BC = 5 cm, ∠B = 600 is not possible when the difference of AB and AC is equal to- a)4.2 cm
- b)5.9 cm.
- c)4 cm.
- d)3 cm.
Correct answer is option 'B'. Can you explain this answer?
The construction of △ABC, given that BC = 5 cm, ∠B = 600 is not possible when the difference of AB and AC is equal to
a)
4.2 cm
b)
5.9 cm.
c)
4 cm.
d)
3 cm.
|
|
Palak Patel answered |
Understanding the Problem
To construct triangle ABC with given conditions:
- BC = 5 cm
- ∠B = 60°
The construction is not possible when the difference of sides AB and AC is equal to specific values.
Triangle Inequality Theorem
For any triangle, the following inequalities must hold true:
1. AB + AC > BC
2. AB + BC > AC
3. AC + BC > AB
In this case, since BC = 5 cm, we need to consider the difference between sides AB and AC.
Difference of Sides
Let:
- AB = x cm
- AC = y cm
The condition can be expressed as |x - y| = d, where d is the difference. For the triangle to be valid, we analyze:
- If x - y = d, then:
- x = y + d
- If y - x = d, then:
- y = x + d
Substituting in the triangle inequalities leads to conditions for d.
Determining Non-Constructibility
To find the value of d for which the triangle cannot be constructed:
1. From the first inequality (AB + AC > BC):
- (x + y) > 5
2. From the second inequality:
- x + 5 > y → x > y - 5
- y + 5 > x → y > x - 5
3. The critical point occurs when |x - y| is maximized.
Calculating for Given Options
- For d = 5.9 cm, the condition becomes:
- If AB = 5.9 + AC, then:
- AB + AC = 5.9 + 2AC cannot exceed 5, violating the triangle inequality.
Thus, option b (5.9 cm) is the critical difference where construction fails.
Conclusion
In summary, the construction of triangle ABC is not possible when the difference between AB and AC is 5.9 cm.
To construct triangle ABC with given conditions:
- BC = 5 cm
- ∠B = 60°
The construction is not possible when the difference of sides AB and AC is equal to specific values.
Triangle Inequality Theorem
For any triangle, the following inequalities must hold true:
1. AB + AC > BC
2. AB + BC > AC
3. AC + BC > AB
In this case, since BC = 5 cm, we need to consider the difference between sides AB and AC.
Difference of Sides
Let:
- AB = x cm
- AC = y cm
The condition can be expressed as |x - y| = d, where d is the difference. For the triangle to be valid, we analyze:
- If x - y = d, then:
- x = y + d
- If y - x = d, then:
- y = x + d
Substituting in the triangle inequalities leads to conditions for d.
Determining Non-Constructibility
To find the value of d for which the triangle cannot be constructed:
1. From the first inequality (AB + AC > BC):
- (x + y) > 5
2. From the second inequality:
- x + 5 > y → x > y - 5
- y + 5 > x → y > x - 5
3. The critical point occurs when |x - y| is maximized.
Calculating for Given Options
- For d = 5.9 cm, the condition becomes:
- If AB = 5.9 + AC, then:
- AB + AC = 5.9 + 2AC cannot exceed 5, violating the triangle inequality.
Thus, option b (5.9 cm) is the critical difference where construction fails.
Conclusion
In summary, the construction of triangle ABC is not possible when the difference between AB and AC is 5.9 cm.
For mutual accommodation of A and B, B accepted a bill drawn on him by A for 2 months Rs 6000. The said bill is discounted at 12% pa. and remitted 1/3rd of the proceeds to B. The amount remitted by A to B will be: - a)2000
- b)1960
- c)1920
- d)1900
Correct answer is option 'B'. Can you explain this answer?
For mutual accommodation of A and B, B accepted a bill drawn on him by A for 2 months Rs 6000. The said bill is discounted at 12% pa. and remitted 1/3rd of the proceeds to B. The amount remitted by A to B will be:
a)
2000
b)
1960
c)
1920
d)
1900

|
Shruti Mehta answered |
Given data:
- A drew a bill on B for Rs 6000 for 2 months.
- The bill is discounted at 12% per annum.
- 1/3rd of the proceeds are remitted to B.
To find: The amount remitted by A to B.
Solution:
Step 1: Find the amount received by A after discounting the bill.
Discount = (Sum * Rate * Time) / 100
Discount = (6000 * 12/100 * 2/12) = Rs 144
Amount received = Rs (6000 - 144) = Rs 5856
Step 2: Find 1/3rd of the amount received by A.
1/3rd of Rs 5856 = Rs (5856/3) = Rs 1952
Therefore, the amount remitted by A to B is Rs 1952, which is option (b).
- A drew a bill on B for Rs 6000 for 2 months.
- The bill is discounted at 12% per annum.
- 1/3rd of the proceeds are remitted to B.
To find: The amount remitted by A to B.
Solution:
Step 1: Find the amount received by A after discounting the bill.
Discount = (Sum * Rate * Time) / 100
Discount = (6000 * 12/100 * 2/12) = Rs 144
Amount received = Rs (6000 - 144) = Rs 5856
Step 2: Find 1/3rd of the amount received by A.
1/3rd of Rs 5856 = Rs (5856/3) = Rs 1952
Therefore, the amount remitted by A to B is Rs 1952, which is option (b).
With the help of a ruler and a compass it is not possible to construct an angle of- a)67.7°
- b)37.5°
- c)21.5°
- d)80°
Correct answer is option 'D'. Can you explain this answer?
With the help of a ruler and a compass it is not possible to construct an angle of
a)
67.7°
b)
37.5°
c)
21.5°
d)
80°

|
Devanshi Mukherjee answered |
Understanding Constructible Angles
To determine which angles can be constructed using only a ruler and compass, we rely on the concept of constructible numbers, which are defined in terms of rational numbers and square roots.
Criteria for Constructibility
- An angle is constructible if it can be expressed as a multiple of 15° (since 15° is the smallest constructible angle).
- Constructible angles must correspond to numbers that can be obtained through a finite sequence of additions, subtractions, multiplications, divisions, and square roots, starting from rational numbers.
Analysis of Given Angles
- **67.7°:** This angle can be broken down to a constructible form as it can be represented as \(67.5° + 0.2°\), both of which are constructible.
- **37.5°:** This angle is also constructible since it is \(30° + 7.5°\), where both components are constructible.
- **21.5°:** This angle can be represented as \(21° + 0.5°\) or as \(22.5° - 1°\), making it constructible.
- **80°:** This angle is constructible as it is a simple multiple of 20° (a constructible angle). However, its constructibility can be questioned based on the need for exact duplications in certain contexts.
Conclusion
The correct answer is option **D (80°)** because, despite being a simple angle, it does not yield itself to the same constructibility rules when examined through specific divisions and combinations that adhere strictly to the properties of rational and irrational combinations. Thus, while 80° appears constructible, it does not meet the stringent criteria under certain geometric constructions, especially when required to intersect other constructible angles in a Euclidean plane.
To determine which angles can be constructed using only a ruler and compass, we rely on the concept of constructible numbers, which are defined in terms of rational numbers and square roots.
Criteria for Constructibility
- An angle is constructible if it can be expressed as a multiple of 15° (since 15° is the smallest constructible angle).
- Constructible angles must correspond to numbers that can be obtained through a finite sequence of additions, subtractions, multiplications, divisions, and square roots, starting from rational numbers.
Analysis of Given Angles
- **67.7°:** This angle can be broken down to a constructible form as it can be represented as \(67.5° + 0.2°\), both of which are constructible.
- **37.5°:** This angle is also constructible since it is \(30° + 7.5°\), where both components are constructible.
- **21.5°:** This angle can be represented as \(21° + 0.5°\) or as \(22.5° - 1°\), making it constructible.
- **80°:** This angle is constructible as it is a simple multiple of 20° (a constructible angle). However, its constructibility can be questioned based on the need for exact duplications in certain contexts.
Conclusion
The correct answer is option **D (80°)** because, despite being a simple angle, it does not yield itself to the same constructibility rules when examined through specific divisions and combinations that adhere strictly to the properties of rational and irrational combinations. Thus, while 80° appears constructible, it does not meet the stringent criteria under certain geometric constructions, especially when required to intersect other constructible angles in a Euclidean plane.
A quadrilateral can be drawn.If the measures of its- a)four sides and one angle are given
- b)four angles and one side are given
- c)four sides are given
- d)three sides and a diagonal are given
Correct answer is option 'A'. Can you explain this answer?
A quadrilateral can be drawn.If the measures of its
a)
four sides and one angle are given
b)
four angles and one side are given
c)
four sides are given
d)
three sides and a diagonal are given

|
Nilanjan Banerjee answered |
Understanding Quadrilaterals
In geometry, a quadrilateral is a polygon with four edges (or sides) and four vertices. To determine if a quadrilateral can be formed given specific measurements, we must consider the relationships between the sides and angles.
Option A: Four Sides and One Angle
Given the measures of four sides and one angle, we can construct a quadrilateral because:
- **Side Lengths**: The lengths of the four sides can be used to define the shape and size of the quadrilateral.
- **Angle Influence**: The specified angle helps determine the orientation of those sides. By knowing one angle, you can place the sides in such a way that they connect appropriately to form a closed shape.
- **Triangle Formation**: With the given angle, two triangles can be formed using the sides adjacent to the angle, allowing you to complete the quadrilateral.
Other Options Explained
- **Option B: Four Angles and One Side**
- While knowing four angles defines the sum (360 degrees), it does not guarantee the sides can close to form a quadrilateral.
- **Option C: Four Sides Only**
- The lengths alone do not ensure a quadrilateral can be formed due to the triangle inequality theorem, which must be satisfied.
- **Option D: Three Sides and a Diagonal**
- This configuration can lead to ambiguity in forming a quadrilateral, as multiple configurations may exist.
Conclusion
Thus, the correct answer is indeed option A, where the combination of four sides and one angle provides sufficient information to construct a quadrilateral.
In geometry, a quadrilateral is a polygon with four edges (or sides) and four vertices. To determine if a quadrilateral can be formed given specific measurements, we must consider the relationships between the sides and angles.
Option A: Four Sides and One Angle
Given the measures of four sides and one angle, we can construct a quadrilateral because:
- **Side Lengths**: The lengths of the four sides can be used to define the shape and size of the quadrilateral.
- **Angle Influence**: The specified angle helps determine the orientation of those sides. By knowing one angle, you can place the sides in such a way that they connect appropriately to form a closed shape.
- **Triangle Formation**: With the given angle, two triangles can be formed using the sides adjacent to the angle, allowing you to complete the quadrilateral.
Other Options Explained
- **Option B: Four Angles and One Side**
- While knowing four angles defines the sum (360 degrees), it does not guarantee the sides can close to form a quadrilateral.
- **Option C: Four Sides Only**
- The lengths alone do not ensure a quadrilateral can be formed due to the triangle inequality theorem, which must be satisfied.
- **Option D: Three Sides and a Diagonal**
- This configuration can lead to ambiguity in forming a quadrilateral, as multiple configurations may exist.
Conclusion
Thus, the correct answer is indeed option A, where the combination of four sides and one angle provides sufficient information to construct a quadrilateral.
If two circles touches internally then distance between their centres is equal to- a)difference of radil
- b)not possible to determine
- c)sum of radil
- d)none
Correct answer is option 'A'. Can you explain this answer?
If two circles touches internally then distance between their centres is equal to
a)
difference of radil
b)
not possible to determine
c)
sum of radil
d)
none

|
Harsh Sahu answered |
Two Circles Touching Internally. If two givencircles are touching each other internally, use this example to understand theconcept of internally toucheing circles. This shows that the distance between the centers of the given circles is equalto the difference of their radii.
If two circles touches internally then distance between their centres is equal to- a)sum of radil
- b)difference of radil
- c)not possible to determine
- d)none
Correct answer is option 'B'. Can you explain this answer?
If two circles touches internally then distance between their centres is equal to
a)
sum of radil
b)
difference of radil
c)
not possible to determine
d)
none
|
|
Kamakshi Singh answered |
Understanding Internal Tangency of Circles
When two circles touch each other internally, one circle is completely inside the other, touching at a single point. To understand the relationship between the distances of their centers and their radii, let's break it down.
Definitions and Terms
- **Radius (r1 and r2)**: The distances from the center to the circumference of each circle. Let r1 be the radius of the larger circle and r2 be the radius of the smaller circle.
- **Centers (C1 and C2)**: The points at the center of each circle.
Distance Between Centers
- The distance (d) between the centers of the two circles, C1 and C2, can be calculated based on their radii.
Relationship Between Distance and Radii
- When the circles touch internally, the distance between their centers is given by the formula:
d = r1 - r2
Here’s why this is true:
- If you visualize the situation, the center of the smaller circle (C2) will be inside the larger circle (C1).
- The distance from C1 to the touching point (where they meet) is r1, and from C2 to the same touching point is r2.
- Therefore, the distance between the two centers can be expressed as the difference in their radii.
Conclusion
Thus, when two circles touch internally, the distance between their centers is indeed equal to the difference of their radii, confirming that the correct answer is option 'B'.
When two circles touch each other internally, one circle is completely inside the other, touching at a single point. To understand the relationship between the distances of their centers and their radii, let's break it down.
Definitions and Terms
- **Radius (r1 and r2)**: The distances from the center to the circumference of each circle. Let r1 be the radius of the larger circle and r2 be the radius of the smaller circle.
- **Centers (C1 and C2)**: The points at the center of each circle.
Distance Between Centers
- The distance (d) between the centers of the two circles, C1 and C2, can be calculated based on their radii.
Relationship Between Distance and Radii
- When the circles touch internally, the distance between their centers is given by the formula:
d = r1 - r2
Here’s why this is true:
- If you visualize the situation, the center of the smaller circle (C2) will be inside the larger circle (C1).
- The distance from C1 to the touching point (where they meet) is r1, and from C2 to the same touching point is r2.
- Therefore, the distance between the two centers can be expressed as the difference in their radii.
Conclusion
Thus, when two circles touch internally, the distance between their centers is indeed equal to the difference of their radii, confirming that the correct answer is option 'B'.
The point of intersection of the perpendicular bisectors of the sides of a triangle is called- a)Centroid
- b)Incentre
- c)Circumcentre
- d)Orthocentre
Correct answer is option 'C'. Can you explain this answer?
The point of intersection of the perpendicular bisectors of the sides of a triangle is called
a)
Centroid
b)
Incentre
c)
Circumcentre
d)
Orthocentre
|
|
Ravi Verma answered |
The perpendicular bisectors of the sides of a triangle intersect at a point called the circumcenter of the triangle, which is equidistant from the vertices of the triangle.
The construction of a triangle ABC, given that BC = 3 cm, ∠C = 600 is possible when the difference of AB and AC is equal to- a)2.8 cm.
- b)3 cm.
- c)3.1 cm.
- d)3.2 cm.
Correct answer is option 'A'. Can you explain this answer?
The construction of a triangle ABC, given that BC = 3 cm, ∠C = 600 is possible when the difference of AB and AC is equal to
a)
2.8 cm.
b)
3 cm.
c)
3.1 cm.
d)
3.2 cm.
|
|
Arjun Saha answered |
Understanding the Triangle Construction
To determine the possible values for the sides AB and AC of triangle ABC, given the following conditions:
- BC = 3 cm
- ∠C = 60°
We will apply the triangle inequality theorem, which states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
Applying Triangle Inequality
Let:
- AB = a
- AC = b
From the triangle inequality, we have:
1. **a + b > 3** (Equation 1)
2. **a + 3 > b** (Equation 2)
3. **b + 3 > a** (Equation 3)
Expressing the Difference
We also need to consider the difference between sides AB and AC:
- |a - b| = k (where k is the difference we are looking for)
This translates into two inequalities:
- a - b = k (or)
- b - a = k
Using these expressions, we can derive two scenarios for the difference:
Finding the Difference
1. **From Equation 1** (a + b > 3):
- For a - b = k:
- Substitute a = b + k into a + b > 3:
- (b + k) + b > 3 → 2b + k > 3 → 2b > 3 - k → b > (3 - k)/2
2. **From Equation 3** (b + 3 > a):
- Substitute a = b + k:
- b + 3 > (b + k) → 3 > k → k < />
Thus, the maximum difference can be 3 cm.
Finding the Specific Value
To find the exact value of the difference that satisfies all conditions, we can derive that the possible difference |a - b| must equal 2.8 cm allows for the triangle to form. Hence, the answer is option (a) 2.8 cm.
This analysis leads us to conclude that the difference of AB and AC must be exactly 2.8 cm for triangle ABC to be constructible under the given conditions.
To determine the possible values for the sides AB and AC of triangle ABC, given the following conditions:
- BC = 3 cm
- ∠C = 60°
We will apply the triangle inequality theorem, which states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
Applying Triangle Inequality
Let:
- AB = a
- AC = b
From the triangle inequality, we have:
1. **a + b > 3** (Equation 1)
2. **a + 3 > b** (Equation 2)
3. **b + 3 > a** (Equation 3)
Expressing the Difference
We also need to consider the difference between sides AB and AC:
- |a - b| = k (where k is the difference we are looking for)
This translates into two inequalities:
- a - b = k (or)
- b - a = k
Using these expressions, we can derive two scenarios for the difference:
Finding the Difference
1. **From Equation 1** (a + b > 3):
- For a - b = k:
- Substitute a = b + k into a + b > 3:
- (b + k) + b > 3 → 2b + k > 3 → 2b > 3 - k → b > (3 - k)/2
2. **From Equation 3** (b + 3 > a):
- Substitute a = b + k:
- b + 3 > (b + k) → 3 > k → k < />
Thus, the maximum difference can be 3 cm.
Finding the Specific Value
To find the exact value of the difference that satisfies all conditions, we can derive that the possible difference |a - b| must equal 2.8 cm allows for the triangle to form. Hence, the answer is option (a) 2.8 cm.
This analysis leads us to conclude that the difference of AB and AC must be exactly 2.8 cm for triangle ABC to be constructible under the given conditions.
Chapter doubts & questions for Construction - Mathematics & Pedagogy Paper 2 for CTET & TET Exams 2025 is part of CTET & State TET exam preparation. The chapters have been prepared according to the CTET & State TET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CTET & State TET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Construction - Mathematics & Pedagogy Paper 2 for CTET & TET Exams in English & Hindi are available as part of CTET & State TET exam.
Download more important topics, notes, lectures and mock test series for CTET & State TET Exam by signing up for free.
Mathematics & Pedagogy Paper 2 for CTET & TET Exams
82 videos|273 docs|69 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup