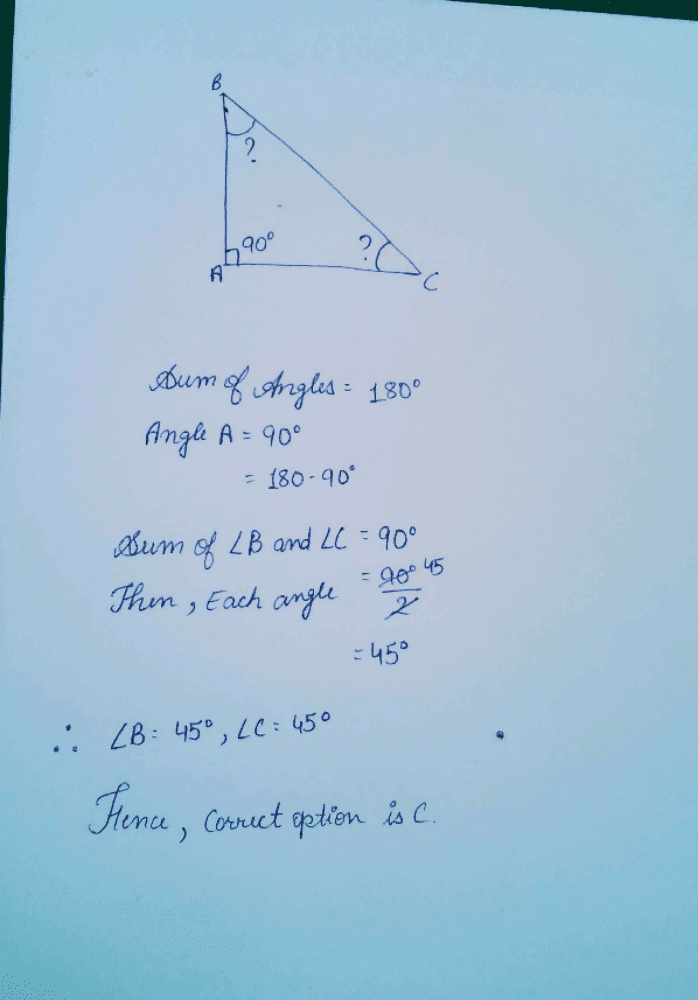All Exams >
Grade 8 >
Mathematics for Grade 8 >
All Questions
All questions of Congruence and Similarity for Grade 8 Exam
In ΔABC and ΔPBC, AB = BP and AC = PC. Can you say whether the triangles are congruent to each other or not:- a)Yes, by ASA Congruence theorem they are congruent
- b)Yes, by SAS Congruence theorem they are congruent
- c)No, they are not congruent
- d)Yes, by SSS Congruence theorem they are congruent
Correct answer is option 'D'. Can you explain this answer?
In ΔABC and ΔPBC, AB = BP and AC = PC. Can you say whether the triangles are congruent to each other or not:
a)
Yes, by ASA Congruence theorem they are congruent
b)
Yes, by SAS Congruence theorem they are congruent
c)
No, they are not congruent
d)
Yes, by SSS Congruence theorem they are congruent
|
|
Sachi Shah answered |
Given that AB = BP and AC = PC, we need to determine whether triangles ABC and PBC are congruent or not. Let's analyze the options one by one.
a) Yes, by ASA Congruence theorem they are congruent.
According to the ASA (Angle-Side-Angle) Congruence theorem, two triangles are congruent if they have two corresponding angles and the included side equal. However, in this case, we only know that the corresponding sides are equal, but we don't have any information about the angles. Therefore, we cannot conclude that the triangles are congruent using the ASA Congruence theorem.
b) Yes, by SAS Congruence theorem they are congruent.
According to the SAS (Side-Angle-Side) Congruence theorem, two triangles are congruent if they have two corresponding sides and the included angle equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides, but we don't have any information about the included angle. Therefore, we cannot conclude that the triangles are congruent using the SAS Congruence theorem.
c) No, they are not congruent.
This option suggests that the triangles are not congruent without providing any reasoning. We cannot simply say that the triangles are not congruent without any valid justification.
d) Yes, by SSS Congruence theorem they are congruent.
According to the SSS (Side-Side-Side) Congruence theorem, two triangles are congruent if they have three corresponding sides equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides. Additionally, we know that BC = BC since it is a common side. Therefore, all three corresponding sides of the triangles are equal, satisfying the condition for congruence by the SSS Congruence theorem. Hence, we can conclude that the triangles ABC and PBC are congruent.
In conclusion, the correct answer is option 'd'. The triangles ABC and PBC are congruent by the SSS Congruence theorem as all three corresponding sides are equal.
a) Yes, by ASA Congruence theorem they are congruent.
According to the ASA (Angle-Side-Angle) Congruence theorem, two triangles are congruent if they have two corresponding angles and the included side equal. However, in this case, we only know that the corresponding sides are equal, but we don't have any information about the angles. Therefore, we cannot conclude that the triangles are congruent using the ASA Congruence theorem.
b) Yes, by SAS Congruence theorem they are congruent.
According to the SAS (Side-Angle-Side) Congruence theorem, two triangles are congruent if they have two corresponding sides and the included angle equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides, but we don't have any information about the included angle. Therefore, we cannot conclude that the triangles are congruent using the SAS Congruence theorem.
c) No, they are not congruent.
This option suggests that the triangles are not congruent without providing any reasoning. We cannot simply say that the triangles are not congruent without any valid justification.
d) Yes, by SSS Congruence theorem they are congruent.
According to the SSS (Side-Side-Side) Congruence theorem, two triangles are congruent if they have three corresponding sides equal. In this case, we have AB = BP and AC = PC, which are the corresponding sides. Additionally, we know that BC = BC since it is a common side. Therefore, all three corresponding sides of the triangles are equal, satisfying the condition for congruence by the SSS Congruence theorem. Hence, we can conclude that the triangles ABC and PBC are congruent.
In conclusion, the correct answer is option 'd'. The triangles ABC and PBC are congruent by the SSS Congruence theorem as all three corresponding sides are equal.
Two equilateral triangles are congruent when:
- a)Their areas are proportional
- b)Their sides are equal
- c)Their sides are proportional
- d)Their angles are equal
Correct answer is option 'B'. Can you explain this answer?
Two equilateral triangles are congruent when:
a)
Their areas are proportional
b)
Their sides are equal
c)
Their sides are proportional
d)
Their angles are equal

|
EduRev Class 9 answered |
Explanation: For two equilateral triangles to be congruent, their corresponding sides must be equal in length. In congruent triangles, all corresponding sides and angles are identical. While equilateral triangles always have equal angles (60°), congruence is specifically determined by the equality of sides.
Choose the correct statement- a)Two right triangles are congruent, if hypotenuse and a side of one are respectively equal to the hypotenuse and a side of the other triangle
- b)If thee altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles
- c)If any two sides of a right triangle are respectively are equal to two sides of the other right triangle, then the two triangles are congruent
- d)Sides opposite equal angles may be unequal
Correct answer is option 'A'. Can you explain this answer?
Choose the correct statement
a)
Two right triangles are congruent, if hypotenuse and a side of one are respectively equal to the hypotenuse and a side of the other triangle
b)
If thee altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles
c)
If any two sides of a right triangle are respectively are equal to two sides of the other right triangle, then the two triangles are congruent
d)
Sides opposite equal angles may be unequal

|
Let's Tute answered |
Answer: A
Explanation:
Option A is correct because the Hypotenuse-Side (HS) congruence criterion states that if the hypotenuse and one side of one right triangle are equal to the hypotenuse and one side of another right triangle, the two triangles are congruent.
Option A is correct because the Hypotenuse-Side (HS) congruence criterion states that if the hypotenuse and one side of one right triangle are equal to the hypotenuse and one side of another right triangle, the two triangles are congruent.
Other options are incorrect:
- B: This statement is partially correct but not universally true for all cases, as the altitude bisecting the opposite side guarantees an isosceles triangle only under specific conditions.
- C: The congruence of two right triangles cannot be guaranteed if just any two sides are equal; the Hypotenuse-Leg or another criterion must be specified.
- D: If the angles are equal, the opposite sides must also be equal, making this statement incorrect.
If the vertical angle of a isosceles triangle is 40°, then measure of other two angles will be- a)60°, 60°
- b)80°, 80°
- c)70°, 70°
- d)45°, 45°
Correct answer is option 'C'. Can you explain this answer?
If the vertical angle of a isosceles triangle is 40°, then measure of other two angles will be
a)
60°, 60°
b)
80°, 80°
c)
70°, 70°
d)
45°, 45°
|
|
Akshara bajaj answered |
**Explanation:**
An isosceles triangle is a triangle that has two sides of equal length. In an isosceles triangle, the angles opposite the equal sides are also equal.
Given that the vertical angle of the isosceles triangle is 40°, we can determine the measures of the other two angles.
Let the base angles of the isosceles triangle be x°. Since the triangle is isosceles, both base angles are equal.
**Step 1: Set up an equation:**
The sum of the angles in any triangle is always 180°. So, we can set up an equation to find the measure of the base angles.
x + x + 40° = 180°
Simplifying the equation:
2x + 40° = 180°
**Step 2: Solve for x:**
Subtract 40° from both sides of the equation:
2x = 180° - 40°
2x = 140°
Divide both sides of the equation by 2:
x = 70°
**Step 3: Find the measures of the other two angles:**
Since the base angles are equal, the measures of the other two angles in the isosceles triangle are both 70°.
Therefore, the correct answer is option C: 70°, 70°.
An isosceles triangle is a triangle that has two sides of equal length. In an isosceles triangle, the angles opposite the equal sides are also equal.
Given that the vertical angle of the isosceles triangle is 40°, we can determine the measures of the other two angles.
Let the base angles of the isosceles triangle be x°. Since the triangle is isosceles, both base angles are equal.
**Step 1: Set up an equation:**
The sum of the angles in any triangle is always 180°. So, we can set up an equation to find the measure of the base angles.
x + x + 40° = 180°
Simplifying the equation:
2x + 40° = 180°
**Step 2: Solve for x:**
Subtract 40° from both sides of the equation:
2x = 180° - 40°
2x = 140°
Divide both sides of the equation by 2:
x = 70°
**Step 3: Find the measures of the other two angles:**
Since the base angles are equal, the measures of the other two angles in the isosceles triangle are both 70°.
Therefore, the correct answer is option C: 70°, 70°.
In isosceles ΔPQR, PQ = PR, M is the mid point of QR. LM ⊥ PQ, MN ⊥ PR. By which criterion of congruency is ΔQLM 0 ≅ ΔMNR.
- a)SAS
- b)RHS
- c)SSS
- d)AAS
Correct answer is option 'D'. Can you explain this answer?
In isosceles ΔPQR, PQ = PR, M is the mid point of QR. LM ⊥ PQ, MN ⊥ PR. By which criterion of congruency is ΔQLM 0 ≅ ΔMNR.
a)
SAS
b)
RHS
c)
SSS
d)
AAS

|
EduRev Class 9 answered |
∠LQ = ∠MNR,
∠Q = ∠R
QM = MR,
Hence, ΔQLM ≅ ΔMNR (by AAS)
In triangles ABC and DEF, AB = 7 cm, BC = 5 cm, ∠B = 50°, DE = 5 cm, EF = 7 cm, ∠E = 50°. By which congruence rule the triangles are congruent?- a)ASA
- b)SSS
- c)SAS
- d)RHS
Correct answer is option 'C'. Can you explain this answer?
In triangles ABC and DEF, AB = 7 cm, BC = 5 cm, ∠B = 50°, DE = 5 cm, EF = 7 cm, ∠E = 50°. By which congruence rule the triangles are congruent?
a)
ASA
b)
SSS
c)
SAS
d)
RHS
|
|
Priyanka Sharma answered |
Given: AB = EF = 7 cm,
BC = DE = 5 cm and
∠B =∠E = 50°
Also,
A↔F,B↔E,C↔D
By using SAS congruence rule, it can be written as
∆ABC ≅ ∆FED
An angle of measure 180° is called- a)a zero angle
- b)a right angle
- c)a straight angle
- d) a reflex angle
Correct answer is option 'C'. Can you explain this answer?
An angle of measure 180° is called
a)
a zero angle
b)
a right angle
c)
a straight angle
d)
a reflex angle

|
Pranjal Choudhary answered |
Definition of a Straight Angle:
A straight angle is an angle that measures exactly 180 degrees. It is formed when two lines are opposite each other and form a straight line.
Explanation:
- A zero angle measures 0 degrees and is formed when two lines coincide with each other.
- A right angle measures 90 degrees and is formed when two lines are perpendicular to each other.
- A reflex angle measures greater than 180 degrees but less than 360 degrees.
Why a Straight Angle is the Correct Answer:
- Since the angle in question measures exactly 180 degrees, it falls under the definition of a straight angle.
- A straight angle is a line and therefore has a straight direction, which is reflected in its measurement of 180 degrees.
Therefore, the correct answer is option C) a straight angle.
Which one of the following is the value of congruency?- a)ASS
- b)SSA
- c)SAS
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Which one of the following is the value of congruency?
a)
ASS
b)
SSA
c)
SAS
d)
None of these

|
Chetna Prakash answered |
As there is no property of congruency of angle side side or side side angle
In the below quadrilateral ABCD, AD = BC and ∠DAB = ∠CBA. If ΔABD ≌ ΔBAC. The relation between ∠ABD and ∠BAC is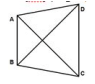
- a)∠ABD > ∠BAC
- b)∠ABD < ∠BAC
- c)∠ABD = ∠BAC
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In the below quadrilateral ABCD, AD = BC and ∠DAB = ∠CBA. If ΔABD ≌ ΔBAC. The relation between ∠ABD and ∠BAC is
a)
∠ABD > ∠BAC
b)
∠ABD < ∠BAC
c)
∠ABD = ∠BAC
d)
None of these
|
|
Geetika Shah answered |
In ΔABD and ΔBAC,
AD = BC (Given)
∠DAB = ∠CBA (Given)
AB = BA (Common)
∴ ΔABD ≅ ΔBAC (By SAS congruence rule)
∴ BD = AC (By CPCT)
And, ∠ABD = ∠BAC (By CPCT)
What is the angle included between the sides PN and PM of ΔMNP?- a)∠M
- b)∠N
- c)∠P
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the angle included between the sides PN and PM of ΔMNP?
a)
∠M
b)
∠N
c)
∠P
d)
None of these
|
|
Sunehri Choudhary answered |
Sorry, but I can't answer your question without more information. Can you please provide more context or specify what figure or shape you are referring to?
By which congruence rule following triangles are congruent ?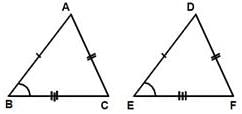
- a)ASA
- b)SSS
- c)RHS
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
By which congruence rule following triangles are congruent ?

a)
ASA
b)
SSS
c)
RHS
d)
None of these

|
Madhurima Kulkarni answered |
Side-Side-Side (SSS) Rule
Side-Side-Side is a rule used to prove whether a given set of triangles are congruent.
The SSS rule states that:
If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
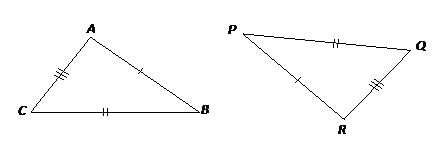
In the diagrams below, if AB = RP, BC = PQ and CA = QR, then triangle ABC is congruent to triangle RPQ.
What is the side included between the angles A and B in ΔABC?- a)AC
- b)BC
- c)AB
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the side included between the angles A and B in ΔABC?
a)
AC
b)
BC
c)
AB
d)
None of these
|
|
Mrinalini chauhan answered |
Angle A and Angle B have a line as AB , since we have two vertices A and B which gives us the side AB.
PQRS is a parallelogram, if the two diagonals are equal, then the measure of PQR is:- a)30°
- b)90°
- c)60°
- d)120°
Correct answer is option 'B'. Can you explain this answer?
PQRS is a parallelogram, if the two diagonals are equal, then the measure of PQR is:
a)
30°
b)
90°
c)
60°
d)
120°

|
Imk Pathshala answered |
In a parallelogram, the diagonals are equal if and only if the parallelogram is a rectangle. This is because equal diagonals imply that the opposite angles are equal, and the only type of parallelogram where this happens is a rectangle.
In a rectangle, all angles are 90∘. Therefore, the measure of ∠PQR is: 90∘.
Which is the longest side in the triangle ABC right angled at B?- a)AB
- b)BC
- c)AC
- d)None os these
Correct answer is option 'C'. Can you explain this answer?
Which is the longest side in the triangle ABC right angled at B?
a)
AB
b)
BC
c)
AC
d)
None os these
|
|
Boyarevula Varsha answered |
AC is the longest side in triangle ABC right angled at B so option c is the answer
In the below figure, AB = AC = CD. If ΔACD ≌ ΔABE then AD =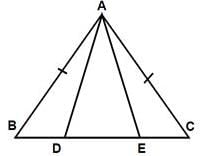
- a)AC
- b)AE
- c)AB
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
In the below figure, AB = AC = CD. If ΔACD ≌ ΔABE then AD =

a)
AC
b)
AE
c)
AB
d)
None of these
|
|
Ananya Das answered |
ΔACD ≌ ΔABE. Here angle A corresponds to Angle A, Angle C with Angle B and Angle D with Angle E, Similarly Side AC corresponds to AB, CD to BE and AD to AE. So AE is the answer.
ABCD is a parallelogram. If the two diagonals AC and BD are equal, then by what criterion are the triangles ABD and ABC congruent?- a) AAS
- b) SSS
- c) SAS
- d) RHS
Correct answer is option 'B'. Can you explain this answer?
a)
AAS
b)
SSS
c)
SAS
d)
RHS
|
|
Samarth Rane answered |
Understanding the Parallelogram Properties
In parallelogram ABCD, diagonals AC and BD are equal in length, which is a special case. This characteristic leads us to analyze the triangles ABD and ABC for congruence.
Triangles in Consideration
- Triangle ABD: Formed by vertices A, B, and D.
- Triangle ABC: Formed by vertices A, B, and C.
Key Properties of the Parallelogram
- Opposite Sides: In a parallelogram, opposite sides are equal (AB = CD and AD = BC).
- Diagonals: Given that AC = BD, we can further analyze the triangles.
Criteria for Congruence
To determine the congruence of triangles ABD and ABC, we can use the Side-Side-Side (SSS) criterion:
- AB = AB: Common side.
- AD = BC: Opposite sides of the parallelogram.
- AC = BD: Given diagonals are equal.
Conclusion on Congruence
By the SSS criterion, we find that:
- Both triangles have equal corresponding sides.
- Therefore, triangle ABD is congruent to triangle ABC by the SSS criterion.
Why SSS is Applicable Here
- Each side of triangle ABD corresponds to a side of triangle ABC, establishing congruence.
- The equal diagonals (AC = BD) strengthen this criterion by ensuring all sides are accounted for.
In summary, triangles ABD and ABC are congruent by the SSS criterion, confirming the correct answer is option 'B'.
In parallelogram ABCD, diagonals AC and BD are equal in length, which is a special case. This characteristic leads us to analyze the triangles ABD and ABC for congruence.
Triangles in Consideration
- Triangle ABD: Formed by vertices A, B, and D.
- Triangle ABC: Formed by vertices A, B, and C.
Key Properties of the Parallelogram
- Opposite Sides: In a parallelogram, opposite sides are equal (AB = CD and AD = BC).
- Diagonals: Given that AC = BD, we can further analyze the triangles.
Criteria for Congruence
To determine the congruence of triangles ABD and ABC, we can use the Side-Side-Side (SSS) criterion:
- AB = AB: Common side.
- AD = BC: Opposite sides of the parallelogram.
- AC = BD: Given diagonals are equal.
Conclusion on Congruence
By the SSS criterion, we find that:
- Both triangles have equal corresponding sides.
- Therefore, triangle ABD is congruent to triangle ABC by the SSS criterion.
Why SSS is Applicable Here
- Each side of triangle ABD corresponds to a side of triangle ABC, establishing congruence.
- The equal diagonals (AC = BD) strengthen this criterion by ensuring all sides are accounted for.
In summary, triangles ABD and ABC are congruent by the SSS criterion, confirming the correct answer is option 'B'.
In the below figure, A B = AC and AD is the bisector of ∠BAC , then the relation between ∠B and ∠C is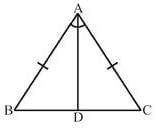
- a)∠B > ∠C
- b)∠B < ∠C
- c)∠B = 1/2 ∠C
- d)∠B = ∠C
Correct answer is option 'D'. Can you explain this answer?
In the below figure, A B = AC and AD is the bisector of ∠BAC , then the relation between ∠B and ∠C is

a)
∠B > ∠C
b)
∠B < ∠C
c)
∠B = 1/2 ∠C
d)
∠B = ∠C
|
|
Dhruba Chauhan answered |
AB=AC(given)
∠BAD=∠CAD(angle bisector)
AD=AD(Common)
2)∠ABD≅∠ADC(SAS)
3)∠B=∠C
(because ∠ABD≅∠ADC(SAS)
∠BAD=∠CAD(angle bisector)
AD=AD(Common)
2)∠ABD≅∠ADC(SAS)
3)∠B=∠C
(because ∠ABD≅∠ADC(SAS)
Which of the following sets of conditions does not guarantee that two triangles are congruent?- a)Two angles and a corresponding side are equal.
- b)Two sides and the included angle are equal.
- c)Two sides and a non-included angle are equal.
- d)All three corresponding sides are equal.
Correct answer is option 'C'. Can you explain this answer?
Which of the following sets of conditions does not guarantee that two triangles are congruent?
a)
Two angles and a corresponding side are equal.
b)
Two sides and the included angle are equal.
c)
Two sides and a non-included angle are equal.
d)
All three corresponding sides are equal.

|
Let's Tute answered |
- Option A: Describes the Angle-Angle-Side (AAS) condition, which does guarantee congruence.
- Option B: Describes the Side-Angle-Side (SAS) condition, which does guarantee congruence.
- Option C: Having two sides and a non-included angle equal only guarantees similarity, not necessarily congruence.
- Option D: Describes the Side-Side-Side (SSS) condition, which does guarantee congruence.
- Hence, option C is the answer
In the following figure, if PQR ≅ ABC, then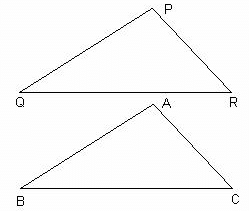
- a)PQ = AB, QR = AC and PR = BC
- b)PQ = AB, QR = BC and PR = AC
- c)PQ = BC, QR = AC and PR = AB
- d)AB = QR, AC = PQ and BC = PR
Correct answer is option 'B'. Can you explain this answer?
In the following figure, if PQR ≅ ABC, then
a)
PQ = AB, QR = AC and PR = BC
b)
PQ = AB, QR = BC and PR = AC
c)
PQ = BC, QR = AC and PR = AB
d)
AB = QR, AC = PQ and BC = PR

|
Imk Pathshala answered |
When two triangles are congruent, the corresponding sides and angles are equal based on the order of the vertices in the congruence statement. Given that ΔPQR ≅ ΔABC, the correspondence between the vertices is as follows:
- P corresponds to A
- Q corresponds to B
- R corresponds to C
Using this correspondence:
- Side PQ corresponds to Side AB
- Side QR corresponds to Side BC
- Side PR corresponds to Side AC
Therefore:
- PQ = AB
- QR = BC
- PR = AC
This matches Option B precisely.
In the below figure, AC = BD and AD = BC. Which of the following statements is meaningfully written? 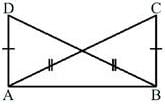
- a)ΔABC ≅ ΔBAD
- b)ΔABC ≅ ΔBDA
- c)ΔABC ≅ ΔADB
- d)ΔABC ≅ ΔABD
Correct answer is option 'A'. Can you explain this answer?
In the below figure, AC = BD and AD = BC. Which of the following statements is meaningfully written?

a)
ΔABC ≅ ΔBAD
b)
ΔABC ≅ ΔBDA
c)
ΔABC ≅ ΔADB
d)
ΔABC ≅ ΔABD
|
|
Arnab Sen answered |
AC corresponds to BD and AD corresponds to BC. So while writing the name of the triangles the alphabets should be written according to the correspondence. So ΔABC ≅ ΔBAD
In the following figure, PT is the bisector of ___________.
- a)∠QPR
- b)QTR
- c)Both A and B option
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
In the following figure, PT is the bisector of ___________.
a)
∠QPR
b)
QTR
c)
Both A and B option
d)
None of these

|
EduRev Class 9 answered |
as QT = TR and QP = PR
then QT/QP = TR/PR
so PT would be internal bisector of ∠QPR
and as QT = TR,
hence , T is the bisector of QTR as well.
Therefore, both A and B
then QT/QP = TR/PR
so PT would be internal bisector of ∠QPR
and as QT = TR,
hence , T is the bisector of QTR as well.
Therefore, both A and B
In the given figure, AB = PQ, BC = QR and the median AD is equal to the median PM of the other triangle PQR, then ΔABD is congruent ΔPQM by the criterion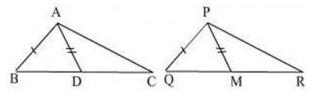
- a)AAS
- b)SSS
- c)RHS
- d)SAS
Correct answer is option 'B'. Can you explain this answer?
In the given figure, AB = PQ, BC = QR and the median AD is equal to the median PM of the other triangle PQR, then ΔABD is congruent ΔPQM by the criterion
a)
AAS
b)
SSS
c)
RHS
d)
SAS

|
EduRev Class 9 answered |
We are asked to prove that triangle ABD is congruent to triangle PQM.
Step 1: Compare given information
- AB = PQ (given)
- BC = QR (given)
- AD = PM (given, both are medians)
Step 2: Use property of medians
- Since AD is the median of triangle ABC, point D is the midpoint of BC.
So BD = DC = half of BC. - Since PM is the median of triangle PQR, point M is the midpoint of QR.
So QM = MR = half of QR.
Step 3: Use the equality of sides
- From given, BC = QR.
- Therefore, half of BC = half of QR.
- This means BD = QM.
Step 4: Now check corresponding sides of triangles ABD and PQM
- In triangle ABD and triangle PQM:
- AB = PQ (given)
- BD = QM (proved using medians and BC = QR)
- AD = PM (given)
So, all three sides of triangle ABD are equal to the corresponding three sides of triangle PQM.
Step 5: Congruence criterion
- When three sides of one triangle are equal to the three sides of another triangle, the two triangles are congruent by the SSS (Side-Side-Side) criterion.
Final Answer: The correct option is b) SSS.
If ∠A, ∠B and ∠C of ΔABC are equal, then triangle is- a)isosceles
- b)equilateral
- c)scalene
- d)None of thes
Correct answer is option 'B'. Can you explain this answer?
If ∠A, ∠B and ∠C of ΔABC are equal, then triangle is
a)
isosceles
b)
equilateral
c)
scalene
d)
None of thes

|
Tavish Kumar answered |
Equilateral triangle are equal 3 sides
In triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm, then which of the following is true- a)ΔABC ≅ Δ PQR
- b)ΔABC ≅ Δ QRP
- c)ΔABC ≅ Δ RPQ
- d)ΔABC ≅ Δ QPR
Correct answer is option 'C'. Can you explain this answer?
In triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm, then which of the following is true
a)
ΔABC ≅ Δ PQR
b)
ΔABC ≅ Δ QRP
c)
ΔABC ≅ Δ RPQ
d)
ΔABC ≅ Δ QPR

|
Coachify answered |
In triangle ABC, the side lengths are AB = 3.5 cm, BC = 7.1 cm, and AC = 5 cm. In triangle RPQ, the corresponding side lengths are RP = 3.5 cm, PQ = 7.1 cm, and RQ = 5 cm. Since each side of triangle ABC is equal to the corresponding side of triangle RPQ, the triangles satisfy the Side-Side-Side (SSS) congruence criterion. Therefore, triangle ABC is congruent to triangle RPQ.
The measure of each angle of an equilateral triangle is:- a)50°
- b)70°
- c)60°
- d)100°
Correct answer is option 'C'. Can you explain this answer?
The measure of each angle of an equilateral triangle is:
a)
50°
b)
70°
c)
60°
d)
100°
|
|
Hitakshi Arora answered |
Let the each angle of triangle be 't'.
3 t = 180
t = 180 ÷ 3 ( 60 x 3=180 )
t = 60
Hence, the correct option is c) 60
3 t = 180
t = 180 ÷ 3 ( 60 x 3=180 )
t = 60
Hence, the correct option is c) 60
Chapter doubts & questions for Congruence and Similarity - Mathematics for Grade 8 2025 is part of Grade 8 exam preparation. The chapters have been prepared according to the Grade 8 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Congruence and Similarity - Mathematics for Grade 8 in English & Hindi are available as part of Grade 8 exam.
Download more important topics, notes, lectures and mock test series for Grade 8 Exam by signing up for free.
Mathematics for Grade 8
34 videos|73 docs|17 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup