All Exams >
ACT >
Mathematics for ACT >
All Questions
All questions of Polynomials for ACT Exam
What is the coefficient of x3 in a polynomial 6x4 + 3x2 + 8x + 5?- a)6
- b)3
- c)8
- d)0
Correct answer is option 'D'. Can you explain this answer?
What is the coefficient of x3 in a polynomial 6x4 + 3x2 + 8x + 5?
a)
6
b)
3
c)
8
d)
0

|
Orion Classes answered |
Coefficient is the number which is multiplied with respective variable.
In the given polynomial 6x4 + 3x2 + 8x + 5, there is not an expression containing x3. So we can write 6x4 + 3x2 + 8x + 5 as 6x4 + 0x3 + 3x2 + 8x + 5. We can see that 0 is multiplied with expression x3, so coefficient of x3 is 0.
In the given polynomial 6x4 + 3x2 + 8x + 5, there is not an expression containing x3. So we can write 6x4 + 3x2 + 8x + 5 as 6x4 + 0x3 + 3x2 + 8x + 5. We can see that 0 is multiplied with expression x3, so coefficient of x3 is 0.
A quadratic polynomial can have at most __________ terms.- a)1
- b)4
- c)2
- d)3
Correct answer is option 'D'. Can you explain this answer?
A quadratic polynomial can have at most __________ terms.
a)
1
b)
4
c)
2
d)
3
|
|
Ayesha Joshi answered |
A polynomial of degree 2 is called quadratic polynomial.
Quadratic polynomials are of the form ax2 + bx + c and it can contain at most three terms namely ax2, bx and c. Thus, we can say that a quadratic polynomial can have at most three terms.
Similarly, a polynomial of degree 1 is called linear polynomial and a polynomial of degree 3 is called cubic polynomial.
Quadratic polynomials are of the form ax2 + bx + c and it can contain at most three terms namely ax2, bx and c. Thus, we can say that a quadratic polynomial can have at most three terms.
Similarly, a polynomial of degree 1 is called linear polynomial and a polynomial of degree 3 is called cubic polynomial.
What do we get after factorising x2 + 6x - 27?- a)(x + 9)(x - 3)
- b)(x - 9)(x + 3)
- c)(x - 9)(x - 3)
- d)(x + 9)(x + 3)
Correct answer is option 'A'. Can you explain this answer?
What do we get after factorising x2 + 6x - 27?
a)
(x + 9)(x - 3)
b)
(x - 9)(x + 3)
c)
(x - 9)(x - 3)
d)
(x + 9)(x + 3)
|
|
Ayesha Joshi answered |
To factorise x2 + 6x - 27, we have to find two numbers ‘a’ and ‘b’ such that a + b = 6 and a * b = 27.
For that we have to find factors of -27, which are ±1, ±3, ±9.
Now we have to arrange two numbers from these numbers such that a + b = 6 and a * b = 27.
By considering this, we get two numbers +9 and -3
9 + (-3) = 6 and 9*-3 = -27
Now after manipulating terms, we get x2 + 9x - 3x - 27.
x2 + 9x - 3x - 27 = x(x + 9) - 3(x + 9)
= (x + 9)(x - 3).
For that we have to find factors of -27, which are ±1, ±3, ±9.
Now we have to arrange two numbers from these numbers such that a + b = 6 and a * b = 27.
By considering this, we get two numbers +9 and -3
9 + (-3) = 6 and 9*-3 = -27
Now after manipulating terms, we get x2 + 9x - 3x - 27.
x2 + 9x - 3x - 27 = x(x + 9) - 3(x + 9)
= (x + 9)(x - 3).
What do we get after factorising x3 + 8y3+ z3 – 4xyz?- a)(x + 2y + z) (x2 + 4y2 + z2 – 5xy – 2yz – zx)
- b)(x + 2y + z) (x2 + 4y2 + z2 – 4xy – 2yz – zx)
- c)(x + 2y + z) (x2 + 4y2 + z2 – 2xy – 2yz – zx)
- d)(x + 2y + z) (x2 + 4y2+ z2 – 3xy – 2yz – zx)
Correct answer is option 'C'. Can you explain this answer?
What do we get after factorising x3 + 8y3+ z3 – 4xyz?
a)
(x + 2y + z) (x2 + 4y2 + z2 – 5xy – 2yz – zx)
b)
(x + 2y + z) (x2 + 4y2 + z2 – 4xy – 2yz – zx)
c)
(x + 2y + z) (x2 + 4y2 + z2 – 2xy – 2yz – zx)
d)
(x + 2y + z) (x2 + 4y2+ z2 – 3xy – 2yz – zx)
|
|
Ayesha Joshi answered |
We know that a3 + b3 + c3 – 3abc = (a + b - c)(a2 + b2 + c2 – ab – bc – ca)
In x3 + 8y3 + y3 – 6xyz, a = x, b = 2y and c = z
By using the above equation, we get x3 + 8y3 + z3 – 4xyz = (x + 2y + z) (x2 + (2y)2 + z2 – x(2y) – (2y)(z) – zx)
= (x + 2y + z) (x2 + 4y2 + z2 – 2xy – 2yz – zx).
In x3 + 8y3 + y3 – 6xyz, a = x, b = 2y and c = z
By using the above equation, we get x3 + 8y3 + z3 – 4xyz = (x + 2y + z) (x2 + (2y)2 + z2 – x(2y) – (2y)(z) – zx)
= (x + 2y + z) (x2 + 4y2 + z2 – 2xy – 2yz – zx).
If the polynomial f(x) = x2 + kx - 15, is exactly divisible by x - 5, then the value of k is _______- a)3
- b)2
- c)-3
- d)-2
Correct answer is option 'D'. Can you explain this answer?
If the polynomial f(x) = x2 + kx - 15, is exactly divisible by x - 5, then the value of k is _______
a)
3
b)
2
c)
-3
d)
-2
|
|
Oliver Ramirez answered |
To determine the value of k in the polynomial f(x) = x^2 + kx - 15, we need to check if the polynomial is exactly divisible by x - 5.
To check if the polynomial is divisible by x - 5, we can use the remainder theorem. According to the remainder theorem, if a polynomial f(x) is divided by x - a and the remainder is zero, then f(a) = 0.
So, let's substitute x = 5 into the polynomial and check if the result is zero.
Substituting x = 5 into f(x), we get:
f(5) = (5)^2 + k(5) - 15
= 25 + 5k - 15
= 5k + 10
If the polynomial is exactly divisible by x - 5, then f(5) should be equal to zero.
Setting f(5) = 0, we have:
5k + 10 = 0
Solving for k, we get:
5k = -10
k = -10/5
k = -2
Therefore, the value of k is -2.
Hence, the correct answer is option 'D' (-2).
To check if the polynomial is divisible by x - 5, we can use the remainder theorem. According to the remainder theorem, if a polynomial f(x) is divided by x - a and the remainder is zero, then f(a) = 0.
So, let's substitute x = 5 into the polynomial and check if the result is zero.
Substituting x = 5 into f(x), we get:
f(5) = (5)^2 + k(5) - 15
= 25 + 5k - 15
= 5k + 10
If the polynomial is exactly divisible by x - 5, then f(5) should be equal to zero.
Setting f(5) = 0, we have:
5k + 10 = 0
Solving for k, we get:
5k = -10
k = -10/5
k = -2
Therefore, the value of k is -2.
Hence, the correct answer is option 'D' (-2).
What do we get after factoring 49x2 - 28xy + .4y2?- a)(7x + 2y)2
- b)(49x - 4y)2
- c)(7x - 2y)2
- d)(7x - 28y)2
Correct answer is option 'C'. Can you explain this answer?
What do we get after factoring 49x2 - 28xy + .4y2?
a)
(7x + 2y)2
b)
(49x - 4y)2
c)
(7x - 2y)2
d)
(7x - 28y)2
|
|
Ayesha Joshi answered |
We know that a2 - 2ab + .b2 = (a - b)2
49x2 - 28xy + .4y2 can also be written as (7x)2 - 2(7)(2)xy + (2y)2
Here, a = 7x and b = 2y.
Therefore, 49x2 - 28xy + .4y2 = (7x)2 - 2(7)(2)xy + (2y)2
= (7x - 2y)2.
49x2 - 28xy + .4y2 can also be written as (7x)2 - 2(7)(2)xy + (2y)2
Here, a = 7x and b = 2y.
Therefore, 49x2 - 28xy + .4y2 = (7x)2 - 2(7)(2)xy + (2y)2
= (7x - 2y)2.
27 * 29 = __________ (calculate without direct calculation).- a)783
- b)753
- c)763
- d)793
Correct answer is option 'A'. Can you explain this answer?
27 * 29 = __________ (calculate without direct calculation).
a)
783
b)
753
c)
763
d)
793
|
|
Ayesha Joshi answered |
We know that (a + b) * (a + c) = a2 + (b + c)a + bc
27 * 29 can also be written as (25 + 2) * (25 + 4)
Now using above identity, 27 * 29 = (25 + 2) * (25 + 4)
= 252 + (2 + 4)25 + (4)(2)
= 625 + 6(25) + 8
= 625 + 150 + 8
= 783.
27 * 29 can also be written as (25 + 2) * (25 + 4)
Now using above identity, 27 * 29 = (25 + 2) * (25 + 4)
= 252 + (2 + 4)25 + (4)(2)
= 625 + 6(25) + 8
= 625 + 150 + 8
= 783.
26 * 34 = __________ (calculate without direct calculation).- a)900
- b)884
- c)916
- d)844
Correct answer is option 'B'. Can you explain this answer?
26 * 34 = __________ (calculate without direct calculation).
a)
900
b)
884
c)
916
d)
844
|
|
Ayesha Joshi answered |
26 * 34 can also be written as (30 - 4) * (30 + 4)
We know that (a - b) * (a + b) = a2 - b2
Similarly, 26 * 34 = (30 - 4) * (30 + 4)
= 302 – 42
= 900 – 16
= 884.
We know that (a - b) * (a + b) = a2 - b2
Similarly, 26 * 34 = (30 - 4) * (30 + 4)
= 302 – 42
= 900 – 16
= 884.
If we add, 7xy + 5yz – 3zx, 4yz + 9zx – 4y and –3xz + 5x – 2xy, then the answer is- a)5xy + 9yz +3zx + 5x – 4y
- b)5xy – 9yz +3zx – 5x – 4y
- c)5xy + 10yz +3zx + 15x – 4y
- d)5xy + 10yz +3zx + 5x – 6y
Correct answer is option 'A'. Can you explain this answer?
If we add, 7xy + 5yz – 3zx, 4yz + 9zx – 4y and –3xz + 5x – 2xy, then the answer is
a)
5xy + 9yz +3zx + 5x – 4y
b)
5xy – 9yz +3zx – 5x – 4y
c)
5xy + 10yz +3zx + 15x – 4y
d)
5xy + 10yz +3zx + 5x – 6y
|
|
Ayesha Joshi answered |
Given, 7xy + 5yz – 3zx, 4yz + 9zx – 4y and –3xz + 5x – 2xy.
If we add the three expressions, then we need to combine the like terms together.
(7xy – 2xy) + (5yz + 4yz) – 3zx + 9zx – 3xz – 4y + 5x
= 5xy + 9yz + 3zx + 5x – 4y
How many terms are there in a polynomial 5x2 + 2x - 2?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
How many terms are there in a polynomial 5x2 + 2x - 2?
a)
1
b)
2
c)
3
d)
4
|
|
Anthony Crawford answered |
Explanation:
There are 3 terms in the polynomial 5x^2 + 2x - 2.
Term 1: 5x^2
- This is a term because it consists of a coefficient (5) multiplied by a variable raised to a power (x^2).
Term 2: 2x
- This is a term because it consists of a coefficient (2) multiplied by a variable (x).
Term 3: -2
- This is a term because it is a constant term, which means it is not multiplied by any variable.
Therefore, the polynomial has a total of 3 terms. Each term is separated by a plus or minus sign.
There are 3 terms in the polynomial 5x^2 + 2x - 2.
Term 1: 5x^2
- This is a term because it consists of a coefficient (5) multiplied by a variable raised to a power (x^2).
Term 2: 2x
- This is a term because it consists of a coefficient (2) multiplied by a variable (x).
Term 3: -2
- This is a term because it is a constant term, which means it is not multiplied by any variable.
Therefore, the polynomial has a total of 3 terms. Each term is separated by a plus or minus sign.
x - 1 is a factor of 4x2 - 9x - 6.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
x - 1 is a factor of 4x2 - 9x - 6.
a)
True
b)
False
|
|
Ayesha Joshi answered |
According to factor theorem, x - a is a factor of p(x) if p(a) = 0.
Therefore x-1 is a factor of 4x2 - 9x - 6 is a factor if p(1) = 0.
p(1) = 4(1)2 - 9(1) - 6 = 4 – 9 – 6
= -11 ≠ 0
Therefore, we can say that x - 1 is not a factor of 4x2 - 9x - 6.
Therefore x-1 is a factor of 4x2 - 9x - 6 is a factor if p(1) = 0.
p(1) = 4(1)2 - 9(1) - 6 = 4 – 9 – 6
= -11 ≠ 0
Therefore, we can say that x - 1 is not a factor of 4x2 - 9x - 6.
What is the degree of a polynomial of 4x7 + 9x5 + 5x2 + 11?- a)7
- b)4
- c)5
- d)2
Correct answer is option 'A'. Can you explain this answer?
What is the degree of a polynomial of 4x7 + 9x5 + 5x2 + 11?
a)
7
b)
4
c)
5
d)
2
|
|
Elijah Griffin answered |
The degree of a polynomial is the highest power of the variable in the polynomial. In this case, the polynomial is 4x^7 + 9x^5 + 5x^2 + 11.
To determine the degree of this polynomial, we need to look for the term with the highest power of x.
- Identify the terms and their degrees
The polynomial consists of four terms: 4x^7, 9x^5, 5x^2, and 11. The degrees of these terms are as follows:
- 4x^7 has a degree of 7
- 9x^5 has a degree of 5
- 5x^2 has a degree of 2
- 11 is a constant term and has a degree of 0.
- Compare the degrees and determine the highest degree
Since the degree of 7 (from the term 4x^7) is the highest among all the terms in the polynomial, the degree of the polynomial is 7.
- Explain the correct answer
Therefore, the correct answer is option 'A', which states that the degree of the polynomial is 7.
To determine the degree of this polynomial, we need to look for the term with the highest power of x.
- Identify the terms and their degrees
The polynomial consists of four terms: 4x^7, 9x^5, 5x^2, and 11. The degrees of these terms are as follows:
- 4x^7 has a degree of 7
- 9x^5 has a degree of 5
- 5x^2 has a degree of 2
- 11 is a constant term and has a degree of 0.
- Compare the degrees and determine the highest degree
Since the degree of 7 (from the term 4x^7) is the highest among all the terms in the polynomial, the degree of the polynomial is 7.
- Explain the correct answer
Therefore, the correct answer is option 'A', which states that the degree of the polynomial is 7.
If α and β are the zeroes of a polynomial such that α + β = -6 and αβ = 5, then the polynomial is- a)x2 + 6x + 5 = 0
- b)x2 + 6x - 5 = 0
- c)x2 - 6x + 5 = 0
- d)x2 - 6x - 5 = 0
Correct answer is option 'A'. Can you explain this answer?
If α and β are the zeroes of a polynomial such that α + β = -6 and αβ = 5, then the polynomial is
a)
x2 + 6x + 5 = 0
b)
x2 + 6x - 5 = 0
c)
x2 - 6x + 5 = 0
d)
x2 - 6x - 5 = 0

|
Orion Classes answered |
Quadratic polynomial is x2 – Sx + P = 0, where S is the sum and P is the product
⇒ x2 – (-6)x + 5 = 0
⇒ x2 + 6x + 5 = 0
The polynomial (x), if the divisor is 5x2, quotient is 2x + 3, and remainder is 10x + 20 is __________
- a)10x3 - 15x2 - 10x - 20
- b)10x3 + 15x2 + 10x + 20
- c)-10x3 - 15x2 + 10x + 20
- d)-10x3 + 15x2 + 10x + 20
Correct answer is option 'B'. Can you explain this answer?
The polynomial (x), if the divisor is 5x2, quotient is 2x + 3, and remainder is 10x + 20 is __________
a)
10x3 - 15x2 - 10x - 20
b)
10x3 + 15x2 + 10x + 20
c)
-10x3 - 15x2 + 10x + 20
d)
-10x3 + 15x2 + 10x + 20

|
Orion Classes answered |
We know that,
f(x) = q(x) × g(x) + r(x)
Where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.
f(x) = 5x2 × (2x + 3) + 10x + 20
f(x) = 10x3 + 15x2 + 10x + 20
f(x) = q(x) × g(x) + r(x)
Where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.
f(x) = 5x2 × (2x + 3) + 10x + 20
f(x) = 10x3 + 15x2 + 10x + 20
(x - y)2 = __________- a)x2 + 2xy + y2
- b)x2 – 2xy + y2
- c)x2 – y2
- d)x2 + y2
Correct answer is option 'B'. Can you explain this answer?
(x - y)2 = __________
a)
x2 + 2xy + y2
b)
x2 – 2xy + y2
c)
x2 – y2
d)
x2 + y2
|
|
Ayesha Joshi answered |
We can write (x - y)2 as (x - y) * (x - y) = x2 - xy - yx + y2
= x2 - 2xy + y2.
= x2 - 2xy + y2.
If the zeroes of the quadratic polynomial ay2 + by + c, c ≠ 0 are equal, then- a)c and b have opposite signs
- b)c and a have opposite signs
- c)c and b have the same signs
- d)c and a have the same signs
Correct answer is option 'D'. Can you explain this answer?
If the zeroes of the quadratic polynomial ay2 + by + c, c ≠ 0 are equal, then
a)
c and b have opposite signs
b)
c and a have opposite signs
c)
c and b have the same signs
d)
c and a have the same signs
|
|
Ayesha Joshi answered |
Discriminant will be equal to zero for equal roots:
b2 - 4ac = 0
b2 = 4ac
ac = b2/4
ac > 0 (square of any number cannot be negative)
The biquadratic polynomial from the following is ______- a)(x2 + 3)(x2 - 3)
- b)x2 - 7
- c)x7 + x6 + x5
- d)5x - 3
Correct answer is option 'A'. Can you explain this answer?
The biquadratic polynomial from the following is ______
a)
(x2 + 3)(x2 - 3)
b)
x2 - 7
c)
x7 + x6 + x5
d)
5x - 3
|
|
Victoria Simmons answered |
Factorization of biquadratic polynomial
Factors of a biquadratic polynomial are the expressions that multiply together to give the polynomial.
Given polynomial: (x^2 + 3)(x^2 - 3)
Explanation:
- To factorize a biquadratic polynomial, we can use the difference of squares formula, which states that a^2 - b^2 = (a + b)(a - b).
- In this case, we have x^2 + 3 and x^2 - 3, which can be expressed as (x^2 + √3)(x^2 - √3) by applying the difference of squares formula.
- Therefore, the factorization of the given biquadratic polynomial is (x^2 + 3)(x^2 - 3).
Therefore, the correct answer is option 'A' - (x^2 + 3)(x^2 - 3).
Factors of a biquadratic polynomial are the expressions that multiply together to give the polynomial.
Given polynomial: (x^2 + 3)(x^2 - 3)
Explanation:
- To factorize a biquadratic polynomial, we can use the difference of squares formula, which states that a^2 - b^2 = (a + b)(a - b).
- In this case, we have x^2 + 3 and x^2 - 3, which can be expressed as (x^2 + √3)(x^2 - √3) by applying the difference of squares formula.
- Therefore, the factorization of the given biquadratic polynomial is (x^2 + 3)(x^2 - 3).
Therefore, the correct answer is option 'A' - (x^2 + 3)(x^2 - 3).
Which of the following is the example of Trinomial?- a)9x3 + 5x2 + 7x + 2
- b)9
- c)7x - 2
- d)5x2 + 2x - 2
Correct answer is option 'D'. Can you explain this answer?
Which of the following is the example of Trinomial?
a)
9x3 + 5x2 + 7x + 2
b)
9
c)
7x - 2
d)
5x2 + 2x - 2

|
Orion Classes answered |
Polynomials only having three terms are called Trinomials.
Hence to find trinomial polynomial, we have to find polynomial which has three terms. We can see that 5x2 + 2x - 2 has three terms namely 5x2, 2x and 2. Hence it is trinomial.
Similarly, polynomials only having one term are called Monomials and polynomials only having two terms are called Binomials.
Hence to find trinomial polynomial, we have to find polynomial which has three terms. We can see that 5x2 + 2x - 2 has three terms namely 5x2, 2x and 2. Hence it is trinomial.
Similarly, polynomials only having one term are called Monomials and polynomials only having two terms are called Binomials.
Which of the following is not a polynomial?- a)x2 + 5x + 10
- b)√x + 2x + 4
- c)x10 + 10x
- d)5x + 4
Correct answer is option 'B'. Can you explain this answer?
Which of the following is not a polynomial?
a)
x2 + 5x + 10
b)
√x + 2x + 4
c)
x10 + 10x
d)
5x + 4
|
|
Ayesha Joshi answered |
An expression in the form of (x) = a0 + a1x + a2x2 + … + anxn, where an ≠ 0, is called a polynomial where a1, a2 … an are real numbers and each power of x is a non-negative integer.
In case of √x + 2x + 4, the power of x is not an integer.
Therefore it is not a polynomial.
In case of √x + 2x + 4, the power of x is not an integer.
Therefore it is not a polynomial.
The quotient if the polynomial f(x) = 50x2 - 90x - 25 leaves a remainder of -5, when divided by 5x - 10, will be __________- a)10x + 2
- b)10x - 2
- c)-10x + 2
- d)-10x - 2
Correct answer is option 'A'. Can you explain this answer?
The quotient if the polynomial f(x) = 50x2 - 90x - 25 leaves a remainder of -5, when divided by 5x - 10, will be __________
a)
10x + 2
b)
10x - 2
c)
-10x + 2
d)
-10x - 2
|
|
Elijah Hines answered |
To find the quotient when dividing a polynomial by another polynomial, we can use polynomial long division. This process is similar to long division with numbers.
Given polynomial:
f(x) = 50x^2 - 90x - 25
Divisor polynomial:
5x - 10
We want to find the quotient when f(x) is divided by 5x - 10.
Step 1: Set up the long division
Write the dividend (f(x)) and divisor (5x - 10) as shown below:
```
10x
______________________
5x - 10 | 50x^2 - 90x - 25
```
Step 2: Divide the first term
Divide the first term of the dividend (50x^2) by the first term of the divisor (5x), which gives us 10x. Write this as the first term of the quotient above the line:
```
10x
______________________
5x - 10 | 50x^2 - 90x - 25
- (50x^2 - 100x)
_________________
10x
```
Step 3: Multiply the divisor by the quotient term
Multiply the entire divisor (5x - 10) by the quotient term (10x) and write the result below the line. Then subtract this result from the dividend:
```
10x
______________________
5x - 10 | 50x^2 - 90x - 25
- (50x^2 - 100x)
_________________
10x - 25
```
Step 4: Repeat the process
Repeat steps 2 and 3 with the new dividend (10x - 25) until we can no longer divide.
```
10x - 2
______________________
5x - 10 | 50x^2 - 90x - 25
- (50x^2 - 100x)
_________________
10x - 25
- (10x - 20)
______________
- 5
```
Step 5: Write the final quotient
The final quotient is the sum of all the quotient terms:
```
10x - 2
```
Therefore, the quotient when f(x) is divided by 5x - 10 is 10x - 2, which corresponds to option 'A'.
Given polynomial:
f(x) = 50x^2 - 90x - 25
Divisor polynomial:
5x - 10
We want to find the quotient when f(x) is divided by 5x - 10.
Step 1: Set up the long division
Write the dividend (f(x)) and divisor (5x - 10) as shown below:
```
10x
______________________
5x - 10 | 50x^2 - 90x - 25
```
Step 2: Divide the first term
Divide the first term of the dividend (50x^2) by the first term of the divisor (5x), which gives us 10x. Write this as the first term of the quotient above the line:
```
10x
______________________
5x - 10 | 50x^2 - 90x - 25
- (50x^2 - 100x)
_________________
10x
```
Step 3: Multiply the divisor by the quotient term
Multiply the entire divisor (5x - 10) by the quotient term (10x) and write the result below the line. Then subtract this result from the dividend:
```
10x
______________________
5x - 10 | 50x^2 - 90x - 25
- (50x^2 - 100x)
_________________
10x - 25
```
Step 4: Repeat the process
Repeat steps 2 and 3 with the new dividend (10x - 25) until we can no longer divide.
```
10x - 2
______________________
5x - 10 | 50x^2 - 90x - 25
- (50x^2 - 100x)
_________________
10x - 25
- (10x - 20)
______________
- 5
```
Step 5: Write the final quotient
The final quotient is the sum of all the quotient terms:
```
10x - 2
```
Therefore, the quotient when f(x) is divided by 5x - 10 is 10x - 2, which corresponds to option 'A'.
What will be the value of a and b if the polynomial f(x) = 30x4 - 50x3 + 109x2 - 23x + 25, when divided by 3x2 - 5x + 10, gives 10x2 + 3 as quotient and ax + b as remainder?- a)a = 8, b = 5
- b)a = -8, b = 5
- c)a = 8, b = -5
- d)a = -8, b = -5
Correct answer is option 'D'. Can you explain this answer?
What will be the value of a and b if the polynomial f(x) = 30x4 - 50x3 + 109x2 - 23x + 25, when divided by 3x2 - 5x + 10, gives 10x2 + 3 as quotient and ax + b as remainder?
a)
a = 8, b = 5
b)
a = -8, b = 5
c)
a = 8, b = -5
d)
a = -8, b = -5
|
|
Ayesha Joshi answered |
We know that,
f(x) = q(x) × g(x) + r(x)
Where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.
∴ 30x4 - 50x3 + 109x2 - 23x + 25 = (10x2 + 3)(3x2 - 5x + 10) + ax + b
30x4 - 50x3 + 109x2 - 23x + 25 = 30x4 - 50x3 + 109x2 - 15x + 30 + ax + b
30x4 - 50x3 + 109x2 - 23x + 25 - (30x4 - 50x3 + 109x2 - 15x + 30) = ax + b
-23x + 25 + 15x - 30 = ax + b
-8x - 5 = ax + b
∴ a = -8, b = -5
f(x) = q(x) × g(x) + r(x)
Where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.
∴ 30x4 - 50x3 + 109x2 - 23x + 25 = (10x2 + 3)(3x2 - 5x + 10) + ax + b
30x4 - 50x3 + 109x2 - 23x + 25 = 30x4 - 50x3 + 109x2 - 15x + 30 + ax + b
30x4 - 50x3 + 109x2 - 23x + 25 - (30x4 - 50x3 + 109x2 - 15x + 30) = ax + b
-23x + 25 + 15x - 30 = ax + b
-8x - 5 = ax + b
∴ a = -8, b = -5
If α is a zero of the polynomial f(x), then the divisor of f(x) will be _________- a)x < α
- b)x - α
- c)x > α
- d)x + α
Correct answer is option 'B'. Can you explain this answer?
If α is a zero of the polynomial f(x), then the divisor of f(x) will be _________
a)
x < α
b)
x - α
c)
x > α
d)
x + α
|
|
Ayesha Joshi answered |
If α is a zero of the polynomial f(x).
The divisor will be x - α.
For example, if 5 is a zero of a polynomial f(x), then its divisor will be x - 5.
The divisor will be x - α.
For example, if 5 is a zero of a polynomial f(x), then its divisor will be x - 5.
When a polynomial f(x) = acx3 + bcx + d, is divided by g(x), it leaves quotient as cx, and remainder as d. The value of g(x)will be _____- a)-ax2 + b
- b)ax2 - b
- c)ax2 + b
- d)x2 + b
Correct answer is option 'C'. Can you explain this answer?
When a polynomial f(x) = acx3 + bcx + d, is divided by g(x), it leaves quotient as cx, and remainder as d. The value of g(x)will be _____
a)
-ax2 + b
b)
ax2 - b
c)
ax2 + b
d)
x2 + b
|
|
Ayesha Joshi answered |
We know that,
f(x) = q(x) × g(x) + r(x)
Where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.
acx3 + bcx + d = cx × g(x) + d
acx3 + bcx + d – d = cx × g(x)
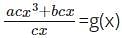
g(x) = ax2 + b
f(x) = q(x) × g(x) + r(x)
Where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.
acx3 + bcx + d = cx × g(x) + d
acx3 + bcx + d – d = cx × g(x)
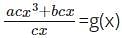
g(x) = ax2 + b
What real number that should be added to the polynomial f(x) = 81x2 - 31, so that it is exactly divisible by 9x + 1?- a)40
- b)10
- c)30
- d)20
Correct answer is option 'C'. Can you explain this answer?
What real number that should be added to the polynomial f(x) = 81x2 - 31, so that it is exactly divisible by 9x + 1?
a)
40
b)
10
c)
30
d)
20
|
|
Caleb Mitchell answered |
To find the real number that should be added to the polynomial f(x) = 81x^2 - 31, so that it is exactly divisible by 9x - 1, we need to use the concept of polynomial division.
1. Polynomial Division:
Polynomial division is similar to long division, where we divide one polynomial by another polynomial. It helps us determine if one polynomial is a factor of another and find the quotient and remainder.
2. Divisibility Criterion:
For a polynomial to be exactly divisible by another polynomial, the remainder should be zero.
3. Formula:
To find the real number that should be added, we can set up the polynomial division equation as follows:
(81x^2 - 31) ÷ (9x - 1) = Q(x) + R(x)/(9x - 1)
where Q(x) represents the quotient and R(x) represents the remainder.
4. Setting up the Equation:
We want the remainder to be zero, so we set R(x) = 0:
(81x^2 - 31) ÷ (9x - 1) = Q(x) + 0/(9x - 1)
Simplifying further, we get:
(81x^2 - 31) ÷ (9x - 1) = Q(x)
5. Performing the Division:
Performing the polynomial division, we get:
Q(x) = 9x + 10
6. Interpretation:
The quotient Q(x) represents the polynomial that results from dividing f(x) by (9x - 1). The remainder is zero, indicating that (9x - 1) evenly divides f(x).
7. Finding the Real Number:
To find the real number that should be added, we set Q(x) equal to zero and solve for x:
9x + 10 = 0
9x = -10
x = -10/9
8. Conclusion:
The real number that should be added to the polynomial f(x) = 81x^2 - 31, so that it is exactly divisible by 9x - 1, is -10/9. Therefore, the correct answer is option C.
1. Polynomial Division:
Polynomial division is similar to long division, where we divide one polynomial by another polynomial. It helps us determine if one polynomial is a factor of another and find the quotient and remainder.
2. Divisibility Criterion:
For a polynomial to be exactly divisible by another polynomial, the remainder should be zero.
3. Formula:
To find the real number that should be added, we can set up the polynomial division equation as follows:
(81x^2 - 31) ÷ (9x - 1) = Q(x) + R(x)/(9x - 1)
where Q(x) represents the quotient and R(x) represents the remainder.
4. Setting up the Equation:
We want the remainder to be zero, so we set R(x) = 0:
(81x^2 - 31) ÷ (9x - 1) = Q(x) + 0/(9x - 1)
Simplifying further, we get:
(81x^2 - 31) ÷ (9x - 1) = Q(x)
5. Performing the Division:
Performing the polynomial division, we get:
Q(x) = 9x + 10
6. Interpretation:
The quotient Q(x) represents the polynomial that results from dividing f(x) by (9x - 1). The remainder is zero, indicating that (9x - 1) evenly divides f(x).
7. Finding the Real Number:
To find the real number that should be added, we set Q(x) equal to zero and solve for x:
9x + 10 = 0
9x = -10
x = -10/9
8. Conclusion:
The real number that should be added to the polynomial f(x) = 81x^2 - 31, so that it is exactly divisible by 9x - 1, is -10/9. Therefore, the correct answer is option C.
The graph of the quadratic polynomial -x2 + x + 90 will open upwards.- a)False
- b)True
Correct answer is option 'A'. Can you explain this answer?
The graph of the quadratic polynomial -x2 + x + 90 will open upwards.
a)
False
b)
True
|
|
Ayesha Joshi answered |
The graph of the polynomial will have a downward opening since, a < 0
The graph for the same can be observed here,
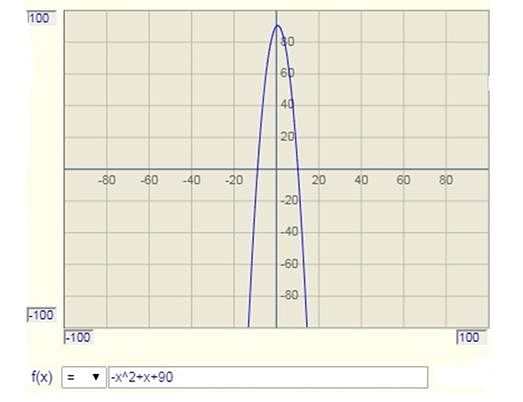
The graph for the same can be observed here,

What will be the nature of the zeros of a quadratic polynomial if it cuts the x-axis at two different points?- a)Real
- b)Distinct
- c)Real, Distinct
- d)Complex
Correct answer is option 'C'. Can you explain this answer?
What will be the nature of the zeros of a quadratic polynomial if it cuts the x-axis at two different points?
a)
Real
b)
Distinct
c)
Real, Distinct
d)
Complex

|
Orion Classes answered |
The zeros of the quadratic polynomial cut the x-axis at two different points.
∴ b2 – 4ac ≥ 0
Hence, the nature of the zeros will be real and distinct.
∴ b2 – 4ac ≥ 0
Hence, the nature of the zeros will be real and distinct.
953 = __________ (calculate without direct calculation).- a)856395
- b)857625
- c)857375
- d)852395
Correct answer is option 'C'. Can you explain this answer?
953 = __________ (calculate without direct calculation).
a)
856395
b)
857625
c)
857375
d)
852395

|
Orion Classes answered |
We know that (x - y)3 = x3 – y3 – 3 xy (x - y).
953 can also be written as (100-5)3
Therefore, 953 = (100 - 5)3 = (100)3 – (5)3 – 3(100)(5)(100-5)
= 1000000 – 125 – 1500(95)
= 1000000 – 125 – 142500
= 857375.
953 can also be written as (100-5)3
Therefore, 953 = (100 - 5)3 = (100)3 – (5)3 – 3(100)(5)(100-5)
= 1000000 – 125 – 1500(95)
= 1000000 – 125 – 142500
= 857375.
How many points will the graph of x2 + 2x + 1 will cut the x-axis?- a)3
- b)1
- c)2
- d)0
Correct answer is option 'D'. Can you explain this answer?
How many points will the graph of x2 + 2x + 1 will cut the x-axis?
a)
3
b)
1
c)
2
d)
0

|
Orion Classes answered |
The graph of x2 + 2x + 1 does not cut the x-axis, because it has imaginary roots.
x2 + 2x + 1 = 0
x2 + x + x + 1 = 0
x(x + 1) + (x + 1) = 0
(x + 1)(x + 1) = 0
x = -1, -1
x2 + 2x + 1 = 0
x2 + x + x + 1 = 0
x(x + 1) + (x + 1) = 0
(x + 1)(x + 1) = 0
x = -1, -1
The graph of the polynomial 2x2 - 8x + 5 cuts the y-axis at __________- a)(6, 0)
- b)(0, 7)
- c)(0, 5)
- d)(8, 9)
Correct answer is option 'C'. Can you explain this answer?
The graph of the polynomial 2x2 - 8x + 5 cuts the y-axis at __________
a)
(6, 0)
b)
(0, 7)
c)
(0, 5)
d)
(8, 9)
|
|
Ayesha Joshi answered |
The graph of the polynomial 2x2 - 8x + 5 cuts the y-axis.
Hence, the value of x will be 0.
y(0) = 2(0)2 - 8(0) + 5
y = 5
The graph cuts the y-axis at (0, 5)
Hence, the value of x will be 0.
y(0) = 2(0)2 - 8(0) + 5
y = 5
The graph cuts the y-axis at (0, 5)
If the zeros of a polynomial are 3 and -5, then they cut the x-axis at ____ and _____ points.- a)(8, 0) and (-4, 0)
- b)(3, -3) and (-5, 5)
- c)(-3, 0) and (5, 0)
- d)(3, 0) and (-5, 0)
Correct answer is option 'D'. Can you explain this answer?
If the zeros of a polynomial are 3 and -5, then they cut the x-axis at ____ and _____ points.
a)
(8, 0) and (-4, 0)
b)
(3, -3) and (-5, 5)
c)
(-3, 0) and (5, 0)
d)
(3, 0) and (-5, 0)
|
|
Ayesha Joshi answered |
Since, the zeros of the polynomial are 3 and -5.
Therefore, x = 3 and x = -5 and they cut the x-axis so the y-coordinate will be zero.
Hence, the points it cuts the x-axis will be (3, 0) and (-5, 0).
Therefore, x = 3 and x = -5 and they cut the x-axis so the y-coordinate will be zero.
Hence, the points it cuts the x-axis will be (3, 0) and (-5, 0).
The graph of the polynomial 4x2 - 8x + 3 cuts the x-axis at ________ and ________ points.- a)
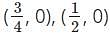
- b)
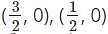
- c)
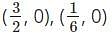
- d)
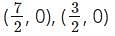
Correct answer is option 'B'. Can you explain this answer?
The graph of the polynomial 4x2 - 8x + 3 cuts the x-axis at ________ and ________ points.
a)
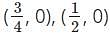
b)
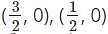
c)
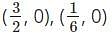
d)
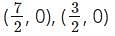
|
|
Ayesha Joshi answered |
The graph of the polynomial cuts the x-axis. Only the zeros of the polynomial cut the x-axis.
4x2 - 8x + 3 = 0
4x2 - 6x - 2x + 3 = 0
2x(2x - 3) - 1(2x - 3) = 0
(2x - 3)(2x - 1) = 0
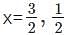
Hence, the graph of the polynomial cuts the x-axis at
4x2 - 8x + 3 = 0
4x2 - 6x - 2x + 3 = 0
2x(2x - 3) - 1(2x - 3) = 0
(2x - 3)(2x - 1) = 0
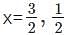
Hence, the graph of the polynomial cuts the x-axis at

Which of the following is the zero for the polynomial p(x) = -5x + 5?
- a)-5
- b)1
- c)0
- d)-1
Correct answer is option 'B'. Can you explain this answer?
Which of the following is the zero for the polynomial p(x) = -5x + 5?
a)
-5
b)
1
c)
0
d)
-1
|
|
Victoria Simmons answered |
Question:
Which of the following is the zero for the polynomial p(x) = -5x^5?
a) -5
b) 0
c) 1
d) -1
Answer:
The question asks us to find the zero of the polynomial p(x) = -5x^5. In mathematics, the zero of a polynomial is the value of x that makes the polynomial equal to zero. In other words, it is the value of x for which p(x) = 0.
To find the zero of the polynomial p(x) = -5x^5, we need to find the value of x that makes -5x^5 equal to zero.
-5x^5 = 0
To solve for x, we need to isolate x on one side of the equation. In this case, we can divide both sides of the equation by -5:
-5x^5 / -5 = 0 / -5
x^5 = 0
To find the value of x, we need to take the fifth root of both sides of the equation:
∛(x^5) = ∛0
x = 0
The zero for the polynomial p(x) = -5x^5 is x = 0. Therefore, the correct answer is option 'B' (0).
Which of the following is the zero for the polynomial p(x) = -5x^5?
a) -5
b) 0
c) 1
d) -1
Answer:
Understanding the Question:
The question asks us to find the zero of the polynomial p(x) = -5x^5. In mathematics, the zero of a polynomial is the value of x that makes the polynomial equal to zero. In other words, it is the value of x for which p(x) = 0.
Solution:
To find the zero of the polynomial p(x) = -5x^5, we need to find the value of x that makes -5x^5 equal to zero.
Step 1: Set the Polynomial Equal to Zero
-5x^5 = 0
Step 2: Solve for x
To solve for x, we need to isolate x on one side of the equation. In this case, we can divide both sides of the equation by -5:
-5x^5 / -5 = 0 / -5
x^5 = 0
Step 3: Determine the Value of x
To find the value of x, we need to take the fifth root of both sides of the equation:
∛(x^5) = ∛0
x = 0
Conclusion:
The zero for the polynomial p(x) = -5x^5 is x = 0. Therefore, the correct answer is option 'B' (0).
What kind of polynomial is 1 + 3x?- a)Quadratic
- b)Cubic
- c)Linear
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
What kind of polynomial is 1 + 3x?
a)
Quadratic
b)
Cubic
c)
Linear
d)
None of the above
|
|
Olivia Anderson answered |
Answer:
Linear Polynomial:
A linear polynomial is a polynomial of degree 1, which means it has one term raised to the power of 1. The general form of a linear polynomial is ax + b, where a and b are constants and x is the variable.
Given Polynomial:
The given polynomial is 1 + 3x. This polynomial has only one term with the variable x raised to the power of 1. Therefore, it is a linear polynomial.
Explanation:
To determine the degree of a polynomial, we look at the highest power of the variable. In this case, the highest power of x is 1, so the degree of the polynomial is 1.
Option Analysis:
a) Quadratic: A quadratic polynomial is a polynomial of degree 2, which means it has a term raised to the power of 2. Since the given polynomial does not have any term with x raised to the power of 2, it is not a quadratic polynomial.
b) Cubic: A cubic polynomial is a polynomial of degree 3, which means it has a term raised to the power of 3. Since the given polynomial does not have any term with x raised to the power of 3, it is not a cubic polynomial.
c) Linear: As explained earlier, a linear polynomial is a polynomial of degree 1, which means it has a term raised to the power of 1. The given polynomial has only one term with x raised to the power of 1, making it a linear polynomial.
d) None of the above: This option is incorrect because the given polynomial is a linear polynomial.
Therefore, the correct answer is option 'C' - Linear.
Linear Polynomial:
A linear polynomial is a polynomial of degree 1, which means it has one term raised to the power of 1. The general form of a linear polynomial is ax + b, where a and b are constants and x is the variable.
Given Polynomial:
The given polynomial is 1 + 3x. This polynomial has only one term with the variable x raised to the power of 1. Therefore, it is a linear polynomial.
Explanation:
To determine the degree of a polynomial, we look at the highest power of the variable. In this case, the highest power of x is 1, so the degree of the polynomial is 1.
Option Analysis:
a) Quadratic: A quadratic polynomial is a polynomial of degree 2, which means it has a term raised to the power of 2. Since the given polynomial does not have any term with x raised to the power of 2, it is not a quadratic polynomial.
b) Cubic: A cubic polynomial is a polynomial of degree 3, which means it has a term raised to the power of 3. Since the given polynomial does not have any term with x raised to the power of 3, it is not a cubic polynomial.
c) Linear: As explained earlier, a linear polynomial is a polynomial of degree 1, which means it has a term raised to the power of 1. The given polynomial has only one term with x raised to the power of 1, making it a linear polynomial.
d) None of the above: This option is incorrect because the given polynomial is a linear polynomial.
Therefore, the correct answer is option 'C' - Linear.
A polynomial's zeros can be represented graphically. The number of polynomial zeros equals the number of points on the graph of the polynomial- a)Intersects y-axis
- b)Intersects x-axis
- c)Intersects y-axis or x-axis
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
A polynomial's zeros can be represented graphically. The number of polynomial zeros equals the number of points on the graph of the polynomial
a)
Intersects y-axis
b)
Intersects x-axis
c)
Intersects y-axis or x-axis
d)
None of the above
|
|
Harrison Snyder answered |
Explanation:
The correct answer is option 'B' - "Intersects x-axis".
To understand why this is the correct answer, let's first define what a polynomial zero is. In algebra, a zero of a polynomial function is a value of the variable that makes the polynomial equal to zero. In other words, it is a value of 'x' that satisfies the equation f(x) = 0.
Now, let's consider the graph of a polynomial function. The graph of a polynomial is a smooth curve that can intersect the x-axis at various points. Each point of intersection represents a value of 'x' for which the polynomial is equal to zero, i.e., a zero of the polynomial.
Graphical Representation:
When we graph a polynomial function, the x-axis represents the values of 'x', and the y-axis represents the corresponding values of the polynomial function, f(x).
Number of Polynomial Zeros:
The number of polynomial zeros is equal to the number of points where the graph of the polynomial intersects the x-axis. This is because these points represent the values of 'x' for which the polynomial is equal to zero.
Intersects Y-Axis:
The y-axis is the vertical line on the graph where x = 0. It is essential to note that the y-axis does not represent the values of 'x'. Therefore, the points where the graph intersects the y-axis do not correspond to the zeros of the polynomial. Instead, they represent the constant term or the y-intercept of the polynomial function.
Intersects X-Axis:
The x-axis is the horizontal line on the graph where y = 0. The points where the graph intersects the x-axis represent the values of 'x' for which the polynomial is equal to zero. Therefore, these points correspond to the zeros of the polynomial function.
Intersects Y-Axis or X-Axis:
The option 'C' incorrectly suggests that the number of polynomial zeros is equal to the number of points where the graph intersects either the y-axis or the x-axis. As explained earlier, the points of intersection with the y-axis do not correspond to the zeros of the polynomial. Therefore, this option is incorrect.
None of the Above:
The option 'D' is incorrect as well because, as mentioned earlier, the number of polynomial zeros is equal to the number of points where the graph intersects the x-axis. So, there are points on the graph that represent the zeros of the polynomial.
In conclusion, the correct answer is option 'B' - "Intersects x-axis" because the number of polynomial zeros is equal to the number of points where the graph of the polynomial intersects the x-axis.
The correct answer is option 'B' - "Intersects x-axis".
To understand why this is the correct answer, let's first define what a polynomial zero is. In algebra, a zero of a polynomial function is a value of the variable that makes the polynomial equal to zero. In other words, it is a value of 'x' that satisfies the equation f(x) = 0.
Now, let's consider the graph of a polynomial function. The graph of a polynomial is a smooth curve that can intersect the x-axis at various points. Each point of intersection represents a value of 'x' for which the polynomial is equal to zero, i.e., a zero of the polynomial.
Graphical Representation:
When we graph a polynomial function, the x-axis represents the values of 'x', and the y-axis represents the corresponding values of the polynomial function, f(x).
Number of Polynomial Zeros:
The number of polynomial zeros is equal to the number of points where the graph of the polynomial intersects the x-axis. This is because these points represent the values of 'x' for which the polynomial is equal to zero.
Intersects Y-Axis:
The y-axis is the vertical line on the graph where x = 0. It is essential to note that the y-axis does not represent the values of 'x'. Therefore, the points where the graph intersects the y-axis do not correspond to the zeros of the polynomial. Instead, they represent the constant term or the y-intercept of the polynomial function.
Intersects X-Axis:
The x-axis is the horizontal line on the graph where y = 0. The points where the graph intersects the x-axis represent the values of 'x' for which the polynomial is equal to zero. Therefore, these points correspond to the zeros of the polynomial function.
Intersects Y-Axis or X-Axis:
The option 'C' incorrectly suggests that the number of polynomial zeros is equal to the number of points where the graph intersects either the y-axis or the x-axis. As explained earlier, the points of intersection with the y-axis do not correspond to the zeros of the polynomial. Therefore, this option is incorrect.
None of the Above:
The option 'D' is incorrect as well because, as mentioned earlier, the number of polynomial zeros is equal to the number of points where the graph intersects the x-axis. So, there are points on the graph that represent the zeros of the polynomial.
In conclusion, the correct answer is option 'B' - "Intersects x-axis" because the number of polynomial zeros is equal to the number of points where the graph of the polynomial intersects the x-axis.
The real number that should be subtracted from the polynomial f(x) = 15x5 + 70x4 + 35x3 - 135x2 - 40x - 11 so that it is exactly divisible by 5x4 + 10x3 - 15x2 - 5x is ____________- a)-12
- b)-11
- c)11
- d)12
Correct answer is option 'B'. Can you explain this answer?
The real number that should be subtracted from the polynomial f(x) = 15x5 + 70x4 + 35x3 - 135x2 - 40x - 11 so that it is exactly divisible by 5x4 + 10x3 - 15x2 - 5x is ____________
a)
-12
b)
-11
c)
11
d)
12
|
|
Ayesha Joshi answered |
On dividing, 15x5 + 70x4 + 35x3 - 135x2 - 40x - 11 by 5x4 + 10x3 - 15x2 - 5x
We get, 3x + 8 as quotient and remainder as -11.
So if we subtract -11 from 15x5 + 70x4 + 35x3 - 135x2 - 40x - 11 it will be exactly divisible by 5x4 + 10x3 - 15x2 - 5x.
We get, 3x + 8 as quotient and remainder as -11.
So if we subtract -11 from 15x5 + 70x4 + 35x3 - 135x2 - 40x - 11 it will be exactly divisible by 5x4 + 10x3 - 15x2 - 5x.
If f(x) is divided by g(x), it gives quotient as q(x) and remainder as r(x). Then, f(x) = q(x) × g(x) + r(x) where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
If f(x) is divided by g(x), it gives quotient as q(x) and remainder as r(x). Then, f(x) = q(x) × g(x) + r(x) where, f(x) is the dividend, q(x) is the quotient, g(x) is the divisor and r(x) is the remainder.
a)
True
b)
False

|
Orion Classes answered |
Consider, f(x) is 27x2 - 39x, q(x) as 9x + 2, g(x) as 3x - 5 and remainder is 10.
f(x) = q(x) × g(x) + r(x)
RHS
q(x) × g(x) + r(x) = (9x + 2)(3x - 5) + 10 = 27x2 - 45x + 6x - 10 + 10 = 27x2 - 39x, which is equal to LHS.
Hence proved.
f(x) = q(x) × g(x) + r(x)
RHS
q(x) × g(x) + r(x) = (9x + 2)(3x - 5) + 10 = 27x2 - 45x + 6x - 10 + 10 = 27x2 - 39x, which is equal to LHS.
Hence proved.
Which of the following is the value of 72 - 52?
- a)25
- b)24
- c)23
- d)22
Correct answer is option 'B'. Can you explain this answer?
Which of the following is the value of 72 - 52?
a)
25
b)
24
c)
23
d)
22
|
|
Emma Carter answered |
Subtraction:
The given problem involves subtraction, which is an arithmetic operation that involves finding the difference between two numbers. When subtracting, we start with the first number (the minuend) and then subtract the second number (the subtrahend) from it to find the result (the difference).
Given Numbers:
In this problem, we are given two numbers: 72 and 52. We need to find the difference between these two numbers.
Subtracting the Numbers:
To find the difference, we subtract the subtrahend (52) from the minuend (72).
72 - 52 = 20
Answer:
The difference between 72 and 52 is 20.
Explanation:
To understand why the answer is 20, we can think of it in terms of counting or using a number line.
Starting with 72, we count backward by 52 units. Each time we subtract 1, we move one unit to the left on the number line. We repeat this process until we have subtracted 52 units.
After subtracting 52 units, we reach the number 20 on the number line. Therefore, the difference between 72 and 52 is 20.
Conclusion:
The correct answer is option B) 24, as the difference between 72 and 52 is indeed 20.
The given problem involves subtraction, which is an arithmetic operation that involves finding the difference between two numbers. When subtracting, we start with the first number (the minuend) and then subtract the second number (the subtrahend) from it to find the result (the difference).
Given Numbers:
In this problem, we are given two numbers: 72 and 52. We need to find the difference between these two numbers.
Subtracting the Numbers:
To find the difference, we subtract the subtrahend (52) from the minuend (72).
72 - 52 = 20
Answer:
The difference between 72 and 52 is 20.
Explanation:
To understand why the answer is 20, we can think of it in terms of counting or using a number line.
Starting with 72, we count backward by 52 units. Each time we subtract 1, we move one unit to the left on the number line. We repeat this process until we have subtracted 52 units.
After subtracting 52 units, we reach the number 20 on the number line. Therefore, the difference between 72 and 52 is 20.
Conclusion:
The correct answer is option B) 24, as the difference between 72 and 52 is indeed 20.
A polynomial of degree p has- a)Only one zero
- b)At least p zeroes
- c)More than p zeroes
- d)At most p zeroes
Correct answer is option 'D'. Can you explain this answer?
A polynomial of degree p has
a)
Only one zero
b)
At least p zeroes
c)
More than p zeroes
d)
At most p zeroes
|
|
Joseph Simmons answered |
Polynomial of Degree p:
- A polynomial is an algebraic expression consisting of variables and coefficients, combined using addition, subtraction, multiplication, and non-negative integer exponents.
- The degree of a polynomial is the highest power of the variable in the polynomial.
- A polynomial of degree p can be written as:
P(x) = a_px^p + a_{p-1}x^{p-1} + ... + a_1x + a_0
Number of Zeroes:
- Zeroes of a polynomial are the values of x for which the polynomial evaluates to zero.
- In other words, a value x is a zero of a polynomial if P(x) = 0.
- The number of zeroes of a polynomial can be equal to or less than the degree of the polynomial.
Option D - At most p zeroes:
- This option means that the polynomial can have a maximum of p zeroes.
- It indicates that the number of zeroes of the polynomial is not necessarily equal to the degree of the polynomial.
- Let's consider an example to understand this concept.
Example:
- Consider a polynomial of degree 3: P(x) = x^3 - 2x^2 + x - 1.
- We can find the zeroes of this polynomial by setting P(x) = 0 and solving for x.
- However, in this case, the polynomial may not have exactly 3 zeroes.
- It could have fewer zeroes depending on the nature of the polynomial.
- In this example, the polynomial has only 1 zero: x = 1.
- Therefore, this example illustrates that a polynomial of degree 3 can have at most 3 zeroes, but it may have fewer zeroes.
Conclusion:
- A polynomial of degree p can have at most p zeroes.
- The number of zeroes can be less than p, depending on the nature of the polynomial.
- Option D, "At most p zeroes," correctly describes the possible number of zeroes for a polynomial of degree p.
- A polynomial is an algebraic expression consisting of variables and coefficients, combined using addition, subtraction, multiplication, and non-negative integer exponents.
- The degree of a polynomial is the highest power of the variable in the polynomial.
- A polynomial of degree p can be written as:
P(x) = a_px^p + a_{p-1}x^{p-1} + ... + a_1x + a_0
Number of Zeroes:
- Zeroes of a polynomial are the values of x for which the polynomial evaluates to zero.
- In other words, a value x is a zero of a polynomial if P(x) = 0.
- The number of zeroes of a polynomial can be equal to or less than the degree of the polynomial.
Option D - At most p zeroes:
- This option means that the polynomial can have a maximum of p zeroes.
- It indicates that the number of zeroes of the polynomial is not necessarily equal to the degree of the polynomial.
- Let's consider an example to understand this concept.
Example:
- Consider a polynomial of degree 3: P(x) = x^3 - 2x^2 + x - 1.
- We can find the zeroes of this polynomial by setting P(x) = 0 and solving for x.
- However, in this case, the polynomial may not have exactly 3 zeroes.
- It could have fewer zeroes depending on the nature of the polynomial.
- In this example, the polynomial has only 1 zero: x = 1.
- Therefore, this example illustrates that a polynomial of degree 3 can have at most 3 zeroes, but it may have fewer zeroes.
Conclusion:
- A polynomial of degree p can have at most p zeroes.
- The number of zeroes can be less than p, depending on the nature of the polynomial.
- Option D, "At most p zeroes," correctly describes the possible number of zeroes for a polynomial of degree p.
What is the degree of 0?- a)Not defined
- b)1
- c)2
- d)0
Correct answer is option 'A'. Can you explain this answer?
What is the degree of 0?
a)
Not defined
b)
1
c)
2
d)
0
|
|
Ayesha Joshi answered |
Degree of the zero polynomial is not defined.
Zero polynomial is denoted by 0, and degree for that is not defined.
Zero polynomial is denoted by 0, and degree for that is not defined.
If p(x) is a polynomial of degree one and p(y) = 0, then y is said to be- a)Zero of p(x)
- b)Value of p(x)
- c)Constant of p(x)
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If p(x) is a polynomial of degree one and p(y) = 0, then y is said to be
a)
Zero of p(x)
b)
Value of p(x)
c)
Constant of p(x)
d)
None of the above
|
|
Ayesha Joshi answered |
Let p(x) = mx + n
Put x = y
p(y) = my + n = 0
So, y is zero of p(x).
What is the degree of a polynomial 7?- a)7
- b)1
- c)0
- d)2
Correct answer is option 'C'. Can you explain this answer?
What is the degree of a polynomial 7?
a)
7
b)
1
c)
0
d)
2
|
|
Ayesha Joshi answered |
Degree of a non-zero constant polynomial is zero.
We can see that given polynomial 7 contain only one term and that is constant. 7 can also be written as 7x0.
Hence degree of 7 is zero.
We can see that given polynomial 7 contain only one term and that is constant. 7 can also be written as 7x0.
Hence degree of 7 is zero.
Which of the following is the zero for the polynomial f(x) = 2x + 7?- a)-2/7
- b)7/2
- c)2/7
- d)-7/2
Correct answer is option 'D'. Can you explain this answer?
Which of the following is the zero for the polynomial f(x) = 2x + 7?
a)
-2/7
b)
7/2
c)
2/7
d)
-7/2
|
|
Sophia Lewis answered |
Explanation:
To find the zero of a polynomial, we need to solve the equation f(x) = 0. In this case, the polynomial is f(x) = 2x - 7.
Step 1:
Set the polynomial equation equal to zero:
2x - 7 = 0
Step 2:
To solve for x, isolate the variable by adding 7 to both sides of the equation:
2x = 7
Step 3:
To isolate x, divide both sides of the equation by 2:
x = 7/2
The zero of the polynomial f(x) = 2x - 7 is x = 7/2.
Explanation of options:
a) -2/7: This is not the zero of the polynomial because substituting -2/7 into the polynomial does not result in zero.
b) 7/2: This is the correct zero of the polynomial, as shown in the explanation above.
c) 2/7: This is not the zero of the polynomial because substituting 2/7 into the polynomial does not result in zero.
d) -7/2: This is not the zero of the polynomial because substituting -7/2 into the polynomial does not result in zero.
Therefore, the correct answer is option 'D', which is x = -7/2.
To find the zero of a polynomial, we need to solve the equation f(x) = 0. In this case, the polynomial is f(x) = 2x - 7.
Step 1:
Set the polynomial equation equal to zero:
2x - 7 = 0
Step 2:
To solve for x, isolate the variable by adding 7 to both sides of the equation:
2x = 7
Step 3:
To isolate x, divide both sides of the equation by 2:
x = 7/2
The zero of the polynomial f(x) = 2x - 7 is x = 7/2.
Explanation of options:
a) -2/7: This is not the zero of the polynomial because substituting -2/7 into the polynomial does not result in zero.
b) 7/2: This is the correct zero of the polynomial, as shown in the explanation above.
c) 2/7: This is not the zero of the polynomial because substituting 2/7 into the polynomial does not result in zero.
d) -7/2: This is not the zero of the polynomial because substituting -7/2 into the polynomial does not result in zero.
Therefore, the correct answer is option 'D', which is x = -7/2.
What do we get after expanding (p + 3q - 2z)2?- a)p2 + 9q2 + 4z2 + 6pq – 12qz + 4zp
- b)p2 + 9q2 + 4z2 + 12pq + 12qz + 4zp
- c)p2 + 9q2 + 4z2 – 12pq – 12qz – 4zp
- d)p2 + 9q2 + 4z2 + 6pq – 12qz – 4zp
Correct answer is option 'D'. Can you explain this answer?
What do we get after expanding (p + 3q - 2z)2?
a)
p2 + 9q2 + 4z2 + 6pq – 12qz + 4zp
b)
p2 + 9q2 + 4z2 + 12pq + 12qz + 4zp
c)
p2 + 9q2 + 4z2 – 12pq – 12qz – 4zp
d)
p2 + 9q2 + 4z2 + 6pq – 12qz – 4zp
|
|
Abigail Russell answered |
To expand the expression (p + 3q - 2z)^2, we use the formula for expanding a binomial square:
(a + b)^2 = a^2 + 2ab + b^2
In this case, a = p and b = 3q - 2z. So, we have:
(p + 3q - 2z)^2 = p^2 + 2(p)(3q - 2z) + (3q - 2z)^2
Expanding the second term:
2(p)(3q - 2z) = 6pq - 4pz
Expanding the third term:
(3q - 2z)^2 = (3q)^2 - 2(3q)(2z) + (2z)^2
= 9q^2 - 12qz + 4z^2
Putting it all together, we get:
(p + 3q - 2z)^2 = p^2 + 6pq - 4pz + 9q^2 - 12qz + 4z^2
So, the expanded expression is:
p^2 + 6pq - 4pz + 9q^2 - 12qz + 4z^2
(a + b)^2 = a^2 + 2ab + b^2
In this case, a = p and b = 3q - 2z. So, we have:
(p + 3q - 2z)^2 = p^2 + 2(p)(3q - 2z) + (3q - 2z)^2
Expanding the second term:
2(p)(3q - 2z) = 6pq - 4pz
Expanding the third term:
(3q - 2z)^2 = (3q)^2 - 2(3q)(2z) + (2z)^2
= 9q^2 - 12qz + 4z^2
Putting it all together, we get:
(p + 3q - 2z)^2 = p^2 + 6pq - 4pz + 9q^2 - 12qz + 4z^2
So, the expanded expression is:
p^2 + 6pq - 4pz + 9q^2 - 12qz + 4z^2
When x = -1, which of the following is the value of f(x) = 5x − 4x2 + 3?- a)3
- b)-6
- c)-12
- d)6
Correct answer is option 'B'. Can you explain this answer?
When x = -1, which of the following is the value of f(x) = 5x − 4x2 + 3?
a)
3
b)
-6
c)
-12
d)
6
|
|
Ayesha Joshi answered |
If x = -1, then f(x) = 5x − 4x2 + 3 would be f(-1) = 5(-1) − 4(-1)2 + 3. It further results in -5 - 4 + 3. Further calculation leads to the outcome as -6. Therefore, according to the derivation, an observation can be made that the value of f(x) = 5x − 4x2 + 3 would be -6 when x = -1.
If a quadratic polynomial's discriminant, D, is greater than zero, the polynomial has- a)two real and equal roots
- b)two real and unequal roots
- c)imaginary roots
- d)no roots
Correct answer is option 'B'. Can you explain this answer?
If a quadratic polynomial's discriminant, D, is greater than zero, the polynomial has
a)
two real and equal roots
b)
two real and unequal roots
c)
imaginary roots
d)
no roots
|
|
Rajeev Kumar answered |
If the discriminant of a quadratic polynomial, D > 0, then the polynomial has two real and unequal roots.
The graph of a quadratic polynomial cuts the x-axis at only one point. Hence, the zeros of the quadratic polynomial are equal and real.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The graph of a quadratic polynomial cuts the x-axis at only one point. Hence, the zeros of the quadratic polynomial are equal and real.
a)
True
b)
False
|
|
Xavier Hughes answered |
Answer:
To understand why the statement is true, let's first revisit the concept of zeros of a quadratic polynomial and the graph of a quadratic function.
Quadratic Polynomial:
A quadratic polynomial is a polynomial of degree 2, written in the form ax^2 + bx + c, where a, b, and c are constants and a ≠ 0.
Zeros of a Quadratic Polynomial:
The zeros (also known as roots or x-intercepts) of a quadratic polynomial are the values of x for which the polynomial equals zero. In other words, the zeros are the x-values at which the graph of the quadratic polynomial intersects the x-axis.
Graph of a Quadratic Polynomial:
The graph of a quadratic polynomial is a parabola. Depending on the coefficients, the parabola can open upwards (concave up) or downwards (concave down). If the parabola intersects the x-axis at two distinct points, the zeros are real and unequal. If the parabola is tangent to the x-axis at only one point, the zeros are equal and real.
Explanation of the Statement:
The given statement states that the graph of a quadratic polynomial cuts the x-axis at only one point. This means that the parabola representing the quadratic polynomial is tangent to the x-axis at a single point. In this case, the parabola does not intersect the x-axis at any other point. Therefore, there is only one value of x for which the quadratic polynomial equals zero, which implies that the zeros of the quadratic polynomial are equal and real.
Conclusion:
Based on the explanation above, we can conclude that the statement is true. When the graph of a quadratic polynomial cuts the x-axis at only one point, the zeros of the quadratic polynomial are equal and real.
To understand why the statement is true, let's first revisit the concept of zeros of a quadratic polynomial and the graph of a quadratic function.
Quadratic Polynomial:
A quadratic polynomial is a polynomial of degree 2, written in the form ax^2 + bx + c, where a, b, and c are constants and a ≠ 0.
Zeros of a Quadratic Polynomial:
The zeros (also known as roots or x-intercepts) of a quadratic polynomial are the values of x for which the polynomial equals zero. In other words, the zeros are the x-values at which the graph of the quadratic polynomial intersects the x-axis.
Graph of a Quadratic Polynomial:
The graph of a quadratic polynomial is a parabola. Depending on the coefficients, the parabola can open upwards (concave up) or downwards (concave down). If the parabola intersects the x-axis at two distinct points, the zeros are real and unequal. If the parabola is tangent to the x-axis at only one point, the zeros are equal and real.
Explanation of the Statement:
The given statement states that the graph of a quadratic polynomial cuts the x-axis at only one point. This means that the parabola representing the quadratic polynomial is tangent to the x-axis at a single point. In this case, the parabola does not intersect the x-axis at any other point. Therefore, there is only one value of x for which the quadratic polynomial equals zero, which implies that the zeros of the quadratic polynomial are equal and real.
Conclusion:
Based on the explanation above, we can conclude that the statement is true. When the graph of a quadratic polynomial cuts the x-axis at only one point, the zeros of the quadratic polynomial are equal and real.
Which of the following is a quadratic polynomial?- a)x + 3x3 + 1
- b)7x + 3
- c)2x2 + x - 1
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a quadratic polynomial?
a)
x + 3x3 + 1
b)
7x + 3
c)
2x2 + x - 1
d)
None of the above
|
|
Ayesha Joshi answered |
Since the degree at the highest level for the polynomial 2x2 + x - 1 is two according to variables, it is to be a quadratic polynomial. On the other hand, 7x + 3 is a linear polynomial. Furthermore, x + 3x3 + 1 is a polynomial that is cubic
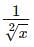 is a polynomial.
is a polynomial.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
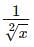 is a polynomial.
is a polynomial.a)
True
b)
False
|
|
Ayesha Joshi answered |
For an expression to be a polynomial, exponent of variable has to be whole number.
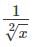 can be written as x-1/2. We can see that exponent of x is -1/2 which is not whole number (W = {0, 1, 2, 3…}). Hence, 1x√2 is not a polynomial.
can be written as x-1/2. We can see that exponent of x is -1/2 which is not whole number (W = {0, 1, 2, 3…}). Hence, 1x√2 is not a polynomial.
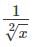 can be written as x-1/2. We can see that exponent of x is -1/2 which is not whole number (W = {0, 1, 2, 3…}). Hence, 1x√2 is not a polynomial.
can be written as x-1/2. We can see that exponent of x is -1/2 which is not whole number (W = {0, 1, 2, 3…}). Hence, 1x√2 is not a polynomial.A real number is called zeros of the polynomial p(x) if _________- a)p(α) = 4
- b)p(α) = 1
- c)p(α) ≠ 0
- d)p(α) = 0
Correct answer is option 'D'. Can you explain this answer?
A real number is called zeros of the polynomial p(x) if _________
a)
p(α) = 4
b)
p(α) = 1
c)
p(α) ≠ 0
d)
p(α) = 0
|
|
Isabella Hayes answered |
Definition of Zeros of a Polynomial:
Zeros of a polynomial are the real numbers that make the polynomial equal to zero when substituted for the variable.
Explanation of the Correct Answer:
Option D: p(α) = 0
This option is the correct answer because the zeros of a polynomial are the values of the variable that make the polynomial equal to zero. In other words, if a real number α is a zero of the polynomial p(x), then p(α) = 0. This is a fundamental property of zeros of polynomials.
Therefore, the correct statement to define zeros of a polynomial is p(α) = 0.
Understanding the Other Options:
- Option A: p(α) = 4
This statement does not define the zeros of the polynomial. Zeros of a polynomial are the values that make the polynomial equal to zero, not any other constant.
- Option B: p(α) = 1
Similarly, this statement does not define the zeros of the polynomial. Zeros are the values that make the polynomial equal to zero, not 1.
- Option C: p(α) ≠ 0
This statement does not accurately define the zeros of the polynomial. Zeros are the values that make the polynomial equal to zero, not any value other than zero.
In Conclusion:
The correct definition of zeros of a polynomial is when the polynomial evaluated at a real number α results in p(α) = 0. This is a fundamental concept in algebra and is crucial in understanding the roots of polynomial functions.
Zeros of a polynomial are the real numbers that make the polynomial equal to zero when substituted for the variable.
Explanation of the Correct Answer:
Option D: p(α) = 0
This option is the correct answer because the zeros of a polynomial are the values of the variable that make the polynomial equal to zero. In other words, if a real number α is a zero of the polynomial p(x), then p(α) = 0. This is a fundamental property of zeros of polynomials.
Therefore, the correct statement to define zeros of a polynomial is p(α) = 0.
Understanding the Other Options:
- Option A: p(α) = 4
This statement does not define the zeros of the polynomial. Zeros of a polynomial are the values that make the polynomial equal to zero, not any other constant.
- Option B: p(α) = 1
Similarly, this statement does not define the zeros of the polynomial. Zeros are the values that make the polynomial equal to zero, not 1.
- Option C: p(α) ≠ 0
This statement does not accurately define the zeros of the polynomial. Zeros are the values that make the polynomial equal to zero, not any value other than zero.
In Conclusion:
The correct definition of zeros of a polynomial is when the polynomial evaluated at a real number α results in p(α) = 0. This is a fundamental concept in algebra and is crucial in understanding the roots of polynomial functions.
Chapter doubts & questions for Polynomials - Mathematics for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polynomials - Mathematics for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Mathematics for ACT
144 videos|100 docs|61 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup











