All Courses
Get the App Signup / Login
Sign in Open App
All Exams  >   ACT  >   Mathematics for ACT  >   All Questions

All questions of Ratio and Proportion for ACT Exam

A farmer has cows and buffaloes in the ratio 3:1. If he buys 10 more cows and 2 more buffaloes, the given ratio becomes 4:1. What is the current number of cows?
  • a)
    3
  • b)
    6
  • c)
    9
  • d)
    12
  • e)
    15
Correct answer is option 'B'. Can you explain this answer?

Tejas Gupta answered
Let's assume that the current ratio of cows to buffaloes is 3x:1x, where x is a constant.

According to the given information, if the farmer buys 10 more cows and 2 more buffaloes, the ratio becomes 4:1.

So, the new ratio of cows to buffaloes is (3x+10):(1x+2) = 4:1

Cross-multiplying, we get:

4(1x+2) = 3x+10

Simplifying:

4x+8 = 3x+10

x = 2

Therefore, the current ratio of cows to buffaloes is 3x:1x = 6:2 or 3:1

To find the current number of cows, we can use the ratio:

Let the current number of cows be 3y and the current number of buffaloes be y.

Then, 3y+10: y+2 = 4:1

Cross-multiplying, we get:

4( y+2) = 3y+10

Simplifying:

y = 4

Therefore, the current number of cows is 3y = 3(4) = 12.

Hence, the correct option is (b) 12.
Clear all your doubts with EduRev

A packet X contains pens, pencils and erasers in the ratio 1:2:3. Packet Y contains pens and pencils in the ratio 4:5.  If the total number of pens and pencils in both the packets combined is 13 and 20 respectively. What is the number of erasers in Packet X?
  • a)
    5
  • b)
    10
  • c)
    15
  • d)
    20
  • e)
    25
Correct answer is option 'C'. Can you explain this answer?

Lavanya Menon answered
Let the number of pens, pencils and erasers in packet X be x, 2x, and 3x, respectively.
Likewise, we can let the number of pens and pencils in packet Y be 4y and 5y. Therefore, we have:
x + 4y = 13
and
2x + 5y = 20
Multiplying the first equation by 2 and subtracting that from the second equation, we have:

⇒ -3y = -6

⇒ y = 2

So x + 2(4) = 13 and hence x = 5.
Since the number of erasers is 3x, the number of erasers is 3(5) = 15.

In triangle ABC, ∠ABC is 7/20  times less than ∠ACB, and ∠ACB is  2/3 times greater than ∠BAC. What is the measure of ∠BAC?
  • a)
    40o
  • b)
    48o
  • c)
    52o
  • d)
    60o
  • e)
    72o
Correct answer is option 'B'. Can you explain this answer?

Meera Rana answered
Given:
  • In ΔABC, let the measure of ∠BAC be ao , ∠ABC be bo and ∠ACB be co
To Find:
ao = ?
Approach:
  1. To find the value of ao we need to draft an equation in terms of ao only. We are given the value of co in terms of ao , and using the given information, we can infer the value of bo in terms of ao .
  2. We know another relation between ao, bo, co, - The Angle Sum Property. By using the values of bo and co in terms of a in the Angle Sum relation, we can find the value of ao
Working out:
Looking at the answer choices, we see that the correct answer is Option B

If A: B is 5: 7 and B: C is 14: 9, then what is the value of square of ratio of A and C?
  • a)
    81/64
  • b)
    100/81
  • c)
    121/100
  • d)
    144/121
  • e)
    169/144
Correct answer is option 'B'. Can you explain this answer?

Chirag Sen answered
Given:
A:B = 5:7
B:C = 14:9

To find:
(A/C)^2

Solution:
Let's assume a common value for B, say 14.
Then, from the first ratio, we can say that A = 5/7 * 14 = 10.
Similarly, from the second ratio, we can say that C = 9/14 * 14 = 9.

So, A:C = 10:9.
Therefore, (A/C)^2 = (10/9)^2 = 100/81.

Hence, the answer is option B (100/81).

Three persons named A, B and C work in succession to build a machine. At first, Person A works alone and builds 1/3rd of the machine and then leaves. After person A leaves, person B works alone and builds 1/4th of the remaining machine and then leaves. After person B leaves, person C works alone and builds 1/5th of the remaining machine and then leaves. What fraction of the machine remains to be built?
  • a)
    1/5
  • b)
    2/5
  • c)
    3/7
  • d)
    13/60
  • e)
    5/8
Correct answer is option 'B'. Can you explain this answer?

Arka Basu answered
Solution:
Let us assume that the total work is represented by 'W'. Then, we have:

Person A completes 1/3rd of the machine, so the remaining work is (2/3)W.
Person B completes 1/4th of the remaining machine, so the work remaining after B is (3/4) × (2/3)W = (1/2)W.
Person C completes 1/5th of the remaining machine, so the work remaining after C is (4/5) × (1/2)W = (2/5)W.

Therefore, the fraction of the machine that remains to be built is (2/5) or option B.

Explanation:
The problem involves successive work done by three persons, and we need to find the fraction of the machine that remains to be built after all three persons have worked. To solve the problem, we use the concept of fractions to represent the work done by each person and the work remaining after each person completes their part.

We start by assuming that the total work is represented by 'W'. Then, we use fractions to represent the work done by each person. Person A completes 1/3rd of the machine, so the remaining work is (2/3)W. Person B completes 1/4th of the remaining machine, so the work remaining after B is (3/4) × (2/3)W = (1/2)W. Person C completes 1/5th of the remaining machine, so the work remaining after C is (4/5) × (1/2)W = (2/5)W.

Therefore, the fraction of the machine that remains to be built is (2/5) or option B.

If a : b = 7 : 5, b : c = 9 : 11, find a : b : c?
  • a)
    42 : 33 : 55
  • b)
    63 : 45 : 55
  • c)
    55 : 39 : 45
  • d)
    62 : 89 : 20
  • e)
    65 : 30 : 63
Correct answer is option 'B'. Can you explain this answer?

Kalyan Nair answered
Given: a:b = 7:5 and b:c = 9:11

To find: a:b:c

Solution:

We can use the concept of proportionality here. If a:b = 7:5, then we can write:

a = (7/5) b

Similarly, if b:c = 9:11, then we can write:

c = (11/9) b

Substituting the value of b in the above equation, we get:

c = (11/9) (5/7) a

c = (55/63) a

Therefore, a:b:c = a:b:(55/63)a

We can simplify this ratio by multiplying all the terms by 63 (the LCM of 1, 7, and 9):

a:b:c = 63a/5 : 63b/7 : 55a/9

a:b:c = 63a : 45b : 55a (Canceling out the common factors)

a:b:c = 63:45:55

Hence, the answer is option B) 63:45:55.

Gerald and James each had a few one dollar bills. After James gave 16 one dollar bills to Gerald, the ratio of the number of bills that James and Gerald respectively had was 14/11  Gerald now returned 8 one dollar bills to James, thereby increasing the ratio of the number of bills that James and Gerald respectively had to 16/9  What was the ratio of the number of bills that James and Gerald respectively had originally?
  • a)
    18/7
  • b)
    46/29
  • c)
    3/2
  • d)
    74/51
  • e)
    2/3
Correct answer is option 'A'. Can you explain this answer?

Meera Rana answered
Given:
  • Let Gerald originally have g bills and James have j bills
  • Number of one dollar bills that Gerald had after James gave him 16 one dollar bills = g + 16
  • Number of one dollar bills that James after he gave Gerald 16 one dollar bills = j - 16
    • So, we can write  
  • Number of one dollar bills that Gerald had after he returned 8 one dollar bills to James = g + 16 – 8
  • Number of one dollar bills that James had after he got 8 one dollar bills from Gerald = j – 16 + 8
    • So, we can write  
To Find: J/g = ?
Approach:
  1. We’re given 2 relations for j and g. Using these, we’ll:
    • Either find the values of j and g, and thus solve for the required ratio.
    • Or directly solve for the ratio J/g
Working out:
  • So, the above equation simplifies to: 11x-14 = 2(9x-16)
Looking at the answer choices, we see that the correct answer is Option A

Peter gifted a packet of chocolates to each of the guests who came to his birthday party. Each packet was identical and contained x chocolates of flavor A, y chocolates of flavor B and z chocolates of flavor C, where x, y and z are positive integers. If the total number of chocolates in a packet was not greater than 50, then how many guests attended his birthday party?
(1) Peter used a total of 21 chocolates of flavor A, 28 chocolates of flavor B and 42 chocolates of flavor C to prepare all the packets.
(2) The numbers of chocolates of flavors A, B and C in each packet were in the ratio  3: 4: 6 respectively.
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. 
  • c)
    BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. 
  • d)
    EACH statement ALONE is sufficient. 
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?

Aarav Sharma answered
Steps 1 & 2: Understand Question and Draw Inferences
Notice that:
(i) Each packet contains x, y and z number of chocolates of flavor A, B and C respectively.
(ii) The packet cannot hold more than 50 chocolates. In other words, x + y + z ≤ 50
If N friends come to his party, then the total number of flavor A, flavor B and flavor C chocolates are Nx, Ny and Nz respectively.
Notice that the total number of chocolates of flavor A, flavor B and flavor C have at least one common factor: N, the number of friends who attended his party.
Step 3: Analyze statement 1
The numbers 21, 28 and 42 represent the total number of flavor A, flavor B and flavor C chocolates.
=> Nx = 21
Ny = 28
Nz = 42
The common factors of Nx, Ny and Nz are 1 and 7.So, the number of friends could be 1 or 7.
Case I: N = 1
=> x = 21, y = 28, z = 42.
=> x + y + z = 91
Since x + y + z > 50, this case is not possible.
Case II: N = 7
x + y + z = 3 + 4 + 6 = 13, which satisfies x + y + z ≤ 50.
This is the only possible case. Therefore, N = 7.
SUFFICIENT.
Step 4: Analyze statement 2
Since the ratio of the number of chocolates of flavor A, flavor B and flavor C is 3:4:6, we can assume the number of chocolates of flavor A, flavor B and flavor C to be 3k, 4k and 6k respectively. (k can be any positive integer)
If the number of friends who attended Peter’s birthday party is N, then the number of chocolates of flavor A, flavor B and flavor C are 3k×N, 4k×N and 6k×N respectively.
There is no information relating 3kN, 4kN and 6kN, and therefore N cannot be found.
INSUFFICIENT.
Step 5: Analyze Both Statements Together (if needed)
Since we have obtained an answer in Step 3, there is no need to combine the statements.
(A)   is the correct answer.

If two inches are approximately equal to 5 centimeters, how much is the area of a painting in square inches if its area is 2900 square centimeters?
  • a)
    464
  • b)
    1160
  • c)
    7250
  • d)
    18125
  • e)
    22904
Correct answer is option 'A'. Can you explain this answer?

Aisha Gupta answered
Step 1: Question statement and Inferences
We have been provided the relation between inches and centimeters. We have to convert an area of 2900 square centimeters into square inches.
We shall follow the following procedure:
(a) First find out, by the Unitary Method, how many inches are there in 1 centimeter.
(b) Then, find out how many square inches are there in 1 square centimeter.
(c) Lastly, find out how many square inches are there in 2900 square centimeters, which is the required answer.
Step 2: Finding required values
Given: 2 inch = 5 centimeters
Writing this equation in reverse, we get:
5 centimeters = 2 inches
=> 1 centimeter = 2/5 inch ----------------(1)
1 square centimeter = 1 centimeter X 1 centimeter
In order to find out how many square inches is 1 square centimeter, substituting the value of 1 centimeter from equation (1) in the above equation, we get
1 square centimeter = 2/5 inch * 2/5 inch
Since inch*inch is square inches,
1 square centimeter = 4/25 square inches
Step 3: Calculating the final answer
In order to find out how many square inches is 2900 square centimeters, multiplying both sides of the above equation by 2900,
2900 square centimeters = 4/25 * 2900 square inch
2900 square centimeters = 464 square inches
(A) is the correct answer.

The students in a class were asked to vote for their favourite subject. W students voted for mathematics, X students voted for science, Y for history and Z for literature. The ratio of W to Y was 4:5, Z to W was 5:6 and X to Z was 13:10. If each student in the class voted for one of the four subjects above, what percent of the students in the class voted for mathematics?
  • a)
    20%
  • b)
    22.8%
  • c)
    24%
  • d)
    26%
  • e)
    30%
Correct answer is option 'C'. Can you explain this answer?

Gauri Iyer answered
Given:
  • Total students in the class = W + X + Y + Z
  • Favorite subject votes were as under:
    • Mathematics = W
    • Science = X
    • History = Y
    • Literature = Z
To Find: % of students who voted for Mathematics as their favorite subject
Approach:
  1.  % of students who voted for Mathematics as their favorite subject=  
​
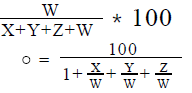
2. So, to find the required percentage, we need to find the values of  
​​
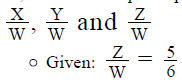
  • We’ll use the given ratios to find the other 2 required values
Working out:
  • Finding Y/W
Looking at the answer choices, we see that the correct answer is Option C

For the team of salespeople in organization X, the amount of incentive provided (I) was found to be directly proportional to the sales in dollars (S) and the sales were found to be directly proportional to the Job satisfaction index (J). If the sales in the month of March of a certain year were $30000, find the value of the job satisfaction index in March?
(1) J = 0.5 whenever S = $10000
(2) I = 100 whenever S = $5000
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. 
  • c)
    BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. 
  • d)
    EACH statement ALONE is sufficient. 
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?

Kiran Chauhan answered
Step 1 & 2: Understand the question and draw inferences
Since I is directly proportional to S, we can write:
I = nS, where n is a constant . . . Equation 1
Since S is directly proportional to J, we can write:
S = mJ, where m is a constant . . . Equation 2
When S = 30,000:
 mJ = 30,000
Thus, in order to find the value of J at S = 30,000, we need to know the value of m.
Step 3: Analyse statement 1
As per Statement 1,
J = 0.5 whenever S = $10000
From Equation 2:
 10000 = m(0.5)
From this equation, we will be able to find a unique value of m
Therefore, Statement 1 is sufficient
Step 4: Analyse statement 2
As per Statement 2,
I = 100 whenever S = $5000
From Equation 1,
 100 = n(5000)
From this equation, we will find the value of n. We will however, have no clue about the value of m.
Therefore, Statement 2 is not sufficient.
Step 5: Analyze statements 1 & 2 together (if needed)
Since we have obtained an answer in Step 3, there is no need to combine the statements.
(A) is the answer.

Peter has an export business and he makes a profit of $12 for every $80 worth of goods that he exports to Europe.  If the currency in Europe is Euro and he exported goods of a total worth of 51000 Euros in the year 2011 and 1 dollar is approximately equal to 0.75 Euros, then what is his profit in 2011 in dollars($)?
  • a)
    7,650
  • b)
    10,200
  • c)
    10,400
  • d)
    11,000
  • e)
    12,000
Correct answer is option 'B'. Can you explain this answer?

Jatin Kapoor answered
To find Peter's profit in dollars, we need to calculate the value of the goods he exported in dollars and then subtract the cost of producing those goods.

1. Calculate the value of the goods exported in euros:
Peter exported goods worth 51,000 euros in 2011.

2. Convert the value of goods exported from euros to dollars:
Given that 1 dollar is approximately equal to 0.75 euros, we can multiply the value of goods exported in euros by the conversion rate to get the value in dollars.

Value in dollars = Value in euros * Conversion rate
Value in dollars = 51,000 euros * 0.75 dollars/euro
Value in dollars = 38,250 dollars

3. Calculate the profit:
Peter makes a profit of $12 for every $80 worth of goods exported.

Profit = (Value in dollars / Value of goods exported) * Profit per $80 worth of goods
Profit = (38,250 dollars / 80 dollars) * 12 dollars
Profit = 45 * 12 dollars
Profit = 540 dollars

Therefore, Peter's profit in 2011 was $540.

The correct answer is option B) 10,200.

A school library consists of literature books and science books in the ratio of 5:6. If 50 more literature books are added to the library and the number of science books is increased by 1/4th of the existing science books, the ratio of the literature books and science books increases to 4:3. If the library consists of only literature and the science books, what is the initial number of books in the library?
  • a)
    60
  • b)
    110
  • c)
    130
  • d)
    140
  • e)
    190
Correct answer is option 'B'. Can you explain this answer?

Gauri Iyer answered
Given:
  • Let the number of literature books be l and the number of science books be s
    • l : s = 5 : 6
  • Number of literature books added = 50
    • Total literature books now = l + 50
  • Number of science books increased = ¼ * s
    • Total science books now = s + ¼ * s
  • New Ratio of literature and science books = 4 : 3
To Find: Initial number of books in the library
  • Value of l + s?
Approach:
  1. To Find the value of l + s, we need to find the values of l and s.
  2. We know that l : s = 5 : 6. So, we need to find another relation between l and s to find unique values of l and s.
  3. We are given that the new number of literature books = l + 50 and the new number of science books is s + ¼ * s. The ratio of these literature and science books is 4 : 3
    • So, we have here another relation between l and s
Working out:
a. So, we have 3l + 150 = 5s, i.e. 5s – 3l = 150…….(2)
3. Adding equations (1) and (2), we have 3l = 150, i.e. l = 50
a. Putting the value of l in equation (2), we have 5s = 150 + 150, i.e. s = 60
4. Hence, initial books in the library = l + s = 50 + 60 = 110
Thus, the library initially had 110 books in total.
Answer : B

In a developing country, the price of a stock is directly proportional to the reciprocal of the inflation in the country, which is in turn directly proportional to the local diesel prices. The price of the stock is 100 currency units when the inflation is 10 units and when the inflation is 12 units, the local price of the diesel is 60 currency units. By how many currency units should the local diesel price fall so that the price of the stock, which is currently at 200 currency units, increases by 25 percent?
  • a)
    5
  • b)
    10
  • c)
    25
  • d)
    30
  • e)
    40
Correct answer is option 'A'. Can you explain this answer?

Gauri Iyer answered
Given:
 where x is a constant and P and I are price of the stock and Inflation respectively
  • Inflation α Local Diesel prices
    • I = bD, where b is a constant and D is the local diesel price.
  • P = 100 when I = 10
  • I = 12 when D = 60
To Find: By how many currency units should the local diesel price fall so that the price of the stock, which is currently at 200 currency units, increases by 25 percent?
  • Current Price stock = 200 currency units.
  • Increased Price stock = 200 *1.25 = 250 currency units
Approach:
  1. Let the current local price of diesel be D and the local price of Diesel at which the price of the stock increases by 25 percent be D’. So, the local Diesel price should fall by (D – D’) units
    • So, we should find the value of D and D’ at the current price and the increased price of the stocks.
  2. We need to find the relation between the price of a stock and the diesel prices
    • We know the relation between price of a stock and the inflation, which is given by 
    • We also know the relation between Inflation and local diesel prices, which is given by I = bD
  3. Using the above relations, we will establish a relation between price of a stock and the local diesel prices.
  4. Once, we establish a relation between price of a stock and the local diesel prices, we will need to find the values of constants b and x to calculate the change needed in local diesel prices when the price of a stock increases by 25 percent.
    • As we are given the price of a stock for a particular level of inflation, we can find the value of x using the relation 
    • Similarly, as we are given the value of inflation for a particular level of local diesel prices, we can find the value of b using the relation I = bD
Working out:
2. Calculating values of x and b
  • Price of a stock = 100 when inflation = 10
    • Using the relation   we can write  
which gives us x = 1000
  • Inflation = 12 when the local diesel prices = 60
    • Using the relation I = bD, we can write 12 =b *60, i.e. b = 1/5
4. So, the fall in local diesel price = 25 – 20 = 5
Hence, the local diesel price should fall by 5 currency units so that the price of
the stock should increase by 25% from 200.
Answer : A

A teacher took a pre-announced test in a class 3/4th. of the students had not prepared for the test. Of the students who had prepared for the test, 2/3rd passed the test. If only 25 percent of the class passed the test, what fraction of the students who had not prepared for the test, failed the test?
  • a)
    1/12
  • b)
    1/9
  • c)
    1/2
  • d)
    2/3
  • e)
    (8over 9)
Correct answer is option 'E'. Can you explain this answer?

Yash Rane answered
Given:
  • Number of students who did not prepare for the test =3/4 of the total student
    • Number of students who prepared for the test = 1/4 of the total student
  • Number of students who prepared and passed the test = 2/3of the students who prepared for the test
  • Number of students who passed the test = 25% of the total students
    • Number of students who failed the test = 75% of the total students
       
To Find: fraction of the students who had not prepared for the test and failed the test?
Approach:
  1. Required Fraction = ​
    • So, we need to either find the values of both “Number of students who did not prepare and failed the test” and “Number of students who did not prepare for the test” or express both of them in terms of a common variable
    • As we are not given any information about the number of students, we will try to express both of them in terms of a common variable
  2. Number of students who did not prepare for the test
    • Let’s assume the total number of students in the class be x.
      As we know that Number of students who did not prepare for the test =  3/4  of the total student, we can find the number of students who did not prepare for the test in terms of x.
    • Also that would give us the number of students who prepared for the test in terms of x.
  3. Number of students who did not prepare for the test and failed the test
    • We know that number of students who failed the test = 75% of the total students
    • Also, number of students who failed the test = Number of students who prepared and failed the test + Number of students who did not prepare and failed the test
    • Now, we know that Number of students who prepared and passed the test =2/3 of the students who prepared for the test.
    • So, number of students who prepared and failed the test = (Number of students who prepared) – (number of students who prepared and passed the test)
    • Using the above relation, we can find the number of students who prepared and failed the test in terms of x.
 
Working out:
  1. Number of students who did not prepare for the test = 3/4  of the total student = 
    • So, number of students who prepared for the test = 
2. Number of students who failed the test = 75% of x = 3/4
3. Also, number of students who failed the test = Number of students who prepared and failed the test + Number of students who did not prepare and failed the test
  • 3/4 =  Number of students who prepared and failed the test + Number of students who did not prepare and failed the test.
  •  Now, we are given that Number of students who prepared and passed the test =  2/3  of the students who prepared for the test =    
  • So, number of students who prepared and failed the test = 
  • Using (3.a), (3.b) and (3.c), we can write    Number of students who did not prepare and failed the test, which gives us the number of students who did not prepare and failed the test =  2/3
Answer  E

A bag contains only two types of coins: 10 cent coins or 1 dollar coins and number of 10 cent coins does not exceed the number of 1 dollar coins. How many 10 cent coins are there in the bag?
(1) The total amount of money in the bag is $16.50.
(2) If five 10-cent coins are removed and replaced with five 1-dollar coins then two-third of all the coins in the bag are 1 dollar coins.
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. 
  • c)
    BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. 
  • d)
    EACH statement ALONE is sufficient. 
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?

Abhishek Kapoor answered
Steps 1 & 2: Understand Question and Draw Inferences
If the number of 10-cent coins are ‘x’ and the number of 1-dollar coins is ‘y’, then we are told that x is less than or equal to y. The question is: what is the value of x?
Also, note that since ‘x’ and ‘y’ are number of coins, they must be non-negative integers.
Step 3: Analyze Statement 1
The total money in the bag due to 10-cent coins = 10x cents
The total money in the bag due to 1-dollar coins = y dollars or 100y cents
Total money in the bag = Total money due to 10-cent coins + Total money due to 1-dollar coins
16.50 * 100 = 10x + 100y
1650 = 10x + 100y
165 = x + 10y
This equation can have several integral solutions such as
if x = 5, y = 16
if x = 15, y = 15
if x = 25, y = 14, and so on.
Since x is less than equal to y, only the first two solutions are possible. ‘x’, whose value has to be found, can be 5 or 15.
INSUFFICIENT.
Step 4: Analyze Statement 2
If five 10-cent coins are replaced with five 1-dollar coins then the number of 10-cent coins become x – 5 and the number of 1-dollar coins become y + 5.
Then, y+5 = 2/3 * (x+y)
3y + 15 = 2x + 2y
y = 2x -15 ------(1)
We have to remember that x and y can only take non-negative integral values and x≤y
 
Substituting y from equation (1) in the given inequality, we have
x≤2x−15x≥15
 
x can have any value greater than or equal to 15.
For example,
if x = 15, then y = 2(15) – 15 = 15
if x = 16, then y = 2(16) – 15 = 17
and so on.
INSUFFCIENT.
Step 5: Analyze both statements together (if needed)
According to the information provided in Statement 1, x = 5 or x = 15.
According to the information provided in Statement 2, x = 15 or x = 16 or x = 17 and so on.
The common solution from the two statements is that x = 15
SUFFICIENT.
(C) is the correct answer.

If a, b, c and d are positive real numbers, is  
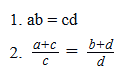
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
  • c)
    BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
  • d)
    EACH statement ALONE is sufficient to answer the question asked.
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?

Aparna Tammana answered
2.(a+c)/c = (b+d)/d
a/c + 1 = b/d + 1
a/c = b/d
a/b = c/d
2 is sufficient to answer
1.ab=cd with this we can't say if a/b = c/d or not
therefore 2 alone is sufficient to answer

The current manager to Direct Report ratio in a company is 1:10. If 50 more Direct Reports are added, the ratio decreases by 50%. How many managers does the company have?
  • a)
    2
  • b)
    5
  • c)
    10
  • d)
    15
  • e)
    20
Correct answer is option 'B'. Can you explain this answer?

Tanishq Choudhury answered
Step 1: Question statement and Inferences
Let the number of managers in the company be M
And the number of Direct Reports be D
It is given that M/D = 1/10
⇒  D = 10M ... Equation 1
When 50 more Direct Reports are added,
Number of Direct Reports = D’ = D + 50
So, the new manager: Direct Report ratio is  
Step 2: Finding required values
It is given that the new ratio is 50% less than the original ratio.
⇒ New Ratio = Original Ratio – 50% of Original Ratio
⇒ New Ratio = ½ (Original Ratio)
Step 3: Calculating the final answer
From Equation 1,
50 = 10M
⇒  M = 5
Therefore, the company has 5 managers.
Looking at the answer choices, we see that Option B is correct
 

Kate plays a game called ‘Fruitball’ in which a fruit is thrown for the player to catch. The fruit that is thrown can be an apple or an orange. A total of 24 fruits are thrown to each player and every time a player catches a fruit, a score of ‘1’ is awarded and every time a fruit is missed a score of ‘0’ is awarded. Kate scores 2/3 of her total points from catching apples and 6 more oranges were thrown at her than apples. If the number of apples that she misses is 1/4 the number of oranges she misses, how much does Kate score in this game of ‘Fruitball’?
  • a)
    6
  • b)
    7
  • c)
    8
  • d)
    9
  • e)
    10
Correct answer is option 'D'. Can you explain this answer?

Sahana Mehta answered
Given:
- Total number of fruits thrown = 24
- Kate scores 2/3 of her total points from catching apples
- Number of oranges thrown = Number of apples thrown + 6
- Number of apples missed = 1/4 * Number of oranges missed

To find:
- Kate's score in the game of Fruitball

Solution:

Let's assume:
- Number of apples thrown = A
- Number of oranges thrown = O

Step 1: Expressing the given information in equations:
- Total number of fruits thrown = A + O = 24 ---- (Equation 1)
- Kate's score from catching apples = 2/3 * Total score = (2/3) * (A / (A + O)) ---- (Equation 2)
- Number of oranges thrown = Number of apples thrown + 6 ---- (Equation 3)
- Number of apples missed = 1/4 * Number of oranges missed ---- (Equation 4)

Step 2: Solving the equations:
From Equation 3, we have:
- O = A + 6

Substituting this value in Equation 1, we get:
- A + (A + 6) = 24
- 2A + 6 = 24
- 2A = 18
- A = 9

Substituting the value of A in Equation 3, we get:
- O = 9 + 6
- O = 15

Step 3: Calculating Kate's score:
From Equation 2, we have:
- Kate's score from catching apples = (2/3) * (9 / (9 + 15))
- Kate's score from catching apples = (2/3) * (9/24)
- Kate's score from catching apples = (2/3) * (3/8)
- Kate's score from catching apples = 1/4

Since Kate scores 1/4 of her total points from catching apples, her total score can be calculated as:
- Total score = (1 / (1/4)) * 1
- Total score = 4

Therefore, Kate's score in the game of Fruitball is 4.

Answer:
The correct answer is option D) 9.

Five friends Alastair, Bell, Cook, Darren and Eoin appeared in an aptitude test. Alastair scored exactly 1/2  of Darren’s score, whose
score was 1/5th  more than Cook’s score. Eoin scored more than Cook and Darren’s score was 3/2 times that of Bell’s score. If the average score (arithmetic mean) of the group was 50, what was the range of the scores of the group?
  • a)
    25
  • b)
    30
  • c)
    35
  • d)
    40
  • e)
    50
Correct answer is option 'D'. Can you explain this answer?

Mrinalini Dasgupta answered
Given:
  • Relation of scores of Alastair, Bell, Cook, Darren and Eoin in an Aptitude test
    • Alastair’s score = ½ * Darren’s Score
    • Darren’s Score = Cook’s score + 1/5* Cook’s score =3/2 * Bell’s score
    • Eoin’s score = Cook’s score + 2/5* Cook’s score
  • Average score of the group = 50
    • So, total score of the group = 50*5 = 250
To Find: Range of the scores of the group
  • Range of the score = Highest score – Lowest Score
Approach:
  1. Range of the score = Highest score – Lowest Score
    • For finding the highest and the lowest score, we need to find the individual scores of all the 5 people
  2. Let’s assume the score of any one person to be x. Let’s assume that person to be Alastair
    • As we are given the relation between the scores of all the 5 people, we will express the scores of other people in terms of x.
  3. Once we get the scores of all the people in terms of x, we know that the sum of their scores is 250.
    • So, equating the sum of the scores of all the 5 people to 250 will give us an equation in x, which will give us a unique value of x.
Working out:
  1. Let Alastair’s score be x……….(1)
  2. Darren’s Score
    • We know that, Alastair’s score = ½ * Darren’s Score
    • So, Darren’s score = 2x………..(2)
  3. Cook’s Score
    • Now, we know that Darren’s Score = Cook’s score + 1/5 * Cook’s score
4. Bell’s Score
​
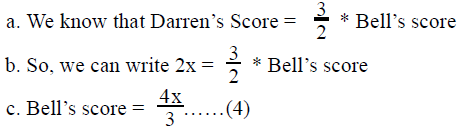
5. Eoin’s Score
6. Also, sum of all the scores = 250
So, the range of the scores of the group is 40.
Answer D

The revenue of a company is directly proportional to the number of customers it serves, which in turn is directly proportional to the
marketing spend of the company. What is the revenue of the company if it spends one million dollars in marketing?
(1) If the company spends $250,000 in marketing, it earns a revenue of ten million dollars
(2) The ratio of revenue of the company to the number of customers it serves is 4:1
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is
    not sufficient to answer the question asked.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is
    not sufficient to answer the question asked.
  • c)
    BOTH statements (1) and (2) TOGETHER are sufficient to
    answer the question asked, but NEITHER statement ALONE
    is sufficient to answer the question asked
  • d)
    EACH statement ALONE is sufficient to answer the question
    asked.
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient to
    answer the question asked, and additional data specific to the
    problem are needed
Correct answer is option 'A'. Can you explain this answer?

Ujwal Iyer answered
Step 1 & 2: Understand Question and Draw Inference
Given: Let revenue = R, Number of customers = C and marketing spend = M
  • R = kC, where k is a proportionality constant
  • C = pM, where p is a proportionality constant
  • So, R = (kp)M . . . (I)
  • So, to answer the question, we need the value of the product of k and p
Step 3 : Analyze Statement 1 independent
  1. If M = 250,000, then R = 106
    • From (I), 106 = (kp)(250,000)
    • From this equation, we can get the value of kp
Thus, Statement 1 alone is sufficient to answer the question.
Step 4 : Analyze Statement 2 independent
  • So, R = 4C
    • As R = kC, we have, k = 4
Since we don’t know the value of p yet, we cannot find the value of product kp Thus, Statement 2 alone is not sufficient to answer the question.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 3, this step is not required
Answer: Option A

2/5more water by weight is added to a salt-sugar-water solution. Before the addition of the water, what is the ratio of the weight of the water to the weight of the solution?
  1. Due to the addition of water, the ratio of the weight of sugar in the solution to the weight of the solution decreases from .
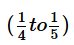  2. After the addition of water, the ratio of the weight of water in the solution to the weight of the solution becomes 7/10
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is
    not sufficient to answer the question asked.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is
    not sufficient to answer the question asked.
  • c)
    BOTH statements (1) and (2) TOGETHER are sufficient to
    answer the question asked, but NEITHER statement ALONE
    is sufficient to answer the question asked.
  • d)
    EACH statement ALONE is sufficient to answer the question
    asked.
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient to
    answer the question asked, and additional data specific to the
    problem are needed.
Correct answer is option 'D'. Can you explain this answer?

Kalyan Nair answered
Step 1 & 2: Understand Question and Draw Inference
Given:
Initial Solution
  • Let the weight of
    • salt = t
    • sugar = g
    • water = w
  • So, weight of whole solution = w + g + t
Final Solution
​
Step 3 : Analyze Statement 1 independent
(1) Due to the addition of water, the ratio of the weight of sugar in the solution to the weight of the solution decreases from to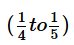 
Initial Solution
Thus, Statement 1 is sufficient.
Step 4 : Analyze Statement 2 independent
(2) After the addition of water, the ratio of the weight of water in the solution to the weight of the solution becomes 7/10
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in each of Steps 3 and 4, this step is not required
Answer: Option D

A store stocks shirts, trousers and suits in the ratio of 4:5:6. If the store stocks only these 3 items, what is the number of items
stocked in the store?
(1) The number of suits is 100 more than the number of shirts stocked in the store
(2) The number of suits is 150 less than the number of shirts and trousers stocked in the store
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is
    not sufficient to answer the question asked.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is
    not sufficient to answer the question asked.
  • c)
    BOTH statements (1) and (2) TOGETHER are sufficient to
    answer the question asked, but NEITHER statement ALONE
    is sufficient to answer the question asked.
  • d)
    EACH statement ALONE is sufficient to answer the question
    asked.
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient to
    answer the question asked, and additional data specific to the
    problem are needed.
Correct answer is option 'D'. Can you explain this answer?

Gauri Iyer answered
Step 1 & 2: Understand Question and Draw Inference
Let the number of shirts, trousers and suits be 4x, 5x and 6x respectively.
Total number of items = 4x +5x+6x = 15x.
 
To find: 15x = ?
To answer this question, we need to find the value of x
Step 3 : Analyze Statement 1 independent
  1. The number of suits is 100 more than the number of shirts stocked in the store
6x – 4x = 100
i.e. 2x = 100
x = 50
Sufficient to answer
Step 4 : Analyze Statement 2 independent
2. The number of suits is 150 less than the number of shirts and trousers stocked in the store
(4x +5x) – 6x = 150
3x = 150
x = 50
Sufficient to answer
Step 5: Analyze Both Statements Together (if needed)
Since, we have a unique answer from steps 3 and 4, this step is not required.
Answer: D

Chapter doubts & questions for Ratio and Proportion - Mathematics for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Ratio and Proportion - Mathematics for ACT in English & Hindi are available as part of ACT exam. Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.

Mathematics for ACT

144 videos|100 docs|61 tests

Top Courses ACT

Signup to see your scores go up within 7 days!

Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup