All Exams >
UCAT >
Decision Making for UCAT >
All Questions
All questions of Probabilistic Reasoning for UCAT Exam
One card is randomly drawn from a pack of 52 cards. What is the probability that the card drawn is a face card(Jack, Queen or King)- a)
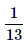
- b)
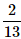
- c)
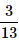
- d)
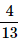
Correct answer is option 'C'. Can you explain this answer?
One card is randomly drawn from a pack of 52 cards. What is the probability that the card drawn is a face card(Jack, Queen or King)
a)
b)
c)
d)
|
Nikita Singh answered |
- Total number of cards, n(S) = 52
- Total number of face cards, n(E) = 12 (4 Jacks, 4 Queens, 4 Kings)
A die is rolled twice. What is the probability of getting a sum equal to 9?- a)
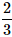
- b)
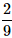
- c)
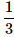
- d)
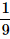
Correct answer is option 'D'. Can you explain this answer?
A die is rolled twice. What is the probability of getting a sum equal to 9?
a)
b)
c)
d)
|
Target Study Academy answered |
Total number of outcomes possible when a die is rolled = 6 (∵ any one face out of the 6 faces)
- Hence, total number of outcomes possible when a die is rolled twice, n(S) = 6 x 6 = 36
E = Getting a sum of 9 when the two dice fall = {(3,6), (4,5), (5,4), (6,3)}
- Hence, n(E) = 4
A bag contains 2 yellow, 3 green and 2 blue balls. Two balls are drawn at random. What is the probability that none of the balls drawn is blue?- a)
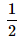
- b)
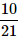
- c)
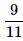
- d)
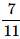
Correct answer is option 'B'. Can you explain this answer?
A bag contains 2 yellow, 3 green and 2 blue balls. Two balls are drawn at random. What is the probability that none of the balls drawn is blue?
a)
b)
c)
d)
|
Future Foundation Institute answered |
Total number of balls = 2 + 3 + 2 = 7
► Let S be the sample space.
- n(S) = Total number of ways of drawing 2 balls out of 7 = 7C2
► Let E = Event of drawing 2 balls, none of them is blue.
- n(E) = Number of ways of drawing 2 balls from the total 5 (= 7-2) balls = 5C2
(∵ There are two blue balls in the total 7 balls. Total number of non-blue balls = 7 - 2 = 5)
Can you explain the answer of this question below:A bag contains 4 black, 5 yellow and 6 green balls. Three balls are drawn at random from the bag. What is the probability that all of them are yellow?
- A:
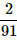
- B:
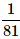
- C:
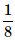
- D:
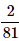
The answer is A.
A bag contains 4 black, 5 yellow and 6 green balls. Three balls are drawn at random from the bag. What is the probability that all of them are yellow?
|
Divey Sethi answered |
Total number of balls = 4 + 5 + 6 = 15
Let S be the sample space.
- n(S) = Total number of ways of drawing 3 balls out of 15 = 15C3
Let E = Event of drawing 3 balls, all of them are yellow.
- n(E) = Number of ways of drawing 3 balls from the total 5 = 5C3
(∵ there are 5 yellow balls in the total balls)
[∵ nCr = nC(n-r). So 5C3 = 5C2. Applying this for the ease of calculation]
What is the probability of selecting a prime number from 1,2,3,... 10 ?- a)
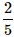
- b)
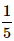
- c)
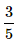
- d)
Correct answer is option 'A'. Can you explain this answer?
What is the probability of selecting a prime number from 1,2,3,... 10 ?
a)
b)
c)
d)
|
|
Nikita Singh answered |
Total count of numbers, n(S) = 10
Prime numbers in the given range are 2,3,5 and 7
Hence, total count of prime numbers in the given range, n(E) = 4
Prime numbers in the given range are 2,3,5 and 7
Hence, total count of prime numbers in the given range, n(E) = 4
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that none of them are selected?- a)
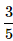
- b)
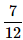
- c)
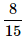
- d)
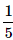
Correct answer is option 'C'. Can you explain this answer?
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that none of them are selected?
a)
b)
c)
d)
|
Anaya Patel answered |
There are 15 boys and 10 girls in a class. If three students are selected at random, what is the probability that 1 girl and 2 boys are selected?
- a)
- b)
- c)
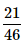
- d)
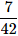
Correct answer is option 'C'. Can you explain this answer?
There are 15 boys and 10 girls in a class. If three students are selected at random, what is the probability that 1 girl and 2 boys are selected?
a)
b)
c)
d)
|
Bank Exams India answered |
Let S be the sample space.
- n(S) = Total number of ways of selecting 3 students from 25 students = 25C3
Let E = Event of selecting 1 girl and 2 boys
- n(E) = Number of ways of selecting 1 girl and 2 boys
15 boys and 10 girls are there in a class. We need to select 2 boys from 15 boys and 1 girl from 10 girls
Number of ways in which this can be done:
15C2 × 10C1
Hence n(E) = 15C2 × 10C1
15C2 × 10C1
Hence n(E) = 15C2 × 10C1
A randomly selected year is containing 53 Mondays then probability that it is a leap year- a)2 / 5
- b)3 / 4
- c)1 / 4
- d)2 / 7
Correct answer is option 'A'. Can you explain this answer?
A randomly selected year is containing 53 Mondays then probability that it is a leap year
a)
2 / 5
b)
3 / 4
c)
1 / 4
d)
2 / 7
|
KS Coaching Center answered |
The correct option is A
- Selected year will be a non leap year with a probability 3/4
- Selected year will be a leap year with a probability 1/4
- A selected leap year will have 53 Mondays with probability 2/7
- A selected non leap year will have 53 Mondays with probability 1/7
- E→ Event that randomly selected year contains 53 Mondays
P(E) = (3/4 × 1/7) + (1/4 × 2/7)
P(Leap Year/ E) = (2/28) / (5/28) = 2/5
P(Leap Year/ E) = (2/28) / (5/28) = 2/5
A card is randomly drawn from a deck of 52 cards. What is the probability getting either a King or a Diamond?- a)
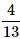
- b)
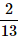
- c)
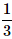
- d)
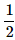
Correct answer is option 'A'. Can you explain this answer?
A card is randomly drawn from a deck of 52 cards. What is the probability getting either a King or a Diamond?
a)
b)
c)
d)
|
Cstoppers Instructors answered |
Total number of cards = 52
Total Number of King Cards = 4
Total Number of King Cards = 4
Total Number of Diamond Cards = 13
Total Number of Cards which are both King and Diamond = 1
Here a card can be both a Diamond card and a King. Hence these are not mutually exclusive events. (Reference : mutually exclusive events) . By Addition Theorem of Probability, we have P(King or a Diamond) = P(King) + P(Diamond) – P(King and Diamond)
John draws a card from a pack of cards. What is the probability that the card drawn is a card of black suit?- a)
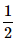
- b)
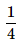
- c)
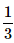
- d)
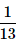
Correct answer is option 'A'. Can you explain this answer?
John draws a card from a pack of cards. What is the probability that the card drawn is a card of black suit?
a)
b)
c)
d)
|
Naroj Boda answered |
Total number of cards, n(S) = 52
Total number of black cards, n(E) = 26
Total number of black cards, n(E) = 26
When two dice are rolled, what is the probability that the sum is either 7 or 11?- a)
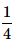
- b)
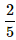
- c)
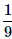
- d)
Correct answer is option 'D'. Can you explain this answer?
When two dice are rolled, what is the probability that the sum is either 7 or 11?
a)
b)
c)
d)
|
|
Target Study Academy answered |
Total number of outcomes possible when a die is rolled = 6 (? any one face out of the 6 faces)
Hence, total number of outcomes possible when two dice are rolled = 6 × 6 = 36
To get a sum of 7, the following are the favourable cases.
(1, 6), (2, 5), {3, 4}, (4, 3), (5, 2), (6,1)
=> Number of ways in which we get a sum of 7 = 6
Hence, total number of outcomes possible when two dice are rolled = 6 × 6 = 36
To get a sum of 7, the following are the favourable cases.
(1, 6), (2, 5), {3, 4}, (4, 3), (5, 2), (6,1)
=> Number of ways in which we get a sum of 7 = 6
To get a sum of 11, the following are the favourable cases. (5, 6), (6, 5) => Number of ways in which we get a sum of 11 = 2
Here, clearly the events are mutually exclusive events. By Addition Theorem of Probability, we have P(a sum of 7 or a sum of 11) = P(a sum of 7) + P( a sum of 11)
5 coins are tossed together. What is the probability of getting exactly 2 heads?- a)
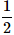
- b)
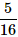
- c)
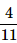
- d)
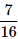
Correct answer is option 'B'. Can you explain this answer?
5 coins are tossed together. What is the probability of getting exactly 2 heads?
a)
b)
c)
d)
|
|
Cstoppers Instructors answered |
Total number of outcomes possible when a coin is tossed = 2 (? Head or Tail)
Hence, total number of outcomes possible when 5 coins are tossed, n(S) = 25
E = Event of getting exactly 2 heads when 5 coins are tossed
n(E) = Number of ways of getting exactly 2 heads when 5 coins are tossed = 5C2
Hence, total number of outcomes possible when 5 coins are tossed, n(S) = 25
E = Event of getting exactly 2 heads when 5 coins are tossed
n(E) = Number of ways of getting exactly 2 heads when 5 coins are tossed = 5C2
A card is randomly drawn from a deck of 52 cards. What is the probability getting an Ace or King or Queen?- a)
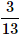
- b)
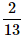
- c)
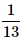
- d)
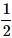
Correct answer is option 'A'. Can you explain this answer?
A card is randomly drawn from a deck of 52 cards. What is the probability getting an Ace or King or Queen?
a)
b)
c)
d)
|
Rhea Reddy answered |
Total number of cards = 52
Total number of Ace cards = 4
Total number of Ace cards = 4
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that only one of them is selected?- a)3/5
- b)2/5
- c)1/5
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
John and Dani go for an interview for two vacancies. The probability for the selection of John is 1/3 and whereas the probability for the selection of Dani is 1/5. What is the probability that only one of them is selected?
a)
3/5
b)
2/5
c)
1/5
d)
None of these
|
Sameer Rane answered |
Let A = the event that John is selected and B = the event that Dani is selected.
Given that 𝑃(𝐴) = 1/3 and 𝑃(𝐵) = 1/5
We know that A is the event that A does not occur and B is the event that B does not occur
Probability that only one of them is selected
What is the probability of drawing a "Queen" from a deck of 52 cards?- a)
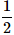
- b)
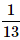
- c)
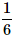
- d)
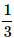
Correct answer is option 'B'. Can you explain this answer?
What is the probability of drawing a "Queen" from a deck of 52 cards?
a)
b)
c)
d)
|
|
Target Study Academy answered |
Total number of cards, n(S) = 52
Total number of "Queen" cards, n(E) = 4
Total number of "Queen" cards, n(E) = 4
Hunar wrote two sections of CAT paper; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?- a)0.75
- b)0.65
- c)0.85
- d)0.95
Correct answer is option 'A'. Can you explain this answer?
Hunar wrote two sections of CAT paper; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?
a)
0.75
b)
0.65
c)
0.85
d)
0.95
|
|
KS Coaching Center answered |
- Let P(QA) = passing QA’s section
- P(V) = passing Verbal section
- So, P(QA/V) = P(QA∩V)/P(V) = 0.6/0.8 = 0.75
Hence, the correct answer is option A.
Three coins are tossed. What is the probability of getting at most two tails?- a)
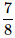
- b)
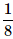
- c)
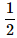
- d)
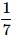
Correct answer is option 'A'. Can you explain this answer?
Three coins are tossed. What is the probability of getting at most two tails?
a)
b)
c)
d)
|
Raghavendra Sharma answered |
Here S = {TTT, TTH, THT, HTT, THH, HTH, HHT, HHH}
Let E = event of getting at most two heads.
Then E = {TTT, TTH, THT, HTT, THH, HTH, HHT}.
Therefore P(E) = n(E)/n(S) = 7/8.
Chapter doubts & questions for Probabilistic Reasoning - Decision Making for UCAT 2025 is part of UCAT exam preparation. The chapters have been prepared according to the UCAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probabilistic Reasoning - Decision Making for UCAT in English & Hindi are available as part of UCAT exam.
Download more important topics, notes, lectures and mock test series for UCAT Exam by signing up for free.
Decision Making for UCAT
16 videos|21 docs|27 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup