All Exams >
SSS 2 >
Physics for SSS 2 >
All Questions
All questions of Simple Harmonic Motion for SSS 2 Exam
What is the phase difference between the displacement and velocity of an object in SHM?- a)0 degrees
- b)45 degrees
- c)90 degrees
- d)180 degrees
Correct answer is option 'C'. Can you explain this answer?
What is the phase difference between the displacement and velocity of an object in SHM?
a)
0 degrees
b)
45 degrees
c)
90 degrees
d)
180 degrees
|
Prasad Shah answered |
Understanding SHM
Simple Harmonic Motion (SHM) is a type of periodic motion where an object oscillates around an equilibrium position. In SHM, two key quantities are displacement and velocity.
Displacement in SHM
- Displacement (x) is the distance of the object from its equilibrium position.
- It varies sinusoidally with time, represented as x(t) = A sin(ωt), where A is the amplitude and ω is the angular frequency.
Velocity in SHM
- Velocity (v) is the rate of change of displacement with respect to time.
- The velocity in SHM can be derived by differentiating displacement: v(t) = dx/dt = Aω cos(ωt).
Phase Relationship
- Displacement and velocity are both sinusoidal functions but differ in their phase.
- Displacement is represented by a sine function, while velocity uses a cosine function.
Phase Difference Explained
- The cosine function can be expressed as a sine function with a phase shift: cos(ωt) = sin(ωt + 90 degrees).
- This means that the velocity function leads the displacement function by 90 degrees.
- In other words, when the displacement is at its maximum, the velocity is zero, and when the displacement is zero, the velocity is at its maximum.
Conclusion
- Therefore, there is a phase difference of 90 degrees between the displacement and velocity of an object in SHM.
- The correct answer to the question is indeed option 'C' – 90 degrees.
Simple Harmonic Motion (SHM) is a type of periodic motion where an object oscillates around an equilibrium position. In SHM, two key quantities are displacement and velocity.
Displacement in SHM
- Displacement (x) is the distance of the object from its equilibrium position.
- It varies sinusoidally with time, represented as x(t) = A sin(ωt), where A is the amplitude and ω is the angular frequency.
Velocity in SHM
- Velocity (v) is the rate of change of displacement with respect to time.
- The velocity in SHM can be derived by differentiating displacement: v(t) = dx/dt = Aω cos(ωt).
Phase Relationship
- Displacement and velocity are both sinusoidal functions but differ in their phase.
- Displacement is represented by a sine function, while velocity uses a cosine function.
Phase Difference Explained
- The cosine function can be expressed as a sine function with a phase shift: cos(ωt) = sin(ωt + 90 degrees).
- This means that the velocity function leads the displacement function by 90 degrees.
- In other words, when the displacement is at its maximum, the velocity is zero, and when the displacement is zero, the velocity is at its maximum.
Conclusion
- Therefore, there is a phase difference of 90 degrees between the displacement and velocity of an object in SHM.
- The correct answer to the question is indeed option 'C' – 90 degrees.
The motion of a simple pendulum is approximately SHM when:- a)The angle of oscillation is small
- b)The angle of oscillation is large
- c)The length of the pendulum is long
- d)The mass of the pendulum is large
Correct answer is option 'A'. Can you explain this answer?
The motion of a simple pendulum is approximately SHM when:
a)
The angle of oscillation is small
b)
The angle of oscillation is large
c)
The length of the pendulum is long
d)
The mass of the pendulum is large
|
Catalyst Learningacademy answered |
The motion of a simple pendulum is approximately SHM when the angle of oscillation is small.
The quality factor (Q-factor) of an oscillating system is a measure of its:- a)Damping
- b)Stiffness
- c)Frequency
- d)Energy
Correct answer is option 'A'. Can you explain this answer?
The quality factor (Q-factor) of an oscillating system is a measure of its:
a)
Damping
b)
Stiffness
c)
Frequency
d)
Energy
|
Sagarika Khanna answered |
Understanding the Q-Factor
The quality factor, or Q-factor, is a dimensionless parameter that characterizes the damping of oscillatory systems, such as springs, pendulums, or electrical circuits.
What is Damping?
Damping refers to the effect of energy dissipation in an oscillating system, which can be caused by friction, resistance, or other forms of energy loss.
Significance of Q-Factor
- Definition: The Q-factor is defined as the ratio of the stored energy to the energy dissipated per cycle.
- High Q: A high Q-factor indicates low damping, meaning the system oscillates for a longer time with less energy loss.
- Low Q: Conversely, a low Q-factor signals high damping, where energy is lost rapidly, resulting in quick cessation of oscillations.
Mathematical Relation
The Q-factor can be expressed mathematically as:
- Q = (Energy stored in the system) / (Energy lost per cycle)
Importance in Applications
- Mechanical Systems: In mechanical systems, a high Q-factor means efficient energy storage, leading to prolonged oscillations.
- Electrical Systems: In circuits, a high Q-factor can enhance the selectivity and sensitivity of resonant circuits, such as in radio transmitters.
Conclusion
Thus, the Q-factor serves as a critical measure of damping in oscillating systems, making option 'A' the correct answer. Understanding the Q-factor helps in designing systems with desired oscillatory behavior, whether in engineering, physics, or technology.
The quality factor, or Q-factor, is a dimensionless parameter that characterizes the damping of oscillatory systems, such as springs, pendulums, or electrical circuits.
What is Damping?
Damping refers to the effect of energy dissipation in an oscillating system, which can be caused by friction, resistance, or other forms of energy loss.
Significance of Q-Factor
- Definition: The Q-factor is defined as the ratio of the stored energy to the energy dissipated per cycle.
- High Q: A high Q-factor indicates low damping, meaning the system oscillates for a longer time with less energy loss.
- Low Q: Conversely, a low Q-factor signals high damping, where energy is lost rapidly, resulting in quick cessation of oscillations.
Mathematical Relation
The Q-factor can be expressed mathematically as:
- Q = (Energy stored in the system) / (Energy lost per cycle)
Importance in Applications
- Mechanical Systems: In mechanical systems, a high Q-factor means efficient energy storage, leading to prolonged oscillations.
- Electrical Systems: In circuits, a high Q-factor can enhance the selectivity and sensitivity of resonant circuits, such as in radio transmitters.
Conclusion
Thus, the Q-factor serves as a critical measure of damping in oscillating systems, making option 'A' the correct answer. Understanding the Q-factor helps in designing systems with desired oscillatory behavior, whether in engineering, physics, or technology.
A particle executes simple harmonic motion between x = -A and x = +A. The time taken for it to go from 0 to A/2 is T1 and to go from A/2 to A is T2. Then- a)T1 < T2
- b)T1 > T2
- c)T1 = T2
- d)T1 = 2T2
Correct answer is option 'A'. Can you explain this answer?
A particle executes simple harmonic motion between x = -A and x = +A. The time taken for it to go from 0 to A/2 is T1 and to go from A/2 to A is T2. Then
a)
T1 < T2
b)
T1 > T2
c)
T1 = T2
d)
T1 = 2T2
|
Diya Iyer answered |
= T2
This statement is not necessarily true. The time taken for the particle to go from 0 to A/2 and from A/2 to A may not be equal in general.
However, if the motion is symmetric about x=0 (i.e., the particle takes the same amount of time to go from 0 to A/2 as it does from 0 to -A/2), then T1 = T2. This is because the total time period of the motion is T = 2T1 = 2T2, and the particle spends half of this time period in each half of the motion, so T1 = T2 = T/2.
This statement is not necessarily true. The time taken for the particle to go from 0 to A/2 and from A/2 to A may not be equal in general.
However, if the motion is symmetric about x=0 (i.e., the particle takes the same amount of time to go from 0 to A/2 as it does from 0 to -A/2), then T1 = T2. This is because the total time period of the motion is T = 2T1 = 2T2, and the particle spends half of this time period in each half of the motion, so T1 = T2 = T/2.
A linear harmonic oscillator of force constant 2 × 106 N/m and amplitude 0.01 m has a total mechanical energy of 160 J.
Its- a)maximum potential energy is 100 J
- b)maximum kinetic energy is 100 J
- c)maximum potential energy is 160 J
- d)maximum potential energy is zero
Correct answer is option 'B,C'. Can you explain this answer?
A linear harmonic oscillator of force constant 2 × 106 N/m and amplitude 0.01 m has a total mechanical energy of 160 J.
Its
Its
a)
maximum potential energy is 100 J
b)
maximum kinetic energy is 100 J
c)
maximum potential energy is 160 J
d)
maximum potential energy is zero
|
Sarthak Khanna answered |
The total energy of the oscillator
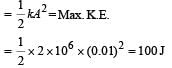
As total mechanical energy = 160 J
The P.E. at equilibrium position is not zero.
P.E. at mean position = (160 – 100) J = 60 J
∴ Max P.E. = (100 + 60 ) J = 160 J.
The P.E. at equilibrium position is not zero.
P.E. at mean position = (160 – 100) J = 60 J
∴ Max P.E. = (100 + 60 ) J = 160 J.
A simple pendulum has time period T1. The point of suspension is now moved upward according to the relation y = Kt2, (K = 1 m/s2) where y is the vertical displacement. The time period now becomes T2. The ratio of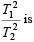 
(g = 10 m/s2)- a)5/6
- b)6/5
- c)1
- d)4/5
Correct answer is option 'B'. Can you explain this answer?
A simple pendulum has time period T1. The point of suspension is now moved upward according to the relation y = Kt2, (K = 1 m/s2) where y is the vertical displacement. The time period now becomes T2. The ratio of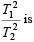
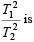
(g = 10 m/s2)
a)
5/6
b)
6/5
c)
1
d)
4/5
|
Jaideep Sengupta answered |
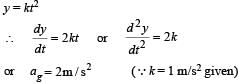
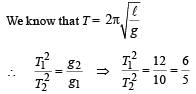
[∵g1 = 10 m/s2 and g2 = g + 2 = 12 m/s2]
Which of the following graphs represents the displacement-time relationship in SHM?- a)Linear graph
- b)Parabolic graph
- c)Sine wave graph
- d)Exponential graph
Correct answer is option 'C'. Can you explain this answer?
Which of the following graphs represents the displacement-time relationship in SHM?
a)
Linear graph
b)
Parabolic graph
c)
Sine wave graph
d)
Exponential graph
|
Gargi Kaur answered |
Understanding Simple Harmonic Motion (SHM)
In simple harmonic motion, the displacement of an object oscillating back and forth is key to understanding its motion. The displacement-time graph is crucial for visualizing this phenomenon.
Characteristics of SHM Displacement-Time Relationship
- Periodic Motion: In SHM, an object moves in a periodic manner, meaning it repeats its motion at regular intervals.
- Sine Wave Form: The displacement of the object as a function of time can be mathematically modeled using sine or cosine functions. This results in a sine wave graph.
- Maxima and Minima: The peaks and troughs of the sine wave represent the maximum positive and negative displacements, respectively. The graph oscillates symmetrically around the equilibrium position.
Why Other Options Are Incorrect
- Linear Graph: Represents uniform motion where displacement changes at a constant rate, unlike SHM, which varies periodically.
- Parabolic Graph: Indicates acceleration changes, typically associated with uniformly accelerated motion, not the oscillatory nature of SHM.
- Exponential Graph: Depicts growth or decay processes, failing to capture the oscillatory or periodic nature of SHM.
Conclusion
The correct representation of the displacement-time relationship in SHM is option 'C', the sine wave graph. This reflects the periodic nature of the motion, showcasing how displacement varies with time in a smooth, oscillatory manner. Understanding this concept is essential for grasping the principles of SHM in physics.
In simple harmonic motion, the displacement of an object oscillating back and forth is key to understanding its motion. The displacement-time graph is crucial for visualizing this phenomenon.
Characteristics of SHM Displacement-Time Relationship
- Periodic Motion: In SHM, an object moves in a periodic manner, meaning it repeats its motion at regular intervals.
- Sine Wave Form: The displacement of the object as a function of time can be mathematically modeled using sine or cosine functions. This results in a sine wave graph.
- Maxima and Minima: The peaks and troughs of the sine wave represent the maximum positive and negative displacements, respectively. The graph oscillates symmetrically around the equilibrium position.
Why Other Options Are Incorrect
- Linear Graph: Represents uniform motion where displacement changes at a constant rate, unlike SHM, which varies periodically.
- Parabolic Graph: Indicates acceleration changes, typically associated with uniformly accelerated motion, not the oscillatory nature of SHM.
- Exponential Graph: Depicts growth or decay processes, failing to capture the oscillatory or periodic nature of SHM.
Conclusion
The correct representation of the displacement-time relationship in SHM is option 'C', the sine wave graph. This reflects the periodic nature of the motion, showcasing how displacement varies with time in a smooth, oscillatory manner. Understanding this concept is essential for grasping the principles of SHM in physics.
One end of a long metallic wire of length L is tied to the ceiling. The other end is tied to a massless spring of spring constant K.A mass m hangs freely from the free end of the spring. The area of cross-section and the Young’s modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to:- a)2π(m /K)1/2
- b)
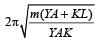
- c)2π[(mYA / KL)1/2
- d)2π[(mL / YA)1/2
Correct answer is option 'B'. Can you explain this answer?
One end of a long metallic wire of length L is tied to the ceiling. The other end is tied to a massless spring of spring constant K.A mass m hangs freely from the free end of the spring. The area of cross-section and the Young’s modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to:
a)
2π(m /K)1/2
b)
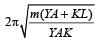
c)
2π[(mYA / KL)1/2
d)
2π[(mL / YA)1/2
|
Sahana Joshi answered |
Let us consider the wire also as a spring. Then the case becomes that of two spring attached in series. The equivalent spring constant is
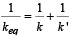
where k' is the spring constant of the wire
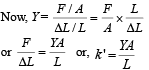
We know that time period of the system
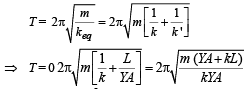
A highly rigid cubical block A of small mass M and side L is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity η such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force F is applied perpendicular to one of the sides faces of A. After the force is withdrawn, block A executes small oscillations the time period of which is given by- a)
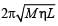
- b)
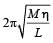
- c)
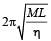
- d)
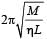
Correct answer is option 'D'. Can you explain this answer?
A highly rigid cubical block A of small mass M and side L is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity η such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force F is applied perpendicular to one of the sides faces of A. After the force is withdrawn, block A executes small oscillations the time period of which is given by
a)
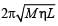
b)
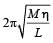
c)
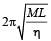
d)
|
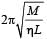
Mira Roy answered |
NOTE : When a force is applied on cubical block A in the horizontal direction then the lower block B will get distorted as shown by dotted lines and A will attain a new position (without distortion as A is a rigid body) as shown by dotted lines.
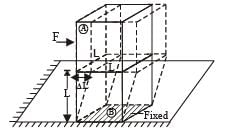
For cubical block B
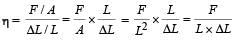
⇒ F = ηLΔL
ηL is a constant
⇒ Force F ∝ ΔL and directed towards the mean position, oscillation will be simple harmonic in nature.
Here, Mω2 = ηL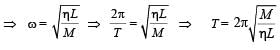
Here, Mω2 = ηL
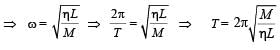
Two bodies M and N of equal masses are suspended from two separate massless springs of spring constants k1 and k2 respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of M to that of N is- a)
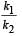
- b)
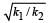
- c)
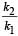
- d)
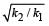
Correct answer is option 'D'. Can you explain this answer?
Two bodies M and N of equal masses are suspended from two separate massless springs of spring constants k1 and k2 respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of M to that of N is
a)
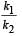
b)
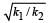
c)
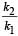
d)
|
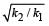
Tejas Chawla answered |
Both the bodies oscillate in simple harmonic motion, for which the maximum velocities will be
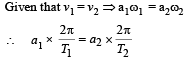
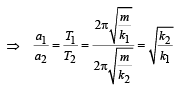
What is Simple Harmonic Motion (SHM)?- a)Motion in a straight line with constant speed
- b)Motion in a circular path with constant speed
- c)Motion back and forth along a line about a stable equilibrium position
- d)Motion in a zigzag pattern with varying speed
Correct answer is option 'C'. Can you explain this answer?
What is Simple Harmonic Motion (SHM)?
a)
Motion in a straight line with constant speed
b)
Motion in a circular path with constant speed
c)
Motion back and forth along a line about a stable equilibrium position
d)
Motion in a zigzag pattern with varying speed
|
|
Catalyst Learningacademy answered |
Simple Harmonic Motion (SHM) refers to the back and forth motion of an object along a line about a stable equilibrium position.
The time period of a simple pendulum depends on:- a)Length of the pendulum and acceleration due to gravity
- b)Amplitude of the pendulum and its mass
- c)Only the length of the pendulum
- d)Only the mass of the pendulum
Correct answer is option 'A'. Can you explain this answer?
The time period of a simple pendulum depends on:
a)
Length of the pendulum and acceleration due to gravity
b)
Amplitude of the pendulum and its mass
c)
Only the length of the pendulum
d)
Only the mass of the pendulum
|
|
Catalyst Learningacademy answered |
The time period of a simple pendulum depends on the length of the pendulum and the acceleration due to gravity.
The force constant of a spring is a measure of its:- a)Elasticity
- b)Mass
- c)Length
- d)Velocity
Correct answer is option 'A'. Can you explain this answer?
The force constant of a spring is a measure of its:
a)
Elasticity
b)
Mass
c)
Length
d)
Velocity
|
KS Coaching Center answered |
The force constant of a spring is a measure of its elasticity.
What is the potential energy of a particle in Simple Harmonic Motion (SHM) given by?- a)U = 1/2 mω²y²
- b)U = 1/2 mωy²
- c)U = 1/2 mωy
- d)U = 1/2 mω²y
Correct answer is option 'A'. Can you explain this answer?
What is the potential energy of a particle in Simple Harmonic Motion (SHM) given by?
a)
U = 1/2 mω²y²
b)
U = 1/2 mωy²
c)
U = 1/2 mωy
d)
U = 1/2 mω²y
|
EduRev SSC CGL answered |
The potential energy of a particle in Simple Harmonic Motion (SHM) is given by U = 1/2 mω²y². This formula represents the energy associated with the position of the particle in the restoring force field of the SHM system.
In Simple Harmonic Motion (SHM), what is the angular frequency defined as?- a)The product of frequency with a factor 2π
- b)The time taken by the particle to complete one oscillation
- c)The maximum displacement in any direction from the mean position
- d)The displacement of the particle from the mean position
Correct answer is option 'A'. Can you explain this answer?
In Simple Harmonic Motion (SHM), what is the angular frequency defined as?
a)
The product of frequency with a factor 2π
b)
The time taken by the particle to complete one oscillation
c)
The maximum displacement in any direction from the mean position
d)
The displacement of the particle from the mean position
|
Ssc Cgl answered |
The angular frequency in Simple Harmonic Motion (SHM) is defined as the product of frequency with a factor 2π. It is denoted by the Greek letter ω and represents the rate of change of phase of a periodic wave or oscillation. The angular frequency is related to the frequency of oscillation in SHM.
What is the time period defined as Simple Harmonic Motion (SHM)?- a)The time taken for a particle to complete one oscillation.
- b)The time taken for a particle to reach its maximum amplitude.
- c)The time taken for a particle to reach its mean position.
- d)The time taken for a particle to reach its extreme position.
Correct answer is option 'A'. Can you explain this answer?
What is the time period defined as Simple Harmonic Motion (SHM)?
a)
The time taken for a particle to complete one oscillation.
b)
The time taken for a particle to reach its maximum amplitude.
c)
The time taken for a particle to reach its mean position.
d)
The time taken for a particle to reach its extreme position.
|
Target Study Academy answered |
In Simple Harmonic Motion, the time period refers to the duration it takes for a particle to complete one full oscillation. This period is crucial in understanding the frequency and behavior of the oscillating system. It is measured as the time required for the particle to move from a point, through its extreme positions, and back to the same point in the same direction. This concept is fundamental in analyzing and predicting the motion of particles undergoing SHM.
How is the velocity of a particle in Simple Harmonic Motion related to its displacement?- a) The velocity is inversely proportional to displacement.
- b) The velocity is directly proportional to displacement.
- c) The velocity is independent of displacement.
- d) The velocity is proportional to the square of displacement.
Correct answer is option 'B'. Can you explain this answer?
How is the velocity of a particle in Simple Harmonic Motion related to its displacement?
a)
The velocity is inversely proportional to displacement.
b)
The velocity is directly proportional to displacement.
c)
The velocity is independent of displacement.
d)
The velocity is proportional to the square of displacement.
|
T.S Academy answered |
In Simple Harmonic Motion, the velocity of a particle is directly proportional to its displacement from the mean position. This relationship implies that as the particle moves away from the equilibrium point, its velocity increases, reaching a maximum at the extreme positions. Understanding this connection between velocity and displacement is crucial in analyzing the dynamics of oscillatory systems and predicting the behavior of particles undergoing SHM.
A block with mass M is conn ected by a massless spring with stiffness constant k to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position x0. Consider two cases: (i) when the block is at x0; and (ii) when the block is at x = x0 + A. In both the cases, a particle with mass m(<M) is softly placed on the block after which they stick to each other. Which of the following statement(s) is (are) true about the motion after the mass m is placed on the mass M?- a)The amplitude of oscillation in the first case chan ges by a factor of
whereas in the second case it remains unchanged. - b)The final time period of oscillation in both the cases is same.
- c)The total energy decreases in both the cases.
- d)The instantaneous speed at x0 of the combined masses decreases in both the cases
Correct answer is option 'A,B,D'. Can you explain this answer?
A block with mass M is conn ected by a massless spring with stiffness constant k to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position x0. Consider two cases: (i) when the block is at x0; and (ii) when the block is at x = x0 + A. In both the cases, a particle with mass m(<M) is softly placed on the block after which they stick to each other. Which of the following statement(s) is (are) true about the motion after the mass m is placed on the mass M?
a)
The amplitude of oscillation in the first case chan ges by a factor of whereas in the second case it remains unchanged.
whereas in the second case it remains unchanged.b)
The final time period of oscillation in both the cases is same.
c)
The total energy decreases in both the cases.
d)
The instantaneous speed at x0 of the combined masses decreases in both the cases
|
|
Mira Roy answered |
Case (i) : Applying conservation of linear momentum.
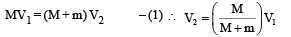
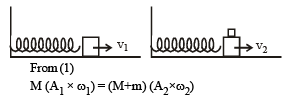
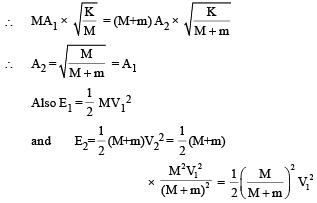
Clearly E2 < E1
The new time Period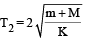
Case (ii) : The new time Period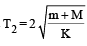
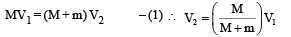
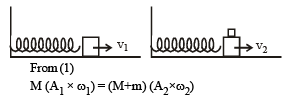
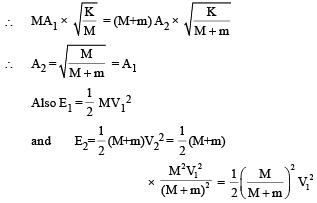
Clearly E2 < E1
The new time Period
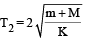
Case (ii) : The new time Period
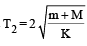
Also A2 = A1
Here E2 = E1
The instantaneous value of speed at Xo of the combined masses decreases in both the cases.
Here E2 = E1
The instantaneous value of speed at Xo of the combined masses decreases in both the cases.
A small block is connected to one end of a massless spring of un-stretched length 4.9 m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2 m and released from rest at t = 0. It then executes simple harmonic motion with angular frequency ω = π/3 rad/s. Simultaneously at t = 0, a small pebble is projected with speed v form point P at an angle of 45° as shown in the figure. Point P is at a horizontal distance of 10 m from O. If the pebble hits the block at t = 1 s, the value of v is (take g = 10 m/s2)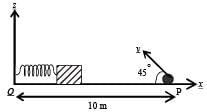
- a)
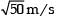
- b)
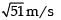
- c)
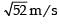
- d)
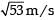
Correct answer is option 'A'. Can you explain this answer?
A small block is connected to one end of a massless spring of un-stretched length 4.9 m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2 m and released from rest at t = 0. It then executes simple harmonic motion with angular frequency ω = π/3 rad/s. Simultaneously at t = 0, a small pebble is projected with speed v form point P at an angle of 45° as shown in the figure. Point P is at a horizontal distance of 10 m from O. If the pebble hits the block at t = 1 s, the value of v is (take g = 10 m/s2)
a)
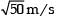
b)
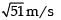
c)
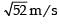
d)
|
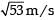
Nandini Nair answered |
A particle free to move along the x-axis has potential energy given by U(x) = k [1–exp(–x2)] for -∞ < x < + ∞, where k is a positive constant of appropriate dimensions. Then- a)at points away from the origin, the particle is in unstable equilibrium
- b)for any finite nonzero value of x, there is a force directed away from the origin
- c)if its total mechanical energy is k/2, it has its minimum kinetic energy at the origin.
- d)for small displacements from x = 0, the motion is simple harmonic
Correct answer is option 'D'. Can you explain this answer?
A particle free to move along the x-axis has potential energy given by U(x) = k [1–exp(–x2)] for -∞ < x < + ∞, where k is a positive constant of appropriate dimensions. Then
a)
at points away from the origin, the particle is in unstable equilibrium
b)
for any finite nonzero value of x, there is a force directed away from the origin
c)
if its total mechanical energy is k/2, it has its minimum kinetic energy at the origin.
d)
for small displacements from x = 0, the motion is simple harmonic
|
Rounak Desai answered |
Let us plot the graph of the mathematical equation
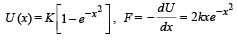
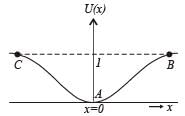
From the graph it is clear that the potential energy is minimum at x = 0. Therefore, x = 0 is the state of stable equilibrium. Now if we displace the particle from x = 0 then for displacements the particle tends to regain the position x = 0 with a force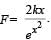 
Therefore for small
values of x we have F ∝ x.
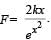Therefore for smallvalues of x we have F ∝ x.
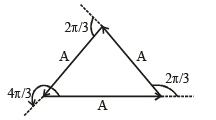
A point mass is subjected to two simultaneous sinusoidal displacements in x-direction, x1(t) = A sin wt and x2(t) =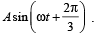 
Adding a third sinusoidal displacement x3(t) = B sin (ωt + φ) brings the mass to a complete rest. The values of B and φ are- a)
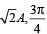
- b)
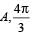
- c)
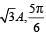
- d)
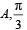
Correct answer is option 'B'. Can you explain this answer?
A point mass is subjected to two simultaneous sinusoidal displacements in x-direction, x1(t) = A sin wt and x2(t) = 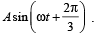Adding a third sinusoidal displacement x3(t) = B sin (ωt + φ) brings the mass to a complete rest. The values of B and φ are
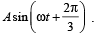Adding a third sinusoidal displacement x3(t) = B sin (ωt + φ) brings the mass to a complete rest. The values of B and φ area)
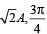
b)
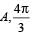
c)
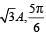
d)
|
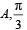
Bhavya Joshi answered |
Two sinusoidal displacements have amplitude A each, with a phase difference of 
It is given that sinusoidal displacement x3(t) brings the mass to a complete rest. This is possible when the amplitude of third is A and is having a phase difference of 
with
respect to x1 (t) as shown in the figure.
It is given that sinusoidal displacement x3(t) brings the mass to a complete rest. This is possible when the amplitude of third is A and is having a phase difference of withrespect to x1 (t) as shown in the figure.
A particle executes simple harmonic motion with a frequency. f. The frequency with which its kinetic energy oscillates is- a)f/2
- b)f
- c)2f
- d)4f
Correct answer is option 'C'. Can you explain this answer?
A particle executes simple harmonic motion with a frequency. f. The frequency with which its kinetic energy oscillates is
a)
f/2
b)
f
c)
2f
d)
4f
|
Devansh Joshi answered |
NOTE : During one complete oscillation, the kinetic energy will become maximum twice.
Therefore the frequency of kinetic energy will be 2f.
Therefore the frequency of kinetic energy will be 2f.
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies ω1 and ω2 and have total energies E1 and E2, respectively. The variations of their momenta p with positions x are shown in the figures.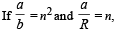 
then the correct equation(s) is(are)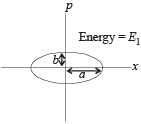
- a)E1ω1 = E2ω2
- b)
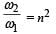
- c)ω1ω2 = n2
- d)
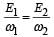
Correct answer is option 'B,D'. Can you explain this answer?
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies ω1 and ω2 and have total energies E1 and E2, respectively. The variations of their momenta p with positions x are shown in the figures. 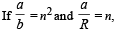then the correct equation(s) is(are)
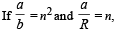then the correct equation(s) is(are) a)
E1ω1 = E2ω2
b)
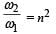
c)
ω1ω2 = n2
d)
|
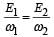
Mihir Patel answered |
Maximum linear momentum in case 1 is (p1)max = mvmax
b = m [aw1] ...(i)
Maximum linear momentum in case 2 is (p2)max = mvmax
R = m [Rω2]
b = m [aw1] ...(i)
Maximum linear momentum in case 2 is (p2)max = mvmax
R = m [Rω2]
∴ 1 = mω2 ...(ii)
Dividing (i) & (ii)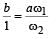 
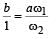
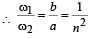∴ B is a correct option.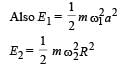
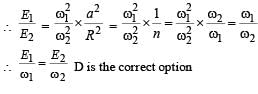
The motion of a mass-spring system is an example of:- a)Simple harmonic motion
- b)Circular motion
- c)Rotational motion
- d)Translational motion
Correct answer is option 'A'. Can you explain this answer?
The motion of a mass-spring system is an example of:
a)
Simple harmonic motion
b)
Circular motion
c)
Rotational motion
d)
Translational motion
|
Paradigm Institute answered |
The motion of a mass-spring system is an example of simple harmonic motion.
Which of the following quantities remains constant during SHM?- a)Total mechanical energy
- b)Acceleration
- c)Displacement
- d)Angular frequency
Correct answer is option 'A'. Can you explain this answer?
Which of the following quantities remains constant during SHM?
a)
Total mechanical energy
b)
Acceleration
c)
Displacement
d)
Angular frequency
|
|
Catalyst Learningacademy answered |
Total mechanical energy remains constant during Simple Harmonic Motion (SHM).
What is the unit for frequency in Simple Harmonic Motion?- a) Hertz
- b) Newton
- c) Joule
- d) Watt
Correct answer is option 'A'. Can you explain this answer?
What is the unit for frequency in Simple Harmonic Motion?
a)
Hertz
b)
Newton
c)
Joule
d)
Watt
|
|
EduRev SSC CGL answered |
The unit for frequency in Simple Harmonic Motion is Hertz, which is equivalent to one oscillation or cycle per second. Frequency represents the number of oscillations completed by a particle in one second and is a crucial parameter in determining the speed and rate of oscillations in SHM. Understanding the unit of frequency is essential for calculating and interpreting various properties of oscillatory systems accurately.
What is the frequency in Simple Harmonic Motion (SHM) defined as?- a)The time taken by the particle to complete one oscillation
- b)The number of oscillations completed by the particle in one second
- c)The maximum displacement in any direction from the mean position
- d)The displacement of the particle from the mean position
Correct answer is option 'B'. Can you explain this answer?
What is the frequency in Simple Harmonic Motion (SHM) defined as?
a)
The time taken by the particle to complete one oscillation
b)
The number of oscillations completed by the particle in one second
c)
The maximum displacement in any direction from the mean position
d)
The displacement of the particle from the mean position
|
|
Ssc Cgl answered |
The frequency in Simple Harmonic Motion (SHM) is defined as the number of oscillations completed by the particle in one second. It is denoted by the Greek letter ν and is the reciprocal of the time period (frequency = 1 / time period).
What does the amplitude represent of Simple Harmonic Motion (SHM)?- a)The maximum velocity attained by the particle.
- b)The maximum distance from the mean position.
- c)The mean position of the particle.
- d)The maximum acceleration experienced by the particle.
Correct answer is option 'B'. Can you explain this answer?
What does the amplitude represent of Simple Harmonic Motion (SHM)?
a)
The maximum velocity attained by the particle.
b)
The maximum distance from the mean position.
c)
The mean position of the particle.
d)
The maximum acceleration experienced by the particle.
|
|
T.S Academy answered |
The amplitude in Simple Harmonic Motion (SHM) signifies the maximum distance that a particle moves away from its mean position during oscillations. It represents the extreme positions reached by the particle as it oscillates back and forth around the equilibrium point. The amplitude is a crucial parameter that influences various aspects of the motion, including energy considerations and the overall behavior of the oscillating system.
What is Simple Harmonic Motion (SHM) defined as?- a)Motion along a curved path under a restoring force
- b)Motion of varying amplitude and frequency
- c)Motion of constant amplitude and single frequency
- d)Motion with irregular frequency changes
Correct answer is option 'C'. Can you explain this answer?
What is Simple Harmonic Motion (SHM) defined as?
a)
Motion along a curved path under a restoring force
b)
Motion of varying amplitude and frequency
c)
Motion of constant amplitude and single frequency
d)
Motion with irregular frequency changes
|
|
Ssc Cgl answered |
Simple Harmonic Motion (SHM) is defined as an oscillatory motion of constant amplitude and of single frequency under a restoring force whose magnitude is proportional to the displacement and always acts towards the mean position. In SHM, the particle's movement is back-and-forth along a straight path centered around the mean position, with the force restoring the particle being directly proportional to the distance of the particle from the mean position.
What is the acceleration of a particle in Simple Harmonic Motion (SHM) at any instant given by?- a)α = d²y / dt² = -ω²y
- b)α = d²y / dt² = -2ωy
- c)α = d²y / dt² = ω²y
- d)α = d²y / dt² = 2ωy
Correct answer is option 'A'. Can you explain this answer?
What is the acceleration of a particle in Simple Harmonic Motion (SHM) at any instant given by?
a)
α = d²y / dt² = -ω²y
b)
α = d²y / dt² = -2ωy
c)
α = d²y / dt² = ω²y
d)
α = d²y / dt² = 2ωy
|
|
T.S Academy answered |
The acceleration of a particle in Simple Harmonic Motion (SHM) at any instant is given by α = d²y / dt² = -ω²y. This expression describes how the acceleration of the particle is directly proportional to its displacement from the mean position but in the opposite direction.
The time period of an object executing SHM is 2 seconds. What is its frequency?- a)0.5 Hz
- b)2 Hz
- c)4 Hz
- d)8 Hz
Correct answer is option 'A'. Can you explain this answer?
The time period of an object executing SHM is 2 seconds. What is its frequency?
a)
0.5 Hz
b)
2 Hz
c)
4 Hz
d)
8 Hz
|
|
Paradigm Institute answered |
Frequency = 1 / Time period = 1 / 2 seconds = 0.5 Hz.
What is the relationship between the frequency and the time period of SHM?- a)They are inversely proportional
- b)They are directly proportional
- c)They are unrelated
- d)They depend on the amplitude of the motion
Correct answer is option 'B'. Can you explain this answer?
What is the relationship between the frequency and the time period of SHM?
a)
They are inversely proportional
b)
They are directly proportional
c)
They are unrelated
d)
They depend on the amplitude of the motion
|
Glance Learning Institute answered |
The frequency and time period of SHM are directly proportional. Frequency = 1 / Time period.
Hooke's Law is applicable to:
- a)Solids, liquids, and gases
- b)Only liquids
- c)Only gases
- d)Only solids
Correct answer is option 'D'. Can you explain this answer?
Hooke's Law is applicable to:
a)
Solids, liquids, and gases
b)
Only liquids
c)
Only gases
d)
Only solids
|
|
Catalyst Learningacademy answered |
Hooke's Law, which describes the relationship between force and displacement in a spring, is applicable to solids, liquids, and gases.
What is the acceleration of a particle at the mean position in Simple Harmonic Motion?- a) Maximum
- b) Zero
- c) Minimum
- d) Constant
Correct answer is option 'B'. Can you explain this answer?
What is the acceleration of a particle at the mean position in Simple Harmonic Motion?
a)
Maximum
b)
Zero
c)
Minimum
d)
Constant
|
|
EduRev SSC CGL answered |
At the mean position in Simple Harmonic Motion, the acceleration of a particle is zero. This means that when the particle is at its equilibrium point, there is no net force acting on it to cause acceleration. As the particle moves away from the mean position, the restoring force accelerates it back towards equilibrium. Understanding this characteristic of SHM helps in interpreting the motion and dynamics of oscillating systems accurately.
What is displacement in Simple Harmonic Motion (SHM) defined as?- a)A physical quantity that changes uniformly with time
- b)The time taken by the particle to complete one oscillation
- c)The number of oscillations completed by the particle in one second
- d)The maximum displacement in any direction from the mean position
Correct answer is option 'A'. Can you explain this answer?
What is displacement in Simple Harmonic Motion (SHM) defined as?
a)
A physical quantity that changes uniformly with time
b)
The time taken by the particle to complete one oscillation
c)
The number of oscillations completed by the particle in one second
d)
The maximum displacement in any direction from the mean position
|
|
Target Study Academy answered |
Displacement in Simple Harmonic Motion (SHM) is defined as a physical quantity which changes uniformly with time and also relative to the mean position in a periodic motion. It represents the position of the particle at any given time during the oscillation.
A uniform cylinder of length L and mass M having cross sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half- submerged in a liquid of density ρ at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is k, the frequency of oscillation of the cylinder is- a)
- b)
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
A uniform cylinder of length L and mass M having cross sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half- submerged in a liquid of density ρ at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is k, the frequency of oscillation of the cylinder is
a)
b)
c)
d)
|
|
Mihir Patel answered |
If x is the displacement then,
The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t = 4 / 3 s is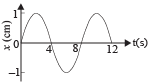
- a)
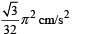
- b)
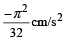
- c)
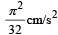
- d)
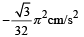
Correct answer is option 'D'. Can you explain this answer?
The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t = 4 / 3 s is
a)
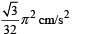
b)
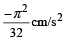
c)
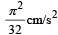
d)
|
|
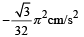
Nandini Nair answered |
From the graph it is clear that the amplitude is 1 cm and the time period is 8 second. Therefore the equation for the S.H.M. is
The velocity (v) of the particle at any instant of time ‘t’ is
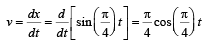
The acceleration of the particle is
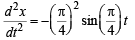
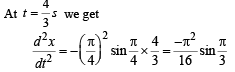
The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The amplitude of the point P is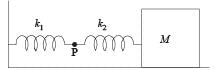
- a)
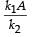
- b)
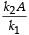
- c)
- d)
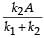
Correct answer is option 'D'. Can you explain this answer?
The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The amplitude of the point P is
a)
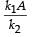
b)
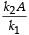
c)
d)
|
|
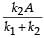
Rounak Desai answered |
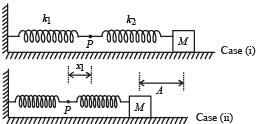
In case (ii), the springs are shown in the maximum compressed position. If the spring of spring constant k1 is compressed by x1 and that of spring constant k2 is compressed by x2 then
x1 + x2 = A … (i)
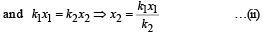
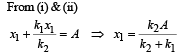
The function x = A sin2 ωt + B cos2 ωt + C sin ωt cosωt represent SHM for which of the option(s)- a)for all value of A, B and C (C ≠ 0)
- b)A = B, C = 2B
- c)A = -B, C = 2B
- d)A = B, C = 0
Correct answer is option 'A,B,C'. Can you explain this answer?
The function x = A sin2 ωt + B cos2 ωt + C sin ωt cosωt represent SHM for which of the option(s)
a)
for all value of A, B and C (C ≠ 0)
b)
A = B, C = 2B
c)
A = -B, C = 2B
d)
A = B, C = 0
|
|
Jaideep Sengupta answered |
The given equation is
x = A sin2 ωt + B cos2 ωt + C sin ωt cos ωt
NOTE THIS STEP
Rearranging the equation in a meaningful form (for interpretation of SHM)
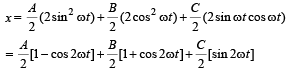
The above equation is that of SHM with amplitude C/2 and angular frequency 2ω. Thus option (a) is correct.
(b) If A = B and C = 2B then x = B + B sin 2ωt
This is equation of SHM. The mean position of the particle executing SHM is not at the origin.
Option (b) is correct.
(c) A = – B, C = 2B; Therefore
x = B cos 2ωt + B sin 2ωt
Let B = X cos φ = X sin φ then
x = X sin 2ωt cos φ + X cos 2ωt sin φ This represents equation of SHM.
(d) A = B, C = 0 and x = A.
This equation does not represents SHM.
This is equation of SHM. The mean position of the particle executing SHM is not at the origin.
Option (b) is correct.
(c) A = – B, C = 2B; Therefore
x = B cos 2ωt + B sin 2ωt
Let B = X cos φ = X sin φ then
x = X sin 2ωt cos φ + X cos 2ωt sin φ This represents equation of SHM.
(d) A = B, C = 0 and x = A.
This equation does not represents SHM.
A uniform rod of length L and mass M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants k. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane.
The rod is gently pushed through a small angle θ in one direction and released. The frequency of oscillation is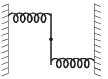
- a)
- b)
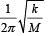
- c)
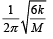
- d)
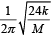
Correct answer is option 'C'. Can you explain this answer?
A uniform rod of length L and mass M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants k. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane.
The rod is gently pushed through a small angle θ in one direction and released. The frequency of oscillation is
The rod is gently pushed through a small angle θ in one direction and released. The frequency of oscillation is
a)
b)
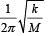
c)
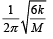
d)
|
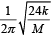
Jatin Dasgupta answered |
Figure shows the rod at an angle θ with respect to its equilibrium position. Both the springs are stretched by length
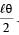
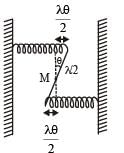
The restoring torque due to the springs τ = – 2 (Restoring force) × perpendicular distance
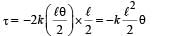... (i)If I is the moment of inertia of the rod about M then
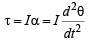… (ii)From (i) & (ii) we get
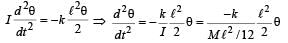
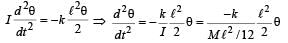
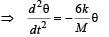
Comparing it with the standard equation of rotational SHM we get
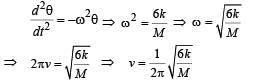
The period of oscillation of a simple pendulum of length L suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination α , is given by- a)
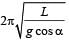
- b)
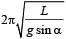
- c)
- d)
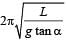
Correct answer is option 'A'. Can you explain this answer?
The period of oscillation of a simple pendulum of length L suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination α , is given by
a)
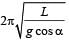
b)
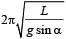
c)
d)
|
|
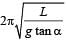
Bhavya Joshi answered |
As shown in the figure, gsina is the pseudo acceleration applied by the observer in the accelerated frame
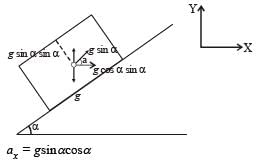
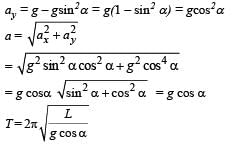
NOTE : Whenever point of suspension is accelerating
use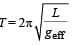
use
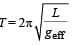
What is the total energy in Simple Harmonic Motion (SHM) given by?- a)Total energy (E) = U + K
- b)Total energy (E) = U - K
- c)Total energy (E) = U x K
- d)Total energy (E) = U / K
Correct answer is option 'A'. Can you explain this answer?
What is the total energy in Simple Harmonic Motion (SHM) given by?
a)
Total energy (E) = U + K
b)
Total energy (E) = U - K
c)
Total energy (E) = U x K
d)
Total energy (E) = U / K
|
Iq Funda answered |
The total energy in Simple Harmonic Motion (SHM) is given by the sum of the potential energy (U) and the kinetic energy (K). It is represented by the formula Total energy (E) = U + K, indicating the combined energy of the particle in SHM.
What is amplitude in Simple Harmonic Motion (SHM) defined as?- a)A physical quantity that changes uniformly with time
- b)The maximum displacement in any direction from the mean position
- c)The number of oscillations completed by the particle in one second
- d)The displacement of the particle from the mean position
Correct answer is option 'B'. Can you explain this answer?
What is amplitude in Simple Harmonic Motion (SHM) defined as?
a)
A physical quantity that changes uniformly with time
b)
The maximum displacement in any direction from the mean position
c)
The number of oscillations completed by the particle in one second
d)
The displacement of the particle from the mean position
|
|
Target Study Academy answered |
Amplitude in Simple Harmonic Motion (SHM) is defined as the maximum displacement in any direction from the mean position. It represents the extreme position that the particle reaches during its oscillatory motion.
The restoring force in SHM is always directed towards:- a)The mean position
- b)The extreme positions
- c)The direction of motion
- d)The direction opposite to motion
Correct answer is option 'A'. Can you explain this answer?
The restoring force in SHM is always directed towards:
a)
The mean position
b)
The extreme positions
c)
The direction of motion
d)
The direction opposite to motion
|
|
KS Coaching Center answered |
The restoring force in SHM is always directed towards the mean position or equilibrium position.
The maximum displacement of an object from its mean position in SHM is called:- a)Amplitude
- b)Period
- c)Frequency
- d)Acceleration
Correct answer is option 'A'. Can you explain this answer?
The maximum displacement of an object from its mean position in SHM is called:
a)
Amplitude
b)
Period
c)
Frequency
d)
Acceleration
|
|
Paradigm Institute answered |
The maximum displacement of an object from its mean position in SHM is called the amplitude.
In SHM, the restoring force is directly proportional to:- a)Displacement
- b)Velocity
- c)Acceleration
- d)Frequency
Correct answer is option 'A'. Can you explain this answer?
In SHM, the restoring force is directly proportional to:
a)
Displacement
b)
Velocity
c)
Acceleration
d)
Frequency
|
|
Paradigm Institute answered |
The restoring force in SHM is directly proportional to the displacement from the equilibrium position.
In SHM, the acceleration is maximum when the displacement is:
- a)Zero
- b)Minimum
- c)Maximum
- d)It does not depend on displacement
Correct answer is option 'C'. Can you explain this answer?
In SHM, the acceleration is maximum when the displacement is:
a)
Zero
b)
Minimum
c)
Maximum
d)
It does not depend on displacement
|
|
KS Coaching Center answered |
In SHM, the acceleration is maximum when the displacement is zero.
Which of the following quantities is not involved in the description of SHM?
- a)Mass
- b)Period
- c)Velocity
- d) Amplitude
Correct answer is option 'D'. Can you explain this answer?
Which of the following quantities is not involved in the description of SHM?
a)
Mass
b)
Period
c)
Velocity
d)
Amplitude
|
|
KS Coaching Center answered |
Mass is not directly involved in the description of Simple Harmonic Motion (SHM). The key quantities involved are amplitude, period, and velocity.
For a particle executing SHM the displacement x is given by x = A coswt. Identify the graph which represents the variation of potential energy (PE) as a function of time t and displacement x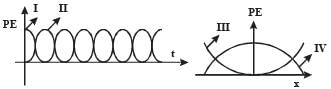
- a)I, III
- b)II, IV
- c)II, III
- d)I, IV
Correct answer is option 'A'. Can you explain this answer?
For a particle executing SHM the displacement x is given by x = A coswt. Identify the graph which represents the variation of potential energy (PE) as a function of time t and displacement x
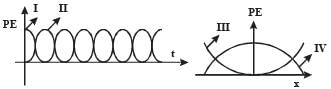
a)
I, III
b)
II, IV
c)
II, III
d)
I, IV
|
|
Tejas Chawla answered |
NOTE : In S.H.M., at extreme position, P.E. is maximum when
t = 0, x = A.
i.e., at time t = 0, the particle executing S.H.M. is at its extreme position.
Therefore P.E. is max. The graph I and III represent the above characteristics.
t = 0, x = A.
i.e., at time t = 0, the particle executing S.H.M. is at its extreme position.
Therefore P.E. is max. The graph I and III represent the above characteristics.
Chapter doubts & questions for Simple Harmonic Motion - Physics for SSS 2 2025 is part of SSS 2 exam preparation. The chapters have been prepared according to the SSS 2 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSS 2 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Simple Harmonic Motion - Physics for SSS 2 in English & Hindi are available as part of SSS 2 exam.
Download more important topics, notes, lectures and mock test series for SSS 2 Exam by signing up for free.
Physics for SSS 2
118 docs|22 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup