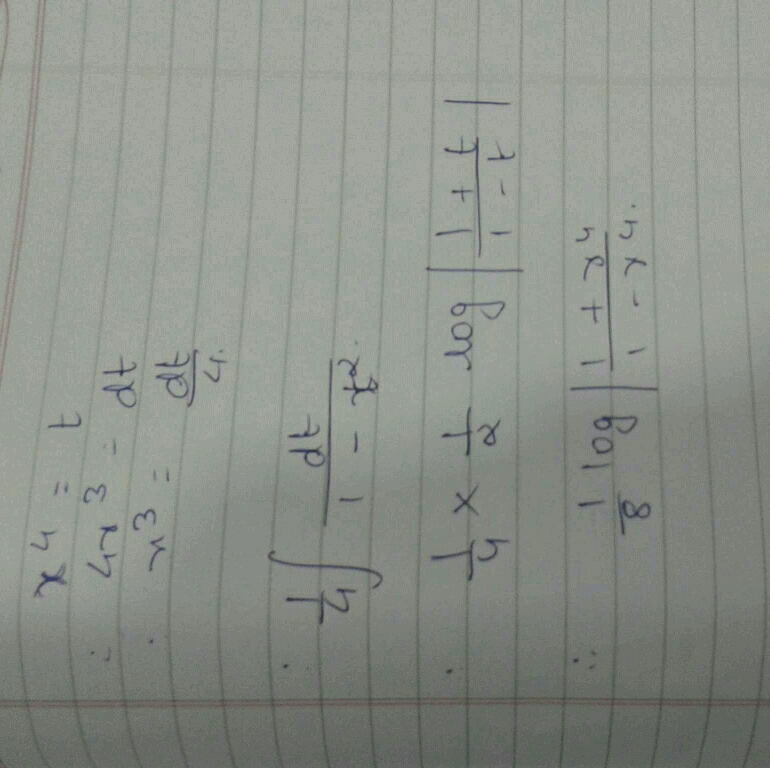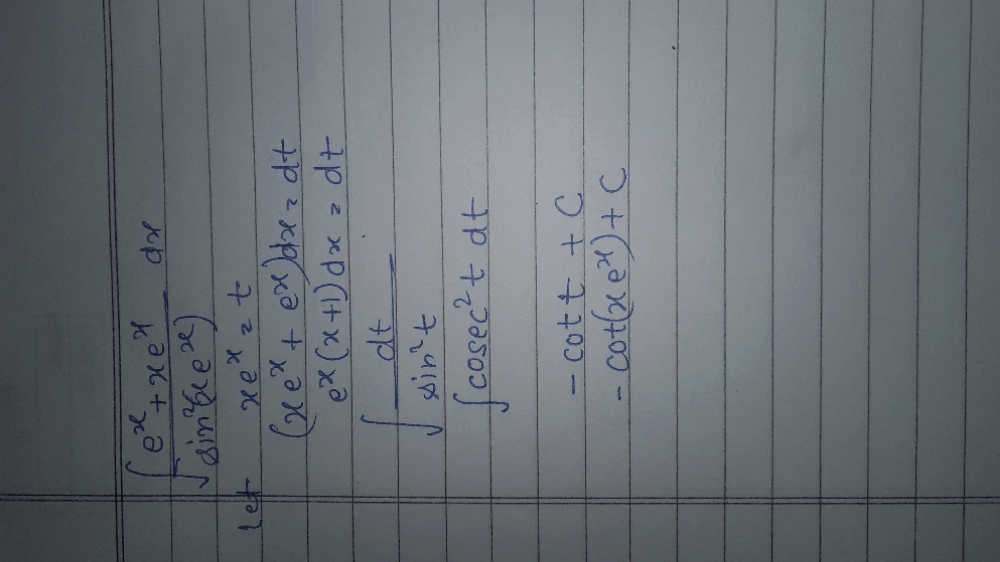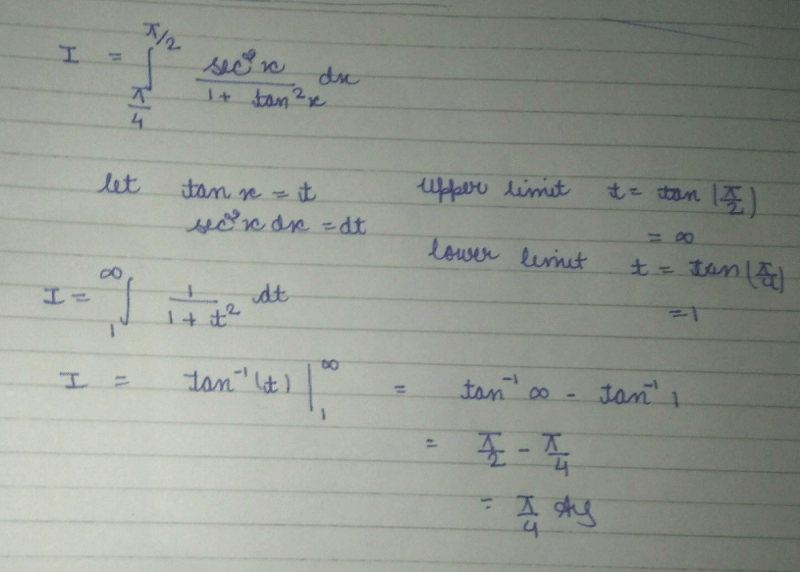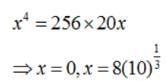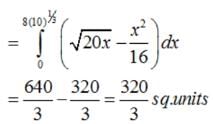All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Integration & Its Applications for JAMB Exam
- a)cos(sin-1x) + c
- b)sin-1x + c
- c)sin(cos-1x) + c
- d)x + c
Correct answer is option 'D'. Can you explain this answer?
a)
cos(sin-1x) + c
b)
sin-1x + c
c)
sin(cos-1x) + c
d)
x + c
|
Divey Sethi answered |
cos(sin-1x)/(1-x2)½……………….(1)
t = sin-1 x
dt = dx/(1-x2)½
Put the value of dt in eq(1)
= ∫cost dt
= sint + c
= sin(sin-1 x) + c
⇒ x + c
t = sin-1 x
dt = dx/(1-x2)½
Put the value of dt in eq(1)
= ∫cost dt
= sint + c
= sin(sin-1 x) + c
⇒ x + c
Integral of sin5x.cos2x is: - a)
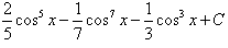
- b)
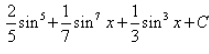
- c)
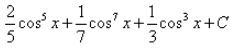
- d)
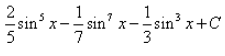
Correct answer is 'A'. Can you explain this answer?
Integral of sin5x.cos2x is:
a)
b)
c)
d)
|
Learners Habitat answered |
So Looking at this integral, we have
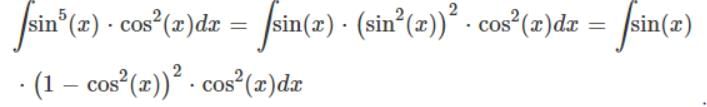
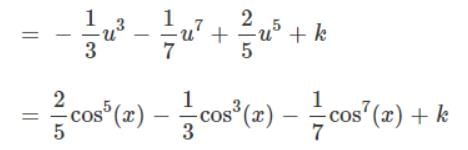
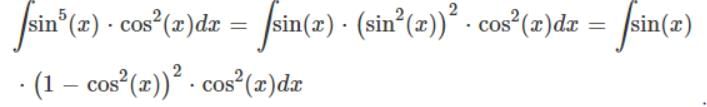
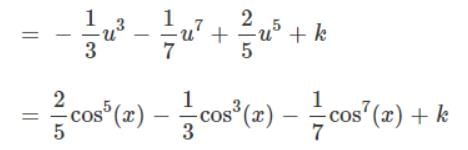
Evaluate: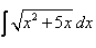 
- a)
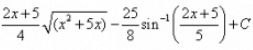
- b)
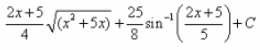
- c)
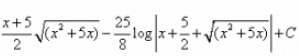
- d)
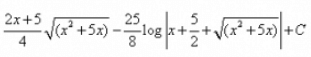
Correct answer is option 'D'. Can you explain this answer?
Evaluate: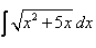
a)
b)
c)
d)
|
|
Leelu Bhai answered |
I = ∫√(x² + 5x)dx= ∫√(x² + 5x + 25/4 - 25/4)= ∫√{(x + 5/2)² - (5/2)²}={1/2(x+5/2)(√x² + 5x)} - {25/8 log{(x + 5/2)+√x²+ 5x}}= {(2x + 5)/4 (√x² + 5x)} - {25/8 log{(x + 5/2)+√x²+ 5x}}Thus, option D is correct...
Evaluate: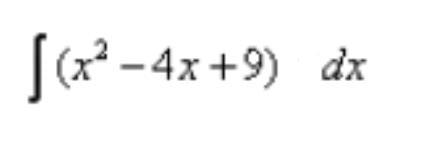 
- a)
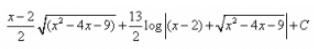
- b)1/√3 arc tan[(x-2)/√5] + C
- c)
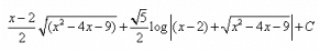
- d)
%7D%7D%7D%2B%7BC%7D)
Correct answer is option 'D'. Can you explain this answer?
Evaluate: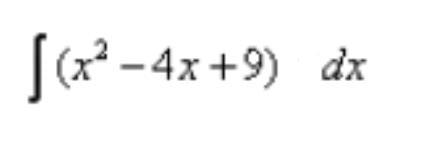
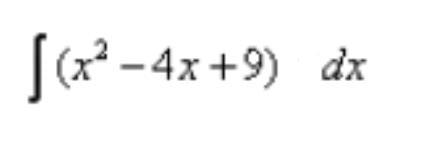
a)
b)
1/√3 arc tan[(x-2)/√5] + C
c)
d)
|
Deepak Kapoor answered |
Let's apply the integral substitution,
substitute 
Now use the standard integral :}}})
substitute back u=(x-2) and add a constant C to the solution,
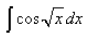
- a)
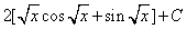, where C is a constant - b)
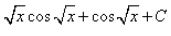, where C is a constant - c)
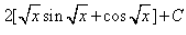, where C is a constant - d)
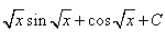, where C is a constant
Correct answer is option 'C'. Can you explain this answer?
a)
, where C is a constantb)
, where C is a constantc)
, where C is a constantd)
, where C is a constant
|
Neha Sharma answered |
q = √x, dq = dx/2√x
⇒ dx = 2q dq
so the integral is 2∫qcosqdq
integration by parts using form
∫uv' = uv − ∫u'v
here u = q, u'= 1 and v'= cosq, v=sinq
so we have 2(qsinq −∫sinqdq)
= 2(qsinq + cosq + C)
= 2(√xsin√x + cos√x + C)
⇒ dx = 2q dq
so the integral is 2∫qcosqdq
integration by parts using form
∫uv' = uv − ∫u'v
here u = q, u'= 1 and v'= cosq, v=sinq
so we have 2(qsinq −∫sinqdq)
= 2(qsinq + cosq + C)
= 2(√xsin√x + cos√x + C)
Evaluate: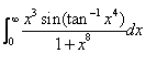 
- a)1/2
- b)1/4
- c)1
- d)1/8
Correct answer is option 'B'. Can you explain this answer?
Evaluate: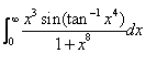
a)
1/2
b)
1/4
c)
1
d)
1/8
|
Sumair Sadiq answered |
This is maths questions I can explain it but you know it is not possible here because this app is not allow to take photo but try it ok let tan inverce 4x =t diff both side wrt x 4x³/1+x⁴ Ka square
x cube / 1+ x8 =dt/4 I = £ 0 se pie by 2 (because when x= 0 t = pie by 2and x = infinity then t = 0 )
I = 1/4 £ 0 se pie by 2 sin t l = 1/4 (- cos t limit 0 se pie by 2 )l = 1/4 ( - cos pie by 2 + cos 0) l = 1/4 ( 0+ 1) l= 1/4 × 1l= 1/4
use my WhatsApp number for further questions but only for study 7060398771
x cube / 1+ x8 =dt/4 I = £ 0 se pie by 2 (because when x= 0 t = pie by 2and x = infinity then t = 0 )
I = 1/4 £ 0 se pie by 2 sin t l = 1/4 (- cos t limit 0 se pie by 2 )l = 1/4 ( - cos pie by 2 + cos 0) l = 1/4 ( 0+ 1) l= 1/4 × 1l= 1/4
use my WhatsApp number for further questions but only for study 7060398771
A function is matched below against an interval where it is supposed to be increasing, Which of the following pairs is incorrectly matched? 
- a)a
- b)b
- c)c
- d)d
Correct answer is option 'B'. Can you explain this answer?
A function is matched below against an interval where it is supposed to be increasing, Which of the following pairs is incorrectly matched?
a)
a
b)
b
c)
c
d)
d
|
Knowledge Hub answered |
Let f (x) = x2 + 6x +6 ⇒ f (x) = 3x (x +4)
Increasing in (-∞,-4) Let ( ) 2 2
f2 (x) = 3x2 - 2x + 1
f2 (x) = 3x2 - 2x + 1
Evaluate: 
- a)
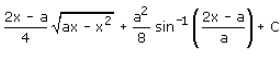
- b)
- c)
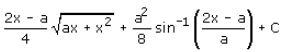
- d)
Correct answer is option 'A'. Can you explain this answer?
Evaluate:
a)
b)
c)
d)
|
Preeti Iyer answered |
(x)½ (a - x)½ dx
= ∫(ax - x2)½ dx
= ∫{-(x2 - ax)½} dx
= ∫{-(x2 - ax + a2/4 - a2/4)½} dx
= ∫{-(x - a/2)2 - a2/4} dx
= ∫{(a/2)2 - (x - a/2)2} dx
= ½(x - a/2) {(a/2)2 - (x - a/2)2} + (a2/4) (½ sin-1(x - a)/a2)
= {(2x - a)/4 (ax - x2)½} + {a2/8 sin-1(2x - a)/a} + c
= ∫(ax - x2)½ dx
= ∫{-(x2 - ax)½} dx
= ∫{-(x2 - ax + a2/4 - a2/4)½} dx
= ∫{-(x - a/2)2 - a2/4} dx
= ∫{(a/2)2 - (x - a/2)2} dx
= ½(x - a/2) {(a/2)2 - (x - a/2)2} + (a2/4) (½ sin-1(x - a)/a2)
= {(2x - a)/4 (ax - x2)½} + {a2/8 sin-1(2x - a)/a} + c
The integration of the function ex.cos3x is:- a)
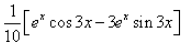
- b)
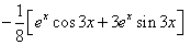
- c)
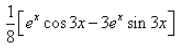
- d)
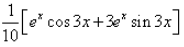
Correct answer is option 'D'. Can you explain this answer?
The integration of the function ex.cos3x is:
a)
b)
c)
d)
|
Om Desai answered |
Let I = ∫ex . cos 3x dx
⇒ I = cos 3x × ∫ex dx − ∫[d/dx(cos 3x) × ∫ex dx]dx
⇒ I = ex cos 3x − ∫(− 3 sin 3x . ex)dx
⇒ I = ex cos 3x + 3∫sin 3x . ex dx
⇒ I = ex cos 3x + 3[sin 3x × ∫ex dx − ∫{ddx(sin 3x) × ∫ex dx}dx]
⇒ I = ex cos 3x + 3[sin 3x . ex − ∫3 cos 3x . ex dx]
⇒ I = ex cos 3x + 3 ex . sin 3x − 9∫ex . cos 3x dx
⇒ I = ex cos 3x + 3 ex . sin 3x − 9I
⇒ 10I = ex cos 3x + 3 ex . sin 3x
⇒ I = 1/10[ex cos 3x + 3 ex . sin 3x] + C
⇒ I = cos 3x × ∫ex dx − ∫[d/dx(cos 3x) × ∫ex dx]dx
⇒ I = ex cos 3x − ∫(− 3 sin 3x . ex)dx
⇒ I = ex cos 3x + 3∫sin 3x . ex dx
⇒ I = ex cos 3x + 3[sin 3x × ∫ex dx − ∫{ddx(sin 3x) × ∫ex dx}dx]
⇒ I = ex cos 3x + 3[sin 3x . ex − ∫3 cos 3x . ex dx]
⇒ I = ex cos 3x + 3 ex . sin 3x − 9∫ex . cos 3x dx
⇒ I = ex cos 3x + 3 ex . sin 3x − 9I
⇒ 10I = ex cos 3x + 3 ex . sin 3x
⇒ I = 1/10[ex cos 3x + 3 ex . sin 3x] + C
is:
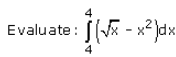
- a)-1
- b)zero
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
a)
-1
b)
zero
c)
1
d)
2
|
Praveen Kumar answered |
∫(0 to 4)(x)1/2 - x2 dx
= [[(x)3/2]/(3/2) - x2](0 to 4)
= [[2x3/2]/3 - x2](0 to 4)
= [[2(0)3/2]/3 - (0)2]] - [[2(4)3/2]/3 - (4)2]]
= 0-0
= 0
= [[(x)3/2]/(3/2) - x2](0 to 4)
= [[2x3/2]/3 - x2](0 to 4)
= [[2(0)3/2]/3 - (0)2]] - [[2(4)3/2]/3 - (4)2]]
= 0-0
= 0
The value of the integral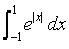 
is:- a)2e – 1
- b)2e + 1
- c)2e
- d)2(e – 1)
Correct answer is option 'D'. Can you explain this answer?
The value of the integral 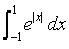is:
is:a)
2e – 1
b)
2e + 1
c)
2e
d)
2(e – 1)
|
Infinity Academy answered |
Correct Answer : d
Explanation : ∫(-1 to 1) e|x| dx
∫(-1 to 0) e|x|dx + ∫(0 to 1) e|x|dx
e1 -1 + e1 - 1
=> 2(e - 1)
Evaluate: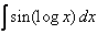 
- a)
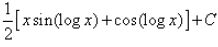
- b)
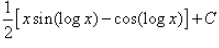
- c)
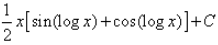
- d)
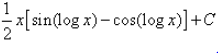
Correct answer is option 'D'. Can you explain this answer?
Evaluate: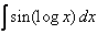
a)
b)
c)
d)
|
Vikas Kapoor answered |
I=∫sin(logx)×1dx
= sin(logx) × x−∫cos(logx) × (1/x)×xdx
= xsin(logx)−∫cos(logx) × 1dx
= xsin(logx)−[cos(logx) × x−∫sin(logx) × (1/x) × xdx]
∴ I=xsin(logx)−cos(logx) × x−∫sin(logx)dx
2I=x[sin(logx)−cos(logx)]
∴ I=(x/2)[sin(logx)−cos(logx)]
= sin(logx) × x−∫cos(logx) × (1/x)×xdx
= xsin(logx)−∫cos(logx) × 1dx
= xsin(logx)−[cos(logx) × x−∫sin(logx) × (1/x) × xdx]
∴ I=xsin(logx)−cos(logx) × x−∫sin(logx)dx
2I=x[sin(logx)−cos(logx)]
∴ I=(x/2)[sin(logx)−cos(logx)]
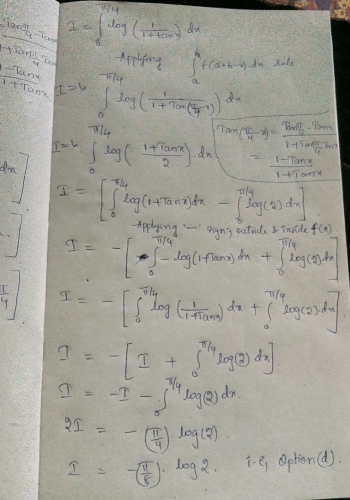
If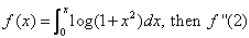 
is- a)2/3
- b)4/5
- c)1
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If 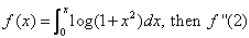is
isa)
2/3
b)
4/5
c)
1
d)
None of these
|
|
Om Desai answered |
In the question, it should be f’(2) instead of f”(2)
Explanation:- f(x) = ∫(0 to x) log(1+x2)
f’(x) = 2xdx/(1+x2)
f’(2) = 2(2)/(1+(2)2)
= 4/5
Explanation:- f(x) = ∫(0 to x) log(1+x2)
f’(x) = 2xdx/(1+x2)
f’(2) = 2(2)/(1+(2)2)
= 4/5
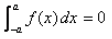
- a)if f(2a – x) = – f(x)
- b)if f(2a – x) = f(x)
- c)if f(- x) = f(x)
- d)if f(- x) = – f(x)
Correct answer is option 'D'. Can you explain this answer?
a)
if f(2a – x) = – f(x)
b)
if f(2a – x) = f(x)
c)
if f(- x) = f(x)
d)
if f(- x) = – f(x)
|
|
Om Desai answered |
∫(-a to a)f(x)dx
= ∫(0 to a) [f(x) + f(-x)] if f(x) is an odd function
⇒ f(-x) = -f(x)
= ∫(0 to a) [f(x) + f(-x)] if f(x) is an odd function
⇒ f(-x) = -f(x)
Evaluate: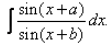 
- a)(x + b) cos(a – b) – sin(a – b).log | sin(x + b) | + C
- b)(x + b) cos(b – a) – sin(b – a).log | sin(x + b) | + C
- c)(x + b) cos(b – a) + sin(b – a).log | sin(x + b) | + C
- d)(x + b) cos(a – b) + sin(a – b).log | sin(x + b) | + C
Correct answer is option 'D'. Can you explain this answer?
Evaluate: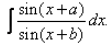
a)
(x + b) cos(a – b) – sin(a – b).log | sin(x + b) | + C
b)
(x + b) cos(b – a) – sin(b – a).log | sin(x + b) | + C
c)
(x + b) cos(b – a) + sin(b – a).log | sin(x + b) | + C
d)
(x + b) cos(a – b) + sin(a – b).log | sin(x + b) | + C
|
Tanuja Kapoor answered |
Create ((X+B) + (A-B)) in numerator and then apply Sin(a+b) formula then you will be able to solve it.
where 
Evaluate: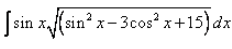 
- a)
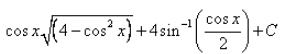
- b)
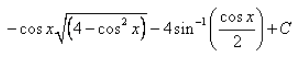
- c)
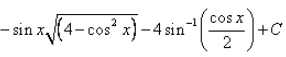
- d)
Correct answer is option 'B'. Can you explain this answer?
Evaluate: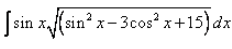
a)
b)
c)
d)
|
|
Om Desai answered |
sin2x = 1 - cos2x
∫sinx(sin2x - 3cos2x + 15)dx
Put cos2x = t
∫sinx(1 - cos2x - 3cos2x + 15)dx
= ∫sinx (16 - 4cos2x)dx
Put t = cosx, differentiate with respect to x, we get
dt/dx = -sinx
= - ∫ [(16 - 4t2)]1/2dt
= -2 ∫ [(2)2 - (t)2]½
= -2{[(2)2 - (t)2]½ + 2sin-1(t/2)} + c
= - cosx {[4 - (cos)2x]½ - 4sin-1(cosx/2)} + c
∫sinx(sin2x - 3cos2x + 15)dx
Put cos2x = t
∫sinx(1 - cos2x - 3cos2x + 15)dx
= ∫sinx (16 - 4cos2x)dx
Put t = cosx, differentiate with respect to x, we get
dt/dx = -sinx
= - ∫ [(16 - 4t2)]1/2dt
= -2 ∫ [(2)2 - (t)2]½
= -2{[(2)2 - (t)2]½ + 2sin-1(t/2)} + c
= - cosx {[4 - (cos)2x]½ - 4sin-1(cosx/2)} + c
is: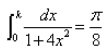 
is:
If 
then the value of k is:- a)7/8
- b)5/8
- c)1/2
- d)3/2
Correct answer is option 'C'. Can you explain this answer?
If 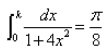then the value of k is:
then the value of k is:a)
7/8
b)
5/8
c)
1/2
d)
3/2
|
Sushil Kumar answered |
Let I=∫(0 to k) 1/[1 + 4x2]dx = π8
Now, ∫(0 to k) 1/[4(1/4 + x2)]dx
= 2/4[tan−1 2x]0 to k
= 1/2tan-1 2k − 0 = π/8
1/2tan−1 2k = π8
⇒ tan−1 2k = π/4
⇒ 2k = 1
∴ k = 1/2
Now, ∫(0 to k) 1/[4(1/4 + x2)]dx
= 2/4[tan−1 2x]0 to k
= 1/2tan-1 2k − 0 = π/8
1/2tan−1 2k = π8
⇒ tan−1 2k = π/4
⇒ 2k = 1
∴ k = 1/2
then
Evaluate: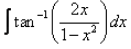
- a)
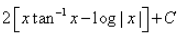
- b)
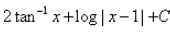
- c)
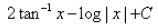
- d)
Correct answer is option 'D'. Can you explain this answer?
Evaluate: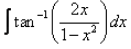
a)
b)
c)
d)
|
Hansa Sharma answered |
Let x=tanθ , so that θ=tan−1x , dx=sec2θdθ
Then the given integral is equivalent to
∫tan−1(2x/(1−x2)dx
=∫tan−1 (2tanθ/(1−tan2θ))⋅sec2θdθ
=∫tan−1tan2θ⋅sec2θdθ
=2×∫θsec2θdθ
(integrate by parts)
=2θ⋅∫sec2θdθ −2⋅∫1⋅(∫sec2θdθ)dθ
=2θtanθ−2⋅∫tanθdθ
=2θtanθ−2loge secθ+c
=2xtan−1x−2loge√1+x2+c
=2xtan−1x−loge(1+x2)+c
Then the given integral is equivalent to
∫tan−1(2x/(1−x2)dx
=∫tan−1 (2tanθ/(1−tan2θ))⋅sec2θdθ
=∫tan−1tan2θ⋅sec2θdθ
=2×∫θsec2θdθ
(integrate by parts)
=2θ⋅∫sec2θdθ −2⋅∫1⋅(∫sec2θdθ)dθ
=2θtanθ−2⋅∫tanθdθ
=2θtanθ−2loge secθ+c
=2xtan−1x−2loge√1+x2+c
=2xtan−1x−loge(1+x2)+c
The normal to the curve x2 + 2xy - 3y2 = 0 at 1,1- a)does not meet the curve again
- b)meet the curve again in second quadrant
- c)meet the curve again in the third quadrant
- d)meet the curve again in forth quadrant
Correct answer is option 'D'. Can you explain this answer?
The normal to the curve x2 + 2xy - 3y2 = 0 at 1,1
a)
does not meet the curve again
b)
meet the curve again in second quadrant
c)
meet the curve again in the third quadrant
d)
meet the curve again in forth quadrant
|
Manisha Mehta answered |
slope of normal at (1, 1) = - 1
∴ Equation of normal y -1 = -1(x -1)
y +x= 2
Solving we get point as (1, 1) and (1/-1/3)
Solving we get point as (1, 1) and (1/-1/3)
So in forth quadrant
Angle between the tangents to the curve y = x 2 - 5x + 6 at the points (2, 0) and (3, 0) is- a)π /2
- b)π /6
- c)π /4
- d)π /3
Correct answer is option 'A'. Can you explain this answer?
Angle between the tangents to the curve y = x 2 - 5x + 6 at the points (2, 0) and (3, 0) is
a)
π /2
b)
π /6
c)
π /4
d)
π /3
|
Nandita Basak answered |
Product of slopes = -1 ⇒ angle between tangents is π/2
onsider the function, f ( x ) =| x - 2 | + | x - 5 | .x∈ R Statement -1 : f ' ( 4) = 0Statement -2 : f is continous in [2, 5], differentiable in (2, 5) and f ( 2) = f ( 5)- a)Statement -1 is true, Statement -2 is true; Statement -2 is not a correct explanation for statement-1.
- b)Statement -1 is true, Statement -2 is false
- c)Statement -1 is false, Statement -2 is true.
- d)Statement-2 is a correct explanation for Statement -1.
Correct answer is option 'A'. Can you explain this answer?
onsider the function, f ( x ) =| x - 2 | + | x - 5 | .x∈ R
Statement -1 : f ' ( 4) = 0
Statement -2 : f is continous in [2, 5], differentiable in (2, 5) and f ( 2) = f ( 5)
a)
Statement -1 is true, Statement -2 is true; Statement -2 is not a correct explanation for statement-1.
b)
Statement -1 is true, Statement -2 is false
c)
Statement -1 is false, Statement -2 is true.
d)
Statement-2 is a correct explanation for Statement -1.
|
Pranav Pillai answered |
f (x ) is constant is [2, 5]
The area of the region bounded by the parabola (y−2)2 = x−1,the tangent to yhe parabola at the point (2 , 3) and the x – axis is equal to- a)12 sq. units
- b)6 sq. units
- c)9 sq. units
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The area of the region bounded by the parabola (y−2)2 = x−1,the tangent to yhe parabola at the point (2 , 3) and the x – axis is equal to
a)
12 sq. units
b)
6 sq. units
c)
9 sq. units
d)
none of these
|
Mohit Patel answered |
Therefore, tangent at (2, 3) is y – 3 = ½ (x – 2). i.e. x – 2y +4 = 0 . therefore required area is
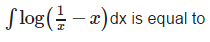
- a)log 2
- b)0
- c)
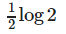
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
a)
log 2
b)
0
c)
d)
none of these
|
Shilpa Saha answered |
∫ log(1-x) dx - ∫ log x dx = 0
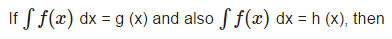
- a)g (x) h (s) = constant
- b)g (x) = h (x).
- c)g (x) - h (x) = constant
- d)h (x) + g (x) = constant
Correct answer is option 'C'. Can you explain this answer?
a)
g (x) h (s) = constant
b)
g (x) = h (x).
c)
g (x) - h (x) = constant
d)
h (x) + g (x) = constant
|
Seblewongel Girma answered |
Integration of a function can have many possibility by adding variable C.
for instance :
take integral of X^2=X^3/3 +C
integral of X^2 can be X^3/3 +1, X^3/3 +2.....
their d/CE is a constant.
for instance :
take integral of X^2=X^3/3 +C
integral of X^2 can be X^3/3 +1, X^3/3 +2.....
their d/CE is a constant.
The area bounded by the parabola y2 = 4x and the line x + y = 3 is- a)32/3
- b)16/3
- c)64/3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The area bounded by the parabola y2 = 4x and the line x + y = 3 is
a)
32/3
b)
16/3
c)
64/3
d)
none of these
|
Gitanjali Tiwari answered |
To find the area bounded by the parabola y^2 = 4x and the line x + y = 3, we need to find the points of intersection between the parabola and the line and then calculate the area between them.
Finding the Points of Intersection:
To find the points of intersection, we can set the equations of the parabola and the line equal to each other and solve for x and y:
y^2 = 4x
x + y = 3
Substituting y = 3 - x into the equation of the parabola, we get:
(3 - x)^2 = 4x
Expanding and rearranging the equation, we get:
9 - 6x + x^2 = 4x
x^2 + 10x - 9 = 0
Now, we can solve this quadratic equation for x using factoring or the quadratic formula. By factoring, we can write it as:
(x + 9)(x - 1) = 0
This gives us two possible values for x: x = -9 and x = 1.
Substituting these values back into the equation of the line, we can find the corresponding y-values:
For x = -9:
y = 3 - (-9) = 3 + 9 = 12
For x = 1:
y = 3 - 1 = 2
So, the points of intersection are (-9, 12) and (1, 2).
Calculating the Area:
To calculate the area bounded by the parabola and the line, we can integrate the difference between the y-values of the parabola and the line over the interval between the x-values of intersection points.
We need to find the integral of (y - (3 - x)) with respect to x, where y is given by the equation of the parabola: y = √(4x).
The integral becomes:
∫[(√(4x) - (3 - x))] dx
Integrating and evaluating this integral from x = -9 to x = 1 gives us the required area:
A = ∫[(√(4x) - (3 - x))] dx (from x = -9 to x = 1)
Simplifying the integral and evaluating it, we get:
A = [(2/3)x^(3/2) + (x^2)/2 - 3x] (from x = -9 to x = 1)
= [2/3 + 1/2 - 3 - ((2/3)(-9)^(3/2) + ((-9)^2)/2 - 3(-9))]
Calculating this expression, we get:
A = [2/3 + 1/2 - 3 - (2/3 - 243/2 + 27)]
= [2/3 + 1/2 - 3 - 2/3 + 243/2 - 27]
= [16/3]
Therefore, the area bounded by the parabola y^2 = 4x and the line x + y = 3 is 16/3.
Finding the Points of Intersection:
To find the points of intersection, we can set the equations of the parabola and the line equal to each other and solve for x and y:
y^2 = 4x
x + y = 3
Substituting y = 3 - x into the equation of the parabola, we get:
(3 - x)^2 = 4x
Expanding and rearranging the equation, we get:
9 - 6x + x^2 = 4x
x^2 + 10x - 9 = 0
Now, we can solve this quadratic equation for x using factoring or the quadratic formula. By factoring, we can write it as:
(x + 9)(x - 1) = 0
This gives us two possible values for x: x = -9 and x = 1.
Substituting these values back into the equation of the line, we can find the corresponding y-values:
For x = -9:
y = 3 - (-9) = 3 + 9 = 12
For x = 1:
y = 3 - 1 = 2
So, the points of intersection are (-9, 12) and (1, 2).
Calculating the Area:
To calculate the area bounded by the parabola and the line, we can integrate the difference between the y-values of the parabola and the line over the interval between the x-values of intersection points.
We need to find the integral of (y - (3 - x)) with respect to x, where y is given by the equation of the parabola: y = √(4x).
The integral becomes:
∫[(√(4x) - (3 - x))] dx
Integrating and evaluating this integral from x = -9 to x = 1 gives us the required area:
A = ∫[(√(4x) - (3 - x))] dx (from x = -9 to x = 1)
Simplifying the integral and evaluating it, we get:
A = [(2/3)x^(3/2) + (x^2)/2 - 3x] (from x = -9 to x = 1)
= [2/3 + 1/2 - 3 - ((2/3)(-9)^(3/2) + ((-9)^2)/2 - 3(-9))]
Calculating this expression, we get:
A = [2/3 + 1/2 - 3 - (2/3 - 243/2 + 27)]
= [2/3 + 1/2 - 3 - 2/3 + 243/2 - 27]
= [16/3]
Therefore, the area bounded by the parabola y^2 = 4x and the line x + y = 3 is 16/3.
Chapter doubts & questions for Integration & Its Applications - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Integration & Its Applications - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup