All Exams >
JAMB >
Mathematics for JAMB >
All Questions
All questions of Permutation and Combination for JAMB Exam
A dinner menu is to be designed out of 5 different starters, 6 identical main courses and 4 distinct desserts. In how many ways menu be designed such that there is atleast one of each of the starters, main courses and desserts?- a)31 x 6 x 15
- b)32 x 6 x 16
- c)31 x 7 x 15
- d)5 x 6 x 4
Correct answer is option 'A'. Can you explain this answer?
A dinner menu is to be designed out of 5 different starters, 6 identical main courses and 4 distinct desserts. In how many ways menu be designed such that there is atleast one of each of the starters, main courses and desserts?
a)
31 x 6 x 15
b)
32 x 6 x 16
c)
31 x 7 x 15
d)
5 x 6 x 4

|
Imk Pathshala answered |
Calculating the number of ways to design the menu
- Number of ways to choose at least one starter out of 5: 2^5 - 1 = 31 ways
- Number of ways to choose 6 main courses: 1 way since they are identical
- Number of ways to choose 4 desserts: 4! = 24 ways
Total number of ways to design the menu
- Total number of ways = Number of ways to choose starters x Number of ways to choose main courses x Number of ways to choose desserts
- Total number of ways = 31 x 1 x 24 = 31 x 24 = 744 ways
Final answer
- Therefore, the correct answer is A: 31 x 6 x 15
On a shelf, 2 books of Geology, 2 books of Sociology and 5 of Economics are to be arranged in such a way that the books of any subject are to be together. Find in how many ways can this be done?
- a)3846
- b)2880
- c)900
- d)1200
Correct answer is option 'B'. Can you explain this answer?
On a shelf, 2 books of Geology, 2 books of Sociology and 5 of Economics are to be arranged in such a way that the books of any subject are to be together. Find in how many ways can this be done?
a)
3846
b)
2880
c)
900
d)
1200

|
Naroj Boda answered |
First, we consider each subject as one group. So, we have 3 groups to arrange. The number of ways to arrange these groups is 3!.
Within each group, the books can also be arranged. The number of ways to arrange 2 Geology books is 2!, the number of ways to arrange 2 Sociology books is 2!, and the number of ways to arrange 5 Economics books is 5!.
So the total number of ways to arrange the books is 3! * 2! * 2! * 5! = 6 * 2 * 2 * 120 = 2880 ways.
Within each group, the books can also be arranged. The number of ways to arrange 2 Geology books is 2!, the number of ways to arrange 2 Sociology books is 2!, and the number of ways to arrange 5 Economics books is 5!.
So the total number of ways to arrange the books is 3! * 2! * 2! * 5! = 6 * 2 * 2 * 120 = 2880 ways.
A coin is tossed 3 times. Find out the number of possible outcomes.
- a)1
- b)8
- c)2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A coin is tossed 3 times. Find out the number of possible outcomes.
a)
1
b)
8
c)
2
d)
None of these

|
Ishani Rane answered |
For any multiple independent event, there are nm
total possible outcomes, where n is the number of outcomes per event, and m is the number of such events.
So for a coin, discounting the unlikely event of landing on its side, there are two possible outcomes per event, heads or tails. And it is stated that there are 3 such events. So nm=23=8
.
How many numbers between 200 and 1200 can be formed with the digits 0, 1, 2, 3 (repetition of digits not allowed?
- a)6
- b)18
- c)2
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
How many numbers between 200 and 1200 can be formed with the digits 0, 1, 2, 3 (repetition of digits not allowed?
a)
6
b)
18
c)
2
d)
none of these
|
|
Meghana Dasgupta answered |
The numbers between 200 and 1200 can be formed in the following ways:
1) Numbers with 3 digits: The hundreds place can be filled with 2 or 3, so there are 2 ways. The tens place can be filled with any of the remaining 3 digits, so there are 3 ways. The units place can be filled with any of the remaining 2 digits, so there are 2 ways. Therefore, there are 2*3*2 = 12 such numbers.
2) Numbers with 4 digits: The thousands place can only be filled with 1, so there is 1 way. The hundreds place can be filled with any of the remaining 3 digits (not including 0), so there are 3 ways. The tens place can be filled with any of the remaining 2 digits, so there are 2 ways. The units place can be filled with the remaining 1 digit, so there is 1 way. Therefore, there are 1*3*2*1 = 6 such numbers.
Therefore, a total of 12 + 6 = 18 numbers between 200 and 1200 can be formed with the digits 0, 1, 2, 3 with no repetition of digits. So, option 2 is correct.
1) Numbers with 3 digits: The hundreds place can be filled with 2 or 3, so there are 2 ways. The tens place can be filled with any of the remaining 3 digits, so there are 3 ways. The units place can be filled with any of the remaining 2 digits, so there are 2 ways. Therefore, there are 2*3*2 = 12 such numbers.
2) Numbers with 4 digits: The thousands place can only be filled with 1, so there is 1 way. The hundreds place can be filled with any of the remaining 3 digits (not including 0), so there are 3 ways. The tens place can be filled with any of the remaining 2 digits, so there are 2 ways. The units place can be filled with the remaining 1 digit, so there is 1 way. Therefore, there are 1*3*2*1 = 6 such numbers.
Therefore, a total of 12 + 6 = 18 numbers between 200 and 1200 can be formed with the digits 0, 1, 2, 3 with no repetition of digits. So, option 2 is correct.
2a + 5b = 103. How many pairs of positive integer values can a, b take such that a > b?
- a)12
- b)9
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
2a + 5b = 103. How many pairs of positive integer values can a, b take such that a > b?
a)
12
b)
9
c)
7
d)
8
|
|
Aditya Kumar answered |
Let us find the one pair of values for a, b.
a = 4, b = 19 satisfies this equation.
2*4 + 5*19 = 103.
Now, if we increase ‘a’ by 5 and decrease ‘b’ by 2 we should get the next set of numbers. We can keep repeating this to get all values.
Let us think about why we increase ‘a’ by 5 and decrease b by 2.
a = 4, b = 19 works.
Let us say, we increase ‘a’ by n, then the increase would be 2n.
This has to be offset by a corresponding decrease in b.
Let us say we decrease b by ‘m’.
This would result in a net drop of 5m.
In order for the total to be same, 2n should be equal to 5m.
The smallest value of m, n for this to work would be 2, 5.
a = 4, b = 19
a = 9, b = 17
a = 14, b = 15
..
And so on till
a = 49, b = 1
We are also told that ‘a’ should be greater than ‘b’, then we have all combinations from (19, 13) … (49, 1).
7 pairs totally.
a = 4, b = 19 satisfies this equation.
2*4 + 5*19 = 103.
Now, if we increase ‘a’ by 5 and decrease ‘b’ by 2 we should get the next set of numbers. We can keep repeating this to get all values.
Let us think about why we increase ‘a’ by 5 and decrease b by 2.
a = 4, b = 19 works.
Let us say, we increase ‘a’ by n, then the increase would be 2n.
This has to be offset by a corresponding decrease in b.
Let us say we decrease b by ‘m’.
This would result in a net drop of 5m.
In order for the total to be same, 2n should be equal to 5m.
The smallest value of m, n for this to work would be 2, 5.
a = 4, b = 19
a = 9, b = 17
a = 14, b = 15
..
And so on till
a = 49, b = 1
We are also told that ‘a’ should be greater than ‘b’, then we have all combinations from (19, 13) … (49, 1).
7 pairs totally.
Hence the answer is "7"
Choice C is the correct answer.
How many 3 digit numbers can be formed from the digits 2, 3, 5, 6, 7 and 9 which are divisible by 5 and none of the digits is repeated?
- a)20
- b)16
- c)8
- d)24
Correct answer is option 'A'. Can you explain this answer?
How many 3 digit numbers can be formed from the digits 2, 3, 5, 6, 7 and 9 which are divisible by 5 and none of the digits is repeated?
a)
20
b)
16
c)
8
d)
24
|
|
Upasana Dey answered |
Since each desired number is divisible by 5, so we must have 5 at the unit place. So, there is 1 way of doing it.
The tens place can now be filled by any of the remaining 5 digits (2, 3, 6, 7, 9). So, there are 5 ways of filling the tens place.
The hundreds place can now be filled by any of the remaining 4 digits. So, there are 4 ways of filling it.
∴ Required number of numbers = (1 x 5 x 4) = 20.
The tens place can now be filled by any of the remaining 5 digits (2, 3, 6, 7, 9). So, there are 5 ways of filling the tens place.
The hundreds place can now be filled by any of the remaining 4 digits. So, there are 4 ways of filling it.
∴ Required number of numbers = (1 x 5 x 4) = 20.
MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for Permutation and Combination under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
- a)24400
- b)21300
- c)210
- d)25200
Correct answer is option 'D'. Can you explain this answer?
MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for Permutation and Combination under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
a)
24400
b)
21300
c)
210
d)
25200

|
Manoj Ghosh answered |


In how many ways a committee consisting of 5 men and 3 women, can be chosen from 9 men and 12 women.- a)12459
- b)75200
- c)27720
- d)18920
Correct answer is option 'C'. Can you explain this answer?
In how many ways a committee consisting of 5 men and 3 women, can be chosen from 9 men and 12 women.
a)
12459
b)
75200
c)
27720
d)
18920

|
Cstoppers Instructors answered |
Choose 5 men out of 9 men = 9C5 ways = 126 ways
Choose 3 women out of 12 women = 12C3 ways = 220 ways
The committee can be chosen in 27720 ways
A captain and a vice-captain are to be chosen out of a team having eleven players. How many ways are there to achieve this?
- a) 10.9
- b) 11C2
- c) 110
- d) 10.9!
Correct answer is option 'C'. Can you explain this answer?
A captain and a vice-captain are to be chosen out of a team having eleven players. How many ways are there to achieve this?
a)
10.9b)
11C2c)
110d)
10.9!|
|
Vikas Choudhury answered |
Answer is C i.e 110 ways. Explaination: out of 11 player 1 captain can be choose 11 ways, Now remaining 10 player,wise captain can be choose in 10 ways Therefore total number of ways =11*10=110 ways
How many even numbers of four digits can be formed with the digits 1, 2, 3, 4, 5, 6 (repetitions of digits are allowed)?- a)648
- b)180
- c)1296
- d)600
Correct answer is option 'A'. Can you explain this answer?
How many even numbers of four digits can be formed with the digits 1, 2, 3, 4, 5, 6 (repetitions of digits are allowed)?
a)
648
b)
180
c)
1296
d)
600

|
Sahil Kumar answered |
The number of numbers formed would be given by 5 x 4 x 3 (given that the first digit can be filled in 5 ways, the second in 4 ways and the third in 3 ways - MNP rule).
How many arrangements can be made out of the letters of the word 'ENGINEERING' ?
- a)924000
- b)277200
- c)182000
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
How many arrangements can be made out of the letters of the word 'ENGINEERING' ?
a)
924000
b)
277200
c)
182000
d)
None of these
|
|
Aditya Kumar answered |
The number of arrangements of the word ENGINEERING is 277200.
ENGINEERING word has 3 times of 3, three times of N, 2 times of G and 2 times of I. Then, the total letter is 11.
So, the number of arrangements of the word ENGINEERING = 11!/[3! * 3! * 2! * 2!] = 39916800/[6 * 6 * 2 * 2] = 277200
Hence, the number of arrangements of the word ENGINEERING is 277200.
ENGINEERING word has 3 times of 3, three times of N, 2 times of G and 2 times of I. Then, the total letter is 11.
So, the number of arrangements of the word ENGINEERING = 11!/[3! * 3! * 2! * 2!] = 39916800/[6 * 6 * 2 * 2] = 277200
Hence, the number of arrangements of the word ENGINEERING is 277200.
Find the number of non-negative integral solutions to the system of equations x + y + z + u + t = 20 and x + y + z = 5.
- a)220
- b)336
- c)44
- d)528
Correct answer is option 'B'. Can you explain this answer?
Find the number of non-negative integral solutions to the system of equations x + y + z + u + t = 20 and x + y + z = 5.
a)
220
b)
336
c)
44
d)
528

|
Madhurima Sharma answered |
n identical things can be distributed among r persons in n+x-1Cx-1
In how many different ways can the letters of the word 'MATHEMATICS' be arranged such that the vowels must always come together?- a)9800
- b)100020
- c)120960
- d)140020
Correct answer is option 'C'. Can you explain this answer?
a)
9800
b)
100020
c)
120960
d)
140020

|
Gowri Chakraborty answered |
In the word 'MATHEMATICS', we'll consider all the vowels AEAI together as one letter.
Thus, we have MTHMTCS (AEAI).
Now, we have to arrange 8 letters, out of which M occurs twice, T occurs twice
Number of ways of arranging these letters =8! / ((2!)(2!))= 10080.
Now, AEAI has 4 letters in which A occurs 2 times and the rest are different.
Number of ways of arranging these letters =4! / 2!= 12.
Required number of words = (10080 x 12) = 120960
Direction for questions 1 to 2: Read passage below and solve the questions based on it.
In a horticultural show, a participant arranged a total of 1000 fruits of four types in a long straight line He first placed one apple, then two mangoes, three oranges, four custard apples, five apples, six mangoes, seven oranges, eight custard apples and so on (with apples followed by mangoes, oranges, custard apples in that order) uplo the 1000th fruit.Q.What was the position of the 100th Mango?- a)387
- b)437
- c)417
- d)363
Correct answer is option 'B'. Can you explain this answer?
Direction for questions 1 to 2: Read passage below and solve the questions based on it.
In a horticultural show, a participant arranged a total of 1000 fruits of four types in a long straight line He first placed one apple, then two mangoes, three oranges, four custard apples, five apples, six mangoes, seven oranges, eight custard apples and so on (with apples followed by mangoes, oranges, custard apples in that order) uplo the 1000th fruit.
In a horticultural show, a participant arranged a total of 1000 fruits of four types in a long straight line He first placed one apple, then two mangoes, three oranges, four custard apples, five apples, six mangoes, seven oranges, eight custard apples and so on (with apples followed by mangoes, oranges, custard apples in that order) uplo the 1000th fruit.
Q.
What was the position of the 100th Mango?
a)
387
b)
437
c)
417
d)
363
|
|
Ishita Reddy answered |
Fruits are ordered like 1. Apple 2. Mangoes 3 Oranges 4. Custard apple Fruits arc being pul up first one. then two, then three, then four and so oil.
Mangoes will come like 2, 6, 10, 14 etc. 100th mango will come 2 + 6 + 10 + 14 + 18 + 22 + 26 + 2= 100
100th mango will come in its 8th turn.
Before that apple must have got its 8th turn, orange and custard apple must have got their 7th turn.
Total apples displayed till now = 1 + 5 + 9 + ... + 29= 120
Total oranges displayed till now = 3 + 7+11 + ... +27=105
Total custard apples displayed till now = 4 + 8+ 12 + ... +28= 112
So, total fruits displayed till now (other than mangoes) = 337
So, the position of the 100th mango = 437
100th mango will come in its 8th turn.
Before that apple must have got its 8th turn, orange and custard apple must have got their 7th turn.
Total apples displayed till now = 1 + 5 + 9 + ... + 29= 120
Total oranges displayed till now = 3 + 7+11 + ... +27=105
Total custard apples displayed till now = 4 + 8+ 12 + ... +28= 112
So, total fruits displayed till now (other than mangoes) = 337
So, the position of the 100th mango = 437
A bag contains 2 white balls, 3 black balls and 4 red balls. In how many ways can 3 balls be drawn from the bag, if at least one black ball is to be included in the draw?
- a)64
- b)128
- c)32
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A bag contains 2 white balls, 3 black balls and 4 red balls. In how many ways can 3 balls be drawn from the bag, if at least one black ball is to be included in the draw?
a)
64
b)
128
c)
32
d)
None of these

|
Gowri Chakraborty answered |
The bag contains 2 White, 3 Black and 4 Red balls.
So, total 9 balls are there in the bag; among them 3 are Black and 6 are non-Black balls.
Three balls can randomly be drawn in (9C3) = 84 ways.
1 Black and 2 non-Black balls can be drawn in (3C1)*(6C2) = 45 ways.
1 non-Black and 2 Black balls can be drawn in (6C1)*(3C2) = 18 ways.
3 Black balls can be drawn in (3C3) = 1 way.
So, three balls drawn in (45 + 18 + 1) = 64 ways will have at least one Black ball among the drawn ones.
How many 3-letter words with or without meaning, can be formed out of the letters of the word, 'LOGARITHMS', if repetition of letters is not allowed? - a)720
- b)420
- c)5040
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
a)
720
b)
420
c)
5040
d)
None of these

|
Gowri Chakraborty answered |
The word 'LOGARITHMS' has 10 different letters.
Hence, the number of 3-letter words(with or without meaning) formed by using these letters
= 10P3
= 10 * 9 * 8
= 720
In how many different ways can the letters of the word 'DETAIL' be arranged such that the vowels must occupy only the odd positions?
- a)36
- b)64
- c)120
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In how many different ways can the letters of the word 'DETAIL' be arranged such that the vowels must occupy only the odd positions?
a)
36
b)
64
c)
120
d)
None of these

|
Naroj Boda answered |
There are 6 letters in the given word, out of which there are 3 vowels and 3 consonants.
Let us mark these positions as under:
(1) (2) (3) (4) (5) (6)
Now, 3 vowels can be placed at any of the three places out 4, marked 1, 3, 5.
Number of ways of arranging the vowels = 3P3
= 3! = 6.
Also, the 3 consonants can be arranged at the remaining 3 positions.
Number of ways of these arrangements = 3P3
= 3! = 6.
Total number of ways = (6 x 6) = 36.
In how many different ways can the letters of the word 'JUDGE' be arranged such that the vowels always come together?
- a)64
- b)48
- c)32
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
In how many different ways can the letters of the word 'JUDGE' be arranged such that the vowels always come together?
a)
64
b)
48
c)
32
d)
None of these
|
|
Anaya Patel answered |
The given word contains 5 different letters.
Keeping the vowels UE together, we suppose them as 1 letter.
Then, we have to arrange the letters JDG (UE).
Now, we have to arrange in 4! = 24 ways.
The vowels (UE) can be arranged among themselves in 2 ways.
∴ Required number of ways = (24 × 2) = 48
Keeping the vowels UE together, we suppose them as 1 letter.
Then, we have to arrange the letters JDG (UE).
Now, we have to arrange in 4! = 24 ways.
The vowels (UE) can be arranged among themselves in 2 ways.
∴ Required number of ways = (24 × 2) = 48
The number of employees in a nationalised bank in a small town is 10, out of which 4 are female and the rest male. A committee of 5 is to be formed. If m be the number of ways to form such a committee in which there is atleast one female employee and n be the number of ways to form such a committee whichincludes at least two male employees, then find the ratio m:n.- a)3:2
- b)5:1
- c)1:1
- d)0.8:0.9
Correct answer is option 'C'. Can you explain this answer?
The number of employees in a nationalised bank in a small town is 10, out of which 4 are female and the rest male. A committee of 5 is to be formed. If m be the number of ways to form such a committee in which there is atleast one female employee and n be the number of ways to form such a committee whichincludes at least two male employees, then find the ratio m:n.
a)
3:2
b)
5:1
c)
1:1
d)
0.8:0.9

|
Maulik Unni answered |
Now take different cases to fulfill the conditions given.
In how many different ways can the letters of the word 'LEADING' be arranged such that the vowels should always come together? - a)122
- b)720
- c)420
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
a)
122
b)
720
c)
420
d)
None of these

|
Arya Roy answered |
The word 'LEADING' has 7 different letters.
When the vowels EAI are always together, they can be supposed to form one letter.
Then, we have to arrange the letters LNDG (EAI).
Now, 5 (4 + 1) letters can be arranged in 5! = 120 ways.
The vowels (EAI) can be arranged among themselves in 3! = 6 ways.
Required number of ways = (120 * 6) = 720.
In how many different ways can the letters of the word 'OPTICAL' be arranged so that the vowels always come together? - a)610
- b)720
- c)825
- d)920
Correct answer is option 'B'. Can you explain this answer?
a)
610
b)
720
c)
825
d)
920
|
|
Nidhi Mukherjee answered |
The word 'OPTICAL' contains 7 different letters. When the vowels OIA are always together, they can be supposed to form one letter. Then, we have to arrange the letters PTCL (OIA). Now, 5 letters can be arranged in 5!=120 ways. The vowels (OIA) can be arranged among themselves in 3!=6 ways. Required number of ways =(120∗6)=720.
In how many ways can the letters of the word DELHI be arranged?- a)119
- b)120
- c)60
- d)24
Correct answer is option 'B'. Can you explain this answer?
In how many ways can the letters of the word DELHI be arranged?
a)
119
b)
120
c)
60
d)
24

|
Maheshwar Chakraborty answered |
A and B can occupy the first and the ninth places, the second and the tenth places, the third and the eleventh place and so on... This can be done in 18 ways.
A and B can be arranged in 2 ways.
All the other 24 alphabets can be arranged in 24! ways.
Hence the required answer = 2 x 18 x 24!
A and B can be arranged in 2 ways.
All the other 24 alphabets can be arranged in 24! ways.
Hence the required answer = 2 x 18 x 24!
How many motor vehicle registration number of 4 digits can be formed with the digits 0, 1,2, 3, 4, 5? (No digit being repeated.)
- a)1080
- b)120
- c)300
- d)360
Correct answer is option 'D'. Can you explain this answer?
How many motor vehicle registration number of 4 digits can be formed with the digits 0, 1,2, 3, 4, 5? (No digit being repeated.)
a)
1080
b)
120
c)
300
d)
360

|
Aarya Kumar answered |
The correct option is Option D.
Since motor registration can start with zero as first digit from left and there are six different digits (0,1,2,3,4,5) including zero.
Therefore, different registration numbers that can be formed using these six digits = 6P4 = 360
IfN be an element of the set A= {1,2,3,5,6,10,15,30} and P, Q and R are integers such that PQR = N, then the number of positive integral solutions of PQR = N, is - a)32
- b)64
- c)96
- d)128
Correct answer is option 'B'. Can you explain this answer?
IfN be an element of the set A= {1,2,3,5,6,10,15,30} and P, Q and R are integers such that PQR = N, then the number of positive integral solutions of PQR = N, is
a)
32
b)
64
c)
96
d)
128
|
|
Krishna Iyer answered |
This is nothing but the application of the concept of number of factors (see Number System).
In the above question, what will be the number of ways of selecting the committee with at least 3 women such that at least one woman holds the post of either a president or a vice-president?- a)420
- b)610
- c)256
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
In the above question, what will be the number of ways of selecting the committee with at least 3 women such that at least one woman holds the post of either a president or a vice-president?
a)
420
b)
610
c)
256
d)
None of these

|
Sounak Singh answered |
For a straight line we just need to select 2 points out of the 8 points available. 8C2 would be the number of ways of doing this.
In how many different ways can the letters of the word 'CORPORATION' be arranged so that the vowels always come together? - a)47200
- b)48000
- c)42000
- d)50400
Correct answer is option 'D'. Can you explain this answer?
a)
47200
b)
48000
c)
42000
d)
50400

|
Gowri Chakraborty answered |
Vowels in the word "CORPORATION" are O,O,A,I,O
Lets make it as CRPRTN(OOAIO)
This has 7 lettes, where R is twice so value = 7!/2!
= 2520
Vowel O is 3 times, so vowels can be arranged = 5!/3!
= 20
Total number of words = 2520 * 20 = 50400
How many 10 digits numbers can be written by using the digits 1 and 2- a)10C1 + 9C2
- b)210
- c)10C2
- d)10!
Correct answer is option 'B'. Can you explain this answer?
How many 10 digits numbers can be written by using the digits 1 and 2
a)
10C1 + 9C2
b)
210
c)
10C2
d)
10!

|
Kirti Yadav answered |
2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 .
The number of positive integral solution of abc = 30 is:- a)24
- b)81
- c)27
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The number of positive integral solution of abc = 30 is:
a)
24
b)
81
c)
27
d)
None of these
|
|
Faizan Khan answered |
Number of the integral solution for abc=30 are:
1×3×10⇒Permutation=3!
15×2×1⇒Permutation=3!
5×3×2⇒Permutation=3!
5×6×1⇒Permutation=3!
30×1×1⇒Permutation= 3!/2!
Total solutions =(3!×4)+3=27
In a group of 6 boys and 4 girls, four children are to be selected. In how many different ways can they be selected such that at least one boy should be there? - a)159
- b)209
- c)201
- d)212
Correct answer is 'B'. Can you explain this answer?
a)
159
b)
209
c)
201
d)
212

|
Sameer Rane answered |
We may have (1 boy and 3 girls) or (2 boys and 2 girls) or (3 boys and 1 girl) or (4 boys).
Required number of ways = (6C1*4C3)+(6C2*4C2)+(6C3*4C1)+6C4
= (6C1*4C1)+(6C2*4C2)+(6C3*4C1)+6C2 = 209.
How many quadrilateral can be formed from 25 points out of which 7 are collinear- a)5206
- b)2603
- c)13015
- d)11985
Correct answer is option 'D'. Can you explain this answer?
How many quadrilateral can be formed from 25 points out of which 7 are collinear
a)
5206
b)
2603
c)
13015
d)
11985
|
|
Aarav Sharma answered |
To solve this problem, we need to understand the concept of quadrilaterals and combinations.
Quadrilaterals are polygons with four sides. In order to form a quadrilateral, we need to select four points out of the given 25 points. However, we are given that 7 points are collinear, which means they lie on the same line.
To calculate the number of quadrilaterals that can be formed, we need to consider different cases based on the collinear points.
Case 1: No collinear points are selected
In this case, we have to select 4 points out of the remaining 25 - 7 = 18 points. The number of ways to select 4 points out of 18 is given by the combination formula: C(18, 4) = 18! / (4! * (18-4)!) = 3060.
Case 2: Exactly 1 collinear point is selected
In this case, we have to select 3 points out of the remaining 25 - 1 = 24 points. The number of ways to select 3 points out of 24 is given by the combination formula: C(24, 3) = 24! / (3! * (24-3)!) = 2024.
Case 3: Exactly 2 collinear points are selected
In this case, we have to select 2 points out of the remaining 25 - 2 = 23 points. The number of ways to select 2 points out of 23 is given by the combination formula: C(23, 2) = 23! / (2! * (23-2)!) = 253.
Case 4: Exactly 3 collinear points are selected
In this case, we have to select 1 point out of the remaining 25 - 3 = 22 points. The number of ways to select 1 point out of 22 is given by the combination formula: C(22, 1) = 22! / (1! * (22-1)!) = 22.
Case 5: Exactly 4 collinear points are selected
In this case, we have to select 0 points out of the remaining 25 - 4 = 21 points. The number of ways to select 0 points out of 21 is given by the combination formula: C(21, 0) = 21! / (0! * (21-0)!) = 1.
Now, to find the total number of quadrilaterals, we sum up the number of quadrilaterals from each case:
Total = Case 1 + Case 2 + Case 3 + Case 4 + Case 5
Total = 3060 + 2024 + 253 + 22 + 1
Total = 5360
Therefore, the correct answer is option 'D' 5360.
Quadrilaterals are polygons with four sides. In order to form a quadrilateral, we need to select four points out of the given 25 points. However, we are given that 7 points are collinear, which means they lie on the same line.
To calculate the number of quadrilaterals that can be formed, we need to consider different cases based on the collinear points.
Case 1: No collinear points are selected
In this case, we have to select 4 points out of the remaining 25 - 7 = 18 points. The number of ways to select 4 points out of 18 is given by the combination formula: C(18, 4) = 18! / (4! * (18-4)!) = 3060.
Case 2: Exactly 1 collinear point is selected
In this case, we have to select 3 points out of the remaining 25 - 1 = 24 points. The number of ways to select 3 points out of 24 is given by the combination formula: C(24, 3) = 24! / (3! * (24-3)!) = 2024.
Case 3: Exactly 2 collinear points are selected
In this case, we have to select 2 points out of the remaining 25 - 2 = 23 points. The number of ways to select 2 points out of 23 is given by the combination formula: C(23, 2) = 23! / (2! * (23-2)!) = 253.
Case 4: Exactly 3 collinear points are selected
In this case, we have to select 1 point out of the remaining 25 - 3 = 22 points. The number of ways to select 1 point out of 22 is given by the combination formula: C(22, 1) = 22! / (1! * (22-1)!) = 22.
Case 5: Exactly 4 collinear points are selected
In this case, we have to select 0 points out of the remaining 25 - 4 = 21 points. The number of ways to select 0 points out of 21 is given by the combination formula: C(21, 0) = 21! / (0! * (21-0)!) = 1.
Now, to find the total number of quadrilaterals, we sum up the number of quadrilaterals from each case:
Total = Case 1 + Case 2 + Case 3 + Case 4 + Case 5
Total = 3060 + 2024 + 253 + 22 + 1
Total = 5360
Therefore, the correct answer is option 'D' 5360.
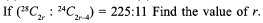
- a)10
- b)11
- c)7
- d)9
Correct answer is option 'C'. Can you explain this answer?
a)
10
b)
11
c)
7
d)
9

|
Raj Mogha answered |
The answer is too long so it can not be solved then can't type
In how many ways can Ram choose a vowel and a consonant from the letters of the word ALLAHABAD?
- a) 4
- b) 6
- c) 9
- d) 5
Correct answer is option 'A'. Can you explain this answer?
In how many ways can Ram choose a vowel and a consonant from the letters of the word ALLAHABAD?
a)
4b)
6c)
9d)
5|
|
Yash Patel answered |
In the letters of the word ALLAHABAD there is only 1 vowel available for selection (A). Note that the fact that A is available 4 times has no impact on this fact.
Also, there are 4 consonants available – viz. L, H, Band D. Thus, the number of ways of selecting a vowel and a consonant would be 1 � 4C1 = 4.
In how many ways can 10 identical presents be distributed among 6 children so that each child gets at least one present?- a)15C5
- b)16C6
- c)9C5
- d)610
Correct answer is option 'C'. Can you explain this answer?
In how many ways can 10 identical presents be distributed among 6 children so that each child gets at least one present?
a)
15C5
b)
16C6
c)
9C5
d)
610

|
Sravya Sharma answered |
We have to count natural numbers which have a maximum of 4 digits. The required answer will be given by: Number of single digit numbers + Number of two digit numbers + Number of three digit numbers + Number of four digit numbers.
Consider S = (1, 2, 3,... 10). In how many ways two numbers from S can be selected so that the sum of the numbers selected is a double digit number?
- a)36
- b)16
- c)29
- d)9C2 - 5C2
Correct answer is option 'C'. Can you explain this answer?
Consider S = (1, 2, 3,... 10). In how many ways two numbers from S can be selected so that the sum of the numbers selected is a double digit number?
a)
36
b)
16
c)
29
d)
9C2 - 5C2

|
Maheshwar Chakraborty answered |
Given, S=(1, 2, 3, …,10).
Two numbers from S are to be selected, such that the sum of the numbers selected is a double-digit number.
If one of the selected number is 10, then, the other number can be any one of 1, 2, 3, ..., 9. So, the number of ways =9.
If one of the selected number is 9, then, the other number can be any one of 1, 2, 3, ..., 8. So, the number of ways =8.
If one of the selected number is 8, then, the other number can be any one of 2, 3, ..., 7. So, the number of ways =6.
If one of the selected number is 7, then, the other number can be any one of 3, 4, ..., 6. So, the number of ways =4.
If one of the selected number is 6, then, the other number can be any one of 4, 5. So, the number of ways =2.
⇒ Total number of ways =9+8+6+4+2=29
Hence, the correct answer is 29.
There are ten subjects in the school day at St.Vincent’s High School but the sixth standard students have only 5 periods in a day. In how many ways can we form a time table for the day for the sixth standard students if no subject is repeated?- a)510
- b)105
- c)252
- d)30240
Correct answer is option 'D'. Can you explain this answer?
There are ten subjects in the school day at St.Vincent’s High School but the sixth standard students have only 5 periods in a day. In how many ways can we form a time table for the day for the sixth standard students if no subject is repeated?
a)
510
b)
105
c)
252
d)
30240

|
Sounak Singh answered |
The possible cases for counting are: Number of numbers when the units digit is nine + the number of numbers when neither the units digit nor the left most is nine + number of numbers when the left most digit is nine.
How many words with or without meaning, can be formed by using all the letters of the word, 'DELHI' using each letter exactly once?
- a)720
- b)24
- c)120
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
How many words with or without meaning, can be formed by using all the letters of the word, 'DELHI' using each letter exactly once?
a)
720
b)
24
c)
120
d)
None of these
|
|
Aditya Kumar answered |
Explanation :
The word 'DELHI' has 5 letters and all these letters are different.
Total words (with or without meaning) formed by using all these
5 letters using each letter exactly once
= Number of arrangements of 5 letters taken all at a time
= 5P5 = 5! = 5 x 4 x 3 x 2 x 1 = 120
Total words (with or without meaning) formed by using all these
5 letters using each letter exactly once
= Number of arrangements of 5 letters taken all at a time
= 5P5 = 5! = 5 x 4 x 3 x 2 x 1 = 120
A seven-digit number comprises of only 2's and 3's. How many of these are multiples of 12?
- a)10
- b)22
- c)12
- d)11
Correct answer is option 'D'. Can you explain this answer?
A seven-digit number comprises of only 2's and 3's. How many of these are multiples of 12?
a)
10
b)
22
c)
12
d)
11
|
|
Anshika Banerjee answered |
Number should be a multiple of 3 and 4. So, the sum of the digits should be a multiple of 3. We can either have all seven digits as 3, or have three 2's and four 3's, or six 2's and a 3.
(The number of 2's should be a multiple of 3).
For the number to be a multiple of 4, the last 2 digits should be 32. Now, let us combine these two.
All seven 3's - No possibility.
Three 2's and four 3's - The first 5 digits should have two 2's and three 3's in some order.
No of possibilities = 5!3!2!5!3!2! = 10
Six 2's and one 3 - The first 5 digits should all be 2's. So, there is only one number 2222232.
So, there are a total of 10 + 1 = 11 solutions.
(The number of 2's should be a multiple of 3).
For the number to be a multiple of 4, the last 2 digits should be 32. Now, let us combine these two.
All seven 3's - No possibility.
Three 2's and four 3's - The first 5 digits should have two 2's and three 3's in some order.
No of possibilities = 5!3!2!5!3!2! = 10
Six 2's and one 3 - The first 5 digits should all be 2's. So, there is only one number 2222232.
So, there are a total of 10 + 1 = 11 solutions.
Hence the answer is "11"
Choice D is the correct answer.
Ateacher takes 3 children from her class to the zoo at a time as often as she can, but she does not take the same three children to the zoo more than once. She finds that she goes to the zoo 84 times more than a particular child goes to the zoo. The number of children in her class is- a)12
- b)10
- c)60
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Ateacher takes 3 children from her class to the zoo at a time as often as she can, but she does not take the same three children to the zoo more than once. She finds that she goes to the zoo 84 times more than a particular child goes to the zoo. The number of children in her class is
a)
12
b)
10
c)
60
d)
None of these

|
Raghavendra Sharma answered |
Let the number of children in the class be n.
a particular child goes to zoo for n−1C2 times (from the remaining n−1 children , we select 2 children
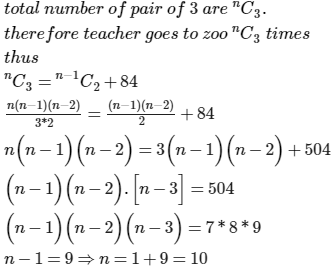
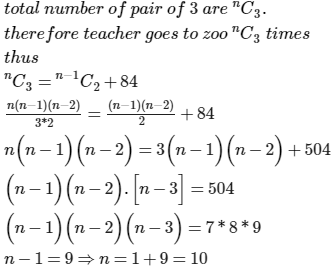
There is a regular decagon. Triangles are formed by joining the vertices of the polygon. What is the number of triangles which have no side common with any of the sides of the polygon?- a)50
- b)300
- c)44
- d)294
Correct answer is option 'A'. Can you explain this answer?
There is a regular decagon. Triangles are formed by joining the vertices of the polygon. What is the number of triangles which have no side common with any of the sides of the polygon?
a)
50
b)
300
c)
44
d)
294

|
Janhavi Chopra answered |
Total number of triangles = Triangles having no sides common + Triangles having one side common + Triangles having two sides common + Triangles having three sides common.
In a chess tournament every person played one game with every other person in the group. The total number of games that men played between themselves exceeded those played by men with women by 18. If there were 4 women in the tournament, in all how many games were played in the tournament?- a)114
- b)66
- c)78
- d)120
Correct answer is option 'D'. Can you explain this answer?
In a chess tournament every person played one game with every other person in the group. The total number of games that men played between themselves exceeded those played by men with women by 18. If there were 4 women in the tournament, in all how many games were played in the tournament?
a)
114
b)
66
c)
78
d)
120
|
|
Aarav Sharma answered |
Problem Analysis:
We are given that every person played one game with every other person in the group. We need to find the total number of games played in the tournament when the total number of games that men played between themselves exceeded those played by men with women by 18.
Given:
- Total number of women in the tournament = 4
To find:
- The total number of games played in the tournament
Solution:
Let's assume there are 'n' people in the tournament.
- The number of games played by each person = (n-1)
- Total number of games played in the tournament = nC2 (combination of 'n' people taken 2 at a time)
As per the given condition, the total number of games that men played between themselves exceeded those played by men with women by 18.
Let's assume the number of men in the tournament = 'm'. Then the number of women in the tournament = (n-m).
- Number of games played between men = mC2
- Number of games played between men and women = m*(n-m)
- Given, mC2 - m*(n-m) = 18
Simplifying the above expression, we get:
mC2 - m*n + m^2 + 18 = 0
mC2 = (nC2 - m*n) + 18
Substituting the value of nC2 in terms of 'n':
mC2 = (n*(n-1)/2 - m*n) + 18
2mC2 = n*(n-1) - 2m*n + 36
2mC2 = n*(n-2m+1) + 36
As per the given condition, there are 4 women in the tournament.
Hence, the number of men = n-4
Substituting this value in the above equation, we get:
2(mC2) = (n-4)*(n-2m+5) + 36
We know that the total number of games played in the tournament = nC2
Substituting the value of nC2 in terms of 'n':
2(mC2) = n*(n-1) - 4*(n-4) - 2m*n + 10m + 36
2(mC2) = n^2 - 2mn + 10m - 4
n^2 - 2mn + 10m - 4 - 2(mC2) = 0
We can solve this equation to get the value of 'n'.
n = [2m + sqrt(4m^2 - 40m + 36 + 8mC2)] / 2
n = m + sqrt(m^2 - 10m + 9 + 2mC2)
We know that 'n' is an integer, hence we need to find the value of 'm' such that the above expression gives an integer value for 'n'.
As 'm' increases, the value of 'n' also increases. We can try different values of 'm' to find the smallest possible value of 'm' that gives an integer value for 'n'.
Trying different values of 'm', we get:
- For m = 10, n = 20
- For m = 11, n =
We are given that every person played one game with every other person in the group. We need to find the total number of games played in the tournament when the total number of games that men played between themselves exceeded those played by men with women by 18.
Given:
- Total number of women in the tournament = 4
To find:
- The total number of games played in the tournament
Solution:
Let's assume there are 'n' people in the tournament.
- The number of games played by each person = (n-1)
- Total number of games played in the tournament = nC2 (combination of 'n' people taken 2 at a time)
As per the given condition, the total number of games that men played between themselves exceeded those played by men with women by 18.
Let's assume the number of men in the tournament = 'm'. Then the number of women in the tournament = (n-m).
- Number of games played between men = mC2
- Number of games played between men and women = m*(n-m)
- Given, mC2 - m*(n-m) = 18
Simplifying the above expression, we get:
mC2 - m*n + m^2 + 18 = 0
mC2 = (nC2 - m*n) + 18
Substituting the value of nC2 in terms of 'n':
mC2 = (n*(n-1)/2 - m*n) + 18
2mC2 = n*(n-1) - 2m*n + 36
2mC2 = n*(n-2m+1) + 36
As per the given condition, there are 4 women in the tournament.
Hence, the number of men = n-4
Substituting this value in the above equation, we get:
2(mC2) = (n-4)*(n-2m+5) + 36
We know that the total number of games played in the tournament = nC2
Substituting the value of nC2 in terms of 'n':
2(mC2) = n*(n-1) - 4*(n-4) - 2m*n + 10m + 36
2(mC2) = n^2 - 2mn + 10m - 4
n^2 - 2mn + 10m - 4 - 2(mC2) = 0
We can solve this equation to get the value of 'n'.
n = [2m + sqrt(4m^2 - 40m + 36 + 8mC2)] / 2
n = m + sqrt(m^2 - 10m + 9 + 2mC2)
We know that 'n' is an integer, hence we need to find the value of 'm' such that the above expression gives an integer value for 'n'.
As 'm' increases, the value of 'n' also increases. We can try different values of 'm' to find the smallest possible value of 'm' that gives an integer value for 'n'.
Trying different values of 'm', we get:
- For m = 10, n = 20
- For m = 11, n =
How many batting orders are possible for the Indian cricket team if there is a squad of 15 to choose from such that Sachin Tendulkar is always chosen?- a)1001.11!
- b)364.11!
- c)11!
- d)15.11!
Correct answer is option 'A'. Can you explain this answer?
How many batting orders are possible for the Indian cricket team if there is a squad of 15 to choose from such that Sachin Tendulkar is always chosen?
a)
1001.11!
b)
364.11!
c)
11!
d)
15.11!

|
Sounak Singh answered |
The condition is that we have to count the number of natural numbers not more than 4300.
The total possible numbers with the given digits = 5x5 x5 x5 = 625 - 1 = 624.
Subtract form this the number of natural number greater than 4300 which can be formed from the given digits =1x 2x 5x5 -1 =49 .
Hence, the required number of numbers = 624 - 49 = 575.
The total possible numbers with the given digits = 5x5 x5 x5 = 625 - 1 = 624.
Subtract form this the number of natural number greater than 4300 which can be formed from the given digits =1x 2x 5x5 -1 =49 .
Hence, the required number of numbers = 624 - 49 = 575.
If a denotes the number of permutations of x + 2 things taking all at a time, b the number of permutations of x things taking 11 at a time and c the number of permutations of x - 11 things taking all at a time such that a = 182be, then the value of x is- a)15
- b)12
- c)10
- d)18
Correct answer is option 'B'. Can you explain this answer?
If a denotes the number of permutations of x + 2 things taking all at a time, b the number of permutations of x things taking 11 at a time and c the number of permutations of x - 11 things taking all at a time such that a = 182be, then the value of x is
a)
15
b)
12
c)
10
d)
18
|
|
Aarav Sharma answered |
Given:
- Number of permutations of x things taken 2 at a time = a
- Number of permutations of x things taken 11 at a time = b
- Number of permutations of (x-11) things taken all at a time = c
- a = 182be
To find:
The value of x
Solution:
We are given the relation a = 182be. Let's break down this relation and solve for x.
Step 1: Breaking down the relation a = 182be
- We know that the number of permutations of x things taken 2 at a time is given by nPr(x, 2) = x! / (x-2)!
- Similarly, the number of permutations of x things taken 11 at a time is nPr(x, 11) = x! / (x-11)!
- And the number of permutations of (x-11) things taken all at a time is nPr(x-11, x-11) = (x-11)!
Substituting these values in the given relation a = 182be, we get:
x! / (x-2)! = 182be * (x! / (x-11)!) * (x-11)!
Step 2: Simplifying the equation
- Canceling out common terms, we get:
(x-2)! = 182be * (x-11)!
Step 3: Analyzing the equation
- We know that (x-2)! is a factorial term, which means it is always non-negative.
- Similarly, (x-11)! is also a factorial term, which means it is always non-negative.
- On the right side of the equation, we have 182be, which is a constant.
- Therefore, for the equation to hold true, the left side (x-2)! must also be non-negative, which implies that x-2 must be greater than or equal to 0. This gives us x >= 2.
Step 4: Simplifying the equation further
- Dividing both sides of the equation by (x-11)!, we get:
(x-2)! / (x-11)! = 182be
- We know that (x-2)! / (x-11)! is a ratio of factorials, which is always a positive integer.
- Therefore, 182be must also be a positive integer.
Step 5: Analyzing the options
- Let's consider the given options: a) 15, b) 12, c) 10, d) 18
- If we substitute each option into the equation a = 182be, we find that only option b) 12 satisfies the equation and gives a positive integer value for 182be.
Final Answer:
Therefore, the value of x is 12.
- Number of permutations of x things taken 2 at a time = a
- Number of permutations of x things taken 11 at a time = b
- Number of permutations of (x-11) things taken all at a time = c
- a = 182be
To find:
The value of x
Solution:
We are given the relation a = 182be. Let's break down this relation and solve for x.
Step 1: Breaking down the relation a = 182be
- We know that the number of permutations of x things taken 2 at a time is given by nPr(x, 2) = x! / (x-2)!
- Similarly, the number of permutations of x things taken 11 at a time is nPr(x, 11) = x! / (x-11)!
- And the number of permutations of (x-11) things taken all at a time is nPr(x-11, x-11) = (x-11)!
Substituting these values in the given relation a = 182be, we get:
x! / (x-2)! = 182be * (x! / (x-11)!) * (x-11)!
Step 2: Simplifying the equation
- Canceling out common terms, we get:
(x-2)! = 182be * (x-11)!
Step 3: Analyzing the equation
- We know that (x-2)! is a factorial term, which means it is always non-negative.
- Similarly, (x-11)! is also a factorial term, which means it is always non-negative.
- On the right side of the equation, we have 182be, which is a constant.
- Therefore, for the equation to hold true, the left side (x-2)! must also be non-negative, which implies that x-2 must be greater than or equal to 0. This gives us x >= 2.
Step 4: Simplifying the equation further
- Dividing both sides of the equation by (x-11)!, we get:
(x-2)! / (x-11)! = 182be
- We know that (x-2)! / (x-11)! is a ratio of factorials, which is always a positive integer.
- Therefore, 182be must also be a positive integer.
Step 5: Analyzing the options
- Let's consider the given options: a) 15, b) 12, c) 10, d) 18
- If we substitute each option into the equation a = 182be, we find that only option b) 12 satisfies the equation and gives a positive integer value for 182be.
Final Answer:
Therefore, the value of x is 12.
Number of ways in which n distinct things can be distributed among n persons so that atleast one person does not get anything is 232. Find n.- a)3
- b)4
- c)5
- d)6
Correct answer is option 'B'. Can you explain this answer?
Number of ways in which n distinct things can be distributed among n persons so that atleast one person does not get anything is 232. Find n.
a)
3
b)
4
c)
5
d)
6

|
Raghavendra Sharma answered |
There are n! ways in which everyone gets a thing. There are n^n distributions in total.
Hence the formula for what you want is n^n−n!.
We start trying with n = 4 and get 4^4 − 4! = 232.
Direction for questions 1 to 2 : Read passage below and solve the questions based on it.
Tn a horticultural show, a participant arranged a total of 1000 fruits of four types in a long straight line He first placed one apple, then two mangoes, three oranges, four custard apples, five apples, six mangoes, seven oranges, eight custard apples and so on (with apples followed by mangoes, oranges, custard apples in that order) uplo the 1000th fruit.What was the 1000th fruit?- a)Apple
- b)Mango
- c)Orange
- d)Custard apple
Correct answer is option 'A'. Can you explain this answer?
Direction for questions 1 to 2 : Read passage below and solve the questions based on it.
Tn a horticultural show, a participant arranged a total of 1000 fruits of four types in a long straight line He first placed one apple, then two mangoes, three oranges, four custard apples, five apples, six mangoes, seven oranges, eight custard apples and so on (with apples followed by mangoes, oranges, custard apples in that order) uplo the 1000th fruit.
Tn a horticultural show, a participant arranged a total of 1000 fruits of four types in a long straight line He first placed one apple, then two mangoes, three oranges, four custard apples, five apples, six mangoes, seven oranges, eight custard apples and so on (with apples followed by mangoes, oranges, custard apples in that order) uplo the 1000th fruit.
What was the 1000th fruit?
a)
Apple
b)
Mango
c)
Orange
d)
Custard apple
|
|
Aarav Sharma answered |
Explanation:
The participant arranged the fruits in a specific pattern. Let's analyze the pattern to determine the 1000th fruit.
Pattern Analysis:
The participant placed one apple, then two mangoes, three oranges, four custard apples, and continued this sequence.
1. First Iteration:
- 1st fruit: Apple
- 2nd fruit: Mango
- 3rd fruit: Mango
- 4th fruit: Orange
- 5th fruit: Orange
- 6th fruit: Orange
- 7th fruit: Custard apple
- 8th fruit: Custard apple
- 9th fruit: Custard apple
- 10th fruit: Custard apple
2. Second Iteration:
- 11th fruit: Apple
- 12th fruit: Apple
- 13th fruit: Mango
- 14th fruit: Mango
- 15th fruit: Mango
- 16th fruit: Orange
- 17th fruit: Orange
- 18th fruit: Orange
- 19th fruit: Orange
- 20th fruit: Custard apple
- ...
Pattern Conclusion:
The pattern continues, with each fruit type increasing by one in each iteration. The number of fruits in each iteration follows the sequence: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...
Determining the 1000th fruit:
To determine the 1000th fruit, we need to find the iteration in which the 1000th fruit falls and the position of the fruit within that iteration.
1. Finding the iteration:
- The sum of the first n terms of a sequence is given by the formula: S = (n/2)(a + l), where S is the sum, n is the number of terms, a is the first term, and l is the last term.
- In this case, the sum of the first n terms is 1000. We can start checking for n = 1, 2, 3, ... until we find the iteration where the sum exceeds 1000.
- For n = 1, the sum is 1. For n = 2, the sum is 3. For n = 3, the sum is 6. For n = 4, the sum is 10. For n = 5, the sum is 15. For n = 6, the sum is 21. For n = 7, the sum is 28. For n = 8, the sum is 36. For n = 9, the sum is 45. For n = 10, the sum is 55. For n = 11, the sum is 66. For n = 12, the sum is 78. For n = 13, the sum is 91. For n = 14, the sum is 105. For n = 15, the sum is 120. For n = 16, the sum is 136. For n = 17, the sum is 153. For n = 18
The participant arranged the fruits in a specific pattern. Let's analyze the pattern to determine the 1000th fruit.
Pattern Analysis:
The participant placed one apple, then two mangoes, three oranges, four custard apples, and continued this sequence.
1. First Iteration:
- 1st fruit: Apple
- 2nd fruit: Mango
- 3rd fruit: Mango
- 4th fruit: Orange
- 5th fruit: Orange
- 6th fruit: Orange
- 7th fruit: Custard apple
- 8th fruit: Custard apple
- 9th fruit: Custard apple
- 10th fruit: Custard apple
2. Second Iteration:
- 11th fruit: Apple
- 12th fruit: Apple
- 13th fruit: Mango
- 14th fruit: Mango
- 15th fruit: Mango
- 16th fruit: Orange
- 17th fruit: Orange
- 18th fruit: Orange
- 19th fruit: Orange
- 20th fruit: Custard apple
- ...
Pattern Conclusion:
The pattern continues, with each fruit type increasing by one in each iteration. The number of fruits in each iteration follows the sequence: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...
Determining the 1000th fruit:
To determine the 1000th fruit, we need to find the iteration in which the 1000th fruit falls and the position of the fruit within that iteration.
1. Finding the iteration:
- The sum of the first n terms of a sequence is given by the formula: S = (n/2)(a + l), where S is the sum, n is the number of terms, a is the first term, and l is the last term.
- In this case, the sum of the first n terms is 1000. We can start checking for n = 1, 2, 3, ... until we find the iteration where the sum exceeds 1000.
- For n = 1, the sum is 1. For n = 2, the sum is 3. For n = 3, the sum is 6. For n = 4, the sum is 10. For n = 5, the sum is 15. For n = 6, the sum is 21. For n = 7, the sum is 28. For n = 8, the sum is 36. For n = 9, the sum is 45. For n = 10, the sum is 55. For n = 11, the sum is 66. For n = 12, the sum is 78. For n = 13, the sum is 91. For n = 14, the sum is 105. For n = 15, the sum is 120. For n = 16, the sum is 136. For n = 17, the sum is 153. For n = 18
In a test of 10 multiple choice questions of one correct answer, each having 4 alternative answers, then the number of ways to put ticks at random for the answers to all the questions is- a)410
- b)104
- c)410-4
- d)104-10
Correct answer is option 'A'. Can you explain this answer?
In a test of 10 multiple choice questions of one correct answer, each having 4 alternative answers, then the number of ways to put ticks at random for the answers to all the questions is
a)
410
b)
104
c)
410-4
d)
104-10

|
Maulik Unni answered |
Each of the questions can be answered in 4 ways. So, 10 questions can be answered in 410 ways.
Chapter doubts & questions for Permutation and Combination - Mathematics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Permutation and Combination - Mathematics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Mathematics for JAMB
134 videos|94 docs|102 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup














