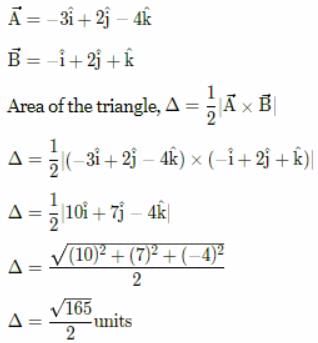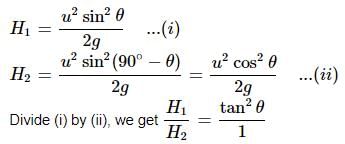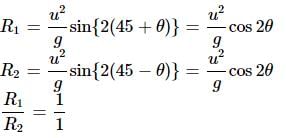All Exams >
JAMB >
Physics for JAMB >
All Questions
All questions of Projectile Motion for JAMB Exam
Two particles are projected simultaneously in the same vertical plane, from the same point, both with different speeds and at different angles with horizontal. The path followed by one, as seen by the other, is- a)A vertical line
- b)A parabola
- c)A hyperbola
- d)A straight line making a constant angle (≠ 90∘) with horizontal
Correct answer is option 'D'. Can you explain this answer?
Two particles are projected simultaneously in the same vertical plane, from the same point, both with different speeds and at different angles with horizontal. The path followed by one, as seen by the other, is
a)
A vertical line
b)
A parabola
c)
A hyperbola
d)
A straight line making a constant angle (≠ 90∘) with horizontal
|
|
Mira Joshi answered |
Let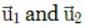 be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.
be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.
The velocities of the two particles after time t are,
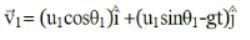
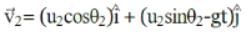
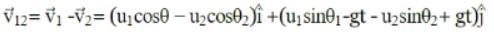

 be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.
be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.The velocities of the two particles after time t are,
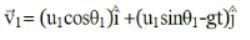
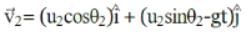
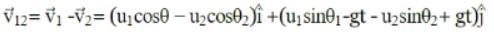

In case of a projectile motion, what is the angle between the velocity and acceleration at the highest point?- a)0°
- b)45°
- c)90°
- d)180°
Correct answer is option 'C'. Can you explain this answer?
In case of a projectile motion, what is the angle between the velocity and acceleration at the highest point?
a)
0°
b)
45°
c)
90°
d)
180°
|
|
Suresh Iyer answered |
At the highest point, velocity is acting horizontally and acceleration ( = acceleration due to gravity) is acting vertically downwards. Therefore, at the highest point the angle between velocity and acceleration is 90∘ .
A girl riding a bicycle with a speed of 5 ms−1 towards north direction, observes rain falling vertically down. If she increases her speed to 10 ms−1, rain appears to meet her at 45∘ to the vertical. What is the speed of the rain?- a)5√2 ms−1
- b)5 ms−1
- c)10√2 ms−1
- d)10 ms−1
Correct answer is option 'A'. Can you explain this answer?
A girl riding a bicycle with a speed of 5 ms−1 towards north direction, observes rain falling vertically down. If she increases her speed to 10 ms−1, rain appears to meet her at 45∘ to the vertical. What is the speed of the rain?
a)
5√2 ms−1
b)
5 ms−1
c)
10√2 ms−1
d)
10 ms−1
|
|
Riya Banerjee answered |
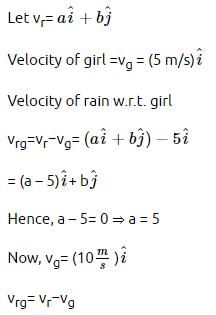
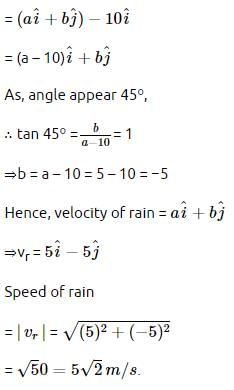
The relation between the time of flight of projectile Tf, and the time to reach the maximum height tm is- a)Tf = 2tm
- b)Tf = tm
- c)Tf = tm/2
- d)Tf = √2 (tm)
Correct answer is option 'A'. Can you explain this answer?
The relation between the time of flight of projectile Tf, and the time to reach the maximum height tm is
a)
Tf = 2tm
b)
Tf = tm
c)
Tf = tm/2
d)
Tf = √2 (tm)
|
|
Raghav Bansal answered |
Time to reach maximum height = tm
Time to reach back to ground = tm
Total time of flight, Tf = tm + tm = 2tm
Time to reach back to ground = tm
Total time of flight, Tf = tm + tm = 2tm
Two particles are projected in air with speed u at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then which one of the following is correct?
(where T1 and T2 are the time of flight.)- a)θ1 > θ2
- b)θ1 = θ2
- c)T1 < T2
- d)T1 = T2
Correct answer is option 'A'. Can you explain this answer?
Two particles are projected in air with speed u at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then which one of the following is correct?
(where T1 and T2 are the time of flight.)
(where T1 and T2 are the time of flight.)
a)
θ1 > θ2
b)
θ1 = θ2
c)
T1 < T2
d)
T1 = T2
|
|
Aarya Ahuja answered |
To fully answer your question, I would need you to provide the angles at which the particles are projected and any other relevant information. Additionally, it seems that part of your question is cut off. Could you please provide the complete question?
A hiker stands on the edge of a cliff 490 m above the ground and throws a stone horizontally with a speed of 15 m s-1. The time taken by the stone to reach the ground is- a)5 s
- b)10 s
- c)12 s
- d)15 s
Correct answer is option 'B'. Can you explain this answer?
A hiker stands on the edge of a cliff 490 m above the ground and throws a stone horizontally with a speed of 15 m s-1. The time taken by the stone to reach the ground is
a)
5 s
b)
10 s
c)
12 s
d)
15 s
|
|
Riya Banerjee answered |
Here, u = 15ms−1
h = 490m
Time taken by the stone to reach the ground is
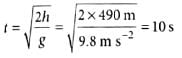
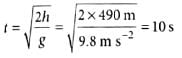
A cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?- a)50 m
- b)100 m
- c)150 m
- d)200 m
Correct answer is option 'A'. Can you explain this answer?
A cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?
a)
50 m
b)
100 m
c)
150 m
d)
200 m
|
|
Meera Singh answered |
Let u be the velocity of projection of the ball. The ball will cover maximum horizontal distance when angle of projection with horizontal, θ = 45∘. Then Rmax = u2/g = 100m
If ball is projected vertically upwards (θ = 90∘) from ground then H attains maximum value.
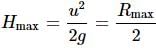
∴ The height to which cricketer can through the ball is = Rmax/2 = 100/2 = 50m.
If ball is projected vertically upwards (θ = 90∘) from ground then H attains maximum value.
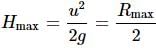
∴ The height to which cricketer can through the ball is = Rmax/2 = 100/2 = 50m.
When air resistance is taken into account while dealing with the motion of the projectile which of the following properties of the projectile, shows an increase?- a)Range
- b)Maximum height
- c)Speed at which it strikes the ground
- d)The angle at which the projectile strikes the ground
Correct answer is option 'D'. Can you explain this answer?
When air resistance is taken into account while dealing with the motion of the projectile which of the following properties of the projectile, shows an increase?
a)
Range
b)
Maximum height
c)
Speed at which it strikes the ground
d)
The angle at which the projectile strikes the ground
|
|
Gaurav Kumar answered |
In the presence of air resistance, the range, maximum height, speed at which the projectile strikes the ground will decreases whereas the angles at which the projectile strikes the ground will increases.
A football is kicked into the air vertically upwards with velocity u. The velocity of the ball at the highest point is- a)u
- b)2u
- c)zero
- d)4u
Correct answer is option 'C'. Can you explain this answer?
A football is kicked into the air vertically upwards with velocity u. The velocity of the ball at the highest point is
a)
u
b)
2u
c)
zero
d)
4u
|
|
Dev Patel answered |
The velocity of the ball at the highest point is zero.
An aeroplane flying horizontally with a speed of 360 km h-1 releases a bomb at a height of 490 m from the ground. If g = 9.8 m s-2, it will strike the ground at- a)10 km
- b)100 km
- c)1 km
- d)16 km
Correct answer is option 'C'. Can you explain this answer?
An aeroplane flying horizontally with a speed of 360 km h-1 releases a bomb at a height of 490 m from the ground. If g = 9.8 m s-2, it will strike the ground at
a)
10 km
b)
100 km
c)
1 km
d)
16 km
|
|
Preeti Iyer answered |
Time taken by the bomb to fall through a height of 490 m
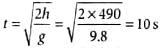
Distance at which the bomb strikes the ground = horizontal velocity x time

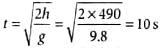
Distance at which the bomb strikes the ground = horizontal velocity x time

A bomb is released by a horizontal flying aeroplane. The trajectory of the bomb is- a)a parabola
- b)a straight line
- c)a circle
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
A bomb is released by a horizontal flying aeroplane. The trajectory of the bomb is
a)
a parabola
b)
a straight line
c)
a circle
d)
a hyperbola
|
|
Riya Banerjee answered |
It is an example of projectile motion. Therefore, the trajectory of the bomb is parabola.
Two projectiles are are fired from the same point with the same speed at angles 60° and 30° respectively. Which one of the follwing is true?- a)Their horizontal ranges will be the same
- b)Their maximum heights will be the same
- c)Their landing velocities will be the same
- d)Their times of flight will be the same
Correct answer is option 'A'. Can you explain this answer?
Two projectiles are are fired from the same point with the same speed at angles 60° and 30° respectively. Which one of the follwing is true?
a)
Their horizontal ranges will be the same
b)
Their maximum heights will be the same
c)
Their landing velocities will be the same
d)
Their times of flight will be the same
|
|
Uday Dasgupta answered |
Horizontal Range
- The horizontal range of a projectile is the distance traveled horizontally before hitting the ground.
- The horizontal range of a projectile is given by the formula R = (v^2 * sin(2θ))/g, where v is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
- When both projectiles are fired from the same point with the same speed, the initial velocity v is the same for both.
- Since sin(2*60°) = sin(120°) = sin(2*30°), the horizontal ranges of the projectiles fired at 60° and 30° will be the same.
Therefore, the correct option is:
a) Their horizontal ranges will be the same
- The horizontal range of a projectile is the distance traveled horizontally before hitting the ground.
- The horizontal range of a projectile is given by the formula R = (v^2 * sin(2θ))/g, where v is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
- When both projectiles are fired from the same point with the same speed, the initial velocity v is the same for both.
- Since sin(2*60°) = sin(120°) = sin(2*30°), the horizontal ranges of the projectiles fired at 60° and 30° will be the same.
Therefore, the correct option is:
a) Their horizontal ranges will be the same
The equations of motion of a projectile are given by x = 36t m and 2y = 96t - 9.8t2 m. The angle of projection is- a)sin−1(4/5)
- b)sin−1(3/5)
- c)sin−1(4/3)
- d)sin−1(3/4)
Correct answer is option 'A'. Can you explain this answer?
The equations of motion of a projectile are given by x = 36t m and 2y = 96t - 9.8t2 m. The angle of projection is
a)
sin−1(4/5)
b)
sin−1(3/5)
c)
sin−1(4/3)
d)
sin−1(3/4)
|
|
Vivek Patel answered |
Given x = 36t
and 2y = 96t − 9.8t2
or y = 48t − 4.9t2
Let the initial velocity of projectile be u and angle of projection θ. Then, Initial horizontal component of velocity,
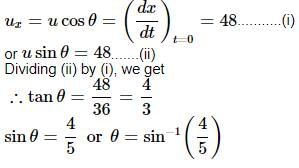
and 2y = 96t − 9.8t2
or y = 48t − 4.9t2
Let the initial velocity of projectile be u and angle of projection θ. Then, Initial horizontal component of velocity,
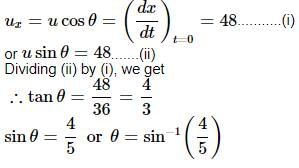
A ball is thrown from the top of a tower with an initial velocity of 10 m s-1 at an angle ot 30° with the horizontal. If it hits the ground at a distance of 17.3 m from the base of the tower, the height of the tower is (Take g = 10 m s-2)- a)5 m
- b)20 m
- c)15 m
- d)10 m
Correct answer is option 'D'. Can you explain this answer?
A ball is thrown from the top of a tower with an initial velocity of 10 m s-1 at an angle ot 30° with the horizontal. If it hits the ground at a distance of 17.3 m from the base of the tower, the height of the tower is (Take g = 10 m s-2)
a)
5 m
b)
20 m
c)
15 m
d)
10 m
|
|
Riya Banerjee answered |
The ball is thrown at an angle, θ = 30o.
Initial velocity of the ball, u = 10 m/s
Horizontal range of the ball, R = 17.3 m
We know that, R = u cosθ t,
where t is the time of flight
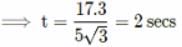
using equation of motion we get:-
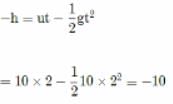
⟹ Height of tower, h = 10 m
We know that, R = u cosθ t,
where t is the time of flight
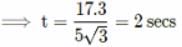
using equation of motion we get:-
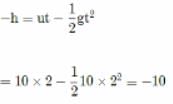
⟹ Height of tower, h = 10 m
The speed of a projectile at its maximum height is √3/2 times its initial speed. If the range of the projectile is P times the maximum height attained by it, then P equals- a)4/3
- b)2√3
- c)4√3
- d)3/4
Correct answer is option 'C'. Can you explain this answer?
The speed of a projectile at its maximum height is √3/2 times its initial speed. If the range of the projectile is P times the maximum height attained by it, then P equals
a)
4/3
b)
2√3
c)
4√3
d)
3/4
|
|
Hansa Sharma answered |
Given √3/2 u = u cos θ
speed at maximum height or cos θ = √3/2 or θ = 30o
speed at maximum height or cos θ = √3/2 or θ = 30o
Given that P Hmax = R
We know Hmax = R tan θ/4
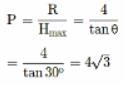
The ceiling of a hall is 40 m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of 56 m s-1 without hitting the ceiling of the hall is- a)25°
- b)30°
- c)45°
- d)60°
Correct answer is option 'B'. Can you explain this answer?
The ceiling of a hall is 40 m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of 56 m s-1 without hitting the ceiling of the hall is
a)
25°
b)
30°
c)
45°
d)
60°
|
|
Suresh Iyer answered |
Here, u = 56 m s-1 Let θ be the angle of projection with the horizontal to have maximum range, with maximum height = 40 m
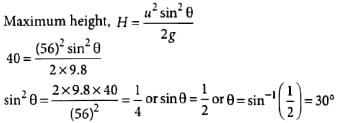
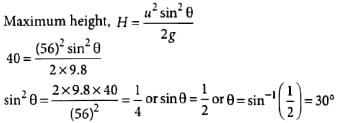
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is:- a)tan−1 (H/R)
- b)tan−1 (2H/R)
- c)tan−1 (4H/R)
- d)tan−1 (4R/H)
Correct answer is option 'C'. Can you explain this answer?
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is:
a)
tan−1 (H/R)
b)
tan−1 (2H/R)
c)
tan−1 (4H/R)
d)
tan−1 (4R/H)
|
|
Nandini Sharma answered |
Understanding Projectile Motion
In projectile motion, the angle of projection determines the trajectory of the projectile. When we denote the horizontal range as \( R \) and the maximum height as \( H \), we can derive the angle of projection.
Key Formulas
- The horizontal range \( R \) of a projectile is given by:
\[
R = \frac{v^2 \sin(2\theta)}{g}
\]
- The maximum height \( H \) attained by a projectile is given by:
\[
H = \frac{v^2 \sin^2(\theta)}{2g}
\]
Where:
- \( v \) = initial velocity
- \( g \) = acceleration due to gravity
- \( \theta \) = angle of projection
Relationship Between H and R
To find the angle \( \theta \), we can manipulate these equations.
1. From the maximum height formula:
\[
v^2 = 2gH \cdot \frac{1}{\sin^2(\theta)}
\]
2. Substituting \( v^2 \) in the range formula:
\[
R = \frac{(2gH / \sin^2(\theta)) \cdot \sin(2\theta)}{g}
\]
3. Simplifying gives:
\[
R = \frac{2H \sin(2\theta)}{\sin^2(\theta)}
\]
Using the identity \( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \):
\[
R = \frac{4H \cos(\theta)}{\sin(\theta)}
\]
4. Rearranging leads to:
\[
\tan(\theta) = \frac{4H}{R}
\]
Final Expression for Angle of Projection
Thus, the angle of projection \( \theta \) can be found using:
\[
\theta = \tan^{-1}\left(\frac{4H}{R}\right)
\]
Hence, the correct choice is option **C**: \( \tan^{-1}\left(\frac{4H}{R}\right) \).
In projectile motion, the angle of projection determines the trajectory of the projectile. When we denote the horizontal range as \( R \) and the maximum height as \( H \), we can derive the angle of projection.
Key Formulas
- The horizontal range \( R \) of a projectile is given by:
\[
R = \frac{v^2 \sin(2\theta)}{g}
\]
- The maximum height \( H \) attained by a projectile is given by:
\[
H = \frac{v^2 \sin^2(\theta)}{2g}
\]
Where:
- \( v \) = initial velocity
- \( g \) = acceleration due to gravity
- \( \theta \) = angle of projection
Relationship Between H and R
To find the angle \( \theta \), we can manipulate these equations.
1. From the maximum height formula:
\[
v^2 = 2gH \cdot \frac{1}{\sin^2(\theta)}
\]
2. Substituting \( v^2 \) in the range formula:
\[
R = \frac{(2gH / \sin^2(\theta)) \cdot \sin(2\theta)}{g}
\]
3. Simplifying gives:
\[
R = \frac{2H \sin(2\theta)}{\sin^2(\theta)}
\]
Using the identity \( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \):
\[
R = \frac{4H \cos(\theta)}{\sin(\theta)}
\]
4. Rearranging leads to:
\[
\tan(\theta) = \frac{4H}{R}
\]
Final Expression for Angle of Projection
Thus, the angle of projection \( \theta \) can be found using:
\[
\theta = \tan^{-1}\left(\frac{4H}{R}\right)
\]
Hence, the correct choice is option **C**: \( \tan^{-1}\left(\frac{4H}{R}\right) \).
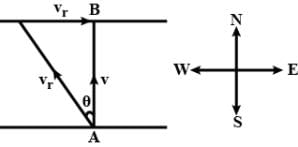
Rain is falling vertically with a speed of 30 ms−1. A woman rides a bicycle with a speed of 12 ms−1 in east to west direction. In which direction she should hold her umbrella?- a)At an angle of tan−1(2/5) with the vertical towards the east.
- b)At angle of tan−1(2/5) with the vertical towards the west.
- c)At angle of tan−1 (5/2) with the vertical towards the east.
- d)At angle of tan−1 (5/2) with the vertical towards the west.
Correct answer is option 'B'. Can you explain this answer?
Rain is falling vertically with a speed of 30 ms−1. A woman rides a bicycle with a speed of 12 ms−1 in east to west direction. In which direction she should hold her umbrella?
a)
At an angle of tan−1(2/5) with the vertical towards the east.
b)
At angle of tan−1(2/5) with the vertical towards the west.
c)
At angle of tan−1 (5/2) with the vertical towards the east.
d)
At angle of tan−1 (5/2) with the vertical towards the west.
|
|
Suresh Iyer answered |
In the figure, 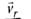 represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle
represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle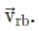 From figure,
From figure,

Therefore, the woman should hold her umbrella at an angle of tan−1(2/5)with the vertical towards the west.
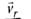 represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle
represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle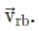 From figure,
From figure,
Therefore, the woman should hold her umbrella at an angle of tan−1(2/5)with the vertical towards the west.
The speed with which the stone hits the ground is- a)15 m s-1
- b)90 m s-1
- c)99 m s-1
- d)49 m s-1
Correct answer is option 'C'. Can you explain this answer?
The speed with which the stone hits the ground is
a)
15 m s-1
b)
90 m s-1
c)
99 m s-1
d)
49 m s-1
|
|
Riya Banerjee answered |
Motion along horizontal direction, ↓+ ve
ux = 15ms−1, ax = 0
vx = ux + axt = 15 + 0 × 10 = 15ms−1
Motion along vertical direction,
uy = 0,ay = g
vy = uy + ayt = 0 + 9.8 × 10 = 98ms−1
∴ Speed of the stone when it hits the ground is
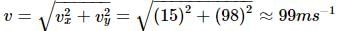
ux = 15ms−1, ax = 0
vx = ux + axt = 15 + 0 × 10 = 15ms−1
Motion along vertical direction,
uy = 0,ay = g
vy = uy + ayt = 0 + 9.8 × 10 = 98ms−1
∴ Speed of the stone when it hits the ground is
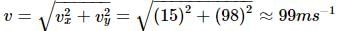

- a)zero
- b)A2B2
- c)AB
- d)√AB
Correct answer is option 'B'. Can you explain this answer?

a)
zero
b)
A2B2
c)
AB
d)
√AB
|
|
Dev Patel answered |
Let θ be angle between vectors 
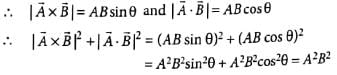
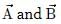
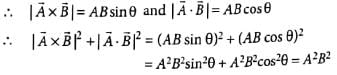
Then the distance from the thrower to the point where the ball returns to the same level is- a)58 m
- b)68 m
- c)78 m
- d)88 m
Correct answer is option 'C'. Can you explain this answer?
Then the distance from the thrower to the point where the ball returns to the same level is
a)
58 m
b)
68 m
c)
78 m
d)
88 m
|
|
Anjali Sharma answered |
Given data,
u = 30ms−1
θ = 300
g = 10ms−2
The distance from the thrower to the point where the ball returns to the same level is


If the angle between the vectors 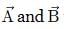 is θ, the value of the product
is θ, the value of the product 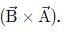
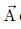 is equal to
is equal to- a)BA2 cos θ
- b)BA2 sin θ
- c)BA2 sin θ cos θ
- d)zero
Correct answer is option 'D'. Can you explain this answer?
If the angle between the vectors 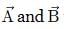 is θ, the value of the product
is θ, the value of the product 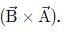
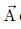 is equal to
is equal to
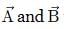 is θ, the value of the product
is θ, the value of the product 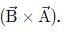
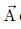 is equal to
is equal toa)
BA2 cos θ
b)
BA2 sin θ
c)
BA2 sin θ cos θ
d)
zero
|
|
Hansa Sharma answered |
We know that scalar triple product is cyclic
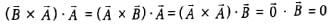
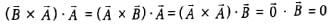
If a body is projected with an angle θ to the horizontal, then- a)Its velocity is always perpendicular to its acceleration.
- b)Its velocity becomes zero at its maximum height.
- c)Its velocity makes zero angle with the horizontal at its maximum height.
- d)The body just before hitting the ground, the direction of velocity coincides with the acceleration.
Correct answer is option 'C'. Can you explain this answer?
If a body is projected with an angle θ to the horizontal, then
a)
Its velocity is always perpendicular to its acceleration.
b)
Its velocity becomes zero at its maximum height.
c)
Its velocity makes zero angle with the horizontal at its maximum height.
d)
The body just before hitting the ground, the direction of velocity coincides with the acceleration.
|
|
Ananya Das answered |
In angular projection, the body at the highest point has velocity = u cosθ in the horizontal direction which makes zero angles with horizontal direction.
If 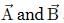 are two vectors, then which of the following is not a correct statement?
are two vectors, then which of the following is not a correct statement?
- a)
- b)
- c)
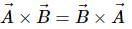
- d)
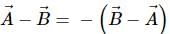
Correct answer is option 'C'. Can you explain this answer?
If 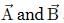 are two vectors, then which of the following is not a correct statement?
are two vectors, then which of the following is not a correct statement?
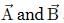 are two vectors, then which of the following is not a correct statement?
are two vectors, then which of the following is not a correct statement?a)
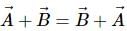
b)
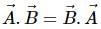
c)
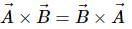
d)
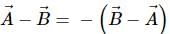
|
|
Lavanya Menon answered |
Vector product of two vectors is anti- commutative.
i.e;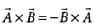
i.e;
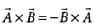
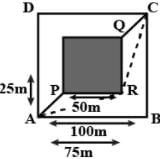
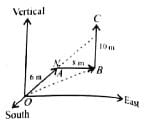
A man wants to reach from A to the opposite corner of the square C (Figure). The sides of the square are 100m each. A central square of 50m × 50m is filled with sand.
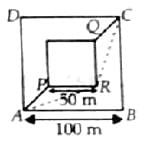
Outside this square, he can walk at a speed 1ms−1. In the central square, he can walk only at a speed of v ms−1(v < 1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?- a)0.18 m s-1
- b)0.81 ms−1
- c)0.5 m s-1
- d)0.95 m s-1
Correct answer is option 'B'. Can you explain this answer?
A man wants to reach from A to the opposite corner of the square C (Figure). The sides of the square are 100m each. A central square of 50m × 50m is filled with sand.

Outside this square, he can walk at a speed 1ms−1. In the central square, he can walk only at a speed of v ms−1(v < 1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?

Outside this square, he can walk at a speed 1ms−1. In the central square, he can walk only at a speed of v ms−1(v < 1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?
a)
0.18 m s-1
b)
0.81 ms−1
c)
0.5 m s-1
d)
0.95 m s-1
|
|
Gaurav Kumar answered |

Consider the straight-line path APQC through the sand. Time is taken to go from A to C via this path
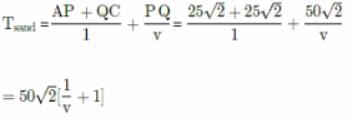
The shortest path outside the sand will be ARC. Time is taken to go from A to C via this path

A cricket ball is thrown at a speed of 30ms−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
(Take g = 10ms−2)- a)2 s
- b)3 s
- c)4 s
- d)5 s
Correct answer is option 'B'. Can you explain this answer?
A cricket ball is thrown at a speed of 30ms−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
(Take g = 10ms−2)
(Take g = 10ms−2)
a)
2 s
b)
3 s
c)
4 s
d)
5 s
|
|
Priya Menon answered |
Here, u = 30ms−1,
θ = 30∘,
g = 10ms−2
The time taken by the ball to return to the same level is
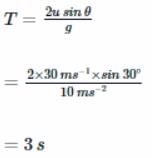
Suppose that two objects A and B are moving with velocities (each with respect to some common frame of reference). Let
(each with respect to some common frame of reference). Let represent the velocity of A with respect to B. Then
represent the velocity of A with respect to B. Then- a)
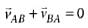
- b)

- c)
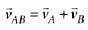
- d)
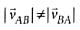
Correct answer is option 'A'. Can you explain this answer?
Suppose that two objects A and B are moving with velocities (each with respect to some common frame of reference). Let
(each with respect to some common frame of reference). Let represent the velocity of A with respect to B. Then
represent the velocity of A with respect to B. Then
 (each with respect to some common frame of reference). Let
(each with respect to some common frame of reference). Let represent the velocity of A with respect to B. Then
represent the velocity of A with respect to B. Thena)
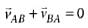
b)

c)
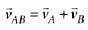
d)
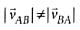
|
|
Gaurav Kumar answered |
Velocity of object A relative to that of B is
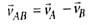
Velocity of object B relative to that of A is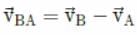
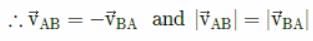
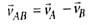
Velocity of object B relative to that of A is
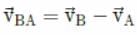
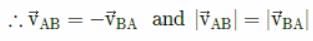
Which of the following is true regarding projectile motion?- a)Horizontal velocity of projectile is constant
- b)Vertical velocity of projectile is constant
- c)Acceleration is not constant
- d)Momentum is constant
Correct answer is option 'A'. Can you explain this answer?
Which of the following is true regarding projectile motion?
a)
Horizontal velocity of projectile is constant
b)
Vertical velocity of projectile is constant
c)
Acceleration is not constant
d)
Momentum is constant
|
|
Raghav Bansal answered |
Horizontal velocity of a projectile is not affected by gravity.
If 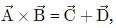 then select the correct alternative.
then select the correct alternative. - a)
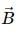 is parallel to
is parallel to 
- b)
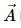 is perpendicular to
is perpendicular to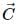
- c)Component of
 Component of
Component of 
- d)Component of
 - Component of
- Component of 
Correct answer is option 'D'. Can you explain this answer?
If 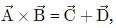 then select the correct alternative.
then select the correct alternative.
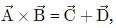 then select the correct alternative.
then select the correct alternative. a)
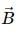 is parallel to
is parallel to 
b)
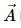 is perpendicular to
is perpendicular to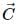
c)
Component of  Component of
Component of 
 Component of
Component of 
d)
Component of  - Component of
- Component of 
 - Component of
- Component of 
|
|
Lavanya Menon answered |
According to definition of cross product 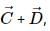 is perpendicular to both
is perpendicular to both
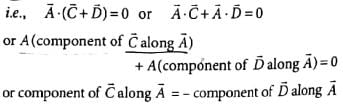
 is perpendicular to both
is perpendicular to both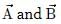
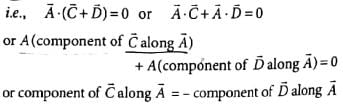
A river is flowing from west to east with a speed 5 ms−1. A swimmer can swim in still water at a speed of 10 ms−1. If he wants to start from point A on south bank and reach opposite point B on north bank, in what direction should he swim?
- a)30∘ east of north
- b)60∘ east of north
- c)30∘ west of north
- d)60∘ west of north
Correct answer is option 'C'. Can you explain this answer?
A river is flowing from west to east with a speed 5 ms−1. A swimmer can swim in still water at a speed of 10 ms−1. If he wants to start from point A on south bank and reach opposite point B on north bank, in what direction should he swim?


a)
30∘ east of north
b)
60∘ east of north
c)
30∘ west of north
d)
60∘ west of north
|
|
Gaurav Kumar answered |
Here, Velocity of swimmer in still water, vs = 10ms−1
Velocity of water flowing in river, vr = 5ms−1
From figure, sinθ = vr/vs = 5/10 = 1/2
θ = sin−1(.1/2) = 30∘ west of north
Velocity of water flowing in river, vr = 5ms−1
From figure, sinθ = vr/vs = 5/10 = 1/2
θ = sin−1(.1/2) = 30∘ west of north
The maximum height attained by the ball is- a)11.25 m
- b)48.2 m
- c)23.5 m
- d)68 m
Correct answer is option 'A'. Can you explain this answer?
The maximum height attained by the ball is
a)
11.25 m
b)
48.2 m
c)
23.5 m
d)
68 m
|
|
Suresh Iyer answered |
The maximum height is given by


Chapter doubts & questions for Projectile Motion - Physics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Projectile Motion - Physics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Physics for JAMB
259 videos|253 docs|230 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup


 on the vector
on the vector  is
is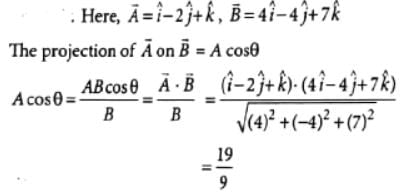
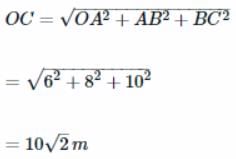
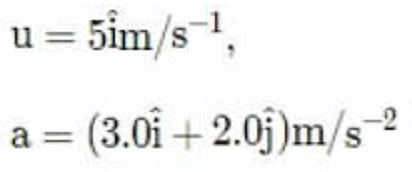
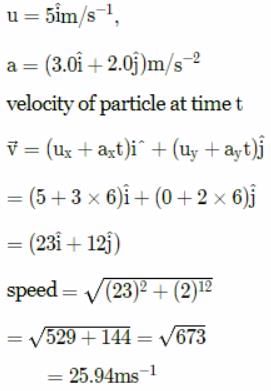
 ×
× 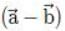 is
is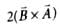
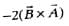
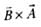
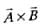
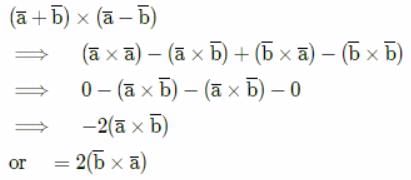
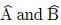 are inclined at an angle θ,Then
are inclined at an angle θ,Then  is
is
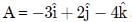 and B =
and B =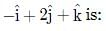 is
is