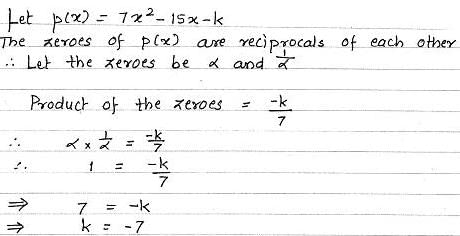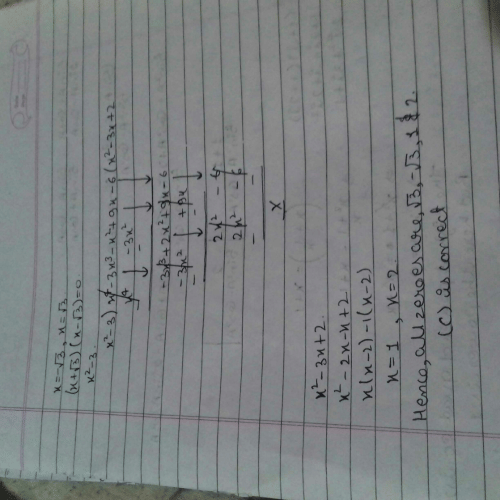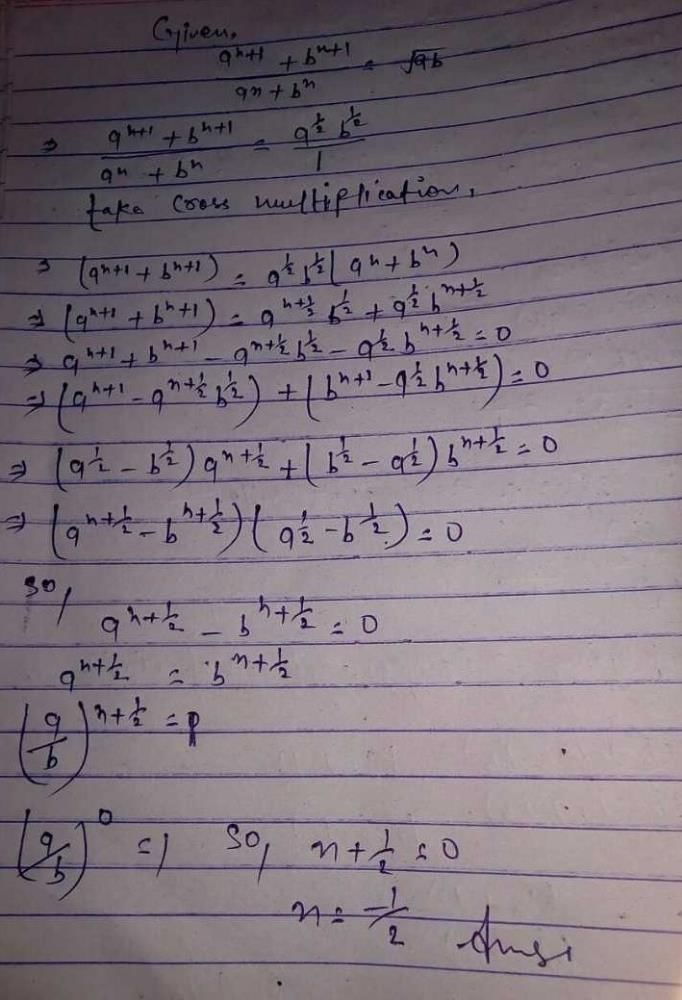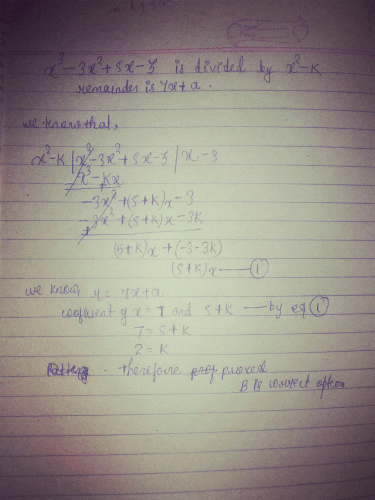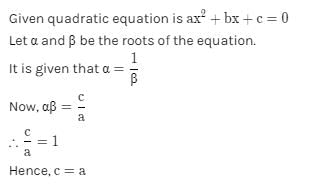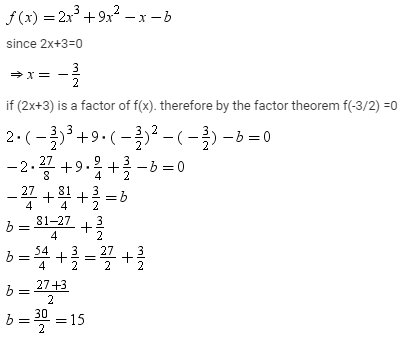All Exams >
EmSAT Achieve >
Mathematics for EmSAT Achieve >
All Questions
All questions of Polynomials for EmSAT Achieve Exam
Can you explain the answer of this question below: If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:- A:14/25
- B:7/5
- C:2/5
- D:7/2
The answer is d.
If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:
A:
14/25
B:
7/5
C:
2/5
D:
7/2
|
Anshu Shah answered |
We have 2 find (1/α + 1/β)
now 1/α + 1/β = (α + β)/ α β (taking LCM)
now by the given poly. we get
(α + β) = -b/a = 7/5
α β = c/a = 2/5
so, (α + β)/ α β = (7/5) / (2/5)
= 7/2
So, 1/α + 1/β = (α + β)/ α β = 7/2
Hence, 1/α + 1/β = 7/2
If one of the factors of x2 + x – 20 is (x + 5), then other factor is- a)(x – 4)
- b)(x – 5)
- c)(x – 6)
- d)(x – 7)
Correct answer is 'A'. Can you explain this answer?
If one of the factors of x2 + x – 20 is (x + 5), then other factor is
a)
(x – 4)
b)
(x – 5)
c)
(x – 6)
d)
(x – 7)
|
Arun Sharma answered |
Using mid-term splitting,
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
- a)6
- b)7
- c)8
- d)9
Correct answer is option 'A'. Can you explain this answer?
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
a)
6
b)
7
c)
8
d)
9
|
Zachary Foster answered |
Given α and β are the zeroes of the polynomial x2 − 5x + k
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
The three zeroes of the polynomial 2x3 + 5x2 – 28x – 15 _____- a)All three are not real numbers
- b)Are all Natural numbers
- c)Are all rational numbers
- d)Are all Integers
Correct answer is option 'C'. Can you explain this answer?
The three zeroes of the polynomial 2x3 + 5x2 – 28x – 15 _____
a)
All three are not real numbers
b)
Are all Natural numbers
c)
Are all rational numbers
d)
Are all Integers
|
Gaurav Kumar answered |
Since the solution is not a complex number, it is a real number. Since rational numbers include all integers, natural numbers and fractions , So the numbers are rational numbers.
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =- a)2
- b)3
- c)1
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =
a)
2
b)
3
c)
1
d)
None of these
|
Pooja Shah answered |
If α and β are the zeros of the polynomial then
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
Now, comparing equation (i) and (ii),we get,
−(α + β) = 3
α + β = −3
−(α + β) = 3
α + β = −3
What value/s can x take in the expression k(x – 10) (x + 10) =0 where k is any real number.- a)100, -100
- b)Infinitely many
- c)Depends on value of k
- d)10, -10
Correct answer is option 'D'. Can you explain this answer?
What value/s can x take in the expression k(x – 10) (x + 10) =0 where k is any real number.
a)
100, -100
b)
Infinitely many
c)
Depends on value of k
d)
10, -10
|
|
Avinash Patel answered |
k(x – 10) (x + 10) =0
⇒ either k=0
Or x-10=0
Or x+10=0
Since we don’t know the value of k
So either x-10=0
x=10
Or x+10=0
x=-10
So values of x can be 10,-10
⇒ either k=0
Or x-10=0
Or x+10=0
Since we don’t know the value of k
So either x-10=0
x=10
Or x+10=0
x=-10
So values of x can be 10,-10
If “1” is a zero of the polynomial P(a) = x2a2 – 2xa + 3x – 2 , then x = ______
- a)2
- b)-2, 1
- c)+2, -2
- d)-2, 0
Correct answer is option 'B'. Can you explain this answer?
If “1” is a zero of the polynomial P(a) = x2a2 – 2xa + 3x – 2 , then x = ______
a)
2
b)
-2, 1
c)
+2, -2
d)
-2, 0
|
|
Pooja Shah answered |
The correct solution of this question is given below:
Here, P(a) = x2a2 - 2xa + 3x - 2
1 is a zero of P(a), so P(1) = 0
Therefore, x212 - 2x.1 + 3x - 2 = 0
x2 + x - 2 = 0
(x + 2)(x - 1) = 0
x = -2, 1
A polynomial of degree three is called ……- a)cubic polynomial
- b)quadratic polynomial
- c)linear polynomial
- d)zero polynomial
Correct answer is option 'A'. Can you explain this answer?
A polynomial of degree three is called ……
a)
cubic polynomial
b)
quadratic polynomial
c)
linear polynomial
d)
zero polynomial
|
Maitri Kulkarni answered |
A cubic polynomial is a polynomial of the form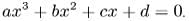 
. A cubic polynomial is a polynomial of degree 3. A univariate cubic polynomial has the form . An equation involving a cubic polynomial is called a cubic equation. A closed-form solution known as the cubic formula exists for the solutions of an arbitrary cubic equation.
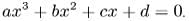. A cubic polynomial is a polynomial of degree 3. A univariate cubic polynomial has the form . An equation involving a cubic polynomial is called a cubic equation. A closed-form solution known as the cubic formula exists for the solutions of an arbitrary cubic equation.Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –- a)x2 – 5x – 14
- b)x2 – 10x – 14
- c)x2 – 5x + 14
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –
a)
x2 – 5x – 14
b)
x2 – 10x – 14
c)
x2 – 5x + 14
d)
None of these
|
|
Amit Kumar answered |
The quadratic equation is of the form x2 - (sum of zeros) x + (product of zeros)
=x2 - 5x - 14
=x2 - 5x - 14
If (x + 1) is a factor of x2 – 3ax + 3a – 7, then the value of a is- a)-2
- b)0
- c)1
- d)-1
Correct answer is option 'C'. Can you explain this answer?
If (x + 1) is a factor of x2 – 3ax + 3a – 7, then the value of a is
a)
-2
b)
0
c)
1
d)
-1
|
|
Anjana Khatri answered |
Since (X+1) is a factor of x^2 - 3ax + 3a - 7
Therefore , x + 1 = 0
or, x=-1
Putting the value of x in the the p(x) = x^2 - 3ax + 3a - 7
or, (-1)^2 - 3(a)(-1) + 3a - 7 = 0
1+3a+3a-7=0
6a=6
or, a=1
Therefore, the value of a = 1.
Direction: Read the following text and answer the following questions on the basis of the same:The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.
If α are 1/α the zeroes of the quadratic polynomial 2x2 – x + 8k, then k is- a)4
- b)1/4
- c)-1/4
- d)2
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.
If α are 1/α the zeroes of the quadratic polynomial 2x2 – x + 8k, then k is
a)
4
b)
1/4
c)
-1/4
d)
2
|
Sun Ray Institute answered |
Given equation, 2x2 – x + 8k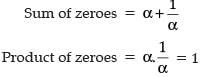
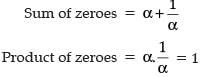
Product of zeroes = c/a = 8k/2
So, 8k/2 = 1
k = 2/8
k = 1/4
Can you explain the answer of this question below:If (x + 1) is a factor of 2x3 + ax2 + 2bx + 1, then find the values of a and b given that 2a – 3b = 4.
- A:
a = 2, b = 2
- B:
a = 5, b = 5
- C:
a = 2, b = 5
- D:
a = 5, b = 2
The answer is d.
If (x + 1) is a factor of 2x3 + ax2 + 2bx + 1, then find the values of a and b given that 2a – 3b = 4.
a = 2, b = 2
a = 5, b = 5
a = 2, b = 5
a = 5, b = 2
|
Vikram Kapoor answered |
Given is the value of a and b.
given that (x+1) is a factor of p(x)
therefore, -1 is a zero of given p(x)
p(x) = 2x3 +ax2 +2bx +1
substituting the value of -1 in the given p(x), we get
p(x)=2*(-1)3 +a *(-1)2 +2*b*(-1)+ 1
= -2 + a -2b + 1
= -1 + a - 2b
or,a - 2b = 1
also given that 2a - 3b = 4
so we got two equations;
a - 2b = 7 ...(1)
2a - 3b = 4 ...(2)
(1)* (2)* (4)- 2 = 2a - 4b = (3)
(2)* 1 = 2a - 3b = 4 (4)
(4) - (3) = [2a - 2a ] + [-3b - (-4b)] = 4 - 2
-3b + 4b = 2
therefore b = 2
substituting the value of bin (3)
2a - 4b = 2
2a - (4*2) = 2
2a - 8 = 2
2a = 2 + 8
2 = 10
a = 10 / 2
therefore a = 5
so we get the value of a and b
that is ; a = 5 and b = 2
given that (x+1) is a factor of p(x)
therefore, -1 is a zero of given p(x)
p(x) = 2x3 +ax2 +2bx +1
substituting the value of -1 in the given p(x), we get
p(x)=2*(-1)3 +a *(-1)2 +2*b*(-1)+ 1
= -2 + a -2b + 1
= -1 + a - 2b
or,a - 2b = 1
also given that 2a - 3b = 4
so we got two equations;
a - 2b = 7 ...(1)
2a - 3b = 4 ...(2)
(1)* (2)* (4)- 2 = 2a - 4b = (3)
(2)* 1 = 2a - 3b = 4 (4)
(4) - (3) = [2a - 2a ] + [-3b - (-4b)] = 4 - 2
-3b + 4b = 2
therefore b = 2
substituting the value of bin (3)
2a - 4b = 2
2a - (4*2) = 2
2a - 8 = 2
2a = 2 + 8
2 = 10
a = 10 / 2
therefore a = 5
so we get the value of a and b
that is ; a = 5 and b = 2
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :- a)5, 6
- b)- 5, - 6
- c)- 5, 6
- d)5, - 6
Correct answer is option 'C'. Can you explain this answer?
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :
a)
5, 6
b)
- 5, - 6
c)
- 5, 6
d)
5, - 6
|
|
Gaurav Kumar answered |
Zeros of the polynomials are the values which gives zero when their value is substituted in the polynomial
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
Find the quadratic polynomial whose zeros are 2 and -6
- a)x2 + 4x + 12
- b)x2 – 4x – 12
- c)x2 + 4x – 12
- d)x2 – 4x + 12
Correct answer is option 'C'. Can you explain this answer?
Find the quadratic polynomial whose zeros are 2 and -6
a)
x2 + 4x + 12
b)
x2 – 4x – 12
c)
x2 + 4x – 12
d)
x2 – 4x + 12
|
Naina Sharma answered |
We know that quadratic equation is of the form x2-(sum of zeros)x+product of zeros
Sum of zeros=2-6=-4
Product of zeros=2*(-6)=-12
x2-(sum of roots )x + product of roots
x2-(-4)x + 12
x2+4x-12
So the equation is x2+4x-12
Sum of zeros=2-6=-4
Product of zeros=2*(-6)=-12
x2-(sum of roots )x + product of roots
x2-(-4)x + 12
x2+4x-12
So the equation is x2+4x-12
The value of 155 mod 9 is- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
The value of 155 mod 9 is
a)
0
b)
1
c)
2
d)
3
|
Raghav Bansal answered |
By the Division algorithm 155 = 9(17) + 2. Where remainder is 155 mod 9.
If two zeroes of a polynomial 4x4 -20x3 +23 x2 + 5x – 6 are ½ and – ½ , the how many more zeroes does it have?- a)3
- b)None
- c)1
- d)2
Correct answer is option 'D'. Can you explain this answer?
If two zeroes of a polynomial 4x4 -20x3 +23 x2 + 5x – 6 are ½ and – ½ , the how many more zeroes does it have?
a)
3
b)
None
c)
1
d)
2
|
Krishna Iyer answered |
The polynomial with degree 4 is a biquadratic equation. And a polynomial has no. of zeros equal to the degree of the polynomial. So total no. of zeros are 4. 2 zeros are already provided to us , so it has 2 more zeros.
Which of the given is the set of zeroes of the polynomial p(x) = 2x3 + x2 – 5x + 2- a)1/2 , -1 , -2
- b)1/2 , 1 , -2
- c)-1/2 , -1 , -2
- d)-1/2 , 1 , -2
Correct answer is option 'B'. Can you explain this answer?
Which of the given is the set of zeroes of the polynomial p(x) = 2x3 + x2 – 5x + 2
a)
1/2 , -1 , -2
b)
1/2 , 1 , -2
c)
-1/2 , -1 , -2
d)
-1/2 , 1 , -2
|
|
Krishna Iyer answered |
We have the polynomial 2x3+x2-5x+2
By Hit and trial method, x=1 is the solution.
Dividing the polynomial by x-1
We get quotient as = 2x2+3x-2
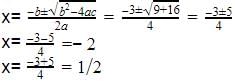
By Hit and trial method, x=1 is the solution.
Dividing the polynomial by x-1
We get quotient as = 2x2+3x-2
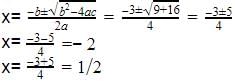
Can you explain the answer of this question below: When x2 – 2x + k divides the polynomial x4 – 6x3 + 16x2 – 25x + 10, the remainder is (x + a) . The value of a is _________
- A:
-3
- B:
3
- C:
-5
- D:
5
The answer is c.
When x2 – 2x + k divides the polynomial x4 – 6x3 + 16x2 – 25x + 10, the remainder is (x + a) . The value of a is _________
-3
3
-5
5
|
|
Pooja Shah answered |
Given that the remainder is (x + a)
⇒ (4k – 25 + 16 – 2k)x + [10 – k(8 – k) ] = x + a
⇒ (2k – 9)x + [10 – 8k + k2 ] = x + a
On comparing both the sides, we get
2k – 9 = 1
⇒ 2k = 10
∴ k = 5
Also 10 – 8k + k2 = a
⇒ 10 – 8(5) + 52 = a
⇒ 10 – 40 + 25 = a
∴ a = – 5
⇒ (4k – 25 + 16 – 2k)x + [10 – k(8 – k) ] = x + a
⇒ (2k – 9)x + [10 – 8k + k2 ] = x + a
On comparing both the sides, we get
2k – 9 = 1
⇒ 2k = 10
∴ k = 5
Also 10 – 8k + k2 = a
⇒ 10 – 8(5) + 52 = a
⇒ 10 – 40 + 25 = a
∴ a = – 5
The value of p when x3 + 9x2 + px – 10 is exactly divisible by (x+ 2 ) is ____- a)1
- b)9
- c)3
- d)6
Correct answer is option 'B'. Can you explain this answer?
The value of p when x3 + 9x2 + px – 10 is exactly divisible by (x+ 2 ) is ____
a)
1
b)
9
c)
3
d)
6
|
Trisha das answered |
Solution:
To find the value of p that makes x^3 + 9x^2 + px + 10 exactly divisible by (x + 2), we can use the remainder theorem.
The remainder theorem states that if a polynomial f(x) is divided by (x - a), then the remainder is f(a).
Therefore, if we divide x^3 + 9x^2 + px + 10 by (x + 2), the remainder will be equal to f(-2), where f(x) = x^3 + 9x^2 + px + 10.
We can find f(-2) by substituting -2 for x in the expression for f(x):
f(-2) = (-2)^3 + 9(-2)^2 + p(-2) + 10
= -8 + 36 - 2p + 10
= 18 - 2p
Since we want the remainder to be zero (i.e. we want (x + 2) to be a factor of x^3 + 9x^2 + px + 10), we must have:
18 - 2p = 0
Solving for p, we get:
p = 9
Therefore, the value of p that makes x^3 + 9x^2 + px + 10 exactly divisible by (x + 2) is 9.
To find the value of p that makes x^3 + 9x^2 + px + 10 exactly divisible by (x + 2), we can use the remainder theorem.
The remainder theorem states that if a polynomial f(x) is divided by (x - a), then the remainder is f(a).
Therefore, if we divide x^3 + 9x^2 + px + 10 by (x + 2), the remainder will be equal to f(-2), where f(x) = x^3 + 9x^2 + px + 10.
We can find f(-2) by substituting -2 for x in the expression for f(x):
f(-2) = (-2)^3 + 9(-2)^2 + p(-2) + 10
= -8 + 36 - 2p + 10
= 18 - 2p
Since we want the remainder to be zero (i.e. we want (x + 2) to be a factor of x^3 + 9x^2 + px + 10), we must have:
18 - 2p = 0
Solving for p, we get:
p = 9
Therefore, the value of p that makes x^3 + 9x^2 + px + 10 exactly divisible by (x + 2) is 9.
Find the sum and the product of the zeroes of the polynomial: x2-3x-10- a)3, 10
- b)-3, -10
- c)3,-10
- d)-3, 10
Correct answer is option 'C'. Can you explain this answer?
Find the sum and the product of the zeroes of the polynomial: x2-3x-10
a)
3, 10
b)
-3, -10
c)
3,-10
d)
-3, 10
|
|
Raghav Bansal answered |
X²-3x-10
x² -(5x-2x)-10
x² - 5x+2x-10
x(x-5)+2(x-5)
(x-5)(x+2)
x=5
x=-2
Sum of zeroes = α+β = 5-2 = 3
α+β = -b/a = -(-3)/1 = 3
Product of zeroes = αβ = 5*-2 = -10
αβ = c/a = -10/1 = -10
x² -(5x-2x)-10
x² - 5x+2x-10
x(x-5)+2(x-5)
(x-5)(x+2)
x=5
x=-2
Sum of zeroes = α+β = 5-2 = 3
α+β = -b/a = -(-3)/1 = 3
Product of zeroes = αβ = 5*-2 = -10
αβ = c/a = -10/1 = -10
If the degree of the dividend is 5 and the degree of the divisor is 3, then the degree of the quotient will be- a)2
- b)1
- c)-2
- d)0
Correct answer is option 'A'. Can you explain this answer?
If the degree of the dividend is 5 and the degree of the divisor is 3, then the degree of the quotient will be
a)
2
b)
1
c)
-2
d)
0
|
|
Vikas Kumar answered |
The degree of the dividend is 5 and that of the divisor is 3;Therefore, if expression with degree 5 is divided by expression with degree 3, then the degree of the quotient is 2.
The value of quadratic polynomial f (x)=2x2– 3x- 2 at x =-2 is ……- a)12
- b)15
- c)-12
- d)16
Correct answer is option 'A'. Can you explain this answer?
The value of quadratic polynomial f (x)=2x2– 3x- 2 at x =-2 is ……
a)
12
b)
15
c)
-12
d)
16
|
|
Amit Kumar answered |
We put the value x=-2 in the polynomial 2x2-3x-2
f(-2)=2(-2)2-3(-2)-2=2*4+6-2=12
f(-2)=2(-2)2-3(-2)-2=2*4+6-2=12
The number of polynomials having zeroes -2 and 5 is:- a)1
- b)3
- c)2
- d)more than 3
Correct answer is option 'D'. Can you explain this answer?
The number of polynomials having zeroes -2 and 5 is:
a)
1
b)
3
c)
2
d)
more than 3
|
|
Amit Kumar answered |
Since the question doesn’t say that there are only 2 zeros of the polynomial we , there can be n number of polynomials which have two of its zeros as -2 and 5 .So the correct answer is more than 3.
The number of polynomials having zeroes as -2 and 5 is:- a)1
- b)2
- c)3
- d)More than 3
Correct answer is option 'D'. Can you explain this answer?
The number of polynomials having zeroes as -2 and 5 is:
a)
1
b)
2
c)
3
d)
More than 3
|
Kamna Science Academy answered |
The polynomials x2-3x-10, 2x2-6x-20, (1/2)x2-(3/2)x-5, 3x2-9x-30, have zeroes as -2 and 5.
The expression that should be subtracted from the polynomial f(x) = x4 + 2x3-13x2 – 12x + 21 so that the resulting polynomial is exactly divisible by g(x) = x2 – 4x + 3 is- a)x2 – 3
- b)2x – 3
- c)x – 4
- d)x2 + 4
Correct answer is option 'B'. Can you explain this answer?
The expression that should be subtracted from the polynomial f(x) = x4 + 2x3-13x2 – 12x + 21 so that the resulting polynomial is exactly divisible by g(x) = x2 – 4x + 3 is
a)
x2 – 3
b)
2x – 3
c)
x – 4
d)
x2 + 4
|
|
Rahul Kapoor answered |
Any division statement can be rewritten in the form of
Dividend = Divisor x Quotient + Remainder.
When the remainder is zero, the dividend is said to be the multiple of the divisor.
When the remainder is not equal to zero, and if it is subtracted from the dividend, then the dividend would become a multiple of divisor.
Dividend = x^4+2x^3-13x^2-12x+21
Divisor = x^2-4x+3
Step 1: Divide the dividend by divisor
Quotient = x^2+6x+8
Remainder = 2x – 3
Step 2: Hence, on subtracting 2x – 3 from the dividend, it will be exactly divisible by the given divisor.
Verification:
On subtracting 2x – 3 from the dividend, we get
x^4+2x^3-13x^2-12x+21-(2x-3) = x^4+2x^3-13x^2-14x+24
Dividing x^4+2x^3-13x^2-14x+24 by x^2-4x+3
Quotient = x^2+6x+8
Remainder = 0
If sum of the zeroes of the polynomial is 4 and their product is 4, then the quadratic polynomial is- a)x2 – 2x + 2
- b)x2 – 4x + 4
- c)x2 + 4x + 4
- d)x2 + 2x + 2
Correct answer is option 'B'. Can you explain this answer?
If sum of the zeroes of the polynomial is 4 and their product is 4, then the quadratic polynomial is
a)
x2 – 2x + 2
b)
x2 – 4x + 4
c)
x2 + 4x + 4
d)
x2 + 2x + 2
|
|
Naina Sharma answered |
Sum of zeros= α+β =4
Product of zeros=αβ=4
We have Quadratic equation as
x2-(Sum of zeros)x+Product of zeros
=x2-4x+4
Product of zeros=αβ=4
We have Quadratic equation as
x2-(Sum of zeros)x+Product of zeros
=x2-4x+4
If the point (5,0) , (0-2) and (3,6) lie on the graph of a polynomial . Then which of the following is a zero of the polynomial?- a)5
- b)6
- c)not defined
- d)-2
Correct answer is option 'A'. Can you explain this answer?
If the point (5,0) , (0-2) and (3,6) lie on the graph of a polynomial . Then which of the following is a zero of the polynomial?
a)
5
b)
6
c)
not defined
d)
-2
|
Sanaya sharma answered |
Explanation:
Since, a zero of a polynomial always lies on the x-axis as a point. In the given question the point (5,0) is a point that lies on x-axis, so its corresponding x value represents zero of the polynomial.
Therefore, 5 is the zero of the polynomial.
Hence, the correct option is A.
You can know more about Geometrical Meaning of the Zeroes of a Polynomial through the document:
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :- a) x2 + 3x – 2
- b)x2 – 2x + 3
- c)x2 – 3x + 2
- d)x2 – 3x – 2
Correct answer is 'C'. Can you explain this answer?
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :
a)
x2 + 3x – 2
b)
x2 – 2x + 3
c)
x2 – 3x + 2
d)
x2 – 3x – 2
|
|
Pooja Shah answered |
Sum of zeros = 3/1
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
If sum of the squares of zeros of the quadratic polynomial f(x) = x2 – 8x + k is 40, find the value of k.- a)12
- b)-12
- c)14
- d)-14
Correct answer is option 'A'. Can you explain this answer?
If sum of the squares of zeros of the quadratic polynomial f(x) = x2 – 8x + k is 40, find the value of k.
a)
12
b)
-12
c)
14
d)
-14
|
|
Shantala nair answered |
p (x)= x^2-8x+k
p (x)=Ax^2+Bx+C(The equation is in this form)
p (x)=Ax^2+Bx+C(The equation is in this form)
Let the zeroes be 'a' and 'b'
It is given that
=> a^2+b^2=40
=> (a+b)^2 - 2ab = 40 ----1
=> a^2+b^2=40
=> (a+b)^2 - 2ab = 40 ----1
sum of zeroes
=> a+b = -B/A = -(-8)/1 = 8
=> a+b = -B/A = -(-8)/1 = 8
Product of zeroes
=> a*b = C/A = k
=> a*b = C/A = k
Substitute these values in the equation1 we get
=> 8^2 - 2k = 40
=> 64 - 2k = 40
=> 2k = 24
=> k = 12
=> 8^2 - 2k = 40
=> 64 - 2k = 40
=> 2k = 24
=> k = 12
Therefore the value of k is 12
If -√5 and √5 are the roots of the quadratic polynomial. Find the quadratic polynomial.- a)x-5
- b)(x-5)(x+5)
- c)x2 – 5
- d)x2 – 25
Correct answer is option 'C'. Can you explain this answer?
If -√5 and √5 are the roots of the quadratic polynomial. Find the quadratic polynomial.
a)
x-5
b)
(x-5)(x+5)
c)
x2 – 5
d)
x2 – 25
|
|
Vikram Kapoor answered |
We have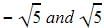 
as the roots which means x + 
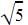and x- 
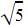are the factors of the quadratic equation. Multiplying x+ 
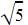and x- 
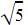and applying a2-b2 we get the equation x2-5.
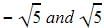as the roots which means x + 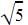and x- 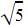are the factors of the quadratic equation. Multiplying x+ 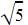and x- 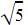and applying a2-b2 we get the equation x2-5.If one zero of 2x2 – 3x + k is reciprocal to the other, then the value of k is :- a)2
- b)-2/3
- c)-3
- d)-3/2
Correct answer is option 'A'. Can you explain this answer?
If one zero of 2x2 – 3x + k is reciprocal to the other, then the value of k is :
a)
2
b)
-2/3
c)
-3
d)
-3/2
|
|
Rajiv Gupta answered |
Given: 2x^2-3x+k ....eq 1
Let the 2 zeroes be α & 1/α
Quadratic form : ax^2+bx+c....eq 2
On comparing eq 1 & eq 2 we get
a=2 ,b = -3, c= k
Product of zeroes = α x 1/α = 1
Product of zeroes= c/a
1= k/ 2
K= 2
The value of k is 2.
Sum and the product of zeroes of the polynomial x2 +7x +10 is - a)10/7 and -10/7
- b)7/10 and -7/10
- c)-7 and 10
- d)7 and -10
Correct answer is option 'C'. Can you explain this answer?
Sum and the product of zeroes of the polynomial x2 +7x +10 is
a)
10/7 and -10/7
b)
7/10 and -7/10
c)
-7 and 10
d)
7 and -10
|
|
Ananya Das answered |
x2 + 7x + 10 = (x + 2)(x + 5)
So, the value of x2 + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0
Therefore, the zeroes of x2 + 7x + 10 are –2 and –5.
Sum of zeroes = -7 = –(Coefficient of x) / (Coefficient of x2)
Product of zeroes = 10 = Constant term / Coefficient of x2
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =- a)- 2
- b)- 1
- c)1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =
a)
- 2
b)
- 1
c)
1
d)
None of these
|
|
Naina Sharma answered |
P(x) = 2x² + 5x + 1
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
Direction: Read the following text and answer the following questions on the basis of the same:
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.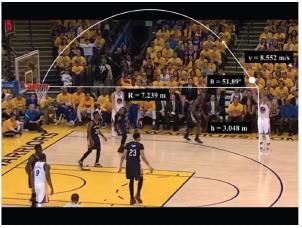
Observe the following graph and answer
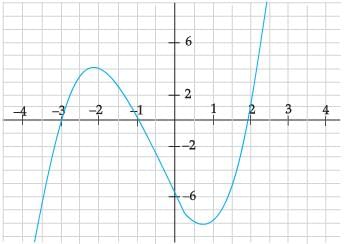In the above graph, how many zeroes are there for the polynomial?- a)0
- b)1
- c)2
- d)3
Correct answer is option 'D'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.
Observe the following graph and answer
In the above graph, how many zeroes are there for the polynomial?
a)
0
b)
1
c)
2
d)
3
|
|
Amit Sharma answered |
The number of zeroes of polynomial is the number of times the curve intersects the x-axis, i.e. attains the value 0.
Here, the polynomial meets the x-axis at 3 points.
So, number of zeroes = 3.
Here, the polynomial meets the x-axis at 3 points.
So, number of zeroes = 3.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion: The sum and product of the zeros of a quadratic polynomial are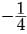 
and 1/4 respectively.Then the quadratic polynomial is 4x2 + x + 1.Reason : The quadratic polynomial whose sum and product of zeros are given is x2-(sum of zeros). x + product of zeros.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: The sum and product of the zeros of a quadratic polynomial are 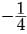and 1/4 respectively.
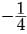and 1/4 respectively.Then the quadratic polynomial is 4x2 + x + 1.
Reason : The quadratic polynomial whose sum and product of zeros are given is x2-(sum of zeros). x + product of zeros.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
EduRev Class 9 answered |
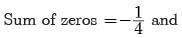
product of zeros = 1/4
Quadratic polynomial be 4x2 + x + 1. So, both A and R are correct and R explains A.
Find the sum and the product of zeroes of the polynomial x2 +7x +10- a)7,-10
- b)7, 10
- c)-7,-10
- d)-7, 10
Correct answer is option 'D'. Can you explain this answer?
Find the sum and the product of zeroes of the polynomial x2 +7x +10
a)
7,-10
b)
7, 10
c)
-7,-10
d)
-7, 10
|
|
Maitri Kulkarni answered |
x2 + 7x + 10 = (x + 2)(x + 5)
So, the value of x2 + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0
Therefore, the zeroes of x2 + 7x + 10 are –2 and –5.
Sum of zeroes = -7 = –(Coefficient of x) / (Coefficient of x2)
Product of zeroes = 10 = Constant term / Coefficient of x2
If α , β are the zeroes of f(x) = px2 – 2x + 3p and α + β = αβ then the value of p is:- a)1/3
- b)-2/3
- c)2/3
- d)-1/3
Correct answer is option 'C'. Can you explain this answer?
If α , β are the zeroes of f(x) = px2 – 2x + 3p and α + β = αβ then the value of p is:
a)
1/3
b)
-2/3
c)
2/3
d)
-1/3
|
|
Ananya Das answered |
The given polynomial is
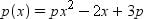
Also, α and β are the zeros of p(x).
and α + β = α × β
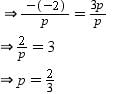
If f(x) is divided by g(x), g(x) ≠ 0, then there exist two polynomials q(x) and r(x) such that- a)r(x) = f(x) g(x) + q(x)
- b)q(x) = f(x) g(x) – r(x)
- c)g(x) = f(x) q (x) + r (x)
- d)f(x) = g (x) q (x) + r (x)
Correct answer is option 'D'. Can you explain this answer?
If f(x) is divided by g(x), g(x) ≠ 0, then there exist two polynomials q(x) and r(x) such that
a)
r(x) = f(x) g(x) + q(x)
b)
q(x) = f(x) g(x) – r(x)
c)
g(x) = f(x) q (x) + r (x)
d)
f(x) = g (x) q (x) + r (x)
|
|
Ananya Das answered |
Dividend = Divisor × Quotient + Remainder.
When we divide f(x) by g(x) then q(x) is quotient and r(x) is remainder.
Therefore, f(x) = g(x) × q(x) + r(x).
When we divide f(x) by g(x) then q(x) is quotient and r(x) is remainder.
Therefore, f(x) = g(x) × q(x) + r(x).
If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:- a)14/25
- b)7/5
- c)2/5
- d)7/2
Correct answer is 'D'. Can you explain this answer?
If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:
a)
14/25
b)
7/5
c)
2/5
d)
7/2
|
Anisha Mukherjee answered |
We have 2 find (1/α + 1/β)
now 1/α + 1/β = (α + β)/ α β (taking LCM)
now by the given poly. we get
(α + β) = -b/a = 7/5
α β = c/a = 2/5
so, (α + β)/ α β = (7/5) / (2/5)
= 7/2
So, 1/α + 1/β = (α + β)/ α β = 7/2
Hence, 1/α + 1/β = 7/2
Assertion (A): A polynomial of degree n cannot have more than n terms.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.- a)Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
- c)The assertion is correct, but the Reason is incorrect.
- d)Assertion is incorrect, but Reason is correct.
Correct answer is option 'D'. Can you explain this answer?
Assertion (A): A polynomial of degree n cannot have more than n terms.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.
a)
Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
c)
The assertion is correct, but the Reason is incorrect.
d)
Assertion is incorrect, but Reason is correct.
|
Khusboo shah answered |
Understanding the Assertion and Reason
The assertion (A) states that a polynomial of degree n cannot have more than n terms. The reason (R) states that the number of coefficients in a polynomial is always one more than its degree. Let's break down these statements.
Assertion (A): Analysis
- A polynomial of degree n is defined as a mathematical expression of the form:
- a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0
- The degree of a polynomial is determined by the highest power of the variable x.
- A polynomial can indeed have fewer than n terms (e.g., x^n + x^2 has 2 terms but is still degree n).
- Therefore, the assertion is incorrect as a polynomial can have more than n terms, as long as terms are combined appropriately.
Reason (R): Analysis
- The reason correctly states that the number of coefficients in a polynomial is always one more than its degree.
- This is because each term has a coefficient, including the constant term (a_0).
- For example, a polynomial of degree 3 (like x^3 + 2x^2 + 3x + 4) has 4 coefficients (a_3, a_2, a_1, and a_0).
Conclusion
- The assertion is incorrect, but the reason is correct.
- Thus, the correct option is D: Assertion is incorrect, but Reason is correct.
This analysis highlights the importance of understanding polynomials and their properties in mathematics.
The assertion (A) states that a polynomial of degree n cannot have more than n terms. The reason (R) states that the number of coefficients in a polynomial is always one more than its degree. Let's break down these statements.
Assertion (A): Analysis
- A polynomial of degree n is defined as a mathematical expression of the form:
- a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0
- The degree of a polynomial is determined by the highest power of the variable x.
- A polynomial can indeed have fewer than n terms (e.g., x^n + x^2 has 2 terms but is still degree n).
- Therefore, the assertion is incorrect as a polynomial can have more than n terms, as long as terms are combined appropriately.
Reason (R): Analysis
- The reason correctly states that the number of coefficients in a polynomial is always one more than its degree.
- This is because each term has a coefficient, including the constant term (a_0).
- For example, a polynomial of degree 3 (like x^3 + 2x^2 + 3x + 4) has 4 coefficients (a_3, a_2, a_1, and a_0).
Conclusion
- The assertion is incorrect, but the reason is correct.
- Thus, the correct option is D: Assertion is incorrect, but Reason is correct.
This analysis highlights the importance of understanding polynomials and their properties in mathematics.
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –- a)x2 + 2x + 3
- b)x2 – 5x + 3
- c)x2 + 5x + 3
- d)x2 + 3x – 5
Correct answer is option 'C'. Can you explain this answer?
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –
a)
x2 + 2x + 3
b)
x2 – 5x + 3
c)
x2 + 5x + 3
d)
x2 + 3x – 5
|
|
Bhaskar Dasgupta answered |
If α, β be the zeros of the quadratic polynomial ,then
(x−α)(x−β) is the quadratic polynomial.
Thus, (x−α)(x−β) is the polynomial.
=x^2−αx−βx+αβ
=x^2−x(α+β)+αβ(i)
(α+β)=−5αβ=3
Now putting the value of (α+β),αβ in equation (i) we get,
x^2−x(−5)+3
=x^2+5x+3
Chapter doubts & questions for Polynomials - Mathematics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polynomials - Mathematics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Mathematics for EmSAT Achieve
146 videos|222 docs|220 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily