All Exams >
EmSAT Achieve >
Mathematics for EmSAT Achieve >
All Questions
All questions of Similarity Theorems for EmSAT Achieve Exam
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion : In ∆ABC , DE|| BC such that AD = (7x - 4)cm, AE = (5 - 2)cm, DB = (3 + 4) cm and EC = 3 cm than x equal to 5.Reason : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distant point, than the other two sides are divided in the same ratio.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'D'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : In ∆ABC , DE|| BC such that AD = (7x - 4)cm, AE = (5 - 2)cm, DB = (3 + 4) cm and EC = 3 cm than x equal to 5.
Reason : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distant point, than the other two sides are divided in the same ratio.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Meera Rana answered |
We have,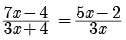
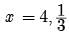
AD/DB = AE/EC
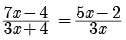
21x2 - 12x = 15x2 + 20x - 6x - 8x
6x2 - 26x + 8 = 0
3x2 - 13x + 4 = 0
3x2 - 12x - x + 4 = 0
3x(x - 4) - 1(x - 4) = 0
(x - 4) (3x - 1) = 0
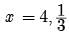
So, A is incorrect but R is correct.
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.Assertion (A): Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, then the area of the larger triangle is 108 cm2.Reason (R): If D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC, then CA2 = CB × CD.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2, then the area of the larger triangle is 108 cm2.
Reason (R): If D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC, then CA2 = CB × CD.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
Krishna Iyer answered |
In case of assertion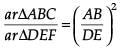
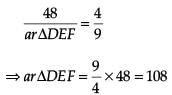
Let ΔABC and ΔDEF are two similar triangles.
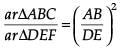
Given that ar ΔABC = 48 cm2. Then,
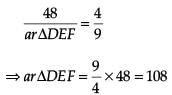
Thus, the area of larger triangle is 108 cm2.
∴ Assertion is correct.
In case of reason:
In ΔBAC and ΔADC,
∠BAC= ∠ADC [Given]
∠BCA= ∠ACD [Common angle]
By AA similarity, ΔBAC ~ ΔADC
Thus,
CA/CD = BC/CA
∴ Reason is correct.
Hence, both assertion and reason are correct but reason is not the correct explanation for assertion.
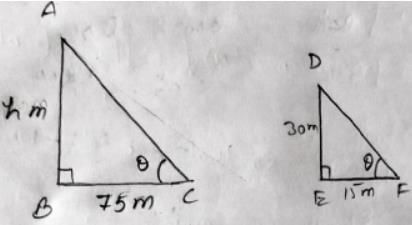
If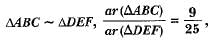 
BC = 21 cm, then EF is equal to- a)9 cm
- b)6 cm
- c)35 cm
- d)25 cm
Correct answer is option 'C'. Can you explain this answer?
If 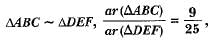BC = 21 cm, then EF is equal to
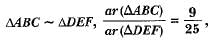BC = 21 cm, then EF is equal toa)
9 cm
b)
6 cm
c)
35 cm
d)
25 cm
|
Imk Pathshala answered |
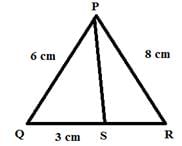
Since, PS is the angle bisector of angle QPR
So, by angle bisector theorem,
QS/SR = PQ/PR
⇒ 3/SR = 6/8
⇒ SR = (3 X 8)/6 cm = 4 cm
It is given that ar(ΔABC) = 81 square units and ar(ΔDEF) = 64 square units. If ΔABC ~ ΔDEF, then- a)AB/DE = 81/64
- b)
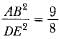
- c)AB/DE = 9/8
- d)AB = 81 units, DE = 64 units
Correct answer is option 'C'. Can you explain this answer?
It is given that ar(ΔABC) = 81 square units and ar(ΔDEF) = 64 square units. If ΔABC ~ ΔDEF, then
a)
AB/DE = 81/64
b)
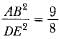
c)
AB/DE = 9/8
d)
AB = 81 units, DE = 64 units
|
|
Imk Pathshala answered |
In triangle ACB and ADC
∠A=∠A
∠ACB = ∠CDA
Therefore triangle ACB and ADC are similar,
Hence
AC/AD = AB/AC
AC2 = AD X AB
82 = 3 x AB
⇒ AB = 64/3
This implies,
BD = 64/3 – AD
⇒ BD = 55/3
∠A=∠A
∠ACB = ∠CDA
Therefore triangle ACB and ADC are similar,
Hence
AC/AD = AB/AC
AC2 = AD X AB
82 = 3 x AB
⇒ AB = 64/3
This implies,
BD = 64/3 – AD
⇒ BD = 55/3
Which geometric figures are always similar?- a)Circles
- b)Circles and all regular polygons
- c)Circles and triangles
- d)Regular polygons
Correct answer is option 'B'. Can you explain this answer?
Which geometric figures are always similar?
a)
Circles
b)
Circles and all regular polygons
c)
Circles and triangles
d)
Regular polygons
|
Raghav Bansal answered |
It can be found that circles map one onto another.So they are similar figures. A regular polygon is a polygon which has the same sides and equal measures of angles. So they are also similar.
QM ⊥ RP and PR2 – PQ2 = OR2 . If∠QPM = 30° , Then ∠MQR is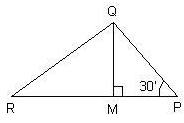
- a)45°
- b)60°
- c)90°
- d)30°
Correct answer is option 'D'. Can you explain this answer?
QM ⊥ RP and PR2 – PQ2 = OR2 . If∠QPM = 30° , Then ∠MQR is
a)
45°
b)
60°
c)
90°
d)
30°
|
|
Krishna Iyer answered |
In triangle PMQ
Angle M = 90°
Angle P = 30°
Angle QMP + Angle MPQ + Angle PQM = 180 degree ( By angle sum property )
90 + 30 + Angle PQM = 180
Angle PQM = 180 - 120
Angle PWM = 60 Degree
QM divides Angle PQR into two equal parts .
Therefore Angle MQR = 30°
Angle M = 90°
Angle P = 30°
Angle QMP + Angle MPQ + Angle PQM = 180 degree ( By angle sum property )
90 + 30 + Angle PQM = 180
Angle PQM = 180 - 120
Angle PWM = 60 Degree
QM divides Angle PQR into two equal parts .
Therefore Angle MQR = 30°
From the given figure, find the unknown x.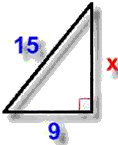
- a)12
- b)225
- c)10
- d)144
Correct answer is option 'A'. Can you explain this answer?
From the given figure, find the unknown x.
a)
12
b)
225
c)
10
d)
144
|
Ishan Choudhury answered |
Since the triangle is a right angled triangle,
Applying Pythagoras Theorem,
H2=P2+B2
152=P2+92
P2=225-81=144
P=12
Applying Pythagoras Theorem,
H2=P2+B2
152=P2+92
P2=225-81=144
P=12
In triangle ABC, if AB = 6√3 cm, AC = 12 cm and BC cm, then ∠B is - a)120°
- b)60°
- c)90°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
In triangle ABC, if AB = 6√3 cm, AC = 12 cm and BC cm, then ∠B is
a)
120°
b)
60°
c)
90°
d)
45°
|
Gaurav Kumar answered |
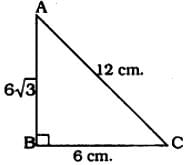
Here largest side is 12 cm.
If the square of the hypotenuse is equal to the square of the other two sides, then it is a right-angled triangle.
If the square of the hypotenuse is equal to the square of the other two sides, then it is a right-angled triangle.
∴ c2 = a2 + b2
AC2 = AB2 + BC2
(12)2 = (63)2 + (6)2
44 = 36 × 3 + 36
144 = 108 + 36
144 = 144
∴ ∆ABC is a right angled triangle and angle opposite to hypotenuse, ∠B = 90°.
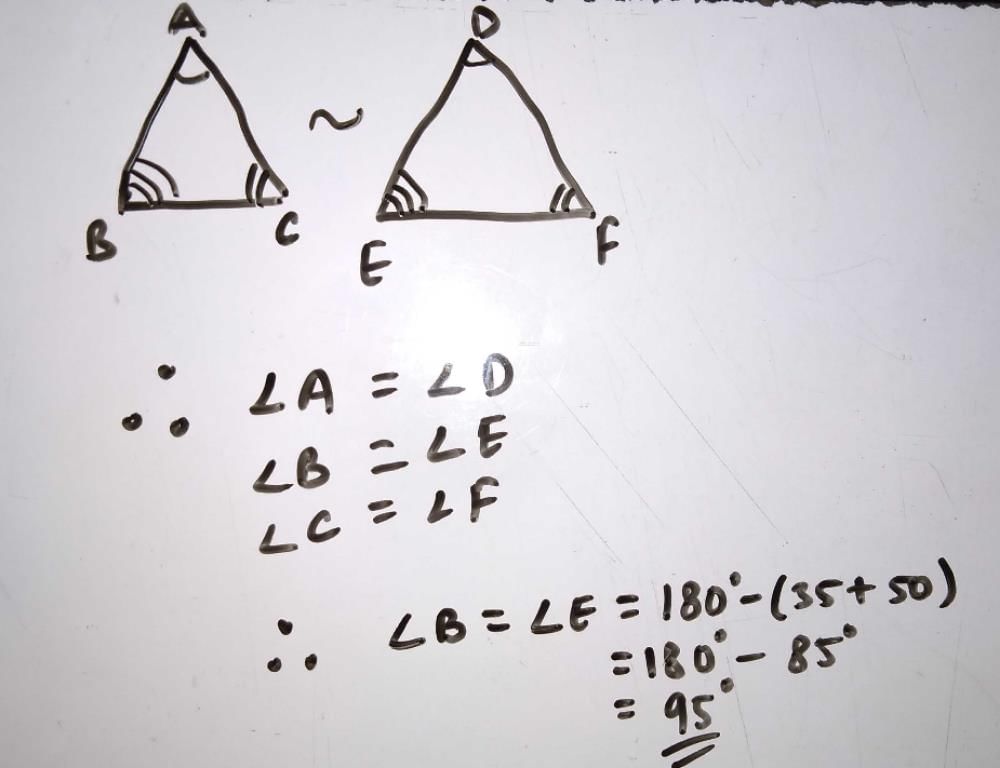
ΔABC ~ ΔPQR, ∠B = 50° and ∠C = 70° then ∠P is equal to- a)50°
- b)60°
- c)40°
- d)70°
Correct answer is option 'B'. Can you explain this answer?
ΔABC ~ ΔPQR, ∠B = 50° and ∠C = 70° then ∠P is equal to
a)
50°
b)
60°
c)
40°
d)
70°
|
|
Radha Iyer answered |
Similar triangles have corresponding angles equal. So Angle Q=Angle B = 50° and Angle R = Angle C = 70° . So by angle sum property, Angle P+Angle Q +Angle R = 180°
Angle P=180° - 50° - 70° = 60°
Angle P=180° - 50° - 70° = 60°
Which pair of the given quadrilaterals is similar?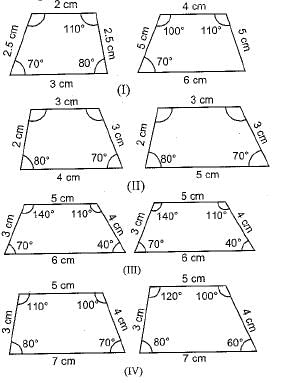
a)I only
b)III onlyc)I and IIId)IVCorrect answer is option 'C'. Can you explain this answer?
|
Naina Sharma answered |
Quadrilaterals are similar if their angles are equal and corresponding sides are proportional.
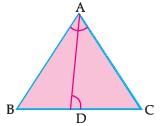
In an equilateral triangle ABC, if AD ⊥ BC. Then- a)3AB2 = 4AD2
- b)2AB2 = 3AD2
- c)3AB2 = 2AD2
- d)4AB2 = 3AD2
Correct answer is option 'A'. Can you explain this answer?
In an equilateral triangle ABC, if AD ⊥ BC. Then
a)
3AB2 = 4AD2
b)
2AB2 = 3AD2
c)
3AB2 = 2AD2
d)
4AB2 = 3AD2
|
|
Raghav Bansal answered |
∆ ABC, in which sides are AB=BC= AC= a units and AD is perpendicular to BC ,
In ∆ADB ,
AB²= AD²+ BD² (by Pythagoras theorem)
a² = AD² + (a/2)² [BD= 1/2BC, since in an equilateral triangle altitude AD is perpendicular bisector of BC ]
a²- a²/4 =AD²
⇒ ( 4a²-a²)/4 = AD²
⇒ 3a² /4 = AD²
⇒ 3AB²/4= AD² [ AB= a]
⇒ 3AB²= 4AD²
What is the diagonal length of a TV screen whose dimensions are 80 x 60 cm?- a)10
- b)100
- c)20
- d)1000
Correct answer is option 'B'. Can you explain this answer?
What is the diagonal length of a TV screen whose dimensions are 80 x 60 cm?
a)
10
b)
100
c)
20
d)
1000
|
Pooja Shah answered |
We have a TV which is a rectangle whose adjacent sides form an angle of 90 degrees so The triangle formed by the two sides and a diagonal will be a right angle. So, Applying Pythagoras Theorem,
(Diagonal)2=802+602=6400+3600=10000
Diagonal=100cm
(Diagonal)2=802+602=6400+3600=10000
Diagonal=100cm
Two congruent triangles are actually similar triangles with the ratio of corresponding sides as.- a)1:2
- b)1:1
- c)1:3
- d)2:1
Correct answer is option 'B'. Can you explain this answer?
Two congruent triangles are actually similar triangles with the ratio of corresponding sides as.
a)
1:2
b)
1:1
c)
1:3
d)
2:1
|
|
Pushkar tiwari answered |
Similar Triangles and Corresponding Sides
Similar triangles are those triangles that have the same shape but may have different sizes. When two triangles are similar, the corresponding angles are the same, and the corresponding sides are proportional. In other words, the ratio of the lengths of the corresponding sides is the same for all pairs of corresponding sides. This ratio is called the scale factor.
Given the statement that "Two congruent triangles are actually similar triangles with the ratio of corresponding sides as," we are asked to determine the scale factor for the corresponding sides of the two triangles.
Option B is the correct answer, and the scale factor is 1:1. This means that the corresponding sides of the two triangles are equal in length.
Explanation of Other Options:
a) 1:2 - This means that the corresponding sides of one triangle are twice as long as the corresponding sides of the other triangle. Therefore, the triangles are not congruent, but they are similar.
c) 1:3 - This means that the corresponding sides of one triangle are three times as long as the corresponding sides of the other triangle. Therefore, the triangles are not congruent, but they are similar.
d) 2:1 - This means that the corresponding sides of one triangle are half as long as the corresponding sides of the other triangle. Therefore, the triangles are not congruent, but they are similar.
Conclusion:
In summary, when two triangles are congruent, they are also similar with a scale factor of 1:1. This means that the corresponding sides of the triangles are equal in length.
Similar triangles are those triangles that have the same shape but may have different sizes. When two triangles are similar, the corresponding angles are the same, and the corresponding sides are proportional. In other words, the ratio of the lengths of the corresponding sides is the same for all pairs of corresponding sides. This ratio is called the scale factor.
Given the statement that "Two congruent triangles are actually similar triangles with the ratio of corresponding sides as," we are asked to determine the scale factor for the corresponding sides of the two triangles.
Option B is the correct answer, and the scale factor is 1:1. This means that the corresponding sides of the two triangles are equal in length.
Explanation of Other Options:
a) 1:2 - This means that the corresponding sides of one triangle are twice as long as the corresponding sides of the other triangle. Therefore, the triangles are not congruent, but they are similar.
c) 1:3 - This means that the corresponding sides of one triangle are three times as long as the corresponding sides of the other triangle. Therefore, the triangles are not congruent, but they are similar.
d) 2:1 - This means that the corresponding sides of one triangle are half as long as the corresponding sides of the other triangle. Therefore, the triangles are not congruent, but they are similar.
Conclusion:
In summary, when two triangles are congruent, they are also similar with a scale factor of 1:1. This means that the corresponding sides of the triangles are equal in length.
In the following figure, find the value of x.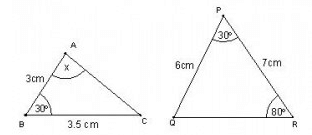
- a)65°
- b)70°
- c)80°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
In the following figure, find the value of x.
a)
65°
b)
70°
c)
80°
d)
30°
|
Ashwani Mishra answered |
The triangles are similar by SAS criterion, So we have, Angle A+Angle B + Angle C=180
x=180-30-80=70 degrees
x=180-30-80=70 degrees
If ΔABC ~ ΔEDF then which of the following is not true?
- a)BC . EF = AC . FD
- b)AB . EF = AC . DE
- c)BC . DE = AB . EF
- d)BC . DE = AB . FD
Correct answer is option 'C'. Can you explain this answer?
If ΔABC ~ ΔEDF then which of the following is not true?
a)
BC . EF = AC . FD
b)
AB . EF = AC . DE
c)
BC . DE = AB . EF
d)
BC . DE = AB . FD
|
Anita Menon answered |
Since △ABC~△EDF
Then, AB/ED = BC/DF = AC/EF
A) BC/DF = AC/EF
⇒BC.EF=AC.FD
So, A) is true
B) AB/ED = AC/EF
⇒AB.EF=AC.DE
So,B) is true
D) AB/ED = BC/DF
BC.DE=AB.EF
So, D) is not true
Therefore, Option C is not true
In the given figure use the similarity of the given triangles to find the value of BD, ΔABC ~ ΔBDC = 90° AB=3, BC=4,AD=2 BD=?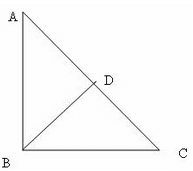
- a)6
- b)10
- c)8/3
- d)5
Correct answer is option 'C'. Can you explain this answer?
In the given figure use the similarity of the given triangles to find the value of BD, ΔABC ~ ΔBDC = 90° AB=3, BC=4,AD=2 BD=?
a)
6
b)
10
c)
8/3
d)
5
|
|
Gaurav Kumar answered |
Solution :
The correct option is Option C.
∆ ABC ~ ∆ BDC = AD/AB = BD/BC = ⅔ = BD/4 = BD = 8/3
In the figure given below, if DE || BC, then x equals :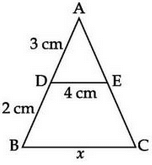
- a)2 cm
- b)4 cm
- c)6.7 cm
- d)3 cm
Correct answer is option 'C'. Can you explain this answer?
In the figure given below, if DE || BC, then x equals :
a)
2 cm
b)
4 cm
c)
6.7 cm
d)
3 cm
|
|
Pooja Shah answered |
We have Angle ADE= Angle ABC
And ANGLE A is common, So by AA criterion of similarity the two triangles are similar so AD/AB=DE/BC
x=5*4/3=6.7
And ANGLE A is common, So by AA criterion of similarity the two triangles are similar so AD/AB=DE/BC
x=5*4/3=6.7
In a triangle ABC, AC= √180 ,AB=6 ,BC=12 .What is ∠B = ?- a)90°
- b)30°
- c)45°
- d)60°
Correct answer is option 'A'. Can you explain this answer?
In a triangle ABC, AC= √180 ,AB=6 ,BC=12 .What is ∠B = ?
a)
90°
b)
30°
c)
45°
d)
60°
|
|
Naina Sharma answered |
We have AB2=36 and BC2=144
Adding both the squares we get
AB2+BC2=36+144=180
=AC2
So , AC is the hypotenuse according to pythagoras theorem , So the angle opposite to it which is B is 90 degrees.
Adding both the squares we get
AB2+BC2=36+144=180
=AC2
So , AC is the hypotenuse according to pythagoras theorem , So the angle opposite to it which is B is 90 degrees.
If ΔPQR ~ ΔXYZ , ∠Q = 50° , ∠R = 70° then ∠X is equal to :- a)50°
- b)60°
- c)70°
- d)120°
Correct answer is option 'B'. Can you explain this answer?
If ΔPQR ~ ΔXYZ , ∠Q = 50° , ∠R = 70° then ∠X is equal to :
a)
50°
b)
60°
c)
70°
d)
120°
|
Yogita Rishi answered |
Angle Q = 50
Angle R= 70
Angle p = ?
now
we know that the angle sum property of a triangle is equal to 180 degree
Angle Q + angle R+ angle P = 180
50 + 70 + angle P = 180
120 + angle P = 180
angle P = 180 - 120
-Angle p = 60
as they both are similar so by corresponding parts of similar triangle
Angle P = Angle X
Angle x = 60....
Angle R= 70
Angle p = ?
now
we know that the angle sum property of a triangle is equal to 180 degree
Angle Q + angle R+ angle P = 180
50 + 70 + angle P = 180
120 + angle P = 180
angle P = 180 - 120
-Angle p = 60
as they both are similar so by corresponding parts of similar triangle
Angle P = Angle X
Angle x = 60....
If ΔDEF ~ ΔABC and DE=AB, what is the relation between the two triangles?- a)They are both right triangles.
- b)ΔDEF ≠ ΔABC
- c)They are both equilateral.
- d)ΔDEF ≅ ΔABC
Correct answer is option 'D'. Can you explain this answer?
If ΔDEF ~ ΔABC and DE=AB, what is the relation between the two triangles?
a)
They are both right triangles.
b)
ΔDEF ≠ ΔABC
c)
They are both equilateral.
d)
ΔDEF ≅ ΔABC
|
|
Naina Sharma answered |
Since DE=AB means that there ratio is 1 which means corresponding sides are equal.Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion . In other words, similar triangles are the same shape, but not necessarily the same size. The triangles are congruent if, in addition to this, their corresponding sides are of equal length.So they are congruent.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are- a)congruent but not similar
- b)similar but not congruent
- c)neither congruent nor similar
- d)congruent as well as similar
Correct answer is option 'B'. Can you explain this answer?
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are
a)
congruent but not similar
b)
similar but not congruent
c)
neither congruent nor similar
d)
congruent as well as similar
|
|
Kiran Mehta answered |
to be congruent, the conditions are
S S S - three sides
S A S - two sides and the included angle
A S A - two angles and one side
R H S - R H S - Right angle, Hypotenuse and one side
But to be similar,
A A A means 3 angles
A A means only two angles ....
in both triangles should be equal.
In the problem, equality of two angles is given, but equality of sides is not given.
So, given triangles are not congruent.
But they are similar.
S S S - three sides
S A S - two sides and the included angle
A S A - two angles and one side
R H S - R H S - Right angle, Hypotenuse and one side
But to be similar,
A A A means 3 angles
A A means only two angles ....
in both triangles should be equal.
In the problem, equality of two angles is given, but equality of sides is not given.
So, given triangles are not congruent.
But they are similar.
=?
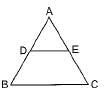
In the given figure, AD/BD = AE/EC and ∠ADE = 70°, ∠BAC = 50°, then angle ∠BCA =
- a)70°
- b)50°
- c)80°
- d)60°
Correct answer is option 'D'. Can you explain this answer?
In the given figure, AD/BD = AE/EC and ∠ADE = 70°, ∠BAC = 50°, then angle ∠BCA =
a)
70°
b)
50°
c)
80°
d)
60°
|
|
Trisha sharma answered |
Explanation: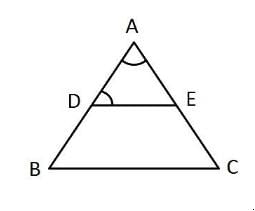
By converse of Thale’s theorem DE II BC
∠ADE = ∠ABC = 70 degree
Given ∠BAC = 50 degree
You can read Important Definitions & Formulas related to Triangles through the document:
In similar triangles ABC and DEF,AG and DH are the medians. What is the value of 
given that 
- a)3/8
- b)1.5/4
- c)50/128
- d)5/8
Correct answer is option 'D'. Can you explain this answer?
In similar triangles ABC and DEF,AG and DH are the medians. What is the value of given that
given that a)
3/8
b)
1.5/4
c)
50/128
d)
5/8
|
Sobha Goswami answered |
Because through the formula of median
In ΔLMN and ΔPQR, ∠L = ∠P, ∠N = ∠R and MN = 2QR. Then the two triangles are- a)Congruent but not similar
- b)Similar but not congruent
- c)neither congruent nor similar
- d)Congrunt as well as similar
Correct answer is option 'B'. Can you explain this answer?
In ΔLMN and ΔPQR, ∠L = ∠P, ∠N = ∠R and MN = 2QR. Then the two triangles are
a)
Congruent but not similar
b)
Similar but not congruent
c)
neither congruent nor similar
d)
Congrunt as well as similar
|
EduRev Class 10 answered |
According to question,
ΔABC ~ ΔDEF,
AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm,
Therefore,
AB/DE = BC/EF = AC/DF
4/6 = BC/9 = AC/12
⇒ 4/6 = BC/9
⇒ BC = 6 cm
And
4/6 = AC/12
⇒ AC = 8 cm
Perimeter = AB + BC + CA
= 4 + 6 + 8
= 18 cm
ΔABC ~ ΔDEF,
AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm,
Therefore,
AB/DE = BC/EF = AC/DF
4/6 = BC/9 = AC/12
⇒ 4/6 = BC/9
⇒ BC = 6 cm
And
4/6 = AC/12
⇒ AC = 8 cm
Perimeter = AB + BC + CA
= 4 + 6 + 8
= 18 cm
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 3 cm, BD = 5 cm, BC = 12.8 cm and DE || BC. Then length of DE (in cm) is- a)4.8 cm
- b)7.6 cm
- c)19.2 cm
- d)2.5 cm
Correct answer is option 'A'. Can you explain this answer?
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 3 cm, BD = 5 cm, BC = 12.8 cm and DE || BC. Then length of DE (in cm) is
a)
4.8 cm
b)
7.6 cm
c)
19.2 cm
d)
2.5 cm
|
|
Meera Rana answered |
GIVEN: In Δ ABC, D and E are points on AB and AC , DE || BC and AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BE = 5 cm.
In Δ ADE and Δ ABC,
∠ADE =∠ABC (corresponding angles)
[DE || BC, AB is transversal]
∠AED =∠ACB (corresponding angles)
[DE || BC, AC is transversal]
So, Δ ADE ~ Δ ABC (AA similarity)
Therefore, AD/AB = AE/AC = DE/BC
[In similar triangles corresponding sides are proportional]
AD/AB = DE/BC
2.4/(2.4+DB) = 2/5
2.4 × 5 = 2(2.4+ DB)
12 = 4.8 + 2DB
12 - 4.8 = 2DB
7.2 = 2DB
DB = 7.2/2
DB = 3.6 cm
Similarly, AE/AC = DE/BC
3.2/(3.2+EC) = 2/5
3.2 × 5 = 2(3.2+EC)
16 = 6.4 + 2EC
16 - 6.4 = 2EC
9.6 = 2EC
EC = 9.6/2
EC = 4.8 cm
Hence,BD = 3.6 cm and CE = 4.8 cm.
In Δ ADE and Δ ABC,
∠ADE =∠ABC (corresponding angles)
[DE || BC, AB is transversal]
∠AED =∠ACB (corresponding angles)
[DE || BC, AC is transversal]
So, Δ ADE ~ Δ ABC (AA similarity)
Therefore, AD/AB = AE/AC = DE/BC
[In similar triangles corresponding sides are proportional]
AD/AB = DE/BC
2.4/(2.4+DB) = 2/5
2.4 × 5 = 2(2.4+ DB)
12 = 4.8 + 2DB
12 - 4.8 = 2DB
7.2 = 2DB
DB = 7.2/2
DB = 3.6 cm
Similarly, AE/AC = DE/BC
3.2/(3.2+EC) = 2/5
3.2 × 5 = 2(3.2+EC)
16 = 6.4 + 2EC
16 - 6.4 = 2EC
9.6 = 2EC
EC = 9.6/2
EC = 4.8 cm
Hence,BD = 3.6 cm and CE = 4.8 cm.
In the given figure perpendiculars are dropped on the common base BD of the given two triangles. AE = 2cm, CF = 3cm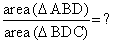 
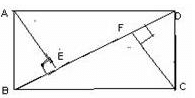
- a)1/3
- b)2/3
- c)4/9
- d)1/9
Correct answer is option 'B'. Can you explain this answer?
In the given figure perpendiculars are dropped on the common base BD of the given two triangles. AE = 2cm, CF = 3cm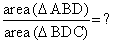
a)
1/3
b)
2/3
c)
4/9
d)
1/9
|
|
Gaurav Kumar answered |
Area of triangle = 1/2 *base*height
Area of ABD=1/2 *BD*2
Area of BDC=1/2*BD*3
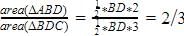
Area of ABD=1/2 *BD*2
Area of BDC=1/2*BD*3
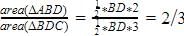
ΔABC ~ ΔDEF Perimeter( ΔABC )= 15 cm, Perimeter( DEF )=25 cm.If AB= 6 cm, then find DE.- a)14
- b)12
- c)10
- d)16
Correct answer is option 'C'. Can you explain this answer?
ΔABC ~ ΔDEF Perimeter( ΔABC )= 15 cm, Perimeter( DEF )=25 cm.If AB= 6 cm, then find DE.
a)
14
b)
12
c)
10
d)
16
|
|
Gaurav Kumar answered |
Ratios of perimeter of similar triangles are equal to the ratio of their sides.
So Perimeter of ABC/perimeter of DEF=15/25=⅗
AB/DE=⅗
DE=6*5/3=10
So Perimeter of ABC/perimeter of DEF=15/25=⅗
AB/DE=⅗
DE=6*5/3=10
In triangle MNS, A and B are points on the sides MN, NS respectively.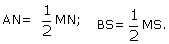 
Then AB is …………………. to NS :- a)Not Perpendicular
- b)Parallel
- c)Perpendicular
- d)Not Parallel
Correct answer is option 'B'. Can you explain this answer?
In triangle MNS, A and B are points on the sides MN, NS respectively. 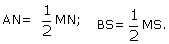Then AB is …………………. to NS :
Then AB is …………………. to NS :a)
Not Perpendicular
b)
Parallel
c)
Perpendicular
d)
Not Parallel
|
|
Anita Menon answered |
In ∆MNS we have,
→ AN = 1/2(MN)
→ AN = (1/2)(MA + AN)
→ AN = (1/2)MA + (1/2)AN
→ AN - (1/2)AN = (1/2)MA
→ AN[1 - (1/2)] = (1/2)MA
→ (1/2)AN = (1/2)MA
→ AN = MA
so, A is mid point of MN .
→ AN = (1/2)(MA + AN)
→ AN = (1/2)MA + (1/2)AN
→ AN - (1/2)AN = (1/2)MA
→ AN[1 - (1/2)] = (1/2)MA
→ (1/2)AN = (1/2)MA
→ AN = MA
so, A is mid point of MN .
similarly,
→ BS = (1/2)(MS)
→ BS = (1/2)(MS)
so, B is mid point of MS .
since AB is a line segment joining the mid points of two sides of ∆MNS .
therefore, → AB || NS { According to Mid point theorem the line segment joining the mid points of two sides of a triangle is parallel to the third side . }
Which of the following is a Pythagorean triplet ?- a)(36,18,43)
- b)(15,20,25)
- c)(3,12,13)
- d)(24,25,26)
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a Pythagorean triplet ?
a)
(36,18,43)
b)
(15,20,25)
c)
(3,12,13)
d)
(24,25,26)
|
Vikram Kapoor answered |
A Pythagorean triple consists of three positive integers a, b, and c, such that a² + b² = c².
a) 432 = 1849
362+182 = 1620
b) 252 = 625
152 + 202 =625
c) 132 = 169
32 + 122 = 153
d) 262 = 676
242 + 252 = 1201
so option b is correct
How far up a wall will an 11m ladder reach, if the foot of the ladder is 4m away from the wall?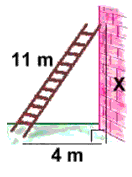
- a)121 m
- b)10 m
- c)10.2 m
- d)16 m
Correct answer is option 'C'. Can you explain this answer?
How far up a wall will an 11m ladder reach, if the foot of the ladder is 4m away from the wall?
a)
121 m
b)
10 m
c)
10.2 m
d)
16 m
|
|
Gaurav Kumar answered |
The height of wall will be the perpendicular for the right angle triangle. So applying pythagoras theorem
H2=P2+B2
11*11=P2+16
P=121-16=10.2 cm
H2=P2+B2
11*11=P2+16
P=121-16=10.2 cm
Which of the following cannot be the sides a right triangle?- a)400mm, 300 mm, 500mm
- b)9 cm, 15 cm, 12 cm
- c)2 cm, 1 cm, √5 cm
- d)9 cm, 5 cm, 7cm
Correct answer is option 'D'. Can you explain this answer?
Which of the following cannot be the sides a right triangle?
a)
400mm, 300 mm, 500mm
b)
9 cm, 15 cm, 12 cm
c)
2 cm, 1 cm, √5 cm
d)
9 cm, 5 cm, 7cm
|
|
Arun Sharma answered |
H2 = P2 + B2
H2 = 81
P2 + B2 = 25 + 49 = 74
H2 ≠ P2+B2.Therefore the sides cannot form a right triangle.
H2 = 81
P2 + B2 = 25 + 49 = 74
H2 ≠ P2+B2.Therefore the sides cannot form a right triangle.
If in triangles ABC and DEF, AB/EF = AC/DE, then they will be similar when- a)∠A = ∠D
- b)∠A = ∠E
- c)∠B = ∠E
- d)∠C = ∠F
Correct answer is option 'B'. Can you explain this answer?
If in triangles ABC and DEF, AB/EF = AC/DE, then they will be similar when
a)
∠A = ∠D
b)
∠A = ∠E
c)
∠B = ∠E
d)
∠C = ∠F
|
Crafty Classes answered |
The altitude divides the opposite side into two equal parts,
Therefore, BD = DC = 4 cm
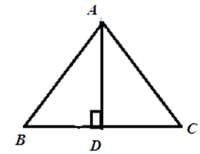
In triangle ABD
AB2 = AD2 + BD2
82 = AD2 + 42
AD2 = 64 – 16
AD2 = 48
AD = 4√3 cm
Therefore, BD = DC = 4 cm
In triangle ABD
AB2 = AD2 + BD2
82 = AD2 + 42
AD2 = 64 – 16
AD2 = 48
AD = 4√3 cm
The monitors of computers are measured along the diagonal. What is the size of the largest monitor that can be placed in a space measuring 17″ x 21″?- a)28″
- b)25″
- c)26″
- d)27″
Correct answer is option 'D'. Can you explain this answer?
The monitors of computers are measured along the diagonal. What is the size of the largest monitor that can be placed in a space measuring 17″ x 21″?
a)
28″
b)
25″
c)
26″
d)
27″
|
|
Kiran Mehta answered |
Since monitors are measured along the diagonals this means we need to use pythagoras theorem for this right angled triangle.
H2 = P2 + B2
=17 * 17 + 21 * 21
=289 + 441 = 730
H=27’’ (Approx)
H2 = P2 + B2
=17 * 17 + 21 * 21
=289 + 441 = 730
H=27’’ (Approx)
In the given figure ΔABC ~ ΔBDC = 90° each. Choose the correct similarity from the given choices.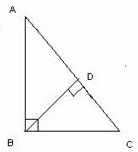
- a)ΔABC ~ ΔCBD
- b)ΔABC ~ ΔDCB
- c)ΔABC ~ ΔBCD
- d)ΔABC ~ ΔBDC
Correct answer is option 'D'. Can you explain this answer?
In the given figure ΔABC ~ ΔBDC = 90° each. Choose the correct similarity from the given choices.
a)
ΔABC ~ ΔCBD
b)
ΔABC ~ ΔDCB
c)
ΔABC ~ ΔBCD
d)
ΔABC ~ ΔBDC
|
|
Naina Sharma answered |
We have Angle C common and Angle B = Angle D
So in similarity we write the name of the triangle in such an order in which the corresponding alphabets denote equal angles . this means that ΔABC ~ ΔBDC that says Angle A = Angle B, Angle B = Angle D, and Angle C = Angle C
So in similarity we write the name of the triangle in such an order in which the corresponding alphabets denote equal angles . this means that ΔABC ~ ΔBDC that says Angle A = Angle B, Angle B = Angle D, and Angle C = Angle C
In right triangled ABC right angled at B ,a line DE is drawn through the mid point D of AB and parallel to BC.If AB=9 cm, BC=12 cm. AE=?- a)13 cm
- b)10 cm
- c)8.5 cm
- d)7.5 cm
Correct answer is option 'D'. Can you explain this answer?
In right triangled ABC right angled at B ,a line DE is drawn through the mid point D of AB and parallel to BC.If AB=9 cm, BC=12 cm. AE=?
a)
13 cm
b)
10 cm
c)
8.5 cm
d)
7.5 cm
|
|
Pooja Shah answered |
In a triangle ABC in which angle B = 90 degree
So, AB is height of the given triangle = 9 cm
Base of triangle i.e, BC = 12 cm
DE is || to BC
D is the mid point of side AB and E is the mid point of side AC
By applying pythagoras
AC2 = AB2 + BC2
AC2 = 9^2 + 12^2
AC2 = 81 + 144
AC2 = 225
AC = root under 225
AC = 15 cm
E is the mid point of AC
Therefore AE = AC / 2
AE = 15 / 2
AE = 7.5 cm
So, AB is height of the given triangle = 9 cm
Base of triangle i.e, BC = 12 cm
DE is || to BC
D is the mid point of side AB and E is the mid point of side AC
By applying pythagoras
AC2 = AB2 + BC2
AC2 = 9^2 + 12^2
AC2 = 81 + 144
AC2 = 225
AC = root under 225
AC = 15 cm
E is the mid point of AC
Therefore AE = AC / 2
AE = 15 / 2
AE = 7.5 cm
A square and a rhombus are always - a)similar
- b)congruent
- c)similar but not congruent
- d)neither similar nor congruent
Correct answer is option 'D'. Can you explain this answer?
A square and a rhombus are always
a)
similar
b)
congruent
c)
similar but not congruent
d)
neither similar nor congruent
|
Kamna Science Academy answered |
Let AC be the ladder of length 5m and BC = 4m be the height of the wall where ladder is placed. If the foot of the ladder is moved 1.6m towards the wall i.e. AD = 1.6 m, then the ladder is slided upward to position E i.e. CE = x m.
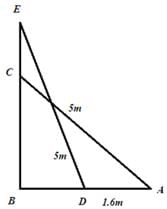
In right triangle ABC
AC2 = AB2 + BC2
⇒52 = AB2 + 42
⇒ AB = 3m
⇒ DB = AB – AD = 3 – 1.6 = 1.4m
In right angled ΔEBD
ED2 = EB2 + BD2
⇒ 52 = EB2 + (1.4)2
⇒ EB = 4.8m
EC = EB – BC = 4.8 – 4 = 0.8m
In right triangle ABC
AC2 = AB2 + BC2
⇒52 = AB2 + 42
⇒ AB = 3m
⇒ DB = AB – AD = 3 – 1.6 = 1.4m
In right angled ΔEBD
ED2 = EB2 + BD2
⇒ 52 = EB2 + (1.4)2
⇒ EB = 4.8m
EC = EB – BC = 4.8 – 4 = 0.8m
In right triangle ABC, right angled at A,A perpendicular is dropped from A to BC, meeting BC at D. Then which of the following is true?- a)ΔADC ~ ΔABD
- b)ΔDCA ~ ΔDABD
- c)ΔDAC ~ ΔDABD
- d)ΔDAC ~ ΔDABA
Correct answer is option 'D'. Can you explain this answer?
In right triangle ABC, right angled at A,
A perpendicular is dropped from A to BC, meeting BC at D. Then which of the following is true?
a)
ΔADC ~ ΔABD
b)
ΔDCA ~ ΔDABD
c)
ΔDAC ~ ΔDABD
d)
ΔDAC ~ ΔDABA
|
|
Naina kapoor answered |
Explanation:
- Let's draw the diagram first.
- From the diagram, we can see that triangle ABD and triangle ACD are both right triangles.
- Therefore, we can use the Pythagorean theorem to find their sides.
- Let's assume that AB = b, AC = c, and BC = a.
- Using Pythagorean theorem, we get:
- AB² + BD² = AD² (for triangle ABD)
- AC² + CD² = AD² (for triangle ACD)
- BC² = AB² + AC² (by Pythagoras theorem)
- Now, we can simplify the above equations to get:
- BD² = AD² - AB² = (AC² + CD²) - AB²
- CD² = AD² - AC² = (AB² + BD²) - AC²
- Substituting the value of BD² and CD² in the above equations, we get:
- AB² + (AC² + CD² - AB²) = AD²
- AC² + (AB² + BD² - AC²) = AD²
- After simplifying, we get:
- AC² = AD² - AB²
- AB² = AD² - AC²
- Therefore, we can say that triangle DAC is similar to triangle DAB by the Angle-Angle-Similarity criterion.
- Thus, option D is the correct answer.
In ΔPQR, ∠P = 60°, ∠Q = 50°. Which side of the triangle is the longest ?- a)PQ
- b)QR
- c)PR
- d)none
Correct answer is option 'A'. Can you explain this answer?
In ΔPQR, ∠P = 60°, ∠Q = 50°. Which side of the triangle is the longest ?
a)
PQ
b)
QR
c)
PR
d)
none
|
Rohini sharma answered |
The context of computing, a program is a set of instructions that tells a computer what to do. It is a sequence of commands or statements that are written in a specific programming language. These instructions can include mathematical calculations, conditional statements, loops, and other operations.
A program is created by a programmer or developer using a text editor or an integrated development environment (IDE). The programmer writes the code in a programming language such as Java, Python, C++, or JavaScript. The code is then compiled or interpreted by a compiler or interpreter, respectively, which converts the code into machine-readable instructions.
Once the program is compiled or interpreted, it can be executed by the computer. The computer reads each instruction and performs the corresponding operation. The program can interact with the user, perform calculations, manipulate data, access files or databases, and perform various other tasks.
Programs can be simple or complex, depending on the requirements and functionality desired. They can be small scripts that automate a specific task or large software applications that have multiple modules and functionalities.
In summary, a program is a set of instructions written in a programming language that tells a computer what to do. It is created by a programmer, compiled or interpreted, and executed by the computer to perform specific tasks or operations.
A program is created by a programmer or developer using a text editor or an integrated development environment (IDE). The programmer writes the code in a programming language such as Java, Python, C++, or JavaScript. The code is then compiled or interpreted by a compiler or interpreter, respectively, which converts the code into machine-readable instructions.
Once the program is compiled or interpreted, it can be executed by the computer. The computer reads each instruction and performs the corresponding operation. The program can interact with the user, perform calculations, manipulate data, access files or databases, and perform various other tasks.
Programs can be simple or complex, depending on the requirements and functionality desired. They can be small scripts that automate a specific task or large software applications that have multiple modules and functionalities.
In summary, a program is a set of instructions written in a programming language that tells a computer what to do. It is created by a programmer, compiled or interpreted, and executed by the computer to perform specific tasks or operations.
In the given fig, P and Q are points on the sides AB and AC respectively of Δ ABC such that AP = 3.5 cm, PB = 7 cm, AQ = 3 cm and QC = 6 cm. If PQ = 4.5 cm, find BC.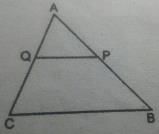
- a)13.5 cme
- b)2. 6 cm
- c)3.4 cm
- d)1. 6 cm
Correct answer is option 'A'. Can you explain this answer?
In the given fig, P and Q are points on the sides AB and AC respectively of Δ ABC such that AP = 3.5 cm, PB = 7 cm, AQ = 3 cm and QC = 6 cm. If PQ = 4.5 cm, find BC.
a)
13.5 cme
b)
2. 6 cm
c)
3.4 cm
d)
1. 6 cm
|
Rahul Kumar answered |
Therefore, by converse of Basic Proportionality Theorem, we have QP || CB
Hence, ∆AQP ~ ∆ACB [Using AA similar condition]
∴ 
⇒
⇒
⇒
⇒
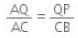
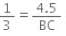
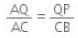
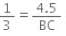
A wood frame for pouring concrete has an interior perimeter of 14 metres. Its length is one metre greater than its width. The frame is to be braced with twelve-gauge steel cross-wires. Assuming an extra half-metre of wire is used at either end of a cross-wire for anchoring, what length of wire should be cut for each brace?- a)14 m
- b)4 m
- c)6 m
- d)60 m
Correct answer is option 'C'. Can you explain this answer?
A wood frame for pouring concrete has an interior perimeter of 14 metres. Its length is one metre greater than its width. The frame is to be braced with twelve-gauge steel cross-wires. Assuming an extra half-metre of wire is used at either end of a cross-wire for anchoring, what length of wire should be cut for each brace?
a)
14 m
b)
4 m
c)
6 m
d)
60 m
|
|
Raghav Bansal answered |
Let width is x
Then length is x+1
Perimeter =x +x + x + 1 + x + 1 = 14
4 x= 12
x = 3
length = 4
Using Pythagoras theorem,
H2 = P2 + B2
=9 + 16 = 25
H = 5cm
An extra half meter on either side will give the length of the wire as 5 + 1 = 6cm
Then length is x+1
Perimeter =x +x + x + 1 + x + 1 = 14
4 x= 12
x = 3
length = 4
Using Pythagoras theorem,
H2 = P2 + B2
=9 + 16 = 25
H = 5cm
An extra half meter on either side will give the length of the wire as 5 + 1 = 6cm
Chapter doubts & questions for Similarity Theorems - Mathematics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Similarity Theorems - Mathematics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Mathematics for EmSAT Achieve
146 videos|222 docs|220 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup