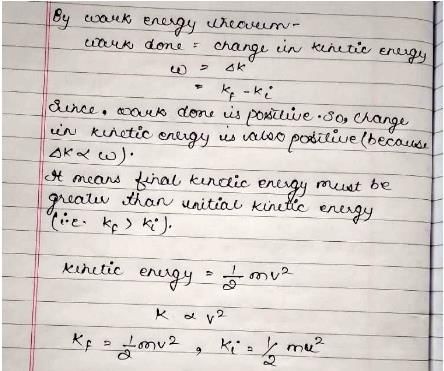All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Work, Energy and Power for EmSAT Achieve Exam
An engine generates a power of 10 kW. In how much time will it raise a mass of 200 kg through a height of 40m.- a)4 sec
- b)10 sec
- c)5 sec
- d)8 sec
Correct answer is option 'D'. Can you explain this answer?
An engine generates a power of 10 kW. In how much time will it raise a mass of 200 kg through a height of 40m.
a)
4 sec
b)
10 sec
c)
5 sec
d)
8 sec
|
Mira Sharma answered |
Power = work done / time
work = force x distance
so power = (force x distance) / time
time = (force x distance) / power
= (2000 N x 40m) / 10000W = 8 seconds
A body dropped from height H reaches the ground with a speed of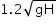 
- a)mgh
- b)-0.28mgH
- c)2gh
- d)0.5gh
Correct answer is option 'B'. Can you explain this answer?
A body dropped from height H reaches the ground with a speed of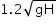
a)
mgh
b)
-0.28mgH
c)
2gh
d)
0.5gh
|
Krishna Iyer answered |
The forces acting on the body are the force of gravity and the air friction. By work energy theorem, the total work done on the body is
W=1/2m(1.2√gH)2−0=0.72mgH
The work done by the force of gravity is mgH.
. Hence, the work done by the air friction is,
=0.72mgH-mgH
=00.28mgH.
W=1/2m(1.2√gH)2−0=0.72mgH
The work done by the force of gravity is mgH.
. Hence, the work done by the air friction is,
=0.72mgH-mgH
=00.28mgH.
What is the dimension of k/m where k is the force constant and m is the mass of the oscillating object?- a)[T2]
- b)[T1]
- c)[T-1]
- d)[T-2]
Correct answer is option 'D'. Can you explain this answer?
What is the dimension of k/m where k is the force constant and m is the mass of the oscillating object?
a)
[T2]
b)
[T1]
c)
[T-1]
d)
[T-2]
|
Preeti Khanna answered |
F=k x (compression in string).
X=L.
a=LT-2.
F=ma.
ma= k L.
LT-2/L=k/m.
T-2=k/m.
X=L.
a=LT-2.
F=ma.
ma= k L.
LT-2/L=k/m.
T-2=k/m.
A person 'A' pushes a body of 5 kg placed on a rough surface of co-efficient of friction 0.3 by a distance of 4 m in 15 seconds. Another person 'B' pushes the body of 7 kg on same surface by a distance of 3 m in the same time. Who has more energy and power?- a)A
- b)B
- c)Both A and B have developed equal power but B has more energy
- d)Both A and B have developed equal power but A has more energy
Correct answer is option 'B'. Can you explain this answer?
A person 'A' pushes a body of 5 kg placed on a rough surface of co-efficient of friction 0.3 by a distance of 4 m in 15 seconds. Another person 'B' pushes the body of 7 kg on same surface by a distance of 3 m in the same time. Who has more energy and power?
a)
A
b)
B
c)
Both A and B have developed equal power but B has more energy
d)
Both A and B have developed equal power but A has more energy
|
Gaurav Kumar answered |
For person A,
Mass of body, m1 = 5kg
Coefficient of friction, μ =0.3
So, The force of friction,
F1= μm1g=0.3 X 5 X 10=15N
Displacement, S1=4m
Therefore,
Work done, W1=15X4=60J
Time taken, t1=15sec
So, Power, P1=60/15=4W
For Person B
Mass of body, m2=7kg
Coefficient of friction, μ =0.3
So, The force of friction,
F1= μm2g=0.3 X 7 X 10=21N
Displacement, S2=3m
Therefore,
Work done, W2=21X3=63J
Time taken, t2=15sec
So, Power, P3=63/15=4.2W
Mass of body, m1 = 5kg
Coefficient of friction, μ =0.3
So, The force of friction,
F1= μm1g=0.3 X 5 X 10=15N
Displacement, S1=4m
Therefore,
Work done, W1=15X4=60J
Time taken, t1=15sec
So, Power, P1=60/15=4W
For Person B
Mass of body, m2=7kg
Coefficient of friction, μ =0.3
So, The force of friction,
F1= μm2g=0.3 X 7 X 10=21N
Displacement, S2=3m
Therefore,
Work done, W2=21X3=63J
Time taken, t2=15sec
So, Power, P3=63/15=4.2W
So person B has more energy and power.
A man A of mass 80 kg runs up a staircase in 12 seconds. Another man of mass 60 kg runs up the same staircase in 11 seconds. The ratio of powers of A and B is :
- a)11:12
- b)9:11
- c)12:11
- d)11:9
Correct answer is option 'D'. Can you explain this answer?
A man A of mass 80 kg runs up a staircase in 12 seconds. Another man of mass 60 kg runs up the same staircase in 11 seconds. The ratio of powers of A and B is :
a)
11:12
b)
9:11
c)
12:11
d)
11:9
|
Naina Sharma answered |
According to question, 60 kg man runs up a staircase in 12 sec.
m₁ = 80 kg
t₁ = 12 sec
=> A 50 kg man runs up the same staircase in 11 sec:
m₂ = 60 kg
t₂ = 11 sec
=> Rate of work done is equals to power.
∴ P = E/ t and E = mgh
∴ P₁ = m₁gh / t₁
P₂ = m₂gh/ t₂
=> The ratio of Power or Rate of work done is:
P₁/P₂ = m₁gh / t₁ / m₂gh/ t₂
= m₁ * t₂ / m₂ * t₁
= 80x11/60x12
= 11 : 9
Thus, the ratio of rate of doing their work is 11 : 9.
An electric motor creates a tension of 4500 N in a hoisting cable and reels it in at the rate of 2 m/s. What is the power of the electric motor?
- a)225W
- b)15kW
- c)9kW
- d)900 W
Correct answer is option 'C'. Can you explain this answer?
An electric motor creates a tension of 4500 N in a hoisting cable and reels it in at the rate of 2 m/s. What is the power of the electric motor?
a)
225W
b)
15kW
c)
9kW
d)
900 W
|
|
Krishna Iyer answered |
F=4500N
v=2ms−1
The power of motor is given by
P=F.v
P=4500×2
P=9000W=9kW
v=2ms−1
The power of motor is given by
P=F.v
P=4500×2
P=9000W=9kW
You are in a lift moving from the 3rd floor to the 12th floor, having a height difference of H = 40 m. Your mass is M = 80 kg and the acceleration due to gravity is g = 10 m/s2. If the elevator moves at a constant speed without stopping, what is the total work performed by all of the forces together (the net force) acting on you?- a)Mgh
- b)-Mgh
- c)0
- d)Mg
Correct answer is option 'C'. Can you explain this answer?
You are in a lift moving from the 3rd floor to the 12th floor, having a height difference of H = 40 m. Your mass is M = 80 kg and the acceleration due to gravity is g = 10 m/s2. If the elevator moves at a constant speed without stopping, what is the total work performed by all of the forces together (the net force) acting on you?
a)
Mgh
b)
-Mgh
c)
0
d)
Mg
|
|
Krishna Iyer answered |
As the final velocity after the action of all forces is 0, therefore the person has 0 net acceleration.
And, as we know that
Fnet = m.anet
Therefore, the net force is 0 and hence, the net work done is also 0.
A body moves under a force such that momentum of the body at any instant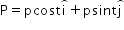 
. What is the rate of work done by the force?- a)
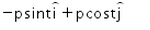
- b)
- c)
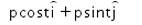
- d)zero
Correct answer is option 'D'. Can you explain this answer?
A body moves under a force such that momentum of the body at any instant 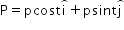. What is the rate of work done by the force?
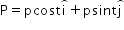. What is the rate of work done by the force?a)
b)
c)
d)
zero
|
Hansa Sharma answered |
P = p Cos(t) i + p Sin(t) j
dP/dt = -p Sin(t) j + p Cos(t) i
Work done, W = P2/2m
Rate of work done = d/dt(P2/2m)
= 2P/2m x dP/dt
= P/m x dP/dt
= -p2.Sin(t).Cos(t) + p2.Sin(t).Cos(t)
=> Rate of work done = 0
Calculate the power developed when the force of 10 N is exerted on a body moving with velocity of 3.65 m/s.- a)36.5W
- b)3.65W
- c)365W
- d)0.365W
Correct answer is option 'A'. Can you explain this answer?
Calculate the power developed when the force of 10 N is exerted on a body moving with velocity of 3.65 m/s.
a)
36.5W
b)
3.65W
c)
365W
d)
0.365W
|
Lavanya Menon answered |
Power =F.V
i.e, Power = force x velocity.
here, force (f)= 10N
and velocity (v) = 3.65 m/s
so, Power = f x v,
i.e, 10 x 3.65 = 36.5 w.
i.e, Power = force x velocity.
here, force (f)= 10N
and velocity (v) = 3.65 m/s
so, Power = f x v,
i.e, 10 x 3.65 = 36.5 w.
How much work is done by a man weighing 80 kgf in raising a stone of weight 20 kgf to the top of a building of height 40 m? (g = 9.8 m/s2)- a)30,900 J
- b)29,678 J
- c)39,200 J
- d)25,000 J
Correct answer is option 'C'. Can you explain this answer?
How much work is done by a man weighing 80 kgf in raising a stone of weight 20 kgf to the top of a building of height 40 m? (g = 9.8 m/s2)
a)
30,900 J
b)
29,678 J
c)
39,200 J
d)
25,000 J
|
Sushil Kumar answered |
Total mass=80+20=100
w=mgh(where m=100, g=9.8, h=40m)
w=100×9.8×40
w=39200J
work done by man weighing 80 kg raising a stone of 20kgf to the top of building of Height is 40m is 39,200J
w=mgh(where m=100, g=9.8, h=40m)
w=100×9.8×40
w=39200J
work done by man weighing 80 kg raising a stone of 20kgf to the top of building of Height is 40m is 39,200J
An elastic spring of force constant k is compressed by an amount x. Then its potential energy will be- a)kx
- b)-kx
- c)
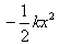
- d)
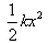
Correct answer is option 'D'. Can you explain this answer?
An elastic spring of force constant k is compressed by an amount x. Then its potential energy will be
a)
kx
b)
-kx
c)
d)
|
Anjana Sharma answered |
F= kx
Now as we know
f.ds = potential energy
differentiate
potential energy = kx .ds
k is a constant .... and diff of x .ds is = x^2 / 2
so here potential energy will be = 1/2 k x^2
How should the force applied on a body be varied with velocity to keep the power of force constant?- a)Force should be inversely proportional to the square root of the velocity of the body
- b)Force should be inversely proportional to the velocity of the body
- c)Force should be directly proportional to the velocity of the body
- d)Force should not be varied. It should remain constant with the velocity
Correct answer is option 'B'. Can you explain this answer?
How should the force applied on a body be varied with velocity to keep the power of force constant?
a)
Force should be inversely proportional to the square root of the velocity of the body
b)
Force should be inversely proportional to the velocity of the body
c)
Force should be directly proportional to the velocity of the body
d)
Force should not be varied. It should remain constant with the velocity
|
|
Anjana Sharma answered |
We know that power (P) = force (F) x velocity (v).
Since the body is moving with acceleration,v changes and as a result of that P also changes,F being constant.
For P to be constant, F v = constant or F ∝ 1/v i.e
Force should be inversely proportional to the velocity of the body.
Thus,as v increases, F should decrease to keep P constant.
In the given figure, what is the work done by the spring force?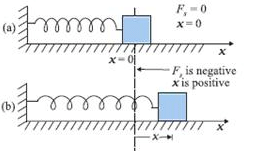
- a)
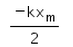
- b)
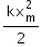
- c)
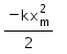
- d)
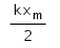
Correct answer is option 'C'. Can you explain this answer?
In the given figure, what is the work done by the spring force?
a)
b)
c)
d)
|
|
Neha Joshi answered |
We know that for a spring with spring constant k, work done by the spring when a compression or expansion is done of some length say x is ½ kx2
Also as the work done is in the opposite direction to that of force applied, we get the sign of the force to be negative.
Also as the work done is in the opposite direction to that of force applied, we get the sign of the force to be negative.
A vehicle of 50 quintal climbs up a hill of 10 m. The potential energy gained by it is (take g = 10 m/s2)- a)5 J
- b)5000 J
- c)500 J
- d)5 x 105 J
Correct answer is option 'D'. Can you explain this answer?
A vehicle of 50 quintal climbs up a hill of 10 m. The potential energy gained by it is (take g = 10 m/s2)
a)
5 J
b)
5000 J
c)
500 J
d)
5 x 105 J
|
|
Geetika Shah answered |
mass = 50 x 100 = 5000 kg, g = 10 m/s2, h = 10 m
Potential energy gained = mgh = 5000 x 10 x 10 = 5 x 105 J
Potential energy gained = mgh = 5000 x 10 x 10 = 5 x 105 J
In an elastic collision in one dimension if a body A collides against the body B of equal mass at rest, then the body A will- a)moves with the same velocity but in opposite direction
- b)move with twice its initial velocity
- c)moves with the same velocity in the same direction
- d)come to rest.
Correct answer is option 'D'. Can you explain this answer?
In an elastic collision in one dimension if a body A collides against the body B of equal mass at rest, then the body A will
a)
moves with the same velocity but in opposite direction
b)
move with twice its initial velocity
c)
moves with the same velocity in the same direction
d)
come to rest.
|
|
Lavanya Menon answered |
Since collision is elastic and mass is same then after velocity exchange A body will stop and B will start moving with A's velocity in the same direction.
When does the potential energy of a spring increase?- a)only when spring is stretched
- b)only when spring is compressed
- c)when spring is neither stretched nor compressed
- d)when spring is compressed or stretched
Correct answer is option 'D'. Can you explain this answer?
When does the potential energy of a spring increase?
a)
only when spring is stretched
b)
only when spring is compressed
c)
when spring is neither stretched nor compressed
d)
when spring is compressed or stretched
|
|
Gaurav Kumar answered |
Potential energy of a spring is proportional to the square of the difference of the springs length and its original length, hence whether it is compressed or stretched the potential the potential energy will eventually increase only.
Two moving particle P and Q are 10 m apart at a certain instant. The velocity of P is 8m/s making an angle 30° with the line joining P and Q and that of Q is 6m/s making an angle 30° with PQ as shown in the figure. Then angular velocity of P with respect to Q is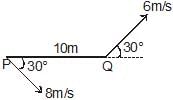 
- a)Zero
- b)0.1 rad/sec
- c)0.4 rad/sec
- d)0.7 rad sec
Correct answer is option 'D'. Can you explain this answer?
Two moving particle P and Q are 10 m apart at a certain instant. The velocity of P is 8m/s making an angle 30° with the line joining P and Q and that of Q is 6m/s making an angle 30° with PQ as shown in the figure. Then angular velocity of P with respect to Q is
a)
Zero
b)
0.1 rad/sec
c)
0.4 rad/sec
d)
0.7 rad sec
|
|
Krishna Iyer answered |
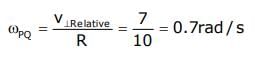
A machine, in an amusement park, consists of a cage at the end of one arm, hinged at O. The cage revolves along a vertical circle of radius r (ABCDEFGH) about its hinge O, at constant linear speedv =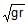 
. The cage is so attached that the man of weight `w' standing on a weighing machine, inside the cage, is always vertical. Then which of the following is correct
- a)The reading of his weight on the machine is the same at all positions
- b)The weight reading at A is greater than the weight reading at E by 2 w.
- c)The weight reading at G = w
- d)The ratio of the weight reading at E to that at A=0
- e)The ratio of the weight reading at A to that at C=2
Correct answer is option 'B,C,D,E'. Can you explain this answer?
A machine, in an amusement park, consists of a cage at the end of one arm, hinged at O. The cage revolves along a vertical circle of radius r (ABCDEFGH) about its hinge O, at constant linear speed
v = 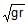. The cage is so attached that the man of weight `w' standing on a weighing machine, inside the cage, is always vertical. Then which of the following is correct
. The cage is so attached that the man of weight `w' standing on a weighing machine, inside the cage, is always vertical. Then which of the following is correcta)
The reading of his weight on the machine is the same at all positions
b)
The weight reading at A is greater than the weight reading at E by 2 w.
c)
The weight reading at G = w
d)
The ratio of the weight reading at E to that at A=0
e)
The ratio of the weight reading at A to that at C=2
|
Crafty Classes answered |
No work is done by a force on an object if- a)The force is always perpendicular to its velocity
- b)The force is always perpendicular to its acceleration
- c)The object is stationary but the point of application of the force moves on the object.
- d)The object moves in such a way that the point of application of the force remains fixed.
Correct answer is option 'A,B'. Can you explain this answer?
No work is done by a force on an object if
a)
The force is always perpendicular to its velocity
b)
The force is always perpendicular to its acceleration
c)
The object is stationary but the point of application of the force moves on the object.
d)
The object moves in such a way that the point of application of the force remains fixed.
|
|
Krishna Iyer answered |
Work done = f.ds
So on perpendicular application for product becomes zero so no work is done
So on perpendicular application for product becomes zero so no work is done
When a ball is allowed to fall from a height of 20 m, 40% of its energy is lost due to impact. After one impact the ball will go up to a height of- a)12 m
- b)15 m
- c)8 m
- d)10 m
Correct answer is option 'A'. Can you explain this answer?
When a ball is allowed to fall from a height of 20 m, 40% of its energy is lost due to impact. After one impact the ball will go up to a height of
a)
12 m
b)
15 m
c)
8 m
d)
10 m
|
|
Lavanya Menon answered |
Before the impact the KE was ½ x m x (2g x 20) = 20mg
And let say v be the velocity after impact and for height h, v2= 2gh
Thus KE = ½ mv2 = ½m2gh = ⅗ x 20mg
Thus we get mgh = 12mg
thus h = 12 m
And let say v be the velocity after impact and for height h, v2= 2gh
Thus KE = ½ mv2 = ½m2gh = ⅗ x 20mg
Thus we get mgh = 12mg
thus h = 12 m
The potential energy of a body at height h is mgh. Then its kinetic energy just before hitting the ground is- a)mgh
- b)
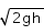
- c)mv2
- d)
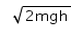
Correct answer is option 'A'. Can you explain this answer?
The potential energy of a body at height h is mgh. Then its kinetic energy just before hitting the ground is
a)
mgh
b)
c)
mv2
d)
|
Om Desai answered |
From the law of conservation of mechanical energy, the potential energy of a body at height h is converted into kinetic energy when it falls down. So, the magnitude of kinetic energy just before hitting the ground is equal to the potential energy at height h which is mgh.
From a waterfall, water is falling at the rate of 100 kg/s on the blades of a turbine. If the height of fall is 100 m, the power delivered to the turbine is- a)100kW
- b)100W
- c)1kW
- d)10kW
Correct answer is option 'A'. Can you explain this answer?
From a waterfall, water is falling at the rate of 100 kg/s on the blades of a turbine. If the height of fall is 100 m, the power delivered to the turbine is
a)
100kW
b)
100W
c)
1kW
d)
10kW
|
|
Nandini Patel answered |
Power = work done / time taken
or P = mgh / t
P = (m/t) gh = 100 x 10 x 100 = 100 kW
Two cylindrical vessels of equal cross-sectional area 16 cm2 contain water up to heights 100 cm and 150 cm, respectively. The vessels are interconnected so that the water levels in them become equal. The work done by the force of gravity during the process is: [Take density of water = 103 kg/m3 and g = 10 ms-2]
- a)0.25 J
- b)12 J
- c)8 J
- d)1 J
Correct answer is option 'D'. Can you explain this answer?
Two cylindrical vessels of equal cross-sectional area 16 cm2 contain water up to heights 100 cm and 150 cm, respectively. The vessels are interconnected so that the water levels in them become equal. The work done by the force of gravity during the process is: [Take density of water = 103 kg/m3 and g = 10 ms-2]
a)
0.25 J
b)
12 J
c)
8 J
d)
1 J
|
Rajeev Saxena answered |
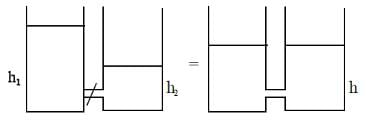
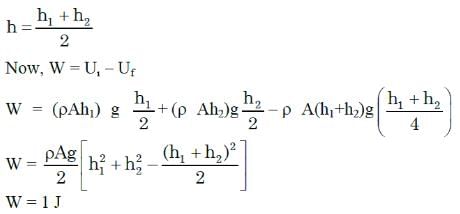
A bomb of mass 4 kg explodes in air into two pieces of masses 3 kg and 1 kg. The smaller mass goes at a speed of 90 m/s. The total energy imparted to two fragments is.- a)2.4 kj
- b)5.4 kj
- c)5.9 kJ
- d)3.8 kJ
Correct answer is option 'B'. Can you explain this answer?
A bomb of mass 4 kg explodes in air into two pieces of masses 3 kg and 1 kg. The smaller mass goes at a speed of 90 m/s. The total energy imparted to two fragments is.
a)
2.4 kj
b)
5.4 kj
c)
5.9 kJ
d)
3.8 kJ
|
|
Raghav Bansal answered |
By conservation of momentum we get the speed of the bigger part let say, v = 1 x90 / 3
Hence we get v = 30
Thus the total KE of the system after collision is ½ (3 X 900 + 1 X 8100)
Thus KE = ½ (10800) = 5400
Now if we apply WET to the system, as no external force has acted upon it, we get
W = ΔKE
= 5400 - 0
= 5.4 kJ
Hence we get v = 30
Thus the total KE of the system after collision is ½ (3 X 900 + 1 X 8100)
Thus KE = ½ (10800) = 5400
Now if we apply WET to the system, as no external force has acted upon it, we get
W = ΔKE
= 5400 - 0
= 5.4 kJ
Which of the following force is non-conservative- a)Restoring force of spring
- b)Force between two stationary masses
- c)Force between two stationary charges
- d)Human push or pull
Correct answer is option 'D'. Can you explain this answer?
Which of the following force is non-conservative
a)
Restoring force of spring
b)
Force between two stationary masses
c)
Force between two stationary charges
d)
Human push or pull
|
|
Anjali Iyer answered |
You mean all force that humans apply, or any push/pull force one person does. A conservative force is the property that the work done in moving a particle between two points is independent of the taken path. A conservative force is dependent only on the position of the object. Eg gravity.
A bomb at rest on a horizontal frictionless surface explodes and breaks into three pieces that fly apart horizontally as shown below. Select all of the following statements that must be true after the bomb has exploded.1. The total kinetic energy of the bomb fragments is the same as that of the bomb before explosion.
2. The total momentum of the bomb fragments is the same as that of the bomb before explosion.
3. The total momentum of all the bomb fragments together is zero.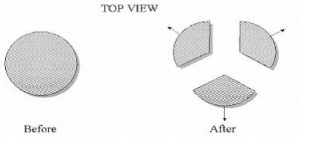
- a)1,2 and 3
- b)1 only
- c)3 only
- d)2 only
Correct answer is option 'C'. Can you explain this answer?
A bomb at rest on a horizontal frictionless surface explodes and breaks into three pieces that fly apart horizontally as shown below. Select all of the following statements that must be true after the bomb has exploded.
1. The total kinetic energy of the bomb fragments is the same as that of the bomb before explosion.
2. The total momentum of the bomb fragments is the same as that of the bomb before explosion.
3. The total momentum of all the bomb fragments together is zero.
2. The total momentum of the bomb fragments is the same as that of the bomb before explosion.
3. The total momentum of all the bomb fragments together is zero.
a)
1,2 and 3
b)
1 only
c)
3 only
d)
2 only
|
|
Naina Sharma answered |
So as no external force acts upon the system, we can say that momentum of the system remains conserved but as an internal force acts that explodes the bomb, the KE of the system is never conserved. But every fragment has some non zero momentum while the bomb initially has zero momentum.
For a varying force work done can be expressed as a- a)product of force and displacement
- b)force divided by the displacement
- c)definite integral of force over displacement
- d)differentiation of force with displacement
Correct answer is option 'C'. Can you explain this answer?
For a varying force work done can be expressed as a
a)
product of force and displacement
b)
force divided by the displacement
c)
definite integral of force over displacement
d)
differentiation of force with displacement
|
|
Krishna Iyer answered |
For a variable force, the work done can be expressed as a definite integral of force over displacement for any system.In case of a variable force, the is calculated with the help of integration. For example, in the case of a spring, the force acting upon any object attached to a horizontal spring can be given as Fs = -kx, where k is the spring constant and x is the displacement of the object attached. We can see that this force is proportional to the displacement of the object from the equilibrium position, hence the force acting at each instant during the compression and extension of the spring will be different. Thus, the infinitesimally small contributions of work done during each instant are to be counted in order to calculate the total work done.
If momentum of an object is doubled, how does its kinetic energy change?- a)increases 4 times
- b)increases 2 times
- c)decreases 4 times
- d)decreases 2 times
Correct answer is option 'A'. Can you explain this answer?
If momentum of an object is doubled, how does its kinetic energy change?
a)
increases 4 times
b)
increases 2 times
c)
decreases 4 times
d)
decreases 2 times
|
|
Naina Bansal answered |
kinetic energy of object = 1/2 mv2
when the momentum of object is doubled,
then, kinetic energy of object = 1/2 m(2v)2
= 1/52 4mv2
= 4[1/2mv2]
so the momentum of an object after doubled is 4 times graeter.
A body is moved along a straight line path by a machine delivering constant power. The distance moved by the body in time t is proportional to:- a)t3/2
- b)t3/4
- c)t1/4
- d)t1/2
Correct answer is option 'A'. Can you explain this answer?
A body is moved along a straight line path by a machine delivering constant power. The distance moved by the body in time t is proportional to:
a)
t3/2
b)
t3/4
c)
t1/4
d)
t1/2
|
Shruti Mehta answered |
A body is moved along a straight line by a machine delivering constant power. The distance moved by the body in time 't' is proportional to.
Can you explain the answer of this question below:An astronomer has total weight of 80 kg. On reaching moon, he climbs up 10 m to enter his aircraft by the ladder. His gravitational potential energy is increased by 1000 J. The value of the gravitational acceleration on the moon is
- A:
2.22 kg
- B:
2.25 kg
- C:
2 N/kg
- D:
1.25 N/kg
The answer is d.
An astronomer has total weight of 80 kg. On reaching moon, he climbs up 10 m to enter his aircraft by the ladder. His gravitational potential energy is increased by 1000 J. The value of the gravitational acceleration on the moon is
2.22 kg
2.25 kg
2 N/kg
1.25 N/kg
|
aakash answered |
Mgh = 80 x 10 x g = 1000
g= 1000 / 800
g = 125 N/ Kg
g= 1000 / 800
g = 125 N/ Kg
A box of mass m is released from rest at position on the frictionless curved track shown. It slides a distance d along the track in time t to reach position 2, dropping a vertical distance h. Let v and a be the instantaneous speed and instantaneous acceleration, respectively, of the box at position 2. Which of the following equations is valid for this situation?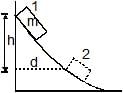 
- a)h = vt
- b)h = (1/2)gt2
- c)mgh = (1/2)mv2
- d)none
Correct answer is option 'C'. Can you explain this answer?
A box of mass m is released from rest at position on the frictionless curved track shown. It slides a distance d along the track in time t to reach position 2, dropping a vertical distance h. Let v and a be the instantaneous speed and instantaneous acceleration, respectively, of the box at position 2. Which of the following equations is valid for this situation?
a)
h = vt
b)
h = (1/2)gt2
c)
mgh = (1/2)mv2
d)
none
|
Imk Pathsala answered |
According to the Work Energy Theorem,
Change in PE = Change in KE
So, mgh = ½ mv2
Hence C
Forum id- 1775160
For complete circle v = √(5gl)
mgh = ½mv2
So, h = 2.5R
Change in PE = Change in KE
So, mgh = ½ mv2
Hence C
Forum id- 1775160
For complete circle v = √(5gl)
mgh = ½mv2
So, h = 2.5R
A stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal smooth surface. The maximum tension the string can withstand is 16 newton. The maximum speed of revolution of the stone without breaking it, will be :- a)20 ms-1
- b)16 ms-1
- c)14 ms-1
- d)12 ms-1
Correct answer is option 'A,C,D'. Can you explain this answer?
A stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal smooth surface. The maximum tension the string can withstand is 16 newton. The maximum speed of revolution of the stone without breaking it, will be :
a)
20 ms-1
b)
16 ms-1
c)
14 ms-1
d)
12 ms-1
|
|
Pooja Shah answered |
T= (mv2max)/r
16 = (16 v2max)/144
v2max = 12 m/s
16 = (16 v2max)/144
v2max = 12 m/s
The launching mechanism of a toy gun consists of a spring of unknown spring constant. When the spring is compressed 0.120 m, the gun, when fired vertically, is able to launch a 35.0-g projectile to a maximum height of 20.0 m above the position of the projectile before firing. Neglecting all resistive forces, determine the spring constant.- a)903 N/m
- b)993 N/m
- c)953 N/m
- d)873 N/m
Correct answer is option 'C'. Can you explain this answer?
The launching mechanism of a toy gun consists of a spring of unknown spring constant. When the spring is compressed 0.120 m, the gun, when fired vertically, is able to launch a 35.0-g projectile to a maximum height of 20.0 m above the position of the projectile before firing. Neglecting all resistive forces, determine the spring constant.
a)
903 N/m
b)
993 N/m
c)
953 N/m
d)
873 N/m
|
Mrinalini Bose answered |
Explanation:
Potential energy of spring converted in to potential energy
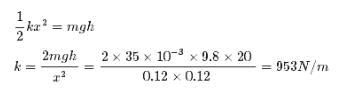
The minimum value of H required so that the particle makes a complete vertical circle is given by- a)5 R
- b)4 R
- c)2.5 R
- d)2 R
Correct answer is option 'C'. Can you explain this answer?
The minimum value of H required so that the particle makes a complete vertical circle is given by
a)
5 R
b)
4 R
c)
2.5 R
d)
2 R
|
|
Hansa Sharma answered |
For complete circle v = √(5gl)
mgh = ½mv2
So, h = 2.5R
mgh = ½mv2
So, h = 2.5R
Which physical quantity is conserved during both elastic and inelastic collision?- a)Kinetic energy
- b)Potential energy
- c)Linear momentum
- d)Velocity
Correct answer is option 'C'. Can you explain this answer?
Which physical quantity is conserved during both elastic and inelastic collision?
a)
Kinetic energy
b)
Potential energy
c)
Linear momentum
d)
Velocity
|
|
Preeti Iyer answered |
Kinetic energy is conserved in elastic collisions, whereas kinetic energy is converted into other forms of energy during an inelastic collision. In both types of collisions, momentum is conserved.
Select the odd one out- a)A stretched bow
- b)Compressed gas
- c)Compressed or elongated spring
- d)Lifted weight
Correct answer is option 'D'. Can you explain this answer?
Select the odd one out
a)
A stretched bow
b)
Compressed gas
c)
Compressed or elongated spring
d)
Lifted weight
|
|
Gaurav Kumar answered |
In A stretched bow. Compressed gas, compressed or elongated spring there is elastic potential energy but the lifted weight there is gravitational force, so the odd one here is lifted weight.
The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed w varies with time t as- a)2 a sin wt
- b)
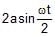
- c)2a cos wt
- d)
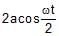
Correct answer is option 'B'. Can you explain this answer?
The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed w varies with time t as
a)
2 a sin wt
b)
c)
2a cos wt
d)
|
|
Naina Sharma answered |
If a particle is moving with angular velocity=ω
Its angle of rotation is given by ωt
Now displacement= length of line AB
Position vector of a particle is given by
R =iacosωt + jasinωt
Ro=ai
displacement =R−Ro
=a(cosωt−1)i+asinωj
d=√[(a(cosωt-1))2+(asinω)2]
=a√(2(1-cosωt))=a√(2×2(sinωt/2)2)=2asinωt/2
Its angle of rotation is given by ωt
Now displacement= length of line AB
Position vector of a particle is given by
R =iacosωt + jasinωt
Ro=ai
displacement =R−Ro
=a(cosωt−1)i+asinωj
d=√[(a(cosωt-1))2+(asinω)2]
=a√(2(1-cosωt))=a√(2×2(sinωt/2)2)=2asinωt/2
A ball of mass 2 kg is raised to the height of 60 m and then dropped from the top. In this case, the quantity which has different magnitude from the other given quantities is- a)Work done by gravity
- b)Potential energy at the top
- c)Velocity just hitting the ground
- d)Kinetic energy before hitting the ground
Correct answer is option 'C'. Can you explain this answer?
A ball of mass 2 kg is raised to the height of 60 m and then dropped from the top. In this case, the quantity which has different magnitude from the other given quantities is
a)
Work done by gravity
b)
Potential energy at the top
c)
Velocity just hitting the ground
d)
Kinetic energy before hitting the ground
|
Aashu answered |
Use work energy thereom At top potential energy= negative of work done by gravity... And at bottom when object is falling same potential energy that was at top will be equal to kinetic energy... So all three are same in magnitude.. Except velocity which will be calculated with the help of kinetic energy.. V=underoot ( 2K/m)
The potential energy in joules of a particle of mass 1 kg moving in a plane is given by U = 3x + 4y, the position coordinates of the point being x and y, measured in meters. If the particle is initially at rest at (6, 4), then- a)Its acceleration is of magnitude 5 m/s2
- b)Its speed when it crosses the y-axis is 10 m/s
- c)It crosses the y-axis (x = 0) at y = _4
- d)It moves in a straight line passing through the origin (0, 0)
Correct answer is option 'A,B,C'. Can you explain this answer?
The potential energy in joules of a particle of mass 1 kg moving in a plane is given by U = 3x + 4y, the position coordinates of the point being x and y, measured in meters. If the particle is initially at rest at (6, 4), then
a)
Its acceleration is of magnitude 5 m/s2
b)
Its speed when it crosses the y-axis is 10 m/s
c)
It crosses the y-axis (x = 0) at y = _4
d)
It moves in a straight line passing through the origin (0, 0)
|
|
Pooja Shah answered |
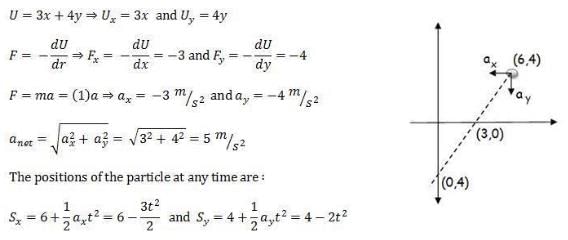
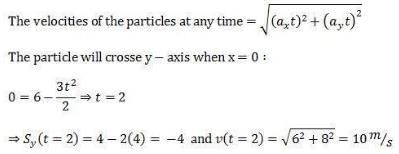Similarly you can find that the particle crosses x - axis at (3, 0) with a velocity 7.07 m/sWork done by force of friction- a)Can be zero
- b)Can be positive
- c)Can be negative
- d)Information insufficient
Correct answer is option 'A,B,C'. Can you explain this answer?
Work done by force of friction
a)
Can be zero
b)
Can be positive
c)
Can be negative
d)
Information insufficient
|
|
Om Desai answered |
Since the motion of the body can be placed in the direction of friction, opposite to the direction of motion and even can not be placed in any motion.
So, Work done by force of friction can be zero, negative, and can be positive.
So, Work done by force of friction can be zero, negative, and can be positive.
Out of a pair of identical springs of spring constants 240 N/m, one is compressed by 10 cm and other is stretched by 10 cm. The difference in P.E. stored in the two springs is:- a)1.2 J
- b)4 J
- c)zero
- d)12 J
Correct answer is option 'C'. Can you explain this answer?
Out of a pair of identical springs of spring constants 240 N/m, one is compressed by 10 cm and other is stretched by 10 cm. The difference in P.E. stored in the two springs is:
a)
1.2 J
b)
4 J
c)
zero
d)
12 J
|
|
Riya Banerjee answered |
P.E. stored in a spring = 1/2Kx2
where x is the extension or compression. In both cases, work is done on the spring.
∴ For the same x, the same potential energy will be stored in the springs.
∴ The difference between the energies is zero.
where x is the extension or compression. In both cases, work is done on the spring.
∴ For the same x, the same potential energy will be stored in the springs.
∴ The difference between the energies is zero.
You are in a lift moving from the 3rd floor to the 12th floor, through a height H. If the elevator moves at a constant speed without stopping, what is the work performed on you by the elevator? Take your body mass as M.- a)Mgh
- b)Mg
- c)-Mgh
- d)-Mg
Correct answer is option 'C'. Can you explain this answer?
You are in a lift moving from the 3rd floor to the 12th floor, through a height H. If the elevator moves at a constant speed without stopping, what is the work performed on you by the elevator? Take your body mass as M.
a)
Mgh
b)
Mg
c)
-Mgh
d)
-Mg
|
|
Hansa Sharma answered |
According to Newton's third law of motion, the force exerted on the floor by the person is equal and opposite the force exerted on the person by the floor.
According to the second law of Newton's law of motion, the net force exerted on the person is equal to the person’s mass times the person’s acceleration.
The net force exerted on the person = Force exerted by the floor+ Force exerted by gravity.
If the elevator goes up with acceleration g, the same is the person inside the elevator.
The work done on the man by the floor is the sum of the change in potential energy and kinetic
energy.
i.e W = Δ P.E + Δ K.E
But the elevator moves at a constant speed, so K.E =0.
W = Δ P.E
The work performed on you by the elevator is force times displacement = -Mgh
Negative sign shows it is moving upwards, i.e., against g.
According to the second law of Newton's law of motion, the net force exerted on the person is equal to the person’s mass times the person’s acceleration.
The net force exerted on the person = Force exerted by the floor+ Force exerted by gravity.
If the elevator goes up with acceleration g, the same is the person inside the elevator.
The work done on the man by the floor is the sum of the change in potential energy and kinetic
energy.
i.e W = Δ P.E + Δ K.E
But the elevator moves at a constant speed, so K.E =0.
W = Δ P.E
The work performed on you by the elevator is force times displacement = -Mgh
Negative sign shows it is moving upwards, i.e., against g.
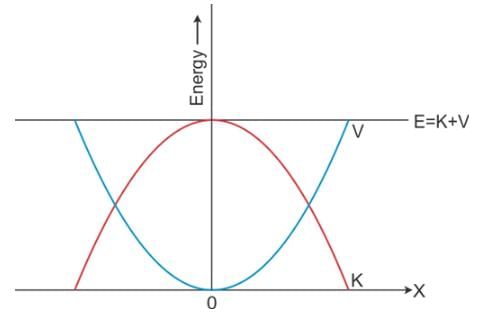
A plot of potential energy and kinetic energy versus displacement x for a block attached to a spring obeying Hooke’s law is- a)a hyperbola
- b)a straight line
- c)an ellipse
- d)a parabola
Correct answer is option 'D'. Can you explain this answer?
A plot of potential energy and kinetic energy versus displacement x for a block attached to a spring obeying Hooke’s law is
a)
a hyperbola
b)
a straight line
c)
an ellipse
d)
a parabola
|
|
Om Desai answered |
The graphs are parabolas as the potential and kinetic energy vary as x2.
There is a sphere of mass m moving with constant velocity v. It hits another sphere of same mass which is at rest. If e is the coefficient of restitution, then the ratio of the velocities of the two spheres after collision will be- a)
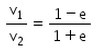
- b)
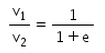
- c)
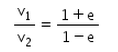
- d)
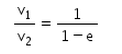
Correct answer is option 'A'. Can you explain this answer?
There is a sphere of mass m moving with constant velocity v. It hits another sphere of same mass which is at rest. If e is the coefficient of restitution, then the ratio of the velocities of the two spheres after collision will be
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
Here, a sphere of mass m moving with a constant velocity v hits another stationary sphere of the same mass. As per the given problem we can write
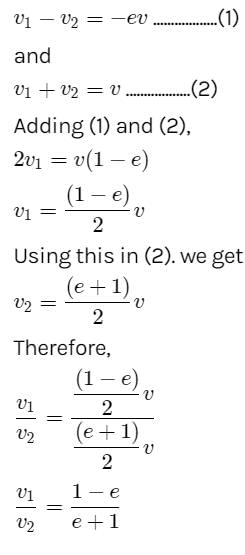
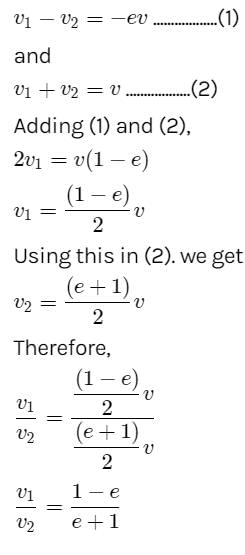
A particle of mass m moving with constant velocity v strikes another particle of same mass m but moving with the same velocity v in opposite direction stick together. The joint velocity after collision will be
- a)zero
- b)2v
- c)v
- d)v/2
Correct answer is option 'A'. Can you explain this answer?
A particle of mass m moving with constant velocity v strikes another particle of same mass m but moving with the same velocity v in opposite direction stick together. The joint velocity after collision will be
a)
zero
b)
2v
c)
v
d)
v/2
|
Soumya Mukherjee answered |
Concept:
- Momentum: momentum is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction.
- The unit of momentum (P) is kg m/s.
- Dimension: [MLT-1]
- Law of conservation of Momentum: A conservation law stating that the total linear momentum of a closed system remains constant through time, regardless of other possible changes within the system.
- P1 = P2
- m1 v1 = m2 v2
- Where, P1 = initial momentum of system, P2 = final momentum of system, m1 = mass of first object, v1 = velocity of first object, m2 = mass of second object and v2 = velocity of second object.
Calculation:
Given: m1 = m kg, m2 = m kg, u1 = v m/s, u2 = -v m/s
Given: m1 = m kg, m2 = m kg, u1 = v m/s, u2 = -v m/s
Let the common velocity of the combined body be V m/s
Mass of combined body M = m + m = 2m
Applying conservation of momentum:
m1 v1 + m2 v2 = M V
mv + (-mv) = 2mV
0 = 2mV
V = 0 m/s
Hence the correct answer will be zero (0) m/s.
Hence the correct answer will be zero (0) m/s.
A particle with constant total energy E moves in one dimension in a region where the potential energy is U(x). The speed of the particle is zero where- a) U(x) = E
- b)U(x) = 0
- c)
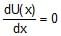
- d)
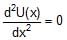
Correct answer is option 'A'. Can you explain this answer?
A particle with constant total energy E moves in one dimension in a region where the potential energy is U(x). The speed of the particle is zero where
a)
U(x) = E
b)
U(x) = 0
c)
d)
|
|
Neha Joshi answered |
If the total energy is E that means that E = U(x) + KE and if KE = 0 then E = U(x)
A 100000 kg engine is moving up a slope of gradient 5o at a speed of 100 m/hr. The coefficient of friction between the engine and the rails is 0.1. If the engine has an efficiency of 4% for converting heat into work, find the amount of coal, the engine has to burn up in one hour. (Burning of 1 kg of coal yields 50000 J.)- a)4.577 Kg
- b)8154 Kg
- c)91.5 Kg
- d)9154 Kg
Correct answer is option 'D'. Can you explain this answer?
A 100000 kg engine is moving up a slope of gradient 5o at a speed of 100 m/hr. The coefficient of friction between the engine and the rails is 0.1. If the engine has an efficiency of 4% for converting heat into work, find the amount of coal, the engine has to burn up in one hour. (Burning of 1 kg of coal yields 50000 J.)
a)
4.577 Kg
b)
8154 Kg
c)
91.5 Kg
d)
9154 Kg
|
EduRev NEET answered |
The forces are shown in Figure.
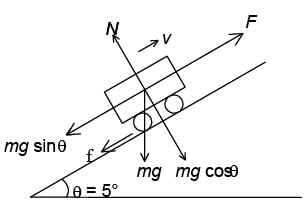
Net force to move the engine up the slope.
F = μN + mg sin θ
= mg (μ cos θ + sin θ)
If the engine has to apply an upward force equal to F, power of engine, P = Fv
where v is the velocity equal to 100 m/hr.
Work done by engine, W = Pt = Fvt
Efficiency of engine,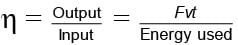
Energy used by engine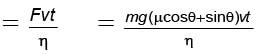
m = 100000 kg, μ = 0.1, θ = 5°, v = 100 m/hr, t = 1 hr
η = 4/100 = 0.04
Energy used by engine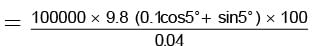
As 1 kg coal yields 50000 J, we have the amount of coal burnt up
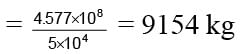
Net force to move the engine up the slope.
F = μN + mg sin θ
= mg (μ cos θ + sin θ)
If the engine has to apply an upward force equal to F, power of engine, P = Fv
where v is the velocity equal to 100 m/hr.
Work done by engine, W = Pt = Fvt
Efficiency of engine,
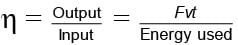
Energy used by engine
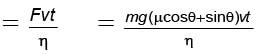
m = 100000 kg, μ = 0.1, θ = 5°, v = 100 m/hr, t = 1 hr
η = 4/100 = 0.04
Energy used by engine
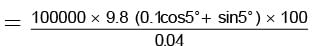
As 1 kg coal yields 50000 J, we have the amount of coal burnt up
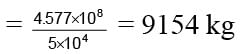
Physically, the notion of potential energy is applicable only to- a)The class of forces where work done against the force gets stored up as energy.
- b)The class of forces where work done against the force gets dissipated
- c)The class of forces where work done against the force gets converted to thermal energy
- d)The class of forces where work done against the force gets converted to kinetic energy
Correct answer is option 'A'. Can you explain this answer?
Physically, the notion of potential energy is applicable only to
a)
The class of forces where work done against the force gets stored up as energy.
b)
The class of forces where work done against the force gets dissipated
c)
The class of forces where work done against the force gets converted to thermal energy
d)
The class of forces where work done against the force gets converted to kinetic energy
|
|
Mahi Nair answered |
Understanding Potential Energy
Potential energy is a crucial concept in physics that applies specifically to certain types of forces. It is essential to grasp which forces allow for the accumulation of energy based on work done against them.
Class of Forces for Potential Energy
- Definition: Potential energy is defined as the energy stored in an object due to its position or configuration.
- Work Done Against Force: The key aspect is that potential energy arises when work is done against a conservative force.
Conservative Forces
- Examples: Gravitational force and elastic force (like a spring) are classic examples of conservative forces.
- Energy Storage: When work is done against these forces, energy is stored in the system, which can later be converted back into kinetic energy or work.
Non-Conservative Forces
- Dissipative Forces: Forces such as friction or air resistance do not allow for the storage of potential energy.
- Energy Dissipation: When work is done against these forces, energy is transformed into thermal energy, not stored.
Key Takeaway
- Potential Energy Applicability: Therefore, the notion of potential energy is applicable only to the class of forces where work done against the force gets stored up as energy. This is why option 'A' is the correct choice.
Understanding these distinctions helps clarify when and how potential energy can be effectively utilized in physical systems.
Potential energy is a crucial concept in physics that applies specifically to certain types of forces. It is essential to grasp which forces allow for the accumulation of energy based on work done against them.
Class of Forces for Potential Energy
- Definition: Potential energy is defined as the energy stored in an object due to its position or configuration.
- Work Done Against Force: The key aspect is that potential energy arises when work is done against a conservative force.
Conservative Forces
- Examples: Gravitational force and elastic force (like a spring) are classic examples of conservative forces.
- Energy Storage: When work is done against these forces, energy is stored in the system, which can later be converted back into kinetic energy or work.
Non-Conservative Forces
- Dissipative Forces: Forces such as friction or air resistance do not allow for the storage of potential energy.
- Energy Dissipation: When work is done against these forces, energy is transformed into thermal energy, not stored.
Key Takeaway
- Potential Energy Applicability: Therefore, the notion of potential energy is applicable only to the class of forces where work done against the force gets stored up as energy. This is why option 'A' is the correct choice.
Understanding these distinctions helps clarify when and how potential energy can be effectively utilized in physical systems.
Chapter doubts & questions for Work, Energy and Power - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Work, Energy and Power - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup