All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Angular Momentum for EmSAT Achieve Exam
A person standing on a rotating platform with his hands lowered outstretches his arms. The angular momentum of the person- a)becomes zero
- b)decreases
- c)remains constant
- d)inreases
Correct answer is option 'C'. Can you explain this answer?
A person standing on a rotating platform with his hands lowered outstretches his arms. The angular momentum of the person
a)
becomes zero
b)
decreases
c)
remains constant
d)
inreases
|
|
Suresh Reddy answered |
Yes because there is absence of any external force or torque so angular momentum will remain constant
here outstretching the hands means internal forces are working.. so moment of inertia increases in this case and to make angular momentum constant when angular velocity decreases.
here outstretching the hands means internal forces are working.. so moment of inertia increases in this case and to make angular momentum constant when angular velocity decreases.
A circus acrobat while performing spins brings his limbs closer to the body. Due to this- a)Moment of inertia increases and angular velocity increases
- b)Moment of inertia decreases and angular velocity decreases
- c)Moment of inertia increases and angular velocity decreases
- d)Moment of inertia decreases and angular velocity increases
Correct answer is option 'D'. Can you explain this answer?
A circus acrobat while performing spins brings his limbs closer to the body. Due to this
a)
Moment of inertia increases and angular velocity increases
b)
Moment of inertia decreases and angular velocity decreases
c)
Moment of inertia increases and angular velocity decreases
d)
Moment of inertia decreases and angular velocity increases

|
Akshay Shah answered |
While in the pike position the body decreases in radius as each segment moves closer to the axis of rotation, resulting in angular velocity increasing and a decrease of moment of inertia. Thus, during a dive, angular momentum is constant meaning that moment of inertia is inversely proportional to angular velocity.
The mass of an electron is 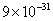 kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of
kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of 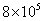 m/s. The angular momentum of electron is
m/s. The angular momentum of electron is- a)2.24 x 10-4 kgm2s-1
- b)3.24 x 10-34 kgm2s-1
- c)4.24 x10-34 kgm2s-1
- d)2.24 x 10-34 kgm2s-1
Correct answer is option 'B'. Can you explain this answer?
The mass of an electron is 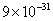 kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of
kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of 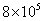 m/s. The angular momentum of electron is
m/s. The angular momentum of electron is
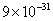 kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of
kg. It revolves around the nucleus of an atom in a circular orbit of radius 4.5 Å, with a speed of 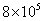 m/s. The angular momentum of electron is
m/s. The angular momentum of electron isa)
2.24 x 10-4 kgm2s-1
b)
3.24 x 10-34 kgm2s-1
c)
4.24 x10-34 kgm2s-1
d)
2.24 x 10-34 kgm2s-1
|
|
Malavika Roy answered |
To find the speed of the electron, we can use the centripetal force formula:
F = mv²/r
Where F is the centripetal force, m is the mass of the electron, v is the speed of the electron, and r is the radius of the orbit.
The centripetal force is provided by the electrostatic force between the electron and the nucleus. This force is given by Coulomb's law:
F = k * (e² / r²)
Where k is the electrostatic constant, e is the charge of the electron, and r is the radius of the orbit.
Since the centripetal force and the electrostatic force are equal, we can set them equal to each other:
mv²/r = k * (e² / r²)
We can solve this equation for v:
v = √((k * e²) / (m * r))
Plugging in the given values:
k = 8.99 x 10^9 Nm²/C² (electrostatic constant)
e = 1.6 x 10^-19 C (charge of the electron)
m = 9 x 10^-31 kg (mass of the electron)
r = 4.5 x 10^-11 m (radius of the orbit)
v = √((8.99 x 10^9 Nm²/C² * (1.6 x 10^-19 C)²) / (9 x 10^-31 kg * 4.5 x 10^-11 m))
v ≈ 2.19 x 10^6 m/s
Therefore, the speed of the electron is approximately 2.19 x 10^6 m/s.
F = mv²/r
Where F is the centripetal force, m is the mass of the electron, v is the speed of the electron, and r is the radius of the orbit.
The centripetal force is provided by the electrostatic force between the electron and the nucleus. This force is given by Coulomb's law:
F = k * (e² / r²)
Where k is the electrostatic constant, e is the charge of the electron, and r is the radius of the orbit.
Since the centripetal force and the electrostatic force are equal, we can set them equal to each other:
mv²/r = k * (e² / r²)
We can solve this equation for v:
v = √((k * e²) / (m * r))
Plugging in the given values:
k = 8.99 x 10^9 Nm²/C² (electrostatic constant)
e = 1.6 x 10^-19 C (charge of the electron)
m = 9 x 10^-31 kg (mass of the electron)
r = 4.5 x 10^-11 m (radius of the orbit)
v = √((8.99 x 10^9 Nm²/C² * (1.6 x 10^-19 C)²) / (9 x 10^-31 kg * 4.5 x 10^-11 m))
v ≈ 2.19 x 10^6 m/s
Therefore, the speed of the electron is approximately 2.19 x 10^6 m/s.
A particle of mass 1 kg is fired from the origin of the co-ordinate axis-making angle 45 with the horizontal. After time t its position vector is 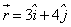 and velocity
and velocity 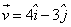 . What is the angular momentum of the particle at that instant?
. What is the angular momentum of the particle at that instant?- a)-25
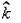
- b)-7
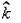
- c)25
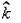
- d)7
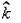
Correct answer is option 'A'. Can you explain this answer?
A particle of mass 1 kg is fired from the origin of the co-ordinate axis-making angle 45 with the horizontal. After time t its position vector is 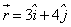 and velocity
and velocity 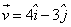 . What is the angular momentum of the particle at that instant?
. What is the angular momentum of the particle at that instant?
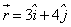 and velocity
and velocity 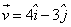 . What is the angular momentum of the particle at that instant?
. What is the angular momentum of the particle at that instant?a)
-25 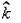
b)
-7 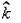
c)
25 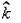
d)
7 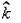
|
|
Anaya Patel answered |
A uniform circular disc of radius 50 cm at rest is free to turn about an axis having perpendicular to its plane and passes through its centre. This situation can be shown by the figure given below:
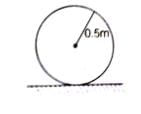
Therefore,

Therefore,
Angular acceleration = α = 2 rad/s2
Angular speed, ω = αt = 4 rad/s
Centripetal acceleration, ac = ω2r
42 x 0.5
=16 x 0.5
= 8m/s2
Linear acceleration at the end of 2 s is,
at = αt = 2 x 0.5 = 1 m/s2
Therefore, the net acceleration at the end of 2.0 sec is given by
An earth satellite is moving around the earth in a circular orbit. In such case, what is conserved?- a)angular momentum
- b)force
- c)linear momentum
- d)velocity
Correct answer is option 'A'. Can you explain this answer?
An earth satellite is moving around the earth in a circular orbit. In such case, what is conserved?
a)
angular momentum
b)
force
c)
linear momentum
d)
velocity
|
|
Preeti Iyer answered |
Angular Momentum is conserved
Mvr = constant
We can say that v is proportional to 1/r. When satellite stays near earth then velocity of the satellite is maximum.
Mvr = constant
We can say that v is proportional to 1/r. When satellite stays near earth then velocity of the satellite is maximum.
kgm2s-1 is the unit of- a)force
- b)angular momentum
- c)tourqe
- d)moment of inertia
Correct answer is option 'B'. Can you explain this answer?
kgm2s-1 is the unit of
a)
force
b)
angular momentum
c)
tourqe
d)
moment of inertia
|
|
Raghav Bansal answered |
L = Iw
L is the angular momentum, I is the MOI and w is the rotational velocity.
[I] = [ML2T0], [w] = [M0L0T-1]
[L] = [MLT-1]
L is the angular momentum, I is the MOI and w is the rotational velocity.
[I] = [ML2T0], [w] = [M0L0T-1]
[L] = [MLT-1]
An earth satellite is moving around the earth in a circular orbit. In such case, what is conserved?- a)force
- b)velocity
- c)angular momentum
- d)linear momentum
Correct answer is option 'C'. Can you explain this answer?
An earth satellite is moving around the earth in a circular orbit. In such case, what is conserved?
a)
force
b)
velocity
c)
angular momentum
d)
linear momentum
|
|
Geetika Shah answered |
An earth satellite is moving in a circular motion due to change in the direction of velocity. Its angular momentum about centre is conserved as there is no external force acting on the system.
The earth rotates about an axis passing through its north and south poles with a period of one day. If it is struck by meteorites, then- a)moment of inertia decreases and angular velocity increases
- b)moment of inertia decreases and angular velocity decreases
- c)moment of inertia increases and angular velocity decreases
- d)moment of inertia increases and angular velocity increases
Correct answer is option 'C'. Can you explain this answer?
The earth rotates about an axis passing through its north and south poles with a period of one day. If it is struck by meteorites, then
a)
moment of inertia decreases and angular velocity increases
b)
moment of inertia decreases and angular velocity decreases
c)
moment of inertia increases and angular velocity decreases
d)
moment of inertia increases and angular velocity increases
|
|
Neha Joshi answered |
Because angular momentum remains constant as the moment of inertia is increasing here so the angular velocity will decrease.
A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rpm. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment if inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.- a)16 rpm
- b)100 rpm
- c)40 rpm
- d)Given data is not sufficient.
Correct answer is option 'B'. Can you explain this answer?
A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rpm. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment if inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
a)
16 rpm
b)
100 rpm
c)
40 rpm
d)
Given data is not sufficient.
|
|
Neha Joshi answered |
Angular momentum is conserved.
I1w1 = I2w2
I2 = (2/5)I1
I1(40) = (2/5)I1w2
w2 = 100 rpm
I1w1 = I2w2
I2 = (2/5)I1
I1(40) = (2/5)I1w2
w2 = 100 rpm
Angular momentum is equal to____.(All the symbols used have their usual meanings)- a)L = I2ω
- b)L = Iω
- c)L = ma
- d)L = I/α
Correct answer is option 'B'. Can you explain this answer?
Angular momentum is equal to____.(All the symbols used have their usual meanings)
a)
L = I2ω
b)
L = Iω
c)
L = ma
d)
L = I/α
|
|
Neha Joshi answered |
Angular momentum is equal to L = Iω. It is the formula.
A sphere of mass 1 kg and radius 1m rotates with a speed of 100 rpm about the axis passing through its centre. Calculate the angular momentum.- a)1.90 kg ms-1
- b)1.90 kg m2s-1
- c)19.0 kg ms-1
- d)19.0 kg m2s-1
Correct answer is option 'B'. Can you explain this answer?
A sphere of mass 1 kg and radius 1m rotates with a speed of 100 rpm about the axis passing through its centre. Calculate the angular momentum.
a)
1.90 kg ms-1
b)
1.90 kg m2s-1
c)
19.0 kg ms-1
d)
19.0 kg m2s-1
|
|
Preeti Iyer answered |
L=Iω2(L- angular momentum)
I(moment of inertia)=mr2
L=1×1×100/60
L=1.6 kgm2s-1
≈1.9 kgm2s-1
I(moment of inertia)=mr2
L=1×1×100/60
L=1.6 kgm2s-1
≈1.9 kgm2s-1
Space craft orientation is based on the principle of:- a)conservation of energy
- b)conservation of linear momentum
- c)conservation of angular momentum
- d)all of the above
Correct answer is option 'C'. Can you explain this answer?
Space craft orientation is based on the principle of:
a)
conservation of energy
b)
conservation of linear momentum
c)
conservation of angular momentum
d)
all of the above
|
|
Anand Kapoor answered |
Conservation of angular momentum is the principle on which spacecraft orientation is based. Angular momentum is a fundamental concept in physics that describes the rotational motion of an object. It is defined as the product of an object's moment of inertia and its angular velocity.
Explanation:
When a spacecraft is in motion, it possesses angular momentum due to its rotation. According to the principle of conservation of angular momentum, the total angular momentum of a system remains constant unless acted upon by an external torque. This means that the spacecraft will continue to rotate at a constant rate unless a torque is applied to change its angular momentum.
In the context of spacecraft orientation, the conservation of angular momentum is crucial for maintaining the stability and control of the spacecraft. Here's how it works:
1. Initial angular momentum: When a spacecraft is launched into space, it has an initial angular momentum that is determined by its moment of inertia and angular velocity.
2. Action and reaction: In the absence of external torques, the spacecraft will continue to rotate at a constant rate due to the conservation of angular momentum. Any action taken by the spacecraft to change its orientation will result in an equal and opposite reaction, as required by Newton's third law of motion.
3. Reaction wheels: To control the spacecraft's orientation, reaction wheels are used. These wheels are motor-driven devices that can change their rotational speed. By spinning the reaction wheels in different directions or changing their speeds, the spacecraft can exert torques on itself and alter its angular momentum.
4. Principle application: By carefully controlling the angular momentum of the reaction wheels, the spacecraft can achieve the desired orientation. For example, if the spacecraft needs to rotate along a particular axis, it can spin one or more reaction wheels in the opposite direction to generate a torque that counteracts the existing angular momentum and causes the spacecraft to rotate.
In conclusion, the conservation of angular momentum is the principle that governs spacecraft orientation. By applying torques through reaction wheels, the spacecraft can change its angular momentum and achieve the desired orientation in space.
Explanation:
When a spacecraft is in motion, it possesses angular momentum due to its rotation. According to the principle of conservation of angular momentum, the total angular momentum of a system remains constant unless acted upon by an external torque. This means that the spacecraft will continue to rotate at a constant rate unless a torque is applied to change its angular momentum.
In the context of spacecraft orientation, the conservation of angular momentum is crucial for maintaining the stability and control of the spacecraft. Here's how it works:
1. Initial angular momentum: When a spacecraft is launched into space, it has an initial angular momentum that is determined by its moment of inertia and angular velocity.
2. Action and reaction: In the absence of external torques, the spacecraft will continue to rotate at a constant rate due to the conservation of angular momentum. Any action taken by the spacecraft to change its orientation will result in an equal and opposite reaction, as required by Newton's third law of motion.
3. Reaction wheels: To control the spacecraft's orientation, reaction wheels are used. These wheels are motor-driven devices that can change their rotational speed. By spinning the reaction wheels in different directions or changing their speeds, the spacecraft can exert torques on itself and alter its angular momentum.
4. Principle application: By carefully controlling the angular momentum of the reaction wheels, the spacecraft can achieve the desired orientation. For example, if the spacecraft needs to rotate along a particular axis, it can spin one or more reaction wheels in the opposite direction to generate a torque that counteracts the existing angular momentum and causes the spacecraft to rotate.
In conclusion, the conservation of angular momentum is the principle that governs spacecraft orientation. By applying torques through reaction wheels, the spacecraft can change its angular momentum and achieve the desired orientation in space.
In case of a projectile, the angular momentum is minimum- a)at some location other than those mentioned above
- b)at the starting point
- c)at the highest point
- d)on return to the ground
Correct answer is option 'B'. Can you explain this answer?
In case of a projectile, the angular momentum is minimum
a)
at some location other than those mentioned above
b)
at the starting point
c)
at the highest point
d)
on return to the ground

|
Imk Pathsala answered |
At the starting point of the projectile, the perpendicular distance from the point of rotation is zero as it's on the ground itself. Since one factor of the product is zero, the angular momentum at the starting point will be zero too.
Relation between torque and angular momentum is similar to the relation between- a)force and linear momentum
- b)energy and displacement
- c)acceleration and velocity
- d)mass and moment of inertia
Correct answer is option 'A'. Can you explain this answer?
Relation between torque and angular momentum is similar to the relation between
a)
force and linear momentum
b)
energy and displacement
c)
acceleration and velocity
d)
mass and moment of inertia
|
|
Jayant Mishra answered |
Torque is the rate of change of angular momentum.
Force in linear motion corresponds to Torque in rotary motion.
Thus, just as Newton’s second law can be written as F=dP/dtF for linear motion, it can be written as T=dL/dt for rotary motion.
A child can balance himself on a moving cycle than on a stationary cycle. Based on- a)Conservation of Angular Momentum
- b)Conservation of Energy
- c)Conservation of Momentum
- d)Conservation of Kinetic Energy Only
Correct answer is option 'A'. Can you explain this answer?
A child can balance himself on a moving cycle than on a stationary cycle. Based on
a)
Conservation of Angular Momentum
b)
Conservation of Energy
c)
Conservation of Momentum
d)
Conservation of Kinetic Energy Only
|
|
Preeti Khanna answered |
Spinning wheels have angular momentum, and when you're sitting on a bike, you and it and its wheels make up a system that obeys the principle of conservation of angular momentum.
Which of the following doesn’t use the application of Conservation of Angular Momentum?- a)Cat landing gently on feet
- b)A skater performing a fast spin
- c)A diver performing somersaults while diving
- d)Fruit falling off the tree
Correct answer is option 'D'. Can you explain this answer?
Which of the following doesn’t use the application of Conservation of Angular Momentum?
a)
Cat landing gently on feet
b)
A skater performing a fast spin
c)
A diver performing somersaults while diving
d)
Fruit falling off the tree
|
|
Jyoti Kapoor answered |
An example of conservation of angular momentum is seen in an ice skater executing a spin, as shown in. ... Conservation of angular momentum is one of the key conservation laws in physics, along with the conservation laws for energy and (linear) momentum.
Other Causes of Fruit Drop. ... A severe pest infestation can also stress the tree enough to cause fruit drop. Sudden changes in temperature, particularly when high temperatures occur at or shortly after fruit set, can cause fruit drop.
What is the relation between torque and angular momentum?- a)T = ωl
- b)
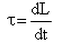
- c)T = L/t
- d)T = lω2
Correct answer is option 'B'. Can you explain this answer?
What is the relation between torque and angular momentum?
a)
T = ωl
b)
c)
T = L/t
d)
T = lω2

|
Imk Pathsala answered |
Option B is the correct answer.
A circus acrobat while performing spins brings his limbs closer to the body. Due to this- a)Angular Momentum is conserved but K.E. is not conserved
- b)Angular Momentum is not conserved and also K.E. is not conserved.
- c)Angular Momentum is not conserved but K.E. is conserved
- d)Angular Momentum is conserved and also K.E. is conserved
Correct answer is option 'A'. Can you explain this answer?
A circus acrobat while performing spins brings his limbs closer to the body. Due to this
a)
Angular Momentum is conserved but K.E. is not conserved
b)
Angular Momentum is not conserved and also K.E. is not conserved.
c)
Angular Momentum is not conserved but K.E. is conserved
d)
Angular Momentum is conserved and also K.E. is conserved

|
Madhavan Patel answered |
Momentum is conserved, but internal kinetic energy is not conserved. (a) Two objects of equal mass initially head directly toward one another at the same speed. (b) The objects stick together (a perfectly inelastic collision), and so their final velocity is zero.
Chapter doubts & questions for Angular Momentum - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Angular Momentum - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









