All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Rotational Work & Energy for EmSAT Achieve Exam
The work done to increase the velocity of a 1500 kg car from 36 km/h to 72 km/h is- a)4.5 × 104 J
- b)2.25 × 105 J
- c)7.5 × 104 J
- d)4.5 × 105 J
Correct answer is option 'B'. Can you explain this answer?
The work done to increase the velocity of a 1500 kg car from 36 km/h to 72 km/h is
a)
4.5 × 104 J
b)
2.25 × 105 J
c)
7.5 × 104 J
d)
4.5 × 105 J
|
Mariam Yousif Al Hamoudi answered |
Understanding Work Done on a Car
To calculate the work done to increase the velocity of the car, we use the concept of kinetic energy (KE). The work done is equal to the change in kinetic energy.
1. Kinetic Energy Formula
The kinetic energy of an object is given by the formula:
- KE = (1/2) * m * v²
Where:
- m = mass of the object (in kg)
- v = velocity of the object (in m/s)
2. Convert Velocities
First, convert the velocities from km/h to m/s:
- 36 km/h = 36 * (1000 m / 3600 s) = 10 m/s
- 72 km/h = 72 * (1000 m / 3600 s) = 20 m/s
3. Calculate Initial and Final Kinetic Energies
- Initial KE (at 10 m/s):
- KE_initial = (1/2) * 1500 kg * (10 m/s)²
- KE_initial = (1/2) * 1500 * 100 = 75000 J
- Final KE (at 20 m/s):
- KE_final = (1/2) * 1500 kg * (20 m/s)²
- KE_final = (1/2) * 1500 * 400 = 300000 J
4. Calculate the Work Done
The work done (W) is the change in kinetic energy:
- W = KE_final - KE_initial
- W = 300000 J - 75000 J = 225000 J
5. Conclusion
The work done to increase the velocity of the car from 36 km/h to 72 km/h is 2.25 × 10^5 J, confirming that the correct answer is option 'B'.
To calculate the work done to increase the velocity of the car, we use the concept of kinetic energy (KE). The work done is equal to the change in kinetic energy.
1. Kinetic Energy Formula
The kinetic energy of an object is given by the formula:
- KE = (1/2) * m * v²
Where:
- m = mass of the object (in kg)
- v = velocity of the object (in m/s)
2. Convert Velocities
First, convert the velocities from km/h to m/s:
- 36 km/h = 36 * (1000 m / 3600 s) = 10 m/s
- 72 km/h = 72 * (1000 m / 3600 s) = 20 m/s
3. Calculate Initial and Final Kinetic Energies
- Initial KE (at 10 m/s):
- KE_initial = (1/2) * 1500 kg * (10 m/s)²
- KE_initial = (1/2) * 1500 * 100 = 75000 J
- Final KE (at 20 m/s):
- KE_final = (1/2) * 1500 kg * (20 m/s)²
- KE_final = (1/2) * 1500 * 400 = 300000 J
4. Calculate the Work Done
The work done (W) is the change in kinetic energy:
- W = KE_final - KE_initial
- W = 300000 J - 75000 J = 225000 J
5. Conclusion
The work done to increase the velocity of the car from 36 km/h to 72 km/h is 2.25 × 10^5 J, confirming that the correct answer is option 'B'.
Moment of inertia, rotational kinetic energy, and angular momentum of a body is I, E, and L respectively then :- a)I = E/L
- b)L = EI
- c)E = 2IL
- d)L = √(2EI)
Correct answer is option 'D'. Can you explain this answer?
Moment of inertia, rotational kinetic energy, and angular momentum of a body is I, E, and L respectively then :
a)
I = E/L
b)
L = EI
c)
E = 2IL
d)
L = √(2EI)
|
Faisal Al Saadi answered |
Understanding the Concepts
To derive the relationship among moment of inertia (I), rotational kinetic energy (E), and angular momentum (L), we need to understand each concept clearly.
Moment of Inertia (I)
- Moment of inertia quantifies how mass is distributed in relation to an axis of rotation.
- It is a measure of an object's resistance to changes in its rotational motion.
Rotational Kinetic Energy (E)
- This is the energy an object possesses due to its rotation.
- The formula for rotational kinetic energy is E = 1/2 Iω², where ω is the angular velocity.
Angular Momentum (L)
- Angular momentum is the product of moment of inertia and angular velocity.
- The formula is L = Iω.
Deriving the Relationship
To find the relationship between E, I, and L, we can manipulate the equations:
1. From L = Iω, we can express ω as:
- ω = L/I
2. Substitute ω into the equation for E:
- E = 1/2 I(L/I)²
- E = 1/2 I(L²/I²)
- E = 1/2 (L²/I)
3. Rearranging gives:
- L² = 2EI
- L = √(2EI)
Conclusion
Thus, the correct relationship is L = √(2EI). This means that angular momentum is directly related to both the rotational kinetic energy and the moment of inertia, confirming that option D is indeed correct.
To derive the relationship among moment of inertia (I), rotational kinetic energy (E), and angular momentum (L), we need to understand each concept clearly.
Moment of Inertia (I)
- Moment of inertia quantifies how mass is distributed in relation to an axis of rotation.
- It is a measure of an object's resistance to changes in its rotational motion.
Rotational Kinetic Energy (E)
- This is the energy an object possesses due to its rotation.
- The formula for rotational kinetic energy is E = 1/2 Iω², where ω is the angular velocity.
Angular Momentum (L)
- Angular momentum is the product of moment of inertia and angular velocity.
- The formula is L = Iω.
Deriving the Relationship
To find the relationship between E, I, and L, we can manipulate the equations:
1. From L = Iω, we can express ω as:
- ω = L/I
2. Substitute ω into the equation for E:
- E = 1/2 I(L/I)²
- E = 1/2 I(L²/I²)
- E = 1/2 (L²/I)
3. Rearranging gives:
- L² = 2EI
- L = √(2EI)
Conclusion
Thus, the correct relationship is L = √(2EI). This means that angular momentum is directly related to both the rotational kinetic energy and the moment of inertia, confirming that option D is indeed correct.
The bullet fired from a gun possesses which form of energy, that can pierce a target?- a)Kinetic Energy
- b)Gravitational Energy
- c)Potential Energy
- d)Nuclear Energy
Correct answer is option 'A'. Can you explain this answer?
The bullet fired from a gun possesses which form of energy, that can pierce a target?
a)
Kinetic Energy
b)
Gravitational Energy
c)
Potential Energy
d)
Nuclear Energy
|
Arien Instructors answered |
The correct answer is Kinetic Energy.
- The kinetic energy of an object is defined as the energy that it possesses due to its motion.
Key Points
- Thus, an object that has motion possesses kinetic energy.
- The amount of kinetic energy that an object has depends upon two variables i.e. the mass (m) of the object and the speed (v) of the object.
- A bullet moves with a large velocity and as such possesses a lot of kinetic energy.
- The work done in piercing the target is derived from the kinetic energy of the bullet.
The expression Iω2/2 represents Rotational ____________
- a)Kinetic energy
- b)Angular momentum
- c)Torque
- d)Power
Correct answer is option 'A'. Can you explain this answer?
The expression Iω2/2 represents Rotational ____________
a)
Kinetic energy
b)
Angular momentum
c)
Torque
d)
Power
|
|
Arien Instructors answered |
CONCEPT:
- Rotational kinetic energy: The energy, which a body has by virtue of its rotational motion, is called rotational kinetic energy.
- A body rotating about a fixed axis possesses kinetic energy because its constituent particles are in motion, even though the body as a whole remains in place.
- Mathematically rotational kinetic energy can be written as -
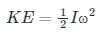
Where I = moment of inertia and ω = angular velocity.
EXPLANATION:
- From above it is clear that,
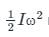represents rotational kinetic energy.
Important Point
If a body is rolling down from a hill at certain height, the body will have- a)Kinetic Energy only
- b)Rotational energy and Kinetic energy only
- c)Potential energy only
- d)Kinetic energy, Rotational energy and potential energy
Correct answer is option 'D'. Can you explain this answer?
If a body is rolling down from a hill at certain height, the body will have
a)
Kinetic Energy only
b)
Rotational energy and Kinetic energy only
c)
Potential energy only
d)
Kinetic energy, Rotational energy and potential energy
|
|
Arien Instructors answered |
CONCEPT:
- When a body moves in a linear direction, it possesses kinetic energy.
- The Kinetic Energy of an object due to its linear speed is given by
E = 1/2 (m × v2)
where m is the mass of a body and v is the speed.
- When a body does the rotational motion, it possesses rotational kinetic energy.
E = 1/2 (I × ω2)
where I is the moment of inertia of the body, and ω is the angular velocity.
- When a body is at a certain height, it has potential energy.
PE = m g h
where m is the mass of a body, g is gravitational acceleration, and h is the height from the earth's surface.
EXPLANATION:
- Kinetic energy: Since the body is moving in a linear direction, so it will have kinetic energy due to its velocity.
- Rotational energy: Along with linear velocity, the body is also revolving i.e. rotating, so it will have rotation energy.
- Potential energy: Since the body is at a certain height, it will have potential energy.
- Hence the body will have all three Kinetic energy, Rotational energy, and potential energy.
- So the correct answer is option 4.
A thin ring of mass 10 kg is rolling on the horizontal ground such that its center of mass has a velocity of 2 m/s. How much work (in joules) needs to be done to stop it?- a)40
- b)20
- c)10
- d)80
Correct answer is option 'A'. Can you explain this answer?
A thin ring of mass 10 kg is rolling on the horizontal ground such that its center of mass has a velocity of 2 m/s. How much work (in joules) needs to be done to stop it?
a)
40
b)
20
c)
10
d)
80
|
|
Arien Instructors answered |
CONCEPT:
Kinetic energy (K.E):
- The energy possessed by a body by virtue of its motion is called kinetic energy.
- The expression for kinetic energy is
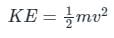
Where m = mass of the body and v = velocity of the body
Rotational Kinetic energy (KE):
- The energy, which a body has by virtue of its rotational motion, is called rotational kinetic energy.
- A body rotating about a fixed axis possesses kinetic energy because its constituent particles are in motion, even though the body as a whole remains in place.
- Mathematically rotational kinetic energy can be written as
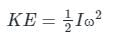
Where I = moment of inertia and ω = angular velocity.
Condition of rolling is
⇒ V = rω
Where ω = angular velocity and V = linear velocity
CALCULATION:
Given - mass (m) = 10 kg and velocity (V) = 2 m/s
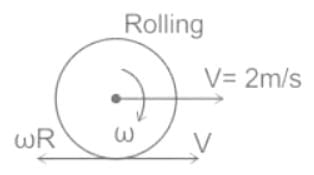
- Moment of inertia of thin circular ring is
⇒ I = mR2
- Work (in joules) needs to be done to stop it is
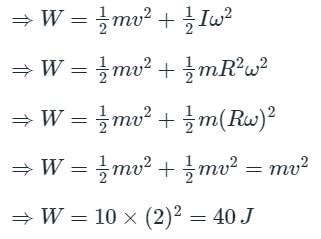
Two discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is- a)
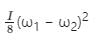
- b)
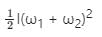
- c)
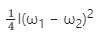
- d)
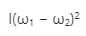
Correct answer is option 'C'. Can you explain this answer?
Two discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is
a)
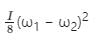
b)
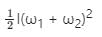
c)
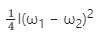
d)
|
|
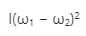
Arien Instructors answered |
Concept:
The moment of inertia is the angular mass or rotational inertia. It is defined as a quantity that decides the amount of torque required for angular acceleration.
The formula of Moment of Inertia is expressed as I = mr2 where m and r is mass and distance from the axis of rotation of the body.
The SI unit of moment of inertia is kg m2.
The kinetic energy of a body in rotational motion is calculated using the formula:
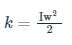
where I is a moment of inertia and w is the angular velocity of the body in rotational motion.
Calculation:
A solid cylinder of mass 10 kg and radius 0.5 m is rotating about its axis at 20 rad/s. How much is it's kinetic energy (in joules)?- a)500
- b)250
- c)1000
- d)2000
Correct answer is option 'B'. Can you explain this answer?
A solid cylinder of mass 10 kg and radius 0.5 m is rotating about its axis at 20 rad/s. How much is it's kinetic energy (in joules)?
a)
500
b)
250
c)
1000
d)
2000
|
|
Arien Instructors answered |
CONCEPT:
Kinetic energy (KE):
- The energy, which a body has by virtue of its rotational motion, is called rotational kinetic energy.
- A body rotating about a fixed axis possesses kinetic energy because its constituent particles are in motion, even though the body as a whole remains in place.
- Mathematically rotational kinetic energy can be written as –
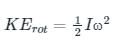
Where I = moment of inertia and ω = angular velocity.
- The moment of inertia of a solid cylinder of mass 'M' and radius 'R' about the axis of the cylinder
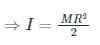
CALCULATION:
Given -
M = 10 kg, R = 0.5 m and ω = 20 rad/s
Mathematically rotational kinetic energy can be written as
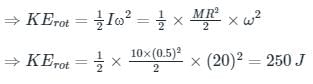
Important Point
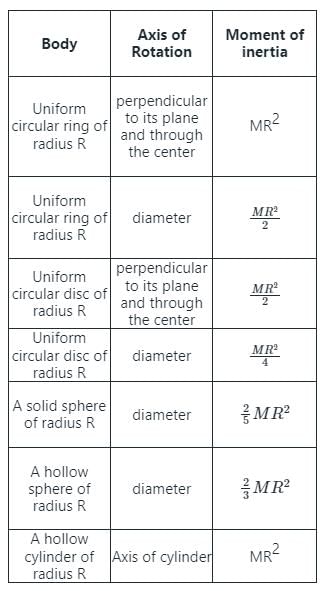
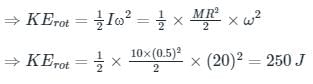
Important Point
The product of torque and angular displacement is __________. - a)Torque
- b)Work
- c)Power
- d)Angular momentum
Correct answer is option 'B'. Can you explain this answer?
The product of torque and angular displacement is __________.
a)
Torque
b)
Work
c)
Power
d)
Angular momentum
|
|
Arien Instructors answered |
CONCEPT:
- Rotational motion: When a block is moving about a fixed axis on a circular path then this type of motion is called rotational motion.
- Torque (τ): It is the twisting force that tends to cause rotation.
- The point where the object rotates is known as the axis of rotation.
Mathematically it is written as,
τ = r F sin θ
Where r is the distance between the axis of rotation and point of application of force, F is force and θ is the angle between r and F.
- Rotational power (P): The rate of work done by torque is called power.
The power associated with torque is given by the product of torque and angular velocity of the body about an axis of rotation i.e.,
⇒ P = τ ω
Where τ = torque and ω = angular velocity
Angular momentum (L) = Rotational inertia (I) × Angular velocity (ω)
EXPLANATION:
Work done by the torque (W) = Torque (τ) × angular displacement (θ)
- The product of torque and angular displacement is work. So option 2 is correct.
EXTRA POINTS:
In rotational dynamics
- Moment of inertia is the analogue of mass
- Angular velocity is analogue of linear velocity
- Angular acceleration is analogue of linear acceleration
Thus, in linear motion mass x velocity = momentum
The analogues of the moment of inertia x angular velocity = angular momentum
A thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. The velocity of the other end when it hits the fioor, assuming that the end which is on the floor does not slip, will be :- a)
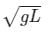
- b)
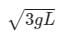
- c)
- d)
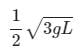
Correct answer is option 'B'. Can you explain this answer?
A thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. The velocity of the other end when it hits the fioor, assuming that the end which is on the floor does not slip, will be :
a)
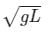
b)
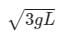
c)
d)
|
|
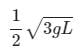
Arien Instructors answered |
CONCEPT:
- Potential Energy: Potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
- Potential energy formula: The formula for potential energy depends on the force acting on the two objects. For the gravitational force the formula is:
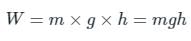
where m is the mass in kilograms, g is the acceleration due to gravity, h is the height in meters.
- Rotational Kinetic Energy: The kinetic energy of a rotating body can be compared to the linear kinetic energy and described in terms of angular velocity.
- Rotational energy occurs due to the object's rotation and is a part of its total kinetic energy. If the rotational energy is considered separately across an object's axis of rotation, the moment of inertia observed.
- Rotational energy is also known as angular kinetic energy defined as: "The kinetic energy due to the rotation of an object and is part of its total kinetic energy".
- Rotational kinetic energy is directly proportional to the rotational inertia and the square of the magnitude of the angular velocity. A rolling object has both translational and rotational kinetic energy.
- Rotational energy occurs due to the object's rotation and is a part of its total kinetic energy. If the rotational energy is considered separately across an object's axis of rotation, the moment of inertia observed.
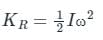
KR is the Rotational Kinetic energy, I is the Moment of Inertia, ω is the angular velocity
CALCULATION:
Using conservation of Energy:
Potential energy = Rotational kinetic energy
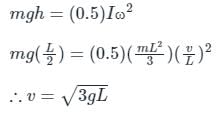
Hence option 2 is the correct answer.
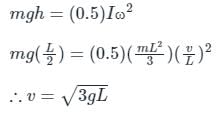
Hence option 2 is the correct answer.
Chapter doubts & questions for Rotational Work & Energy - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Rotational Work & Energy - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily