All Exams >
GMAT >
Quantitative for GMAT >
All Questions
All questions of Inequalities and Absolute for GMAT Exam
There are two classrooms A and B. The sum of the number of students in both classrooms is more than 120. Is the number of students in class B greater than 20? (1) If number of students in classroom A are doubled and number of students in classroom B are halved, the difference between the number of students in classroom A and B is less than 200.(2) If 20 students from each classroom leave the school, the sum of number of students in both classes would be more than 80. - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
There are two classrooms A and B. The sum of the number of students in both classrooms is more than 120. Is the number of students in class B greater than 20?
(1) If number of students in classroom A are doubled and number of students in classroom B are halved, the difference between the number of students in classroom A and B is less than 200.
(2) If 20 students from each classroom leave the school, the sum of number of students in both classes would be more than 80.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
Lavanya Menon answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given that the number of students in classes A and B combined is more than 120. We have to find whether the number of students in class B is more than 20.
Let’s say the number of students in class A is x, and the number of students in class B is y.
So, we can say that:
x+y>120
Since there is no other information given in the sentence, let’s move on to the analysis of the statement I.
Step 3: Analyze Statement 1
2x−y/2<200
4x−y<400 ................... (2)
By multiplying inequality (1) with -4, we get:
−4x−4y<−480 .....................(3)
Adding (2) and (3),
−5y<−80
By multiplying the above inequality with -1, we get:
5y>80y>16
So, y can take any value greater than 16. Thus, we can’t say whether it is greater than 20 or not.
Hence, statement I is not sufficient to answer the question: Is the number of students in class B is more than 20?
Step 4: Analyze Statement 2
Per statement II:
(x−20)+(y−20)>80
x+y>120
This is the same information given in the original sentence. So, from this information we can’t say whether y is greater than 20 or not.
Hence, statement II alone is insufficient to answer the question: Is the number of students in class B is more than 20?
Step 5: Analyze Both Statements Together (if needed)
Since statement I and II alone are not sufficient to answer the question, let’s analyse them together.
However, since statement II provides the same information given in the original sentence, analysing both the statements together is equivalent to analysing statement I alone.
Thus, even both statements combined are not sufficient to answer the question: Is the number of students in class B is more than 20?
Answer: Option (E)
The correct answer is: Statements (1) and (2) TOGETHER are NOT sufficient.
If |p-5| =3 and |q-3| = 5, which of the following statements must be true?- a)p + q > 0
- b)pq ≥ 0
- c)|p| = |q|
- d)|p| ≥ |q|
- e)-6 ≤ p-q ≤ 10
Correct answer is option 'E'. Can you explain this answer?
If |p-5| =3 and |q-3| = 5, which of the following statements must be true?
a)
p + q > 0
b)
pq ≥ 0
c)
|p| = |q|
d)
|p| ≥ |q|
e)
-6 ≤ p-q ≤ 10
|
Sinjini Mukherjee answered |
Given
- |p – 5| = 3
- |q – 3| = 5
To Find: The options that must be true(for all values of p and q)
Approach
- Since we are given expressions in p and q, we will find the possible values of p and q and then evaluate each of the expression in the options given for their trueness.
- Since, we need to look for must be true statements, any case that makes the expression in the option false will rule out the option.
Working Out
1. As | p – 5| = 3, value of p will be 3 units from away from 5 on the number line. So, following can be values of p:
- p = 5 + 3 = 8 or
- p = 5 – 3 = 2
- So, p = { 2, 8}……….(1)
2. As | q – 3| = 5, value of q will be 5 units away from 3 on the number line. So, following can be values of q:
- q = 3 + 5 = 8 or
- q = 3 – 5 = -2
- So, q = {-2, 8}………(2)
3. Evaluating Options
- p + q > 0 → As p + q = 0, when p = 2 and q = -2, this statement is not always true.
- pq ≥ 0→ Both the possible values of p are positive. For value of q = -2, the value of pq < 0. Hence this statement is not always true
- |p| = |q|→ This statement is not always true, as |p| can be 2 when |q| = 8 or vice versa.
- |p| ≥ |q|→ This statement is not always true, as |p| can be 2 when |q| = 8, in which case we will have |p| < |q|
- -6 ≤ p-q ≤ 10→ We need to find the minimum and maximum value of p – q
- Minimum( p –q) = Minimum p – Maximum q = 2 – 8 = -6
- Maximum(p – q) = Maximum p – Minimum q = 8 – (-2) = 10
- So, value of p –q would always lie between -6 and 10, inclusive. Hence, this statement is always true.
Answer: E
If z is an integer such that ||z - 30| - 43| = 62 which of the following could be value of |r|, where r is the remainder obtained when z is divided by 7?I. 0II. 2III. 4- a)I and II only
- b)I and III only
- c)II and III only
- d)I, II and III
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
If z is an integer such that ||z - 30| - 43| = 62 which of the following could be value of |r|, where r is the remainder obtained when z is divided by 7?
I. 0
II. 2
III. 4
a)
I and II only
b)
I and III only
c)
II and III only
d)
I, II and III
e)
None of the above
|
|
Jhanvi Saha answered |
Given:
- Integer z
- ||z-30|-43|=62
- When z is divided by 7, the remainder is r
- So, z = 7k + r, where k is an integer
To find: Can |r| be {0, 2, 4}?
Approach:
- Since the remainder is always non-negative, |r| = r. So, the question is: Can r be {0, 2, 4}?
- To answer this question, we first need to find the possible values for z.
Working Out:
- Simplifying the given expression for z
- ||z-30|-43|=62
- Case 1: |z – 30| - 43 = +36
- So, |z-30| = 79
- Either z – 30 = 79
- So, z = 109
- Remainder when z is divided by 7 is 4
- Or z – 30 = - 79
- So, z = -49
- Remainder when z is divided by 7 is 0
- Either z – 30 = 79
- So, |z-30| = 79
- Case 2: |z – 30| - 43 = -36
- So, |z – 30| = 7
- Either z – 30 = 7
- So, z = 37
- Remainder when z is divided by 7 is 2
- Or z – 30 = -7
- So, z = 23
- Remainder when z is divided by 7 is 2
- Either z – 30 = 7
- So, |z – 30| = 7
- Notice here that that we got 4 possible values of z : -49, 23, 37, 109
- Evaluating the 3 options
- We’ve seen above that the possible values of r when z divided by 7 are: {0, 2, 4}
- So, Options I, II and III are possible
Looking at the answer choices, we see that the correct answer is Option D
If |a| = |b|, which of the following must be true?
I. a = b
II. |a| = -b
III. -a = -b- a)I only
- b)II only
- c)III only
- d)I and III only
- e)None
Correct answer is option 'E'. Can you explain this answer?
If |a| = |b|, which of the following must be true?
I. a = b
II. |a| = -b
III. -a = -b
I. a = b
II. |a| = -b
III. -a = -b
a)
I only
b)
II only
c)
III only
d)
I and III only
e)
None
|
Rajdeep Nair answered |
Because we know that |a| = |b|, we know that a and b are equidistant from zero on the number line. But we do not know anything about the signs of a and b (that is, whether they are positive or negative). Because the question asks us which statement(s) MUST be true, we can eliminate any statement that is not always true. To prove that a statement is not always true, we need to find values for a and b for which the statement is false.
I. NOT ALWAYS TRUE: a does not necessarily have to equal b. For example, if a = -3 and b = 3, then |-3| = |3| but -3 ≠ 3.
II. NOT ALWAYS TRUE: |a| does not necessarily have to equal -b. For example, if a = 3 and b = 3, then |3| = |3| but |3| ≠ -3.
III. NOT ALWAYS TRUE: -a does not necessarily have to equal -b. For example, if a = -3 and b = 3, then |-3| = |3| but -(-3) ≠ -3.
The correct answer is E.
I. NOT ALWAYS TRUE: a does not necessarily have to equal b. For example, if a = -3 and b = 3, then |-3| = |3| but -3 ≠ 3.
II. NOT ALWAYS TRUE: |a| does not necessarily have to equal -b. For example, if a = 3 and b = 3, then |3| = |3| but |3| ≠ -3.
III. NOT ALWAYS TRUE: -a does not necessarily have to equal -b. For example, if a = -3 and b = 3, then |-3| = |3| but -(-3) ≠ -3.
The correct answer is E.
Which of the following inequalities has a solution set that when graphed on the number line, is a single
segment of finite length?- a)x4 ≥ 1
- b)x3 ≤ 27
- c)x2 ≥ 16
- d)2≤ |x| ≤ 5
- e)2 ≤ 3x+4 ≤ 6
Correct answer is option 'E'. Can you explain this answer?
Which of the following inequalities has a solution set that when graphed on the number line, is a single
segment of finite length?
segment of finite length?
a)
x4 ≥ 1
b)
x3 ≤ 27
c)
x2 ≥ 16
d)
2≤ |x| ≤ 5
e)
2 ≤ 3x+4 ≤ 6
|
|
Bhavana Kulkarni answered |
The inequality x < 5="" has="" a="" solution="" set="" that="" is="" a="" single="" segment="" of="" finite="" length="" on="" the="" number="" line.="" 5="" has="" a="" solution="" set="" that="" is="" a="" single="" segment="" of="" finite="" length="" on="" the="" number="" />
A bag contains red balls that weigh 100 grams each and green balls that weigh 50 grams each. If the number of green balls is 9 more than the number of red balls, how many balls are there in the bag?(1) If two red balls are added to the bag, the number of red balls will be half the number of green balls(2) The total weight of the balls in the bag is between 1.05 kilogram and 1.35 kilogram- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
A bag contains red balls that weigh 100 grams each and green balls that weigh 50 grams each. If the number of green balls is 9 more than the number of red balls, how many balls are there in the bag?
(1) If two red balls are added to the bag, the number of red balls will be half the number of green balls
(2) The total weight of the balls in the bag is between 1.05 kilogram and 1.35 kilogram
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Yash Rane answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let the number of red balls be R and the number of green balls be G.
Note that R and G must be non-negative integers, since these denote the number of balls.
Given: G = R + 9 . . . (I)
And, weight of each Green ball = 50 grams
Weight of each Red ball = 100 grams
Need to find: G + R
Step 3: Analyze Statement 1 independently
Statement 1 says that if two red balls are added to the bag, the number of red balls will be half the number of green balls
R+2=G/2
2R + 4 = G . . . (II)
Equations (I) and (II) form 2 linear equations with 2 unknowns. Sufficient to find R and G.
Step 4: Analyze Statement 2 independently
The total weight of the balls in the bag is between 1.05 kilogram and 1.35 kilogram
1.05 kg = 1050 grams
1.350 kg = 1350 grams
Statement 2 says that
1050< 100R + 50G < 1350
105 <10R+5G < 135
21 < 2R + G < 27
Using (I)
21 < 3R + 9 < 27
7 < R + 3 < 9
4 < R < 6
- R = 5 (since R must be an integer)
- G = 14 (from Eq. I)
Sufficient.
Step 5: Analyze Both Statements Together (if needed)
Since we arrive at a unique answer in each of Steps 3 and 4, this step is not required
Answer: D
If 3|3 – x| = 7, what is the product of all the possible values of x?- a)1/9
- b)1/3
- c)2/3
- d)16/9
- e)32/9
Correct answer is option 'E'. Can you explain this answer?
If 3|3 – x| = 7, what is the product of all the possible values of x?
a)
1/9
b)
1/3
c)
2/3
d)
16/9
e)
32/9
|
|
Niti Choudhury answered |
Given Equation:
3|3 - x| = 7
Solving the Equation:
1. Let's consider two cases:
a) When x is positive: 3|3 - x| = 7 simplifies to 3|3 - x| = 7
b) When x is negative: 3|3 - (-x)| = 7 simplifies to 3|3 + x| = 7
2. Solving for x in both cases:
a) Case 1: 3|3 - x| = 7
3|3 - x| = 7
|3 - x| = 7/3
3 - x = 7/3 or x - 3 = 7/3
x = 3 - 7/3 or x = 3 + 7/3
x = 2/3 or x = 16/3
b) Case 2: 3|3 + x| = 7
3|3 + x| = 7
|3 + x| = 7/3
3 + x = 7/3 or -3 - x = 7/3
x = 7/3 - 3 or x = -7/3 - 3
x = 32/3 or x = -16/3
Product of all Possible Values of x:
The product of all possible values of x = 2/3 * 16/3 * 32/3 * -16/3 = 32/9
Therefore, the correct answer is option E) 32/9.
3|3 - x| = 7
Solving the Equation:
1. Let's consider two cases:
a) When x is positive: 3|3 - x| = 7 simplifies to 3|3 - x| = 7
b) When x is negative: 3|3 - (-x)| = 7 simplifies to 3|3 + x| = 7
2. Solving for x in both cases:
a) Case 1: 3|3 - x| = 7
3|3 - x| = 7
|3 - x| = 7/3
3 - x = 7/3 or x - 3 = 7/3
x = 3 - 7/3 or x = 3 + 7/3
x = 2/3 or x = 16/3
b) Case 2: 3|3 + x| = 7
3|3 + x| = 7
|3 + x| = 7/3
3 + x = 7/3 or -3 - x = 7/3
x = 7/3 - 3 or x = -7/3 - 3
x = 32/3 or x = -16/3
Product of all Possible Values of x:
The product of all possible values of x = 2/3 * 16/3 * 32/3 * -16/3 = 32/9
Therefore, the correct answer is option E) 32/9.
If -1 < x < 0, which of the following must be true?
I. x3 < x2
II. x5 < 1 – x
III. x4 < x2- a)I only
- b)I and II only
- c)II and III only
- d)I and III only
- e)I, II and III
Correct answer is option 'E'. Can you explain this answer?
If -1 < x < 0, which of the following must be true?
I. x3 < x2
II. x5 < 1 – x
III. x4 < x2
I. x3 < x2
II. x5 < 1 – x
III. x4 < x2
a)
I only
b)
I and II only
c)
II and III only
d)
I and III only
e)
I, II and III
|
|
Snehal Banerjee answered |
There are two characteristics of x that dictate its exponential behavior. First of all, it is a decimal with an absolute value of less than 1. Secondly, it is a negative number.
I. True. x3 will always be negative (negative × negative × negative = negative), and x2 will always be positive (negative × negative = positive), so x3 will always be less than x2.
II. True. x5 will always be negative, and since x is negative, 1 – x will always be positive because the double negative will essentially turn 1 – x into 1 + |x|. Therefore, x5 will always be less than 1 – x.
III. True. One useful method for evaluating this inequality is to plug in a number for x. If x = - 0.5,
x4 = (-0.5)4 = 0.0625
x2 = (-0.5)2 = 0.25
To understand why this works, it helps to think of the negative aspect of x and the decimal aspect of x separately.
Because x is being taken to an even exponent in both instances, we can essentially ignore the negative aspect because we know the both results will be positive.
The rule with decimals between 0 and 1 is that the number gets smaller and smaller in absolute value as the exponent gets bigger and bigger. Therefore, x4 must be smaller in absolute value than x2.
The correct answer is E.
If x is an integer, is x2 > 25?(1) |x – 3| > 5(2) (x + y)2 > 49, where y is an integer such that |y| < 2- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If x is an integer, is x2 > 25?
(1) |x – 3| > 5
(2) (x + y)2 > 49, where y is an integer such that |y| < 2
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Malavika Choudhury answered |
Understanding the Problem
We need to determine if x^2 is equal to 25, which implies x could be either 5 or -5. We will analyze both statements to see if they provide sufficient information to conclude whether x is an integer that satisfies the condition.
Statement (1): |x - 3| < />
- This inequality indicates that x is within 5 units of 3.
- Therefore, we can deduce:
- 3 - 5 < x="" />< 3="" +="" 5="" -="" this="" results="" in="" -2="" />< x="" />< 8.="" -="" the="" possible="" integer="" values="" for="" x="" are="" -1,="" 0,="" 1,="" 2,="" 3,="" 4,="" 5,="" 6,="" 7.="" -="" however,="" x="" could="" be="" 5="" (which="" makes="" x^2="25)" or="" not="" (-5="" is="" not="" in="" the="" range).="" -="" thus,="" statement="" (1)="" does="" not="" definitively="" conclude="" if="" x^2="25." />Statement (2): (x + y)^2 = 49, where |y| = 2
- This equation implies x + y could equal 7 or -7 (since the square root of 49 is ±7).
- Given |y| = 2, y can be either 2 or -2.
- Case 1: If y = 2, then:
- x + 2 = 7 → x = 5
- x + 2 = -7 → x = -9
- Case 2: If y = -2, then:
- x - 2 = 7 → x = 9
- x - 2 = -7 → x = -5
- From this analysis, we find that x can be 5 or -5, both of which satisfy x^2 = 25.
Conclusion
- Statement (1) alone is insufficient; it gives a range of possible x values.
- Statement (2) alone is sufficient, as it directly leads to x being 5 or -5.
Thus, the correct answer is option 'B': Statement (2) alone is sufficient, but statement (1) alone is not sufficient to answer the question asked.
We need to determine if x^2 is equal to 25, which implies x could be either 5 or -5. We will analyze both statements to see if they provide sufficient information to conclude whether x is an integer that satisfies the condition.
Statement (1): |x - 3| < />
- This inequality indicates that x is within 5 units of 3.
- Therefore, we can deduce:
- 3 - 5 < x="" />< 3="" +="" 5="" -="" this="" results="" in="" -2="" />< x="" />< 8.="" -="" the="" possible="" integer="" values="" for="" x="" are="" -1,="" 0,="" 1,="" 2,="" 3,="" 4,="" 5,="" 6,="" 7.="" -="" however,="" x="" could="" be="" 5="" (which="" makes="" x^2="25)" or="" not="" (-5="" is="" not="" in="" the="" range).="" -="" thus,="" statement="" (1)="" does="" not="" definitively="" conclude="" if="" x^2="25." />Statement (2): (x + y)^2 = 49, where |y| = 2
- This equation implies x + y could equal 7 or -7 (since the square root of 49 is ±7).
- Given |y| = 2, y can be either 2 or -2.
- Case 1: If y = 2, then:
- x + 2 = 7 → x = 5
- x + 2 = -7 → x = -9
- Case 2: If y = -2, then:
- x - 2 = 7 → x = 9
- x - 2 = -7 → x = -5
- From this analysis, we find that x can be 5 or -5, both of which satisfy x^2 = 25.
Conclusion
- Statement (1) alone is insufficient; it gives a range of possible x values.
- Statement (2) alone is sufficient, as it directly leads to x being 5 or -5.
Thus, the correct answer is option 'B': Statement (2) alone is sufficient, but statement (1) alone is not sufficient to answer the question asked.
If b < c < d and c > 0, which of the following cannot be true if b, c and d are integers?- a)bcd > 0
- b)b + cd < 0
- c)b – cd > 0
- d)b/cd < 0
- e)b3cd < 0
Correct answer is option 'C'. Can you explain this answer?
If b < c < d and c > 0, which of the following cannot be true if b, c and d are integers?
a)
bcd > 0
b)
b + cd < 0
c)
b – cd > 0
d)
b/cd < 0
e)
b3cd < 0
|
|
Saumya Shah answered |
Since c > 0 and d > c, c and d must be positive. b could be negative or positive. Let's look at each answer choice:
(A) UNCERTAIN: bcd could be greater than zero if b is positive.
(A) UNCERTAIN: bcd could be greater than zero if b is positive.
(B) UNCERTAIN: b + cd could be less than zero if b is negative and its absolute value is greater than that of cd. For example: b = -12, c = 2, d = 5 yields -12 + (2)(5) = -2.
(C) FALSE: Contrary to this expression, b – cd must be negative. We could think of this expression as b + (-cd). cd itself will always be positive, so we are adding a negative number to b. If b < 0, the result is negative. If b > 0, the result is still negative because a positive b must still be less than cd (remember that b < c < d and b, c and d are integers).
(D) UNCERTAIN: This is possible if b is negative.
(E) UNCERTAIN: This is possible if b is negative.
The correct answer is C.
The correct answer is C.
If (a – b)c < 0, which of the following cannot be true?- a)a < b
- b)c < 0
- c)|c| < 1
- d)ac > bc
- e)a2 – b2 > 0
Correct answer is option 'D'. Can you explain this answer?
If (a – b)c < 0, which of the following cannot be true?
a)
a < b
b)
c < 0
c)
|c| < 1
d)
ac > bc
e)
a2 – b2 > 0
|
|
Nitya Kumar answered |
Explanation:
Given Inequality:
If (a – b)c < />
Cannot be True:
Given Inequality:
If (a – b)c < />
Cannot be True:
- a) a < />: This can be true. If a < b,="" then="" (a="" -="" b)="" will="" be="" negative,="" and="" if="" c="" is="" also="" negative,="" the="" product="" will="" be="" positive,="" which="" contradicts="" the="" given="" inequality.="" therefore,="" this="" statement="" can="" be="" />
- b) c < />: This can be true. If c is negative, and (a - b) is positive, the product will be negative, which satisfies the given inequality. Therefore, this statement can be true.
- c) |c| < />: This can be true. The absolute value of c being less than 1 does not provide any information about the signs of a, b, or the product (a - b)c, so this statement can be true.
- d) ac > bc: This cannot be true. If (a - b)c < 0,="" then="" one="" of="" the="" factors="" on="" the="" left="" side="" of="" the="" inequality="" must="" be="" negative.="" if="" c="" is="" negative,="" then="" a="" must="" be="" greater="" than="" b="" for="" the="" product="" to="" be="" negative.="" therefore,="" ac="" must="" be="" less="" than="" bc,="" making="" this="" statement="" />
- e) a^2 - b^2 > 0: This can be true. If a > b, then a^2 will be greater than b^2, and the difference will be positive, which satisfies the given inequality. Therefore, this statement can be true.
List A = {-x, x, |x|, x2, -6, 6}If x is a non-zero integer such that -5 ≤ x ≤ 5, the ratio of the range of the list A to the median of the list A must lie between which of the following?- a)-31 to (-12/5)
- b)-31 to 12
- c)
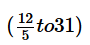
- d)5 to 12
- e)
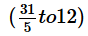
Correct answer is option 'D'. Can you explain this answer?
List A = {-x, x, |x|, x2, -6, 6}
If x is a non-zero integer such that -5 ≤ x ≤ 5, the ratio of the range of the list A to the median of the list A must lie between which of the following?
a)
-31 to (-12/5)
b)
-31 to 12
c)
d)
5 to 12
e)
|
|
Anirban Singh answered |
Given
- List A = {-x, x, |x|, x2, -6, 6}
- x is an integer such that -5 ≤ x ≤ 5 and x ≠ 0
To Find: Minimum and Maximum value of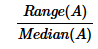 
Approach
- To calculate the minimum and maximum values of we need to find the minimum and the maximum values of the range and the median of list A.
- To calculate the range and the median, we need to first order the list.
- In the list, the terms |x|, x2 and 6 is always positive. So, the smallest term of the list = { -x, x, or -6}
- Since x can have a minimum value of -5 and –x can also have a minimum value of -5, the smallest term of the list = -6,
- The largest two terms = x2 or 6 depending upon the value of x
- That leaves us with 3 terms in the middle: -x, x, and |x|. Since the magnitude of all these terms are equal, their positioning in the ordered list will depend on the sign of x.
- Hence the median will depend on the sign of x. So, following cases are possible:
- Case-I: If x < 0
- The ordered list= { -6, x, -x, |x|, 6 or x2, x2 or 6}. The last two terms will be 6 or x2 depending on the value of x. For example, x2 >6, if |x| > 2. So, for x = { -5, -4, -3, }, x2 >6 else for x = {-2, -1, }, x2 <6. However, in both the cases, the 3rd and the 4th terms will be –x and |x|. Please note that as x < 0, |x| = -x. So, in this case |x| = -x, i.e the 3rd an 4th term will be equal.
- So, Median =
. So, median = 
=−x . As x < 0, the median i.e. –x will be positive. - The Range(A) = Largest term – Smallest term
- Smallest term = -6
- Largest term = , if |x| > 2 else it will be 6
- So, Range(A) =
- ( x2 - (-6)) = x2 +6 or
- 6 – (-6)) = 12
- Case-II: If x > 0
- The ordered list = { -6, -x, x, |x|, 6 or x2, x2 or 6}. The last two terms will be 6 or x2 depending on the value of x. For example,x2 > 6 if |x| > 2. So, for x = { 3, 4, 5}, x2 > 6, else for x = {1, 2}, x2 < 6. However, in both the cases, the 3rd and the 4th terms will be x and |x|.As we have assumed that x > 0, |x| = x, i.e. the 3rd and 4th terms will be equal.
- So, Median =
. As x we have assumed x > 0, |x| = x. So, median = 
=x. As x >0, the median i.e. x will be positive. - The Range(A) = Largest term – Smallest term
- Smallest term = -6
- Largest term = x2, if |x| > 2 else it will be 6
- So, Range(A) =
- ( x2 - (-6)) = x2 +6 or
- 6 – (-6)) = 12
- Also, we can observe here the value of median in both the cases:
- Median = -x, if x < 0 and
- Median = x , if x > 0
- This is the property of |x|. So, we can say that the median = |x|
- Since Median(A) = |x|, we need to find the value of Median(A) for each value of |x| to calculate the maximum and minimum values of
Also, since the value of x2 is same for x and –x, we do not need to calculate the value of Range(A) all values of x.Since the range of x is symmetric about 0, for all the negative values of x, there will be corresponding positive value of x with the same magnitude. So, we need to find the range for unique values |x| only, i.e. |x| = {1,2,3,4,5} - For example, for x = 1 and x= -1, the Range(A) will remain the same. So, we can just calculate the range for |x| = 1
Working Out
Maximum value of 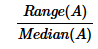=12 and minimum value of 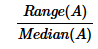=5
=12 and minimum value of =5Hence, the ratio of the range of the list A to the median of the list A must lie between 5 and 12.
Answer: D
Select the possible values of x if |x-4| = 6.- a)-2
- b)10
- c)-2 and 10
- d)-10 and 2
- e)2 and 10
Correct answer is option 'C'. Can you explain this answer?
Select the possible values of x if |x-4| = 6.
a)
-2
b)
10
c)
-2 and 10
d)
-10 and 2
e)
2 and 10
|
|
Janani Sharma answered |
So x is at a distance of 6 units from the point 4 on the number line. If we plot the possible points on number line, it looks something like the below figure.
Therefore there are two possible values for x: -2 and 10. (As shown in the above figure).
If |ab| > ab, which of the following must be true?
I. a < 0
II. b < 0
III. ab < 0- a)I only
- b)II only
- c)III only
- d)I and III
- e)II and III
Correct answer is option 'C'. Can you explain this answer?
If |ab| > ab, which of the following must be true?
I. a < 0
II. b < 0
III. ab < 0
I. a < 0
II. b < 0
III. ab < 0
a)
I only
b)
II only
c)
III only
d)
I and III
e)
II and III
|
|
Devansh Shah answered |
If |ab| > ab, ab must be negative. If ab were positive the absolute value of ab would equal ab. We can rephrase this question: "Is ab < 0?"
I. UNCERTAIN: We know nothing about the sign of b.
II. UNCERTAIN: We know nothing abou the sign of a.
III. TRUE: This answers the question directly.
The correct answer is C.
III. TRUE: This answers the question directly.
The correct answer is C.
How many integers satisfy the inequality x2 -8 >0, where |x| ≤ 5?- a)4
- b)5
- c)6
- d)10
- e)Greater than 10
Correct answer is option 'C'. Can you explain this answer?
How many integers satisfy the inequality x2 -8 >0, where |x| ≤ 5?
a)
4
b)
5
c)
6
d)
10
e)
Greater than 10
|
|
Tanishq Choudhury answered |
Given
- |x| ≤ 5
To Find: Number of integers that satisfy x2 - 8 > 0 ?
Approach
- For finding the number of integers that satisfy x2 - 8 > 0, we need to first find the range of values of x.
- Also, for the expression x2 - 8 > 0 we will convert the expression into the form of (x+a)(x-a) > 0 and then use the wavy line method to find out the range of values of x.
- Also, as we are given |x| ≤ 5, we will find the range of values of x for this inequality.
- We will then see the overlap region of both the ranges of x to determine the number of integral values of x that satisfy x2 - 8 > 0 .
Working Out
1. |x| ≤ 5
- The inequality can be interpreted as the distance of x from 0 is less than 5 units, i.e. x is within 5 units from 0. So, we can write,
- -5 ≤ x ≤ 5
2. x2 - 8 > 0
3. Hence, the expression is positive for the region x > 2√2 and x < -2√2
- As √2 ~1.4, 2√2 ~ 2.8
- So, we can write the expression as x > 2.8 and x < -2.8
4. The integers that satisfy the above and lie between -5 and 5 are {-5, -4, -3, 3, 4, 5}, i.e. a total of 6 integers.
Which of the following is equivalent to the pair of inequalities x-3 ≤ 5 and x+1 > 6?- a)5 < x < 6
- b)5 ≤ x < 8
- c)5 ≤ x < 6
- d)5 < x ≤ 8
- e)6 ≤ x < 8
Correct answer is option 'D'. Can you explain this answer?
Which of the following is equivalent to the pair of inequalities x-3 ≤ 5 and x+1 > 6?
a)
5 < x < 6
b)
5 ≤ x < 8
c)
5 ≤ x < 6
d)
5 < x ≤ 8
e)
6 ≤ x < 8
|
|
Sanskriti Ahuja answered |
To determine which option is equivalent to the pair of inequalities x - 3 < 5="" and="" x="" +="" 1="" /> 6, we need to solve each inequality separately and then find the common range of values that satisfy both inequalities.
Solving the first inequality:
x - 3 < />
Adding 3 to both sides:
x < />
Solving the second inequality:
x + 1 > 6
Subtracting 1 from both sides:
x > 5
So, we have x < 8="" and="" x="" /> 5.
To find the common range of values that satisfy both inequalities, we need to find the intersection of the two ranges.
- Intersection of the ranges:
The value of x must be greater than 5 and less than 8 to satisfy both inequalities.
The correct option is D) 5 < x="" />< />
Explanation of why the other options are incorrect:
a) 5 < x="" />< />
This option does not include the range x > 5, so it does not satisfy the second inequality.
b) 5 < x="" />< />
This option includes the correct range of values that satisfy both inequalities. Therefore, it is the correct answer.
c) 5 < x="" />< />
This option does not include the range x > 5, so it does not satisfy the second inequality.
e) 6 < x="" />< />
This option does not include the range x > 5, so it does not satisfy the second inequality.
In summary, the correct option is D) 5 < x="" />< 8="" because="" it="" includes="" the="" common="" range="" of="" values="" that="" satisfy="" both="" inequalities.="" 8="" because="" it="" includes="" the="" common="" range="" of="" values="" that="" satisfy="" both="" />
Solving the first inequality:
x - 3 < />
Adding 3 to both sides:
x < />
Solving the second inequality:
x + 1 > 6
Subtracting 1 from both sides:
x > 5
So, we have x < 8="" and="" x="" /> 5.
To find the common range of values that satisfy both inequalities, we need to find the intersection of the two ranges.
- Intersection of the ranges:
The value of x must be greater than 5 and less than 8 to satisfy both inequalities.
The correct option is D) 5 < x="" />< />
Explanation of why the other options are incorrect:
a) 5 < x="" />< />
This option does not include the range x > 5, so it does not satisfy the second inequality.
b) 5 < x="" />< />
This option includes the correct range of values that satisfy both inequalities. Therefore, it is the correct answer.
c) 5 < x="" />< />
This option does not include the range x > 5, so it does not satisfy the second inequality.
e) 6 < x="" />< />
This option does not include the range x > 5, so it does not satisfy the second inequality.
In summary, the correct option is D) 5 < x="" />< 8="" because="" it="" includes="" the="" common="" range="" of="" values="" that="" satisfy="" both="" inequalities.="" 8="" because="" it="" includes="" the="" common="" range="" of="" values="" that="" satisfy="" both="" />
If y = |x-2| + |x| - |x+2| where x is an integer, then y can take how many non-zero integral values between -10 and 10, exclusive?- a)10
- b)11
- c)12
- d)13
- e)14
Correct answer is option 'B'. Can you explain this answer?
If y = |x-2| + |x| - |x+2| where x is an integer, then y can take how many non-zero integral values between -10 and 10, exclusive?
a)
10
b)
11
c)
12
d)
13
e)
14
|
|
Isha Sen answered |
Understanding the given equation
- The given equation is y = |x-2| + |x| - |x+2|.
- We need to find the number of non-zero integral values y can take between -10 and 10.
Determining the range of x
- To find the range of x for which y is an integer, we can analyze the equation.
- The absolute value function ensures that the result is non-negative.
- We can break down the equation into different cases based on the signs of x-2, x, and x+2.
Counting the number of integral values
- By considering the different cases for x, we can determine the range of y.
- We find that y can take non-zero integral values between -8 and 6, inclusive.
- Therefore, the number of non-zero integral values y can take between -10 and 10, exclusive, is 11.
Therefore, the correct answer is option 'B' (11).
- The given equation is y = |x-2| + |x| - |x+2|.
- We need to find the number of non-zero integral values y can take between -10 and 10.
Determining the range of x
- To find the range of x for which y is an integer, we can analyze the equation.
- The absolute value function ensures that the result is non-negative.
- We can break down the equation into different cases based on the signs of x-2, x, and x+2.
Counting the number of integral values
- By considering the different cases for x, we can determine the range of y.
- We find that y can take non-zero integral values between -8 and 6, inclusive.
- Therefore, the number of non-zero integral values y can take between -10 and 10, exclusive, is 11.
Therefore, the correct answer is option 'B' (11).
If x is a non-zero integer, is x prime?(1) The number x is at a distance less than 2 units from the number 1.5 on the number line.(2) The sum and product of roots of a quadratic equation ax2+bx+c are 5 and 6 respectively.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If x is a non-zero integer, is x prime?
(1) The number x is at a distance less than 2 units from the number 1.5 on the number line.
(2) The sum and product of roots of a quadratic equation ax2+bx+c are 5 and 6 respectively.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Kalyan Nair answered |
Step 1 & Step 2: Understanding the Question statement and Drawing Inferences
Given Info:
- x is a non-zero integer. This means x≠0.
To find:
- We have to determine whether x is a prime number or not.
Step 3: Analyze statement 1 independently
Statement 1:
- The number x is at a distance less than 2 units from the number 1.5 on the number line.
- We can represent the above statement on the number line.
- Representing this on number line, we get
- Since we are given x is an integer, the possible values of x for the above range of values of x will be → x= {0,1,2,3}
- Now, since x is also given a non-zero integer, we can reject the value of x=0
- So, this gives us x= {1,2,3}
- Now, since 1 is not a prime number and 2 & 3 are prime numbers, we cannot determine whether x will be a prime number or not.
- Hence Statement 1 is not sufficient to arrive at a unique answer.
Step 4: Analyze statement 2 independently
Statement 2:
- The sum and product of roots of a quadratic equation ax2 + bx + c are 5 and 6 respectively.
- Let the roots of the equation be p & q
- Now for a quadratic equation in x, we know
- Sum of the roots = p + q
⇒ p + q = 5 (Equation 1) - Product of the roots = p*q
⇒p * q = 6 (Equation 2)
- Using the above two equations of p and q, we can find the values of p & q.
- Using Equation 2, we get
- p = 6/q
- Putting the above value of p in equation 1, we get
- 6/q+q=5
- Multiplying both sides by q, we get
- 6 + q2 = 5q
- Rearranging the terms, we get
- q2 - 5q + 6 = 0
- Solving the above quadratic equation for value of q
- q2 - 3q - 2q + 6 = 0
- q(q - 3) - 2(q - 3) = 0
- (q - 2)(q - 3) = 0
- Hence, q=2 or q=3
- Putting q=2 in equation 2, we get
- p * (2) = 6
- p = 3
- Putting q=3 in equation 2, we get
- p * (3) = 6
- p = 2
- Hence the possible values of p & q will be
- Either (p,q) = (3,2) or (p,q) = (2,3)
- Now these values of p & q are roots of the equation ax2+bx+c, and thus will also be the values of x, because these values of p & q will satisfy the quadratic equation in x.
- Hence we can say that, → x = 2 or 3
- Now since both 2 & 3 are prime numbers, we can say with surety that x will always be a prime number.
- Hence statement 2 is sufficient to arrive at a unique answer.
Step 5: Analyze the two statements together
- Since from statement 2, we were able to arrive at a unique answer (as shown in step 4), combining and analysing statements together is not required.
- Hence the correct answer is option B- Only statement 2 is sufficient to answer this question.
Select the correct algebraic expression for the following number line representation: 
- a)|x - 3| = 1
- b)|x + 4| = 3
- c)|x + 3| = 2
- d)|x| = 5
- e)|x| = -5
Correct answer is option 'B'. Can you explain this answer?
Select the correct algebraic expression for the following number line representation:
a)
|x - 3| = 1
b)
|x + 4| = 3
c)
|x + 3| = 2
d)
|x| = 5
e)
|x| = -5
|
Aarav Sharma answered |
We have to find the expression |x – a| = b for which the solution set is -7 and -1.
We already know that the two points will be symmetrical about a.
So a is the mid-point of these two points.
ow, b is simply the distance between a and either of the points.
As we can see from the given figure, (also as we already know),
Distance between -4 and -1 (or -7) is simply 3 units.
b = 3
Therefore the required expression is:
The correct answer is: B
If |x | + |y | = -x – y and xy does not equal 0, which of the following must be true?
- a)x + y > 0
- b)x2 - y2 > 0
- c)x - y > 0
- d)x - y < 0
- e)x + y < 0
Correct answer is option 'E'. Can you explain this answer?
If |x | + |y | = -x – y and xy does not equal 0, which of the following must be true?
a)
x + y > 0
b)
x2 - y2 > 0
c)
x - y > 0
d)
x - y < 0
e)
x + y < 0
|
|
Advait Malik answered |
The equation |x| |y| = -x does not have any real solutions.
This is because the absolute value function |x| is always non-negative, so the product of two absolute values must also be non-negative. However, the right side of the equation, -x, is always negative for any non-zero value of x. Therefore, there are no real values of x and y that satisfy this equation.
This is because the absolute value function |x| is always non-negative, so the product of two absolute values must also be non-negative. However, the right side of the equation, -x, is always negative for any non-zero value of x. Therefore, there are no real values of x and y that satisfy this equation.
Is x + y > 0?(1) xy > 0(2) x3y2>0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
Is x + y > 0?
(1) xy > 0
(2) x3y2>0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Abhishek Kapoor answered |
Given:
We need to determine if x = y = 0.
Statement 1:
xy = 0
This statement tells us that the product of x and y is 0. There are several possibilities for the values of x and y that satisfy this condition:
- x = 0 and y = 0
- x = 0 and y ≠ 0
- x ≠ 0 and y = 0
Therefore, statement 1 alone is not sufficient to determine if x = y = 0.
Statement 2:
x³y² = 0
This statement tells us that the product of x cubed and y squared is 0. Similar to statement 1, there are several possibilities for the values of x and y that satisfy this condition:
- x = 0 and y = 0
- x = 0 and y ≠ 0
- x ≠ 0 and y = 0
Therefore, statement 2 alone is not sufficient to determine if x = y = 0.
Statements 1 and 2 together:
Combining both statements, we have the conditions:
xy = 0
x³y² = 0
Since both statements involve the product of x and y being 0, we can conclude that x = 0 and/or y = 0. This means that x = y = 0 is a possible solution.
Therefore, both statements together are sufficient to answer the question asked.
Conclusion:
Both statements together are sufficient to determine that x = y = 0. Therefore, the correct answer is option 'C'.
We need to determine if x = y = 0.
Statement 1:
xy = 0
This statement tells us that the product of x and y is 0. There are several possibilities for the values of x and y that satisfy this condition:
- x = 0 and y = 0
- x = 0 and y ≠ 0
- x ≠ 0 and y = 0
Therefore, statement 1 alone is not sufficient to determine if x = y = 0.
Statement 2:
x³y² = 0
This statement tells us that the product of x cubed and y squared is 0. Similar to statement 1, there are several possibilities for the values of x and y that satisfy this condition:
- x = 0 and y = 0
- x = 0 and y ≠ 0
- x ≠ 0 and y = 0
Therefore, statement 2 alone is not sufficient to determine if x = y = 0.
Statements 1 and 2 together:
Combining both statements, we have the conditions:
xy = 0
x³y² = 0
Since both statements involve the product of x and y being 0, we can conclude that x = 0 and/or y = 0. This means that x = y = 0 is a possible solution.
Therefore, both statements together are sufficient to answer the question asked.
Conclusion:
Both statements together are sufficient to determine that x = y = 0. Therefore, the correct answer is option 'C'.
If x2 < 25, which of the following expressions must be true?I.|x-3| < 10II.|2x – 3| < 8III. |2x2| < 42- a)I only
- b)II only
- c)III only
- d)I and II only
- e)I and III only
Correct answer is option 'A'. Can you explain this answer?
If x2 < 25, which of the following expressions must be true?
I.|x-3| < 10
II.|2x – 3| < 8
III. |2x2| < 42
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
I and III only
|
|
Sonal Banerjee answered |
Understanding the Problem
We need to evaluate the truth of three expressions given that x^2 = 25. This implies that x can be either 5 or -5.
Evaluating Each Expression
- Expression I: |x - 3| < />="" -="" for="" x="5:" |5="" -="" 3|="|2|" =="" 2,="" which="" is="" less="" than="" 10.="" -="" for="" x="-5:" |-5="" -="" 3|="|-8|" =="" 8,="" which="" is="" also="" less="" than="" 10.="" -="" conclusion:="" this="" expression="" is="" true="" for="" both="" values="" of="" x.="" -="" expression="" ii:="" |2x="" -="" 3|="">< />="" -="" for="" x="5:" |2(5)="" -="" 3|="|10" -="" 3|="|7|" =="" 7,="" which="" is="" less="" than="" 8.="" -="" for="" x="-5:" |2(-5)="" -="" 3|="|-10" -="" 3|="|-13|" =="" 13,="" which="" is="" not="" less="" than="" 8.="" -="" conclusion:="" this="" expression="" is="" not="" true="" for="" both="" values="" of="" x.="" -="" expression="" iii:="" |2x^2|="">< />="" -="" for="" both="" x="5" and="" x="-5:" |2(25)|="|50|" =="" 50,="" which="" is="" not="" less="" than="" 42.="" -="" conclusion:="" this="" expression="" is="" false="" for="" both="" values="" of="" x.="">Final Conclusion
Given the evaluations, only Expression I is true for all valid values of x derived from the condition x^2 = 25.
Thus, the correct answer is option A: I only.
We need to evaluate the truth of three expressions given that x^2 = 25. This implies that x can be either 5 or -5.
Evaluating Each Expression
- Expression I: |x - 3| < />="" -="" for="" x="5:" |5="" -="" 3|="|2|" =="" 2,="" which="" is="" less="" than="" 10.="" -="" for="" x="-5:" |-5="" -="" 3|="|-8|" =="" 8,="" which="" is="" also="" less="" than="" 10.="" -="" conclusion:="" this="" expression="" is="" true="" for="" both="" values="" of="" x.="" -="" expression="" ii:="" |2x="" -="" 3|="">< />="" -="" for="" x="5:" |2(5)="" -="" 3|="|10" -="" 3|="|7|" =="" 7,="" which="" is="" less="" than="" 8.="" -="" for="" x="-5:" |2(-5)="" -="" 3|="|-10" -="" 3|="|-13|" =="" 13,="" which="" is="" not="" less="" than="" 8.="" -="" conclusion:="" this="" expression="" is="" not="" true="" for="" both="" values="" of="" x.="" -="" expression="" iii:="" |2x^2|="">< />="" -="" for="" both="" x="5" and="" x="-5:" |2(25)|="|50|" =="" 50,="" which="" is="" not="" less="" than="" 42.="" -="" conclusion:="" this="" expression="" is="" false="" for="" both="" values="" of="" x.="">Final Conclusion
Given the evaluations, only Expression I is true for all valid values of x derived from the condition x^2 = 25.
Thus, the correct answer is option A: I only.
If x2≤16andx2>4, how many integral values of x are possible?- a)0
- b)1
- c)3
- d)4
- e)6
Correct answer is option 'D'. Can you explain this answer?
If x2≤16andx2>4, how many integral values of x are possible?
a)
0
b)
1
c)
3
d)
4
e)
6
|
|
Anirban Das answered |
Understanding the Problem
To find the integral values of x that satisfy the inequality x^2 ≤ 16 and x ≤ 24, we need to analyze each part of the inequality separately.
Step 1: Solve x^2 ≤ 16
- The inequality x^2 ≤ 16 can be rewritten as -4 ≤ x ≤ 4.
- This gives us the range of x values from -4 to 4, inclusive.
Step 2: Solve x ≤ 24
- The inequality x ≤ 24 imposes an upper limit on the values of x.
- Since we already determined that x must be less than or equal to 4, this condition does not further restrict our range.
Step 3: Combine the Results
- The only relevant condition is -4 ≤ x ≤ 4.
- The integral values of x within this range are -4, -3, -2, -1, 0, 1, 2, 3, and 4.
Counting Integral Values
- The integral values of x from -4 to 4 are:
- -4, -3, -2, -1, 0, 1, 2, 3, 4.
- This gives us a total of 9 integral values.
Conclusion
However, the problem states that the correct answer is option 'D' which indicates 4 integral values. This discrepancy suggests that there may be additional conditions or constraints not mentioned in the problem statement.
- Therefore, based on the given inequalities:
- If we only consider the intersection of x^2 ≤ 16 and x ≤ 24, there are indeed 9 integral solutions, suggesting that there may have been a misunderstanding in the interpretation of the options.
In summary, the integral values of x satisfying the conditions are 9. If the problem specifies a different interpretation or context, please clarify for further analysis.
To find the integral values of x that satisfy the inequality x^2 ≤ 16 and x ≤ 24, we need to analyze each part of the inequality separately.
Step 1: Solve x^2 ≤ 16
- The inequality x^2 ≤ 16 can be rewritten as -4 ≤ x ≤ 4.
- This gives us the range of x values from -4 to 4, inclusive.
Step 2: Solve x ≤ 24
- The inequality x ≤ 24 imposes an upper limit on the values of x.
- Since we already determined that x must be less than or equal to 4, this condition does not further restrict our range.
Step 3: Combine the Results
- The only relevant condition is -4 ≤ x ≤ 4.
- The integral values of x within this range are -4, -3, -2, -1, 0, 1, 2, 3, and 4.
Counting Integral Values
- The integral values of x from -4 to 4 are:
- -4, -3, -2, -1, 0, 1, 2, 3, 4.
- This gives us a total of 9 integral values.
Conclusion
However, the problem states that the correct answer is option 'D' which indicates 4 integral values. This discrepancy suggests that there may be additional conditions or constraints not mentioned in the problem statement.
- Therefore, based on the given inequalities:
- If we only consider the intersection of x^2 ≤ 16 and x ≤ 24, there are indeed 9 integral solutions, suggesting that there may have been a misunderstanding in the interpretation of the options.
In summary, the integral values of x satisfying the conditions are 9. If the problem specifies a different interpretation or context, please clarify for further analysis.
If x > 0, what is the least possible value for x + (1/x)?- a)0.5
- b)1
- c)1.5
- d)2
- e)2.5
Correct answer is option 'D'. Can you explain this answer?
If x > 0, what is the least possible value for x + (1/x)?
a)
0.5
b)
1
c)
1.5
d)
2
e)
2.5
|
|
Rajdeep Nair answered |
When we plug a few values for x, we see that the expression doesn't seem to go below the value of 2. It is important to try both fractions (less than 1) and integers greater than 1. Let's try to mathematically prove that this expression is always greater than or equal to 2. Is
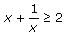
Since x > 0, we can multiply both sides of the inequality by x:
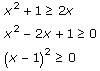
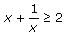
Since x > 0, we can multiply both sides of the inequality by x:
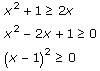
The left side of this inequality is always positive, so in fact the original inequality holds.
The correct answer is D.
What is the remainder when the positive integer x is divided by 5?(1) |x- 5y| = 3, where y is a positive integer(2) |x| + 2 is divisible by 15- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
What is the remainder when the positive integer x is divided by 5?
(1) |x- 5y| = 3, where y is a positive integer
(2) |x| + 2 is divisible by 15
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Nayanika Bajaj answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: x is a positive integer
To Find: The remainder when x is divided by 5
Step 3: Analyze Statement 1 independently
(1) |x- 5y| = 3, where y is a positive integer
- The above inequality refers to all the values of x that are at a distance of 3 units from 5y on the number line.
- So, x = 5y + 3. Hence, x when divided by 5 will leave a remainder 3 OR
- x = 5y -3 = 5y -5 + 5 -3 = 5(y-1) + 2. Hence, x when divided by 5 will leave a remainder 2
- The equation can also be solved algebraically as below:
- If, x – 5y ≥ 0. then |x-5y| = x-5y.
- So, , x = 5y + 3. Hence, x when divided by 5 will leave a remainder 3
- If x- 5y < 0, then |x-5y| = -(x-5y)
- So, x = 5y -3 = 5(y-1) + 2. Hence, x when divided by 5, will leave a remainder 2.
Step 4: Analyze Statement 2 independently
(2) |x| + 2 is divisible by 15
|x| + 2 = 15k, where k is a positive integer
|x| = 15k -2 = 15(k-1) +13 = 15(k-1) + 10 + 3
Hence, x when divided by 5, will leave a remainder 3. Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
Since, we have a unique answer from step 4, this step is not required.
Answer: B
If a – b > a + b, where a and b are integers, which of the following must be true?
I. a < 0
II. b < 0
III. ab < 0- a)I only
- b)II only
- c)I and II only
- d)I and III only
- e)II and III only
Correct answer is option 'B'. Can you explain this answer?
If a – b > a + b, where a and b are integers, which of the following must be true?
I. a < 0
II. b < 0
III. ab < 0
I. a < 0
II. b < 0
III. ab < 0
a)
I only
b)
II only
c)
I and II only
d)
I and III only
e)
II and III only
|
|
Arnab Kumar answered |
If a person is experiencing symptoms of depression, it is important for them to seek help from a medical professional or mental health specialist. Depression is a serious mental health condition that can have significant impacts on a person's well-being, relationships, and daily functioning. A medical professional can accurately diagnose depression and recommend appropriate treatment options, such as therapy, medication, or a combination of both. Additionally, a support system of family, friends, or support groups can also be beneficial in providing emotional support and understanding. It is crucial to remember that seeking help is not a sign of weakness, but rather a courageous step towards improving one's mental health.
If x is a positive number and |-4x + 8| ≥ 2, which of the following statements is correct?- a)No value of x satisfies this inequality
- b)0 < x ≤ 3/2 or x ≥ 5/2
- c)3/2 ≤ x ≤ 5/2
- d)|x| > 1
- e)x|x| < 4
Correct answer is option 'B'. Can you explain this answer?
If x is a positive number and |-4x + 8| ≥ 2, which of the following statements is correct?
a)
No value of x satisfies this inequality
b)
0 < x ≤ 3/2 or x ≥ 5/2
c)
3/2 ≤ x ≤ 5/2
d)
|x| > 1
e)
x|x| < 4
|
|
Pranab Dasgupta answered |
We know that |-4x + 8| = |-(4x -8)| = |4x -8|
Therefore we’re essentially given
|4x−8|≥2
Dividing both sides by 4, we get:
Representing this on the number line: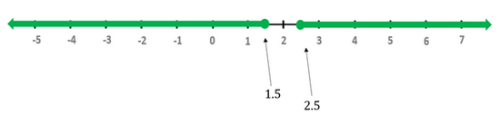 
Therefore we have
x ≥ 2.5 or x ≤ 1.5
Correct Answer: B
If -|x+1| = b, where b is a non-zero integer, which of the following statements must be true?I. b < 0II. x < -bIII. x > b- a)I only
- b)II only
- c)III only
- d)I and II only
- e)I and III only
Correct answer is option 'D'. Can you explain this answer?
If -|x+1| = b, where b is a non-zero integer, which of the following statements must be true?
I. b < 0
II. x < -b
III. x > b
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
I and III only
|
|
Janani Sharma answered |
Given, -|x+1| = b
- |x+1| = -b
- |x – (-1)| = -b
Since the left hand side (modulus) is never negative, we can infer that “-b” on the RHS is positive. (It is already given that b is non-zero).
- -b > 0
- b < 0
Therefore statement I is correct.
Now let us try to represent the given expression on number line and see what it says.
|x – (-1)| = -b
There are two possible values of x (x1, x2) that are at a distance of “-b” from -1. (As shown in the above figure.)
You can see that both these values are to the left side of “-b”.
Therefore both of them are less than “-b”
So statement II is correct.
Also, you can see from the above figure that only one of the possible values of x is greater than b while the other is lesser than b. Therefore statement III is incorrect.
Correct Answer: D
If |x – (9/2)| = 5/2, and if y is the median of a set of p consecutive integers, where p is odd, which of the
following must be true?
I. xyp is odd
II. xy(p2 + p) is even
III. x2y2p2 is even- a)II only
- b)III only I and III
- c)II and III
- d)I, II, and III
Correct answer is option 'A'. Can you explain this answer?
If |x – (9/2)| = 5/2, and if y is the median of a set of p consecutive integers, where p is odd, which of the
following must be true?
I. xyp is odd
II. xy(p2 + p) is even
III. x2y2p2 is even
following must be true?
I. xyp is odd
II. xy(p2 + p) is even
III. x2y2p2 is even
a)
II only
b)
III only I and III
c)
II and III
d)
I, II, and III
|
|
Devansh Shah answered |
The rules of odds and evens tell us that the product will be odd if all the factors are odd, and the product will be even if at least one of the factors is even. In order to analyze the given statements I, II, and III, we must determine whether x and y are odd or even. First, solve the absolute value equation for x by considering both the positive and negative values of the absolute value expression.
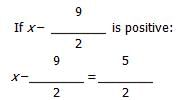
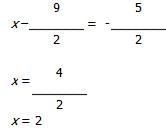
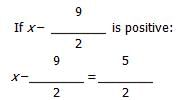
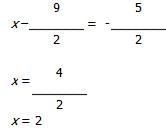
Therefore, x can be either odd or even.
Next, consider the median (y) of a set of p consecutive integers, where p is odd. Will this median necessarily be odd or even? Let's choose two examples to find out:
Example Set 1: 1, 2, 3 (the median y = 2, so y is even)
Example Set 2: 3, 4, 5, 6, 7 (the median y = 5, so y is odd)
Therefore, y can be either odd or even.
Now, analyze the given statements:
I. UNCERTAIN: Statement I will be true if and only if x, y, and p are all odd. We know p is odd, but since x and y can be either odd or even we cannot definitively say that xyp will be odd. For example, if x = 2 then xyp will be even.
II. TRUE: Statement II will be true if any one of the factors is even. After factoring out a p, the expression can be written as xyp(p + 1). Since p is odd, we know (p + 1) must be even. Therefore, the product of xyp(p + 1) must be even.
III. UNCERTAIN: Statement III will be true if any one of the factors is even. The expression can be written as xxyypp. We know that p is odd, and we also know that both x and y could be odd.
The correct answer is A.
Next, consider the median (y) of a set of p consecutive integers, where p is odd. Will this median necessarily be odd or even? Let's choose two examples to find out:
Example Set 1: 1, 2, 3 (the median y = 2, so y is even)
Example Set 2: 3, 4, 5, 6, 7 (the median y = 5, so y is odd)
Therefore, y can be either odd or even.
Now, analyze the given statements:
I. UNCERTAIN: Statement I will be true if and only if x, y, and p are all odd. We know p is odd, but since x and y can be either odd or even we cannot definitively say that xyp will be odd. For example, if x = 2 then xyp will be even.
II. TRUE: Statement II will be true if any one of the factors is even. After factoring out a p, the expression can be written as xyp(p + 1). Since p is odd, we know (p + 1) must be even. Therefore, the product of xyp(p + 1) must be even.
III. UNCERTAIN: Statement III will be true if any one of the factors is even. The expression can be written as xxyypp. We know that p is odd, and we also know that both x and y could be odd.
The correct answer is A.
If a, b, c and d are positive consecutive multiples, not necessarily in that order, of a positive integer x greater than 1, is a + b + c + d ≥ 50?(1) c = 15(2) The difference between d and b is divisible by only four positive integers, one of which is 10.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If a, b, c and d are positive consecutive multiples, not necessarily in that order, of a positive integer x greater than 1, is a + b + c + d ≥ 50?
(1) c = 15
(2) The difference between d and b is divisible by only four positive integers, one of which is 10.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Ruchi Pillai answered |
Steps 1 & 2: Understand Question and Draw Inferences
- x is an integer > 1
- a, b , c, d are integers > 0
- Let the least multiple of x in {a, b, c , d} be xy, where y > 0
- We are taking the least multiple to be xy because we do not know which integer out of a, b, c and d is the least in value. Of course, xy will be equal to one integer out of a, b, c or d.
- So, we can express the other 3 multiples of x in terms of y as: x(y+1), x(y+2), x(y +3)
To Find: Is a + b + c + d ≥ 50?
That is, is xy + x(y+1) +x(y+2) +x(y+3) ≥ 50 ?
Is 4x +6xy ≥ 50 ?
That is, is x(2y + 3) ≥ 25?
So, we need to find a unique answer to the question is x(2y + 3) ≥ 25?
Step 3: Analyze Statement 1 independently
(1) c = 15
As c is a multiple of x, the value of x can be the factors of 15 greater than 1= {3, 5, or 15}. We need to see, if for a value of x, is x(2y+3) ≥ 25?
- If x = 15
- We need to calculate the minimum possible value of y, keeping in mind the constraint that one of the integers, i.e. c = 15
- Minimum possible value of y = 1. For such a case, we will have xy = c = 15. So, minimum possible value of y = 1.
- Minimum value of x(2y+3) = 75 > 25.
- For all values of y, x(2y+3) ≥ 25.
- Is, a + b +c + d ≥ 50> → Yes
- If x = 5
- Minimum Value of y = 1. In this case we will have x(y+2) = c = 15. So, minimum possible value of y = 1
- Minimum value of x(2y+3) = 25 = 25
- For values of y ≥ 1, x(2y+3) ≥ 25
- Is, a +b+c+d ≥ 50> → Yes
- If x = 3
- If we assume here that the minimum possible of y = 1, the maximum possible number out of (a,b,c,d) will be x *(y+3) = 12. So, y = 1 is not the minimum possible value of y.
- For x(y+3) = 15, we need to have a minimum possible value of y + 3 = 5, i.e. y =2
- So, minimum of x(2y+3) = 21 < 25
- For values of y ≥ 3, x(2y+3) ≥ 25
- Is, a +b+c+d ≥ 50> → Yes/No
- If we assume here that the minimum possible of y = 1, the maximum possible number out of (a,b,c,d) will be x *(y+3) = 12. So, y = 1 is not the minimum possible value of y.
As we do not have a unique answer to the question Is, a +b+c+d ≥ 50 , the statement is insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The difference between d and b is divisible by only four positive integers, one of which is 10.
The possible values of difference between d and b can be ={x, 2x, or 3x}. As we are given that the difference between d and b is divisible by 10, we will try to find , if for all values of x and y, is x(2y+3) ≥ 25?
Also, as 10 has four factors (1,2,5 and 10), a number, which is divisible by 10 will be divisible by all the factors of 10. Since |d-b| is divisible by 10 and has only 4 factors, the only possible value of |d-b| = 10
- Case-I:|d – b| = x, i.e. d and b are consecutive multiples. So, x = 10.
- Minimum value of y = 1
- Minimum value of x(2y+3) = 50 > 25
- For all values of y, x(2y+3) ≥ 25.
- Is, a + b +c + d ≥ 50> → Yes
- Case-II:|d-b| = 2x = 10, i.e. x = 5
- Minimum value of y = 1
- Minimum value of x(2y+3) = 25 = 25
- For values of y ≥ 1, x(2y+3) ≥ 25
- Is, a +b+c+d ≥ 50> → Yes
- Case-III:|d-b| = 3x = 10. Not possible as 10 is not divisible by 3
As we have a unique answer to the question Is, a +b+c+d ≥ 50 , the statement is sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step 4, this step is not required
Answer: B
p and q are positive integers such that 2p -10 > -q, and 3q -20 < -p. If m is the minimum possible value of p and n is the maximum possible value of q, then which of the following pairs accurately represents (m, n).- a)(2, 6)
- b)(6, 2)
- c)(3, 6)
- d)(3, 5)
- e)No such values exist.
Correct answer is option 'D'. Can you explain this answer?
p and q are positive integers such that 2p -10 > -q, and 3q -20 < -p. If m is the minimum possible value of p and n is the maximum possible value of q, then which of the following pairs accurately represents (m, n).
a)
(2, 6)
b)
(6, 2)
c)
(3, 6)
d)
(3, 5)
e)
No such values exist.
|
|
Pranab Dasgupta answered |
Given inequalities are:
2p – 10 > -q and 3q – 20 < -p
The question statement asks us to find the minimum possible value of p and the maximum possible value of q.
So to know more about the range of values p and q can take, let us now try to solve these inequalities.
Step 1: Write the given inequalities in the standard form
2p + q -10 > 0 (Let’s call this I)
p + 3q -20 < 0 (Let’s call this II)
Step 2: Eliminate one variable
We can eliminate p from the inequalities by subtracting 2*II from I.
I: 2p + q -10 > 0
2*II: 2p + 6q – 40 < 0
-2*II: -2p – 6q + 40 > 0
Since I and -2*II have the same inequality sign, we can safely add them.
I – 2*II: 2p + q -10 -2p – 6q + 40 > 0
- -5q + 30 > 0
- -5q > -30
- 5q < 30
- q < 6 (Let’s call this III).
Writing III in standard form: q – 6 < 0.
Step 3: Find the value(s) of the eliminated variable
We can use I and III to find the value of p.
I: 2p + q -10 > 0
III: q – 6 < 0
-III: -q + 6 > 0
Since I and –III have the same inequality sign, we can safely add them.
I – III: 2p + q -10 – q + 6 > 0
- 2p – 4 > 0
- p > 2 (Let’s call this IV)
So from III and IV we know that, p > 2 and q < 6
We are also given that p and q are positive integers.
Combining these two pieces of information, we can infer the following:
- Since p > 2 and p is a positive integer, the minimum possible value (just greater than 2) p can take is 3.
- Since q < 6 and q is a positive integer, the maximum possible value (just lesser than 6) q can take is 5
Therefore, m = 3 and n = 5
Correct Answer: D
|x + 3| = |y -4|, where x and y are non-zero integers. If |x| < 5 and |y| < 5, what is the maximum possible value of -|xy|?- a)-12
- b)-6
- c)-4
- d)-2
- e)0
Correct answer is option 'D'. Can you explain this answer?
|x + 3| = |y -4|, where x and y are non-zero integers. If |x| < 5 and |y| < 5, what is the maximum possible value of -|xy|?
a)
-12
b)
-6
c)
-4
d)
-2
e)
0
|
|
Saumya Sharma answered |
Understanding the Equation
The equation |x + 3| = |y - 4| implies two cases based on the properties of absolute values:
- Case 1: x + 3 = y - 4
- Case 2: x + 3 = -(y - 4)
We can simplify both cases to find relationships between x and y.
Finding x and y Values
1. Case 1: x + 3 = y - 4
- Rearranging gives y = x + 7.
2. Case 2: x + 3 = -y + 4
- Rearranging gives y = 7 - x.
Constraints on x and y
We have the constraints |x| < 5="" and="" |y|="" />< 5.="" this="" means:="" -="" x="" can="" be="" in="" the="" range="" {-4,="" -3,="" -2,="" -1,="" 1,="" 2,="" 3,="" 4}.="" -="" y="" can="" also="" be="" in="" the="" range="" {-4,="" -3,="" -2,="" -1,="" 1,="" 2,="" 3,="" 4}="" based="" on="" the="" equations="" derived.="" />Calculating Possible Products
Now we will check the integer pairs (x, y) derived from both cases:
1. From y = x + 7:
- When x = -4, y = 3 → xy = -12
- When x = -3, y = 4 → invalid (y > 5)
- When x = -2, y = 5 → invalid (y > 5)
- When x = -1, y = 6 → invalid (y > 5)
- When x = 1, y = 8 → invalid (y > 5)
- When x = 2, y = 9 → invalid (y > 5)
- When x = 3, y = 10 → invalid (y > 5)
- When x = 4, y = 11 → invalid (y > 5)
2. From y = 7 - x:
- When x = -4, y = 11 → invalid
- When x = -3, y = 10 → invalid
- When x = -2, y = 9 → invalid
- When x = -1, y = 8 → invalid
- When x = 1, y = 6 → invalid
- When x = 2, y = 5 → invalid
- When x = 3, y = 4 → valid, yielding xy = 12
- When x = 4, y = 3 → valid, yielding xy = 12
Finding the Maximum Value of -|xy|
The maximum value of -|xy| (considering valid pairs) is:
- For xy = -12, -|xy| = -(-12) = -12
- For xy = 12, -|xy| = -12
Hence, the maximum possible value of -|xy| is -12.
Selecting the Correct Answer
After evaluating all valid pairs, the final maximum value is -12, aligning with option D.
The equation |x + 3| = |y - 4| implies two cases based on the properties of absolute values:
- Case 1: x + 3 = y - 4
- Case 2: x + 3 = -(y - 4)
We can simplify both cases to find relationships between x and y.
Finding x and y Values
1. Case 1: x + 3 = y - 4
- Rearranging gives y = x + 7.
2. Case 2: x + 3 = -y + 4
- Rearranging gives y = 7 - x.
Constraints on x and y
We have the constraints |x| < 5="" and="" |y|="" />< 5.="" this="" means:="" -="" x="" can="" be="" in="" the="" range="" {-4,="" -3,="" -2,="" -1,="" 1,="" 2,="" 3,="" 4}.="" -="" y="" can="" also="" be="" in="" the="" range="" {-4,="" -3,="" -2,="" -1,="" 1,="" 2,="" 3,="" 4}="" based="" on="" the="" equations="" derived.="" />Calculating Possible Products
Now we will check the integer pairs (x, y) derived from both cases:
1. From y = x + 7:
- When x = -4, y = 3 → xy = -12
- When x = -3, y = 4 → invalid (y > 5)
- When x = -2, y = 5 → invalid (y > 5)
- When x = -1, y = 6 → invalid (y > 5)
- When x = 1, y = 8 → invalid (y > 5)
- When x = 2, y = 9 → invalid (y > 5)
- When x = 3, y = 10 → invalid (y > 5)
- When x = 4, y = 11 → invalid (y > 5)
2. From y = 7 - x:
- When x = -4, y = 11 → invalid
- When x = -3, y = 10 → invalid
- When x = -2, y = 9 → invalid
- When x = -1, y = 8 → invalid
- When x = 1, y = 6 → invalid
- When x = 2, y = 5 → invalid
- When x = 3, y = 4 → valid, yielding xy = 12
- When x = 4, y = 3 → valid, yielding xy = 12
Finding the Maximum Value of -|xy|
The maximum value of -|xy| (considering valid pairs) is:
- For xy = -12, -|xy| = -(-12) = -12
- For xy = 12, -|xy| = -12
Hence, the maximum possible value of -|xy| is -12.
Selecting the Correct Answer
After evaluating all valid pairs, the final maximum value is -12, aligning with option D.
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?- a)3
- b)6
- c)5
- d)4
- e)Infinitely many
Correct answer is option 'C'. Can you explain this answer?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
a)
3
b)
6
c)
5
d)
4
e)
Infinitely many
|
|
Janani Sharma answered |
5x + 4|y| = 55
The equation can be rewritten as 4|y| = 55 - 5x.
Because |y| is non-negative, 4|y| will be non-negative. Therefore, (55 - 5x) cannot take negative values.
The equation can be rewritten as 4|y| = 55 - 5x.
Because |y| is non-negative, 4|y| will be non-negative. Therefore, (55 - 5x) cannot take negative values.
Because x and y are integers, 4|y| will be a multiple of 4.
Therefore, (55 - 5x) will also be a multiple of 4.
55 is a multiple of 5. 5x is a multiple of 5 for integer x. So, 55 - 5x will always be a multiple of 5 for any integer value of x.
So, 55 - 5x will be a multiple of 4 and 5.
i.e., 55 - 5x will be a multiple of 20.
Therefore, (55 - 5x) will also be a multiple of 4.
55 is a multiple of 5. 5x is a multiple of 5 for integer x. So, 55 - 5x will always be a multiple of 5 for any integer value of x.
So, 55 - 5x will be a multiple of 4 and 5.
i.e., 55 - 5x will be a multiple of 20.
Integer values of x > 0 that will satisfy the condition that (55 - 5x) is a multiple of 20:
1. x = 3, 55 - 5x = 55 - 15 = 40.
2. x = 7, 55 - 5x = 55 - 35 = 20
3. x = 11, 55 - 5x = 55 - 55 = 0.
When x = 15, (55 - 5x) = (55 - 75) = -20. Because (55 - 5x) has to non-negative x = 15 or values greater than 15 are not possible.
So, x can take only 3 values viz., 3, 7, and 11.
1. x = 3, 55 - 5x = 55 - 15 = 40.
2. x = 7, 55 - 5x = 55 - 35 = 20
3. x = 11, 55 - 5x = 55 - 55 = 0.
When x = 15, (55 - 5x) = (55 - 75) = -20. Because (55 - 5x) has to non-negative x = 15 or values greater than 15 are not possible.
So, x can take only 3 values viz., 3, 7, and 11.
We have 3 possible values for 55 - 5x. So, we will have these 3 values possible for 4|y|.
Possibility 1: 4|y| = 40 or |y| = 10. So, y = 10 or -10.
Possibility 2: 4|y| = 20 or |y| = 5. So, y = 5 or -5.
Possibility 3: 4|y| = 0 or |y| = 0. So, y = 0.
Number of values possible for y = 5.
Possibility 1: 4|y| = 40 or |y| = 10. So, y = 10 or -10.
Possibility 2: 4|y| = 20 or |y| = 5. So, y = 5 or -5.
Possibility 3: 4|y| = 0 or |y| = 0. So, y = 0.
Number of values possible for y = 5.
The correct choice is (C) and the correct answer is 5.
If |x - 5| = 2|x - 8|, then what is the value of x?(1) |x2 – 100| > 50(2) |x2 – 49| =0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If |x - 5| = 2|x - 8|, then what is the value of x?
(1) |x2 – 100| > 50
(2) |x2 – 49| =0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Geetika Sarkar answered |
Understanding the Equation
To solve |x - 5| = 2|x - 8|, we need to consider different cases based on the definitions of absolute values.
Case 1: x - 5 ≥ 0 (x ≥ 5)
- The equation simplifies to: x - 5 = 2(x - 8)
- Solving gives: x - 5 = 2x - 16 → x = 11
Case 2: x - 5 < 0="" (x="" />< />
- The equation simplifies to: -(x - 5) = 2|x - 8|
- We need to analyze further based on whether x is less than or greater than 8.
- Subcase 2.1: x - 8 ≥ 0 (x ≥ 8)
- This case contradicts our assumption since x cannot be both less than 5 and greater than or equal to 8.
- Subcase 2.2: x - 8 < 0="" (x="" />< />="" -="" the="" equation="" becomes:="" -x="" +="" 5="-2(x" -="" 8)="" -="" solving="" gives:="" -x="" +="" 5="-2x" +="" 16="" →="" x="11," which="" again="" is="" invalid="" for="" x="">< 5.="" thus,="" we="" find="" the="" only="" solution="" is="" x="11." />Evaluating Statements
Statement (1): |x^2 - 100| = 50
- This leads to two equations: x^2 - 100 = 50 or x^2 - 100 = -50.
- Solving gives: x^2 = 150 or x^2 = 50 → x = ±√150 or ±√50, yielding multiple values including x = 11.
Statement (2): |x^2 - 49| = 0
- This simplifies to x^2 - 49 = 0 → x = ±7.
- However, we need to check if x = 11 also satisfies this condition.
Therefore, both statements independently yield x = 11, making option D correct since each statement alone is sufficient.
To solve |x - 5| = 2|x - 8|, we need to consider different cases based on the definitions of absolute values.
Case 1: x - 5 ≥ 0 (x ≥ 5)
- The equation simplifies to: x - 5 = 2(x - 8)
- Solving gives: x - 5 = 2x - 16 → x = 11
Case 2: x - 5 < 0="" (x="" />< />
- The equation simplifies to: -(x - 5) = 2|x - 8|
- We need to analyze further based on whether x is less than or greater than 8.
- Subcase 2.1: x - 8 ≥ 0 (x ≥ 8)
- This case contradicts our assumption since x cannot be both less than 5 and greater than or equal to 8.
- Subcase 2.2: x - 8 < 0="" (x="" />< />="" -="" the="" equation="" becomes:="" -x="" +="" 5="-2(x" -="" 8)="" -="" solving="" gives:="" -x="" +="" 5="-2x" +="" 16="" →="" x="11," which="" again="" is="" invalid="" for="" x="">< 5.="" thus,="" we="" find="" the="" only="" solution="" is="" x="11." />Evaluating Statements
Statement (1): |x^2 - 100| = 50
- This leads to two equations: x^2 - 100 = 50 or x^2 - 100 = -50.
- Solving gives: x^2 = 150 or x^2 = 50 → x = ±√150 or ±√50, yielding multiple values including x = 11.
Statement (2): |x^2 - 49| = 0
- This simplifies to x^2 - 49 = 0 → x = ±7.
- However, we need to check if x = 11 also satisfies this condition.
Therefore, both statements independently yield x = 11, making option D correct since each statement alone is sufficient.
If a = -1/2, which of the following is true?- a)a-2 < a-1 < a
- b)a-2 < a< a-1
- c)a-1 < a-2 < a
- d)a-1 < a < a-2
- e)a < a-1 <a-2
Correct answer is option 'D'. Can you explain this answer?
If a = -1/2, which of the following is true?
a)
a-2 < a-1 < a
b)
a-2 < a< a-1
c)
a-1 < a-2 < a
d)
a-1 < a < a-2
e)
a < a-1 <a-2
|
|
Gitanjali Kumar answered |
If you observe the question along with the option statements, the question is essentially asking us to find the relation between a, a-1, a-2
So we simply need to find the values of each of these. For this, we are given that a = -1/2
We also know that when we are dealing with negative exponents, a-m = 1/am
Therefore a-1 = 1/a = 1/(-1/2) = -2
Similarly, a-2 = 1/a2 = 1/(-1/2)^2 = 1/(1/4) = 4
Therefore we have,
a = -1/2 = -0.5; a-1 = -2; a-2 = 4;
Among these three numbers, -2 is the lowest and 4 is the highest.
Therefore, if we arrange the given numbers in ascending order, we get:
a-1 < a < a-2
Correct Answer: D
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?- a)3
- b)6
- c)5
- d)4
- e)Infinitely many
Correct answer is option 'C'. Can you explain this answer?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
a)
3
b)
6
c)
5
d)
4
e)
Infinitely many
|
|
Nayanika Bajaj answered |
5x + 4|y| = 55
The equation can be rewritten as 4|y| = 55 - 5x.
Because |y| is non-negative, 4|y| will be non-negative. Therefore, (55 - 5x) cannot take negative values.
The equation can be rewritten as 4|y| = 55 - 5x.
Because |y| is non-negative, 4|y| will be non-negative. Therefore, (55 - 5x) cannot take negative values.
Because x and y are integers, 4|y| will be a multiple of 4.
Therefore, (55 - 5x) will also be a multiple of 4.
55 is a multiple of 5. 5x is a multiple of 5 for integer x. So, 55 - 5x will always be a multiple of 5 for any integer value of x.
So, 55 - 5x will be a multiple of 4 and 5.
i.e., 55 - 5x will be a multiple of 20.
Therefore, (55 - 5x) will also be a multiple of 4.
55 is a multiple of 5. 5x is a multiple of 5 for integer x. So, 55 - 5x will always be a multiple of 5 for any integer value of x.
So, 55 - 5x will be a multiple of 4 and 5.
i.e., 55 - 5x will be a multiple of 20.
Integer values of x > 0 that will satisfy the condition that (55 - 5x) is a multiple of 20:
1. x = 3, 55 - 5x = 55 - 15 = 40.
2. x = 7, 55 - 5x = 55 - 35 = 20
3. x = 11, 55 - 5x = 55 - 55 = 0.
When x = 15, (55 - 5x) = (55 - 75) = -20. Because (55 - 5x) has to non-negative x = 15 or values greater than 15 are not possible.
So, x can take only 3 values viz., 3, 7, and 11.
1. x = 3, 55 - 5x = 55 - 15 = 40.
2. x = 7, 55 - 5x = 55 - 35 = 20
3. x = 11, 55 - 5x = 55 - 55 = 0.
When x = 15, (55 - 5x) = (55 - 75) = -20. Because (55 - 5x) has to non-negative x = 15 or values greater than 15 are not possible.
So, x can take only 3 values viz., 3, 7, and 11.
We have 3 possible values for 55 - 5x. So, we will have these 3 values possible for 4|y|.
Possibility 1: 4|y| = 40 or |y| = 10. So, y = 10 or -10.
Possibility 2: 4|y| = 20 or |y| = 5. So, y = 5 or -5.
Possibility 3: 4|y| = 0 or |y| = 0. So, y = 0.
Number of values possible for y = 5.
Possibility 1: 4|y| = 40 or |y| = 10. So, y = 10 or -10.
Possibility 2: 4|y| = 20 or |y| = 5. So, y = 5 or -5.
Possibility 3: 4|y| = 0 or |y| = 0. So, y = 0.
Number of values possible for y = 5.
The correct choice is (C) and the correct answer is 5.
If √[(x + 4)2] = 3,which of the following could be the value of x – 4?- a)-11
- b)-7
- c)-4
- d)-3
- e)5
Correct answer is option 'A'. Can you explain this answer?
If √[(x + 4)2] = 3,which of the following could be the value of x – 4?
a)
-11
b)
-7
c)
-4
d)
-3
e)
5
|
|
Pallavi Sharma answered |
Given Equation:
√[(x + 4)^2] = 3
Solving the Equation:
- Square both sides to eliminate the square root: (x + 4)^2 = 3^2
- Simplify: (x + 4)^2 = 9
- Expand the left side: x^2 + 8x + 16 = 9
- Rearrange the equation: x^2 + 8x + 16 - 9 = 0
- Simplify: x^2 + 8x + 7 = 0
- Factor the quadratic equation: (x + 7)(x + 1) = 0
- Set each factor to zero: x + 7 = 0 or x + 1 = 0
- Solve for x: x = -7 or x = -1
Calculating x - 4:
- Substitute x = -7: -7 - 4 = -11
- Substitute x = -1: -1 - 4 = -5
Conclusion:
Among the given options, only -11 matches the possible value of x - 4 when x = -7. Therefore, the correct answer is option 'A' (-11).
√[(x + 4)^2] = 3
Solving the Equation:
- Square both sides to eliminate the square root: (x + 4)^2 = 3^2
- Simplify: (x + 4)^2 = 9
- Expand the left side: x^2 + 8x + 16 = 9
- Rearrange the equation: x^2 + 8x + 16 - 9 = 0
- Simplify: x^2 + 8x + 7 = 0
- Factor the quadratic equation: (x + 7)(x + 1) = 0
- Set each factor to zero: x + 7 = 0 or x + 1 = 0
- Solve for x: x = -7 or x = -1
Calculating x - 4:
- Substitute x = -7: -7 - 4 = -11
- Substitute x = -1: -1 - 4 = -5
Conclusion:
Among the given options, only -11 matches the possible value of x - 4 when x = -7. Therefore, the correct answer is option 'A' (-11).
If ab > cd and a, b, c and d are all greater than zero, which of the following CANNOT be true?- a)c > b
- b)d > a
- c)b/c > d/a
- d)a/c > d/b
- e)(cd)2 < (ab)2
Correct answer is option 'C'. Can you explain this answer?
If ab > cd and a, b, c and d are all greater than zero, which of the following CANNOT be true?
a)
c > b
b)
d > a
c)
b/c > d/a
d)
a/c > d/b
e)
(cd)2 < (ab)2
|
|
Rajdeep Nair answered |
Let's look at the answer choices one by one:
(A) POSSIBLE: c can be greater than b if a is much bigger than d. For example, if c = 2, b = 1, a = 10 and d = 3, ab (10) is still greater than cd (6), despite the fact that c > b.
(B) POSSIBLE: The same reasoning from (A) applies.
(C) IMPOSSIBLE: Since a, b, c and d are all positive we can cross multiply this fraction to yield ab < cd, the opposite of the inequality in the question.
(D) DEFINITE: Since a, b, c and d are all positive, we can cross multiply this fraction to yield ab > cd, which is the same inequality as that in the question.
(E) DEFINITE: Since a, b, c and d are all positive, we can simply unsquare both sides of the inequality. We will then have cd < ab, which is the same inequality as that in the question.
The correct answer is C.
(A) POSSIBLE: c can be greater than b if a is much bigger than d. For example, if c = 2, b = 1, a = 10 and d = 3, ab (10) is still greater than cd (6), despite the fact that c > b.
(B) POSSIBLE: The same reasoning from (A) applies.
(C) IMPOSSIBLE: Since a, b, c and d are all positive we can cross multiply this fraction to yield ab < cd, the opposite of the inequality in the question.
(D) DEFINITE: Since a, b, c and d are all positive, we can cross multiply this fraction to yield ab > cd, which is the same inequality as that in the question.
(E) DEFINITE: Since a, b, c and d are all positive, we can simply unsquare both sides of the inequality. We will then have cd < ab, which is the same inequality as that in the question.
The correct answer is C.
How many real solutions exist for the equation x2 – 11|x| - 60 = 0?- a)3
- b)2
- c)1
- d)4
- e)None
Correct answer is option 'B'. Can you explain this answer?
How many real solutions exist for the equation x2 – 11|x| - 60 = 0?
a)
3
b)
2
c)
1
d)
4
e)
None
|
|
Anirban Singh answered |
Step 1:
Assign y = |x| and solve for y
Let |x| = y.
We can rewrite the equation x2 - 11|x| - 60 = 0 as y2 - 11y - 60 = 0
The equation can be factorized as y2 - 15y + 4y - 60 = 0
(y - 15) (y + 4) = 0
The values of y that satisfy the equation are y = 15 or y = -4.
Step 2:
We have assigned y = |x|
|x| is always a non-negative number.
So, |x| cannot be -4.
|x| can take only one value = 15.
If |x| = 15, x = 15 or -15.
We can rewrite the equation x2 - 11|x| - 60 = 0 as y2 - 11y - 60 = 0
The equation can be factorized as y2 - 15y + 4y - 60 = 0
(y - 15) (y + 4) = 0
The values of y that satisfy the equation are y = 15 or y = -4.
Step 2:
We have assigned y = |x|
|x| is always a non-negative number.
So, |x| cannot be -4.
|x| can take only one value = 15.
If |x| = 15, x = 15 or -15.
The number of real solutions that exist for x2 – 11|x| - 60 = 0 is 2.
The correct choice is (B) and the correct answer is 2.
Select the possible values of x if |x+4| = 6- a)-2
- b)10
- c)-2 and 10
- d)-10 and 2
- e)2 and 10
Correct answer is option 'D'. Can you explain this answer?
Select the possible values of x if |x+4| = 6
a)
-2
b)
10
c)
-2 and 10
d)
-10 and 2
e)
2 and 10
|
|
Sahana Mehta answered |
The given expression can be written as:
|x - (-4)| = 6
So x is at a distance of 6 units from the point -4 on the number line. If we plot the possible points on number line, it looks something like the below figure.
Therefore there are 2 possible values for x: -10 and 2 (As shown in the above figure).
For how many values of integer n is 0.01 < 3-n+1 < 0.1?- a)0
- b)1
- c)2
- d)3
- e)4
Correct answer is option 'C'. Can you explain this answer?
For how many values of integer n is 0.01 < 3-n+1 < 0.1?
a)
0
b)
1
c)
2
d)
3
e)
4
|
|
Chirag Roy answered |
Given:
- Integer n
To find: Number of integral solutions for the inequality 0.01 < 3-n+1 < 0.1
Approach:
- We will first simplify the complicated-looking inequality 0.01 < 3-n+1 < 0.1
- After simplification, we will look at the integer values of n, that are possible.
Working Out:
- Simplifying the given inequality
- The possible values (integer powers of 3) that lies between 10 and 100 is (33 = 27 & 34 = 81)
Equating 3n-1 to its possible values (33 and 34)
- 3n-1 = 33 ; n -1 = 3 or n = 4
- 3n-1 = 34 ; n -1 = 4 or n = 5
- So, the possible values of n: {4, 5}
- Thus, 2 values of n are possible.
Looking at the answer choices, we see that the correct answer is Option C
If 4x+2<x2+3x−18<0, where x is an integer, what is the value of x ?- a)-6
- b)-5
- c)-4
- d)6
- e)7
Correct answer is option 'B'. Can you explain this answer?
If 4x+2<x2+3x−18<0, where x is an integer, what is the value of x ?
a)
-6
b)
-5
c)
-4
d)
6
e)
7
|
|
Chirag Sen answered |
Given equation:
4x + 2x^2 = 3x^180
Solving the equation:
We can simplify the equation by rearranging it and setting it equal to zero:
2x^2 + 4x - 3x^180 = 0
Factoring the equation:
2x^2 - 3x^180 + 4x = 0
2x^2 - 3x^180 - 2x + 4x = 0
x(2x - 3x^179) - 2(2x - 3x^179) = 0
(2x - 3x^179)(x - 2) = 0
Finding the possible values of x:
From the factored equation, we have two possible values for x:
1) 2x - 3x^179 = 0
2x = 3x^179
2 = 3x^178
x = 2/3^(178)
2) x - 2 = 0
x = 2
Choosing the integer value of x:
Since x has to be an integer, the only integer value of x is 2.
Therefore, the value of x is 2, which means the correct answer is option B (-5).
4x + 2x^2 = 3x^180
Solving the equation:
We can simplify the equation by rearranging it and setting it equal to zero:
2x^2 + 4x - 3x^180 = 0
Factoring the equation:
2x^2 - 3x^180 + 4x = 0
2x^2 - 3x^180 - 2x + 4x = 0
x(2x - 3x^179) - 2(2x - 3x^179) = 0
(2x - 3x^179)(x - 2) = 0
Finding the possible values of x:
From the factored equation, we have two possible values for x:
1) 2x - 3x^179 = 0
2x = 3x^179
2 = 3x^178
x = 2/3^(178)
2) x - 2 = 0
x = 2
Choosing the integer value of x:
Since x has to be an integer, the only integer value of x is 2.
Therefore, the value of x is 2, which means the correct answer is option B (-5).
If (|x| -1)2 > 4, which of the following may be true?I. |x| < 1II. |x +1| < 1III. |x -2|2 ≥ 4- a)I only
- b)II only
- c)III only
- d)I and II only
- e)None of the above
Correct answer is option 'C'. Can you explain this answer?
If (|x| -1)2 > 4, which of the following may be true?
I. |x| < 1
II. |x +1| < 1
III. |x -2|2 ≥ 4
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
None of the above
|
|
Akshay Khanna answered |
Understanding the Inequality
The inequality given is (|x| - 1)² < 4.="" this="" can="" be="" simplified:="" -="" taking="" the="" square="" root="" on="" both="" sides="" gives="" us:="" -="" |x|="" -="" 1="" />< 2="" -="" |x|="" -="" 1="" /> -2
- This leads to two inequalities:
- |x| < 3="" -="" |x|="" /> -1 (which is always true since |x| is always non-negative)
Thus, the valid solution is: |x| < 3.="" />Analyzing Each Statement
Now, let's evaluate each statement based on the derived inequality.
I. |x| < />
- This statement is not necessarily true. While |x| < 1="" would="" satisfy="" the="" original="" inequality,="" it="" is="" not="" a="" requirement="" since="" |x|="" can="" be="" values="" in="" the="" range="" (1,="" 3).="" -="" therefore,="" this="" statement="" may="" not="" be="" true.="" />II. |x + 1| < />
- This implies -1 < x="" +="" 1="" />< 1,="" leading="" to="" -2="" />< x="" />< 0.="" -="" therefore,="" while="" this="" range="" is="" possible,="" it="" does="" not="" necessarily="" hold="" for="" all="" values="" of="" x="" satisfying="" |x|="" />< 3.="" -="" hence,="" this="" statement="" may="" also="" not="" be="" true.="" />III. |x - 2|² < />
- This simplifies to -2 < x="" -="" 2="" />< 2,="" resulting="" in="" 0="" />< x="" />< 4.="" -="" this="" range="" is="" valid="" within="" |x|="" />< 3,="" particularly="" for="" x="" values="" between="" 0="" and="" 3.="" -="" thus,="" this="" statement="" may="" be="" true.="" />Conclusion
The only statement that can be true given the conditions from the inequality is III. Therefore, the correct answer is option 'C'.
The inequality given is (|x| - 1)² < 4.="" this="" can="" be="" simplified:="" -="" taking="" the="" square="" root="" on="" both="" sides="" gives="" us:="" -="" |x|="" -="" 1="" />< 2="" -="" |x|="" -="" 1="" /> -2
- This leads to two inequalities:
- |x| < 3="" -="" |x|="" /> -1 (which is always true since |x| is always non-negative)
Thus, the valid solution is: |x| < 3.="" />Analyzing Each Statement
Now, let's evaluate each statement based on the derived inequality.
I. |x| < />
- This statement is not necessarily true. While |x| < 1="" would="" satisfy="" the="" original="" inequality,="" it="" is="" not="" a="" requirement="" since="" |x|="" can="" be="" values="" in="" the="" range="" (1,="" 3).="" -="" therefore,="" this="" statement="" may="" not="" be="" true.="" />II. |x + 1| < />
- This implies -1 < x="" +="" 1="" />< 1,="" leading="" to="" -2="" />< x="" />< 0.="" -="" therefore,="" while="" this="" range="" is="" possible,="" it="" does="" not="" necessarily="" hold="" for="" all="" values="" of="" x="" satisfying="" |x|="" />< 3.="" -="" hence,="" this="" statement="" may="" also="" not="" be="" true.="" />III. |x - 2|² < />
- This simplifies to -2 < x="" -="" 2="" />< 2,="" resulting="" in="" 0="" />< x="" />< 4.="" -="" this="" range="" is="" valid="" within="" |x|="" />< 3,="" particularly="" for="" x="" values="" between="" 0="" and="" 3.="" -="" thus,="" this="" statement="" may="" be="" true.="" />Conclusion
The only statement that can be true given the conditions from the inequality is III. Therefore, the correct answer is option 'C'.
What is the value of integer x?(1) x + x2 = 0(2) |x| + x2 = 2x- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
What is the value of integer x?
(1) x + x2 = 0
(2) |x| + x2 = 2x
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Nayanika Bajaj answered |
Steps 1 & 2: Understand Question and Draw Inferences
- x is an integer
To Find: Unique value of x
Step 3: Analyze Statement 1 independently
(1) x + x2 = 0
x(1+x) = 0
x = 0 or x = -1
Since we do not have a unique value of x, the statement is insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) |x| + x2 = 2x
- Following cases can occur:
- If x ≥ 0
- Then, |x| = x
- So, the equation in Statement 2 becomes:
- x + x2 = 2x
- x2 - x = 0
- x(x – 1) = 0
- Either x = 0 or 1. Both values satisfy the condition in this case (that x ≥ 0). So, both these values are possible
- If x < 0
- Then, |x| = -x
- So, the equation in Statement 2 becomes:-x + x2 = 2x
- x2 - 3x = 0
- x(x – 3) = 0
- Either x = 0 or 3. Both the values are rejected as we have assumed x < 0
- If x ≥ 0
So, x = 0 or 1. Insufficient to answer.
Alternate Method
As |x| and x2 is always ≥ 0 (irrespective of the value of x), |x| + x2≥ 0. Thus, the equation in statement 2 tells us that 2x ≥ 0.
So, x will never be less than zero. Hence, we can assume |x| = x and solve for the values of x.
As shown above, we'll get: x = 0 or 1.
Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
- From statement 1, we inferred that: x = 0 or -1
- From statement 2, we inferred that: x = 0 or 1
Combining both the statements, we have x = 0. Sufficient to answer.
Answer: C
How many integrals value of x satisfy the inequality (1-x2)(4-x2)(9-x2) > 0 ?- a)0
- b)1
- c)3
- d)5
- e)Greater than 5
Correct answer is option 'B'. Can you explain this answer?
How many integrals value of x satisfy the inequality (1-x2)(4-x2)(9-x2) > 0 ?
a)
0
b)
1
c)
3
d)
5
e)
Greater than 5
|
|
Sounak Iyer answered |
Question Analysis:
We are given the inequality (1 - x^2)(4 - x^2)(9 - x^2) > 0 and we need to determine the number of integral values of x that satisfy this inequality.
Solution:
To solve this inequality, we need to consider the sign of each factor and determine the intervals where the product is positive.
Step 1: Analyzing the Factors:
Let's analyze the sign of each factor individually:
1 - x^2:
- This factor is equal to zero when x = 1 and x = -1.
- It is positive when x < -1="" or="" x="" /> 1, and negative when -1 < x="" />< />
4 - x^2:
- This factor is equal to zero when x = 2 and x = -2.
- It is positive when x < -2="" or="" x="" /> 2, and negative when -2 < x="" />< />
9 - x^2:
- This factor is equal to zero when x = 3 and x = -3.
- It is positive when x < -3="" or="" x="" /> 3, and negative when -3 < x="" />< />
Step 2: Determining the Intervals:
To determine the intervals where the product is positive, we need to consider the following cases:
Case 1: All factors are positive.
- This occurs when x > 3, as all three factors are positive.
Case 2: Two factors are positive.
- This occurs when one factor is negative and the other two factors are positive.
- We have two sub-cases to consider:
1. 1 - x^2 is negative and the other two factors are positive: -1 < x="" />< />
2. 4 - x^2 is negative and the other two factors are positive: -2 < x="" />< />
Case 3: One factor is positive.
- This occurs when two factors are negative and one factor is positive.
- We have three sub-cases to consider:
1. 1 - x^2 is positive and the other two factors are negative: x < />
2. 4 - x^2 is positive and the other two factors are negative: -2 < x="" />< -1="" or="" 1="" />< x="" />< />
3. 9 - x^2 is positive and the other two factors are negative: -3 < x="" />< -2="" or="" 2="" />< x="" />< />
Case 4: All factors are negative.
- This occurs when x < -3,="" as="" all="" three="" factors="" are="" />
Step 3: Counting the Integral Solutions:
To determine the integral solutions, we need to consider the intervals where the product is positive. The integral solutions lie within these intervals.
From the analysis above, we can see that there is only one interval where the product is positive: x > 3. Therefore, there is only one integral value of x that satisfies the inequality.
Answer:
The correct answer is option B) 1.
We are given the inequality (1 - x^2)(4 - x^2)(9 - x^2) > 0 and we need to determine the number of integral values of x that satisfy this inequality.
Solution:
To solve this inequality, we need to consider the sign of each factor and determine the intervals where the product is positive.
Step 1: Analyzing the Factors:
Let's analyze the sign of each factor individually:
1 - x^2:
- This factor is equal to zero when x = 1 and x = -1.
- It is positive when x < -1="" or="" x="" /> 1, and negative when -1 < x="" />< />
4 - x^2:
- This factor is equal to zero when x = 2 and x = -2.
- It is positive when x < -2="" or="" x="" /> 2, and negative when -2 < x="" />< />
9 - x^2:
- This factor is equal to zero when x = 3 and x = -3.
- It is positive when x < -3="" or="" x="" /> 3, and negative when -3 < x="" />< />
Step 2: Determining the Intervals:
To determine the intervals where the product is positive, we need to consider the following cases:
Case 1: All factors are positive.
- This occurs when x > 3, as all three factors are positive.
Case 2: Two factors are positive.
- This occurs when one factor is negative and the other two factors are positive.
- We have two sub-cases to consider:
1. 1 - x^2 is negative and the other two factors are positive: -1 < x="" />< />
2. 4 - x^2 is negative and the other two factors are positive: -2 < x="" />< />
Case 3: One factor is positive.
- This occurs when two factors are negative and one factor is positive.
- We have three sub-cases to consider:
1. 1 - x^2 is positive and the other two factors are negative: x < />
2. 4 - x^2 is positive and the other two factors are negative: -2 < x="" />< -1="" or="" 1="" />< x="" />< />
3. 9 - x^2 is positive and the other two factors are negative: -3 < x="" />< -2="" or="" 2="" />< x="" />< />
Case 4: All factors are negative.
- This occurs when x < -3,="" as="" all="" three="" factors="" are="" />
Step 3: Counting the Integral Solutions:
To determine the integral solutions, we need to consider the intervals where the product is positive. The integral solutions lie within these intervals.
From the analysis above, we can see that there is only one interval where the product is positive: x > 3. Therefore, there is only one integral value of x that satisfies the inequality.
Answer:
The correct answer is option B) 1.
If p > 0, and x2 - 11x + p = 0 has integer roots, how many integer values can 'p' take?- a)6
- b)11
- c)5
- d)10
- e)Infinitely many
Correct answer is option 'C'. Can you explain this answer?
If p > 0, and x2 - 11x + p = 0 has integer roots, how many integer values can 'p' take?
a)
6
b)
11
c)
5
d)
10
e)
Infinitely many
|
|
Malavika Choudhury answered |
Step 1:
The given quadratic equation is x2 - 11x + p = 0.
The sum of the roots of this quadratic equation
The product of the roots of this quadratic equation
Step 2:
The question states that p > 0.
'p' is the product of the roots of this quadratic equation. So, the product of the two roots is positive.
The product of two numbers is positive if either both the numbers are positive or both the numbers are negative.
We also know that the sum of the roots = 11, which is positive.
The sum of two negative numbers cannot be positive.
So, both the roots have to be positive.
Step 3:
We also know that the roots are integers.
So, we have to find different ways of expressing 11 as a sum of two positive integers.
Possibility 1: (1, 10)
Possibility 2: (2, 9)
Possibility 3: (3, 8)
Possibility 4: (4, 7)
Possibility 5: (5, 6)
The given quadratic equation is x2 - 11x + p = 0.
The sum of the roots of this quadratic equation
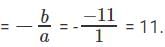
The product of the roots of this quadratic equation
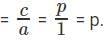
Step 2:
The question states that p > 0.
'p' is the product of the roots of this quadratic equation. So, the product of the two roots is positive.
The product of two numbers is positive if either both the numbers are positive or both the numbers are negative.
We also know that the sum of the roots = 11, which is positive.
The sum of two negative numbers cannot be positive.
So, both the roots have to be positive.
Step 3:
We also know that the roots are integers.
So, we have to find different ways of expressing 11 as a sum of two positive integers.
Possibility 1: (1, 10)
Possibility 2: (2, 9)
Possibility 3: (3, 8)
Possibility 4: (4, 7)
Possibility 5: (5, 6)
Each of these pairs, will result in a different value for p.
So, p can take 5 different values.
So, p can take 5 different values.
The correct choice is (C) and the correct answer is 5.
If a, b, c, and d are integers and ab2c3d4 > 0, which of the following must be positive?
I. a2cd
II. bc4d
III. a3c3d2- a)I only
- b)II only
- c)III only
- d)I and III
- e)I, II, and III
Correct answer is option 'C'. Can you explain this answer?
If a, b, c, and d are integers and ab2c3d4 > 0, which of the following must be positive?
I. a2cd
II. bc4d
III. a3c3d2
I. a2cd
II. bc4d
III. a3c3d2
a)
I only
b)
II only
c)
III only
d)
I and III
e)
I, II, and III
|
|
Rajdeep Nair answered |
First, let’s try to make some inferences from the fact that ab2c3d4 > 0. Since none of the integers is equal to zero (their product does not equal zero), b and d raised to even exponents must be positive, i.e. b2 > 0 and d4 > 0, implying that b2d4 > 0. If b2d4 > 0 and ab2c3d4 > 0, the product of the remaining variables, a and c3 must be positive, i.e. ac3 > 0. As a result, while we do not know the specific signs of any variable, we know that ac > 0 (because the odd exponent c3 will always have the same sign as c) and therefore a and c must have the same sign—either both positive or both negative.
Next, let’s evaluate each of the statements:
I. UNCERTAIN: While we know that the even exponent a2 must be positive, we do not know anything about the signs of the two remaining variables, c and d. If c and d have the same signs, then cd > 0 and a2cd > 0, but if c and d have different signs, then cd < 0 and a2cd < 0.
II. UNCERTAIN: While we know that the even exponent c4 must be positive, we do not know anything about the signs of the two remaining variables, b and d. If b and d have the same signs, then bd > 0 and bc4d > 0, but if b and d have different signs, then bd < 0 and bc4d < 0.
III. TRUE: Since a3c3 = (ac)3 and a and c have the same signs, it must be true that ac > 0 and (ac)3 > 0. Also, the even exponent d2 will be positive. As a result, it must be true that a3c3d2 > 0.
The correct answer is C.
Is the distance between Snape’s home and college greater than 20 kilometers?(1) If Snape drives at a speed of 25 kilometers per hour, he takes less than 1 hour to reach his college from his home.(2) If Snape drives at a speed of 12 kilometers per hour, he takes more than 105 minutes to reach his college from his home- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed
Correct answer is option 'B'. Can you explain this answer?
Is the distance between Snape’s home and college greater than 20 kilometers?
(1) If Snape drives at a speed of 25 kilometers per hour, he takes less than 1 hour to reach his college from his home.
(2) If Snape drives at a speed of 12 kilometers per hour, he takes more than 105 minutes to reach his college from his home
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed
|
|
Abhishek Kapoor answered |
Steps 1 & 2: Understand Question and Draw Inferences
Let the distance between Snape’s home and college be d.
We need to find , if d > 20?
Step 3: Analyze Statement 1 independently
(1) If Snape drives at a speed of 25 kilometers per hour, he takes less than 1 hour to reach his college from his home.
d=s∗t
t=d/s Now we know that the time taken by Snape to reach his college from his home is less than 1 hour. So, t < 1.
As t=d/s , we can write d/s<1
d/25<1
d<25
Insufficient to tell us if d > 20 or not.
Step 4: Analyze Statement 2 independently
(2) If Snape drives at a speed of 12 kilometers per hour, he takes more than 105 minutes to reach his college from his home
d=s∗t
The time taken, t is greater than 105 minutes, which can be written as ((1+45) /60) hours
So, t > ((1+45) /60)
t >((1+3)/4)
t > 7/4
t=d/s, we have d/12>7/4
d > 21
Sufficient to tell us that d > 20.
Step 5: Analyze Both Statements Together (if needed)
This step is not needed as we have a unique answer from step -4
Answer: B
Select the correct algebraic expression for the following number line representation: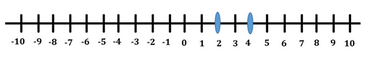
- a)|x - 3| = 1
- b)|x + 4| = 3
- c)|x + 3| = 2
- d)|x| = 5 .
- e)|x| = -5
Correct answer is option 'A'. Can you explain this answer?
Select the correct algebraic expression for the following number line representation:
a)
|x - 3| = 1
b)
|x + 4| = 3
c)
|x + 3| = 2
d)
|x| = 5 .
e)
|x| = -5
|
|
Sahana Mehta answered |
We have to find the expression |x – a| = b for which the solution set is 2 and 4.
We already know that the two points will be symmetrical about a.
So a is the mid-point of these two points.
- a=(2+4)2
- a=3
Now, b is simply the distance between a and either of the points.
As we can see from the given figure, (also as we already know),
Distance between 3 and 4 (or 2) is simply 1 unit.
b = 1
Therefore the required expression is:
|x -3| = 1
The correct answer is: A
If A and B are non-zero numbers such that AB >0, is |A - B| > |A| - |B|?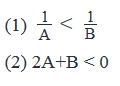
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
If A and B are non-zero numbers such that AB >0, is |A - B| > |A| - |B|?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Mehul Nair answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Given: AB > -0.
- Either A and B are both positive
- Or A and B are both negative
- To find: Is |A - B| > |A| - |B|?
Step 3: Analyze Statement 1 independently
- Since AB is positive, multiplying both sides of the inequality with AB will not change the sign of inequality. We get:
- In order to answer the question, we also need to simplify the expression for |A| - |B|
- If A is
- non-negative, then |A| = A
- negative, then |A| = -A
- Similarly for B
- If A is
- Since we only know that A and B are either both positive or both negative, we’ll have to consider both these cases
- Case 1: A and B are both positive
- This means, |A| = A and |B| = B
- So, |A| - |B| = A - B .. . (II)
- From Equations (I) and (II), we see that
- |A - B| = |A| - |B|
- So, the answer to the question is NO in this case
- Case 2: A and B are both negative
- This means, |A| = -A and |B| = -B
- So, |A| - |B| = -A - (-B) = B - A .. . (III)
- Since A – B is positive, B – A is negative
- Thus, |A| - |B| is negative
- Since a positive number is always greater than a negative number, the answer to the question is: YES
Thus, from the information given in Statement 1, the answer could be YES or NO.
Since we have not been able to determine a unique answer, Statement 1 is not sufficient.
Step 4: Analyze Statement 2 independently
(2) 2A + B < 0
- Remember that in Steps 1 and 2, we’ve inferred that A and B are either both positive or both negative
- If A and B are both positive, then the above inequality is not satisfied (The sum of 2 positive numbers cannot be less than zero)
- Therefore, A and B are both negative
- This means, |A| = -A and |B| = -B
- So, |A| - |B| = -A -(-B) = B - A . .. (I)
- However, we do not know which out of A and B is the bigger number. So, we’ll have to consider both the cases:
- Case 1: A > B
- This means, A – B > 0
- Thus, A – B is positive
- So, |A - B| = A - B . . . (II)
- In this case, B – A is negative. So, from (I), |A| - |B| is negative
- Since a positive number is always greater than a negative number, the answer to the question is: YES
- This means, A – B > 0
- Case 1: A > B
- Case 2: A≤B
- This means, A−B≤0
- Thus, A –B is not positive
- So, |A−B|=−(A−B)=B−A...(III)
-
-
- From (I) and (III), |A - B| = |A| - |B|
- Thus, the answer to the question in this case is: NO
-
- Thus, from the information given in Statement 2, the answer could be YES or NO.
- Since we have not been able to determine a unique answer, Statement 2 is not sufficient.
.
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: B < A
- If A and B are both positive, answer = NO
- If A and B are both negative, answer = YES
- From Statement 2: A and B are both negative
- If B < A, answer = YES
- If B ≥ A, answer = NO
- Combining both statements,
- A and B are both negative
- B < A
- And, answer = YES
Since we could arrive at a unique answer, the two statements together are sufficient.
Answer: Option C
Chapter doubts & questions for Inequalities and Absolute - Quantitative for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Inequalities and Absolute - Quantitative for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Quantitative for GMAT
121 videos|148 docs|111 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily