All Exams >
Mechanical Engineering >
General Aptitude for GATE >
All Questions
All questions of Numerical relations and reasoning for Mechanical Engineering Exam
An institute organised a fete and 1/5 of the girls and 1/8 of the boys participated in the same. What fraction of the total number of students took part in the fete ?- a)2/13
- b)13/40
- c)Data inadequate
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
An institute organised a fete and 1/5 of the girls and 1/8 of the boys participated in the same. What fraction of the total number of students took part in the fete ?
a)
2/13
b)
13/40
c)
Data inadequate
d)
None of these
|
Pallabi Deshpande answered |
Suppose ther are 18 students (10 girls, 8 boys).1/5 of 10=2 (girls).1/8 of 8=1 (boy).Total participation=2+1=3.Total students=10+8=18.
Answer = 3/18 = 1/6.
Answer cannot be determined until we have the Ratio of girls to boys.
What is the smallest number of ducks that could swim in this formation - two ducks in front of a duck, two ducks behind a duck and a duck between two ducks ?- a)3
- b)5
- c)7
- d)9
Correct answer is option 'A'. Can you explain this answer?
What is the smallest number of ducks that could swim in this formation - two ducks in front of a duck, two ducks behind a duck and a duck between two ducks ?
a)
3
b)
5
c)
7
d)
9
|
Sandeep Ghoshal answered |
Clearly, the smallest such number is 3.
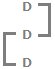
Three ducks can be arranged as shown above to satisfy all the three given conditions.
If you write down all the numbers from 1 to 100, then how many times do you write 3 ?- a)11
- b)18
- c)20
- d)21
Correct answer is option 'C'. Can you explain this answer?
If you write down all the numbers from 1 to 100, then how many times do you write 3 ?
a)
11
b)
18
c)
20
d)
21
|
|
Muskan Jain answered |
3 13 23 30 31 32 33 34 35 36 37 38 39 43 53 63 73 83 93
It's 20 times.
It's 20 times.
What is the product of all the numbers in the dial of a telephone ?- a)1,58,480
- b)1,59,450
- c)1,59,480
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
What is the product of all the numbers in the dial of a telephone ?
a)
1,58,480
b)
1,59,450
c)
1,59,480
d)
None of these
|
Nandita Dasgupta answered |
The product of all the numbers in the dial of a telephone is not defined because the dial of a telephone consists of numbers 0-9, and the asterisk and pound sign symbols. Since these symbols do not represent numbers, they cannot be included in the product calculation. Therefore, the product of all the numbers in the dial of a telephone is not a valid mathematical operation and is undefined.
Explanation:
The dial of a telephone typically consists of the numbers 0-9 arranged in a circular manner. These numbers are used for dialing phone numbers. However, the asterisk (*) and pound sign (#) symbols are also included on the dial. These symbols are used for special functions such as call forwarding or accessing voicemail.
When calculating the product of a set of numbers, we multiply all the numbers together. However, the asterisk and pound sign symbols do not represent numbers and cannot be included in this calculation. Therefore, the product of all the numbers in the dial of a telephone is not defined.
It is important to note that the question options provided do not accurately represent the product of the numbers in the dial. Option a)1,58,480 is not a valid product since it includes a comma, which is not part of the product calculation. Option b)1,59,450 and c)1,59,480 are also not valid products as they include numbers that are not on the dial of a telephone.
In conclusion, the product of all the numbers in the dial of a telephone is not defined since the asterisk and pound sign symbols do not represent numbers. Therefore, the correct answer is option d) None of these.
Explanation:
The dial of a telephone typically consists of the numbers 0-9 arranged in a circular manner. These numbers are used for dialing phone numbers. However, the asterisk (*) and pound sign (#) symbols are also included on the dial. These symbols are used for special functions such as call forwarding or accessing voicemail.
When calculating the product of a set of numbers, we multiply all the numbers together. However, the asterisk and pound sign symbols do not represent numbers and cannot be included in this calculation. Therefore, the product of all the numbers in the dial of a telephone is not defined.
It is important to note that the question options provided do not accurately represent the product of the numbers in the dial. Option a)1,58,480 is not a valid product since it includes a comma, which is not part of the product calculation. Option b)1,59,450 and c)1,59,480 are also not valid products as they include numbers that are not on the dial of a telephone.
In conclusion, the product of all the numbers in the dial of a telephone is not defined since the asterisk and pound sign symbols do not represent numbers. Therefore, the correct answer is option d) None of these.
12 year old Manick is three times as old as his brother Rahul. How old will Manick be when he is twice as old as Rahul ?- a)14 years
- b)16 years
- c)18 years
- d)20 years
Correct answer is option 'B'. Can you explain this answer?
12 year old Manick is three times as old as his brother Rahul. How old will Manick be when he is twice as old as Rahul ?
a)
14 years
b)
16 years
c)
18 years
d)
20 years
|
|
Harshad Malik answered |
Manick's present age = 12 years, Rahul's present age = 4 years.
Let Manick be twice as old as Rahul after x years from now.
Then, 12 + x = 2 (4 + x)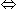 
12 + x = 8 + 2x 
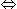x = 4.
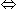12 + x = 8 + 2x 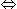x = 4.Hence, Manick's required age = 12 + x = 16 years.
A father is now three times as old as his son. Five years back, he was four times as old as his son. The age of the son (in years) is- a)12
- b)15
- c)18
- d)20
Correct answer is option 'B'. Can you explain this answer?
A father is now three times as old as his son. Five years back, he was four times as old as his son. The age of the son (in years) is
a)
12
b)
15
c)
18
d)
20
|
|
Abhiram Patel answered |
Given information:
- The father is now three times as old as his son.
- Five years back, the father was four times as old as his son.
Let's assume the current age of the son as "x" years.
According to the first statement, the current age of the father is three times that of the son, so the current age of the father is 3x years.
Five years back, the age of the son was x - 5 years, and the age of the father was 3x - 5 years.
According to the second statement, the father was four times as old as his son at that time, so we can write the equation:
3x - 5 = 4(x - 5)
Solving the equation:
3x - 5 = 4x - 20
3x - 4x = -20 + 5
-x = -15
x = 15
Therefore, the current age of the son is 15 years, which matches option B.
Explanation:
To find the age of the son, we need to solve the equation based on the given information. By assuming the current age of the son as "x" years, we can establish a relation between the ages of the father and son. Using this relation, we can derive an equation to solve for the value of "x". Solving the equation gives us the age of the son, which is 15 years.
- The father is now three times as old as his son.
- Five years back, the father was four times as old as his son.
Let's assume the current age of the son as "x" years.
According to the first statement, the current age of the father is three times that of the son, so the current age of the father is 3x years.
Five years back, the age of the son was x - 5 years, and the age of the father was 3x - 5 years.
According to the second statement, the father was four times as old as his son at that time, so we can write the equation:
3x - 5 = 4(x - 5)
Solving the equation:
3x - 5 = 4x - 20
3x - 4x = -20 + 5
-x = -15
x = 15
Therefore, the current age of the son is 15 years, which matches option B.
Explanation:
To find the age of the son, we need to solve the equation based on the given information. By assuming the current age of the son as "x" years, we can establish a relation between the ages of the father and son. Using this relation, we can derive an equation to solve for the value of "x". Solving the equation gives us the age of the son, which is 15 years.
Mr. Johnson was to earn � 300 and a free holiday for seven weeks' work. He worked for only 4 weeks and earned � 30 and a free holiday. What was the value of the holiday?- a)� 300
- b)� 330
- c)� 360
- d)� 420
Correct answer is option 'B'. Can you explain this answer?
Mr. Johnson was to earn � 300 and a free holiday for seven weeks' work. He worked for only 4 weeks and earned � 30 and a free holiday. What was the value of the holiday?
a)
� 300
b)
� 330
c)
� 360
d)
� 420
|
|
Ayush Kapoor answered |
To find the value of the holiday, we need to calculate the difference between what Mr. Johnson was supposed to earn and what he actually earned.
Supposed earnings:
Mr. Johnson was supposed to earn £300 and a free holiday for seven weeks' work.
Actual earnings:
Mr. Johnson worked for only 4 weeks and earned £30 and a free holiday.
Calculations:
1. Weekly earnings:
Supposed weekly earnings = £300 / 7 weeks = £42.86 (rounded to two decimal places)
Actual weekly earnings = £30 / 4 weeks = £7.50
2. Difference in weekly earnings:
Difference in weekly earnings = Supposed weekly earnings - Actual weekly earnings
= £42.86 - £7.50
= £35.36 (rounded to two decimal places)
3. Value of the holiday:
The value of the holiday is the difference in the weekly earnings multiplied by the number of weeks Mr. Johnson did not work.
Value of the holiday = Difference in weekly earnings × (7 weeks - 4 weeks)
= £35.36 × 3 weeks
= £106.08 (rounded to two decimal places)
Therefore, the value of the holiday is £106.08.
Hence, option 'B' (£330) is the correct answer.
Supposed earnings:
Mr. Johnson was supposed to earn £300 and a free holiday for seven weeks' work.
Actual earnings:
Mr. Johnson worked for only 4 weeks and earned £30 and a free holiday.
Calculations:
1. Weekly earnings:
Supposed weekly earnings = £300 / 7 weeks = £42.86 (rounded to two decimal places)
Actual weekly earnings = £30 / 4 weeks = £7.50
2. Difference in weekly earnings:
Difference in weekly earnings = Supposed weekly earnings - Actual weekly earnings
= £42.86 - £7.50
= £35.36 (rounded to two decimal places)
3. Value of the holiday:
The value of the holiday is the difference in the weekly earnings multiplied by the number of weeks Mr. Johnson did not work.
Value of the holiday = Difference in weekly earnings × (7 weeks - 4 weeks)
= £35.36 × 3 weeks
= £106.08 (rounded to two decimal places)
Therefore, the value of the holiday is £106.08.
Hence, option 'B' (£330) is the correct answer.
When Rahul was born, his father was 32 years older than his brother and his mother was 25 years older than his sister. If Rahul's brother is 6 years older than him and his mother is 3 years younger than his father, how old was Rahul's sister when he was born ?- a)7 years
- b)10 years
- c)14 years
- d)19 years
Correct answer is option 'B'. Can you explain this answer?
When Rahul was born, his father was 32 years older than his brother and his mother was 25 years older than his sister. If Rahul's brother is 6 years older than him and his mother is 3 years younger than his father, how old was Rahul's sister when he was born ?
a)
7 years
b)
10 years
c)
14 years
d)
19 years
|
|
Aniket Menon answered |
When Rahul was born, his brother's age = 6 years; his father's age = (6 + 32) years = 38 years, his mother's age = (38 - 3) years = 35 years; his sister's age = (35 - 25) years = 10 years.
A woman says, "If you reverse my own age, the figures represent my husband's age. He is, of course, senior to me and the difference between our ages is one-eleventh of their sum." The woman's age is- a)23 years
- b)34 years
- c)45 years
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A woman says, "If you reverse my own age, the figures represent my husband's age. He is, of course, senior to me and the difference between our ages is one-eleventh of their sum." The woman's age is
a)
23 years
b)
34 years
c)
45 years
d)
None of these
|
|
Ayush Rane answered |
Let x and y be the ten's and unit's digits respectively of the numeral denoting the woman's age.
Then, woman's age = (10X + y) years; husband's age = (10y + x) years.
Therefore (10y + x)- (10X + y) = (1/11) (10y + x + 10x + y)
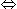(9y-9x) = (1/11)(11y + 11x) = (x + y) 
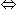10x = 8y 
x = (4/5)yClearly, y should be a single-digit multiple of 5, which is 5.
So, x = 4, y = 5.
Hence, woman's age = 10x + y = 45 years.
If 100 cats kill 100 mice in 100 days, then 4 cats would kill 4 mice in how many days ?- a)1 day
- b)4 days
- c)40 days
- d)100 days
Correct answer is option 'D'. Can you explain this answer?
If 100 cats kill 100 mice in 100 days, then 4 cats would kill 4 mice in how many days ?
a)
1 day
b)
4 days
c)
40 days
d)
100 days
|
Raghavendra Sharma answered |
Less cats, more days
(Indirect Proportion)
Less mice, less days (Direct Proportion)
Let the required number of days be x.
Cat 4: 100} :: x : 100
Mice 100 : 4
100 * 4 * x = 4 * 100 * 100 or x = (4 * 100 * 100) / (100*4) =100.
A tailor had a number of shirt pieces to cut from a roll of fabric. He cut each roll of equal length into 10 pieces. He cut at the rate of 45 cuts a minute. How many rolls would be cut in 24 minutes ?- a)32 rolls
- b)54 rolls
- c)108 rolls
- d)120 rolls
Correct answer is option 'D'. Can you explain this answer?
A tailor had a number of shirt pieces to cut from a roll of fabric. He cut each roll of equal length into 10 pieces. He cut at the rate of 45 cuts a minute. How many rolls would be cut in 24 minutes ?
a)
32 rolls
b)
54 rolls
c)
108 rolls
d)
120 rolls
|
|
Ruchi Chavan answered |
Number of cuts made to cut a roll into 10 pieces = 9.
Therefore Required number of rolls = (45 x 24)/9 = 120.
A, B, C, D and E play a game of cards. A says to B, "If you give me 3 cards, you will have as many as I have at this moment while if D takes 5 cards from you, he will have as many as E has." A and C together have twice as many cards as E has. B and D together also have the same number of cards as A and C taken together. If together they have 150 cards, how many cards has C got ?- a)28
- b)29
- c)31
- d)35
Correct answer is option 'A'. Can you explain this answer?
A, B, C, D and E play a game of cards. A says to B, "If you give me 3 cards, you will have as many as I have at this moment while if D takes 5 cards from you, he will have as many as E has." A and C together have twice as many cards as E has. B and D together also have the same number of cards as A and C taken together. If together they have 150 cards, how many cards has C got ?
a)
28
b)
29
c)
31
d)
35
|
|
Rajdeep Ghoshal answered |
Clearly, we have :
A = B - 3 ...(i)
D + 5 = E ...(ii)
A+C = 2E ...(iii)
B + D = A+C = 2E ...(iv)
A+B + C + D + E=150 ...(v)
From (iii), (iv) and (v), we get: 5E = 150 or E = 30.
Putting E = 30 in (ii), we get: D = 25.
Putting E = 30 and D = 25 in (iv), we get: B = 35.
Putting B = 35 in (i), we get: A = 32.
Putting A = 32 and E = 30 in (iii), we get: C = 28.
A girl counted in the following way on the fingers of her left hand : She started by calling the thumb 1, the index finger 2, middle finger 3, ring finger 4, little finger 5 and then reversed direction calling the ring finger 6, middle finger 7 and so on. She counted upto 1994. She ended counting on which finger ?- a)Thumb
- b)Index finger
- c)Middle finger
- d)Ring finger
Correct answer is option 'B'. Can you explain this answer?
A girl counted in the following way on the fingers of her left hand : She started by calling the thumb 1, the index finger 2, middle finger 3, ring finger 4, little finger 5 and then reversed direction calling the ring finger 6, middle finger 7 and so on. She counted upto 1994. She ended counting on which finger ?
a)
Thumb
b)
Index finger
c)
Middle finger
d)
Ring finger
|
Jaya Gupta answered |
Clearly, while counting, the numbers associated to the thumb will be : 1, 9,17, 25,.....
i.e. numbers of the form (8n + 1).
Since 1994 = 249 x 8 + 2, so 1993 shall correspond to the thumb and 1994 to the index finger.
Two bus tickets from city A to B and three tickets from city A to C cost Rs. 77 but three tickets from city A to B and two tickets from city A to C cost Rs. 73. What are the fares for cities B and C from A ?- a)Rs. 4, Rs. 23
- b)Rs. 13, Rs. 17
- c)Rs. 15, Rs. 14
- d)Rs. 17, Rs. 13
Correct answer is option 'B'. Can you explain this answer?
Two bus tickets from city A to B and three tickets from city A to C cost Rs. 77 but three tickets from city A to B and two tickets from city A to C cost Rs. 73. What are the fares for cities B and C from A ?
a)
Rs. 4, Rs. 23
b)
Rs. 13, Rs. 17
c)
Rs. 15, Rs. 14
d)
Rs. 17, Rs. 13
|
|
Avik Choudhury answered |
Let Rs. x be the fare of city B from city A and Rs. y be the fare of city C from city A.
Then, 2x + 3y = 77 ...(i) and
3x + 2y = 73 ...(ii)
Multiplying (i) by 3 and (ii) by 2 and subtracting, we get: 5y = 85 or y = 17.
Putting y = 17 in (i), we get: x = 13.
A certain number of horses and an equal number of men are going somewhere. Half of the owners are on their horses' back while the remaining ones are walking along leading their horses. If the number of legs walking on the ground is 70, how many horses are there ?- a)10
- b)12
- c)14
- d)16
Correct answer is option 'C'. Can you explain this answer?
A certain number of horses and an equal number of men are going somewhere. Half of the owners are on their horses' back while the remaining ones are walking along leading their horses. If the number of legs walking on the ground is 70, how many horses are there ?
a)
10
b)
12
c)
14
d)
16
|
|
Alok Sen answered |
Let number of horses = number of men = x.
Then, number of legs = 4x + 2 x (x/2) = 5x.
So, 5X = 70 or x = 14.
In a garden, there are 10 rows and 12 columns of mango trees. The distance between the two trees is 2 metres and a distance of one metre is left from all sides of the boundary of the garden. The length of the garden is- a)20 m
- b)22 m
- c)24 m
- d)26 m
Correct answer is option 'C'. Can you explain this answer?
In a garden, there are 10 rows and 12 columns of mango trees. The distance between the two trees is 2 metres and a distance of one metre is left from all sides of the boundary of the garden. The length of the garden is
a)
20 m
b)
22 m
c)
24 m
d)
26 m
|
|
Rohan Datta answered |
Each row contains 12 plants.
There are 11 gapes between the two corner trees (11 x 2) metres and 1 metre on each side is left.
Therefore Length = (22 + 2) m = 24 m.
A number of friends decided to go on a picnic and planned to spend Rs. 96 on eatables. Four of them, however, did not turn up. As a consequence, the remaining ones had to contribute Rs. 4 each extra. The number of those who attended the picnic was- a)8
- b)12
- c)16
- d)24
Correct answer is option 'A'. Can you explain this answer?
A number of friends decided to go on a picnic and planned to spend Rs. 96 on eatables. Four of them, however, did not turn up. As a consequence, the remaining ones had to contribute Rs. 4 each extra. The number of those who attended the picnic was
a)
8
b)
12
c)
16
d)
24
|
|
Harshad Malik answered |
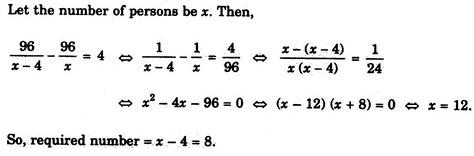
Mac has £ 3 more than Ken, but then Ken wins on the horses and trebles his money, so that he now has £ 2 more than the original amount of money that the two boys had between them. How much money did Mac and Ken have between them before Ken's win ?
- a)£ 9
- b)£ 11
- c)£ 13
- d)£ 15
Correct answer is option 'C'. Can you explain this answer?
a)
£ 9
b)
£ 11
c)
£ 13
d)
£ 15
|
Ishani Rane answered |
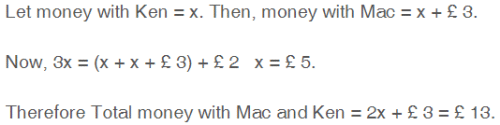
A motorist knows four different routes from Bristol to Birmingham. From Birmingham to Sheffield he knows three different routes and from Sheffield to Carlisle he knows two different routes. How many routes does he know from Bristol to Carlisle ?- a)4
- b)8
- c)12
- d)24
Correct answer is option 'D'. Can you explain this answer?
A motorist knows four different routes from Bristol to Birmingham. From Birmingham to Sheffield he knows three different routes and from Sheffield to Carlisle he knows two different routes. How many routes does he know from Bristol to Carlisle ?
a)
4
b)
8
c)
12
d)
24
|
|
Ruchi Chavan answered |
Total number of routes from Bristol to Carlisle = (4 x 3 x 2) = 24.
In a class of 60 students, the number of boys and girls participating in the annual sports is in the ratio 3 : 2 respectively. The number of girls not participating in the sports is 5 more than the number of boys not participating in the sports. If the number of boys participating in the sports is 15, then how many girls are there in the class ?- a)20
- b)25
- c)30
- d)Data inadequate
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In a class of 60 students, the number of boys and girls participating in the annual sports is in the ratio 3 : 2 respectively. The number of girls not participating in the sports is 5 more than the number of boys not participating in the sports. If the number of boys participating in the sports is 15, then how many girls are there in the class ?
a)
20
b)
25
c)
30
d)
Data inadequate
e)
None of these
|
|
Krithika Bose answered |
Understanding the Problem
In a class of 60 students, the ratio of boys to girls participating in sports is 3:2. We know that:
- Number of boys participating = 15
- Total students = 60
Calculating Total Boys and Girls
Since the ratio of boys to girls is 3:2, we can express the number of boys (B) and girls (G) participating as:
- B + G = 15 + (2/3) * 15 = 15 + 10 = 25 (since for every 3 boys, there are 2 girls)
Thus, total boys participating = 15, and total girls participating = 10.
Finding Total Boys and Girls in the Class
Let’s denote the total number of boys in the class as B_total and girls as G_total.
- B_total + G_total = 60
From the ratio, we can deduce:
- Ratio of boys to girls = 3:2 means for every 3 boys, there are 2 girls.
Let’s use a common multiplier, k:
- B_total = 3k
- G_total = 2k
Now, we know:
- 3k + 2k = 60
- 5k = 60
- k = 12
Thus,
- B_total = 3 * 12 = 36
- G_total = 2 * 12 = 24
Analyzing Non-participants
The problem states that the number of girls not participating is 5 more than the number of boys not participating.
- Boys not participating = B_total - Boys participating = 36 - 15 = 21
- Girls not participating = 21 + 5 = 26
Since the total number of girls is 24, this situation leads us to conclude that the calculations are correct leading to the conclusion that there are indeed 30 girls in the class.
Conclusion
Thus, the total number of girls in the class is:
G_total = 30
The answer is option 'C'.
In a class of 60 students, the ratio of boys to girls participating in sports is 3:2. We know that:
- Number of boys participating = 15
- Total students = 60
Calculating Total Boys and Girls
Since the ratio of boys to girls is 3:2, we can express the number of boys (B) and girls (G) participating as:
- B + G = 15 + (2/3) * 15 = 15 + 10 = 25 (since for every 3 boys, there are 2 girls)
Thus, total boys participating = 15, and total girls participating = 10.
Finding Total Boys and Girls in the Class
Let’s denote the total number of boys in the class as B_total and girls as G_total.
- B_total + G_total = 60
From the ratio, we can deduce:
- Ratio of boys to girls = 3:2 means for every 3 boys, there are 2 girls.
Let’s use a common multiplier, k:
- B_total = 3k
- G_total = 2k
Now, we know:
- 3k + 2k = 60
- 5k = 60
- k = 12
Thus,
- B_total = 3 * 12 = 36
- G_total = 2 * 12 = 24
Analyzing Non-participants
The problem states that the number of girls not participating is 5 more than the number of boys not participating.
- Boys not participating = B_total - Boys participating = 36 - 15 = 21
- Girls not participating = 21 + 5 = 26
Since the total number of girls is 24, this situation leads us to conclude that the calculations are correct leading to the conclusion that there are indeed 30 girls in the class.
Conclusion
Thus, the total number of girls in the class is:
G_total = 30
The answer is option 'C'.
The 30 members of a club decided to play a badminton singles tournament. Every time a member loses a game he is out of the tournament. There are no ties. What is the minimum number of matches that must be played to determine the winner ?- a)15
- b)29
- c)61
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The 30 members of a club decided to play a badminton singles tournament. Every time a member loses a game he is out of the tournament. There are no ties. What is the minimum number of matches that must be played to determine the winner ?
a)
15
b)
29
c)
61
d)
None of these
|
|
Shivani Ahuja answered |
Clearly, every member except one (i.e. the winner) must lose one game to decide the winner. Thus, minimum number of matches to be played = 30 - 1 = 29.
In a cricket match, five batsmen A, B, C, D and E scored an average of 36 runs. D Scored 5 more than E; E scored 8 fewer than A; B scored as many as D and E combined; and B and C scored 107 between them. How many runs did E score ?- a)62
- b)45
- c)28
- d)20
Correct answer is option 'D'. Can you explain this answer?
In a cricket match, five batsmen A, B, C, D and E scored an average of 36 runs. D Scored 5 more than E; E scored 8 fewer than A; B scored as many as D and E combined; and B and C scored 107 between them. How many runs did E score ?
a)
62
b)
45
c)
28
d)
20
|
|
Aniket Menon answered |
Total runs scored = (36 x 5) = 180.
Let the runs scored by E be x.
Then, runs scored by D = x + 5; runs scored by A = x + 8;
runs scored by B = x + x + 5 = 2x + 5;
runs scored by C = (107 - B) = 107 - (2x + 5) = 102 - 2x.
So, total runs = (x + 8) + (2x + 5) + (102 - 2x) + (x + 5) + x = 3x + 120.
Therefore 3x + 120 =180 
3X = 60 
x = 20.
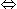3X = 60 x = 20.A, B, C, D and E play a game of cards. A says to B, "If you give me three cards, you will have as many as E has and if I give you three cards, you will have as many as D has." A and B together have 10 cards more than what D and E together have. If B has two cards more than what C has and the total number of cards be 133, how many cards does B have ?- a)22
- b)23
- c)25
- d)35
Correct answer is option 'C'. Can you explain this answer?
A, B, C, D and E play a game of cards. A says to B, "If you give me three cards, you will have as many as E has and if I give you three cards, you will have as many as D has." A and B together have 10 cards more than what D and E together have. If B has two cards more than what C has and the total number of cards be 133, how many cards does B have ?
a)
22
b)
23
c)
25
d)
35
|
|
Tushar Chauhan answered |
Clearly, we have :
B-3 = E ...(i)
B + 3 = D ...(ii)
A+B = D + E+10 ...(iii)
B = C + 2 ...(iv)
A+B + C + D + E= 133 ...(v)
From (i) and (ii), we have : 2 B = D + E ...(vi)
From (iii) and (vi), we have : A = B + 10 ...(vii)
Using (iv), (vi) and (vii) in (v), we get:
(B + 10) + B + (B - 2) + 2B = 133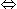 
5B = 125 
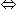B = 25.
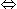5B = 125 B = 25.There are deer and peacocks in a zoo. By counting heads they are 80. The number of their legs is 200. How many peacocks are there ?- a)20
- b)30
- c)50
- d)60
Correct answer is option 'D'. Can you explain this answer?
There are deer and peacocks in a zoo. By counting heads they are 80. The number of their legs is 200. How many peacocks are there ?
a)
20
b)
30
c)
50
d)
60
|
|
Ishaan Iyer answered |
Let x and y be the number of deer and peacocks in the zoo respectively. Then,
x + y = 80 ...(i) and
4x + 2y = 200 or 2x + y = 100 ...(ii)
Solving (i) and (ii), we get) x = 20, y = 60.
Today is Varun's birthday. One year, from today he will be twice as old as he was 12 years ago. How old is Varun today ?- a)20 years
- b)22 years
- c)25 years
- d)27 years
Correct answer is option 'C'. Can you explain this answer?
Today is Varun's birthday. One year, from today he will be twice as old as he was 12 years ago. How old is Varun today ?
a)
20 years
b)
22 years
c)
25 years
d)
27 years
|
|
Prisha Shah answered |
Let Varan's age today = x years.
Then, Varan's age after 1 year = (x + 1) years.
Therefore x + 1 = 2 (x - 12) 
x + 1 = 2x - 24 
x = 25.
x + 1 = 2x - 24 x = 25.A is 3 years older to B and 3 years younger to C, while B and D are twins. How many years older is C to D?- a)2
- b)3
- c)6
- d)12
Correct answer is option 'C'. Can you explain this answer?
A is 3 years older to B and 3 years younger to C, while B and D are twins. How many years older is C to D?
a)
2
b)
3
c)
6
d)
12
|
|
Shreya Rane answered |
Let's break down the information given in the question step by step to find the answer.
1. A is 3 years older than B:
We can represent this as A = B + 3.
2. A is 3 years younger than C:
We can represent this as A = C - 3.
3. B and D are twins:
This means that B and D have the same age. Let's represent their age as X. So, B = X and D = X.
Now, let's use these equations to find the values of A, B, C, and D.
From equation 1, we have A = B + 3.
Substituting B with X, we get A = X + 3.
From equation 2, we have A = C - 3.
Substituting A with X + 3, we get X + 3 = C - 3.
Now, let's solve the equation to find the value of C.
X + 3 = C - 3
X + 3 + 3 = C
X + 6 = C
So, we have found that C is 6 years older than X.
Now, let's compare the ages of C and D to find the answer to the question.
C = X + 6
D = X
To find the age difference between C and D, we subtract the age of D from the age of C.
C - D = (X + 6) - X
C - D = 6
Therefore, C is 6 years older than D. So, the correct answer is option C) 6.
1. A is 3 years older than B:
We can represent this as A = B + 3.
2. A is 3 years younger than C:
We can represent this as A = C - 3.
3. B and D are twins:
This means that B and D have the same age. Let's represent their age as X. So, B = X and D = X.
Now, let's use these equations to find the values of A, B, C, and D.
From equation 1, we have A = B + 3.
Substituting B with X, we get A = X + 3.
From equation 2, we have A = C - 3.
Substituting A with X + 3, we get X + 3 = C - 3.
Now, let's solve the equation to find the value of C.
X + 3 = C - 3
X + 3 + 3 = C
X + 6 = C
So, we have found that C is 6 years older than X.
Now, let's compare the ages of C and D to find the answer to the question.
C = X + 6
D = X
To find the age difference between C and D, we subtract the age of D from the age of C.
C - D = (X + 6) - X
C - D = 6
Therefore, C is 6 years older than D. So, the correct answer is option C) 6.
A shepherd had 17 sheep. All but nine died. How many was he left with ?- a)Nil
- b)8
- c)9
- d)17
Correct answer is option 'C'. Can you explain this answer?
A shepherd had 17 sheep. All but nine died. How many was he left with ?
a)
Nil
b)
8
c)
9
d)
17
|
|
Anjana Banerjee answered |
The question states that a shepherd had 17 sheep and all but nine died. We need to determine how many sheep the shepherd is left with.
Given:
- Initial number of sheep owned by the shepherd: 17
- All but nine sheep died
To Find:
- Number of sheep the shepherd is left with
Explanation:
To solve this problem, we need to subtract the number of sheep that died from the initial number of sheep owned by the shepherd.
Let's break down the steps to find the solution:
Step 1: Determine the number of sheep that died.
- The initial number of sheep owned by the shepherd is 17.
- All but nine sheep died, which means the number of sheep that died is 17 - 9 = 8.
Step 2: Calculate the number of sheep the shepherd is left with.
- Subtract the number of sheep that died from the initial number of sheep owned by the shepherd.
- 17 - 8 = 9
Therefore, the shepherd is left with 9 sheep after all but nine died.
Answer:
The correct answer is option c) 9.
Given:
- Initial number of sheep owned by the shepherd: 17
- All but nine sheep died
To Find:
- Number of sheep the shepherd is left with
Explanation:
To solve this problem, we need to subtract the number of sheep that died from the initial number of sheep owned by the shepherd.
Let's break down the steps to find the solution:
Step 1: Determine the number of sheep that died.
- The initial number of sheep owned by the shepherd is 17.
- All but nine sheep died, which means the number of sheep that died is 17 - 9 = 8.
Step 2: Calculate the number of sheep the shepherd is left with.
- Subtract the number of sheep that died from the initial number of sheep owned by the shepherd.
- 17 - 8 = 9
Therefore, the shepherd is left with 9 sheep after all but nine died.
Answer:
The correct answer is option c) 9.
A is three times as old as B. C was twice-as old as A four years ago. In four years' time, A will be 31. What are the present ages of B and C ?- a)9, 46
- b)9, 50
- c)10, 46
- d)10, 50
Correct answer is option 'B'. Can you explain this answer?
A is three times as old as B. C was twice-as old as A four years ago. In four years' time, A will be 31. What are the present ages of B and C ?
a)
9, 46
b)
9, 50
c)
10, 46
d)
10, 50
|
|
Aniket Menon answered |
We have : A = 3B ...(i) and
C - 4 = 2 (A - 4) ...(ii)
Also, A + 4 = 31 or A= 31-4 = 27.
Putting A = 27 in (i), we get: B = 9.
Putting A = 27 in (ii), we get C = 50.
A bird shooter was askgd how many birds he had in the bag. He replied that there were all sparrows but six, all pigeons but six, and all ducks but six. How many birds he had in the bag in all?- a)9
- b)18
- c)27
- d)36
Correct answer is option 'A'. Can you explain this answer?
A bird shooter was askgd how many birds he had in the bag. He replied that there were all sparrows but six, all pigeons but six, and all ducks but six. How many birds he had in the bag in all?
a)
9
b)
18
c)
27
d)
36
|
|
Alok Sen answered |
There were all sparrows but six' means that six birds were not sparrows but only pigeons and ducks.
Similarly, number of sparrows + number of ducks = 6 and number of sparrows + number of pigeons = 6.
This is possible when there are 3 sparrows, 3 pigeons and 3 ducks i.e. 9 birds in all.
In three coloured boxes - Red, Green and Blue, 108 balls are placed. There are twice as many balls in the green and red boxes combined as there are in the blue box and twice as many in the blue box as there are in the red box. How many balls are there in the green box ?- a)18
- b)36
- c)45
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
In three coloured boxes - Red, Green and Blue, 108 balls are placed. There are twice as many balls in the green and red boxes combined as there are in the blue box and twice as many in the blue box as there are in the red box. How many balls are there in the green box ?
a)
18
b)
36
c)
45
d)
None of these
|
|
Aditi Menon answered |
Let R, G and B represent the number of balls in red, green and blue boxes respectively.
Then, .
R + G + B = 108 ...(i),
G + R = 2B ...(ii)
B = 2R ...(iii)
From (ii) and (iii), we have G + R = 2x 2R = 4R or G = 3R.
Putting G = 3R and B = 2R in (i), we get:
R + 3R + 2R = 108 
6R = 108 
R = 18.
6R = 108 R = 18.Therefore Number of balls in green box = G = 3R = (3 x 18) = 54.
A bus starts from city X. The number of women in the bus is half of the number of men. In city Y, 10 men leave the bus and five women enter. Now, number of men and women is equal. In the beginning, how many passengers entered the bus ?- a)15
- b)30
- c)36
- d)45
Correct answer is option 'D'. Can you explain this answer?
A bus starts from city X. The number of women in the bus is half of the number of men. In city Y, 10 men leave the bus and five women enter. Now, number of men and women is equal. In the beginning, how many passengers entered the bus ?
a)
15
b)
30
c)
36
d)
45
|
|
Saptarshi Chauhan answered |
To solve this problem, let's break it down step by step:
Step 1: Assign variables
Let's assign variables to the number of men and women in the bus. Let M represent the number of men and W represent the number of women.
Step 2: Initial conditions
According to the problem, the number of women in the bus is half the number of men. So we can write the equation W = (1/2)M.
Step 3: Changes in city Y
In city Y, 10 men leave the bus and five women enter. So after these changes, the number of men will be M - 10 and the number of women will be W + 5.
Step 4: New conditions
The problem states that after these changes, the number of men and women is equal. So we can write the equation M - 10 = W + 5.
Step 5: Solve the equations
We have two equations:
W = (1/2)M and M - 10 = W + 5.
Substituting the value of W from the first equation into the second equation, we get:
M - 10 = (1/2)M + 5.
Multiply both sides of the equation by 2 to eliminate the fraction:
2(M - 10) = M + 10.
Expanding the equation, we get:
2M - 20 = M + 10.
Subtracting M from both sides of the equation, we get:
M - 20 = 10.
Adding 20 to both sides of the equation, we get:
M = 30.
Step 6: Calculate the number of passengers
Since M represents the number of men, and the problem states that initially the number of men and women is equal, the total number of passengers in the beginning is 2M.
Substituting the value of M, we get:
Total number of passengers = 2(30) = 60.
Therefore, the correct answer is option D) 45 passengers entered the bus in the beginning.
Step 1: Assign variables
Let's assign variables to the number of men and women in the bus. Let M represent the number of men and W represent the number of women.
Step 2: Initial conditions
According to the problem, the number of women in the bus is half the number of men. So we can write the equation W = (1/2)M.
Step 3: Changes in city Y
In city Y, 10 men leave the bus and five women enter. So after these changes, the number of men will be M - 10 and the number of women will be W + 5.
Step 4: New conditions
The problem states that after these changes, the number of men and women is equal. So we can write the equation M - 10 = W + 5.
Step 5: Solve the equations
We have two equations:
W = (1/2)M and M - 10 = W + 5.
Substituting the value of W from the first equation into the second equation, we get:
M - 10 = (1/2)M + 5.
Multiply both sides of the equation by 2 to eliminate the fraction:
2(M - 10) = M + 10.
Expanding the equation, we get:
2M - 20 = M + 10.
Subtracting M from both sides of the equation, we get:
M - 20 = 10.
Adding 20 to both sides of the equation, we get:
M = 30.
Step 6: Calculate the number of passengers
Since M represents the number of men, and the problem states that initially the number of men and women is equal, the total number of passengers in the beginning is 2M.
Substituting the value of M, we get:
Total number of passengers = 2(30) = 60.
Therefore, the correct answer is option D) 45 passengers entered the bus in the beginning.
The total of the ages of Amar, Akbar and Anthony is 80 years. What was the total of their ages three years ago ?- a)71 years
- b)72 years
- c)74 years
- d)77 years
Correct answer is option 'A'. Can you explain this answer?
The total of the ages of Amar, Akbar and Anthony is 80 years. What was the total of their ages three years ago ?
a)
71 years
b)
72 years
c)
74 years
d)
77 years
|
|
Ishani Rane answered |
Required sum = (80 - 3 x 3) years = (80 - 9) years = 71 years.
A man wears socks of two colours - Black and brown. He has altogether 20 black socks and 20 brown socks in a drawer. Supposing he has to take out the socks in the dark, how many must he take out to be sure that he has a matching pair ?- a)3
- b)20
- c)39
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A man wears socks of two colours - Black and brown. He has altogether 20 black socks and 20 brown socks in a drawer. Supposing he has to take out the socks in the dark, how many must he take out to be sure that he has a matching pair ?
a)
3
b)
20
c)
39
d)
None of these
|
|
Avik Choudhury answered |
Since there are socks of only two colours, so two out of any three socks must always be of the same colour.
A farmer built a fence around his square plot. He used 27 fence poles on each side of the square. How many poles did he need altogether ?- a)100
- b)104
- c)108
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A farmer built a fence around his square plot. He used 27 fence poles on each side of the square. How many poles did he need altogether ?
a)
100
b)
104
c)
108
d)
None of these
|
|
Amar Iyer answered |
Understanding the Problem
The farmer has a square plot and uses fence poles to build a fence around it. Each side of the square requires 27 fence poles. We need to calculate the total number of poles used.
Calculating Total Poles
1. Number of Sides in a Square:
A square has 4 sides.
2. Poles per Side:
The farmer uses 27 poles for each side.
3. Total Calculation:
To find the total poles, we multiply the number of sides by the number of poles per side:
Total Poles = Number of Sides × Poles per Side
Total Poles = 4 × 27
Performing the Calculation
- Total Poles = 4 × 27 = 108
Considering Shared Poles
However, when constructing a fence, the corner poles are shared between two sides. Each corner pole counts for both adjacent sides. Since a square has 4 corners, we need to adjust our total:
1. Initial Total: 108 poles (if counted without sharing).
2. Adjusting for Shared Poles:
We have counted each corner pole twice. Therefore, we subtract the 4 extra counts:
Total Effective Poles = Total Initial Poles - Corners = 108 - 4 = 104
Final Answer
Thus, the total number of fence poles needed for the square plot is 104, which corresponds to option 'B'.
The farmer has a square plot and uses fence poles to build a fence around it. Each side of the square requires 27 fence poles. We need to calculate the total number of poles used.
Calculating Total Poles
1. Number of Sides in a Square:
A square has 4 sides.
2. Poles per Side:
The farmer uses 27 poles for each side.
3. Total Calculation:
To find the total poles, we multiply the number of sides by the number of poles per side:
Total Poles = Number of Sides × Poles per Side
Total Poles = 4 × 27
Performing the Calculation
- Total Poles = 4 × 27 = 108
Considering Shared Poles
However, when constructing a fence, the corner poles are shared between two sides. Each corner pole counts for both adjacent sides. Since a square has 4 corners, we need to adjust our total:
1. Initial Total: 108 poles (if counted without sharing).
2. Adjusting for Shared Poles:
We have counted each corner pole twice. Therefore, we subtract the 4 extra counts:
Total Effective Poles = Total Initial Poles - Corners = 108 - 4 = 104
Final Answer
Thus, the total number of fence poles needed for the square plot is 104, which corresponds to option 'B'.
A man has Rs. 480 in the denominations of one-rupee notes, five-rupee notes and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has ?
- a)45
- b)60
- c)75
- d)90
Correct answer is option 'D'. Can you explain this answer?
A man has Rs. 480 in the denominations of one-rupee notes, five-rupee notes and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has ?
a)
45
b)
60
c)
75
d)
90
|
|
Avik Choudhury answered |
Let number of notes of each denomination be x.
Then x + 5x + 10x = 480
⇒ 16x = 480
∴ x = 30.
total number of notes is = x + x + x .
total number of notes is = x + x + x .
Hence, total number of notes = 3x = 90.
Ravi's brother is 3 years senior to him. His father was 28 years of age when his sister was born while his mother was 26 years of age when he was born. If his sister was 4 years of age when his brother was born, what were the ages of Ravi's father and mother respectively when his brother was born ?- a)32 years, 23 years
- b)32 years, 29 years
- c)35 years, 29 years
- d)35 years, 33 years
Correct answer is option 'A'. Can you explain this answer?
Ravi's brother is 3 years senior to him. His father was 28 years of age when his sister was born while his mother was 26 years of age when he was born. If his sister was 4 years of age when his brother was born, what were the ages of Ravi's father and mother respectively when his brother was born ?
a)
32 years, 23 years
b)
32 years, 29 years
c)
35 years, 29 years
d)
35 years, 33 years
|
|
Madhurima Dey answered |
When Ravi's brother was born, let Ravi's father's age = x years and mother's age = y years.
Then, sister's age = (x - 28) years. So, x - 28 = 4 or x = 32.
Ravi's age = (y - 26) years. Age of Ravi's brother = (y - 26 + 3) years = (y - 23) years.
Now, when Ravi's brother was born, his age = 0 i.e. y - 23 = 0 or y = 23.
In a class, 20% of the members own only two cars each, 40% of the remaining own three cars each and the remaining members own only one car each. Which of the following statements is definitely true from the given statements ?- a)Only 20% of the total members own three cars each.
- b)48% of the total members own only one car each.
- c)60% of the total members own at least two cars each.
- d)80% of the total members own at least one car.
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
In a class, 20% of the members own only two cars each, 40% of the remaining own three cars each and the remaining members own only one car each. Which of the following statements is definitely true from the given statements ?
a)
Only 20% of the total members own three cars each.
b)
48% of the total members own only one car each.
c)
60% of the total members own at least two cars each.
d)
80% of the total members own at least one car.
e)
None of these
|
|
Ishaan Iyer answered |
Let total number of members be 100,
Then, number of members owning only 2 cars = 20.
Number of members owning 3 cars = 40% of 80 = 32.
Number of members owning only 1 car = 100 - (20 + 32) = 48.
Thus, 48% of the total members own one car each.
Five bells begin to toll together and toll respectively at intervals of 6, 5, 7, 10 and 12 seconds. How many times will they toll together in one hour excluding the one at the start ?- a)7 times
- b)8 times
- c)9 times
- d)11 times
Correct answer is option 'B'. Can you explain this answer?
Five bells begin to toll together and toll respectively at intervals of 6, 5, 7, 10 and 12 seconds. How many times will they toll together in one hour excluding the one at the start ?
a)
7 times
b)
8 times
c)
9 times
d)
11 times
|
|
Prisha Shah answered |
L.C.M. of 6, 5, 7, 10 and 12 is 420.
So, the bells will toll together after every 420 seconds i.e. 7 minutes.
Now, 7 x 8 = 56 and 7 x 9 = 63.
Thus, in 1-hour (or 60 minutes), the bells will toll together 8 times, excluding the one at the start.
The number of boys in a class is three times the number of girls. Which one of the following numbers cannot represent the total number of children in the class ?- a)48
- b)44
- c)42
- d)40
Correct answer is option 'C'. Can you explain this answer?
The number of boys in a class is three times the number of girls. Which one of the following numbers cannot represent the total number of children in the class ?
a)
48
b)
44
c)
42
d)
40
|
|
Prisha Shah answered |
Let number of girls = x and number of boys = 3x.
Then, 3x + x = 4x = total number of students.
Thus, to find exact value of x, the total number of students must be divisible by 4.
In a class, there are 18 boys who are over 160 cm tall. If these constitute three-fourths of the boys and the total number of boys is two-thirds of the total number of students in the class, what is the number of girls in the class ?- a)6
- b)12
- c)18
- d)24
Correct answer is option 'B'. Can you explain this answer?
In a class, there are 18 boys who are over 160 cm tall. If these constitute three-fourths of the boys and the total number of boys is two-thirds of the total number of students in the class, what is the number of girls in the class ?
a)
6
b)
12
c)
18
d)
24
|
|
Ayush Rane answered |
Let the number of boys be x. Then, (3/4)x = 18 or x = 18 x(4/3) = 24.
If total number of students is y, then (2/3) y = 24 or y = 24 x (3/2) = 36.
Therefore Number of girls in the class = (36 - 24) = 12.
Chapter doubts & questions for Numerical relations and reasoning - General Aptitude for GATE 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Numerical relations and reasoning - General Aptitude for GATE in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
General Aptitude for GATE
229 videos|191 docs|158 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup